轴力图的画法
材料力学内力图绘制详细讲解
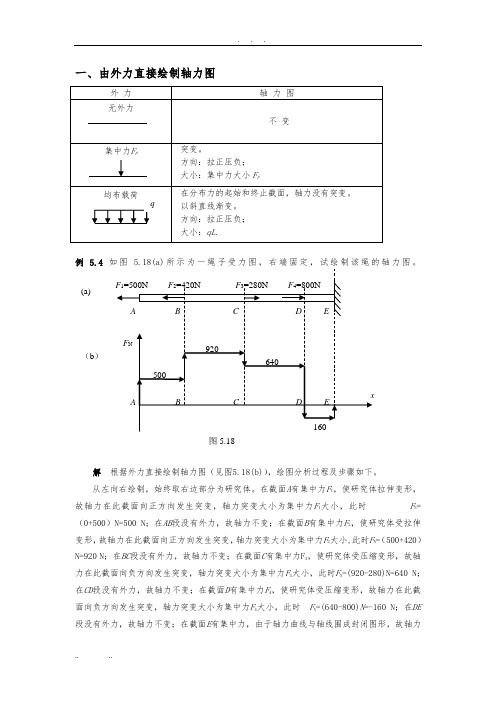
一、由外力直接绘制轴力图例 5.4 力图。
解 根据外力直接绘制轴力图(见图5.18(b)),绘图分析过程及步骤如下。
从左向右绘制,始终取右边部分为研究体。
在截面A 有集中力F 1,使研究体拉伸变形,故轴力在此截面向正方向发生突变,轴力突变大小为集中力F 1大小,此时 F N =(0+500)N=500 N ;在AB 段没有外力,故轴力不变;在截面B 有集中力F 2,使研究体受拉伸变形,故轴力在此截面向正方向发生突变,轴力突变大小为集中力F 2大小,此时F N =(500+420)N=920 N ;在BC 段没有外力,故轴力不变;在截面C 有集中力F 3,使研究体受压缩变形,故轴力在此截面向负方向发生突变,轴力突变大小为集中力F 3大小,此时F N =(920-280)N=640 N ;在CD 段没有外力,故轴力不变;在截面D 有集中力F 4,使研究体受压缩变形,故轴力在此截面向负方向发生突变,轴力突变大小为集中力F 4大小,此时 F N =(640-800)N =-160 N ;在DE 段没有外力,故轴力不变;在截面E 有集中力,由于轴力曲线与轴线围成封闭图形,故轴力(b )(a)突变为0。
例5.5有一根阶梯轴受力如图5.19(a)所示,试绘制阶梯轴的轴力图。
图5.19解从右向左绘制,始终取左变部分为研究体。
根据外力直接绘制轴力图(见图5.19(b)),绘图分析过程及步骤如下:在截面A有集中力F1,使研究体压缩变形,故轴力在此截面向负方向发生突变,轴力突变大小为集中力F1大小,此时F N=(0-10)kN=-10 kN;在AB段有均匀分布载荷,使研究体受拉伸变形,故轴力以斜直线规律向正方向渐变,轴力渐变大小为均匀分布载荷大小,此时F N=(-10+10×2)kN=10 kN;在截面B没有力,故此截面轴力没有变化;在BC段没有外力,故轴力不变;在截面C有集中力F2,使研究体受拉伸变形,故轴力在此截面向正方向发生突变,轴力突变大小为集中力F2大小,此时F N=(10+10)kN=20 kN;在CD段没有外力,故轴力不变;在截面D有集中力,由于轴力曲线与轴线围成封闭图形,故轴力突变为0.二、由外力直接绘制扭矩图外力扭矩图无外力不变集中力F P突变。
拉压杆件轴力图的矢量画法

其 中, 跳 跃 矢 量 的具 体 画 法 为 : 跳跃 矢 量 的起 点 , 为 上段 保 持 矢 量 的终 点 。跳 跃 矢 量 方 向 , 需要 根 据 外 力 方 向与 位 置 坐标 轴 正 方 向是 否 一 致判 断 , 当外 力 方 向与位 置 坐 标 轴 正方 向一 致 时 , 跳 跃 矢量 指 向轴 力 减
中 图分 类 号 : G 7 1 2 文 献 标识 码 :A 文章编号 : 1 6 7 1 — 5 9 9 3 ( 2 0 1 5 ) 0 1 — 0 0 4 1 — 0 2
引 言
( 一) 计算 量 大 。 需 根据 外 力 作 用 点个 数 , 将 构件 分段, 逐 段 列 平 衡方 程 , 才 能 求解 出每 段 内力 。 外 力数 量越多, 平 衡 方 程数 量 也 越 多 , 计 算 量 就越 大 , 计 算 效
若将上述例子的a截面的所受外力变成未知且该杆件仍受力平衡即得如图4所示的悬臂梁受力悬臂梁受力图在解决这类杆件轴力图绘制时若采用矢量画法则不必像截面法那样先根据力的平衡方程计算截面处的外力然后再按一般过程进行计算并绘图而可以直接利用矢量的相应性质从杆件已知外力端向未知外力端依次绘制矢量而省去计算未截面处的外力绘制出相应的轴力图
一
( 二) 判 断 内力 的 实 际正 负 号 较 为 麻 烦 。判 断每 段 截 面 内力 的正 负 号方 法 , 一 般 为 先 假 设 该段 内力 为 正 ,再 由所 列 的平 衡 方 程 求 解 出的 内力 的 正 负号 , 判 断 出 内力 的实 际 正 负号 。 同样 , 当 外 力数 量 越 多 时 , 内 力 的方 向需 要 判 断 的次 数 也就 越 多 。
拉压杆 件轴 力 图的矢量 画法
02-2-2 画轴力图 课件在线观看

画轴力图
♦画轴力图
轴力图
轴力随横截面位置而变化的图。
♦画轴力图
二、算例
—等直杆其受力情况如下图所示,请作杆的轴力 图。
1
40kN
55^N 25^N
A 600 B
C 500
• 300.
20蚪
D 400E
♦画轴力图
FR \A 600 B
40kN -300 -
55^N 25^N
20蚪
C 500. D 400 ・E
解: (1)求支座反力
-FR -40 +55 -25 +20 = 0
FR = 10kN
♦画轴力图
⑵求48段内的轴力
FR
_ .0kN
55伊 25"
20kN
|A 60 0 B
■ 300 ・
E C 500. D 400 -
、 FN
F = FN1
— F FN1
R
=R
0=
+10(kN)
(+)
♦画轴力图
(3)求3C段内的轴
力
璃 _F - 40 = 0 = FN2 FR + 40 = +50(kN) (+)
♦画轴力图
(4)求CQ段内的轴力
—凡3 - 25 + 20 = 0 FN3 = _5(kN)(―)
♦画轴力图 (5)求QE段内的轴力
FR
』0kN
、 55kN 25kN
► —.
20kN
\A 600 B . 300.
妇 C 500
E
o
々4
20kN
F 4 = +20(kN)(+)
05-轴力与轴力图

材料力学大连理工大学王博轴力与轴力图F 1 F 2 F 3 一、轴力F N (Axial force)—— 拉压杆的内力 截面法步骤——截断、取半、画内力、平衡mm轴力与轴力图0x F =∑N 120F F F -+=, N 12F F F =-F N F 1 F 2 mm取左半和取右半计算内力,结果是一样的因此,可选择简单的一侧计算轴力,另一侧作为校核 小讨论N 3F F =12F F =-F 1 F 2 F 3m m F NF 1 F 2 m mF N F 3 mm取左半 取右半知识点:轴力 Axial force定义——内力主矢的法向分量求法——截面法 Method of section步骤:截开,取半,画内力,平衡大小= 截面任一侧所有外力的代数和正负号——拉伸为正(离开截面)单位—— N , kNQ:1 理论力学里怎么定义的力的正负?2 轴力为什么依据变形来定义正负呢? (好处?)问题:如何描述不同截面的轴力既简单又直观? 方法: 1. 临用时逐个截面计算2. 写方程式3. 画几何图线—— 轴力图: 横坐标——杆的轴线纵坐标——轴力数值二、轴力图 Axial force diagram F 1 F 2 F 3 F 3 1 12 2 33解:1.各段轴力计算: 例题1 作图示杆的轴力图 10kN20kN 20kN 10kN A D B C 11 2 2 3 3 F N(kN ) 10 1010N110kN ,F =N210kN ,F =-N320kNF =- 2.作轴力图1. 与杆平行对齐画2. 标明内力的性质(F N )3. 标明内力单位4. 正确画出内力沿轴线的变化规律5. 标明内力的正负号6. 注明特殊截面的内力数值(极值)轴力图要求 10kN20kN 20kN 10kN AD BC F N(kN ) 10 1010例题2 A CBF l 1 l 2 12 12.42 F N (kN) x 1 F F N1 F F N2 l 1 x 2-l 1 1 1 x 1 22 x 212.98 已知:A 1=3 ㎝2 , A 2=4 ㎝2 , l 1= l 2= 50m , F =12 kN , γ = 0.028 N/㎝3 求:作轴力(考虑自重) 解:(1) 计算轴力 AB 段: F N1 = F +γA 1x 1 (0≤x 1≤l 1) BC 段: F N2 =F + γ A 1l 1+γ A 2 (x 2-l 1) (l 1≤x 2≤l 1+l 2)(2) 绘轴力图。
工程力学教学课件:2–2 轴力及轴力图

P P
5
一、概念 轴向拉压的外力特点:外力的合力作用线与杆的轴线重合。 轴向拉压的变形特点:杆的变形主要是轴向伸缩,伴随横向 缩扩。 轴向拉伸:杆的变形是轴向伸长,横向缩短。 轴向压缩:杆的变形是轴向缩短,横向变粗。
6
二、 工 程 实 例
7
8
内力
指由外力作用所引起的、物体内相邻部分之间分布内 力系的合成(附加内力)。
计算杆在截开面上的未知内力(此时截开面上的内力 对所留部分而言是外力)。
10
1. 轴力的概念: (在轴向载荷作用下,杆件横截面上的唯一 内力分量--就是轴力)
m
P
P
m
P
m FN
FN = P
m
P
m
P
m
P
m FN
FN = P
m
11
2. 轴力的正负规定: FN 与外法线同向,为正轴力(拉力) FN
FN与外法线反向,为负轴力(压力)
24
补充例题:
例题2-2:试作此杆的轴力图。
q
F
F
l
解: FR
F
l
2l
l
1
F2 q
3
1
F 2
3
F F'=2ql FR
F
FR = F
F F F
25
补充例题: FR = F FR = F FR = F
FR = F
1
F2
q
3
Fx
1
F2
3
FN1 = F
FN3 = F
F
Fq
F N2
F
x1
F F Fx1 l
杆件横截面面上的正应力由题目可见斜截面mm的方位角为40ommm50om于是斜截面上的正应力与切应力分别为应力方向如图示221引言22轴力及轴力图23拉压杆应力与圣维南原理第二章轴向拉伸和压缩24材料在拉伸和压缩时的力学性能25应力集中26失效许用应力与强度条件27胡克定律拉压杆变形28拉压静不定问题29连接部分的强度21引言工程中有很多构件例如屋架中的杆是等直杆作用于杆上的外力的合力的作用线与杆的轴线重合
02-2-2 画轴力图 课件在线观看

第二章拉伸压缩与剪切轴向拉压的内力计算2.1画轴力图2.2拉(压)杆横截面上的应力2.3拉(压)杆斜截面上的应力2.4材料拉伸时的力学性能2.5第二章拉伸压缩与剪切材料压缩时的力学性能2.6剪切和挤压的实用计算2.10失效、许用应力和强度计算2.7轴向拉压时杆件的变形2.8应力集中的概念2.9画轴力图画轴力图画轴力图xF NO一、轴力图轴力随横截面位置而变化的图。
一等直杆其受力情况如下图所示,请作杆的轴力图。
CABD 600300500400E40kN55kN 25kN 20kN 画轴力图二、算例FR画轴力图CA B D600300500400E40kN55kN25kN20kN解:(1) 求支座反力R 405525200F--+-+=R 10kNF=F R画轴力图CA B D 600300500400E40kN 55kN 25kN 20kN (2) 求AB 段内的轴力1F RF N1N1R 0F F -=N1R 10(kN)()F F ==++F R画轴力图CA BD 600300500400E40kN55kN 25kN20kN(3) 求BC 段内的轴力N2R 400F F --=2F R40kNF N2N2R 4050(kN)()F F =+=++F R画轴力图CABD 600300500400E40kN55kN 25kN20kN(4) 求CD 段内的轴力N325200F --+=N35(kN)()F =--20kN25kN3F N3F R画轴力图CABD 600300500400E40kN55kN 25kN20kN(5) 求DE 段内的轴力420kNF N4)((kN)N ++=204F发生在BC 段内任一横截面上 画轴力图Nmax 50(kN)F =(6) 画轴力图C AB D 600300500400E 40kN 55kN 25kN 20kN F 5010520++NKN x。
材料力学内力图绘制详解

一、由外力直接绘制轴力图例 如图(a)所示为一绳子受力图,右端固定,试绘制该绳的轴力图。
解 根据外力直接绘制轴力图(见图(b)),绘图分析过程及步骤如下。
从左向右绘制,始终取右边部分为研究体。
在截面A 有集中力F 1,使研究体拉伸变形,故轴力在此截面向正方向发生突变,轴力突变大小为集中力F 1大小,此时 F N =(0+500)N=500 N ;在AB 段没有外力,故轴力不变;在截面B 有集中力F 2,使研究体受拉伸变形,故轴力在此截面向正方向发生突变,轴力突变大小为集中力F 2大小,此时F N =(500+420)(b )(a)N=920 N;在BC段没有外力,故轴力不变;在截面C有集中力F3,使研究体受压缩变形,故轴力在此截面向负方向发生突变,轴力突变大小为集中力F3大小,此时F N=(920-280)N=640 N;在CD段没有外力,故轴力不变;在截面D有集中力F4,使研究体受压缩变形,故轴力在此截面向负方向发生突变,轴力突变大小为集中力F4大小,此时F N=(640-800)N=-160 N;在DE 段没有外力,故轴力不变;在截面E有集中力,由于轴力曲线与轴线围成封闭图形,故轴力突变为0。
例有一根阶梯轴受力如图(a)所示,试绘制阶梯轴的轴力图。
图解从右向左绘制,始终取左变部分为研究体。
根据外力直接绘制轴力图(见图(b)),绘图分析过程及步骤如下:在截面A有集中力F1,使研究体压缩变形,故轴力在此截面向负方向发生突变,轴力突变大小为集中力F1大小,此时F N=(0-10)kN=-10 kN;在AB段有均匀分布载荷,使研究体受拉伸变形,故轴力以斜直线规律向正方向渐变,轴力渐变大小为均匀分布载荷大小,此时F N=(-10+10×2)kN=10 kN;在截面B没有力,故此截面轴力没有变化;在BC段没有外力,故轴力不变;在截面C有集中力F2,使研究体受拉伸变形,故轴力在此截面向正方向发生突变,轴力突变大小为集中力F2大小,此时F N=(10+10)kN=20 kN;在CD段没有外力,故轴力不变;在截面D有集中力,由于轴力曲线与轴线围成封闭图形,故轴力突变为0.二、由外力直接绘制扭矩图例如图(a)所示圆轴,左端固定、右端自由,受到三个集中力偶作用,试绘制其内力图。
材料力学-轴力图的绘制方法

低碳钢的 20— 27% 60% 为塑性材料
总复习
保证拉(压)杆不
拉(压)杆的强度条件
因强度不足发生破
坏的条件
max [ ]
等直杆
max
FN, max A
[ ]
强度计算的三种类型:
(1)强度校核
max
FN,max A
[ ]
(2)截面选择
A FN,max
[ ]
(3)计算许可荷载
总复习
e —
30
弹性极限31
32
E
E tan 梁横力弯曲时横截面上的应力
梁的挠曲线近似微分方程及其积分
33
3总4 复习
35
低碳钢试件拉伸时的力学性能
0
两个塑性指标:
断后伸长率 l1 l0 100% 断面收缩率 A0 A1 100%
l0
A0
5% 为塑性材料 5% 为脆性材料
l 1 FN l EA
即
E
称为单轴应力状态下的胡克定律。
总复习
轴向拉(压)杆的变形·胡克定律
d1 d
F
F
l l1
ν
或 -ν
n -- 横向变形因数或泊松比
0 n 0.5
总复习
例1:已知:A1=2cm2,A2=4cm2,F1=4kN,F2=10kN,
E=2×105MPa。试求杆的总变形。
C1、C2为常数,由梁的边界条件(包括位移约 束和连续条件)确定。
A
B
A
B
wA=0
wB=0
总复习
wA=0 θA=0
例6:将正确答案填入下列各题的空格中。
(1)梁变形时,横截面的挠度是指截面形心
沿
