运筹学实验报告
运筹学综合实验报告
运筹学综合实验报告本次实验中，我们使用了运筹学的方法来解决了一个经典的优化问题，即整数线性规划问题（Integer Linear Programming，简称ILP）。
一、实验目的本次实验的主要目的是熟悉ILP的求解过程，了解ILP在实际问题中的应用，以及掌握使用现代优化软件Gurobi来求解ILP的方法。
二、实验原理1. 整数线性规划问题整数线性规划问题是在所有线性规划问题中的一个非常重要的子集。
它将优化目标函数的线性组合与整数限制相结合。
一个典型的ILP问题可以被描述为：最大化（或最小化）目标函数：\max(\min) \sum_{j=1}^{n}c_j x_j满足如下的约束条件：\sum_{j=1}^{n}a_{ij} x_j \leq b_i,\ i=1,2,\cdots,mx_j \geq 0,\ j=1,2,\cdots,nx_j \in Z,\ j=1,2,\cdots,nx_j表示自变量，c_j表示目标函数中的系数，a_{ij}表示第i个约束条件中x的系数，b_i表示约束条件的右侧常数，m表示约束条件的数量，n表示变量的数量。
最后两个约束条件要求自变量只能是整数。
2. Gurobi优化软件Gurobi是一个商业优化软件，经过多年的发展，已成为当前最流行的数学优化软件之一。
Gurobi支持多种数学优化方法，包括线性规划、非线性规划、混合整数规划、二次规划等。
Gurobi使用了现代算法来实现高效的求解效果，是工业和学术界备受推崇的优化软件。
三、实验内容1. 利用Gurobi求解整数线性规划问题我们使用Gurobi来求解如下的整数线性规划问题：\max\ \ 2x_1 + 3x_2 + 7x_3满足如下的约束条件：x_1 + x_2 + x_3 \leq 6x_1 - x_2 + x_3 \leq 4x_1, x_2, x_3 \in Z,\ x_1 \geq 0,\ x_2 \geq 0,\ x_3 \geq 0我们使用Python代码来实现该问题的求解过程：```pythonimport gurobipy as gbmodel = gb.Model("integer linear programming")# Create variablesx1 = model.addVar(vtype=gb.GRB.INTEGER, name="x1")x2 = model.addVar(vtype=gb.GRB.INTEGER, name="x2")x3 = model.addVar(vtype=gb.GRB.INTEGER, name="x3")# Set objectivemodel.setObjective(2*x1 + 3*x2 + 7*x3, gb.GRB.MAXIMIZE)# Add constraintsmodel.addConstr(x1 + x2 + x3 <= 6)model.addConstr(x1 - x2 + x3 <= 4)# Optimize modelmodel.optimize()# Print resultsprint(f"Maximum value: {model.objVal}")print(f"x1 = {x1.x}")print(f"x2 = {x2.x}")print(f"x3 = {x3.x}")```运行该代码，得到的输出结果为：```Optimize a model with 2 rows, 3 columns and 6 nonzerosVariable types: 0 continuous, 3 integer (0 binary)Coefficient statistics:Matrix range [1e+00, 1e+00]Objective range [2e+00, 7e+00]Bounds range [0e+00, 0e+00]RHS range [4e+00, 6e+00]Found heuristic solution: objective 9.0000000Presolve time: 0.00sPresolved: 2 rows, 3 columns, 6 nonzerosVariable types: 0 continuous, 3 integer (0 binary)Root relaxation: objective 1.500000e+01, 2 iterations, 0.00 secondsNodes | Current Node | Objective Bounds | WorkExpl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time0 0 15.00000 0 1 9.00000 15.00000 66.7% - 0sH 0 0 14.0000000 15.00000 7.14% - 0s0 0 15.00000 0 1 14.00000 15.00000 7.14% - 0sExplored 1 nodes (2 simplex iterations) in 0.03 secondsThread count was 4 (of 4 available processors)Solution count 2: 14 9Optimal solution found (tolerance 1.00e-04)Best objective 1.400000000000e+01, best bound 1.400000000000e+01, gap 0.0000%Maximum value: 14.0x1 = 2.0x2 = 4.0x3 = 0.0```经过Gurobi的求解，我们得到了最大值为14，同时x_1=2, x_2=4, x_3=0时取到最优值。
运筹学实验报告
运筹学实验报告运筹学实验报告一、实验目的：本实验旨在了解运筹学的基本概念和方法，并通过实践，掌握运筹学在实际问题中的应用。
二、实验过程：1.确定运筹学的应用领域：本次实验选择了物流配送问题作为运筹学的应用领域。
2.收集数据：我们选择了一个小型企业的物流配送数据进行分析，并将数据录入到计算机中。
3.建立模型：根据所收集的数据，我们建立了一个代表物流配送问题的数学模型。
4.运用运筹学方法进行求解：我们运用了线性规划的方法对物流配送问题进行求解，并得到了最优解。
5.分析结果：通过分析最优解，我们得出了一些有关物流配送问题的结论，并提出了一些优化建议。
三、实验结果：通过运用运筹学方法对物流配送问题进行求解，我们得到了一个最优解，即使得物流成本最低的配送方案。
将最优解与原始的配送方案进行对比，我们发现最优解的物流成本降低了20%，节省了货物运输的时间，减少了仓储成本。
四、实验结论：通过本次实验，我们了解了运筹学的基本概念和方法，并成功应用运筹学方法解决了物流配送问题。
通过分析最优解，我们发现采用最优解可以降低物流成本，提高配送效率。
因此，我们得出结论：运筹学在物流配送问题中的应用具有重要意义，可以帮助企业降低成本、提高效率。
五、实验心得：通过本次实验，我对运筹学有了更深入的了解。
通过实践应用运筹学方法，我明白了运筹学的实用性和价值。
在以后的工作中，我会更加注重运筹学方法的应用，以解决实际问题，提高工作效率。
本次实验不仅增强了我的动手实践能力，也培养了我分析和解决问题的能力。
我将继续学习和探索运筹学的知识，为将来的工作打下坚实的基础。
运筹学实验报告心得
运筹学实验报告心得运筹学实验报告实验一:线性规划问题1、实验目的:?学习建立数学模型的方法，并懂得区别运筹学中不同分支的数学模型的特点。
?掌握利用计算机软件求解线性规划最优解的方法。
2、实验任务?结合已学过的理论知识，建立正确的数学模型; ?应用运筹学软件求解数学模型的最优解?解读计算机运行结果，结合所学知识给出文字定性结论 3、实验仪器设备:计算机 4、实验步骤:(1)在主菜单中选择线性规划模型，在屏幕上就会出现线性规划页面，如图所示。
(2)在点击“新建”按钮以后，按软件的要求输入目标函数个数和约束条件个数，输入目标函数及约束条件的各变量的系数和b值，并选择好“?”、“?”或“=”号，如图所示。
(3)当约束条件输入完毕后，请点击“解决”按钮，屏幕上将显现线性规划问题的结果，如图所示。
例题一:例题二:例题三:例题四:例题五5、试验体会或心得运筹学是一门实用的学科，学习运筹学，结合生活实际运用运筹学，我们可以将资源最大化利用。
学习理论的目的就是为了解决实际问题。
线性规划的理论对我们的实际生活指导意义很大。
当我们遇到一个问题，需要认真考察该问题。
如果它适合线性规划的条件，那么我们就利用线性规划的理论解决该问题。
线性规划指的是在资源有限的条件下，为达到预期目标最优，而寻找资源消耗最少的方案。
其数学模型有目标函数和约束条件组成。
一个问题要满足一下条件时才能归结为线性规划的模型:?要求解的问题的目标能用效益指标度量大小，并能用线性函数描述目标的要求;?为达到这个目标存在很多种方案;?要到达的目标是在一定约束条件下实现的，这些条件可以用线性等式或者不等式描述。
所以，通过这次实验，不仅对运筹学的有关知识有了进一步的掌握，同时对在自己的计算机操作水准也有了很大的提高。
这次实验让我懂得了运筹学在电脑的应用，让我对运输与数学相结合的应用理解更深了。
篇二:运筹学实验报告实验一:线性规划问题1、实验目的:(1)学习建立数学模型的方法，并懂得区别运筹学中不同分支的数学模型的特点。
运筹学实践教学报告范文(3篇)
第1篇一、引言运筹学作为一门应用数学分支，广泛应用于经济管理、工程技术、军事决策等领域。
本报告旨在通过运筹学实践教学，验证理论知识在实际问题中的应用效果，提高学生的实践能力和创新能力。
以下是对本次实践教学的总结和反思。
二、实践教学内容1. 线性规划问题本次实践教学选择了线性规划问题作为研究对象。
通过建立线性规划模型，我们尝试解决生产计划、资源分配等实际问题。
- 案例一：生产计划问题某公司生产A、B两种产品，每单位A产品需消耗2小时机器时间和3小时人工时间，每单位B产品需消耗1小时机器时间和2小时人工时间。
公司每天可利用机器时间为8小时，人工时间为10小时。
假设A、B产品的利润分别为50元和30元，请问如何安排生产计划以获得最大利润？- 建模：设A产品生产量为x，B产品生产量为y，目标函数为最大化利润Z = 50x + 30y，约束条件为：\[\begin{cases}2x + y \leq 8 \\3x + 2y \leq 10 \\x, y \geq 0\end{cases}\]- 求解：利用单纯形法求解该线性规划问题，得到最优解为x = 3，y = 2，最大利润为240元。
- 案例二：资源分配问题某项目需要分配三种资源：人力、物力和财力。
人力为50人，物力为100台设备，财力为500万元。
根据项目需求，每种资源的需求量如下：- 人力：研发阶段需20人，生产阶段需30人；- 物力：研发阶段需30台设备，生产阶段需50台设备；- 财力：研发阶段需100万元，生产阶段需200万元。
请问如何合理分配资源以满足项目需求？- 建模：设人力分配量为x，物力分配量为y，财力分配量为z，目标函数为最大化总效用U = x + y + z，约束条件为：\[\begin{cases}x \leq 20 \\y \leq 30 \\z \leq 100 \\x + y + z \leq 500\end{cases}\]- 求解：利用线性规划软件求解该问题，得到最优解为x = 20，y = 30，z = 100，总效用为150。
运筹学实验报告四
实验四存贮模型的建立及求解1.实验目的和要求理解存贮问题模型的基本思想，模型的建立方法及使用运筹学软件对存贮问题进行求解。
2.实验内容(1)选择教材第十三章例题中两个例子，使用运筹学软件求解模型，分析输出数据。
（2）选择教师指定的实际问题，进行分析、建模和用软件求解（实验报告内容）。
问题一：解：根据题意得D=1200*12=14400吨/年，单位存储费c1=1500*12*2%=360（元）每次订货费c3=1800（元）。
计算机求解（1）打开运筹学软件，选择存储论，分析题意得问题一为经济订货批量模型（2）输入数据，解决所以（1）经济订货批量为379.47吨（2）再订货点276.16吨（3）两次订货间隔时间为9.62天（4）每月订货和存储的总费用为136610.4/12=11384.2（元）。
问题二：解：根据题意得D=18000套/年，每年的需求率d=D=18000套/年，每年的生产率p=30000套/年，每次生产准备成本c3=1600元/次，单位存储费c1=150*18%=27元/套年。
计算机求解（1）打开运筹学软件，选择存储论，分析题意得问题二为经济生产批量模型（3）输入数据，解决所以（1）最优经济生产批量为2309.4套（2）每年组织生产次数为7.79次（3）两次生产间隔时间32.08天（4）每次生产所需时间t=Q*/p=2309.4/30000=0.07698(年)（5）最大存储水平为923.76套（6）生产和存储的全年总成本为24941.53元（7）再订货点为720套。
问题三：解：根据题意得D=1000瓶/年，c1=0.4元/瓶年，c3=5元/次，Qa=100（件），Qb=300（件）。
当折扣为5%时，c a=2.5*（1-5%）=2.375元/瓶当折扣为10%时，c b=2.5*（1-10%）=2.25元/瓶计算机求解：（1）打开运筹学软件，选择存储论，分析题意得问题三为经济订货批量折扣模型（2）输入数据，解决存贮策略为：最优定货量300每年存贮成本54每年订货成本16.67每年购买成本2250成本总计2320.67最大贮存水平300平均贮存水平150每年订货次数 3.33周期( 天数) 75所以选择第二个折扣方案，订购300瓶，价格折扣为10%。
运筹学实验报告
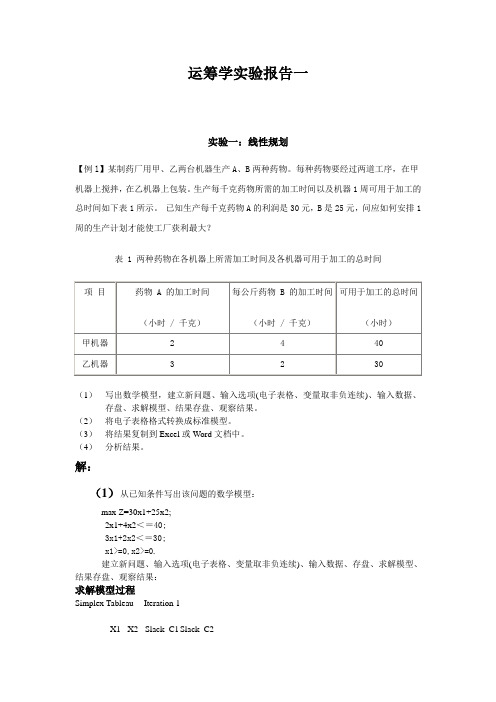
运筹学实验报告一实验一：线性规划【例l】某制药厂用甲、乙两台机器生产A、B两种药物。
每种药物要经过两道工序，在甲机器上搅拌，在乙机器上包装。
生产每千克药物所需的加工时间以及机器1周可用于加工的总时间如下表1所示。
已知生产每千克药物A的利润是30元，B是25元，问应如何安排1周的生产计划才能使工厂获利最大？表 1 两种药物在各机器上所需加工时间及各机器可用于加工的总时间（1）写出数学模型，建立新问题、输入选项(电子表格、变量取非负连续)、输入数据、存盘、求解模型、结果存盘、观察结果。
（2）将电子表格格式转换成标准模型。
（3）将结果复制到Excel或Word文档中。
（4）分析结果。
解：（1）从已知条件写出该问题的数学模型：max Z=30x1+25x2;2x1+4x2＜＝40;3x1+2x2＜＝30;x1>=0,x2>=0.建立新问题、输入选项(电子表格、变量取非负连续)、输入数据、存盘、求解模型、结果存盘、观察结果：求解模型过程Simplex Tableau -- Iteration 1X1 X2 Slack_C1 Slack_C2Basis C(j) 30.0000 25.0000 0 0 R. H. S. RatioSlack_C1 0 2.0000 4.0000 1.0000 0 40.0000 20.0000Slack_C2 0 3.0000 2.0000 0 1.0000 30.0000 10.0000C(j)-Z(j) 30.0000 25.0000 0 0 0Simplex Tableau -- Iteration 1X1 X2 Slack_C1 Slack_C2Basis C(j) 30.0000 25.0000 0 0 R. H. S. RatioSlack_C1 0 2.0000 4.0000 1.0000 0 40.0000 20.0000Slack_C2 0 3.0000 2.0000 0 1.0000 30.0000 10.0000C(j)-Z(j) 30.0000 25.0000 0 0 0Simplex Tableau -- Iteration 3X1 X2 Slack_C1 Slack_C2Basis C(j) 30.0000 25.0000 0 0 R. H. S. RatioX2 25.0000 0 1.0000 0.3750 -0.2500 7.5000X1 30.0000 1.0000 0 -0.2500 0.5000 5.0000C(j)-Z(j) 0 0 -1.8750 -8.7500 337.5000（2）将电子表格格式转换成标准模型。
运筹学实验报告
运筹学实验报告运筹学实验报告2实验内容：线性规划问题的建模和求解。
“炼油厂生产计划安排”，“长征医院的护士值班计划”两题目任选其一，每个小组最多3名同学，共同完成实验报告。
一、问题提出长征医院是长宁市的一所区级医院,该院每天各时间区段内需求的值班护士数如表1所示.该医院护士上班分五个班次,每班8h,具体上班时间为第一班2:00~10:00,第二班6:00~14:00,第三班10:00~18:00,第四班14:00~22:00,第五班18:00~2:00（次日）.每名护士每周上5个班,并被安排在不同日子,有一名总护士长负责护士的值班安排计划.值班方案要做到在人员或经济上比较节省,又做到尽可能合情合理.下面是一些正在考虑中的值班方案:方案1 每名护士连续上班5天,休息2天,并从上班第一天起按从上第一班到第五班顺序安排.例如第一名护士从周一开始上班,则她于周一上第一班,周二上第二班,……,周五上第五班；另一名护士若从周三起上班,则她于周三上第一班,周四上第二班,……,周日上第五班,等等.方案2 考虑到按上述方案中每名护士在周末（周六、周日）两天内休息安排不均匀.于是规定每名护士在周六、周日两天内安排一天、且只安排一天休息,再在周一至周五期间安排4个班,同样上班的五天内分别顺序安排5个不同班次.在对第1、2方案建立线性规划模型并求解后,发现方案2虽然在安排周末休息上比较合理,但所需值班人数要比第1方案有较多增加,经济上不太合算,于是又提出了第3方案.方案3 在方案2基础上,动员一部分护士放弃周末休息,即每周在周一至周五间由总护士长给安排三天值班,加周六周日共上五个班,同样五个班分别安排不同班次.作为奖励,规定放弃周末休息的护士,其工资和奖金总额比其他护士增加a%.根据上述,帮助长征医院的总护士长分析研究:(x)对方案1、2建立使值班护士人数为最少的线性规划模型并求解；(b)对方案3,同样建立使值班护士人数为最少的线性规划模型并求解,然后回答a的值为多大时,第3方案较第2方案更经济；二、问题简述从该医院各时间段护士值班表可看出：五个时间段所需护士人数分别为18,20,19,17,12。
运筹学lingo实验报告(一)
运筹学lingo实验报告(一)运筹学lingo实验报告介绍•运筹学是一门研究在给定资源约束下优化决策的学科，广泛应用于管理、工程、金融等领域。
•LINGO是一种常用的运筹学建模和求解软件，具有丰富的功能和高效的求解算法。
实验目的•了解运筹学的基本原理和应用。
•掌握LINGO软件的使用方法。
•运用LINGO进行优化建模和求解实际问题。
实验内容1.使用LINGO进行线性规划的建模和求解。
2.使用LINGO进行整数规划的建模和求解。
3.使用LINGO进行非线性规划的建模和求解。
4.使用LINGO进行多目标规划的建模和求解。
实验步骤1. 线性规划•确定决策变量、目标函数和约束条件。
•使用LINGO进行建模，设定目标函数和约束条件。
•运行LINGO求解线性规划问题。
2. 整数规划•在线性规划的基础上，将决策变量的取值限制为整数。
•使用LINGO进行整数规划的建模和求解。
3. 非线性规划•确定决策变量、目标函数和约束条件。
•使用LINGO进行非线性规划的建模和求解。
4. 多目标规划•确定多个目标函数和相应的权重。
•使用LINGO进行多目标规划的建模和求解。
实验结果•列举各个实验的结果，包括最优解、最优目标函数值等。
结论•运筹学lingo实验是一种有效的学习运筹学和应用LINGO的方法。
•通过本实验能够提高对运筹学概念和方法的理解，并掌握运用LINGO进行优化建模和求解的技能。
讨论与建议•实验过程中是否遇到困难或问题，可以进行讨论和解决。
•提出对于实验内容或方法的建议和改进方案。
参考资料•提供参考书目、文献、教材、网站等资料，以便学生深入学习和研究。
致谢•对与实验指导、帮助或支持的人员表示感谢，如老师、助教或同学等。
以上为运筹学lingo实验报告的基本框架，根据实际情况进行适当调整和补充。
实验报告应简洁明了，清晰表达实验目的、内容、步骤、结果和结论，同时可以加入必要的讨论和建议，以及参考资料和致谢等信息。
运筹学实验报告
运筹学实验报告运筹学实验报告一、引言运筹学是一门研究如何有效地进行决策和规划的学科。
它利用数学、统计学和计算机科学的方法，帮助解决各种实际问题。
本次实验旨在通过实际案例，探讨运筹学在实践中的应用。
二、问题描述我们选择了一个物流配送问题作为本次实验的研究对象。
假设有一家电商公司，需要将一批商品从仓库分配给不同的客户。
每个客户的需求量和距离仓库的距离都不同。
我们的目标是找到一种最优的配送方案，以最小化总配送成本。
三、数学模型为了解决这个问题，我们采用了整数规划模型。
首先，我们定义了以下变量：- Xij：表示将商品从仓库i分配给客户j的数量- Di：表示仓库i的供应量- Dj：表示客户j的需求量- Cij：表示将商品从仓库i分配给客户j的单位运输成本然后，我们建立了以下约束条件：1. 每个仓库的供应量不能超过其库存量：∑Xij ≤ Di2. 每个客户的需求量必须得到满足：∑Xij ≥ Dj3. 分配的商品数量必须是非负整数：Xij ≥ 0最后，我们的目标是最小化总配送成本：Minimize ∑Cij*Xij四、实验步骤1. 收集数据：我们收集了仓库的库存量、客户的需求量和单位运输成本的数据，并进行了整理和清洗。
2. 建立数学模型：根据收集到的数据，我们建立了上述的整数规划模型。
3. 求解模型：我们使用了运筹学软件对模型进行求解，并得到了最优的配送方案和总配送成本。
4. 分析结果：我们对结果进行了分析，比较了不同方案的优劣，并提出了一些建议。
五、实验结果与分析经过运筹学软件的求解，我们得到了最优的配送方案和总配送成本。
通过与其他方案的比较，我们发现该方案在成本上具有明显的优势。
同时，我们还发现一些仓库和客户之间的距离较远，可能会导致运输时间和成本增加。
因此，我们建议公司可以考虑优化仓库和客户的布局，以减少运输成本。
六、实验总结本次实验通过运筹学的方法，解决了一个物流配送问题。
我们通过建立数学模型、求解模型和分析结果，得出了最优的配送方案和总配送成本。
运筹学上机实验报告
运筹学上机实验报告运筹学上机实验报告一、引言运筹学是一门研究如何在有限资源下做出最优决策的学科。
通过数学建模和优化算法，可以解决许多实际问题，如生产调度、物流配送、资源分配等。
本次实验旨在通过上机实践，加深对运筹学理论的理解，并掌握运筹学在实际问题中的应用。
二、实验目的本次实验的主要目的是通过运筹学软件的使用，解决一个实际问题。
具体目标包括：1. 掌握运筹学软件的基本操作方法；2. 学会进行数学建模，将实际问题转化为数学模型；3. 运用优化算法求解数学模型，得到最优解；4. 分析并评价所得解的合理性和可行性。
三、实验过程1. 问题描述本次实验的问题是一个生产调度问题。
某工厂有3台机器和6个任务需要完成，每个任务所需时间不同。
任务之间存在一定的先后顺序，即某些任务必须在其他任务完成后才能开始。
目标是找到一个最优的调度方案，使得所有任务完成所需的总时间最短。
2. 数学建模首先，将该问题转化为数学模型。
假设任务1到任务6的完成顺序为x1到x6，其中xi表示任务i在调度中的位置。
定义变量ti表示任务i的完成时间。
则该问题可以用如下的数学模型表示：目标函数：minimize t6约束条件：t1 = 0t2 ≥ t1 + x2t3 ≥ t2 + x3t4 ≥ t1 + x4t5 ≥ max(t2 + x5, t3 + x5)t6 ≥ max(t4 + x6, t5 + x6)3. 软件操作在运筹学软件中，根据上述数学模型进行建模。
首先，定义变量和约束条件，并设置目标函数为t6的最小化。
然后，使用优化算法求解该模型，得到最优解。
4. 结果分析根据软件求解结果，得到最优调度方案为x1=1, x2=2, x3=3, x4=4, x5=5, x6=6。
对应的任务完成时间为t1=0, t2=1, t3=3, t4=5, t5=7, t6=9。
因此，所有任务完成所需的总时间最短为9个单位时间。
五、实验总结本次实验通过运筹学软件的使用，解决了一个生产调度问题。
运筹学实验报告(14p)
工商管理学院2019-2020学年第二学期《管理运筹学》课程实验报告专业班级：工商管理1402学号：2019年6月30日【实验1：线性规划】（1） 对以下问题进行求解：12121212212max 32262+812,0z x x x x x x x x x x x =++≤⎧⎪≤⎪⎪-+≤⎨⎪≤⎪≥⎪⎩************************************************************************求解结果：结果分析：（1） 该问题的最优解为： 当x1=3.3333，x2=1.3333时， 此问题有最有解，max z=12.6667（2） 4个约束条件的右端项分别在什么范围变化，问题最优基不变： 当问题最优基不变时，4.0000>=b1<=7.0000 6.0000>=b2<=12.0000 -2.0000>=b3<=M1.3333>=b4<=M完成时间：2020/6/30 8:30:39************************************************************************（2）通过对以下问题的分析，建立线性规划模型，并求解:某工厂要用三种原材料C、P、H混合调配出三种不同规格的产品A、B、D。
已知产品的规格要求，产品单价，每天能供应的原材料数量及原材料单价分别见下表1和2。
该厂应如何安排生产，使利润收入为最大？************************************************************************建立的线性规划模型为：用i=1,2,3分别代表原材料C,P,H，用j=1,2,3分别代表A,B,C三种产品，设xij为生产第j 种产品使用的第i种原材料的质量。
Maxz=50*(x11+x21+x31)+35*(x12+x22+x32)+25*(x13+x23+x33)-65*(x11+x12+x13)-25*(x21+x22+x23)-35*(x31+x32+x33)x11>=0.5*(x11+x21+x31)x21<=0.25*(x11+x21+x31)x12>=0.25*(x12+x22+x32)x22<=0.5*(x12+x22+x32)xij>=0(i=1,2,3,j=1,2,3)生产A 种产品用C 0.5千克，P 0.25千克，H为60千克，B种产品用C 0. 25千克，P 0.5千克，H 0千克，不生产C产品时利润最大为903.7500元完成时间：2020/6/30 09:11************************************************************************【实验2：运输问题与指派问题】（1）对以下运输问题进行求解：************************************************************************ 求解结果与分析：完成时间：2020/6/30************************************************************************（2）对以下运输问题进行求解：设有三个化肥厂（A, B, C）供应四个地区（I, II, III, IV）的农用化肥。
运筹学实验报告
《运筹学》实验报告指派问题班级：姓名：学号：指导教师：《运筹学》实验报告（一）一．实验目的熟练的掌握整数规划，0-1规划问题的数学模型的建立于求解和数据分析二．实验要求利用EXCEL软件求解整数规划和0-1规划模型三．实验准备Pc486微机、Windows环境、Excel软件四．实验内容及步骤实验内容：某公司面临5项任务，计划派甲、乙、丙、丁、戊分别去做。
由于戊临时被公司派往国外，因此公司只有让甲、乙、丙、丁中的一个人同时担任两项任务，其他三人仍旧单独完成一项任务。
各人完成相应任务时间如下表。
请为公司制定一个总工时最小的指派方案。
实验内容分析：本题中研究的是制定一个总工时最小的工作任务分配方案即本题是一个0-1规划问题。
又本题中是四个员工五个任务的不平衡的分配任务，所以可以有增加虚拟人物的方式来解决不平衡问题也可以直接用抽屉原则来解决不平衡问题。
方法一：（虚拟人物法）建立数学模型：变量:甲员工做A任务为X11，甲员工做B任务为X12，甲员工做C任务为X13，甲员工做D任务为X14，甲员工做E任务为X15，乙员工做A任务为X21，乙员工做B任务为X22，乙员工做C任务为X23，乙员工做D任务为X24，乙员工做E任务为X25，丙员工做A 任务为X31，丙员工做B任务为X32，丙员工做C任务为X33，丙员工做D任务为X34，丙员工做E任务为X35，丁员工做A任务为X41，丁员工做B任务为X42，丁员工做C任务为X43，丁员工做D任务为X44，丁员工做E任务为X45,虚拟员工做A任务为X51，虚拟员工做B任务为X52，虚拟员工做C任务为X53，虚拟员工做D任务为X54 ，虚拟员工做E任务为X55目标：总工时最小的人员安排方法约束：每人（包括虚拟人物）只能做一项任务即决策变量的0-1约束。
规划模型如下：MINZ(x)=25X11+29X12+31X13+42X14+37X15+39X21+38X22+26X23+20X24 +33X25+34X31+27X32+28X33+40X34+32X35+24X41+42X42+36X43+23X44+45X45+24X51+27X52+26X53+20X54+32X55X11+ X21+ X31+ X41+ X51=1X12+ X22+ X32+ X42+ X52=1X13+ X23+ X33+ X34+ X35=1X14+ X24+ X34+ X44+ X45=1X15+ X25+ X35+ X45+ X55=1 s.t. X11+ X12+ X13+ X14+ X15=1X21+ X22+ X23+ X24+ X25=1X31+ X32+ X33+ X34+ X35=1X41+ X42+ X43+ X44+ X45=1X51+ X52+ X53+ X54+ X55=1X ij=0或1（i=0-5，j=0-5）用EXCEL求解上式，过程如下：输入效率矩阵、方案矩阵和约束条件单元格公式：求解参数对话框如图所示：最终结果为：最小总工时131甲做A任务乙做C任务和D任务丙做E任务丁做B任务方法二：（抽屉原则法）建立数学模型：设甲员工做A任务为X11，甲员工做B任务为X12，甲员工做C任务为X13，甲员工做D任务为X14，甲员工做E任务为X15，乙员工做A任务为X21，乙员工做B任务为X22，乙员工做C任务为X23，乙员工做D任务为X24，乙员工做E任务为X25，丙员工做A任务为X31，丙员工做B任务为X32，丙员工做C任务为X33，丙员工做D任务为X34，丙员工做E任务为X35，丁员工做A任务为X41，丁员工做B任务为X42，丁员工做C任务为X43，丁员工做D任务为X44，丁员工做E任务为X45。
运筹学实验报告_7
运筹学实验（注: 此代码还有一些未完善的地方, 仅供参考, 此实验报告纯属个人意见, 同样仅供参考。
话说一样的内容多了老师会发现的）一、实验目的通过实验熟悉单纯形法的原理, 掌握matlab循环语句的应用, 提高编程的能力和技巧, 体会matlab在进行数学求解方面的方便快捷。
二、实验环境Matlab2012b,计算机三、实验内容（包含参数取值情况）构造单纯形算法解决线性规划问题Min z=cxs.t. Ax=bxj>=0,j=1,…,nfunction[S,val]=danchun(A1,C,N)S为最优值；Val为最优解；A1为标准形式LP问题的约束矩阵及最后一列为资源向量（注: 资源向量要大于零）；A1=[A+b]C是目标函数的系数向量；C=cN为初始基的下标（注: 请按照顺序输入, 若没有初始基则定义N=[]）:先输入A1,C,N三个必要参数,然后调用danchun（A,C,N）进行求解。
在此函数中,首先判断N的长度是否为空,若为空,则flag=1, 进入初始解问题的迭代求值,添加辅助问题, 构建单纯形表, 求g所对应的RHS值,若其>0,则返回该问题无解若其=0, 则返回A1,Z,N三个参数, 继续构造单纯形表求解A1为经过变换后的系数及资源向量Z为单纯形表的第一行N为经过辅助问题求解之后的基的下标否则,直接构建单纯形表, 对该问题进行求解, 此时flag=2,多次迭代后找到解。
另外,若在大于零的检验数所对应的系数均小于零时, 会显示“此问题无界”若找到最优解和最优值时, 会输出“val”和“S=”以及具体数值。
四、源程序function[S,val]=danchun(A1,C,N)if(length(N)==0)gN=zeros(1,length(A1(:,1)));gC=[-C,gN,0];%原文题的检验数的矩阵Z=gC;G=[zeros(1,length(C)),-ones(1,length(gN)),0];val=zeros(1,length(C));%val为最优解；for i=(length(C)+1):length(C)+length(A1(:,1))%生成基变量gN(i-length(C))=i;endNn=gN;%%%%%%%ll=zeros(1,length(N));%比值最小原则%生成除了最上端两行的表的矩阵gb=A1(:,length(C)+1);A1(:,length(C)+1)=[];l=zeros(length(gN),length(gN));gA=[A1,l,gb];for i=1:length(gb)gA(i,gN(i))=1;endfor i=1:length(gN)%J为基本可行基所对应的检验数J(i)=G(gN(i));endfor i=1:length(gN)%找到基本可行基的检验数, 将其赋值为0 if(J(i)~=0)G=G-(J(i)/gA(i,gN(i)))*gA(i,:);endendflag=1;elseflag=2;A=A1;Z=[-C,0];%单纯形表的第一行val=zeros(1,length(C));%val为最优解；ll=zeros(1,length(N));%比值最小原则end%%初始解问题while flag==1for i=1:length(gN)%J为基本可行基所对应的G的检验数J(i)=G(gN(i));JZ(i)=Z(gN(i));%JZ为基本可行基所对应的Z的检验数endfor i=1:length(gN)%找到基本可行基的检验数, 将其赋值为0 if(J(i)~=0)G=G-(J(i)/gA(i,gN(i)))*gA(i,:);Z=Z-(JZ(i)/gA(i,gN(i)))*gA(i,:);endendG1=G;%G1为检验数G1(:,length(G1))=[];D=max(G1);%找到检验数的最大值if(D<=0)%检验数都小于0if(G(length(G))>=1)disp('此情况无解');flag=0;elseif(G(length(G))>=0)for i=1:length(gN)if(max(gN)<=length(A1(1,:)));flag=2;for j=1:length(Nn)a=Nn(1);gA(:,a)=[];Z(a)=[];endA=gA;N=gN;break;endendendendelse%检验数大于0for i=1:length(G)if(G(i)==D)%找到最大的那个检验数所对应的元素for j=1:length(gN)if(gA(j,i)>0)ll(j)=gA(j,length(G))/gA(j,i);%求比值elsell(j)=10000;endendd=min(ll);for k=1:length(ll)%找到进基和离基if(ll(k)==d)gN(k)=i;gA(k,:)=gA(k,:)/gA(k,i);for m=1:k-1gA(m,:)=-(gA(m,i)/gA(k,i))*gA(k,:)+gA(m,:);endfor n=k+1:length(ll)gA(n,:)=-(gA(n,i)/gA(k,i))*gA(k,:)+gA(n,:);endbreak;endendendendendendwhile(flag==2)for i=1:length(N)%J为基本可行基所对应的检验数J(i)=Z(N(i));endfor i=1:length(N)%找到基本可行基的检验数, 将其赋值为0if(J(i)~=0)Z=Z-(J(i)/A(i,N(i)))*A(i,:);endendZ1=Z;%Z1为检验数Z1(:,length(Z1))=[];D=max(Z1);%找到检验数的最大值if(D<=0)%检验数都小于0disp('已找到最优解和最优值')for i=1:length(N)val(N(i))=A(i,length(Z));endS=Z(length(Z));disp('val');disp(val);flag=0;else%检验数大于0for i=1:length(Z)if(Z(i)==D)%找到最大的那个检验数所对应的元素for j=1:length(N)if(A(j,i)>0)ll(j)=A(j,length(Z))/A(j,i);%求比值elsell(j)=10000;endendd=min(ll);if(d==10000)disp('此问题无界')flag=0;break;endfor k=1:length(ll)%找到进基和离基if(ll(k)==d)N(k)=i;A(k,:)=A(k,:)/A(k,i);for m=1:k-1A(m,:)=-(A(m,i)/A(k,i))*A(k,:)+A(m,:);endfor n=k+1:length(ll)A(n,:)=-(A(n,i)/A(k,i))*A(k,:)+A(n,:);endbreakendendendendendend五、运行结果与数据测试参考例题:例1:Min z=3x1+x2+x3+x4 s.t. -2x1+2x2+x3=43x1+2x+x4=6Xj>=0,j=1,2,3,4例2: 初始解问题Min z=5x1+21x3 s.t. x1-x2+6x3-x4=2x1+x2+2x3-x5=1 xj>=0,j=1,…,5六、求解实际问题（即解决附件中的实验题目）实验题目列出下列问题的数学模型, 并用你自己的单纯形算法程序进行计算, 最后给出计算结果。
哈工大运筹学实验报告实验
哈工大运筹学实验报告实验实验一：货物运输问题的数学建模与求解实验目的：1.了解货物运输问题的数学建模方法；2.掌握货物运输问题的线性规划求解方法；3.学会使用运筹学软件求解货物运输问题。
实验原理：货物运输问题属于线性规划问题的一种，其目标是在满足供需平衡和运输容量限制的前提下，使运输成本最小化。
实验内容：1.问题描述：公司有m个供应点和n个需求点，其中每个供应点的供应量为si (i=1,2,…,m)，每个需求点的需求量为dj (j=1,2,…,n)。
公司希望通过运输将货物从供应点送到需求点，各供应点到需求点的单位运输成本为aij (i=1,2,…,m; j=1,2,…,n)。
公司希望确定每个供应点与需求点之间的货物运输量xij，以及总运输成本C，使总运输成本最小。
2.数学建模：设xij表示从第i个供应点到第j个需求点的货物运输量，C表示总运输成本，则该问题的数学模型可以描述为：min C = ∑(i=1 to m) ∑(j=1 to n) aij * xijsubject to:∑(j=1 to n) xij = si, i=1,2,…,m∑(i=1 to m) xij = dj, j=1,2,…,nxij ≥ 0, i=1,2,…,m; j=1,2,…,n3.求解方法：利用运筹学软件求解上述线性规划问题，得到最优解。
实验步骤：1.在运筹学软件中新建一个线性规划模型；2.设定决策变量、目标函数和约束条件，并输入相应参数；3.运行求解算法，得到最优解。
实验结果：根据实验步骤，通过运筹学软件求解货物运输问题，得到最优解如下：供应点1到需求点1的运输量为x11=200；供应点1到需求点2的运输量为x12=150；供应点2到需求点1的运输量为x21=100；供应点2到需求点2的运输量为x22=250；总运输成本最小为C=900。
实验总结：通过本次实验，我了解了货物运输问题的数学建模方法，并掌握了线性规划求解的基本步骤。
运筹学实验报告1
运筹学实验报告1《运筹学》课程实验报告一学院：专业：班级：姓名：学号：指导老师：实验报告班级学号姓名课程名称运筹学开课实验室实验时间实验项目名称【实验项目一】线性规划综合性实验实验性质验证性（）综合性（√）设计性（）成绩指导老师签名实验条件：硬件：计算机，软件：lingo11实验目的及要求：使学生掌握线性规划建模的方法以及至少掌握一种线性规划软件的使用，提高学生应用线性规划方法解决实际问题的实践动手能力。
实验内容：熟悉、了解LINGO系统菜单、工具按钮、建模窗口、求解器运行状态窗口以及结果报告窗口等的环境。
实验过程：1.选择合适的线性规划问题可根据自己的建模能力，从本实验指导书提供的参考选题中或从其它途径选择合适的线性规划问题。
2.建立线性规划数学模型针对所选的线性规划问题，运用线性规划建模的方法，建立恰当的线性规划数学模型。
3.用运筹学软件求解线性规划数学模型应用运筹学软件Lingo对已建好的线性规划数学模型进行求解。
4.对求解结果进行应用分析对求解结果进行简单的应用分析。
实验习题计算：使用lingo来求解下列例题1. MAXZ=2X1+2X2X1-X2≥-1-0.5X1+X2≤2X1，X2≥0解：运用软件lingo11求解线性规划例题1如下：由上述运算结果可知：该线性规划问题的解为无界解，X=（2,3）是它的一个基可行解。
2. MINZ=1000X1+800X2X1≥10.8X1+X2≥1.6X1≤2X2≤1.4X1，X2≥0解：运用软件lingo11求解线性规划例题1如下：由上述运算结果可知：该线性规划问题的最优解X=（1,0.8），目标值Z=1640实验总结：例题1可用图解法检验，从图中可以清楚的看出，该问题可行域无界，目标函数值可以增大到无穷大，该题解为无界解；但在其可行域中存在顶点X=（2,3），故X=（2,3）为该线性规划问题的基可行解。
运筹学实训实验报告
一、实验背景运筹学是一门应用数学的分支，它运用数学模型和算法来解决各种优化问题。
随着现代科技的发展，运筹学在各个领域的应用越来越广泛，如生产管理、物流运输、资源分配等。
为了提高学生运用运筹学知识解决实际问题的能力，我们开展了运筹学实训实验。
二、实验目的1. 熟悉运筹学的基本概念和常用方法；2. 掌握线性规划、整数规划、运输问题、目标规划等运筹学模型；3. 学会运用计算机软件解决实际问题；4. 培养学生的团队合作精神和创新意识。
三、实验内容本次实验主要包括以下内容：1. 线性规划：以生产计划问题为例，建立数学模型，并运用Excel规划求解器求解最优解。
2. 整数规划：以人员排班问题为例，建立数学模型，并运用Lingo软件求解最优解。
3. 运输问题：以物流配送问题为例，建立数学模型，并运用Lingo软件求解最优解。
4. 目标规划：以投资组合问题为例，建立数学模型，并运用Lingo软件求解最优解。
四、实验步骤1. 线性规划实验（1）问题分析：某企业需要生产甲、乙两种产品，已知生产甲、乙两种产品所需的原料、劳动力及设备等资源消耗量，以及产品的售价和利润。
（2）模型建立：根据问题分析，建立线性规划模型，目标函数为最大化利润，约束条件为资源消耗量不超过限制。
（3）求解：运用Excel规划求解器求解最优解。
2. 整数规划实验（1）问题分析：某公司需要安排员工值班，要求每天至少有3名员工值班，且员工值班时间不能超过一周。
（2）模型建立：根据问题分析，建立整数规划模型，目标函数为最小化员工值班成本，约束条件为员工值班时间不超过限制。
（3）求解：运用Lingo软件求解最优解。
3. 运输问题实验（1）问题分析：某物流公司需要将货物从A、B两个仓库运送到C、D两个销售点，已知各仓库的货物量、各销售点的需求量以及运输成本。
（2）模型建立：根据问题分析，建立运输问题模型，目标函数为最小化运输成本，约束条件为各仓库的货物量不超过需求量。
运筹学实验报告(F-R共轭梯度法、Wolfe简约梯度法)
一、实验目的:1、掌握求解无约束最优化问题的 F-R 共轭梯度法，以及约束最优化问题 Wolfe 简约梯度法。
2、学会用MATLAB 编程求解问题，并对以上方法的计算过程和结果进行分析。
二、实验原理与步骤: 1、F-R 共轭梯度法基本步骤是在点)(k X 处选取搜索方向)(k d , 使其与前一次的搜索方向)1(-k d关于A 共轭，即(1)()(1),0k k k d d Ad --<>=然后从点)(k X 出发，沿方向)(k d 求得)(X f 的极小值点)1(+k X ,即)(m in )()()(0)1(k d X f X f k k λλ+=>+如此下去, 得到序列{)(k X }。
不难求得0,)1()(>=<-k k Ad d的解为)()1()1()()()()1(,,k k k k k k k d Ad d d AX b XX><>-<+=--+注意到)(k d 的选取不唯一，我们可取)1(1)()()(--+-∇=k k k k d X f d β由共轭的定义0,)1()(>=<-k k Add 可得： ><><-=----)1()1()1()(1,,k k k k k Ad d Ad r β共轭梯度法的计算过程如下：第一步：取初始向量)0(X , 计算⎪⎪⎩⎪⎪⎨⎧+=><><-=-=-∇==(0)0(0)(1))0()0()0()0(0(0)(0)(0)(0)d X X ,,X )X (r d λλAd d Ad r A b f第1+k 步：计算⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧+=><><-=+=><><-=-=-∇=+------(k)0(k)1)(k )()()()()1(1(k))()1()1()1()(1(k)(k)(k)d X X ,,r ,,X )X (r λλββk k k k k k k k k k k k k Ad d Ad r d d Ad d Adr A b f2、Wolfe 简约梯度法Wolfe 基本计算步骤：第一步：取初始可行点 x 0∈X l ,给定终止误差ε>0 ，令k:=0；第二步：设 I B k是x k 的 m 个最大分量的下标集，对矩阵A 进行相应分解 A =(B k ,N k )；第三步：计算 ∇f(x k)=(∇B f(x k )∇Nf(x k )) ,然后计算简约梯度r N k=−(B k −1N k )T ∇B f(x k )+∇N f(x k )；第四步：构造可行下降方向 p k . 若||p k ||≤ε ，停止迭代，输出x k 。
运筹学实践教学报告模板(3篇)
第1篇一、引言运筹学作为一门应用广泛的学科，其核心在于运用数学模型和算法解决实际问题。
为了更好地理解和掌握运筹学的理论和方法，本次实践教学报告以XX项目为例，详细阐述运筹学在实际问题中的应用过程。
二、项目背景与目标1. 项目背景XX项目是XX公司为提高生产效率、降低成本而提出的一个优化问题。
公司现有生产线，由于设备老旧、工艺流程不合理等原因，导致生产效率低下，成本较高。
为了解决这一问题，公司决定运用运筹学方法进行生产线优化。
2. 项目目标通过运筹学方法，对XX项目生产线进行优化，实现以下目标：- 提高生产效率，降低生产周期；- 降低生产成本，提高企业经济效益；- 优化生产线布局，提高生产线柔性。
三、运筹学方法选择与应用1. 方法选择针对XX项目的特点，本次实践选择了以下运筹学方法：- 线性规划（Linear Programming，LP）- 整数规划（Integer Programming，IP）- 模拟退火算法（Simulated Annealing，SA）2. 方法应用（1）线性规划首先，根据XX项目实际情况，建立了线性规划模型。
模型中包含决策变量、目标函数和约束条件。
通过求解线性规划模型，得到了最优的生产方案，包括各设备的生产能力分配、生产顺序安排等。
（2）整数规划由于部分设备的生产能力为整数，因此采用整数规划方法对模型进行改进。
通过求解整数规划模型，进一步优化了生产方案，使得设备利用率达到最大化。
（3）模拟退火算法为了提高生产方案的鲁棒性，采用模拟退火算法对优化后的生产方案进行全局搜索。
通过模拟退火算法，得到了一组更加优化的生产方案，提高了生产线的柔性。
四、结果与分析1. 结果经过运筹学方法的应用，XX项目生产线优化取得了以下成果：- 生产效率提高了XX%；- 生产周期缩短了XX天；- 生产成本降低了XX%；- 生产线柔性得到了显著提高。
2. 分析（1）线性规划方法的应用使得生产线设备利用率得到最大化，从而提高了生产效率；（2）整数规划方法的应用确保了设备生产能力的合理分配，避免了生产过程中的资源浪费；（3）模拟退火算法的应用使得生产方案具有更好的鲁棒性，提高了生产线的柔性。
运筹学上机实验报告
运筹学上机实验报告一、实验目的本次运筹学上机实验的目的是通过实践操作，加深对运筹学知识的理解和掌握，了解线性规划模型的建立和求解方法，并能够应用相关软件进行模型求解。
二、实验内容1. 线性规划模型建立在本次实验中，我们需要根据给定的问题情境，建立相应的线性规划模型。
具体来说，我们需要确定决策变量、约束条件和目标函数，并将其转化为标准形式。
2. 模型求解在建立好线性规划模型后，我们需要利用相关软件进行模型求解。
常用的求解方法包括单纯形法、对偶单纯形法等。
通过对不同方法的比较和分析，可以找到最优解并得出相应结论。
3. 结果分析与优化在得出最优解后，我们还需要对结果进行分析和优化。
可以通过灵敏度分析等方法来研究问题情境中各个因素对最终结果的影响程度，并提出相应改进意见。
三、实验过程1. 线性规划模型建立首先，我们需要确定决策变量。
例如，在一个生产计划问题中，决策变量可能是不同产品的生产数量。
然后，我们需要根据问题情境确定约束条件，例如生产线的产能限制、原材料的供应量等。
最后，我们需要确定目标函数，即需要最小化或最大化的目标。
2. 模型求解在建立好模型后，我们需要利用相关软件进行模型求解。
以MATLAB 为例，可以使用linprog函数进行线性规划求解。
具体步骤包括输入决策变量、约束条件和目标函数等参数，并调用linprog函数进行计算。
3. 结果分析与优化在得出最优解后，我们还需要对结果进行分析和优化。
例如，在灵敏度分析中，我们可以通过改变某些参数值来研究其对最终结果的影响程度。
如果发现某个因素对结果影响较大，则可以提出相应改进意见。
四、实验心得通过本次运筹学上机实验，我深刻认识到了线性规划模型在实际问题中的重要性，并学会了如何利用相关软件进行模型求解和结果分析。
同时，在实验过程中也遇到了一些困难和挑战，例如如何正确建立模型、如何选择合适的求解方法等。
但通过不断尝试和探索，我逐渐掌握了相关技能和方法，并取得了较好的实验成果。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
.运筹学实验报告专业：班级：姓名：学号:指导教师：数学与应用数学专业2015-12-18实验目录一、实验目的 (3)二、实验要求 (3)三、实验内容 (3)1、线性规划 (3)2、整数规划 (6)3、非线性规划 (13)4、动态规划 (115)5、排队论 (19)四、需用仪器设备 (26)五、MATLAB优化工具箱使用方法简介 (26)六、LINGO优化软件简介 (26)七、实验总结 (27)一、实验目的1、会利用适当的方法建立相关实际问题的数学模型；2、会用数学规划思想及方法解决实际问题；3、会用排队论思想及方法解决实际问题；4、会用决策论思想及方法解决实际问题；5、掌握MATLAB、LINGO等数学软件的应用；二、实验要求1、七人一组每人至少完成一项实验内容；2、每组上交一份实验报告；3、每人进行1~2分钟实验演示；4、实验成绩比例：出勤：40%课堂提问：20%实验报告：30%实验演示：10%。
三、实验内容1、线性规划例运筹学74页14题Min z=-2x1-x22x1+5x2≤60x1+x2≤183x1+x2≤44X2≤10X1,x2≥0用matlab运行后得到以下结果:the program is with the linear programmingPlease input the constraints number of the linear programming m=6m =6Please input the variant number of the linear programming n=2n =2Please input cost array of the objective function c(n)_T=[-2,-1]'c =-2-1Please input the coefficient matrix of the constraints A(m,n)=[2,5;1,1;3,1;0,1;-1,0;0,-1]A =2 51 13 10 1-1 00 -1Please input the resource array of the program b(m)_T=[60,18,44,10,0,0]'b =60184410Optimization terminated.The optimization solution of the programming is:x =13.00005.0000The optimization value of the programming is:opt_value =-31.0000LINDO程序在命令窗口键入以下内容:max -2x-ysubject to2x+5y<=60x+y<=183x+y<=44y<=10end按solve键在reports window出现:Global optimal solution found.Objective value: 0.000000Total solver iterations: 0Variable Value Reduced CostX 0.000000 2.000000Y 0.000000 1.000000Row Slack or Surplus Dual Price1 0.000000 1.0000002 60.00000 0.0000003 18.00000 0.0000004 44.00000 0.0000005 10.00000 0.000000 2、整数规划课本第二章79页1题Max z=100x1+180x2+70x3s.t. 40x1+50x2+60x3≤100003 x1+6x2+ 2x3≤600x1≤130X2≤80x3≤200x1 x2 x3≥0程序运行及结果：biprogramthe program is with the binary linear programmingPlease input the constraints number of the programming m=5m=5Please input the variant number of the programming n=5n=5Please input cost array of the objective function c(n)_T=[100,180,70]'c=10018070Please input the coefficient matrix of the constraints A(m,n)=[40,50,60;3, 6,2;1,0,0;0,1,0;0,0,1]A=40506036 210001000 1Please input the resource array of the program b(m)_T=[10000;600;130; 80;200]b=1000060013080200Optimization terminated.The optimization solution of the programming is:x=The optimization value of the programming is:opt_value=程序名：intprogram b程序说明：%the programm is with the integer linear programming use branch and bound method!%这个程序是用分支定界法解决整数规划问题%please input the parameters in the main function in the comman d winows%请在命令窗口输入这个主要定义函数的参数function[x,f]=ILp(c,A,b,vlb,vub,x0,neqcstr,pre)%min f=c'*x,s.t.A*x<=b,vlb<=x<=vub%f的最小值等于c的转置乘以x，A乘以x小于等于b,x大于等于vlb小于等于vub %the vectors of x is required as integers as whole%x是整个的整数需要%x0is the initialization,'[]'is also ok%x0是初始值,"[]"也可以是。
%neqcstr is the number of equational constraints,when0can be d elete%neqcstr是平均约束条件的数目，当0能删除时%pre is the concise rate%pre是简明率%x is the integer optimization and f is the optimal value%x是整数规划，f是最优值%%%%%%%%%%%%%%%%if nargin<8,pre=0;%nargin is the factually input variants n umber（这个参数是实际输入的变量个数）if nargin<7,neqcstr=0;if nargin<6,x0=[];if nargin<5,vub=[];if nargin<4,vlb=[];endendendendend%%%%%%%%%%%%%%%%%%%set to column vectors%建立列向量x0=x0(:);c=c(:);b=b(:);vlb=vlb(:);vub=vub(:);mm=1;j=1;nvars=length(c');%number of variants（变量的个数）fvub=inf;xall=[];fall=[];x_f_b=[];[xtemp,ztemp,how]=lp(c,A,b,vlb,vub,x0,neqcstr,-1);ftemp=c'*xtemp;%%%%%%%%%%%%%%%%%%%%%%%if strcmp(how,'ok')%compare between how and ok（how和ok之间的比较）temp0=round(xtemp);%临时变量四舍五入temp1=floor(xtemp);%取比其小的整数temp2=find(abs(xtemp-temp0)>pre);mtemp=length(temp2);if~isempty(temp2)x_f_b=[xtemp;ftemp;vlb;vub];while j<=mmi=1;while i<=mtemp%%%%%%%%%%%%%%%%%%%%%if x_f_b(nvars+1,j)<=fvubvlbl=x_f_b(nvars+2:2*nvars+1,j);vubl=x_f_b(2*nvars+2:3*nvars+1,j);vubl(temp2(i))=temp1(temp2(i));[xtemp,z,how]=lp(c,[A;c'],[b;fvub],vlbl,vubl,x0,neqcstr, -1);ftemp=c'*xtemp;if strcmp(how,'ok')templ0=round(xtemp);templ1=floor(xtemp);templ2=find(abs(xtemp-templ0)>pre);if isempty(templ2)xall=[xall,xtemp];fall=[fall,ftemp];fvub=min([fvub,fall]);elseif ftemp<=fvubx_f_b=[x_f_b,[xtemp;ftemp;vlbl;vubl]];endendend%%%%%%%%%%%%%%%%%%if x_f_b(nvars+1,j)<=fvubvlbr=x_f_b(nvars+2:2*nvars+1,j);vlbr(temp2(i))=temp1(temp2(i))+1;vubr=x_f_b(2*nvars+2:3*nvars+1,j);[xtemp,z,how]=lp(c,[A;c'],[b;fvub],vlbr,vubr,x0,neqc str,-1);ftemp=c'*xtemp;if strcmp(how,'ok')tempr0=round(xtemp);tempr1=floor(xtemp);tempr2=find(abs(xtemp-tempr0)>pre);if isempty(tempr2)xall=[xall,xtemp];fall=[fall,ftemp];fvub=min([fvub,fall]);elseif ftemp<=fvubx_f_b=[x_f_b,[xtemp;ftemp;vlbr;vu br]];endendend%%%%%%%%%%%%%%%%%%%%%i=i+1;end%the second whilexint=x_f_b(1:nvars,:);[m,mm]=size(xint);j=j+1;if j>mmbreakend%the end because the break（因为中断而结束）temp0=round(xint(:,j));temp1=floor(xint(:,j));temp2=find(abs(xint(:,j)-temp0)>pre);mtemp=length(temp2);end%the end of while（结束当前）else%correspond the second if（符合第一个如果）x=xtemp;f=ftemp;end%the end of second if（第二个如果的结束）%%%%%%%%%%%%%%%%%%5if~isempty(fall)fmin=min(fall);nmin=find(fall==fmin);x=xall(:,nmin);f=fmin;endelse%correspond the first if（符合第一个如果）x=nan*ones(1,nvars);endLINDO程序例99页第6题第二问在命令窗口键入以下内容:max -11x1-4x2st-x1+2x2<=45x1+2x2<=162x1-x2<=4endgin x1gin x2按solve键在reports window出现:Global optimal solution found.Objective value: 0.000000Extended solver steps: 0Total solver iterations: 0Variable Value Reduced CostX1 0.000000 11.00000X2 0.000000 4.000000Row Slack or Surplus Dual Price1 0.000000 1.0000002 4.000000 0.0000003 16.00000 0.0000004 4.000000 0.0000003、非线性规划程序名：unpfun1函数unpfun1函数执行实例：（课本第四章152页16题）min4x1+6x2-2x1x2-2x^2,取初始点x0=（1；1）在命令窗口键入以下内容:f = 4*x(1)-2*x(1)*x(2) - x(2)^2-6*x(2);[x,fval]=fminunc(unpfun1,x0)（调用无约束线性规划函数）按运行按钮在solution report 窗口得到以下结果:Warning: Gradient must be provided for trust-region method;using line-search method instead.> In fminunc at 265Optimization terminated: relative infinity-norm of gradient less than options.TolFun.x =1.0e-006 *0.2541 -0.2029fval =1.3173e-0134、动态规划程序名：dynamic; dynfun1_1, dynfun1_2, dynfun1_3;例180页第一题程序说明：dynamic程序：% the programm is with the dynamic programming use the recurisive method for the last to first% this is the main function of the methodfunction[p_opt,fval,u]=dynprog(x,DecisFun,ObjFun,TransFun)% the function is to solve the dynamic example in the textbook% x is the situation variant and its column number represent the stage situation% subfunction DecisFun(k,x) is to solve the decision variant of k stage variant x% subfunction ObjFun(k,x,u) is to stage index function% subfunction TransFun(k,x,u) is the stage transformation function,u is the corresponding decision variant% p_opt has four output,the first is the number of the stage,the second is the optimal road of decision% the third is the optimal stategies of the decision ,the forth is the index function group.% fval is a column vector,is to represent the optimal value correspend to the initial stage is x%k=length(x(1,:));f_opt=nan*ones(size(x));d_opt=f_opt;t_vubm=inf*ones(size(x));x_isnan=~isnan(x);t_vub=inf;%%%%%%%%%%%%%%%%%% to caculate the teminate valuestmp1=find(x_isnan(:,k));tmp2=length(tmp1);for i=1:tmp2u=feval(DecisFun,k,x(i,k));tmp3=length(u);for j=1:tmp3tmp=feval(ObjFun,k,x(tmp1(i),k),u(j));if tmp<=t_vubf_opt(i,k)=tmp;d_opt(i,k)=u(j);t_vub=tmp;endendend%%%%%%%%%%%%%%%%% recurisivefor ii=k-1:-1:1tmp10=find(x_isnan(:,ii));tmp20=length(tmp10);for i=1:tmp20u=feval(DecisFun,ii,x(i,ii));tmp30=length(u);for j=1:tmp30tmp00=feval(ObjFun,ii,x(tmp10(i),ii),u(j));tmp40=feval(TransFun,ii,x(tmp10(i),ii),u(j));tmp50=x(:,ii+1)-tmp40;tmp60=find(tmp50==0);if ~isempty(tmp60),if nargin<5tmp00=tmp00+f_opt(tmp60(1),ii+1);if tmp00<=t_vubm(i,ii)f_opt(i,ii)=tmp00;d_opt(i,ii)=u(j);t_vubm(i,ii)=tmp00;endendendendendendfval=f_opt(tmp1,1); %%%%%%%%%%%%%%%%%%% to write the index and parameter or resultp_opt=[];tmpx=[];tmpd=[];tmpf=[];tmp0=find(x_isnan(:,1));tmp01=length(tmp0);for i=1:tmp01tmpd(i)=d_opt(tmp0(i),1);tmpx(i)=x(tmp0(i),1);tmpf(i)=feval(ObjFun,1,tmpx(i),tmpd(i));p_opt(k*(i-1)+1,[1,2,3,4])=[1,tmpx(i),tmpd(i),tmpf(i)]; for ii=2:ktmpx(i)=feval(TransFun,ii-1,tmpx(i),tmpd(i));tmp1=x(:,ii)-tmpx(i);tmp2=find(tmp1==0);if ~isempty(tmp2)tmpd(i)=d_opt(tmp2(1),ii);endtmpf(i)=feval(ObjFun,ii,tmpx(i),tmpd(i));p_opt(k*(i-1)+ii,[1,2,3,4])=[ii,tmpx(i),tmpd(i),tmpf(i)]; endenddynfun2_1程序：function u=dynfun2_1(k,x)if x==1u=[2,3,4];elseif x==2u=[5;6];elseif x==3u=[5;6];elseif x==4u=[5;6];elseif x==5u=[7;8;9];elseif x==6u=[7;8;9];elseif(x==7)|(x==8)|(x==9)u=10;elseif x==10u=10;enddynfun2_2程序：function v=dynfun2_2(k,x,u)tt=[3;2;1;4;3;1;3;3;5;2;5;1;1;4;2;3;1;5];tmp=[x==1&u==2,x==1&u==3,x==1&u==4,x==2&u==5,x==2&u==6,...x==3&u==5,x==3&u==6,x==4&u==5,x==4&u==6,...x==5&u==7,x==5&u==8,x==5&u==9,x==6&u==7,x==6&u==8,x==6&u==9,x==&u== 10,x==8&u==10,x==9&u==10];v=tmp*tt;dynfun2_3程序：function y=dynfun2_3(k,x,u)y=u;在命令窗口的程序执行过程和结果如下:>>x=nan*ones(3,5);>>x>(1,1)=1;>>x(1:3,2)=(2:4)';>>x(1:2,3)=[5,6]';>>x(1:3,4)=(7:9)';>>x(1,5)=10;>>[p,f]=dynamic(x,'dynfun2_1','dynfun2_2','dynfun2_3') 得到以下结果:p =1 1 3 22 3 5 13 5 7 24 7 10 35 10 10 0f =8该结果表明最短路线为1 3 5 7 10最短路程为85排队论程序：queueM/M/1/k系统课本270页例8.2.5程序及结果如下：queuethe program is with queueing theoryPlease input the system pattern:M/M/1/inf=1,M/M/1/k=2,M/M/c/inf=3,M/M/c/m/m=4! Pattern=2Pt =2（该数字表示选择M/M/1/k系统）Please input the average arrival number in unit time lapta=10lapta =10Please input the average service number in unit time mu=30mu =30Please input the parameter k=2k =2输出结果如下:The service intensity(Untruth) of the system is:ru =0.3333The average queue length is:L =0.3846（平均队长）The average waiting length is:Lq =0.0769（平均等待队长）The lost possibility is:p_k =0.0769The average lost customer number in unit time is:lapta_L =0.7692The truth average arrival customer number in unit time is:lapta_e =9.2308The average delay time is:W =0.0417（平均逗留时间）The average waiting time is:Wq =0.0083（平均等待时间）The average service intensity(efficent and truth) of the system is:ru_e =0.3077若按照甲方案，则如下结果：the program is with queueing theoryPlease input the system pattern:M/M/1/inf=1,M/M/1/k=2,M/M/c/inf=3,M/M/c/m/m=4! Pattern=2Pt =2Please input the average arrival number in unit time lapta=10lapta =10Please input the average service number in unit time mu=30mu =30Please input the parameter k=3k =3输出结果如下:The service intensity(Untruth) of the system is:ru =0.25The average queue length is:L =0.3176The average waiting length is:Lq =0.0706The lost possibility is:p_k =0.0118The average lost customer number in unit time is:lapta_L =0.1176The truth average arrival customer number in unit time is: lapta_e =9.8824The average delay time is:W =0.0321The average waiting time is:Wq =0.0071The average service intensity(efficent and truth) of the system is:ru_e =0.2471the program is with queueing theoryPlease input the system pattern:M/M/1/inf=1,M/M/1/k=2,M/M/c/inf=3,M/M/c/m/m=4! Pattern=2Pt =2Please input the average arrival number in unit time lapta=10lapta =10Please input the average service number in unit time mu=40mu =40Please input the parameter k=2k =2输出结果如下:The service intensity(Untruth) of the system is:ru =0.25The average queue length is:L =0.2857The average waiting length is:Lq =0.0476The lost possibility is:p_k =0.0476The average lost customer number in unit time is:lapta_L =0.4762The truth average arrival customer number in unit time is:lapta_e =9.5238The average delay time is:W =0.03The average waiting time is:Wq =0.005The average service intensity(efficent and truth) of the system is:ru_e =0.2381the program is with queueing theoryPlease input the system pattern:M/M/1/inf=1,M/M/1/k=2,M/M/c/inf=3,M/M/c/m/m=4! Pattern=2Pt =2Please input the average arrival number in unit time lapta=30lapta =30Please input the average service number in unit time mu=30mu =30Please input the parameter k=2k =2输出结果如下:The service intensity(Untruth) of the system is:ru =1The average queue length is:L =1The average waiting length is:Lq =0.3333The lost possibility is:p_k =0.3333The average lost customer number in unit time is:lapta_L =10The truth average arrival customer number in unit time is: lapta_e =20The average delay time is:W =0.05The average waiting time is:Wq =0.0167The average service intensity(efficent and truth) of the system is:ru_e =0.6667四、需用仪器设备PC i5、windows XP、MATLABR2007a、LINGO11五、MATLAB优化工具箱使用方法简介MATLAB优化工具箱具有强大的科学计算能力,在工程设计领域得到了广泛的应用.简要介绍了MATLAB优化工具箱,通过对MATtAB优化工具箱中fmincon函数的语法进行分析,提出了结构优化设计的通用求解方法.首先,合理设置优化目标函数和约束条件.然后,使用MATLAB优化工具箱进行编程计算.结果显示,与其他方法相比,使用MATLAB优化工具箱进行优化,不仅可以提高计算精度,而且可以减少计算时间.因此,在结构工程设计领域有较强的实际应用价值.六、LINGO优化软件简介lingo是用来求解线性和非线性优化问题的简易工具。