全等三角形12.2三角形全等的判定第2课时边角边教学课件新版新人教版
八年级数学上册 12.2三角形全等的判定第2课时边角边课件2_6-10
∴△ABD≌△ACD(Sห้องสมุดไป่ตู้S).
∴ ∠BAD=∠CAD,
变式2
已知:如图,AB=AC, BD=CD,E为AD上一点,
求证: BE=CE.
证明: 在△ABD和△ACD中,
AB=AC BD=CD AD=AD
(已知), (已知), (公共边),
∴△ABD≌△ACD(SSS). ∴ ∠BAD=∠CAD,
在△ABE和△ACE中,
AB=AC (已知),
∠BAD=∠CAD
(已证),
AD=AD (已证),
∴△ABD≌△ACD(SAS).
∴ BD=CD.
变式1
已知:如图,AB=AC, BD=CD,
求证: ∠ BAD= ∠ CAD.
证明:
在△ABD和△ACD中, AB=AC (已知), BD=CD (已知), AD=AD (公共边),
A E
即 AF=CE.
B
在△AFD和△CEB中,
AD=CB (已知),
∠A=∠C
(已证),
AF=CE (已证),
∴△AFD≌△CEB(SAS).
D
F C
4.已知:如图,AB=AC,AD是△ABC的角平分线,
求证:BD=CD.
证明: ∵AD是△ABC的角平分线,
∴ ∠BAD=∠CAD,
在△ABD和△ACD中,
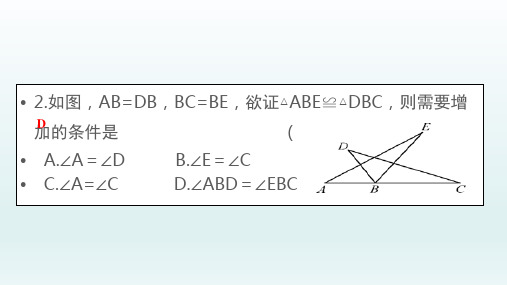
• 2.如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则需要增
加D 的条件是
()
• A.∠A=∠D • C.∠A=∠C
B.∠E=∠C D.∠ABD=∠EBC
3.如图,点E、F在AC上,AD//BC,AD=CB,AE=CF.
求证:△AFD≌△CEB.
第3套人教初中数学八上 12.2 三角形全等的判定课件2 【通用,最新经典教案】

【预习导学】
二、自学检测:学生自主完成,小组内展示、点评,教师巡视。5分钟
1、如图1,AB=DB,BC=BE,欲证△ABE≌△DBC,则需要增加的条件是( )
D
A、∠A=∠D B、∠E=∠C C、∠A=∠C D、∠ABD=∠EBC
练一练
下列长度的各组线段能否组成一个三角形?
(1)15cm、10cm、7cm (2) 4cm、5cm、10cm
(3) 3cm、8cm、5cm
(4) 4cm、5cm、6cm
只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.
做一做:
1、已知两条边长分别为3cm、5cm,你可以 画出几个符合条件的等腰三角形?并求符合 条件的等腰三角形的周长.
如图三角形中,假设有一只小蚂蚁要从点B出 发沿着三角形的边爬到点C,去捉小瓢虫,它有 几条路线可以选择?各条路线的长一样吗?
A
由“两点之间,线段最短”
可以得到AB+AC>BC
同理可得:
AC+BC>AB,
B
C
AB+BC>AC
结论
三角形的三边有这样的关系: 三角形两边的和大于第三边
猜一猜,两边之差与第三边有何关系: 三角形任何两边的差小于第三边
(4)已知等腰三角形的两边长分别为8cm,3cm,
则这三角形的周长为 ( )
(A) 14cm
(B)19cm
(C) 14cm或19cm (D) 不确定
我学会了 1、三角形的三边关系定理; 2、 (1)判断三条已知线段能否组成三角形时,采用一种较为简便的判法:若最短边与较长边的和
12.2三角形全等的判定第2课时 边角边

下列说法中: ① DA 平分∠ EDF ;②△ EBD≌△FCD ;
三、解答题(共36分)
16 . (10 分 ) 如图 , 已知∠ 1 =∠ 2 , AC = AE , BC= D
BC上,求证:AB=AD.
证明:∵∠1=∠2,∠AOE=∠DOC,∴∠E=∠C
AE,BC=DE,∴△ABC≌△ADE(SAS),∴AB=A
要补充的一个条件是( C )
A.∠B=∠C B.∠D=∠E
C.∠BAC=∠EAD D.∠B=∠E
4.(3分)如图,若线段AB,CD互相平分且相交于点O
错误的是( D )
A.AD=BC B.∠C=∠D
C.AD∥BC D.OB=OC
5.(3分)如图所示,AC=DF,BD=EC,AC∥DF,∠
80°,∠B=30°,则∠F=_______. 70°
△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正
二、填空题(每小题4分,共8分)
14.如图,在△ABC中,AB=BC=CA,∠ABC=∠
BD=CE,AD与BE相交于点F,则∠AFE=______. 60
15.如图,在△ABC中,AB=AC,AD是角平分线, ④AD⊥BC.正确的是____________.( 填序号) ①②③④
:CD⊥BE.
证△ABE≌△ACD(SAS),得∠ACD=∠ABE=45°
∠ACB+∠ACD=45°+45°=90°,即CD⊥BE
• • • • • • • • • • • • • • • • • • • •
1、快乐总和宽厚的人相伴,财富总与诚信的人相伴,聪明总与高尚的人相伴,魅力总与幽默的人相伴,健康总与阔达的人相伴。 2、人生就有许多这样的奇迹,看似比登天还难的事,有时轻而易举就可以做到,其中的差别就在于非凡的信念。 3、影响我们人生的绝不仅仅是环境,其实是心态在控制个人的行动和思想。同时,心态也决定了一个人的视野和成就,甚至一生。 4、无论你觉得自己多么了不起,也永远有人比更强;无论你觉得自己多么不幸,永远有人比你更不幸。 5、也许有些路好走是条捷径,也许有些路可以让你风光无限,也许有些路安稳又有后路,可是那些路的主角,都不是我。至少我会觉得,那些路不是自己想要的。 6、在别人肆意说你的时候,问问自己,到底怕不怕,输不输的起。不必害怕,不要后退,不须犹豫,难过的时候就一个人去看看这世界。多问问自己,你是不是已经为了梦想而竭尽全力了? 7、人往往有时候为了争夺名利,有时驱车去争,有时驱马去夺,想方设法,不遗余力。压力挑战,这一切消极的东西都是我进取成功的催化剂。 8、真想干总会有办法,不想干总会有理由;面对困难,智者想尽千方百计,愚者说尽千言万语;老实人不一定可靠,但可靠的必定是老实人;时间,抓起来是黄金,抓不起来是流水。 9、成功的道路上,肯定会有失败;对于失败,我们要正确地看待和对待,不怕失败者,则必成功;怕失败者,则一无是处,会更失败。 10、一句简单的问候,是不简单的牵挂;一声平常的祝福,是不平常的感动;条消息送去的是无声的支持与鼓励,愿你永远坚强应对未来,胜利属于你! 11、行为胜于言论,对人微笑就是向人表明:我喜欢你,你使我快乐,我喜欢见到你。最值得欣赏的风景,就是自己奋斗的足迹。 12、人生从来没有真正的绝境。无论遭受多少艰辛,无论经历多少苦难,只要一个人的心中还怀着一粒信念的种子,那么总有一天,他就能走出困境,让生命重新开花结果。 13、当机会呈现在眼前时,若能牢牢掌握,十之八九都可以获得成功,而能克服偶发事件,并且替自己寻找机会的人,更可以百分之百的获得成功。 14、相信自己,坚信自己的目标,去承受常人承受不了的磨难与挫折,不断去努力去奋斗,成功最终就会是你的! 15、相信你做得到,你一定会做到。不断告诉自己某一件事,即使不是真的,最后也会让自己相信。 16、当你感到悲哀痛苦时,最好是去学些什么东西。领悟会使你永远立于不败之地。 17、出发,永远是最有意义的事,去做就是了。当一个人真正觉悟的一刻,就是他放弃追寻外在世界的财富,开始追寻他内心世界的真正财富。 18、幻想一步成功者突遭失败,会觉得浪费了时间,付出了精力,却认为没有任何收获;在失败面前,懦弱者痛苦迷茫,彷徨畏缩;而强者却坚持不懈,紧追不舍。 19、进步和成长的过程总是有许多的困难与坎坷的。有时我们是由于志向不明,没有明确的目的而碌碌无为。但是还有另外一种情况,是由于我们自己的退缩,与自己“亲密”的妥协没有坚持到底的意志,才使得机会逝去,颗粒无收。 20、任何人都不可以随随便便的成功,它来自完全的自我约束和坚韧不拔的毅力。永远别放弃自己,哪怕所有人都放弃了你。
12.2 三角形全等的判定 第2课时 课件-人教版数学八年级上册

学习目标
1.探索并掌握用“边角边”的方法判定三角形全等,能运用“边角边” 证明简单的三角形全等问题,提高学生分析和解决问题的能力.
2.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论 的过程,逐步养成用数学语言表达与交流的习惯.
复习引入
1.通过上节课的学习我们知道两个三角形只有一个或 两个条件相等时,不能保证两个三角形全等. 2.给出三个条件时,有四种可能.
池塘可以直接到达点A和B.连接AC并延长到点D,使CD=CA.连接BC并延长到点E, 使CE=CB.连接DE,那么量出DE的长就是A,B的距离,为什么?
证明:分在析C∆AA:BCC构D和造∆边DE角C 边中,条件
1 2
CB C∆EABC≌∆DEC
∴∆ABC≌∆DEC (SAS) ∴AB=DE
AB = DE
画法:(1)画∠DB′E=∠B;
不一定全等.
(2)在射线B′D上截取B′A′=BA;
(3)以A′为圆心,以AC长为半径画弧,此时只要∠C≠90°,弧线一定和射
线B′E交于两点C′,F.
课堂练习
1.如图,两车从南北方向的路段AB的A端出发,分别向东、向西行进相同的距离,到 达C,D两地.此时C,D到B的距离相等吗?为什么?
【结论】两边和它们的夹角分别相等的两个三角形全等 (简写为“边角边”或“SAS”)
几何语言:
在∆ABC 和∆A′B′C′中,
AB = A′B′ ∠A = ∠A′ AC = A′C′
是两边的 “夹角”
∴∆ABC≌∆A′B′C′ (SAS).
C
A C′
B
A′
B′
例题分析
如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点C不经过
人教版数学八上 12.2三角形全等的判定(二)(SAS)同步上课课件(共20张PPT)

∴ △AOB ≌△ A′ O B′ (SAS). ∴ AB = A′ B′(全等三角形的对应边相等).
因此的A′B′长度就是这座大山A处与B处的距离.
五、课堂小结
本节课学习了---知识有: 方法有:
六、当堂检测
1.如图,将两根钢条AA′,BB′的中点O连在一起, 使AA′,BB′可以绕着点O自由转动,就做成了一 个测量工件,则AB的长等于内槽宽A′B′,那么 判定△AOB≌△A′OB′的理由是( A )
A.边角边
B.角边角
C.边边边
D.角角边
2.若AB=AC,则添加一个什么条件可得
△ABD≌ △ACD?
A
//
△ABD≌ △ACD
\
/
B
S
SA
S
AD=AD ∠BABD=C∠DCAD AB=AC
D C
3.如图,点B、F、C、E在一条直线上, AB∥DE且 FB=CE,AB=DE.求证:AC∥DF.
A
问题2 今天老师准备了上课的教具三角形,可是 不小心弄坏了,聪明的你能根据老师给出的剩下部分 的边和角的大小,重新制作一个形状、大小都一样的 三角形吗?(两边分别长13cm、20cm,两边的夹角为 60° )
尺规作图,探究边角边的判定方法
画法:
(1) 画∠DAE = 60° ;
(2)在射线AD上截取
A.1对
B.2对
C.3对Βιβλιοθήκη D.4对2.(武汉中考)如图,AC和BD相交于点O,OA=OC,OB=OD.求 证:DC∥AB.
(第1题)
(第2题)
1.下图中全等的三角形有( )
图1
图2
图3
图4
A.图1和图2
B.图2和图3
12.2三角形全等的判定2边角边 初中八年级上册数学教案教学设计课后反思 人教版

教师姓名朱文辉单位名称阿克苏市第四中学填写时间2020.08.22学科数学年级/册八年级上册教材版本人教版课题名称12.2三角形全等的判定(2)边角边难点名称探究“边角边”证明两个三角形全等的条件难点分析从知识角度分析为什么难1.六取三的正确取舍;2.两边一角的两种位置关系;3.刚学的知识还不能熟练地应用。
难点教学方法 1.探究法;2.练习巩固。
教学环节教学过程导入在上节课的讨论中,我们发现三角形中只给一个条件或两个条件时,都不能保证所画出的三角形一定全等.给出三个条件时,有四种可能,能说出是哪四种吗?(三内角、三条边、两边一内角、两内角一边.)这四种情况中我们已经研究了两种,三内角对应相等不能保证两三角形一定全等;三条边对应相等的两三角形全等.今天我们接着研究第三种情况:“两边一内角”知识讲解(难点突破)在上节课的讨论中,我们发现三角形中只给一个条件或两个条件时,都不能保证所画出的三角形一定全等.给出三个条件时,有四种可能,能说出是哪四种吗?(三内角、三条边、两边一内角、两内角一边.)这四种情况中我们已经研究了两种,三内角对应相等不能保证两三角形一定全等;三条边对应相等的两三角形全等.今天我们接着研究第三种情况:“两边一内角”课堂练习(难点巩固) 例2,如图,有—池塘,要测池塘两端A 、B 的距离,可先在平地上取一个可以直接到达A 和B 的点C ,连接AC 并延长到D ,使CD =CA ,连接BC 并延长到E ,使CE =CB .连接DE ,那么量出DE 的长就是A 、B 的距离,为什么?(总结:明确证明分别属于两个三角形的线段相等或者角相等的问题,常常通过证明这两个三角形全等来解决.)小练、已知:如图AB=AC,AD=AE,∠BAC=∠DAE 求证: △ABD≌△ACE 继续思考:如何解决以下问题?求证:1.BD=CE 2. ∠B= ∠C小结1.根据边角边公理判定两个三角形全等,要找出两边及夹角对应相等的三个条件.2.找使结论成立所需条件,要充分利用已知条件(包括给出图形中的隐含条件,如公共边、公共角等),并要善于运用学过的定义、公理、定理。
新人教版八年级数学上册《12.2三角形全等的判定(2)》优课件

形不一定全等。
B
CD
知识梳理: A
A
B
C
SSA不能
A
判定全等
B
C
DD
B D
通过本课时的学习,需要我们掌握: 1.根据边角边定理判定两个三角形全等,要找出两边 及夹角对应相等的三个条件. 2.找使结论成立所需条件,要充分利用已知条件 (包括给出图形中的隐含条件,如公共边、公共角等), 并要善于运用学过的定义、公理、定理.
把一长一短的两根细木棍的一端用螺钉铰合在一起,
使长木棍的另一端与射线BC的端点B重合,适当调整
好长木棍与射线BC所成的角后,固定住长木棍,把
短木棍摆起来.
如图,在△ABC 和△ABD 中.
A
AB =AB,AC = AD,∠B =∠B,
但△ABC 和△ABD 不全等.
有两边及其中一边的对
角分别相等的两个三角
解:在△AEC和△ADB中
C
_A_E__=__A_D_(已知)
D
∠A= ∠A( 公共角)
A
E
B
_A_C___=_A__B_(已知)
∴ △AEC≌△ADB( SAS )
6.根据题中条件,分别找出各题中的全等三角形.
A 40°
B
A
B
D
C
D
C (2)
F
(1)
40 °E
(2)△ADC≌△CBA 根据 “SAS”
全等 ④
D
5
① 及夹角对应相等的两个三角形全等
两边
B
C OB=OC
证明:在△ABO和△CDO中,
OA=OC ∠AOB=∠COD OB=OD, ∴ △ABO≌△CDO(SAS), ∴∠C=∠A. ∴AB∥CD.
新人教版八年级数学上学期《三角形全等的判定边角边》公开课课件

AD
∵ AE=DE(已知)
∠AEB=∠DEC(对顶角相等) B BE=CE(已知)
∴3. △如A图BE4,≌△在D△CEA.BE(和S.△AD.BSE.中),A AB=DB,请你添加一个适当的条件,
E 图3 C ED
使得△ABE≌△DBE,添加的条件是
___________________________.
45°
2. 画∠ MAB= 45°; 3. 在射线AM上截取
A
B AC=2.5cm;
4. 连结BC .
△ ABC即为所求.
把你画的三角形与其他同学画的三角形进行比较,或 将你画的三角形剪下,放在其他同学画的三角形上,看看 是否完全重合.
在△ABC和△A′B′C′中,已知AB=A′B′, ∠A=∠A′,AC=A′C′ .
B
图4
4. 如图5,有一池塘,要测池塘两端A、B的距离,
可先在平地上取一个可以直接到达A和B的点C,连结
AC并延长到D,使CD=CA.连结BC并延长到E,使
CE=CB.连结DE,那么DE的长就是A、B的距离.你
知道其中的道理吗?
A
B
已知:AD与BE相交于点C, CA=CD,
1
C
CB=CE .
2
求证:AB=DE .
三角形全等的判定
---边角边
温故知新
1. 如果两个三角形只有一组对应相等的 元素,那么它可以分为几种情况? 不一定全
一边、一角
等
2. 如果两个三角形只有两组对应相等的
元素,那么它可以分为几种情况? 不一定全
一边一角、两边、两角
等
3. 如果两个三角形有三组对应相等的元 素,那么它可以分为几种情况?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
讲授新课
一 三角形全等的判定(“边角边”定理)
问题:已知一个三角形的两条边和一个角,那么这两条边
与这一个角的位置上有几种可能性呢?
A
A
B
C
“两边及夹角”
B
C
“两边和其中一边的对角”
它们能判定两个三角 形全等吗?
探究活动1:SAS能否判定的两个三角形全等
尺规作图画出一个△A′B′C′,使A′B′=AB,A′C′=AC, ∠A′=∠A (即使两边和它们的夹角对应相等). 把画好的△A′B′C′ 剪下,放到△ABC上,它们全等吗?
C
A
B
C
A
B
作法:
(1)画∠DA'E=∠A;
(2)在射线A'E上截取
A'C'=AC ,在射线A'D上截取
A'B'=AB ;
(3)连接B'C '.
E C′
A′
D
B′
思考: ① △A′ B′ C′ 与 △ABC 全等吗? 如何验证?
②这两个三角形全等是满 足哪三个条件?
知识要点
“边角边”判定方法
文字语言:两边和它们的夹角分别相等的两个三角形全等
在△AMD与△BND中
AM=BN ∠A=∠B AD=BD
(已证) (已证) (已知)
∴△AMD≌△BND(SAS) ∴DM=DN.
课堂小结
内容
有两边及夹角对应相等的两个三角 形全等(简写成 “SAS”)
边 角 边 应 用 为证明线段和角相等提供了新的证法
注意
1.已知两边,必须找“夹角” 2. 已知一角和这角的一夹边,必须找 这角的另一夹边
A
(SAS)
边: AB=CB(已知),
B
角: ∠ABD= ∠CBD(已知),
边: BD=BD(公共边).
?
D C
证明: 在△ABD 和△ CBD中,
AB=CB(已知),
∠ABD= ∠CBD(已知),
BD=BD(公共边),
∴ △ ABD≌△CBD ( SAS).
变式1:
已知:如图,AB=CB,∠1= ∠2.
三边对应相等的两个三角形全等(可以简写为
“边边边”或“SSS”).
A
2.符号语言表达: 在△ABC和△ DEF中
AB=DE BC=EF CA=FD ∴ △ABC ≌△ DEF(SSS)
B
D
E
C F
除了SSS外,还有其他情况吗?
当两个三角形满足六个条件中的3个时,有四种情况:
三角
×
三边
√
两边一角
?
两角一边
已知:如图, AB=DB,CB=EB,∠1=∠2,求证:∠A=∠D.
证明:∵ ∠1=∠2(已知), ∴∠1+∠DBC= ∠2+ ∠DBC(等式的性质),
即∠ABC=∠DBE. 在△ABC和△DBE中,
AB=DB(已知), ∠ABC=∠DBE(已证), CB=EB(已知), ∴△ABC≌△DBE(SAS). ∴ ∠A=∠D(全等三角形几何语言:
在△ABC 和△ DEF中,
A F
B
AB = DE, ∠A =∠D, AC =AF ,
必须是两边 “夹角”
∴ △ABC ≌△ DEF(SAS).
D
E
典例精析
例1 :如果AB=CB ,∠ ABD= ∠ CBD,那么
△ ABD 和△ CBD 全等吗?
分析: △ ABD ≌△ CBD.
M
D
C
结论 全等.
A
B
有两边和其中一边的对角分别相等的两个三角形不一定
典例精析
例3 下列条件中,不能证明△ABC≌△DEF的是( C )
A.AB=DE,∠B=∠E,BC=EF B.AB=DE,∠A=∠D,AC=DF C.BC=EF,∠B=∠E,AC=DF D.BC=EF,∠C=∠F,AC=DF
解析:要判断能不能使△ABC≌△DEF,应看所给出的条件是不是两边和这两边的夹 角,只有选项C的条件不符合,故选C.
第十二章 全等三角形 12.2三角形全等的判定
第2课时 “边角边”
学习目标
1.探索并正确理解三角形全等的判定方法“SAS”.(重情境点引)入 2.会用“SAS”判定方法证明两个三角形全等及进行简单的应用.(重 点)
3.了解“SSA”不能作为两个三角形全等的条件.(难点)
1.回顾三角形全等的判定方法1
AE=AE (公共边),
能力提升
5.如图,已知CA=CB,AD=BD, M,N分别是CA,CB的中点, 求证:DM=DN. 证明: 连接CD,如图所示;
在△ABD与△CBD中 CA=CB (已知)
AD=BD (已知)
CD=CD (公共边) ∴△ACD≌△BCD(SSS) ∴∠A=∠B 又∵M,N分别是CA,CB的中点, ∴AM=BN
∴△ABD≌△ACD(SAS).
∴ BD=CD.
变式1
已知:如图,AB=AC, BD=CD,
求证: ∠ BAD= ∠ CAD.
证明:
在△ABD和△ACD中, AB=AC (已知), BD=CD (已知), AD=AD (公共边),
∴△ABD≌△ACD(SSS).
∴ ∠BAD=∠CAD,
变式2
已知:如图,AB=AC, BD=CD,E为AD上一点,
延长到点E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离,为
什么?
证明:在△ABC 和△DEC 中,
A
AC = DC(已知),
∠ACB =∠DCE (对顶角相等),
·C
CB=EC(已知) ,
∴△ABC ≌△DEC(SAS),∴AB =DE , E
(全等三角形的对应边相等).
B D
归纳证明线段相等或者角相等时,常常通过证明它们是全等三角形的对应边或 对应角来解决.
∠A=∠C
(已证),
AF=CE (已证),
∴△AFD≌△CEB(SAS).
D
F C
4.已知:如图,AB=AC,AD是△ABC的角平分线,
求证:BD=CD.
证明: ∵AD是△ABC的角平分线,
∴ ∠BAD=∠CAD,
在△ABD和△ACD中,
AB=AC (已知),
∠BAD=∠CAD
(已证),
AD=AD (已证),
方法总结:判断三角形全等时,注意两边与其中一边的对角相等的两个三角形 不一定全等.解题时要根据已知条件的位置来考虑,只具备SSA时是不能判定三 角形全等的.
当堂练习
1.在下列图中找出全等三角形进行连线.
30º
Ⅰ
ⅢⅢ
30º
2.如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则需要增加的条件是 ( D)
证明: ∵DB 平分∠ ADC, ∴∠1=∠2.
在△ABD与△CBD中,
B
AD=CD (已知),
∠1=∠2 (已证),
BD=BD (公共边),
∴△ABD≌△CBD(SAS),
∴∠A=∠C.
A
1 D
2
C
例2:如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个
可以直接到达A和B的点C,连接AC并延长到点D,使CD=CA,连接BC并
求证: BE=CE.
证明: 在△ABD和△ACD中,
AB=AC BD=CD AD=AD
(已知), (已知), (公共边),
∴△ABD≌△ACD(SSS). ∴ ∠BAD=∠CAD,
在△ABE和△ACE中,
∴△ABE≌△ACE(SAS).
AB=AC (已知), ∠BAD=∠CAD
(已证),
∴
BE=CE.
探究活动2:SSA能否判定两个三角形全等
想一想:
如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC.固定住
长木棍,转动短木棍,得到△ABD.这个实验说明了什么?
A
△ABC和△ABD满足
AB=AB ,AC=AD,
∠B=∠B,但△ABC与
△ABD不全等.
B
C
D
画一画: 画△ABC 和△DEF,使∠B =∠E =30°, AB =DE =5 cm ,AC =DF =3 cm .观察所得的两个三角形是否全等?
A.∠A=∠D C.∠A=∠C
B.∠E=∠C D.∠ABD=∠EBC
3.如图,点E、F在AC上,AD//BC,AD=CB,AE=CF.
求证:△AFD≌△CEB.
证明:
∵AD//BC, ∴ ∠A=∠C,
∵AE=CF, ∴AE+EF=CF+EF,
A E
即 AF=CE.
B
在△AFD和△CEB中,
AD=CB (已知),
求证:(1) AD=CD;
(2) DB 平分∠ ADC.
B
证明: 在△ABD与△CBD中,
AB=CB (已知),
∠1=∠2 (已知),
BD=BD (公共边),
∴△ABD≌△CBD(SAS),
∴AD=CD,∠3=∠4, ∴DB 平分∠ ADC.
1 2
A
3 D
4
C
变式2:
已知:AD=CD,DB平分∠ADC ,求证:∠A=∠C.
