图像的几何变换的两种实现(旋转、平移、放大、缩小)
图形的变换

图形的变换
图形的变换是指将一个图形经过一系列操作,变换为另外
一个图形的过程。
常见的图形变换包括平移、旋转、缩放
和翻转等。
1. 平移:平移是指将图形沿着一个方向移动一定的距离。
平移后的图形与原图形形状完全相同,只是位置发生了改变。
2. 旋转:旋转是指将图形绕着一个固定点旋转一定的角度。
旋转后的图形保持原来的形状,只是方向或位置发生了改变。
3. 缩放:缩放是指按照一定的比例改变图形的大小。
缩放
后的图形与原图形形状相似,只是大小发生了改变。
4. 翻转:翻转是指将图形沿着某个轴对称翻转。
翻转后的
图形与原图形形状完全相同,只是左右或上下发生了改变。
图形变换在几何学、计算机图形学和计算机视觉等领域中有广泛的应用。
通过对图形进行变换,可以实现图形的组合、变形和动画效果等。
抛物线的几何变换

抛物线的几何变换抛物线是一种常见的曲线形状,它在几何学中有着重要的应用。
通过对抛物线进行几何变换,我们可以得到一系列有趣的结果和应用。
本文将就抛物线的几何变换进行详细探讨。
我们来讨论抛物线的平移变换。
平移是指将图形沿着平行于某个方向的直线移动一定的距离。
对于抛物线来说,平移变换可以使得抛物线在平面上的位置发生改变,但其形状和大小保持不变。
通过平移变换,我们可以将抛物线的顶点从原点移动到任意位置,从而得到不同位置的抛物线。
接下来,我们来探讨抛物线的缩放变换。
缩放是指改变图形的大小,使得图形的各个部分相对于原图形的位置保持不变。
对于抛物线来说,缩放变换可以使得抛物线的形状变得更加扁平或者更加瘦长。
通过缩放变换,我们可以调整抛物线的曲率和尺寸,从而满足不同的需求。
除了平移和缩放变换,我们还可以对抛物线进行旋转变换。
旋转是指将图形绕着某个点或者某个轴进行旋转,使得图形的各个部分相对于原图形的位置保持不变。
对于抛物线来说,旋转变换可以使得抛物线沿着顶点或者其他点进行旋转,从而改变抛物线的朝向和方向。
通过旋转变换,我们可以得到不同方向的抛物线,具有更多的应用场景。
我们还可以对抛物线进行镜像变换。
镜像是指通过某个直线将图形的各个部分对称翻转,使得图形的对称轴上的点保持不变。
对于抛物线来说,镜像变换可以使得抛物线关于某个直线对称,从而得到与原抛物线关于对称轴对称的抛物线。
通过镜像变换,我们可以得到一对关于对称轴对称的抛物线,具有更多的几何特性。
我们来谈论一下抛物线的平移、缩放、旋转和镜像的组合变换。
通过将这些变换结合起来,我们可以得到更加复杂的抛物线图形。
例如,我们可以先进行平移变换,将抛物线移动到指定位置,然后再进行缩放变换,调整抛物线的大小,最后进行旋转变换,改变抛物线的方向。
这样,我们可以得到一个全新的抛物线图形,具有丰富的几何特征。
抛物线的几何变换是一种有趣且实用的数学工具。
通过对抛物线进行平移、缩放、旋转和镜像变换,我们可以得到各种不同形状和特性的抛物线图形。
图形的几何变换

图形的几何变换图形的几何变换是指对于一个图形,在平面上或空间中进行比例、旋转、平移、对称等操作后,得到的新图形。
这种操作可以改变图形的大小、方向、位置等特征,广泛运用于数学、物理、美术、计算机图形等领域。
以下从不同变换类型的角度分析图形的几何变换。
一、比例变换比例变换是指将一个图形沿着某个中心点或轴线进行等比例伸缩的变换。
其结果通常是一个形状相似但大小不同的新图形。
比例变换可以分为放大和缩小两种情况,当比例因子大于1时,为放大;比例因子小于1时,为缩小。
比例变换常见的应用包括模型制作、图形的等比例缩放等。
二、旋转变换旋转变换是指将一个图形沿着某个轴心或轴线进行旋转的变换。
旋转变换可分为顺时针旋转和逆时针旋转两种情况,其结果是一个相似但方向不同的新图形。
旋转变换的角度通常用弧度制表示,旋转角度为正时为逆时针旋转,为负时为顺时针旋转,常见的应用包括风车的运动、建筑设计的转角变换等。
三、平移变换平移变换又叫做移动变换,是指将一个图形沿着某个方向进行平移的变换。
平移变换可以将图形整体沿着平移向量的方向进行移动,其结果是一个与原图形相同但位置不同的新图形。
平移变换常见的应用包括机器人的运动、物体的位移等。
平移变换也可以看作是比例变换的特殊情况,比例因子为1,即不改变图形的大小。
四、对称变换对称变换是指将一个图形沿着某个轴线进行翻折的操作。
对称变换可以分为对称、反对称和正交对称三种类型。
对称变换的结果通常是一个与原图形相等但位置镜像对称的新图形。
对称变换在分形几何、美术设计等领域都有着广泛的应用。
五、仿射变换仿射变换是指图形在平面上或空间中进行非等比例伸缩、旋转、平移和投影等操作时的变换。
仿射变换的结果通常是一个与原图形相似但有略微变形的新图形。
仿射变换包括平移变换、旋转变换、比例变换和剪切变换等。
其应用领域包括医学图像处理、计算机图形学等。
总结图形的几何变换在现代科技和艺术中有着广泛的应用。
比例变换常用于造型、模型制作和图形的等比例缩放;旋转变换常用于旋转花纹、风车运动、建筑转角的变化等;平移变换常用于运动控制、物体的位移等;对称变换常用于几何分形、美术设计等领域;仿射变换则是结合了以上变换操作的高级变换,其应用范围更加广泛。
mfc空间几何变换之图像平移、镜像、旋转、缩放详解

MFC空间几何变换之图像平移、镜像、旋转、缩放详解一. 图像平移前一篇文章讲述了图像点运算(基于像素的图像变换),这篇文章讲述的是图像几何变换:在不改变图像容的情况下对图像像素进行空间几何变换的处理方式。
点运算对单幅图像做处理,不改变像素的空间位置;代数运算对多幅图像做处理,也不改变像素的空间位置;几何运算对单幅图像做处理,改变像素的空间位置,几何运算包括两个独立的算法:空间变换算法和灰度级插值算法。
空间变换操作包括简单空间变换、多项式卷绕和几何校正、控制栅格插值和图像卷绕,这里主要讲述简单的空间变换,如图像平移、镜像、缩放和旋转。
主要是通过线性代数中的齐次坐标变换。
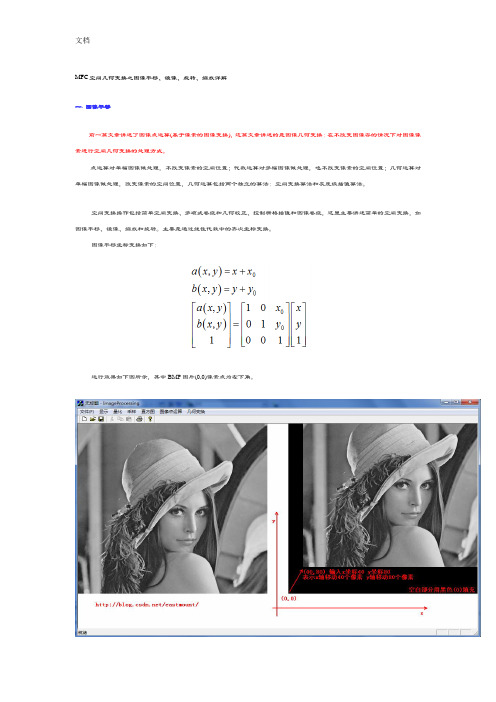
图像平移坐标变换如下:运行效果如下图所示,其中BMP图片(0,0)像素点为左下角。
其代码核心算法:1.在对话框中输入平移坐标(x,y) m_xPY=x,m_yPY=y2.定义Place=dlg.m_yPY*m_nWidth*3 表示当前m_yPY行需要填充为黑色3.新建一个像素矩阵ImageSize=new unsigned char[m_nImage]4.循环整个像素矩阵处理for(int i=0 ; i<m_nImage ; i++ ){if(i<Place) {ImageSize[i]=black;continue;}//黑色填充底部从小往上绘图else if(i>=Place && countWidth<dlg.m_xPY*3) {//黑色填充左部分ImageSize[i]=black;countWidth++; continue;}else if(i>=Place && countWidth>=dlg.m_xPY*3) {//图像像素平移区域ImageSize[i]=m_pImage[m_pImagePlace];//原(0,0)像素赋值过去m_pImagePlace++;countWidth++;if(countWidth==m_nWidth*3) {//一行填满m_pImagePlace走到(0,1)number++;m_pImagePlace=number*m_nWidth*3;}}}5.写文件绘图fwrite(ImageSize,m_nImage,1,fpw)第一步:在ResourceView资源视图中,添加Menu子菜单如下:(注意ID号)第二步:设置平移对话框。
几何变换的认识与运算

几何变换的认识与运算几何变换是指在二维或三维的空间中,通过对图形进行平移、旋转、缩放和翻转等操作,改变图形的位置、方向、形状和大小。
它是几何学中的重要概念,被广泛应用于计算机图形学、建筑设计、工程制图等领域。
本文将介绍几种常见的几何变换,并探讨其运算规则。
一、平移变换平移变换是指将图形沿着平行于某个方向的矢量移动一段距离,使图形保持原有的形状和大小不变。
平移变换可以用一个向量来表示,该向量的大小和方向决定了平移的距离和方向。
例如,对于一个平面上的图形,如一个矩形,我们可以将它沿着x轴正方向平移10个单位,沿着y轴正方向平移5个单位。
这个平移变换可以表示为(10, 5),其中10表示x方向的平移距离,5表示y方向的平移距离。
二、旋转变换旋转变换是指将图形围绕一个点或者一个轴进行旋转,使图形相对于旋转中心点产生旋转。
旋转变换可以用一个角度来表示,该角度决定了旋转的方向和幅度。
例如,对于一个平面上的图形,如一个正方形,我们可以将它围绕原点逆时针旋转45度。
这个旋转变换可以表示为45°,其中45°表示逆时针旋转的角度。
三、缩放变换缩放变换是指改变图形的大小,使图形的各个部分相对于原始大小进行伸缩。
缩放变换可以用一个比例因子来表示,该比例因子决定了缩放的程度。
例如,对于一个平面上的图形,如一个圆形,我们可以将它在x方向上缩小为原来的一半,在y方向上缩放为原来的两倍。
这个缩放变换可以表示为(0.5, 2),其中0.5表示x方向上的缩放比例,2表示y方向上的缩放比例。
四、翻转变换翻转变换是指将图形沿着一条轴进行对称映射,使图形相对于轴发生左右或上下的镜像翻转。
翻转变换可以用一个方向来表示,该方向决定了翻转的轴线。
例如,对于一个平面上的图形,如一个三角形,我们可以将它沿着x轴进行上下翻转。
这个翻转变换可以表示为x轴,其中x轴表示沿着x轴进行翻转。
几何变换的运算规则可以通过矩阵相乘的方式来表示。
MFC空间几何变换之图像平移、镜像、旋转、缩放详解
MFC空间几何变换之图像平移、镜像、旋转、缩放详解一. 图像平移前一篇文章讲述了图像点运算(基于像素的图像变换),这篇文章讲述的是图像几何变换:在不改变图像容的情况下对图像像素进行空间几何变换的处理方式。
点运算对单幅图像做处理,不改变像素的空间位置;代数运算对多幅图像做处理,也不改变像素的空间位置;几何运算对单幅图像做处理,改变像素的空间位置,几何运算包括两个独立的算法:空间变换算法和灰度级插值算法。
空间变换操作包括简单空间变换、多项式卷绕和几何校正、控制栅格插值和图像卷绕,这里主要讲述简单的空间变换,如图像平移、镜像、缩放和旋转。
主要是通过线性代数中的齐次坐标变换。
图像平移坐标变换如下:运行效果如下图所示,其中BMP图片(0,0)像素点为左下角。
其代码核心算法:1.在对话框中输入平移坐标(x,y) m_xPY=x,m_yPY=y2.定义Place=dlg.m_yPY*m_nWidth*3 表示当前m_yPY行需要填充为黑色3.新建一个像素矩阵 ImageSize=new unsigned char[m_nImage]4.循环整个像素矩阵处理for(int i=0 ; i<m_nImage ; i++ ){if(i<Place) {ImageSize[i]=black; continue;} //黑色填充底部从小往上绘图else if(i>=Place && countWidth<dlg.m_xPY*3) {//黑色填充左部分ImageSize[i]=black; countWidth++; continue;}else if(i>=Place && countWidth>=dlg.m_xPY*3) {//图像像素平移区域ImageSize[i]=m_pImage[m_pImagePlace];//原(0,0)像素赋值过去m_pImagePlace++; countWidth++;if(countWidth==m_nWidth*3) { //一行填满 m_pImagePlace走到(0,1)number++; m_pImagePlace=number*m_nWidth*3;}}}5.写文件绘图fwrite(ImageSize,m_nImage,1,fpw)第一步:在ResourceView资源视图中,添加Menu子菜单如下:(注意ID号)第二步:设置平移对话框。
编程实现一幅图像的平移、镜像、旋转、缩小和放大。
编程实现⼀幅图像的平移、镜像、旋转、缩⼩和放⼤。
课程设计任务书学⽣姓名: zhh 专业班级:通信1002班指导教师:徐⽂君⼯作单位:信息⼯程学院题⽬: 通信⼯程应⽤技术综合训练与实习初始条件:1.数字图像处理课程相关知识。
2.Matlab软件的软件编程应⽤与仿真。
要求完成的主要任务:任务:编程实现⼀幅图像的平移、镜像、旋转、缩⼩和放⼤。
要求:1.给出所⽤算法的理论依据和必要的推导过程。
2.给出原始图像和处理后的图像。
时间安排:序号设计内容所⽤时间1根据设计任务确定实验⽅案2天2根据实验条件进⾏电路的测试,并对结果进⾏分析7天3撰写课程设计报告1天合计2周指导教师签名: 年⽉⽇系主任签名: 年⽉⽇⽬录摘要..................................................................................I Abstract ............................................................................. II 1 图像的⼏何变换.. (1)1.1图像⼏何变换内容 (1)1.2 Matlab仿真使⽤的主要函数 (1)2图像的平移变换 (3)2.1图像平移变换原理 (3)2.2图像平移变换的matlab实现 (3)3图像的镜像变换 (4)3.1 图像镜像变换原理 (5)3.2 图像镜像变换的matlab实现 (6)4图像的旋转变换 (6)4.1图像旋转变换原理 (7)4.2 图像旋转变换的matlab实现 (8)5图像的⽐例变换 ..................................................... 错误!未定义书签。
5.1 图像⽐例变换原理 (10)5.2 图像⽐例变换的matlab实现 (10)6 ⼼得体会 (14)参考⽂献 (15)附录 (16)摘要图像是对三维实际景物的平⾯投影,图形图像处理主要是通过计算机对图像进⾏处理,从⽽达到预期的效果的技术。
如何进行平移旋转翻转等几何变换
如何进行平移旋转翻转等几何变换如何进行平移、旋转、翻转等几何变换几何变换是几何学中重要的概念,广泛应用于计算机图形学、游戏开发、计算机辅助设计和工程制图等领域。
通过几何变换,我们可以改变图形的位置、方向和形状,从而达到我们想要的效果。
本文将介绍如何进行平移、旋转和翻转等几何变换,并提供示例说明。
一、平移变换平移变换是指在平面内将图形沿着某个方向移动一定的距离。
平移变换不改变图形的大小和形状,只改变其位置。
对于平面上的一个点(x, y),平移变换的公式为:新的坐标点 = (x + dx, y + dy)其中,dx和dy分别代表在x轴和y轴上的平移距离。
例如,如果要将一个点(2, 3)沿x轴正方向平移3个单位,沿y轴正方向平移2个单位,则变换后的新坐标为(5, 5)。
平移变换也可以用矩阵进行表示。
平移变换矩阵如下所示:[1 0 dx][0 1 dy][0 0 1]二、旋转变换旋转变换是指将图形绕某个点旋转一定的角度。
通过旋转变换,我们可以改变图形的方向和位置。
对于平面上的一个点(x, y),绕原点旋转θ度后的新坐标计算公式为:新的坐标点= (x * cosθ - y * sinθ, x * sinθ + y * cosθ)其中,θ为旋转角度。
例如,如果要将点(1, 1)绕原点逆时针旋转45度,则变换后的新坐标为(0, √2)。
旋转变换也可以用矩阵进行表示。
旋转变换矩阵如下所示:[cosθ -sinθ 0][sinθ cosθ 0][0 0 1]三、翻转变换翻转变换是指将图形关于某个轴或某个点进行对称翻转。
翻转变换有水平翻转和垂直翻转两种情况。
1. 水平翻转:对于平面上的一个点(x, y),关于x轴进行水平翻转后的新坐标计算公式为:新的坐标点 = (x, -y)例如,将点(2, 3)关于x轴进行水平翻转,则变换后的新坐标为(2, -3)。
2. 垂直翻转:对于平面上的一个点(x, y),关于y轴进行垂直翻转后的新坐标计算公式为:新的坐标点 = (-x, y)例如,将点(2, 3)关于y轴进行垂直翻转,则变换后的新坐标为(-2, 3)。
数字图像的几何运算
数字图像的几何运算
数字图像的几何运算是指对图像进行几何变换的操作。
几何变换包括平移、旋转、缩放、翻转等操作,通过这些操作可以改变图像的位置、角度、大小和方向。
数字图像的几何运算在图像处理、计算机视觉、图形学等领域有着广泛的应用。
平移是将图像沿着水平方向和垂直方向进行移动的操作。
平移变换可以通过将图像的像素点进行位移来实现。
对于二维图像而言,平移变换可以表示为:
T(x, y) = (x + dx, y + dy)
(x, y)为原始图像中的像素点坐标,(dx, dy)为平移向量。
对于彩色图像,需要对每个像素点的RGB分量进行平移。
垂直翻转变换可以表示为:
除了以上几种基本的几何运算,还有其他一些常用的几何运算,包括仿射变换、透视变换等。
这些运算可以通过矩阵运算来实现。
仿射变换可以通过将图像的像素点坐标进行线性变换来实现。
透视变换可以通过将图像的像素点坐标进行非线性变换来实现。
数字图像的几何运算在数字图像处理中有着广泛的应用。
在计算机视觉中,通过对图像进行几何运算可以实现目标检测、目标跟踪等功能。
在图形学中,通过对图像进行几何运算可以实现图形变换、图形合成等功能。
在图像处理中,通过对图像进行几何运算可以实现图像校正、图像增强等功能。
基本的几何变换
基本的几何变换几何变换是数学中一个重要的概念,指的是通过平移、旋转、缩放等操作来改变几何图形的形状、大小或位置。
在计算机图形学和计算机视觉领域,几何变换也扮演着至关重要的角色。
本文将介绍几个基本的几何变换,包括平移、旋转、缩放和镜像。
1. 平移在几何变换中,平移是指通过将图形沿着指定的方向移动一定的距离来改变图形的位置。
平移操作可以用以下公式表示:x' = x + dxy' = y + dy其中(x, y)是原始图形上的坐标,(x', y')是平移后的坐标,dx和dy 分别是在x和y方向上的平移量。
2. 旋转旋转是指通过围绕一个指定的点或轴旋转图形来改变图形的方向或角度。
旋转操作可以用以下公式表示:x' = x * cosθ - y * sinθy' = x * sinθ + y * cosθ其中(x, y)是原始图形上的坐标,(x', y')是旋转后的坐标,θ表示旋转的角度。
3. 缩放缩放是指通过改变图形的尺寸来改变图形的大小。
缩放操作可以用以下公式表示:x' = x * scaleXy' = y * scaleY其中(x, y)是原始图形上的坐标,(x', y')是缩放后的坐标,scaleX和scaleY分别表示在x和y方向上的缩放比例。
4. 镜像镜像是指通过将图形沿着一个轴对称折叠来改变图形的位置或方向。
镜像操作可以用以下公式表示:x' = -xy' = -y其中(x, y)是原始图形上的坐标,(x', y')是镜像后的坐标。
这些基本的几何变换可以单独应用于图形,也可以组合在一起以实现更复杂的效果。
通过灵活组合这些变换操作,我们可以实现各种各样的几何变换,用于图像处理、游戏开发、计算机辅助设计等领域。
总结几何变换是一种重要的数学概念,可以通过平移、旋转、缩放和镜像等操作来改变几何图形的形状、大小和位置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
面向对象程序设计学号:************ 学生所在学院:信息工程学院****************教师所在学院:信息工程学院2013级实现图像的几何变换电子信息工程信息工程学院摘要:几何变换是最常见的图像处理手段,通过对变形的图像进行几何校正,可以得出准确的图像。
常用的几何变换功能包括图像的平移、图像的镜像变换、图像的转置、图像的缩放、图像的旋转等等。
目前数字图像处理的应用越来越广泛,已经渗透到工业、航空航天、军事等各个领域,在国民经济中发挥越来越大的作用。
作为数字图像处理的一个重要部分,本文接受的工作是如何Visual C++编程工具设计一个完整的应用程序,实现经典的图像几何变换功能。
程序大概分为两大部分:读写BMP图像,和数字图像的几何变换。
即首先用Visual C++创建一个单文档应用程序框架,在实现任意BMP图像的读写,打印,以及剪贴板操作的基础上,完成经典的图像几何变换功能。
图像几何变换的Visual C++编程实现,为校内课题的实现提供了一个实例。
关键字:图像处理;几何变换(图像的平移、缩放、转置、旋转和镜像变换);BMP图像;Visual C++一、引言图像几何变换是指用数学建模的方法来描述图像位置、大小、形状等变化的方法。
在实际场景拍摄到的一幅图像,如果画面过大或过小,都需要进行缩小或放大。
如果拍摄时景物与摄像头不成相互平行关系的时候,会发生一些几何畸变,例如会把一个正方形拍摄成一个梯形等。
这就需要进行一定的畸变校正。
在进行目标物的匹配时,需要对图像进行旋转、平移等处理。
在进行三维景物显示时,需要进行三维到二维平面的投影建模。
因此,图像几何变换是图像处理及分析的基础。
图像几何变换是计算机图像处理领域中的一个重要组成部分,也是值得深讨的一个重要课题。
在图像几何变换中主要包括图像的放缩、图像的旋转、图像的移动、图像的镜像、图像的块操作等内容,几何变换不改变图像的像素值,只改变像素所在的几何位置。
从广义上说,图像是自然界景物的客观反映,是人类认识世界和人类本身的重要源泉。
图像对我们并不陌生。
我们生活在一个信息时代,科学研究和统计表明,人类从外界获得的信息约有75%来自视觉系统,也就是从图像中获得的。
所以对数字图像的处理便显得尤为重要了。
本文主要深讨了图像的几何变换(主要包括图像的平移、转置、缩放、旋转、镜像等)理论,并在此基础上用Visual C++实现的过程。
1.3.2研究方法方法一:利用Windows 本身就提供了一个API函数SetWorldTransForm来实现图片旋转、位移及其他变形,这个函数是对一个设备上下文DC进行操作,通过坐标转换来实现各种功能的。
方法二:通过图像进行平移、旋转、转置、镜像、缩放后重新计算各点新像素完成几何变换。
自定义一个图像处理的Cdibapi类,把一般处理图像时要用到的函数实现封装在这个类中,该类用于实现DIB对象的绘制,DIB对象调色板的创建,DIB 对象的读取与存储,图像线性变换,图像灰度拉伸等。
然后把在视类中实现图像平移,图像镜像,图像转置,图像缩放及图像旋转的函数调用和实现。
二、正文2.1灰度图灰度图(Grayscale)是指只含亮度信息,不含色彩信息的图像。
因此,要表示灰度图,就需要把亮度值进行量化。
通常划分为0到255共256个级别,0最暗(全黑),255最亮(全白)。
BMP格式的文件中并没有灰度图这个概念,但是可以很容易的用BMP文件来表示灰度图。
方法是用256色的调色板,只不过这个调色板有点特殊,每一项的RGB值都是相同的。
也就是说RGB值从(0,0,0),(1,1,1)一直到(255,255,255)。
(0,0,0)是全黑色,(255,255,255)是全白色,中间的是灰色。
2.2调色板调色板结构LOGPALETTE,该结构定义如下:typedef struct tagLOGPALETTE{WORD palVersion; //调色板的板本号,应该指定该值为0x300;WORD palNumEntries;//调色板中的表项数,对于灰度图像该值为256;PALETEENTRY palPalEntry[1];//调色板中的颜色表项,由于该表项的数目不一定,所以这里数组长度定义为1,灰度图像对应的该数组的长度为256}LOGPALETTE;颜色表项结构PALETTEENTRY定义了调色板中的每一个颜色表项的颜色和使用方式,定义如下:typedef struct tagPALETTEENTRY{BYTE peRed; //R分量值;BYTE peGreen; //G分量值;BYTE peBlue; //B分量值;BYTE peFlags; // 该颜色被使用的方式,一般情况下设为"0";}PALETTEENTRY;Windows系统使用调色板管理器来管理与调色板有关的操作,通常活动窗口的调色板即是当前系统调色板,所有的非活动窗口都必须按照此系统调色板来显示自己的颜色,此时调色板管理器将自动的用系统调色板中的最近似颜色来映射相应的显示颜色。
如果窗口或应用程序按自己的调色板显示颜色,就必须将自己的调色板载入到系统调色板中,这种操作叫作实现调色板,实现调色板包括两个步骤:1. 首先将调色板选择到设备上下文中,可以通过CDC::SelectPalette() 选入设备上下文2. 然后在设备上下文中实现调色板,可以通过 CDC::RealizePalette()实现设备调色板。
1.2.4BMP文件中DIB的结构DIB是标准的Windows位图格式,BMP文件中包含了一个DIB。
一个BMP文件大体上分成如下4个部分:位图文件头(只用于BMP文件)ArrayBITMAPINFOHEADER位图信息头Palette调色板DIB图像数据2.3图像的几何变换基础知识图像的几何变换,通常包括图像的平移、图像的镜像变换、图像的转置、图像的缩放和图像的旋转等。
图2.1 程序基本框架图2.3.1图像的平移图像的平移是几何变换中最简单的变换之一。
图像平移就是将图像中所有的点都按照指定的平移量水平、垂直移动。
设(x0,y0)坐标将变为(x1,y1)。
显然(x0,y0)和(x1,y1)的关系如下:{x1=x0+tx y1=y0+ty用矩阵表示如下:[x1y11]=[1 0 tx0 1 ty0 0 1][x0y01]对该矩阵求逆,可以得到逆变换:[x0y01]=[1 0 −tx0 1 −ty0 0 1][x1y11]即{x0=x1−txy0=y1−ty这样,平移后的图像上的每一点都可以在原图像中找到对应的点。
例如,对于新图中的(0,0)像素,代入上面的方程组,可以求出对应原图中的像素(-tx,-ty)。
如果tx或ty大于0,则(-tx,-ty)不在原图中。
对于不在原图中的点,可以直接将它的像素值统一设置为0或则255(对于灰度图就是黑色或白色)。
同样,若有点不在原图中,也就说明原图中有点被移出显示区域。
如果不想丢失被移出的部分图像,可以将新生成的图像宽度扩大|tx|,高度扩大|ty|。
2.3.2图像的镜像图像的镜像变换分为两种:一种是水平镜像,另外一种是垂直镜像。
图像的水平镜像操作是将图像的左半部分和右半部分以图像垂直中轴线为中心镜像进行对换;图像的垂直镜像操作是将图像上半部分和下半部分以图像水平中轴线为中心镜像进行对换。
设图像高度为lHeight,宽度为lWidth,原图中(x0,y0)经过水平镜像后坐标将变为(lWidth-x0,y0),其矩阵表达式为:[x1y11]=[−1 0 lWidth0 1 ty0 0 1][x0y01]逆运算表达式为:[x0y01]=[−1 0 lWidth0 1 00 0 1][x1y11]即同样,(x0,y0)经过垂直镜像后坐标将变为(x0,lHeight-y0),其矩阵表达式为:[x1y11]=[1 0 00 −1 lHeight0 0 1][x0y01]逆运算矩阵表达式为:[x0y01]=[1 0 00 −1 lHeight0 0 1][x1y11]即{x0=x1y0=lHeight−y12.3.3图像的转置图像的转置操作是将图像像素的x坐标和y坐标互换。
该操作将改变图像的大小,图像的高度和宽度将互换。
转置表达式:[x1y11]=[1 0 tx0 1 ty0 0 1][x0y01]它的逆矩阵表达式:[x0y01]=[1 0 tx0 1 ty0 0 1][x1y11]即{x0=x1y0=y12.3.4图像的缩放上面的几种图像几何变换中都是1:1的变换,而图像的缩放操作将会改变图像的大小,产生的图像中的像素可能在原图中找不到相应的像素点,这样就必须进行近似处理。
一般的方法是直接赋值为和它最相近的像素值,也可以通过一些插值算法来计算。
下面的代码直接采用了前一种做法。
假设图像x轴方向缩放比率为fx,y轴方向缩放比率为fy,那么原图中点(x0,y0)对应与新图中的点(x1,y1)的转换矩阵为:[x1y11]=[fx 0 00 fy 00 0 1][x0y01]其逆运算如下:[x0y01]=[1/fx 0 00 1/fy 00 0 1][x1y11]即{x0=x1/fxy0=y1/fy例如,当fx=fy=0.5时,图像被缩放到一半大小,此时缩小后图像中的(0,0)像素对应于原图中的(0,0)像素;(0,1)像素对应于原图中的(0,2)像素;(1,0)像素对应于原图中的(2,0)像素,以此类推。
在原图基础上,每行隔一个像素取一点,每隔一行进行操作。
其实是将原图每行中的像素重复取值一遍,然后每行重复一次。
2.3.5图像的旋转一般图像的旋转是以图像的中心为原点,旋转一定的角度。
旋转后,图像的大小一般会改变。
和图像平移一样,既可以把转出显示区域的图像截去,也可以扩大图像范围以显示所有的图像。
可以推导一下旋转运算的变换公式。
如下图所示,点(x0,y0)经过旋转θ度后坐标变成(x1,y1)。
在旋转前:{x0=γcos(θ) y0=γsin(θ)转置后:{x1=γcos(α−θ)=γcos (α)cos (θ)+γsin (α)sin (θ)=x0cos (θ)+y0sin (θ)y1=γsin(α−θ)=γsin(α)cos(θ)−γcos(α)sin(θ)=−x0sin(θ)+y0cos (θ)写成矩阵表达式为:[x1y11]=[cos(θ) sin (θ) 0−sin(θ)cos (θ) 00 0 1][x0y01]其逆运算如下:[x0y01]=[cos(θ) −sin (θ) 0sin(θ)cos (θ) 00 0 1][x1y11]有了上面的转换公式,就可以非常方便的编写出实现图像旋转的函数。
