3第二章 化工过程系统的稳态模拟与分析
化工系统工程__化工过程系统稳态模拟与分析(可编辑)

化工系统工程__化工过程系统稳态模拟与分析2 化工过程系统稳态模拟与分析概述通过对化工工艺流程系统进行稳态模拟与分析也就是对过程系统建立模型并对模型进行求解可以解决下述三方面的问题①过程系统的分析与模拟②过程系统设计③过程系统参数优化①过程系统的分析模拟对某个给定的过程系统模型进行模拟求解可得出该系统的全部状态变量从而可以对该过程系统进行工况分析如图21所示②过程系统设计当对某个或某些系统变量提出设计规定要求时通过调整某些决策变量使模拟结果满足设计规定要求如图22所示③过程系统参数优化过程系统模型与最优化模型联解得到一组使工况目标函数最佳的决策变量优化变量从而实施最佳工况如图所示 2 化工过程系统稳态模拟与分析相关的基本概念 1 系统为了某种目标由共同的物料流或信息流联系在一起的单元组合而形成的整体称为系统 2 子系统组成系统的系统下一层次的事物简单系统子系统就是某个单元复杂系统它的子系统又可能包含有子系统基本概念 3 系统的特性由两方面构成 1系统内各个单元的特性复杂系统则是各子系统的特性 2系统流程的结构特性树结构和再循环结构的概念 4 过程拓扑将过程流程图转换为信息流程图再把信息流程图转变为过程矩阵的过程称为过程拓扑过程流程→信息流程用有向线段表示信息流用方框表示设备或节点信息流程→过程矩阵将信息流程数字化使计算机可以识别根据信息流图可以得出过程矩阵 2.1 过程系统模拟的基本方法过程系统模拟计算量大且复杂手工计算难以完成计算机和计算技术的发展为过程系统的整体研究提供了技术手段各种类型的过程系统模拟软件不断出现但就其模拟计算求解方法而言可以归纳为三类序贯模块法 Sequentia1 Modular Method 面向方程法 Equation Oriented Method 联立方程法联立模块法 Stmultaneously Modular Method 2 11过程系统模拟的序贯模块法序贯模块法按照由各种单元模块组成的过程系统的结构序贯的对各单元模块进行计算从而完成该过程系统的模拟计算的方法序贯模块法对过程系统的模拟以单元模块的模拟计算为基础依据单元模块入口的物流信息以及足够的定义单元特性的信息计算出单元出口物流的信息序贯模块法的优点与实际过程的直观联系强模拟系统软件的建立维护和扩充都很方便易于通用化计算出错时易于诊断出错位置序贯模块法的主要缺点计算效率较低尤其是解决设计和优化问题时计算效率更低序贯模块法计算效率低的原因只能根据模块的输入物流信息计算输出物流信息在进行系统模拟的过程中对有再循环物流单元模块的计算需要考虑断裂物流收敛计算使问题复杂 2 12 过程系统模拟的面向方程法面向方程法将描述整个过程系统的数学方程式联立求解从而得出模拟计算结果的方法面向方程法又称联立方程法面向方程法的优点可以根据问题的要求灵活地确定输入输出变量而不受实际物流和流程结构的影响模型中所有的方程可同时计算和同步收敛面向方程法的问题形成通用软件比较困难不能利用现有大量丰富的单元模块缺乏与实际流程的直观联系计算失败之后难于诊断错误所在对初值的要求比较苛刻计算技术难度较大等 2 13 过程系统模拟的联立模块法联立模块法将过程系统的简化模型方程与单元模块严格模型交替求解又被称作双层法 2.2 过程系统模拟的序贯模块法 2.2.1序贯模块法的基本原理单元模块依据相应过程单元的数学模型和求解算法编制而成的子程序如图28 a 中的闪蒸单元可依据闪蒸单元模型和算法编制成闪蒸单元模块单元模块的单向性结定单元模块的输入物流变量及参数可计算出相应的输出物流变量但不能由检出变量计算输入变量也不能由输入输出变量计算模块参数序贯模块法的基本思想从系统入口物流开始经过对该物流变量进入的单元模块的计算得到输出物流变量这个输出物流变量就是下一个相邻单元的输入物流变量依次逐个的计算过程系统中的各个单元最终计算出系统的输出物流计算得出过程系统中所有的物流变量值即状态变量值 2.2.2 再循环物流的断裂当涉及的系统为无再循环流的树形结构时序贯模块法的模拟计算顺序可以按过程单元的排列顺序一一顺利完成用序贯模块法处理具有再循环物流系统的模拟计算时需要用到系统分解断裂 Tearing 和收敛 Convergence 等多项技术 Step1 假定断裂物流S4的变量值然后依次计算单元模块ABC得到物流S4的变量值 Step2利用收敛单元比较S4与S4的相应变量值若不等则改变S4为新的变量值重复Step1过程直到S4与S4两个变量值相等为止问题收敛单元设置在哪个物流处既如何选择断裂物流本问题中不仅可以是物流S4处也可以设置在物流S2或S3处对于复杂系统收敛单元设置的位置不同其效果也将不同究竟设置在何处为好这要通过断裂技术去解决如何得到新的S4变量值如何保证计算收敛如何加快收敛取决于收敛算法还与断裂物流变量的特性有关 2.2.2 再循环物流的断裂 1 断裂的基本概念首先考察方程组的断裂假设有一个由四个方程四个未知变量组成的方程组也可以由另外的方式进行求解例如假设x2的猜值则 f1解出x3 f2解出x4 f3解出x1 最后利用f4来检验最初没定的猜值x2 是否正确如果f4为零则可认为得到了方程组的解若此处的f4 不为零则需修正x2的值再重新进行迭代计算这样可将四维求解问题降阶成了四个一维问题通过迭代计算把高级方程组降阶为低级方程组的办法称为断裂考察过程系统中的不可分隔子系统如图211断裂物流可以选为S10当然也可以选为S11选择不同的断裂物流则其相应的迭代序列也不一样从表面上看上列的两种计算序列似乎没有什么很大的区别但由于系统中各物流及其变量特性的不同在收敛计算上常是有很大差异的如变量个数的多少方程求解的难易程度等如何选择断裂物流确定迭代序列是实施序贯模块法进行过程系统模拟计算过程中必须要解决的问题 2 断裂方法的研究早在20世纪60年代初就有人提出了断裂的思想此后随着流程模拟技术的不断发展有关研究断裂的文章不断出现他们提出判断最佳断裂的准则分为四类 1 断裂的物流数最少 2 断裂物流的变量数最少 3 断裂物流的权重因子之和最少 4 断裂回路的总次数最少另一种归纳 1断裂的流股数目最少 2断裂流股包含的变量数目最少 3对每一流股选定一个权因子该权因子数值反映了断裂该流股时迭代计算的困难程度应当使所有的断裂流股权因子数值总和最小4选择一组断裂流股使直接代入法具有最好的收敛特性四条准则是一般性的原则 3 回路矩阵过程系统中的简单回路可以用回路矩阵 1oop/stream Matrix 表示矩阵中的行代表回路列代表物流若某回路i中包括有物流J则相应的矩阵元素aij=1否则为空白或零不独立的列 f 1 与 f 值较大的列相比较若某列中的非零元素与 f 值较大列的非零元素同行则该列相对于 f 值大的列不独立如S2的f 值较大与其余小于它的列相比较会发现S2的非零元素为C行和A行而S1列C行非零 S3A行非零其余列中无与S2同行的非零的元素则判别出 S1 S3相对于S2不独立表示为 S1 S3 S2 S5 S6 S4 流股断裂方法一L - R 分解法 L – R分解法遵循的原则断裂流股数目最少且将所有循环路打开例现有一个为最大循环网的不可分割子系统其信息流图如下1 42 53 S4 S3 S2 S1 S6 S5 S7 S8 4流股断裂方法分析在这个信息流程图中有 8个流股S1S2 S8 五个节点12345构成了ABCD四个环路 1 4 2 5 3 S4 S3 S2 S1 S6 S5 S7 S8 A D C B在Lee – Rudd 法中首先分析信息流图再用环路矩阵表示出来 A B C D 环路S1 S2 S3 S4 S5 S6 S7 S8 01 1 0 0 0 0 0 0 00 0 0 0 1 1 1 1 01 0 0 0 0 0 0 0 11 1 1 0 流股 f R 1 42 53 S4 S3 S2 S1 S6 S5 S7 S8A C DB 矩阵做法Si 流股若在 A 环中出现则标 1若不出现则标 0例如 A 环由S2S3 两流股构成其余为零矩阵中还有加和行用f 表示它由每一列中的非零元素加和构成加和列R它将每一行非零元素加和构成 f 称为环路频率代表某流股出现在所有环路中的次数R 称为环路的秩代表某环路中包含的流股总数经运算可得出加和 f 和R值环路矩阵成为下面样子 A B C D S1 S2 S3 S4 S5 S6 S7 S8 0 1 1 00 0 0 0 0 0 0 0 0 0 1 1 1 1 0 1 0 0 0 0 0 0 0 1 1 1 10 R 2 2 3 4 f 1 2 1 2 1 1 2 1 不独立的列 A B C D S1 S2 S3 S4 S5S6 S7 S8 0 1 1 0 0 00 0 0 0 0 0 0 0 11 1 1 0 1 0 0 0 00 0 0 1 1 1 1 0 R 2 2 34 f 1 2 1 2 1 1 2 1 不独立的列基本概念工艺流程图过程流程过程拓扑举例信息流图-13 序贯模块法的基础是单元模块子程序通常单元模块与过程单元是一一对应的过程单元的输入物流变量即为单元模块的输入单元模块的输出即为过程单元的输出物流变量如 A B H G F E C D 系统分解对复杂系统将所有模型方程全部联立求解很困难直接用序贯法又存在相互影响这时可将该系统分成几个相对独立的部分各自联解再序贯求解将大的复杂系统分解为若干个小的子系统的过程称为大系统的分解目的是识别出不可分割子系统 AB H G F ECD 不可分割子系统不相关子系统 A B H G FE C D A B C A B CG F E D 流股断裂 Tearing 一般对于大系统分解得到的子系统已是不可分隔的如ABC构成的当这样的子系统仍很复杂时联立求解仍困难若断开某一个流股则可采用序贯法求解而断开的流股变量则作为迭代变量选择断裂流股是该技术的关键 A B H G F E C D 断裂物流迭代计算步骤如下该方程组可以通过联立求解得到它的解图210 描述了断裂的过程其中流股x2称为断裂流股该流股只有一个变量x2 称为迭代变量流股的收敛性指的就是其中变量x2 的收敛性能问题如果不选择流股x2是否可达到简化的目的。
化工过程模拟教学大纲

《化工过程模拟》课程教学大纲课程编码:课程类别:必修适用专业及层次:化学、应用化学等化工相关专业;本科学分:3分总学时数:48学时(其中理论学时24,实验学时24)先修课程:化工原理,物理化学,一种高级计算机语言一、课程的性质、目的和任务《化工过程模拟》是化学工程与工艺专业的一门专业选修课程。
其目的是给本专业大三的学生,在完成《化工原理》、《物理化学》等专业基础课程之后,为造就过程工程概念,及早了解并逐步适应当代化学工业的数字化和信息化的趋势,打下初步的基础。
学生通过本课程的学习之后,能够掌握化工流程和单元设备模拟与优化的基本原理、方法步骤,掌握用常用计算机软件解决化工过程开发、设备设计和实际工程模拟优化等问题的初步技能。
二、课程教学的基本要求1、使学生理解并初步掌握化工过程和单元操作的数学建模的基本要领,并对典型过程和典型单元操作的模拟问题做上机练习。
2、掌握化工流程和单元设备模拟与优化的基本原理、方法步骤3、掌握用常用计算机软件解决化工过程开发、设备设计和实际工程模拟优化等问题的初步技能。
4、在后续的毕业设计过程中,学生可以利用本课程所学到的知识技能,最大限度地利用计算机软件技术进行工艺和设备计算,以及工艺和设备的优化。
三、课程教学内容第一章绪论【授课学时】(1学时)【教学内容】1.1过程模拟的一般方法:物理模拟与数学模拟的联系与区别;化工系统模拟的层次;数学模型的类型。
1.2数学模拟的用途及限制:化工开发放大试验和数学模拟的关系;化工设计中的数学模拟方法;化工厂生产操作的数学模拟方法;数学模拟方法的限制。
1.3过程模拟与优化:两个不同层次的概念(过程系统结构优化,过程参数优化),过程模拟和优化间关系。
【教学要求】了解过程模拟的用处以及数学模拟和优化的关系、掌握过程模拟的概念和一般方法,熟练掌握化工过程模拟与优化的基础核心地位。
【教学重难点】1、数学模拟的用途及限制2、数学模型化的步骤第二章单元过程的稳态模拟【授课学时】(5个理论学时+6个实验学时)【教学内容】2.1基本概念:流程系统的工况特性;稳态过程和稳态过程模拟;两类过程模拟类型(模拟型与设计型);过程模拟基本环节;变量选择和自由度分析。
2化工过程系统模拟
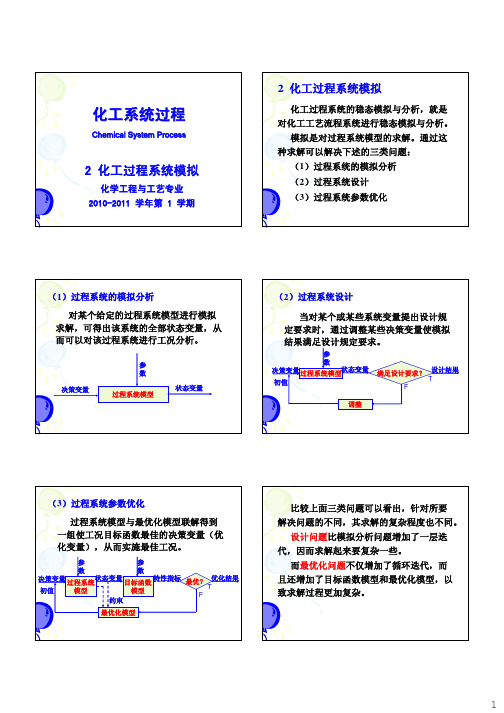
设计问题比模拟分析问题增加了一层迭 代,因而求解起来要复杂一些。
而最优化问题不仅增加了循环迭代,而 且还增加了目标函数模型和最优化模型,以 致求解过程更加复杂。
1
2.1 过程系统模拟基本介绍
如果一个生产系统A是比较复杂的系 统,而不能预知其效果如何,则可以找另 外一个比较简单的系统B,其操作特性与系 统A相同,但是比A容易进行实验或解算。 因而,为了预知系统A的效果,就可以用实 验系统B的性能来代替A。
数学模拟的优越性
1、试验的经济性。 2、加大放大倍数。 3、外延性。 4、互换性。 5、研究稳定性和灵敏度。 6、研究控制方式。 7、提供深入系统的技术资料。
1、试验的经济性。用数学模型在电子计算 机上进行试验,可以省略大量物质装备及物料 消耗,因而比在实际装置上实验来的更加迅速、 经济和详尽。模拟可以压缩或放大时间刻度, 有点类似用电影摄像机使动作过程加速或减慢 一样,从而使系统特性更易于被观察。
化工系统过程
Chemical System Process
2 化工过程系统模拟
化学工程与工艺专业 2010-2011 学年第 1 学期
2 化工过程系统模拟
化工过程系统的稳态模拟与分析,就是 对化工工艺流程系统进行稳态模拟与分析。
模拟是对过程系统模型的求解。通过这 种求解可以解决下述的三类问题:
(1)过程系统的模拟分析 (2)过程系统设计 (3)过程系统参数优化
2.1.4 模拟问题的实质
为了归纳出稳态过程模拟问题的一 般化实质,明确地描述一个模拟问 题,我们必须对以下几个方面的信息 有一个精确的数学描述:
化工系统工程稳态模拟

通过模拟实验代替实际实验,可以大大缩短新产品的研发 周期,降低研发成本。
02
化工系统稳态模拟基础
化工系统简介
01
02
03
化工系统
指由多个化学反应和物理 过程组成的复杂系统,包 括原料的输入、反应过程、 产物的输出等。
化工系统的特点
具有高度的复杂性、非线 性、时变性和不确定性, 涉及大量的物质、能量和 信息流动。
背景
随着化工行业的快速发展,生产过程越来越复杂,对生产过程的控制和优化要 求也越来越高。稳态模拟作为化工系统工程中的重要技术手段,能够为实际生 产提供理论支持和指导。
稳态模拟的定义和重要性
定义
稳态模拟是指对化工生产过程中的物料平衡、能量平衡和 化学反应等进行的数学建模和计算机模拟。在稳态模拟中 ,系统的状态参数(如温度、压力、流量等)不随时间变 化。
06
结论与展望
结论
稳态模拟是化工系统工程中的重要手段,通过模拟可以预测实际生产过程中可能出 现的各种情况,为优化生产和提高经济效益提供有力支持。
稳态模拟技术在化工生产中得到了广泛应用,不仅提高了生产效率,还降低了能耗 和环境污染,为可持续发展做出了贡献。
稳态模拟技术在实际应用中仍存在一些挑战和限制,如模型精度、计算效率和数据 可靠性等方面的问题,需要进一步研究和改进。
重要性
稳态模拟的重要性主要体现在以下几个方面
1. 优化工艺参数
通过模拟不同工艺参数下的系统性能,可以找到最优的工 艺参数组合,提高产品质量和生效率。
2. 降低能耗
通过模拟不同操作条件下的能耗情况,可以找出最优的能 源利用方案,降低生产成本。
3. 提高安全性
通过模拟潜在的危险操作和事故情况,可以预测系统的安 全性能,及时发现和解决潜在的安全隐患。
化工系统第2章

5
对于方程组
x1 2 x2 5 0 (1) ( 2) x1 x2 2 0
可以有如下两种不同写法
x1 2 x1 2 x2 5 x1 x1 x1 x2 2 x2 x2 x1 x2 2 x2 x1 3 x2 5
切线方程的解
20
例:简单蒸馏时,某时刻釜中残液量与低沸点组 成 x 之间有如下关系式
F0 x0 1 1 x ln (ln ln ) F 1 x 1 x0
对于苯-甲苯物系,α=2.5,开始物系中含苯60%,甲 苯40%,若残液量为原料加料量的一半时,试求残 x ( k ) x ( k 1) ε取 液中苯含量。 收敛判据选 0.0001 F0 1 0 .6 1 x 2 .5 l n ln 解:依题意可得 l n F0 2.5 1 x 1 0 .6 2
则得牛顿迭代公式
x
( k 1)
x
(k )
f (x ) (k ) f (x )
(k )
牛顿法实际上是把非线性方程 f ( x ) 0 逐步线性化
f ( x ( k ) ) 就是在点
x
(k )
处的斜率,因此,牛顿法
是用切线来不断近似曲线的。
2015/9/1 19
牛顿迭代法示意图
切线
2015/9/1
2015/9/1 21
1 x ) ln(x ) 0.7402 0 整理得到 2.5 ln(
令 f(x)=2.5ln(1-x)-ln(x)+0.7402,则
f ( x ) 2.5 1 1 x x
取x 0 =0.4 则f(x0)=0.3794 f '(x0)=-6.6666 x1=x0- f (x0)/f '(x0)=0.4569 则
化工过程模拟与分析第二章化工过程系统数学模拟方法【精选】

化工单元模型和模块 钝性流动器械 ; 活性分离器械 ; 平衡级器械 ; 压力变化器械 ; 温度变化器械; 化学反应器;
模型与模块
化工单元模型组成 方程组成 1. 物料衡算方程;
2. 能量衡算方程;
方程独立性
3. 设备约束方程:描述物料通过时发生变化所遵从 的关系;
4. 其它方程 :摩尔分率约束方程 ,物性关联式 。
2、确定与过程有关的设备特性参数和操作参数;
3、确定单元过程从外界得到的热量和功;
4、列出表示各物流之间有关变量约束关系的全部独立 方程;
物料、能量和动量守恒方程,压力平衡,化学平衡, 相平衡,反应动力学,传热、传质速率,流动阻力方 程。
模型自由度
描述一个系统的状态所需变量的数目与建立这些变量 之间关系的独立方程的数目之差,称为此系统的自由 度(degree of freedom)。
第二章 化工过程系统数学模拟方法
2.1 模型化的基本概念
三种数学模型 1、机理模型 P2 P1 32 l u d 2
2、统计模型 cp a bT cT 2 dT3 ... f T
3、混合模型 带部分返混的管式催化反应器模型
单元建模步骤
1、确定单元过程输入、输出流股变量中的独立变量数;
若否,则k=k+1,则返回2)继续迭代。
收敛标准也可为: f xk ?
xk
关于牛顿法的注记
1. 牛顿法是局部收敛算法,且收敛有条件;
2. 初始点选择不同,导致迭代次数变化;
3. 导数可以利用差分代替,切线可用割线代替;
4. 牛顿法具有二阶收敛速度。
收敛速度定义:
lim
k
xk1 x xk x n
2.123化工过程系统稳态模拟

③非线性
2.2.1 稀疏线性方程组的直接求解方法
(1)稀疏性(Sparseness)
设线性方程组为: A·X = b 式中:A — n×n 阶矩阵; X — n 维向量; B — n 维向量。 系数矩阵 A 中,若大部分元素是零,而非零元素占很小比例,则为稀疏矩 阵(sparse matrix),稀疏性用稀疏比φ 描述: 非零元素数N φ= ——————————×100% A中元素总数(n×n)
2.2.3 非线性方程组的迭代求解方法
(1)直接迭代法与部分迭代法
对于非线性方程组 F(X)= 0
可以化为等价形式:G(X)- X = 0 由此构成直接迭代法(也称“不动点迭代法”)的公式:
1
0
0
2Leabharlann -1-10
0
-4
0
2
3
=
0
3
2
0
0
1
·
0
0
-2
0
1
3
(3)Bending & Hutchison 法
Bending & Hutchison 法是以主元素 Gauss 消去法为基础的
一种求解方法。
求解过程的特点是: 只存贮非零元素; 只对非零元素进行运算。
设线性方程组 A·X = b,经消元后转化为 U·X = b′,U为 上三角阵,方程组的求解可以通过自上而下“回代”求出X。
出现的顺序接着编号。
⑤ 从最后选择的那个主元素开始,按相反的顺序进行回代,依次求出
各
变量值。
【例2.2】 稀疏线性方程组:
1 3 2 x1 x 2 0
① ② ③ ④ ⑤ ⑥
3
x1 x 3 0
化工过程模拟与分析(第二章化工过程系统数学模拟方法)

联立方程法基本问题
1、针对稀疏方程的解法; 2、初始值确定; 3、方程解法的选择。
三、联立模块法(Simultaneous modular approach)
研究背景 联立方程法的缺点:
1、方程求解和出错诊断困难 2、先前开发的模块被浪费 原理 将严格单元模型线性化产生只包含流股输入、 输出信息的近似线性模型,将之联立形成过程系统 的线性模型并求解。
模 型
总流量及物流性质的计算与加合器相同
FOUT j j FOUT
若给定j物流占总流的分率
FOUTj fOUTj,k /X OUTj,k 给定k出口物流的组份流量
反应器的化学计量模型及其线性化
流程模拟软件提供的反应器模型:
1. 化学计量模型 转化率和一个或多个反应程度;
2. 多相化学平衡反应器 每个反应偏离平衡的程度;
zi 1 Ki f 0 i 1 1 K i 1
c
V F
气相分率
求解出气相分率之后,则可获得其他所有状态变量
确定F, z, PF, TF, P, T值
给出气液相组成x和y的估计值
计算 Ki=Ki ( x, y, P, T ) 以x, y的计算值 作为新的估计值
平衡闪蒸的不同类型
闪蒸类型 Ⅰ Q,P 设计变量 T,V 状态变量
Ⅱ
Ⅲ Ⅳ
Q,T
Q,V V,T
P,V
P,T P,Q
Ⅴ
Ⅵ 各类
V,P
P,T
T,Q
V,Q
F,PF,TF,zi(i=1,2…,c-1)xi,yi,zc,L,HF,HL,HV, Ki(i=1,2,…,c-1)
模型的求解
对于情况V,若相平衡系数Ki已知,则可将物料平 衡、相平衡和组分约束方程组转化为一个非线性方程
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
方程的主元素选择过程
2.4 过程系统模拟的联立模块法
Simultaneously modular method simulating the process system
两种系统模拟方法的比较
Comparison of two system simulation methods 内容 占用存储空间 迭代循环圈 计算效率 指定设计变量 对初值要求 计算错误诊断 编制、修改程序 序贯模块法 小 多 低 不灵活 低 易 较易 面向方程法 大 少 高 灵活 高 难 较难
x4 y4 x1 y1 x2 y2 x3 y3
2.4.2 建立简化模型的切断方式
Establishment of tearing mode for simple model 流股全切断方式类似于面向方程法。主要区别在 于后者是严格模型方程,变量数也要大得多。 因此,对于较大系统,流股全切断方式建立的简 化模型方程数是很大的。
Ak和Bk。将Ak和Bk代入,得到线性方程组。 过程系统的模型方程组一般由线性方程和非线性方程组
成,因而线性化的对象应该是非线性方程。
2.3.3 联立拟线性方程组法解大型 稀疏非线性方程组
Solution of couple imitate-linear equation 2、稀疏线性方程组的解法 稀疏非线性方程组 稀疏线性方程组
回路切断方式:
相当于把若干个单元作为一个“虚拟单元”处理, 建立虚拟单元的简化模型。 虚拟单元所包含的各单元间的连接流股变量则不 出现在简化模型中,从而大大降低了简化模型的维数。
2.4.2 建立简化模型的切断方式
Establishment of tearing mode for simple model 通常以循环回路为一个虚拟单元,切断再循环流 股,故称为回路切断方式。
2.3.3 联立拟线性方程组法解大型 稀疏非线性方程组
Solution of couple imitate-linear equation
降维求解
大型稀疏非线性方程组
线性化后,联立求解
迭代
误差
线性化后方程组的解
2.3.3 联立拟线性方程组法解大型 稀疏非线性方程组
Solution of couple imitate-linear equation 1、线性化方法 对于n维非线性方程组 用n维线性方程组逼近 F(x) = 0 F( x) ≈ Ax + B = 0
1
该拟线性方程组的解(用下标QL表示)为:
xQL A B
作台劳展开可得到牛顿迭代解(下标NR):
x
k 1 NR
x (J ) F (x )
k k
k 1
2.3.3 联立拟线性方程组法解大型 稀疏非线性方程组
Solution of couple imitate-linear equation 式中J为雅可比矩阵:
2.4.1 联立模块法的原理
Principle of Simutaneous modular method 初值的选取方法: (1) 猜值; (2)用序贯模块法迭代求解几次,得到个点的初值。
联立模块法的计算效率主要依赖于简化模型的形式。
2.4.2 建立简化模型的切断方式
Establishment of tearing mode for simple model 简化模型对象范围的划分:
x 3 y=G(x) x 虚拟单元 1 2 y=G(x)
作业: 查找甲苯加氢脱烷基过程的合成 工艺路线及工艺参数
回
顾
物料衡算 Material balance
相平衡 Phase-equilibria 传递方程 Equations of transport 化学反应动力学 Chemical kinetics
在求解大型稀疏线性方程组时,应尽可能减少填充,否 则会使计算效率下降。 减少填充与提高数值稳定性和计算精度是矛盾的。如, 为减少填充,需把55作为主元素,但如果它的绝对值很小, 会引入较大的误差,使计算精度、数值稳定性变差。
2.3.3 联立拟线性方程组法解大型 稀疏非线性方程组
Solution of couple imitate-linear equation 主元容限: 通常把绝对值最大的元素作为主元,进行消元。目 的是提高计算精度。但如果这样选取的主元导致较大的 填充,将引起计算效率的下降。往往选择一个绝对值不 是最大,且不会引起填充量过大的元素作为主元。 人为规定一个界限ε>0。当矩阵元素的绝对值大于 ε,该元素就具备了作为主元的资格,若它引入的填充 量也不是很大,就可定为主元。这个界限称为主元容限。 经验给定,但应满足提高计算精度和减少填充量的统一 要求。
入非零元素 。
新出现的非零元素称作填充量,填充时与消元成零的非零
元素之差称作填充增量。填充量与主元选取的次序有关。
高斯消去法就是通过矩阵的行变换达到消元的目的,从 而将方程组的系数矩阵由对称矩阵变为三角矩阵,最后 获得方程组的解。
假定a11≠0,我们首先保留矩阵的第一行,并利用它来 消去其余三行中的第一列。
化工过程分析的作用
能量衡算 Energy balance
2.3.3 联立拟线性方程组法解大型 稀疏非线性方程组
Solution of couple imitate-linear equation 牛顿迭代具有二阶收敛特性。下面方程也具有二阶收敛。
xQL
k 1
( A ) B
k 1
k
Ax
k
k 1
B
k
系数A和B均是向量x的函数。
从x的第k次近似解xk可以计算得到Jk、F(xk),从而得到
{状态变量} 图2-24 联立模块法
2.4.1 联立模块法的原理
Principle of Simutaneous modular method 特点: ①把序贯模块法中最费时、收敛最慢的回路迭代计算, 用由简化模型组成的方程组的联解而代之,使计算加速,尤 其是处理有多重再循环流或有设计规定要求的问题时具有较 好的收敛行为。因此,联立模块法计算效率较高。 ② 因单元模块数比之过程方程数要少得多,所以简化 模型方程组的维数比面向方程法也小得多,求解起来也容易 得多。 ③能利用大量原有的丰富的序贯模块软件。可在原有 序贯模块模拟器上修改得到联立模块模拟器。
2.4.1 联立模块法的原理
Principle of Simutaneous modular method 优点: ① 计算效率较高; ② 对初值要求较低; ③ 迭代循环圈较少; ④ 计算出错时诊断较容易; ⑤ 能利用大量原有的软件。
2.4.1 联立模块法的原理
Principle of Simutaneous modular method
2.3.3 联立拟线性方程组法解大型 稀疏非线性方程组
Solution of couple imitate-linear equation 挑选主元素的过程: ① 选择纵列最小的变量,如不止一个,任选其一; ② 在与此变量有关的方程中,选择橫列最小的方程所对 应的元素作为主元; ③ 如果橫列最小的方程不止一个,则选择绝对值最大的 元素作为主元;
联立模块法与序贯模块法的共同之处在于面向模块;与面向方程 法共同在于联立求解过程系统模型方程。
2.4.1 联立模块法的原理
Principle of Simutaneous modular method
严格模块
1
2
…….
n
简化模型方程
由于简化模型是严格模块的近似,所以计算结果往往不是 联立解 问题的解,必须用严格模块对这组解进行计算,修正简化模 型的系数。重复这一过程,直到收敛到原问题的解。
第一行与第一列非零元素间的交叉点会出现新的填充量
2.3.3 联立拟线性方程组法解大型 稀疏非线性方程组
Solution of couple imitate-linear equation
常规消去法:
通常采用下列两方面的技术 a.只对非零元素进行计算 b.只存储非零元素 (如压缩存储技术)
不经济的 计算效率低
2.3.3 联立拟线性方程组法解大型 稀疏非线性方程组
Solution of couple imitate-linear equation 填充量:
用高斯消去法进行消元过程的同时,会在原来零元素处引
2.3.3 联立拟线性方程组法解大型 稀疏非线性方程组
Solution of couple imitate-linear equation
完成主元选择后的增广矩阵
2.3.3 联立拟线性方程组法解大型 稀疏非线性方程组
Solution of couple imitate-linear equation
2.3.3 联立拟线性方程组法解大型 稀疏非线性方程组
Solution of couple imitate-linear equation
④ 检验选出主元的绝对值是否大于用户给出的主元容限。 不大于,则返回①,否则进行下一步; ⑤ 用这样选择出的主元进行常规的高斯消元,然后返回①。 上述过程中,步骤①和②都是为了避免填充。而 步骤③和④是为了保证计算精度和系数矩阵非奇异。
F( x) ≈ Ax + B = 0
x
k 1 NR
x (J ) F (x )
k k
k 1
k 1 xNR x k ( J k ) 1 ( Ak x k B k )
令J=A
k 1 k 1 xNR x k ( Ak ) 1 ( Ak x k B k ) ( Ak ) 1 B k xQL
2.3.3 联立拟线性方程组法解大型 稀疏非线性方程组
Solution of couple imitate-linear equation
