通信电子技术电子调频波与调相的比较
调频与调相

1
Nout 4 2 A2
fm fm
(2
f
)2
N0df
2 3A2
N0
f
3 m
解调后,输出信噪比为
Sout
Nout
KF2M E m
t
2 3A2 2N0 fm3
3A2 KF2M
2N0
f
3 m
E m
t
2
因为
FM
K FM
| m(t) |max fm
Sout
Nout
3
2 FM
E m
no(t) 可以看成ns(t)经过微分器,而 ns (t) V (t)sin( ' (t))是一个均值为0,
功率为N0BFM的低通型窄带噪声,其带宽范围
BFM 2
, BFM 2
。
微分器的传输响应函数为
H () 1 j 2A
所以,经过微分后噪声的功率谱密度为
1
4 2 A2
(2
f
)2
N0
经过低通[-fm,fm]后,噪声概率为
2 FM
Si n0 fm
m(t) ,0
A2 m(t)2,
2
A | m(t) |max
改善门限效应的方法
加重和去加重 锁相环解调* 负反馈解调等*
加重和去加重
输出噪声呈抛物线形式
经过鉴频器后,噪声的功率谱密度变为抛物线)型, 即在信号的低频处,噪声的功率谱密度小,而在信号 的高频处,信号的功率谱密度大。由于一般信号在高 频分量处,信号的功率本身就小,因此高频分量处的 信噪比就较差。这实际上影响着调频的输出信噪比。
m t'
t m
d
则对m(t)’调相等价于对m(t)调频。
高频电子线第7章频率调制与解调详解

第7章 频率调制与解调
7.1 角度调制信号分析
二、信号的频域分析 1. 调频波的展开式
因为 e jmf sin t 是周期为2π/Ω的周期性时间函数,可以将它展开为傅氏
级数,其基波角频率为Ω,即
e jm f sin t
J n (m f )e jnt
n
式中Jn(mf)是宗数为mf的n阶第一类贝塞尔函数。
计算。
西安电子科技大学ISN国家重点实验室——付卫红
第7章 频率调制与解调
7.1 角度调制信号分析
三、调频信号的功率
调频信号uFM(t)在电阻RL上消耗的平均功率为
PFM
uF2M (t) RL
因为 uFM Uc Jn (mf ) cos(Ct nt) n-
由于余弦项的正交性,总和的均方值等于各项均方值的总和, 则:
第7章 频率调制与解调
7.1 角度调制信号分析
二、信号的频域分析
3. 调频信号的带宽
当mf很小时,如mf<0.5,为窄频带调频,此时
uFM (t) UC [J0 (m f ) cosct J1(m f ) cos(c )t -
J1(mf ) cos(c )t]
-
0
由于边频分量的合成 矢量与载波垂直,故 也叫正交调制
|Jn(mf)| ≥0.01
n/mf 4 3 2 1
0 4 8 12 16 20
mf
|Jn(mf)|≥0.01时的n/mf曲线
西安电子科技大学ISN国家重点实验室——付卫红
第7章 频率调制与解调
7.1 角度调制信号分析
二、信号的频域分析 3. 调频信号的带宽
n/mf 4
由图可见,当mf很大时,n/mf趋近于
第7章 频率调制

16
《通信电子电路》
第7章 频率调制与解调
Jn (mf) 1 .0 0 .8 0 .6 0 .4 0 .2 0 -0 .2 -0 .4 0 1 2 3 4 5 6 7 8 9 10 11 12 mf J0 J1 J2 J3 J4 J5 J6
J7
J8 J9 J1 0
图7-3 第一类贝塞尔函数曲线
17
u U cost
uc Uc cosc t
Umax Uc (1 ma )
Uc
Umin U c (1 ma )
2
《通信电子电路》
第7章 频率调制与解调
概 述
在无线通信中,频率调制和相位调制是又一类重要的 调制方式。 1 、频率调制又称调频 (FM) ,它是使高频振荡信号的频 率按调制信号的规律变化(瞬时频率变化的大小与调制信号 成线性关系),而振幅保持恒定的一种调制方式。调频信号 的解调称为鉴频或频率检波。 2 、相位调制又称调相 (PM) ,它的瞬时相位按调制信号
调频信号的瞬时相位(t)是瞬 时角频率 ω(t) 对时间的积分,即:
t
(t ) c m cos t
(7-2)
0 为信号的起始角频率。 式中,
0
(t ) ( )d 0
为了分析方便,不妨设φ0=0,则 式(7-2)变为:
t
0
m ( )d ct sin t ct m f sin t
Δm大小影响有效频带宽度
c
mf=2
c
mf=2
Ω大小影响频谱间隔 二者共同影响有效带宽
c
mf=5
c
mf=5
高频电子线路最新版课后习题解答第七章——角度调制与解调答案

第七章 思考题与习题7.1 什么是角度调制?解:用调制信号控制高频载波的频率(相位),使其随调制信号的变化规律线性变化的过程即为角度调制。
7.2 调频波和调相波有哪些共同点和不同点,它们有何联系?解:调频波和调相波的共同点调频波瞬时频率和调相波瞬时相位都随调制信号线性变化,体现在m f MF ∆=;调频波和调相波的不同点在:调频波m f m f k V Ω∆=与调制信号频率F 无关,但f m f k V M Ω=Ω与调制信号频率F 成反比;调相波p p m M k V Ω=与调制信号频率F 无关,但m f m f k V Ω∆=Ω与调制信号频率F 成正比;它们的联系在于()()d t t dtϕω=,从而具有m f MF ∆=关系成立。
7.3 调角波和调幅波的主要区别是什么?解:调角波是载波信号的频率(相位)随调制信号的变化规律线性变化,振幅不变,为等福波;调幅波是载波信号的振幅随调制信号的变化规律线性变化,频率不变,即高频信号的变化规律恒定。
7.4 调频波的频谱宽度在理论上是无限宽,在传送和放大调频波时,工程上如何确定设备的频谱宽度? 解:工程上确定设备的频谱宽度是依据2m BW f =∆确定7.5为什么调幅波调制度 M a 不能大于1,而调角波调制度可以大于1?解:调幅波调制度 M a 不能大于,大于1将产生过调制失真,包络不再反映调制信号的变化规律;调角波调制度可以大于1,因为f fcmmV M k V Ω=。
7.6 有一余弦电压信号00()cos[]m t V t υωθ=+。
其中0ω和0θ均为常数,求其瞬时角频率和瞬时相位解: 瞬时相位 00()t t θωθ=+ 瞬时角频率0()()/t d t dt ωθω==7.7 有一已调波电压1()cos()m c t V A t t υωω=+,试求它的()t ϕ∆、()t ω∆的表达式。
如果它是调频波或调相波,它们相应的调制电压各为什么?解:()t ϕ∆=21A t ω,()()12d t t A t dtϕωω∆∆==若为调频波,则由于瞬时频率()t ω∆变化与调制信号成正比,即()t ω∆=()f k u t Ω=12A t ω,所以调制电压()u t Ω=1fk 12A t ω 若为调相波,则由于瞬时相位变化()t ϕ∆与调制信号成正比,即 ()t ϕ∆=p k u Ω(t )所以调制电压()u t Ω=1pk 21A t ω 由此题可见,一个角度调制波可以是调频波也可以是调相波,关键是看已调波中瞬时相位的表达式与调制信号:与调制信号成正比为调相波,与调制信号的积分成正比(即瞬时频率变化与调制信号成正比)为调频波。
通信电子线路考试课后题复习解析

丁250 X lO^rad/s}00i x Rji I尺a1 +R Z +P T】+誇+雳2-5 井联i 皆航回路如图题2-5所示"已知通频带•电容「•若回路总电导为 &曰心工=q+仏 +氐九试证明:- 4K A/U iC fl 若给宦「=初pF’ZBFu :=启MHs 禺=13kO. & = 10kn, J R R u 曲事少? 灯证阴 由于Q = R 护C =蛙M因此有® =警=迸匸 N 吿gc = 2^/u.r • 2nC = ^f b ,C 避毕.代人数携拇CJ==畫扛 X 6 X 10s X 20 X 10 12 = 0, 75 X 10 3S — 0. 75mS 園此 G|p = 6 — G E — G D = a 75 — 1/10 ― 1/13 = a 573mS 即心=L 75kn2-6 回路如图題 所示.已 m r=0. 8^H TQ… = 100T C, =Ci =20pF,C 6 = 5pF, = i okn.c,.-2O PF *R r = skn*试计算回路谐振频率、谐振电pru 不计隔 与尽 时八有 戟品质因數Qi.和通频带.由已知条件得/?: =占凤.=Rr, — 4R (, — 20kQ 匸;=注c L = (c ;^cj CL= T C L = 5P FCv=C s + C ;r + ^4^ = S+5+LO-2OpF则谐振频率/Q =i^te =39-8MHz 或八谐振电阻有載品质因数2-15 在图题2 -15中*已知用T AM (调幅'波段的中械遍谐回路的苗扳频牢人』 4苗kHz.空载Q 值为 MC.线圈初级圈效为160 匝’次级圈数为10匝•初级中心據饪至F 端阿数 为召0 Rs ,C-=200pF*Ri = LkQ . W s = 16ka… 试求 回路电越L 、有载Q 值和通频带.制由已知条件得L =事=612. 3%H屁=Qu/a^C = i74e 9Skfi盹■隔〃圧〃尺;.-凡# (骨)'隔“(等:)比° 73. 92kQQ_ =— 42. Z l因此 *圈 St 2-5图题2-6图竝2 15/ = 50MH;时,250 7012. SMEUM3夕=零*MHz ■ 绘參■弄錯刚■睥刑2-19 晶 I* 1? 3IX ;fiC 的特征频率 A - 250MHz,= 50,求该管在 /= lMUz t 2OMHz*5OMHz 时的 I 川值.解由“可得h = f 訂佝=5MHz⑴当/=lMHz 时,满足此时於U 禺= 5<h 这时R 不陽f 变化*即相呀于低 频的情况:(2)当/ = 20,50MHz 时,满足所哦3 H 某一晶捧管谐振功率放大器*设已知E 「= 2AW ・-250mA.兀= 5W.电压 利用系数等于】.求1心•杯P“R “解(1)电压利用乘数~ = H 则U “ =氐=24V*代士J 皿・T* =器士416mA<3)几二£2 = 24X0*/>C = P S -P…^6-5 = 1W可知fm 为 416mA ・乐为 83, 2^£,片 为 1 W,R e 为 57. 60“3-16 匕球晶阵営输出持性酣罐甲便和怖瞬峨跆导乩片弓①杓/VV.用忧晶侔當愿战 的谐振功放电路的 E r -24V.fl =70s ,Z™*=2,2A,«I . (70*)0t Z53tffl C70">-0, +36.并工 作衽临界状态.试计算凡•几沖 和尺卄解{" P s = E, /H > = E r /c^au < 70*) - 2. 2 XO. 253 X 24 = 13T 36W ⑵ U…. = ~Mrr"=E — U.严24 -鳥-2L25V则化=*心心=寺UJX 21. 25X2,2X0.436 = 10. 19Wp(3)蕈h 才=o. 7$• s代入数信得心=22. I6fl可知几为IS 】9W*入为l3.3£Wq 为0.托求e 为22. 16Q./ = 20MHz 时. ⑷(瓦一【人』4- 10 题图表示二回路振荡器的交流等效电路,假定有以下六种情况::C3------- 1二 C1 :TC 2 3 L2试问哪几种情况可能振荡?等效为哪种类型的振荡当f>f 1,即f :. ------- 时,ce 是容性; 2 兀(Li G fvf,即 '「'L 3C 3cb 是感性;由于可取f 同时满足上述条件。
通信电子电路(第六章)于洪珍

单频正弦波和三角波时的调频信号调相信号的有关波形。 图6.1 单频正弦波和三角波时的调频信号调相信号的有关波形。
6.2角度调制信号的基本特性 角度调制信号的基本特性
一、调频信号
设载波信号为: 设载波信号为: 调制信号为: 调制信号为:
u(t ) = Um cos(ωct +ϕ0 )
uΩ(t )
则调频信号瞬时角频率: 则调频信号瞬时角频率: 瞬时角频率
频偏、相偏、调制指数比较(单音调制) 频偏、相偏、调制指数比较(单音调制)
FM PM
) ∆ω(t(rad / s) k f UΩm cos Ωt = ∆ωm cos Ωt − kPUΩm sinΩt = −mpΩsinΩt ( ∆ϕ(t(rad ) ) (
k f UΩm Ω sinΩt = mf sinΩt kPUΩm cos Ωt = mp cos Ωt
0
t
为比例系数(调频灵敏度)。 k f 为比例系数(调频灵敏度)。
表明FM信号的振幅恒定 uFM (t ) = Um cos[ωct + k f ∫ uΩ (t )dt +ϕ0 ] 表明 信号的振幅恒定 瞬时角频率是在固定的载频 ωc 上叠加一个与调制信号电压成正比 的角频率偏移(角频偏)。 的角频率偏移(角频偏)。 角频偏: 角频偏:
dθ(t ) 由于频率是相位的微分ω(t ) = ,故相位的变化必将引起频率的 dt
变化,反之亦然。所以调频信号与调相信号在时域特性、频谱宽度、 变化,反之亦然。所以调频信号与调相信号在时域特性、频谱宽度、 时域特性 调制与解调的原理和实现方法等方面都有密切的联系 的原理和实现方法等方面都有密切的联系。 调制与解调的原理和实现方法等方面都有密切的联系。 调频和调相都表现为载波信号的瞬时相位受到调变, 调频和调相都表现为载波信号的瞬时相位受到调变,故统称为角度调 制(Angle Modulation)。 。
高频电子线路复习提纲与习题答案(1)
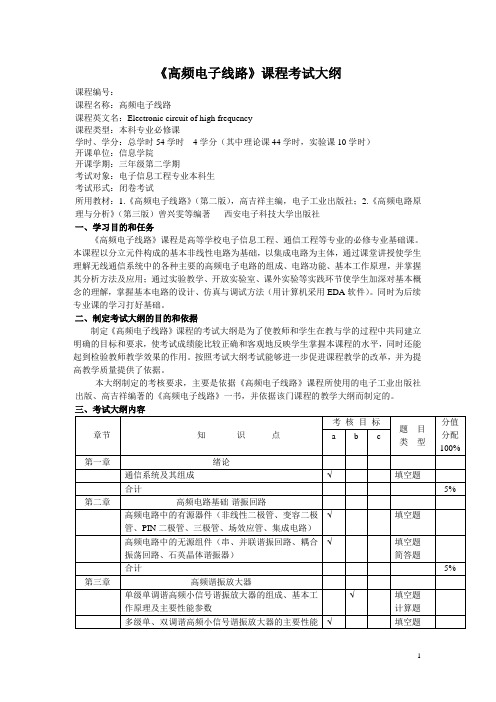
《高频电子线路》课程考试大纲课程编号:课程名称:高频电子线路课程英文名:Electronic circuit of high frequency课程类型:本科专业必修课学时、学分:总学时54学时4学分(其中理论课44学时,实验课10学时)开课单位:信息学院开课学期:三年级第二学期考试对象:电子信息工程专业本科生考试形式:闭卷考试所用教材:1.《高频电子线路》(第二版),高吉祥主编,电子工业出版社;2.《高频电路原理与分析》(第三版)曾兴雯等编著西安电子科技大学出版社一、学习目的和任务《高频电子线路》课程是高等学校电子信息工程、通信工程等专业的必修专业基础课。
本课程以分立元件构成的基本非线性电路为基础,以集成电路为主体,通过课堂讲授使学生理解无线通信系统中的各种主要的高频电子电路的组成、电路功能、基本工作原理,并掌握其分析方法及应用;通过实验教学、开放实验室、课外实验等实践环节使学生加深对基本概念的理解,掌握基本电路的设计、仿真与调试方法(用计算机采用EDA软件)。
同时为后续专业课的学习打好基础。
二、制定考试大纲的目的和依据制定《高频电子线路》课程的考试大纲是为了使教师和学生在教与学的过程中共同建立明确的目标和要求,使考试成绩能比较正确和客观地反映学生掌握本课程的水平,同时还能起到检验教师教学效果的作用。
按照考试大纲考试能够进一步促进课程教学的改革,并为提高教学质量提供了依据。
本大纲制定的考核要求,主要是依据《高频电子线路》课程所使用的电子工业出版社出版、高吉祥编著的《高频电子线路》一书,并依据该门课程的教学大纲而制定的。
三、考试大纲内容说明:1、考试形式:分为闭卷、开卷、闭卷+开卷、实验操作、实验操作+闭卷考试等,本课程采用闭卷考试形式。
2、所用教材:包括书名,作者名,出版社,版次。
3、考试对象:分为年级,学期。
4、考核目标:其中a、b、c,分别表示a:了解;b:掌握;c:熟练掌握。
四、内容要求:第一章选频网络1.掌握LC串并联谐振回路的谐振特性;2.串并联阻抗转换(在同一工作频率处);3.接入系数的计算(电容抽头、电感抽头、变压器等);4.耦合回路(1)反射阻抗的概念(2)耦合系数(3)耦合因数(4)频率特性及通频带第二章高频小信号放大器1.单级单调谐放大器掌握电路分析方法,画交流等效电路,求谐振放大电路的电压增益、功率增益、通频带、选择性。
4-15 调频与调相

4.5.3 调角波的频谱及频带宽度
一、频谱
vFM (t) J0 (m f )
J1(m f )[cos(0 )t cos(0 )t] J2 (m f )[cos(0 2)t cos(0 2)t] J3(m f )[cos(0 3)t cos(0 3)t]
(2) BW0.1 2(75 1) 152KHz
n0
Jn (mf ) 是以mf为宗数的n阶第一类贝赛尔函数。
4.5.3 调角波的频谱及频带宽度
一、频谱
vFM (t) J0 (m f )
J1(m f )[cos(0 )t cos(0 )t] J2 (m f )[cos(0 2)t cos(0 2)t]
1、频谱数量? 2、各分量相位关系? 3、带宽?
fI
本 振 信 号
fL
fI
镜像 干扰
fK
f
上节内容回顾与扩展
混频器的干扰
交叉调制系数
Kf
干扰信号所转移的调制 有用信号调制
1 2
f '''VS0Vk20m2 cos 2t f 'VS0m1 cos 1t
结论:
1 m2 2 m1
f f
''' '
Vk20
(1)交叉调制是由非线性器件中的三次项或更高次
调相 瞬时相位 (t) 0t kpV cosΩt 0
mp
kpV
Dp
瞬时频率 (t) 0 kpV sin Ωt
4.5.2 数学表达式与相关参数
以单音调制波为例 调制信号 vΩ (t) VΩ cost
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
根据调频波的数学表达式以及瞬时角频率)(t ω和瞬时相位)(t ϕ的基本关系可知: 调频波的调频系数Ω∆=Ω=Ωω
m
f f U k m 调频波的最大角频偏m f f U k t u k ΩΩ==∆max )(ω 调频波的最大相移f t f t
m dt
t u k t ==∆=∆⎰⎰Ωmax 0max 0)()(ωϕ
根据调相波的数学表达式以及瞬时角频率)(t ω和瞬时相位)(t ϕ的基本关系可知:
调相波的调相系数m p p U k m Ω=∆=ϕ
调相波的最大相移m p p U k m Ω==∆ϕ 调相波的最大角频偏m p p U k dt t du k dt t d ΩΩΩ==∆=∆max
max )()(ϕω 由此可知,在调频中,最大角频偏ω∆与调制信号频率Ω无关,最大相移ϕ∆则与调制信号频率Ω成反比;在调相中,最大角频偏ω∆与调制信号频率Ω成正比,最大相移ϕ∆则与调制信号频率Ω无关。
这是两种调制的根本区别。
