稳态误差分析例题
自动控制原理--控制系统的稳态误差

二、给定作用下的稳态误差
设系统开环传递函数为:
其中K为开环增益,v为系统中含有的积分环节数 对应于v=0,1,2的系统分别称为0型,Ⅰ型和Ⅱ型系统。
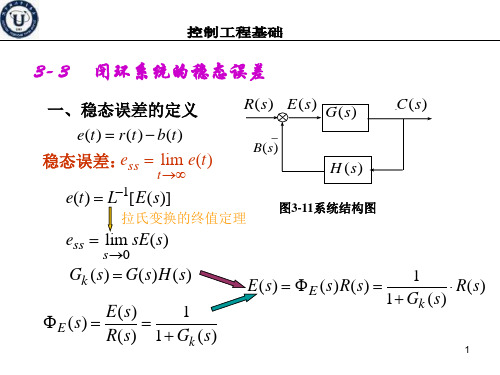
稳态误差的定义
• 误差定义为输入量与反馈量的差值
• 稳态误差为误差的稳态值 • 如果需要可以将误差转换成输出量的量纲
• 稳态误差不仅与其传递函数有关,而且与输入 信号的形式和大小有关。其终值为:
稳态误差计算
误差的定义:
E(s) R(s) B(s)
lim ess ()
( L1[ E ( s )])
(1)系统是稳定的; (2)所求信号的终值要存在。
例27 已知系统如图3-36所示。当输入信号 rt ,1干t扰信 号 n时t,求1t系 统的总的稳态误差。
Ns
Rs
Es
K1
K2 s
Y s
Bs
图3-36 例3-15系统结构图
解:⑴对于本例,只要参数 K1, K均2大于零,则系统一定是稳 定的。
⑵在r t 信1t号 作用下(此时令 n)t 0
s0
s0
1 s K1K2
K2 s K1K2
1 s
1 K1
由以上的分析和例题看出,稳态误差不仅与系统本身
的结构和参数有关,而且与外作用有关。利用拉氏变换
的终值定理求得的稳态误差值或者是零,或者是常数,
或者是无穷大,反映不出它随时间的变化过程。另外,
对于有些输入信号,例如正弦函数,是不能应用终值定
最后由终值定理求得稳态误差 ess
ess
稳态误差分析例题

× r2(t)=t
G 2 (s)
s(s
7(s 3) 4)(/8 ess= 8/21
r3(t)=t2
8(0.5s 1)
G 3 (s) s2 (0.1s 1)
× Ⅱ型 k=8 ess=1/8
例题3 求图示系统的essn。
n(t)=1(t)
s2
An2 2 n s
n2
s0
s
得(s)
s2
0.95 3.3462 2 0.344 3.346s 3.3462
s2
10.636 2.3s 11.196
开环传递函数
G(s)
s2
10.636 2.3s 0.56
2.
Gc (s)
kc s
0 < kc < 0.12
kh
ts=3T=0.03/kh=0.3
E(s) R(s)
1
30
H(s) 1 G(s)H(s) s(s 10)
∴kh=0.1
ess= 3
例题5 1、试求出该系统的开环传递函数及参数;
2、确定串联校正装置的传递函数,使系统 对阶跃输入的稳态误差为零。
设无零点的单位反馈二阶系统h(t)曲线如图所示,
λ2k2=T1+T2
即: λ1 = 1/k2
分子只有s3项时,由终值定理可得: λ2=(T1+T2)/k2
例题2
已知单位反馈系统开
环传递函数为G(s),输
入为r(t),试求稳态误
差ess。
r1(t)=1(t)
10
G1(s) (0.1s 1)(0.5s 1)
解:
系统2不稳定,∴ ess→∞ 系统3的A=2, ∴ ess=1/4
3-5稳态误差的分析与计算

0型 系统
m
K (TjS 1) G(s) j1
n
(TiS 1)
i 1
抛物线输入 Ⅱ型系统
系统开环传递函数中 不含积分环节
KPlim G(s)K
s0
ess
1 1 K
阶跃输入时,误差系数=K
输出始终不会等于输入,存在稳态误差
Klim SG (s)0 斜坡输入时,误差系数=0
e s 0 ss 稳态误差无穷大(输出不能跟随输入)
三种典型输入下对应于“0”“I”“Ⅱ”型三 种系统
有九种情况,误差的计算公式列表如下:
给定输入
给定稳态误差的终值 0型系统 I型系统 Ⅱ型系统
1(t)
1/(1+K)
0
0
t
∞1/K0源自t2/2∞∞1/K
注意: (1) 尽管将阶跃输入、速度输入及加速度输入下 系统的误差分别称之为位置误差、速度误差和加 速度误差,但对速度误差、加速度误差而言并不 是指输出与输入的速度、加速度不同,而是指输 出与输入之间存在一确定的稳态位置偏差。
i1 n1
(is1) (k2s2 2kks1)
k1 n2
(Tjs1) (Tl2s2 2lls1)
j1
l1
稳态误差系数仅与系统参数K、(积分环节个数—系统 型号)有关,对应=0、1、2 称 0、I、Ⅱ型系统
0、I、Ⅱ型三种系统 分别三种典型输入 稳态误差有九种情况
阶跃输入 斜坡输入
0型系统 I型系统
3. 稳态误差与系统传递系数有关
4. 稳态误差与扰动有关
本章结束
给定输入下的稳态误差与稳态误差系数
阶跃输入下:
e ssr
1
1 K
P
KPlimG(s) s0
第三章(4)系统的稳态误差

S ( S 2 n S n )
2 2 2
eSS lim SE(s) lim
S 0 S 0
S 2 n K d n S 2 2 n S n
2 2
2 Kd n
只要令
Kd
2
n
就可以实现系统在稳态时无误差地跟踪单位斜 坡输入。
R0 ess 1 K
p
K K G ( s ) H ( s ) G0 ( s ) H 0 ( s ) S S
(3 63)
Kp
K , 0 , 1
R0 const, 0 ess 1 K , 1 0
结论:
若要求对于阶跃作用下不存在稳态误差, 则必须选用Ⅰ型及Ⅰ型以上的系统 .
Kd 2
n
时,稳态时系统的
输出能无误差地跟踪单位斜坡输入 )
C ( s)
—
图3-18 控制系统的方块图
证明: 闭环传递函数
(1 K d S ) n C (s) 2 R( s ) S 2 n S n 2
G 2 ( H ) G2H NE ( S ) 1 G1G 2 ( H ) 1 G1G 2 H
系统总的稳态误差:
ess lim e(t ) lim sE ( s)
t s 0
lim s RE ( s) R( s) lim s NE ( s) N ( s)
2
C ( s)
(1 K d S ) n
2 2
S 2 2 n S n
1 2 S
R(s)
2
E ( s ) R( s) C ( s) (1 K d S ) n
2
实验七 控制系统的稳态误差分析
实验七 控制系统的稳态误差分析一、 实验目的1、 研究系统在单位阶跃输入下的稳态误差变化。
2、 掌握系统型次及开环增益对稳态误差的影响。
3、 在Multisim 仿真平台上建立二阶电路,通过示波器观测控制系统稳态误差变化情况。
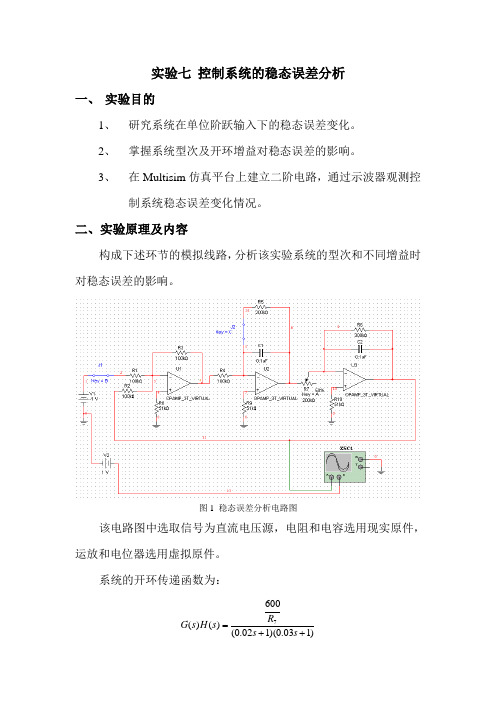
二、实验原理及内容构成下述环节的模拟线路,分析该实验系统的型次和不同增益时对稳态误差的影响。
图1 稳态误差分析电路图该电路图中选取信号为直流电压源,电阻和电容选用现实原件,运放和电位器选用虚拟原件。
系统的开环传递函数为:)103.0)(102.0(600)()(7++=s s R s H s G其中:R 7为电位器从系统的开环传递函数知,本系统属于0型系统,并且开环增益7600R K =,则系统的稳态误差K Ro e ss +=1。
三、实验步骤1、将开关J2断开,电位器R 7调到100K Ω进行实验,观察示波器中响应曲线稳态误差的情况(见图2)。
2、将开关J2闭合,调节电位器的数值(利用A 键),观测稳态误差的大小变化以及收敛的速度。
(1)当电位器R 7为200K Ω时,输出波形见图3(2)当电位器R 7为100K Ω时,输出波形见图4(3)当电位器R 7为50K Ω时,输出波形见图5图2 J2断开时的稳态误差分析曲线图3 R7=200KΩ时误差分析曲线图4 R7=100KΩ时误差分析曲线实验八 一阶系统频率特性测量一、实验目的1、加深了解系统及元件频率特性的物理概念。
2、掌握系统及元件频率特性的测量方法,根据所测得的频率特性做出波特图。
二、实验内容构成下述环节的模拟线路,使用仿真软件中的波特图一加深对惯性环节的频率特性的理解,通过测量值的变化规律得到系统的幅频特性和相频特性。
1、 测量原理若输入信号11()sin m u t U t ω=,则在稳态时,其输出信号为22()sin()m u t U t ωϕ=+,改变输入信号的角频率值ω,便可以测得两组随ω变化的值----12m mu u 和ϕ,进而可以通过测量值的变化规律得到系统的幅频特性和相频特性。
稳态误差的总结分析和例解

稳态误差的总结分析和例解控制系统稳态误差是系统控制准确度的一种度量,通常称为稳态性能。
只有当系统稳定时,研究稳态误差才有意义,对不能稳定的系统,根本不存在研究稳态误差的可能性。
一、 误差与稳态误差1、输入端的定义:对图一,比较输出得到:E(s)=R(s)-H(s)*Y(s)称E(s)为误差信号,简称误差图一2、输出端的定义:将图一转换为图二,便可定义输出端的稳态误差,并且与输入端的稳态误差有如下关系:E ’(s)=E(s)/H(s)输入端定义法可测量实现,输出端定义法常无法测量,因此只有数学意义,以后在不做特别说明时,系统误差总是指输入端定义误差。
图二再有误差的时域表达式:也有:e(t)= [E(S)]= [Φe (s)*R(S)]其中Φe (s)是误差传递函数,定义为:Φe (s)==根据拉氏变换终值定理,由上式求出稳态误差:(T j s+1)e ss (∞)= =二、 系统类型一般的,定义一个分子为m 阶次,分母为n 阶次的开环传递函数为:[]1()()()()ts ss e t L E s e t e t -==+G(S)H(S)=K为开环增益,ν表示系统类型数,ν=0,表示0型系统;ν=1表示Ⅰ型系统;当ν大于等于2时,除了符合系统外,想使得系统稳定相当困难。
四、阶跃输入下的ess(∞)与静态位置误差系数Kpr(t)=R*1(t),则有:ess (∞)=νν用Kp表示静态位置误差系数:ess(∞)==其中: Kp=且有一般式子:Kp=ν∞ν五、斜坡输入下的ess(∞)与静态速度误差系数Kvr(t)=Rt,则有:ess (∞)=ν用Kv表示静态速度误差系数:ess(∞)==其中: Kv=六、加速度输入下的ess(∞)与静态加速度误差系数Kar(t)=Rt2/2,则有: ess (∞)=ν、用Kv表示静态速度误差系数: ess(∞)==其中: Kv=且有: Ka=、七、扰动状况下的稳态误差系统的模型如图三所示对扰动状况下的稳态误差仍然有输入端与输出端的两种定义:图三1、输入端定义法:扰动状况下的系统的稳态误差传递函数:由拉氏变换终值定理,求得扰动状况下的稳态误差为:2、输出端定义法:212()'()0()()1()()()G s E s Y s N s G s G s H s =-=-+记Φe (s) =为误差传递函数,其中G(s)为:G(s)=G 1(s)*G 2(s)*H(s)八、减小或者消除稳态误差的措施: (1)保证系统中各个环节(或元件),特别是反馈回路中元件的参数具有一定的精度和恒定性;(2)对输入信号而言,增大开环放大系数(开环增益),以提高系统对给定输入的跟踪能力;(3)对干扰信号而言,增大输入和干扰作用点之间环节的放大系数(扰动点之前的前向通道增益),有利于减小稳态误差;(4)增加系统前向通道中积分环节数目,使系统型号提高,可以消除不同输入信号时的稳态误差。
求系统的稳态误差-太原科技大学
4
K
1 Kv
E ( s ) E ( s ) R( s )
1 R( s ) 1 Gk ( s)
1 R( s) 3 s
单位抛物线输入信号作用下系统的稳态误差 1 s 3 1 1 s ess lim R( s) 3 s 0 1 Gk ( s ) lim s 2 Gk ( s ) s
K1 T1 s 1
K2 s(T2 s 1)
C ( s) ·
1 1 K v K1K 2 n(t ) 1(t ) 时,扰动误差 G2 ( s) 1 1 essn lim s ( ) K1 s 0 1 Gk ( s ) s 线性系统符合叠加原理,给定和扰动同时作用下系统 1 1 1 K2 的误差 15 ess essr essn K1K 2 K1 K1K 2
sK 2 K 3 lim 2 0 s 0 s (T0 s 1) K1K 2 K 3 (TI s 1)
14
四、给定和扰动同时作用下系统的误差分析 例3-10 图3-15所示系统,求系统的稳态误差 N ( s)
r (t ) t
n(t ) 1(t )
R(s)
_
解: 系统开环传递函数为
12
K1
K2 s
N ( s)
· K3 C ( s) T0 s 1
N ( s)
K1
K2 s
K3 C· ( s) T0 s 1
图3-14 例3-9系统结构图 n(t ) 1(t ) K 2 K3 s K1K 2 K 3 s (T0 s 1) 1 lim Gk ( s ) ssb s (T0 s 1) s 0 1 K1K 2 K 3 s K3 s (T0 s 1) s T0 s 1 1 K 2 K3 1 ssa lim lim s 0 1 K1K 2 K 3 s K1 s 0 s (T0 s 1) K1K 2 K 3 s (T0 s 1) 有稳态误差,其值与扰动作 sK 3 lim 0 用点和误差 E ( s )之间的比例 s 0 s (T0 s 1) K1K 2 K 3 系数成反比
第六节稳态误差分析

Thursday, July 11, 2013
扰动误差与积分环节的关系
e 可见, ssn 不仅与 Gk (s), N (s)有关,还与G2 (s) 有关(扰动点到输 出点之间的那部分前向通道传递函数)。
[例子]:考虑下面两个系统。
N (s ) N (s )
R(s)
-
k1
k2 s
+
(a )
k3 C (s ) R(s) Ts 1
Thursday, July 11, 2013
2
给定输入时的稳态误差表达式
一、给定输入值作用下系统的误差分析 这时,不考虑扰动的影响。由图b,可以写出随动系统的误 差 E (s)为(见右图):
R(s)
E (s )
E ( s) 1 1 , E ( s) R( s ) R(s) 1 G1G2 H 1 G1G2 H
s 0
当 0,1时,K a lim s (1, 2) kG 0 ( s) 0, essr s 0 1 当 2时,K a lim kG 0 ( s ) k , essr s 0 k k 当 3时,K a lim G0 ( s) , essr 0 s 0 s
Thursday, July 11, 2013
12
稳态误差的例子||例3-9
N (s ) k 1 T s 1 2、 再令 R( s ) 0, N (t ) 2 s 2 N ( s) C ( s) 1 Ts s k R(s) E (s ) + C (s) k1 2 s (Ts 1) ' N ( s) 1 k1k 2 Ts s k1k 2 s(Ts 1) Ts 2 s kn Ts 2 s ' C ( s) N ( s) 2 N ( s) Ts s k1k2 Ts s k1k2 Tn s 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
λ2k2=T1+T2
即: λ1 = 1/k2
分子只有s3项时,由终值定理可得: λ2=(T1+T2)/k2
例题2
已知单位反馈系统开
环传递函数为G(s),输
入为r(t),试求稳态误
差ess。
r1(t)=1(t)
10
G1(s) (0.1s 1)(0.5s 1)
解:
系统2不稳定,∴ ess→∞ 系统3的A=2, ∴ ess=1/4
r=0
5
s
2
c(t)
(0.1s+1)(0.5s+1)
∴essn=
-limsC(s) s→0
=
0
几点说明
(2)
① 增益
③ 差异
② 型别
例题4
已知图示系统的调节时间ts= 0.3秒,
试求r(t)=3t时输出端定(义s) 的 误差1终/ k值h ess。
R(s)
1 C(s)
0.01s / kh 1
0.01s
解:
(1)
1
C(s)=
5 (0.1s+1)(0.5s+1) s s(0.1s+1)(0.5s+1)+10
∵系统稳定
r=0
2
(0.1s+1)(0.5s+1)
5 s
c(t)
∴essn=
-limsC(s) s→0
=
-1/2
(1)
(2) C(s)=
2s
1 s
s(0.1s+1)(0.5s+1)+10
n(t)=1(t)
1.25
0.95
0
1
解
1.25
ess 0.05
% 0.3 0.95
tp 1s
0.95
=0.344,n 3.346
或 者 令G(s) 19
解 得G(s)
as 2 19bs 1 1.786s2 4.1s
1
0
1
1、由于 h() 0.95
由 h() lims(s)
设
1A
(s)
0.95
线性系统时域分析
稳态误差例题
例题
λ1s+ λ2s2
E(s) R(s)
k1
求图示系统中的λ1、λ2,使系统由 一阶无差系统变为三阶无差系统。
k2
C(s)
s(T1s+1)(T2s+1)
解或:者由(s1) Φer(s) =
1+
(G1s(s)2求s2出)kG2 (s)后 s1(T1Gs+(1s) (T2s+1)
kh
ts=3T=0.03/kh=0.3
E(s) R(s)
1
30
H(s) 1 G(s)H(s) s(s 10)
∴kh=0.1
ess= 3
例题5 1、试求出该系统的开环传递函数及参数;
2、确定串联校正装置的传递函数,使系统 对阶跃输入的稳态误差为零。
设无零点的单位反馈二阶系统h 2 n s
n2
s0
s
得(s)
s2
0.95 3.3462 2 0.344 3.346s 3.3462
s2
10.636 2.3s 11.196
开环传递函数
G(s)
s2
10.636 2.3s 0.56
2.
Gc (s)
kc s
0 < kc < 0.12
k1k2
s(T1s+1)(T2s+1)
s(T1s 1)(T2s 1) (1s 2s2 )k2
s(T1s+1)(T2s+1)+k1k2
因为一阶无差所以系统稳定,则当
,ess令= Glsi→m(0ss)Φ为er3(型s)R即(s)可。
=
lim
s→0
s
T1T2s3
k1k2
∴ λ1k2=1
A
s3
=0
√ 0型 k=10 ess=1/11
× r2(t)=t
G 2 (s)
s(s
7(s 3) 4)(s2 2s
2)
Ⅰ型
k=21/8 ess= 8/21
r3(t)=t2
8(0.5s 1)
G 3 (s) s2 (0.1s 1)
× Ⅱ型 k=8 ess=1/8
例题3 求图示系统的essn。
n(t)=1(t)
