辐射的量子理论
量子光学

必须指出的是,光量子学说的提出,成功的解释了光电效应现象的实验结果,促进了光电检测理论、光电检 测技术和光电检测器件等学科领域的飞速发展;因此,从这个意义上讲,爱因斯坦是光电检测理论之父。不仅如 此,光量子学说的提出最终导致了量子光学的建立,所以说它是量子光学发展的源头和起点;因此,从这个意义 上讲,爱因斯坦是量子光学的先驱和创始人。尤为重要的是,爱因斯坦在其光量子学说中所提出的有关光量子这 一概念,几经发展形成了当今的光子这一概念,最终导致光子学理论的建立,并由此带动了光子技术、光子工程 和光子产业的迅猛发展;可见,光量子学说是光子学、光子技术、光子工程和光子产业的发端;因此,从这个意 义上讲,爱因斯坦是光子学、光子技术、光子工程和光子产业的先导。除此而外,爱因斯坦在研究二能级系统的 黑体辐射问题时曾提出了受激辐射、受激吸收和自发辐射这三个概念,并形式的引入了爱因斯坦受激辐射系数、 受激吸收系数和自发辐射系数这三个系数等等;特别是受激辐射这一概念的提出,最终导致了激光器的发明、激 光的出现和激光理论的诞生,直至形成了当今的激光技术、激光工程和激光产业;因此,从这个意义上讲,爱因 斯坦本人是当之无愧的激光之父和激光理论的先驱。
图5研究实验
图6量子光学除了单个原子的自发辐射外,还有多个原子在一起时产生的相干自发辐射,也称超辐射。
发展历程
01
光电效应
02
理论体系
03
推向深入
04
学科成就
06
理论规则
05
激光之父
图7 M·普朗克提出了能量子假设众所周知,光的量子学说最初由A.Einstein于1905年在研究光电效应现象 时提出来的[注:光电效应现象包括外光电效应、内光电效应和光电效应的逆效应等等,爱因斯坦本人则是因为研 究外光电效应现象并从理论上对其做出了正确的量子解释而获得诺贝尔物理学奖;这是量子光学发展史中的第一 个重大转折性历史事件,同时又是量子光学发展史上的第一个诺贝尔物理学奖。尽管爱因斯坦终生对科学的贡献 是多方面的(例如,他曾建立狭义相对论和广义相对论等等),但他本人却只获得这唯一的一次诺贝尔物理学奖]。
霍金辐射理论

霍金辐射理论
霍金辐射理论是由英国物理学家斯蒂芬·霍金于1974年提出的量子力学理论,用以描述黑洞的辐射现象。
根据一般相对论,黑洞具有非常强大的引力,以至于连光也无法逃脱其吸引。
然而,霍金通过量子效应的考虑,提出了一个新的理论,即黑洞会通过辐射的方式丢失质量和能量,最终会完全蒸发消失。
具体而言,霍金辐射理论将量子场论和黑洞的物理性质结合起来,通过研究在黑洞的事件视界附近产生和消失的虚粒子,得出了黑洞的辐射机制。
根据该理论,黑洞表面上会产生一对虚粒子,其中一个粒子逃脱黑洞,形成辐射,而另一个粒子则被黑洞吸收,使黑洞质量减小。
据霍金辐射理论,这种辐射通常被称为“霍金辐射”或“霍金效应”。
它预言了黑洞的温度和辐射功率与其质量和表面积成反比关系。
较小质量的黑洞辐射更强烈,辐射时间更短。
当黑洞质量非常低时,辐射效应会更加显著,而当质量趋近于无穷大时,辐射效应趋近于零。
霍金辐射理论的提出对黑洞物理学和量子力学领域有着重要的影响。
它解决了黑洞会一直吞噬物质而不断增长的矛盾,同时也与量子力学的基本原理相符合。
然而,目前尚未有实验证据能够直接证实霍金辐射的存在,因为黑洞辐射非常微弱且难以观测到。
不过,随着技术的进步,人们对于验证该理论的努力正在进行中。
量子力学解释黑体辐射谱

量子力学解释黑体辐射谱黑体辐射谱是指由具有完全吸收和完全发射性质的物体所辐射出的电磁波谱。
在经典物理学中,黑体辐射无法得到很好的解释,而量子力学的发展则提供了更准确的解释和计算方法。
量子力学的基本原理是,微观粒子的能量是量子化的,也就是说,存在一个最小的能量单位,即光子。
光子是电磁波的粒子化表现,其能量与光的频率有关系,由普朗克公式E=hf给出,其中h为普朗克常数,f为光的频率。
在黑体辐射中,物体吸收的能量会导致其内部电子发生激发和跃迁,而发射出的能量会形成辐射光子。
根据量子力学的原理,能量的量子化导致了辐射光子的能量也是离散的。
具体来说,当物体处于较高的温度时,其内部的电子会被激发到较高的能级上,当电子从一个能级跃迁到另一个能级时,能量差可以用一个光子的能量来表示,这个光子的能量对应着一个特定的波长或频率。
根据量子力学的理论,我们可以计算出黑体辐射谱的分布。
普朗克黑体辐射定律给出了黑体辐射功率与波长或频率的关系。
根据定律,黑体辐射功率与波长的关系可以用一个公式来表示,即普朗克公式:B(λ, T) = (2hc^2/λ^5) × (1/(e^(hc/λkT) - 1)其中,B(λ, T)表示单位时间内单位面积的黑体辐射功率,λ表示波长,T表示温度,h为普朗克常数,c为光速,k为玻尔兹曼常数。
根据普朗克公式,我们可以得到黑体辐射谱的分布图像,即黑体辐射谱线。
在低频段(长波段),辐射能量较低,谱线呈现为一个平缓的曲线;随着频率的增加,能量也随之增加,曲线逐渐变得陡峭。
当频率趋近于无穷大时,辐射能量趋于零。
这个分布被称为黑体辐射曲线,也被称为普朗克曲线。
量子力学的解释还提供了对黑体辐射的理论计算。
通过量子力学的数学模型,我们可以计算特定温度下的黑体辐射谱线,并与实验数据进行比较。
这种计算可以更准确地描述和解释黑体辐射的特性。
总的来说,量子力学提供了对黑体辐射谱的解释和计算方法。
通过量子化的能量和光子的概念,我们可以理解和描述黑体辐射谱线的分布规律。
第十四章量子物理基础11

n
波长范围
2,3,4,… 紫外区 91~121.5nm
3,4,5,… 可见光区 364.5~656.3nm
4,5,6,… 近红外区 0.820~1.875μm
5,6,7,… 中红外区 1.46~4.05μm
6,7,8,… 中红外区 2.28~7.46μm
第一节 初始的量子理论
五、玻尔的氢原子理论 玻尔理论的基本假设
转的自旋运动。根据量子力学的计算,电子的自旋角动
量Ls为:
Ls
s(s 1),
s1 2
它在外磁场方向(z轴的方向)的分量Lsz为:
Lsz ms,
1 ms 2
s称为自旋量子数,ms叫做自旋磁量子数。
L l(l 1) h l(l 1) 2π
第二节 四个量子数
五、四个量子数
量子数
可能的取值
(
1 22
1 n2 )
n 3,4,5
里德伯公式
f
c
R
c
(
1 k2
1 n2
)
式中k取1,2,3,…; n是从k+1开始取值的正整数。 这里整数k决定谱线系,n则决定谱线系中的各条谱线。
第一节 初始的量子理论
五、玻尔的氢原子理论
氢原子光谱的各谱线系
谱线系 k 赖曼系 1 巴耳末系 2 帕邢系 3 布喇开系 4 普芬德系 5
为了使薛定谔方程有合理的解,电子绕核运动的角动量L 在外磁场方向(一般取为z轴方向)的分量Lz必须满足以 下量子化条件:
Lz ml
ml=0,±1,±2,…±l 。ml 称为磁量子数
L l(l 1) h l(l 1) 2π
第二节 四个量子数
四、电子自旋与自旋磁量子数
黑体辐射、普朗克能量子假设、光电效应、康普顿效应

实验装置
包括光源、光电管、电压表和电流表 等。
实验操作
实验现象
当入射光频率达到一定值时,光电流出现; 入射光频率越高,光电流越大;当电压达到 一定值时,光电流消失,即出现截止电压。
用不同频率的光照射光电管,观察电 流表示数的变化。
爱因斯坦光电子理论要点
光子假设
01
爱因斯坦提出光是由一份一份的能量子组成,每一份能量子称
光电效应、康普顿效应在现代科技中应用
要点一
光电效应
光电效应是指光照在物质上,引起电 子从束缚状态进入自由状态,从而产 生电流的现象。光电效应在现代科技 中有着广泛的应用,如太阳能电池、 光电传感器等。
要点二
康普顿效应
康普顿效应是指X射线或伽马射线与 物质相互作用时,光子将部分能量转 移给电子,使得光子的频率降低、波 长增长的现象。康普顿效应在医学、 材料科学等领域有着重要的应用,如 放射治疗、材料无损检测等。
实验基础和理论依据。
04 康普顿效应发现过程及科 学价值
康普顿散射实验简介
01
02
03
实验背景
研究X射线通过物质时的 散射现象。
实验装置
X射线管、散射物质(通 常为石墨)、探测器等。
实验过程
X射线照射到散射物质上, 探测器测量散射光的角度 和波长。
散射结果分析与解释
散射光波长变长
实验发现散射光的波长比入射光波长要长,且散射角越大,波长 变化越明显。
普朗克的能量子假设不仅解决了当时物理 学中的一些难题,还推动了物理学的发展 。在能量子假设的基础上,人们逐渐发现 了微观粒子的波粒二象性、不确定性原理 等重要概念,建立了量子力学、量子场论 等现代物理学理论,推动了人类对自然界 的认识不断深入。
普朗克黑体辐射量子理论
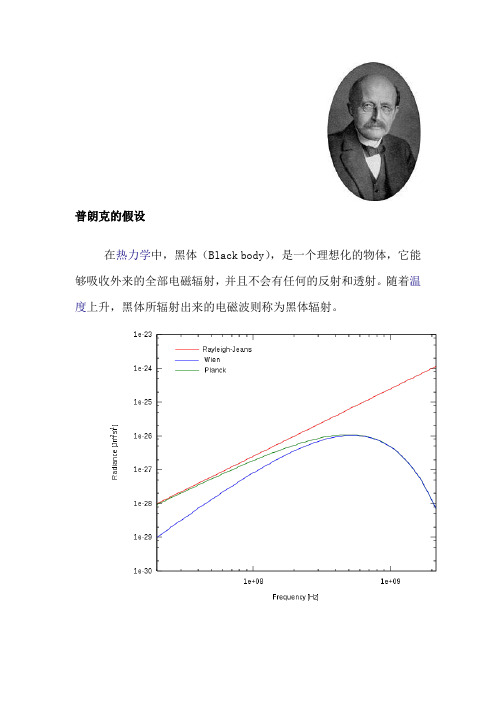
普朗克的假设在热力学中,黑体(Black body),是一个理想化的物体,它能够吸收外来的全部电磁辐射,并且不会有任何的反射和透射。
随着温度上升,黑体所辐射出来的电磁波则称为黑体辐射。
“紫外灾难”:在经典统计理论中,能量均分定律预言黑体辐射的强度在紫外区域会发散至无穷大,这和事实严重违背马克斯·普朗克于1900年建立了黑体辐射定律的公式,并于1901年发表。
其目的是改进由威廉·维恩提出的维恩近似(至于描述黑体辐射的另一公式:由瑞利勋爵和金斯爵士提出的瑞利-金斯定律,其建立时间要稍晚于普朗克定律。
由此可见瑞利-金斯公式所导致的“紫外灾难”并不是普朗克建立黑体辐射定律的动机。
)。
维恩近似在短波范围内和实验数据相当符合,但在长波范围内偏差较大;而瑞利-金斯公式则正好相反。
普朗克得到的公式则在全波段范围内都和实验结果符合得相当好。
在推导过程中,普朗克考虑将电磁场的能量按照物质中带电振子的不同振动模式分布。
得到普朗克公式的前提假设是这些振子的能量只能取某些基本能量单位的整数倍,这些基本能量单位只与电磁波的频率有关,并且和频率成正比。
这即是普朗克的能量量子化假说,这一假说的提出比爱因斯坦为解释光电效应而提出的光子概念还要至少早五年。
然而普朗克并没有像爱因斯坦那样假设电磁波本身即是具有分立能量的量子化的波束,他认为这种量子化只不过是对于处在封闭区域所形成的腔内的微小振子而言的,用半经典的语言来说就是束缚态必然导出量子化。
普朗克没能为这一量子化假设给出更多的物理解释,他只是相信这是一种数学上的推导手段,从而能够使理论和经验上的实验数据在全波段范围内符合。
不过最终普朗克的量子化假说和爱因斯坦的光子假说都成为了量子力学的基石。
爱因斯坦的光电子假设截止电压,最大动能,极限频率,几乎瞬时发射,偏振方向经典理论无法完美解释以上现象1905年,爱因斯坦发表论文《关于光的产生和转化的一个试探性观点》,对于光电效应给出另外一种解释。
量子物理学中的量子自发辐射与受激辐射

量子物理学中的量子自发辐射与受激辐射量子自发辐射和受激辐射是量子物理学中重要的现象,它们在原子和分子的能级跃迁过程中起着关键作用。
本文将探讨这两种辐射现象的基本原理、特性和应用。
量子自发辐射是指原子或分子在外界干扰下,自发地从一个能级跃迁到另一个能级,并辐射出一个光子的过程。
这种辐射是随机的,其发生概率与能级之间的跃迁概率有关。
根据爱因斯坦的关系式,量子自发辐射的速率与能级之间的跃迁概率成正比。
量子自发辐射在自然界中广泛存在,例如,太阳的辐射就是由大量原子和分子的量子自发辐射所产生的。
受激辐射是指原子或分子在外界干扰下,从一个能级跃迁到另一个能级,并且受到一个已经存在的光子的刺激,辐射出与刺激光子相同频率、相同相位和相同方向的光子。
这种辐射是非随机的,其发生概率与刺激光子的强度和频率有关。
受激辐射的速率与刺激光子的强度成正比,与能级之间的跃迁概率成正比。
受激辐射是激光的基本原理之一,激光的产生就是通过受激辐射的过程。
量子自发辐射和受激辐射在原子和分子的能级跃迁过程中有着重要的应用。
在光谱学中,通过研究物质在不同能级之间跃迁时所产生的辐射,可以获得物质的结构和性质信息。
量子自发辐射的频率和强度可以用于确定物质的能级结构和能级之间的跃迁概率。
受激辐射的频率和强度可以用于激光技术,激光在医疗、通信、材料加工等领域有着广泛的应用。
在量子自发辐射和受激辐射的研究中,量子力学的理论框架被广泛应用。
量子力学描述了微观粒子的波粒二象性和量子态的演化规律。
量子自发辐射和受激辐射的发生过程可以通过量子力学的波函数演化来描述。
量子力学的波函数演化方程,如薛定谔方程和密度矩阵方程,可以用于计算量子自发辐射和受激辐射的速率和概率。
除了在理论研究中的应用,量子自发辐射和受激辐射也在实验室中得到了广泛的研究。
通过实验可以测量和控制量子自发辐射和受激辐射的频率、强度和相位。
例如,通过调节外界条件和材料的性质,可以控制量子自发辐射和受激辐射的速率和频率。
大学物理15-1黑体辐射普朗克能量子假设

THANKS FOR WATCHING
感谢您的观看
05 结论
对黑体辐射和普朗克能量子假设的理解
黑体辐射
黑体辐射是物理学中的一个基本概念,它描述了一个理想化 的物体在特定温度下发射电磁辐射的方式。普朗克能量子假 设指出,黑体辐射的能量只能以离散的量子形式发射或吸收 ,每个量子的大小与频率成正比。
普朗克能量子假设
普朗克提出,黑体辐射的能量只能以离散的量子形式发射或 吸收,每个量子的大小与频率成正比。这一假设为量子力学 的发展奠定了基础,是理解微观世界中能量传递和转换的关 键。
能源利用
普朗克能量子假设对于能源利用具有重要启示。例如,在太阳能电池中,光子的 能量被转换成电能。通过理解量子力学原理,可以提高太阳能电池的效率,为可 再生能源利用提供更多可能性。
信息技术
量子力学原理在信息技术领域也有广泛应用。例如,量子计算利用量子比特进行 信息处理,具有超越传统计算机的潜力。通过深入研究和应用量子力学原理,可 以推动信息技术的发展和创新。
04 黑体辐射与普朗克能量子 假设的关系
黑体辐射与量子力学的联系
黑体辐射是物理学中一个经典 的热辐射模型,它描述了一个 理想物体在特定温度下发射的 电磁辐射。
量子力学是描述微观粒子运动 和相互作用的物理学理论。
黑体辐射的实验结果与量子力 学的基本原理密切相关,表明 光和物质在微观层面上具有波 粒二象性。
过程
为了解决这一难题,普朗克提出了能 量子假设,认为能量不是连续变化的, 而是以离散的能量子形式传递。
普朗克能量子假设的内容
01
02
03
内容概述
普朗克假设能量只能以离 散的能量子形式传递,并 且每个能量子的大小与频 率成正比。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(10.3.5)
受激吸收一个光子跃迁速率为
wafi = 2πηn g fikλ 2δ (E f − Ei − ηωk )
(10.3.6)
对末态光子动量和极化求和得
∑ ∑ Γfai = wafi = 2πηn g fikλ 2δ (E f − Ei − ηωk )
kλ
kλ
(10.3.7)
用同自发辐射中同样的方法 在偶极近似下单位时间感应吸收 速率为
∫ ∫ + 1
(iη)2
t
0 dt2
t2 0
dt1
∧
H
I
(t2
)
∧
H
I
(t1
)Φ(0)
+
Λ
若取(10.2.2)前两项 称一级玻恩近似
(10.2.2)
自发辐射一级玻恩近似解释
相互作用使初态 i 演化为
∫ Φ
=
1
+
1 iη
t 0
dt1
H
1
(t
)
i
在此态中出现态 f 的概率振幅为
∫ c fi =
fΦ=
f
(10.3.3)
在推倒(10.3.3)式时利用的n-1个光子系统态矢量的归一化条件
2
1 (n −1)!
(ck+λ )n−1
0
=
1 (n −1)!
0 (ckλ )n−1(ck+λ )n−1 0
=1
跃迁矩阵元为化为
(10.3.4)
f
H1 i
=η
n g ei( E f −Ei −ηωk )t / η fikλ
1 iη
t
0 dt1 H1(t1) i
于是由 i 跃迁到 f 的跃迁速率是
w fi
=
d dt
c fi
2
(10.2.3) (10.2.4)
(10.2.5)
跃迁速率是一个很重要的描写跃迁过程的物理量 由它可以算 出许多可以直接实验测量的量 如激发态的寿命 光谱线的强 度 散射截面等
设初态中有一个i态电子 自发辐射动量为 k 极化为 ελ
符随时间的指数函数关系 故(10.1.15)式给出的也就是相互作用哈
密顿算符在相互作用会景中的形式
若将(10.1.16)式作一次分部积分
和ε
* λ
=
ελ (Θ
A+
=
A)
可证明
g* µνkλ
=
g µν −kλ
并利用横波条件ελ ⋅ k = 0
(10.1.17)
这里暂不考虑相互作用算符中与A2有关的部分 因为它对一级近
µν −kλ µ ν k′λ′
µνk ′λ ′
⋅
1 n!
(ck+λ
)
n
ai+
0
(10.3.9)
算符乘积正规化手续后
f
H1 i
=η
n + 1g e−i(E f −Ei −ηωk )t / η fi − kλ
(10.3.10)
于是电子辐射光子过程的跃迁速率为
∑ ∑ Γfei = wwfi = 2πη(n +1) g fi−kλ 2δ (E f − Ei − ηωk ) (10.3.11)
磁场相互作用的影响而发生 电子场与电磁场相互作用对电子的 影响可看成一种微扰 可用微扰方法讨论自发辐射
相互作用绘景态矢量随时间的变化
iη
∂
Φ(t)
=
∧
HI
Φ(t)
∂t
(10.2.1)
∧
H I 为相互作用哈密顿算符 (10.2.1)式可用迭代法求解
结果为
∫ Φ(t) = Φ(0) + 1
iη
t
∧
0 dt1 H I (t1)Φ(0)
µν −kλ ν µ kλ
其中
(10.1.11) (10.1.12) (10.1.13)
(10.1.14)
(10.1.15)
∫ g µνkλ
=
−
e m
2π Vηωk
ϕ
* µ
eik
⋅x
[ε
λ
⋅
pϕν
( x)]dx
=− e m
2π Vηωk
ϕµ eik⋅xελ ⋅ p ϕν
10.1.16)
其中 p = −iη∇ 在写出(10.1.14)和(10.1.15)式时应用了自由场算
x ϕi
在长波近似下 自发辐射跃迁速率可表为
∫ ∑ Γ
s fi
=
e2ω 3 2πηc3
ελ ⋅ x fi 2 dΩ
λ
(10.2.17)
因 ex fi ≡ d fi 是原子的电偶极矩矩阵 所以长波近似也称为电
偶极近似
对于极化光辐射的情况 (10.2.17)中不对极化方向求和 对非 极化光辐射做如下计算
似中的电子发射或吸收一个光子的过程没有贡献
10.2 自发辐射
自发辐射 电子受电子场—电磁场相互作用而自发辐射光子的过 程
在一次量子化理论中 由于能级的稳定性 自发辐射是不可 能发生的 完整的光发射和吸收理论要借助二次量子化方法
讨论自发辐射的方法 由自发辐射定义知电子自发辐射光子是电子受到电子场与电
i
µνkλ
(10.2.7)
对于式中的算符乘积采取归一化办法 可得
0
a
f
ckλ
aν+
aµ
c+ k ′λ
′ai+
0
= δ kk′δ λλ′δ fν δ iµ
(10.2.7)式简化为
f
H1 i
= ηg e−i(Ei −E f −ηωk )t / η fi − kλ
再应用
∫ ∫ e dt t −iEt1 /η
Γfai
=
n
4e2ω 2 3ηc3
2
x fi
(10.3.8)
其中
ω = (E f − Ei ) / η
受激吸收
在初态存在光子时 电子辐射光子过程的矩阵元一般可表为
f H1 i = 0 a f
1 (n +
1)!
(ckλ
)
n+1
∑ ⋅ (η
g a a c e ) +
+ −i( Eµ −Eν −ηωk′ )t / η
[ ] ∫ H
R 0
=
1 8π
E 2 (x,t) + B2 (x,t) dx
∫ = 1 8π
1
c
2
∂A ∂t
2
+
(∇
×
A)2
dx
10.1.5)
组成
二次量子化系统的哈密顿算符 波函数 ψ (x, t) 和ψ ∗ (x, t) 以及
A 都变成算符 二次量子化系统的哈密顿算符可表为
H = H0 + H1 + H2
由于动量方向变化的连续性 求和变为积分
∑ ∫ ∫ → V
k (2π )3
dk
=
V (2π
)3
k 2dkdΩ
对末态光子有 ηωk = cηk
因此
k 2dk
=
ω
2 k
ηc3
d (ηωk
)
于是得到跃迁速率
∫ ∑ Γ
s fi
=
Vω 2 (2π )2 c3
g fi−kλ 2dΩ
λ
(10.2.13)
自发辐射电偶极近似 下面用偶极近似计算自发辐射跃迁速率 已知
在长波近似下
g fi−kλ
=
−
e m
2π Vηω
ϕf
ελ ⋅p ϕi
在相互作用绘景中 坐标算符的运动方程是
∧
dx dt
=
1∧ [x,
iη
H0]
=
1∧ (x
iη
H0
−
H0
∧
x)
=
p m
(10.2.15) (10.2.16)
于是在H0表象中 有
ϕ f p ϕi
=
m iη
(
Ei
−
Ef
)
ϕ
f
x ϕi
= −imω ϕ f
(10.3.1)
[ck′λ′ , (ck+λ )n ] = n(ck+λ )算符乘积在真空态中的平均值变为
1 n!(n −1)!
0 a f (ckλ )n−1 aµ+aν ck′λ′ (ck+λ )n ai+
0
= nδ kk′δ λλ′δ fµδ iν
x fi ≠ 0 要求 l = l′ ±1, m = m, m′ ±1
于是
∫ Γs ( nlm → n′l ′m′ )
=
4e2ω 3 3ηc3
(l +1) /(2l +1)
l /(2l +1)
∝ 0
Rn′l′
(r ) Rnl
(r)r
3dr
2
可看出 寿命与磁量子数无关 所以应对初态的可能
值 m态求平均 对末态m'求和 即
光子组成的系统 电子受到感应作用吸收了一个光子而转化为f
态的电子
与此过程对应的初态 末态的态矢量为
i
=
1 n!
(ck+λ
)
n
ai+
0
f = 0 af
1 (n −
1)!
(ckλ
)
n−1
相互作用哈密顿算符为
∑ H1 = η
g a a c e +
i( Eµ −Eν −ηωk )t / η
µνkλ µ ν k′λ′
