第一章流体的流动阻力
化工原理第一章第四节流体流动现象
任意截面的总机械能是相等的,即:
3000
6 6'
E1 E2 E3 E4 E5 E6 E
2 2'
2 2 u12 p1 u2 p2 u3 p3 E gz1 gz2 gz3 2 2 2 2 2 2 u4 p4 u5 p5 u6 p6 gz4 gz5 gz6 2 2 2
式中:
2 1
2
1 h 2
1
u2 2 m
s
2 2
2
d2 184 而u1 u2 2 6.7712m s 100 d1
hf1-2=11.38J/kg
Hale Waihona Puke u u p1 z1g p2 z2 g h f 12 2 2
2 2
2 2' 24m
2m 1 1'
u1 p1 u2 p2 gz1 we gz2 h f 12 2 2
由已知: Z1=0,
Z2=24+2=26m,
P1=0(表) u10
P2= 6.15×104Pa(表压)
hf1-2= 160J/kg
Vs 34.5 u2 2.49 m s 2 2 d 0.07 3600 4 4
1000 500
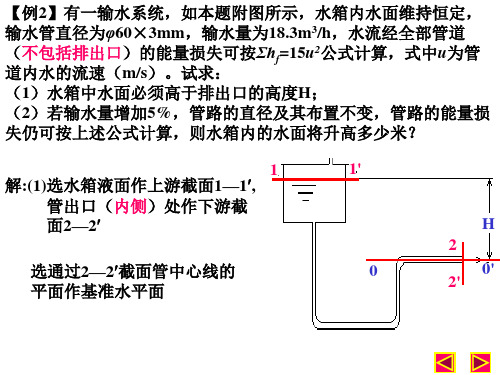
【例4】水在本题附图所示的虹吸管内作定态流动,管路直 径没有变化,水流经管路的能量损失可以忽略不计,试计 算管内截面2-2 、3-3、4-4 、5-5 处的压强。大气压强为 1.0133×105Pa。图中所标注的尺寸均以mm计。 4 解: 选择2-2 截面做基准水平面 4' 3 3' 理想流体,没有外部能量加入, 1 1' 5 5' 因此,根据理想流体柏努利方程,
化工原理ppt-第一章流体流动

其单位为J/kg。
2022/8/11
34
二、流体系统的质量守恒与能量守恒
2. 柏努利方程
(1) 总能量衡算
4)外加能量 流体输送机械(如泵或风机)向流体作功。单位质量流体所获得
的机械能。用We表示,单位J/kg。 5)能量损失
液体流动克服自身粘度而产生摩擦阻力,同时由于管路局部装置 引起的流动干扰、突然变化而产生的阻力。流体流动时必然要消耗 部分机械能来克服这些阻力。单位质量流体克服各种阻力消耗的机 械能称为能量损失。用Σhf ,单位J/kg。
2022/8/11
27
知识运用
【1-3】某自来水厂要求安装一根输水量为30m3/h的管道,试选择一合 适的管子。
解:水的密度:1000kg/m3, 体积流量:Vs=30000/(3600×1000)=0.0083(m3/s)
查表水流速范围,取u=1.8m3/s
根据d 4Vs
u
d 4Vs 4 30 / 3600 0.077 m 77mm
22
一、流体流量和流速
2.流速
单位时间内流体质点在流动方向上所流经的距离。
(1)平均流速:u=Vs/A (m/s)
关系:G =u
(2)质量流速:G=Ws/A (kg/(m2·s))
2022/8/11
23
一、流体流量和流速
3.圆形管道直径的选定
2022/8/11
24
一、流体流量和流速
3.圆形管道直径的选定
2022/8/11
8
二、流体压力
2.表压与真空度
表压和真空度
p 当地大气压,
表压强=绝对压强-大气压强
p 当地大气压,
真空度=大气压强-绝对压强
化工原理第一章 流体流动

§1.3 流体流动的基本方程
质量守恒 三大守恒定律 动量守恒 能量守恒
§1.3.1 基本概念
一.稳态流动与非稳态流动 流动参数都不随时间而变化,就称这种流动为稳态流 动。否则就称为非稳态流动。 本课程介绍的均为稳态流动。
§1.3.1 基本概念
二、流速和流量
kg s 质量流量,用WS表示, 流量 3 体积流量,用 V 表示, m s S
=0 的流体
位能 J/kg
动能 静压能 J/kg J/kg
流体出 2 2
实际流体流动时:
2 2 u1 p1 u2 p gz1 we gz2 2 wf 2 2
摩擦损失 J/kg 永远为正
流体入 ------机械能衡算方程(柏努利方程) 1
z2
有效轴功率J/kg
z1 1
二、 液体的密度
液体的密度基本上不随压强而变化,随温度略有改变。 获得方法:(1)纯液体查物性数据手册
(2)液体混合物用公式计算:
液体混合物:
1
m
xwA
A
xwB
B
xwn
n
三、气体的密度
气体是可压缩流体,其值随温度和压强而变,因此 必须标明其状态。当温度不太低,压强不太高,可当作理
想气体处理。
理想气体密度获得方法: (1)查物性数据手册 (2)公式计算: 或
注:下标0表示标准状态。
对于混合气体,也可用平均摩尔质量Mm代替M。
混合气体的密度,在忽略混合前后质量变化条件下, 可用下式估算(以1 m3混合气体为计算基准):
m A x VA B x VB n x Vn
2
2
气体
第一章 流体流动

气体密度 一般温度不太低,压强不太高时气体可按理想气 体考虑,所以理想气体密度可由理想气体状态方程 导出: T0 p M pM m
v
RT
0
Tp 0
0 22.4 ,kg / m
3
混合气体密度
ρm= ρ1y1+ ρ2y2+ …+ ρnyn
MT0 p 22.4Tp 0
式 y1、y2……yn——气体混合物各组分的体积分数 ρ1、 ρ2、…、 ρn—气体混合物中各组分的密度,kg/m3; ρm——气体混合物的平均密度,kg/m3;
2.2 流体静力学基本方程的应用
1、压力的测量 (1) U型管压差计 构造: U型玻璃管内盛指示液A 指示液:指示液A(蓝色)与被测液B(白)互不相溶,且ρA>ρB 原理:图中a、b两点在相连通的同一静止流体内,并且在 同一水平面上,故a、b两点静压力相等,pa=pb。 对a、b两点分别由静力学基本方程,可得 pa= p1+ρB· g(Z+R) pb= p2+ρB· gZ+ρAgR
三、流体的研究方法
连续介质假说:流体由无数个连续的质点组
成。﹠质点的运动过程是连 续的 质点:由许多个分子组成的微团,其尺寸比 容器小的多,比分子自由程大的多。 (宏观尺寸非常小,微观尺寸又足够大)
四、流体的物理性质
◆密度ρ 单位体积流体的质量,称为流体的密度,其表 m 达式为
V
式中 ρ——流体的密度,kg/m3; m——流体的质量,kg; V——流体的体积,m3。 流体的密度除取决于自身的物性外,还与其温 度和压力有关。液体的密度随压力变化很小,可 忽略不计,但随温度稍有改变;气体的密度随温 度和压力变化较大。
pA=p0+ ρgz pB=p0+ ρi gR 又∵ pA=pB
化工原理第一章流体流动知识点总结

第一章流体流动一、流体静力学:压强,密度,静力学方程二、流体基本方程:流速流量,连续性方程,伯努利方程三、流体流动现象:牛顿粘性定律,雷诺数,速度分布四、摩擦阻力损失:直管,局部,总阻力,当量直径五、流量的测定:测速管,孔板流量计,文丘里流量计六、离心泵:概述,特性曲线,气蚀现象和安装高度8■绝对压力:以绝对真空为基准测得的压力。
■表压/真空度 :以大气压为基准测得的压力。
表 压 = 绝对压力 - 大气压力真空度 = 大气压力 - 绝对压力1.1流体静力学1.流体压力/压强表示方法绝对压力绝对压力绝对真空表压真空度1p 2p 大气压标准大气压:1atm = 1.013×105Pa =760mmHg =10.33m H 2O112.流体的密度Vm =ρ①单组分密度),(T p f =ρ■液体:密度仅随温度变化(极高压力除外),其变化关系可从手册中查得。
■气体:当压力不太高、温度不太低时,可按理想气体状态方程计算注意:手册中查得的气体密度均为一定压力与温度下之值,若条件不同,则需进行换算。
②混合物的密度■ 混合气体:各组分在混合前后质量不变,则有nn 2111m φρφρφρρ+++= RTpM m m=ρnn 2211m y M y M y M M +++= ■混合液体:假设各组分在混合前后体积不变,则有nmn12121w w w ρρρρ=+++①表达式—重力场中对液柱进行受力分析:液柱处于静止时,上述三力的合力为零:■下端面所受总压力 A p P 22=方向向上■上端面所受总压力 A p P 11=方向向下■液柱的重力)(21z z gA G -=ρ方向向下p 0p 2p 1z 1z 2G3.流体静力学基本方程式g z p g z p 2211+=+ρρ能量形式)(2112z z g p p -+=ρ压力形式②讨论:■适用范围:适用于重力场中静止、连续的同种不可压缩性流体;■物理意义:在同一静止流体中,处在不同位置流体的位能和静压能各不相同,但二者可以转换,其总和保持不变。
1.4流体流动阻力

hf
l d
2g
m
压力损失
pf
l d
u2
2
Pa
该公式层流与湍流均适用;
注意 p与 pf 的区别。
5
返回
三、层流时的摩擦系数
速度分布方程
又
1 u 2 umax
umax
( p1 p2 )
4l
R2
R d 2
32lu
( p1 p2 ) d 2
32lu
pf d 2
(2)结果具有普遍性,便于推广。 基础:量纲一致性
即每一个物理方程式的两边不仅数值相等, 而且每一项都应具有相同的量纲。
8
返回
基本定理:白金汉(Buckingham)π 定理 设影响某一物理现象的独立变量数为n个,
这些变量的基本因次数为m个,则该物理现象可 用N=(n-m)个独立的无量纲数群表示。 湍流时压力损失的影响因素:
——哈根-泊谡叶 (Hagen-Poiseuille)方程
6
返回
能量损失
32lu Wf d 2
层流时阻力与速度的一次方成正比 。
变形:
Wf
32lu d 2
64 l du d
u2 2
64 l Re d
u2 2
比较得
64
Re
7
返回
四、湍流时的摩擦系数 1. 量纲分析法 目的:(1)减少实验工作量;
2
流体的摩擦力: F A πdl
定态流动时
( p1
πd 2 p2 ) 4
πdl
Wf
4l
d
化工原理 第五节 流动阻力
管
化工原理
第一章 流体流动
6/18
莫狄(Moody)图
0.10 0.09 0.08 0.07 0.06 0.05 0.04
l u wf d 2
d
2
0.05 0.04 0.03 0.02 0.015 0.01 0.008 0.006 0.004 0.002
0.03 0.025
64 Re
阻力平方区
d
0.02
水力光滑管 Re
层 流 区
103 2
0.015
0.01 0.009 0.008
过 渡 区
4 68 104 2
Re,
d
0.001 0.000 0.0006 0.0004 0.0002 0.0001 0.00005 0.00001
化工原理
0 0.5
u2 小管中的大速度
第一章 流体流动
17/18
化工原理
第一章 流体流动
18/18
化工原理
第一章 流体流动
19/18
蝶阀化工Biblioteka 理 第一章 流体流动20/18
(动画2)
化工原理 第一章 流体流动
21/18
(动画3)
化工原理 第一章 流体流动
22/18
总结:
管路系统的总阻力损失为
Re
0.04 0.03 0.025 0.02 0.015
Re , d
d
0.01 0.008 0.006 0.004 0.002
d
0.001 0.000 0.0006 0.0004
0.0002 随着 Re 数的增大,/d 对的影响越来越重要, 0.0001 0.00005 相反,Re 数对的影响却越来越弱。Why? 0.01
流体在管内的流动阻力
l / d:管子的长径比;
du
Pf
: 雷诺数Re;反映流体的流动状态和湍动程度
u
2
: 欧拉准数,以Eu表示 。表示压力降与惯性力之比
数群(4)=变量(7)-基本因次(3)
3)数据处理
湍流流动,实验证明,l/d的指数b=1 。
Pf
l u 2 p f d 2 p f l u2 hf d 2
—— 圆形直管阻力所引起能量损失的通式( 对于滞流或 湍流都适用),范宁公式。 λ为无因次的系数,称为摩擦因数 。
f (Re, / d )
2、 层流时的直管阻力损失
P 2 d umax 2u umax R R 4l 2 d 2 Pf P d 2 u 2u ( ) 32 l 4l 2
个无因次数群,减少变量数目。
π定理: i=n-m i----无因次数群个数 n----物理量个数 m----量纲个数
3)数据处理:建立过程的无因次数群之间的关系。 一般常采用幂函数形式π1=kπ2απ3β 线性化:1ogπ1=1ogk+α1ogπ2+β1ogπ3 线性回归参数:k、α、β
因次分析法 特点:通过因次分析法得到数目较少的无因次变量,按无因 次变量组织实验,从而大大减少了实验次数,使实验简 便易行。 依据:因次一致性原则 白金汉(Buckinghan)所提出的π定理。 凡是根据基本的物理规律导出的物理量方 因次一致原则 : 程 f ( , ,... ) 0, 1 2 i 式中各项的因次必然相同,也就是说,物理 量方程式左边的因次应与右边的因次相同。
用幂函数表示为:p f 各物理量的因次:
k.d l u
a b c e f
p ML1t 2 3 ML1t 1 L ML
化工基础概论 第一章 流体流动与输送
Re 4000 时,是湍流流动; 2000 Re 4000时,有时出现层流,有时出现湍流,是一个不稳定的区域,称
为过渡区。在一般工程计算中,当 Re 2000 时可按湍流处理。
1.2.3直管阻力的计算
经过大量的实验研究发现,流体流过直管的阻力与其流体的动能 u2/2、管长 l 成 正比,与其管径成反比,即:
l u2 hf d 2
(J/kg)
(1-7)
式中 h f ——直管阻力,J/kg;
——摩擦系数;
l ——直管长度,m; d ——管内径,m;
u ——流体在管内的平均流速,m/s。
1.2.3直管阻力的计算
式(1-7)为直管阻力计算通式,称为范宁公式。范宁公式还可以写成以下两种 形式:
le u 2 h d 2
' f
(J/kg)
(1-13)
式中:d、u、 分别为与管件相连接的直管管件、管内流体平均流速以及摩擦系 数。各种管件和阀门的当量长度可由有关手册查得,表 1-1 列出了常见管件的
le d 值,即当量长度 le 与管内径 d 的比值。
1.2.5减小流动阻力的途径
(1)减小直管阻力的途径
l u 2 p f d 2
(Pa) (m)
(1-8) (1-9)
l u2 Hf d 2g
式中 p f ——直管压力降,Pa;
H f ——直管损失压头,m。
范宁公式不仅适用于层流, 也适用于湍流的阻力计算, 但式中摩擦系数 的 处理方法不同。 当流体在圆形直管内作层流流动时:
•
1.1.2流量
(1)体积流量
(2)质量流量
(1)体积流量
单位时间内流经管道任一截面上的流体体积量,称为体积流量,用符号 VS 或 Vh 表示,单位为 m3/s 或 m3/h。
第四讲流体的流动阻力(第一章)
0.5
u∞
u∞
0.376 .2 x (Re0 x )
0.8
δ
A
x0
x
层流内层
平板上的流动边界层
x增加,湍流边界层的厚度δ比层流边界层的厚度δ增加得快
圆形直管中:
u
u∞ δ
u∞ δ
u∞ δ
u∞
x0
圆管进口处层流边界层的发展
x0(进料段距离)以后为充分发展的流动
x0 0.0575 Re ——适用于层流流动 d
p1 p2 2 2 ur (R r ) 4l
或
p1 p2 2 r2 ur R (1 2 ) 4l R
可见,圆形直管内层流流动的速度分布为一抛物线 壁面处速度最小,0
管中心处速度最大 umax
p1 p2 2 R 4l
Re ≤2000
umax
u
层流时流体在圆管中的速度分布
lgHf d
c b e 45°
a
lguc
lguc´
lgu
下临界点 上临界点
三、流体的流动型态(Type of flow pattern)
2 u 流型判据——雷诺(Reynolds)准数: Re u L M d L 3 du L L0 M 0T 0 Re T M
损失。
⑤
流动边界层的分离 流体绕固体表面的流动
(a)当流速较小时 流体贴着固体壁缓慢流过 (爬流)。
(b) 流速不断提高,达到某一程度时,边界层分离
分离点
驻点
A B u( uB、pA减小至pB、p / x 0 A u 0)增加至
BC
uB减小至u( 、pB增加至pC、p / x 0 C u 0)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
的圆形管。当量直径用de表示,水力半径用rH表示。
我们来一下圆管的直径:
内径为d,长为l,其内部可供流体流过的体积
为πd2l/4,其被润湿的内表面积为πdl,因此有 下列关系:
π 2 πd d l 流通截面积 4 4 d 4 4 4 πdl πd 润湿周边长
2
对非圆形管:可以类比上式而得到其当量直径为:
实际管的当量粗糙度 管壁粗糙度对阻力系数λ的影响首先是在人工 粗糙管中测定得。人工粗糙管是将大小相同得砂 粒均匀地粘着在普通管壁上,人为地造成粗糙度, 因而其粗糙度可以精确测定。工业管道内壁得凸 出物形状不同,高度也参差不齐,粗糙度无法精 确测定。实践上通过试验测得阻力损失并计算λ 值,然后由图1-27反求处相当得相对粗糙度,称 为实际管道得当量相对粗糙度。由当量相对粗糙
与壁面间出现边界层分离,产生漩涡,因此有能
量损失。
②突然缩小
突然缩小时,流体在顺压强梯度下流动,不
致于发生边界层脱离现象,因此在收缩部分不会 发生明显的阻力损失。但流体有惯性,流道将继 续收缩至O-O面后又扩大。这时,流体在逆压强梯 度下流动,也就产生了边界层分离和漩涡。因此 也就产生了机械能损失,由此可见,突然缩小造
流通截面积 d 4 润湿周边长
对长a,宽b为的矩形管道:
ab d e 4 2a b
当a>3b时,此式误差比较大。
对于外管内径为d1,内管外径为d2的套管环
隙
π 2 2 d1 d 2 4 d e 4 d1 d 2 π d1 d 2
• 一套管换热器,内管与外管均为光滑管, 直径分别为垆 30x2.5mm与 56X3mm。平 均温度为400C的水以每小时10m3的流量流 过套管的环隙。试估算水通过环隙时每米 管长的压强降。
二、层流时的摩擦系数
l u 32 Lu p f h f p 2 d 2 d
2
上式称为哈根-泊谡叶方程,是流体在圆直管
内作层流流动时的阻力计算式,Δp是层流时流体
的内摩擦力引起的压力降。层流时压力降Δp与流
速u成正比,
管壁粗糙度可用: 绝对粗糙度ε(ε指壁面凸出部分的平均高度) 相对粗糙度ε/d ε相同的管道,直径d不同,对λ的影响就不
1阻力系数法
• 克服局部阻力所引起的能量损失可表示为 2 动能 u / 2的一个函数
u2 即 hf 2 2 u p f ' 2 式中 称为局部阻力系数。下面列举几种常用的局部阻力系数的求法。
'
⑴突然扩大与突然缩小
①突然扩大
流体流过如图所示的突然扩大管道时,由于
流股离开壁面成一射流注入了扩大的截面中,然 后才扩张道充满整个截面。由于流道突然扩大, 下游压强上升,流体在逆压强梯度下流动,射流
4l 4 2 l u 2 hf dl u2 d 2
8 2 u
长径比,无因次
l u hf d 2
摩擦因数
2
l u △ p f hf d 2
动能
2
上式就是范宁(Fanning)公式。范宁公式既适用层流, 也适用湍流。λ是无因次的系数,称为摩擦系数,它是雷 诺数的函数或者是雷诺数与管壁粗糙度的函数。
度可以求出当量得绝对粗糙度
非圆形管的当量直径 前面讨论得都是圆形管道。在工业生产中经常 会遇到非圆形截面的管道或设备。如套管换热器 环隙,列管换热器管间,长方形的通分管等。对 于非圆形管内的流体流动,必须找到一个与圆形 管直径相当的量,为此类似当量粗糙度引入当量 直径的概念,以表示非圆形管相当与直径为多少
成的阻力主要还在于突然扩大。
1
2
2
0
1
1
2
2
0
1
a. 突然扩大
b. 突然缩小
进口与出口
当流体从小管流到大容器,如流到大空间时,
S1/S2≈0,则ζ=1 。而当流体从大容器流到
小管,S2/S1≈0,则ζ=0.5 。 注意流体流速用小管内的流速计算阻力。
管件与阀门
二、当量长度法
能产生与局部阻力相同的沿程阻力所需的
1.5
流体流动阻力
流体流动阻力产生的原因是流体有粘性,在流
动中产生内摩擦力,而内摩擦力是阻碍流体流动的
力,即阻力,可见,流体的粘性是产生流体流动阻
力的内因。根据前面的讨论可知,流体只有在渡过
固体壁面(管壁或设备壁)时,才能促使流体内部产
生相对运动(即产生内摩擦)。所以说,壁面及其形 状等因素是流体流动阻力产生的外因。
同。故一般用相对粗糙度ε/d来考虑对λ的影响。
①层流:层流时,管壁上凹凸不平的地方都被有
规则的流体层所覆盖,而流速又比较缓慢,流体
质点对管壁凸出部分不会有碰撞作用,所以层流
时λ与ε无关,粗糙度的大小并未改变层流的速
度分布和内摩擦规律。
②湍流时,前面我们已知道,湍流时靠管壁处总 是存在一层层流内层,其厚度设为δb,若δb > ε,则此时管壁粗糙度对λ的影响与层流相近,
流体在流动过程中要克服这些阻力,需要消耗一部 分能量,这一能量即为柏努利方程式中的∑hf项。 流体流动阻力也相应分为直管阻力(或称沿程阻力)
生产用管路主要由直管和管件、阀门等两部分组成,
和局部阻力两类。
流体在直管中的流动阻力
一、直管阻力计算式 如附图所示,不可压缩性流体以速度u在内径
下面对一段水平直管内流动的流体作受力分析,
管道长度
le u p d 2
/ f
2
le 称为管件或阀门的当量长度,其单位为m。
管路系统中的总能量损失
管路系统中的总能量损失常称为总阻力损失,
是管路上全部直管阻力与局部阻力之和。
l le u hf d 2
2
h f 管路系统中的总能量损失,J/kg
le 管路系统全部管件与阀门等的当量长度之
为d 的管内作稳定流动。 作用在截面1-1′上的力为
F1 p1 A1 p1
4
d2 d2
F2 p2 A2 p2
4
F1 F2 ( p1 p2 )
4
d2
F S dl
( p1 p2 )
4
d 2 dl
4l p1 p2 hf d
和,m
l 管路系统各段直管的总长度,m
u
流体流经管路的流速,m/s
1.5.2管路上的局部阻力
化工管路中的管件种类繁多,流体流过各种管件
都会产生阻力损失。和直管阻力的沿程均匀分布
不同,这种阻力损失是由管件内的流道多变所造 成,因而称为局部阻力损失。局部阻力损失是由 于流道的急剧变化使流动边界层分离,所产生的 大量漩涡,使流体质点运动受到干扰,因此即使 流体在直管内是层流流动,但当它通过管件或阀 门时也是很容易变成湍流。
• 解:设套管的外管内径为d1,内管的外径为d2。水通过 环隙的流速为
• 水的流通截面A= = 0.001 26m2
• 所以
u=ห้องสมุดไป่ตู้2.2m/s
• 环隙的当量直径为 de=4rH
•
rH .
• 所以 de=4x. =d1-d2=0.05-0.03=0.02m
• 由本教材附录七查得水在400C时, 992kg/m3, =65.6x10-5Pa· s。 • 于是 Re= =6.65X104 • 从计算结果可知属于紊流.从图1-27光滑管的曲线上查得 在此Re值下. • 根据是1-43a得水通过环隙时每米管长得压降为 •
若δb<ε,则管壁突出部分便伸入湍流区与流体
质点发生碰撞,便湍流加剧,此时ε对λ的影响
便成的主要因素。Re越大,层流内层越薄,这种
影响越显著。当Re增大到一定程度,层流内层薄
得使表面得凸出完全暴露在湍流区内,则在增大
Re,只要ε一定,λ就一定了,此时就进入了阻 力平方区,即阻力损失与u2成正比:hf∝u2 。
