几何画板实验一
巧用几何画板 开展数学实验教学

思 维, 更好 地完 成 教学 任 务创 造 了优 为
异 的条件 。 信 息 技术 与语 文 教学 有机 地 整合 ,
点燃 了绚丽 多 彩 的语 文世 界, 语文 课 为 堂注 入新 的活 力, 打造 一片 新 的天 空, 提
稿 件 编 号 : P 0 2 6 1107
作者 简介:张建军,本科 ,中教 高级。陈唐 明,本科 ,中教 高级 。
AB > F2 度 量 线 段 B M
,
该方程 的解 , 因此 方程 X ‘一( 口一1 =0无解 。从而 由 )
师: ( 稍作 停顿 )有没 有 同学有不 同看 法 ? 片刻沉 默之 后, 有学 生举手 , 示意他 回答 。 笔者 生2 :我 觉 得 有 点 问题 。原 方 程 有 唯 一 解 , 方 程 对
住, 管雪 花 曲线 的 周长 趋 向于 无 穷大 , 尽 但雪 花 曲线 永远 不会超 出这 个正 方形 。
此 时, 出 问题 :() 圆相 交 的条件 是什 么?2两 半 提 1两 ( ) 径之 差 是 多少 ?3怎 样 使两 圆相 交 ?4点P 足 的几 何 条 () () 满 件是什 么?5怎样 出现 双 曲线 的两支 ?6通过上 述实 验, () () 你
问题 的 能力 , 时培 养 了学生 自主 探 索 能 力与 合 作交 流 同 意 识 。真 正做 到 了知识 与技 能 、方法 与过程 、情 感态 度 与价 值观 “ 三维 目标 ”的和 谐统 一 。
三 、利 用 “ 何 画 板 ”做 数 学 实 验 —— 几 在运 动 与变 化 中突 破 静 态思 维 的束 缚
美, 学 生看 后 心 旷神 怡 、浮 想联 翩 。激 发 了学 生 的好 让 奇心 和 内心 探 索 未 知世 界 的欲 望, 以饱满 的热 情 投入 到 数 学 学 习 中 。而 在 学生 亲 自实 践操 作 中, 不仅 能 及 时巩 固所 学 知识 , 增 强 了学 生 发现 问题 、分 析 问题 、解 决 还
几何画板中的度量功能实验报告:椭圆的画法

几何画板中的度量功能实验报告一、 实验目的1. 学习应用数学知识原理来指导绘制圆锥曲线。
2. 掌握几何画板中的建立坐标系,绘制已知点以及运用几何画板中内置计算器计算比值的方法,掌握度量菜单的用法。
3. 应用几何画板中的操作类按钮的功能动态显示圆锥曲线的变化状况。
二、 实验原理圆锥曲线基本定义,椭圆的参数方程以及椭圆的标准方程。
实验内容:根据椭圆的不同定义,标准方程以及参数方程,绘制不同的椭圆曲线。
三、 实验仪器PC 计算机; 软件工具:几何画板5.04 四、实验课时:6课时 五、实验步骤 (一)知识储备椭圆的第一定义:平面内与两定点F 1、F 2(即焦点)的距离的和等于常数的动点P 的轨迹叫做椭圆. 其数学表达式为:|PF 1|+|PF 2|=2a (2a >|F 1F 2|),焦距:|F 1F 2|=2c ≤2a.椭圆的第二定义:平面内到定点F(c ,0)的距离和到定直线l :ca x 2=(F 不在l 上)的距离之比为常数,即离心率ace =(0<e<1)的点的轨迹是椭圆. (二)椭圆的画法:1、根据椭圆的第一定义画椭圆:2种画法。
2、缩放法画椭圆3、双圆法画椭圆(三)各种画法的实验步骤1、根据椭圆的第一定义画椭圆:有两种画法 画法一:(1)新建页:【文件】-【文档选项】-【增加页】-【空白页面】,命名为:根据椭圆的第一定义画椭圆——画法一。
(2)构造控制台:选择【线段工具】,在空白处画线段AB ,选中线段AB ,【构造】-【构造线段上的点】(点C ),选中点C ,【度量】-【点的值】(xx ____上在AB C ),【数据】-【计算】-输入 :上在____1AB C ,选中比值,鼠标右击-【标记比值】。
(3)画圆:选择【点工具】,在空白处,作点D 、点E ,双击点D ,选中点E ,【变换】-【缩放】-【按标记比进行缩放】-【确定】,得到点E ’(通过拖动点C ,可以控制点E ’的位置,从而改变下面的椭圆的离心率。
几何画板实验报告册

几何画板实验报告册几何画板实验报告册一、引言几何画板是一种用于绘制几何图形的工具,它由一个平面板和一些固定在板上的钉子组成。
通过在钉子之间穿线,我们可以创造出各种美丽的几何图形。
本实验报告将介绍几何画板的原理、实验过程以及实验结果,并对其应用进行探讨。
二、实验原理几何画板的原理基于线段之间的连线。
当我们在画板上选择两个钉子,并用线段连接它们时,我们可以得到一条直线。
同样,当我们选择三个钉子并连接它们时,我们可以得到一个三角形。
通过在不同的钉子之间连接线段,我们可以创造出更复杂的几何图形,如四边形、五边形等。
三、实验过程1. 准备实验材料:几何画板、彩色线或线团。
2. 将几何画板放在平坦的桌面上。
3. 选择两个钉子,并在它们之间拉一条线段,得到一条直线。
4. 选择三个钉子,并在它们之间拉线段,得到一个三角形。
5. 继续选择更多的钉子,并在它们之间拉线段,创造出更多的几何图形。
6. 使用不同颜色的线团,使图形更加鲜明。
7. 拍摄实验过程中的照片,以备后续分析。
四、实验结果通过实验,我们创造了多个几何图形,包括直线、三角形、四边形、五边形等。
这些图形在几何学中具有重要的意义,并且在日常生活中也有广泛的应用。
通过使用不同颜色的线团,我们可以使图形更加美观,增加观赏性。
五、实验分析几何画板实验不仅仅是一种简单的娱乐活动,它还有着深远的教育意义。
通过实践操作,我们可以更直观地理解几何学中的基本概念和定理。
例如,在创造三角形的过程中,我们可以体验到三条边之间的关系,从而更深入地理解三角形的性质。
此外,几何画板实验还培养了我们的观察力和创造力,激发了我们对几何学的兴趣。
六、应用探讨几何画板不仅可以用于教学和学习,还可以应用于其他领域。
例如,在建筑设计中,几何画板可以帮助建筑师绘制精确的图纸,并确保建筑结构的几何形状符合要求。
在艺术创作中,几何画板可以成为艺术家创作灵感的来源,帮助他们创造出独特而美丽的几何艺术作品。
小学数学实验2210几何画板如何制作平行线

小学数学实验2210几何画板如何制作平行线制作平行线的方法有许多种,以下是一种简单的方法:
材料:
-2210几何画板
-铅笔
-直尺
-量角器(可选)
步骤:
1.准备画板:在画板上找到一个合适的位置,清洁画板确保表面平整。
2.画出基准线:使用直尺,画一条直线,作为平行线的基准线。
这条
基准线可以是任意长度和方向。
3.确定平行线的距离:使用直尺,在基准线的任意一点上,测量出与
基准线平行的距离。
这个距离可以是任意长度,可以使用直尺上的刻度线
进行测量。
4.确定平行线的位置:在基准线上选择一个起点,使用直尺以所测得
的距离,在基准线上画出一点。
这个点将成为平行线上的一个点。
5.连接两点:使用直尺,将新画出的点与基准线上的起点连接起来,
画一条直线。
6.判断平行关系:使用直尺,将直线与基准线进行比较。
如果它们是
平行的,那么它们之间的距离将保持不变。
可以使用直尺的刻度线进行测量,以验证距离是否相等。
注意事项:
-在制作平行线时,直尺应该放置平稳,确保直线的笔直。
-使用铅笔绘制直线时,要保持适量的压力,以免将直尺移动,导致
直线不准确。
-可以使用量角器来确保所画的线与基准线之间的夹角一致,以确保
平行关系。
制作平行线的方法还有很多种,以上介绍的只是其中的一种简单方法。
在实际操作中,可以根据需要选用不同的方法,以便更方便地绘制平行线。
同时,不同的实验目标和实验要求也可能需要采用不同的制作方法。
几何画板实验报告.doc

%1.实验目的:学会使用变换中的旋转按钮
%1.实验步骤:
%1画出一条线段;
%1选中线段左端点双击,标记中心;
%1选中线段和另-端点,选择变换中的旋转按钮,并设置旋转角度为
90°,然后在依次做出另外两条边。
%1.实验结果
实验二
一实验内容:构造三角形的中线
二实验目的:学会构造线段中点
三实验步骤:
%1单击线段工具,构造出一个三角形ABC;
%1选中线段AB,执行构造-中点命令,构造出AB中点D
%1单击线段工具,连接CD.
四实验结果
实验三
一实验内容:构造三角形的外心
二实验目的:学会构造线段的中垂线
三实验步骤:
%1单击线段工具,构造出一个三角形ABC;
%1选中线段AB,执行构造■中点命令,构造出AB中点D,同时选中
AB和D,执行构造-垂线
%1在AC±重复②,两垂线交点即为外心
四实验结果
一实验内容:绘制三角形的内心
二实验目的:学会构造巳知角的平分线
三实验步骤:
%1画出任意三点A, B, C,选中A,B.C三画,执行构造-线段,构造 出三角形ABC;
%1依次选中B,A,C,执行构造-角平分线,构造出ZBAC的角平分线i;
%1按照②的步骤做出ZABC的角平分线j;
%1选中i, j,执行构造■中点命令,构造出三角形内心D;
%1选中i, j,执行显示-隐藏平分线,隐藏平分线。
四实验结果:
实验一五
一实验内容:绘制函
三实验步骤:
%1执行绘图-定义坐标系命令,新建坐标系,并将原点坐标的标签设 为0;
%1执行数据-新建函数命令,新建函数y = r;
几何画板基本操作实验报告

几何画板基本操作实验报告一、实验目的1、认识几何画板2、能够使用几何画板的基本绘图工具绘制简单的图形3、掌握动画按钮的制作方法。
二、实验原理通过点的变化来引起动态参数的变化,从而充分体现正弦函数振幅,周期以及初相的变化而引起的函数图像的变化。
三、实验内容绘制函数sin()y A xωφ=+的图像,观察函数的振幅、周期和初象分别与Aωφ、、之间的关系。
四、实验课时:4课时五、实验步骤(略)1、绘制方法:线段坐标法和参数法2、绘制步骤(1)线段坐标法:①新建页:【文件】-【文档选项】-【增加页】-【空白页面】,命名为:三角函数——线段坐标法。
②绘制坐标系:点击【绘图】-【定义坐标系】,右击【隐藏网格】③设置角度单位:【编辑】-【参数选项】,将角度的单位改为【弧度】④选定自变量:在x轴上任取一点F,【度量】-【横坐标】,度量值为X F⑤选取动态的振幅、周期:在x轴上选取两个点H、I,选中两点,点击【变换】→【平移】,固定距离为1厘米,固定角度为90°。
选中H、H’构造射线,并在射线上选取一点,右击此点【属性】-【标签】-(改变振幅A)。
再次选中此点,【度量】-【纵坐标】,并将度量值的标签改为“A”。
选中I、I’构造射线,并在射线上选取一点,右击此点【属性】-【标签】-(改变周期ω)。
再次选中此点,【度量】-【纵坐标】,并将度量值的标签改为“ω”。
⑥选取动态的初相位:选中原点D和单位点E,【构造】-【以圆心和圆周上的点作圆】,【构造】-【圆上的点】,将圆上的点标签改为“改变初相位φ”,依次选中点E、D、改变初相位φ,【度量】-【角度】,将度量的角度值标签改为“φ”。
⑦建立函数并绘制图像:【数据】-【计算】→运用A、ω、φ输入:A*sin(ω*X F+φ),点击确定。
依次选中X F、Asin(ωX F+φ),【绘图】-【绘制点()(P)】,点的标签为“J”,【选中点J】-【选中点F】-【构造】-【轨迹】⑧隐藏不需要显示的对象:选中要隐藏的对象,【编辑】-【操作类按钮】-【显示/隐藏】,点击按钮:【隐藏对象】。
几何画板实验报告
选中线段BC和点A构造垂线,垂足为H,同理得到垂足L、K,三条垂线的交点为M;
选中点A和M构造线段,再选中线段AM构造中点O,同理得到点N、P;
选中点E、P、O构造过三点的弧,选中点O、D、E构造过三点的弧;
4、作出两圆的内外公切线。
外公切线步骤:
构造两圆C、D,圆心分别为C、D(注:圆C的半径大于圆D的半径);
S移至点P处,并设置动画按钮。
③同理作出点V在圆O的另一半弧上,标记角度QOV,分别使三角形KBL绕点K、三角形MEN绕点M,按标记角度旋转,并设置点V的动画按钮。
4、(1)用轨迹功能绘出球面,
(2)运用缩放、平移、轨迹功能绘出球冠。
实验步骤:
作一个圆A,过点A作一平行的直线交圆A于点C,取圆上一点D,选中点D、直线
选中点C、D,构造直线CD;
在圆D上任意取一点F,连接构造线段DF;
选中点C、线段DF,构造平行线交圆C于点G、P
选中点G、F,再构造直线GF交直线CD于点H;
选中点D、H,构造线段DH,再构造线段DH的中点M;
依次选中M、D(H),接着“构造”—“以圆心和圆周上的点作圆”—“生成一个圆M交圆D于点O和N;
作一圆o用直线连接点op交圆于点q依次选中点opq作过三点的弧作弧上一点s用虚线段连接点os依次选中点sop标记角度双击点i选中三角形ijc的三边和顶点jc按标记角度旋转得到三角形ijc将点s移至点p处并设置动画按钮
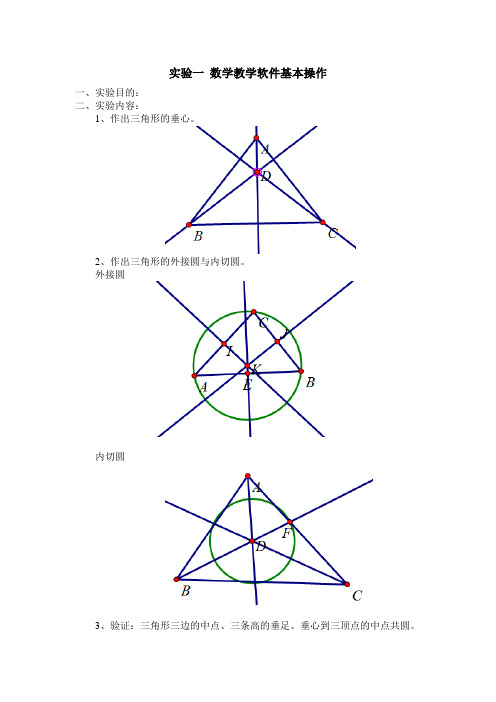
实验一数学教学软件基本操作
一、实验目的:
二、实验内容:
1、作出三角形的垂心。
2、作出三角形的外接圆与内切圆。
分别构造出直线OH和直线NH,即为所求的外公切线。
几何画板基本操作实验报告

几何画板基本操作实验报告1. 实验目的通过本实验,我们旨在探索和熟悉几何画板的基本操作,包括创建几何图形、编辑图形属性、进行几何变换等。
2. 实验环境•操作系统:Windows 10•软件:几何画板版本2.03. 实验步骤3.1 创建一个几何图形在几何画板中,我们可以通过以下步骤创建一个几何图形:1.打开几何画板软件。
2.在工具栏中选择所需的几何图形工具,例如直线、矩形、圆等。
3.在画板上点击并拖动鼠标,确定图形的位置和尺寸。
4.松开鼠标左键,完成图形的创建。
3.2 编辑图形属性在几何画板中,我们可以对已经创建的图形进行属性编辑,包括颜色、线条粗细、填充颜色等。
1.选中需要编辑属性的图形。
2.在属性栏中选择所需的属性编辑选项,例如颜色选择器、线条粗细调节器等。
3.根据需要调整属性值。
4.属性值调整完成后,点击确认按钮,应用新的属性值。
3.3 进行几何变换在几何画板中,我们可以对已经创建的图形进行各种几何变换,包括平移、旋转、缩放等。
1.选中需要进行几何变换的图形。
2.在变换工具栏中选择所需的几何变换工具,例如平移工具、旋转工具、缩放工具等。
3.根据需要拖动鼠标或调节值,完成几何变换。
4.点击确认按钮,应用几何变换。
4. 实验结果我们在几何画板中按照以上步骤进行了几何图形的创建、属性编辑和几何变换等操作,实验结果如下:1.创建了一个直线图形,并通过属性编辑修改了颜色和线条粗细。
2.创建了一个矩形图形,并通过属性编辑修改了填充颜色。
3.进行了平移、旋转和缩放等几何变换操作,使图形发生变化。
5. 实验分析通过本次实验,我们掌握了几何画板的基本操作技巧,进一步了解了几何图形的创建、属性编辑和几何变换等内容。
几何画板作为一个强大且易于操作的软件工具,能够帮助我们有效地进行几何图形的绘制和编辑工作。
不仅可以用于教学和研究领域,还可以应用于工程设计和艺术创作等方面。
同时,几何画板还具有以下优点:•界面友好:几何画板提供直观的界面,易于操作和学习。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
步骤:
一、(1)任意作两个圆,圆 ,圆 (圆 半径大于圆 ),
(2)连接两圆圆心,以其为直径做圆,记为圆 ,
(3)以 为圆心,两圆的半径差为半径做小圆,
(4)连接 与小圆和圆 的交点作直线,交圆 于 ,分别过 作
的垂线,则得到两圆的外切线。
二、(1)任意作两个圆,圆 ,圆 (圆 半径大于圆 ),
实验一.数学教学软件(几何画板)基本操作
实验内容:
1、做出三角形的垂心。
2、做出三角形的外接圆与内切圆。
3、验证:三角形三边的中点、三条高的垂足、垂心到顶点的中点共圆。
4、作出两圆的内外公切线。
第一题:做出三角形的垂心。
步骤:
分别作三角形 三边的垂线,交于一点 ,
则可得到 为三角形的垂心:
第二题:做出三角形的外接圆与内切圆。
步骤:
(1)作出三边中点,
(2)作三条高的垂足,交于一点,段,分别作出线段中垂线,交于一点。即这些点的圆心 ,
(5)以圆心到以上任意点距离为半径作圆,这些点都在这个圆上,共圆。
所以可知三角形三边的中点、三条高的垂足、垂心到顶点的中点共圆。
存在问题:由于对软件和知识点的不熟悉,实验过程中需要思考后才能制作出需要的图形。
步骤:
(1)作出三角形 两条边的中垂线,交于一点 就是外接圆圆心,以外接圆圆心到顶点距离为半径做圆,就是外接圆。
(2)做出三角形 两个角的角平分线,交于一点 就是内切圆圆心,再过任意一边与内切圆圆心垂线,交相应边于一点,以内切圆圆心到垂足的距离为半径做圆就是内切圆。
则可得到三角形的内切圆和外接圆:
第三题:验证:三角形三边的中点、三条高的垂足、垂心到顶点的中点共圆。
(2)连接两圆圆心,以其为直径做圆,记为圆 ,
(3)以 为圆心,两圆的半径和为半径做大圆,
(4)连接 与大圆和圆 的交点作直线,交圆 于 ,分别过 作
的垂线,则得到两圆的内切线。
则得到两圆的内外公切线:
实验结论及其存在的问题:
结论:通过本次实验学会了几何画板的基本的绘图方法,第一题学会如何使用几何画板绘制垂线;第二题学会如何绘制角平分线和圆;第三题学会掌握一些基本操作,并证明了三角形三边的中点、三条高的垂足、垂心到顶点的中点共圆,用几何画板直观的表现出来;第四题通过画两圆的外切线和内切线,让我们知道利用几何画板制图时要运用数学的思想方法,才会得到我们想要的图形。既熟练了几何画板的使用,又锻炼了我们的思维能力。
