概率论例题
概率论总结及例题
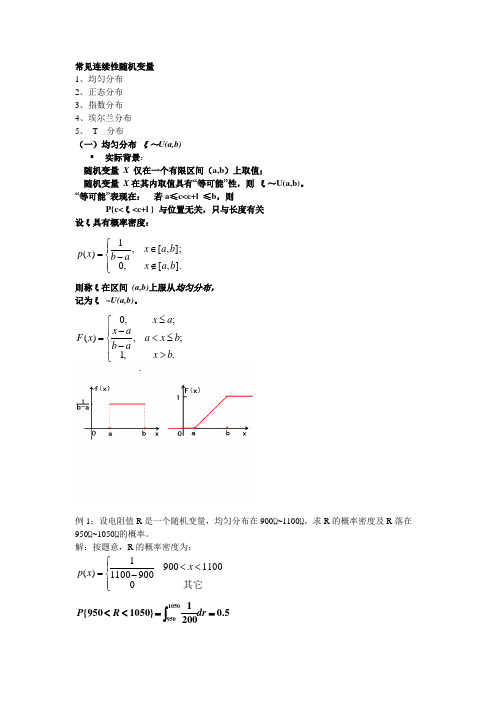
常见连续性随机变量1、均匀分布2、正态分布3、指数分布4、埃尔兰分布5、 T 分布(一)均匀分布 ξ~U(a,b)▪ 实际背景:随机变量 X 仅在一个有限区间(a,b )上取值;随机变量 X 在其内取值具有“等可能”性,则 ξ~U(a,b)。
“等可能”表现在: 若a ≤c<c+l ≤b ,则P{c<ξ<c+l } 与位置无关,只与长度有关设ξ具有概率密度:则称ξ在区间 (a,b)上服从均匀分布,记为ξ ~U(a,b)。
例1:设电阻值R 是一个随机变量,均匀分布在900Ώ~1100Ώ,求R 的概率密度及R 落在 950Ώ~1050Ώ的概率。
解:按题意,R 的概率密度为:⎪⎩⎪⎨⎧∉∈-=].,[,0];,[,1)(b a x b a x a b x p ⎪⎩⎪⎨⎧>≤<--≤=.,1;,;,0)(b x b x a a b a x a x x F ⎪⎩⎪⎨⎧<<-=其它0110090090011001)(x x p 5.02001}1050950{1050950==<<⎰dr R P例2 ξ ~ U (2, 5). 现在对 ξ 进行三次独立观测,试求至少有两次观测值大于 3 的概率.解:记 A = { ξ > 3 },则 P (A ) = P ( ξ> 3) = 2/3设 Y 表示三次独立观测中 A 出现的次数,则 Y ~ B (3, 2/3),所求概率为P (Y ≥2) =P (Y =2)+P (Y =3)=20/27(二)正态分布(normal distribution )记为ξ ~ N (μ, σ2),其中σ >0, μ 是任意实数.➢ μ 是位置参数➢ σ 是尺度参数.正态分布的性质(1) p (x ) 关于μ 是对称的. 在μ 点 p (x ) 取得最大值.(2) 若σ 固定, μ 改变, p (x )左右移动, 形状保持不变.(3) 若μ 固定, σ 改变,σ 越大曲线越平坦; σ 越小曲线越陡峭标准正态分布N (0, 1)密度函数记为 ϕ(x ),分布函数记为 Φ(x ).Φ(x ) 的计算(1) x ≥ 0 时, 查标准正态分布函数表.(2) x < 0时, 用 若 ξ ~ N (0, 1), 则(1) P (ξ < a ) = Φ(a );(2) P (ξ≥a ) =1-Φ(a );(3) P (a ≤ξ<b ) = Φ(b )Φ-(a );(4) 若a ≥ 0, 则P (|ξ|<a ) = P (-a <ξ<a ) = Φ(a )Φ-(-a ) = Φ(a )- [1- Φ(a )] = 2Φ(a )-1230233*********C C =+⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭2()(),22x p x x μσ⎧⎫-⎪⎪=--∞<<∞⎨⎬⎪⎪⎩⎭R x dt e x F x t ∈=⎰∞---,21)(222)(σμσπ1(1) (0),2Φ=(2)()1()x x Φ-=-Φ()1().x x Φ=-Φ-例2.5.1 设 ξ ~ N (0, 1), 求P (ξ>-1.96) , P (|ξ|<1.96)解: P (ξ>-1.96)= 1- Φ(-1.96) = 1-(1- Φ(1.96)) = Φ(1.96)= 0.975 (查表得)P (|ξ|<1.96)= 2 Φ(1.96)-1= 2 ⨯0.975-1= 0.95例2.5.2 设 ξ ~ N (0, 1), P (ξ ≤ b ) = 0.9515, P (ξ ≤ a ) = 0.04947, 求 a , b . 解: Φ(b ) = 0.9515 >1/2,所以 b > 0,反查表得: Φ(1.66) = 0.9515,故 b = 1.66而 Φ(a ) = 0.0495 < 1/2,所以 a < 0,Φ(-a ) = 0.9505, 反查表得:Φ(1.65) = 0.9505,故 a = - 1.65一般正态分布的标准化 结论1 设 ξ ~ N (μ, σ 2), 结论2:若 ξ ~ N (μ, σ 2), 则 若 ξ ~ N (μ, σ2), 则P (ξ<a ) = , P (ξ>a ) = 例2.5.3 设ξ ~ N (10, 4), 求 P (10<ξ<13), P (|ξ-10|<2).解: P (10<ξ<13) = Φ(1.5)Φ-(0) = 0.9332 - 0.5= 0.4332P (|ξ -10|<2) = P (8<ξ<12)= 2Φ(1)-1= 0.6826例2.5.4 设 ξ ~ N (μ, σ 2), P (ξ ≤ -5) = 0.045,P (ξ ≤ 3) = 0.618, 求 μ 及 σ.解:μ = 1.76σμξη-=()x F x μσ-=Φ⎛⎫ ⎪⎝⎭a μσ-⎛⎫Φ ⎪⎝⎭1a μσ-⎛⎫-Φ ⎪⎝⎭5 1.6930.3μσμσ+⎧=⎪⎪⎨-⎪=⎪⎩σ =4课堂练习(1)已知ξ~ N(3, 22), 且P{ξ>k} = P{ξ≤k}, 则k = ( ).课堂练习(2)设ξ~ N(μ, 42), η~ N(μ, 52), 记p1 = P{ξ≤μ-4},p2 = P{η≥μ +5}, 则( )①对任意的μ,都有p1 = p2②对任意的μ,都有p1 < p2③只个别的μ,才有p1 = p2④对任意的μ,都有p1 > p2课堂练习(3)设ξ~ N(μ , σ2), 则随σ的增大,概率P{| ξ-μ | <σ} ( )①单调增大②单调减少③保持不变④增减不定▪例假设在设计公共汽车车门的高度时,要求男子的碰头机会在1%以下,设男子的身高ξ(cm)服从正态分布,ξ~ N (170,36),问车门高度至少应为多高?实际背景:如果一个随机现象是由大量微小的相互独立的因素共同构成,那么描述这种随机现象的随机变量通常被认为服从或近似服从正态分布.在自然现象和社会现象中,大量随机变量都服从或近似服从正态分布。
概率论期末知识要点及书写规范例题

1 −1 e 3 fX (x) = 3 0
x>0 el se
2 y fY ( y ) = 0
0 ≤ y ≤1 其他
求 : E ( XY ) 和 E ( X + Y )
ˆ x = −46.1557, ˆ =y − b a
经验回归直线方程为: 经验回归直线方程为:
∧ ∧
(3分)
Xi p
0 1/2
1 1/2
∑ P{ X
k=0
3
= k }P { A X = k }
k = 0,1, 2, 3,
…7分
∑
k=0
3
k P{X = k}⋅ 6
3
k 3− k P{ X = k } = C 3 C3 / C 63 ,
1 6
∑ kP { X
k=0
= k} =
1 1 3 1 EX = ⋅ = 6 6 2 4
解法1: (1) X的可能取值为0,1,2,3,X 的 k 3− k 3 概率分布为 P{ X = k } = C3 C3 / C6 , k = 0,1, 2, 3, 即 因此, EX=0×1/20+1×9/20+2×9/20+3×1/20=3/2 5分
已知甲、 已知甲、乙两箱中装有同种产品, 其中甲箱 装有3件合格品和3件次品, 乙箱中装有3件合格 品, 从甲箱中任取3件放入乙箱后, 求: (1) 乙箱中次品件数X的数学期望; 的数学期望; (2) 从乙箱中任取一件产品是次品的概率. (2)设A表示事件“从乙箱中任意取出的一 件产品是次品”, 根据全概率公式, 有
(3分) (2分)
3 × 0.6 P ( B1 A) P ( B1 ) P ( A | B1 ) 5 = 0.517(4分) P ( B1 | A) = = = 0.696 P ( A) P ( A)
概率论典型例题

P{ X 0} P{ X 2}
P{ X 0} P{ X 2} P{ X 5}
22 . 29
---
例2 设离散型随机变量 X 的分布函数为
0, x 1,
a,
1 x 1,
F
(
x
)
2 3
a,
1 x 2,
a b, x 2.
且 P{ X 2} 1 ,试确定常数a,b,并求 X 的分布律. 2
---
例5 设某仪器上装有三只独立工作的同型号电子 元件,其寿命(单位 : 小时)都服从同一指数分布,其
中参数 1 600,试求在仪器使用的最初200小时
内,至少有一只元件损坏的概率a. [思路] 以 Ai (i 1,2,3) 分别表示三个电子元件“在 使用的最初 200 小时内损坏”的事件, 于是 a P{ A1 A2 A3 } 1 P( A1 A2 A3 )
C B AB.
---
例3 假设目标出现在射程之内的概率为0.7,这时 射击命中目标的概率为0.6, 试求两次独立射击至 少有一次命中目标的概率.
[思路] 引进事件 A {目标进入射程}; Bi {第i次射击命中目标}, i 1,2.
故所求概率为事件B B1 B2的概率,由于目标 不在射程之内是不可能命中目标的, 因此 , 可利 用全概率公式来求解.
---
例4 设有来自三个地区的各10名、15名和25名考 生的报名表,其中女生的报名表分别为3份、7份和
5 份, 随机地取一个地区的报名表,从中先后抽出 两份.
(1) 求先抽到的一份是女生表的概率 p;
(2)已知后抽到的一份表是男生表,求先抽到 的一份是女生表的概率 p.
[思路] 由于抽到的表与来自哪个地区有关,故此 题要用全概率公式来讨论.
概率论典型例题

20
4
故Y
~
B
⎛ ⎜⎝
3,
1 4
⎞ ⎟⎠
。
于是
C P{Y = 2} =
2⎛ 3 ⎜⎝
1 4
⎞2 ⎟⎠
⎛ ⎜⎝
3 4
⎞ ⎟⎠
=
9 64
。
注:本例既需要掌握二项分布的由来及其概率分布,还需掌握连续型随机变
量由密度函数求其在某个区间上的取值概率。 有离散也有连续,需要区分清楚,
掌握牢固,这是容易出问题的地方。
解:(1)当 y > 0 时,
FY ( y) = P(Y
≤
y)
=
P
⎛ ⎜⎝
1 X
≤
y
⎞ ⎟⎠
=
P
⎛ ⎜⎝
1 X
≤
0
⎞ ⎟⎠
+
P
⎛ ⎜⎝
0
<
1 X
≤
y
⎞ ⎟⎠
当 y < 0 时,
=
P(X
<
0) +
⎛ P⎜
⎝
X
≥
1 y
⎞ ⎟ ⎠
=
FX
(0) +1−
FX
⎛ ⎜ ⎝
1 y
⎞ ⎟
;
⎠
FY ( y) =
P(Y
≤
X2 0
1
4
9
pk 0.1 0.3 0.3 0.3
注:对离散型随机变量,其函数的分布列的求法比较简单。只要从分布列定
义中包含的两部分:可能取值与对应概率出发,必定能求出。
另外,值得提醒的是,如果分布列中有未知参数,一定要通过分布列的性质
(一般是归一性的应用),将其求出,再进行其他计算。
《概率论与数理统计》典型例题

《概率论与数理统计》典型例题第一章 随机事件与概率例1.已知事件,A B 满足,A B 与同时发生的概率与两事件同时不发生的概率相等,且()P A p =,则()P B = 。
分析:此问题是考察事件的关系与概率的性质。
解:由题设知,()(P AB P A B =∩),则有()()()1()1()()()P AB P A B P A B P A B P A P B P AB ===−=−−+∩∪∪而,故可得。
()P A p =()P B =1p −注:此题具体考察学生对事件关系中对偶原理,以及概率加法公式的掌握情况,但首先要求学生应正确的表示出事件概率间的关系,这三点都是容易犯错的地方。
例2.从10个编号为1至10的球中任取1个,则取得的号码能被2或3整除的概率为 。
分析:这是古典概型的问题。
另外,问题中的一个“或”字提示学生这应该是求两个事件至少发生一个的概率,即和事件的概率,所以应考虑使用加法公式。
解:设A :“号码能被2整除”,B :“号码能被3整除”,则53(),()1010P A P B ==。
只有号码6能同时被2和3整除,所以1()10P AB =,故所求概率为 5317()()()()10101010P A B P A P B P AB =+−=+−=∪。
注:这是加法公式的一个应用。
本例可做多种推广,例如有60只球,又如能被2或3或5整除。
再如直述从10个数中任取一个,取得的数能被2或3整除的概率为多少等等。
例3.对于任意两事件,若,则 A B 和()0,()0P A P B >>不正确。
(A )若AB φ=,则A 、B 一定不相容。
(B )若AB φ=,则A 、B 一定独立。
()若C AB φ≠,则A 、B 有可能独立。
()若D AB φ=,则A 、B 一定不独立。
分析:此问题是考察事件关系中的相容性与事件的独立性的区别,从定义出发。
解:由事件关系中相容性的定义知选项A 正确。
概率论例题汇总

边缘分布为
7
若改为无放回摸球,则(X,Y)的联合分布律为
X
Y
0
3 10 3 10 3 5
1
3 10 1 10 2 5
3 5 2 5
X
Y
0
9 25 6 25
3 5
1
6 25 4 25 2 5 3 5 2 5
0
1
0
1
边缘分布为
与有放回的情况比较, 两者的联合分布完全不同,
i 1
5 0.1 2 0.2 1 0.3 4 0.4 1 .
EX 2 xi2 pi
i 1 4
4 0.1 1 0.2 0 0.3 1 0.4 1 .
24
例2 设随机变量 X ~ N (0,1), 求 E ( X 2 ) 解 E( X )
4 xy, 0 x 1, 0 y 1 (1) f1 ( x, y ) 其他 0,
8 xy, 0 x y, 0 y 1 (2) f 2 ( x, y ) 其他 0,
讨论X ,Y 是否独立?
16
4 xy, 0 x 1, 0 y 1 f1 ( x, y ) 其他 0, 1 解 (1)经计算得边缘密度为
( 3 ) 概 率 P{ X Y 1 } .
y x
解 (1)
1 0
x 0
f ( x , y ) dxdy
0 1 x
dx cy( 2 x ) dy
c 1 5 24 2 ( 2 x ) x dx c 1 , c . 5 2 0 24
概率论典型例题共102页

38、若是没有公众舆论的支持,法律 是丝毫 没有力 量的。 ——菲 力普斯 39、一个判例造出另一个判例,它们 迅速累 聚,进 而变成 法律。 ——朱 尼厄斯
40、人类法律,事物有规律,这是不 容忽视 的。— —爱献 生
21、要知道对好事的称颂过于夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
23、一切节省,归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰,决心到最后会全部推倒。——莎士比亚
25、学习是劳动,是充满思想的劳动。——乌申斯基
谢谢!
概率论第一章例题

1
333 2000
250 2000
83 2000
3. 4
例4 某接待站在某一周曾接待过 12次来访,已知 所有这 12 次接待都是在周二和周四进行的,问是 否可以推断接待时间是有规定的.
解 假设接待站的接待时间没有
规定,且各来访者在一周的任一天
中去接待站是等可能的.
17 27
解 将产品编号, 1, 2, 3 为一等品 ; 4 号为二等品 . 以 (i, j) 表示第一次、第二次分别取到第 i 号、第
j 号产品, 则试验的样本空间为 {(1,2), (1,3), (1,4), (2,1), (2,3), (2,4) , ,
(4,1), (4,2), (4,3)},
因为 333 2000 334, 所以 P( A) 333 ,
6
2000
由于 2000 250, 故得 P(B) 250 .
8
2000
由于 83 2000 84, 得 P( AB) 83 .
24
2000
于是所求概率为
P( AB) 1 {P( A) P(B) P( AB)}
3. 古典概型的基本模型:摸球模型
(1) 无放回地摸球
问题1 设袋中有4 只白球和 2只黑球, 现从袋中无
放回地依次摸出2只球,求这2只球都是白球的概率.
解 设 A {摸得 2 只球都是白球},
基本事件总数为 A62,
AP所( A包)含 基A42 本A62事件52.的个数为或A42,
不考虑顺序
C42种 C22种
2个
2个
因此第1、2个杯子中各有两个球的概率为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
概率论例题
例1.设某班车起点站上车人数X 服从参数为λ(λ>0)的泊松分布,并且中途不再有人上车。
而车上每位乘客在中途下车的概率为p )1p 0(<<,且中途下车与否相互独立,以Y 表示在中途下车的人数。
试求(1)(X,Y )的联合概率分布律;(2)求Y 的分布律(列)。
解:X 可能的取值是0,1,2,…..,k ,…,n ,... P{X =k }=
!
k e k λ
λ-
Y 可能的取值是0,1,2,…,r ,…,k
P{x =k, y =r }=P{x=k}P{y=r/x=k}=
!
k e k λ
λ-r k r r k q p C - r=0,1,2,…,k
当r>k 时,P{x=k, y=r}=0, Y 的边缘分布
P{Y = r }=∑+∞
===0
},{k r y k x P =∑+∞
====0
}/{}{k k x r y P k x P =∑
+∞
=--r
k r k r r k k
q p C e k λλ!
=∑+∞
=--+--r k r k r
q r r k k k k p e )(!)
1()1(!
1)
(λλλ =∑+∞=---r k r
k r
rq r k r p e )()!
(1!1)(λλ
=rq r e r p e --!1)(λλ=rp r e r p -!)(λ r = 0, 1, 2, … , 验证Y 的分布律
∑+∞
==0
}{r r y P = 1 ?
例2. 解 因为η只取非负值,所以当0y ≤时,
2()()
()
F y P y P y ηηξ=<=<
=
当
0y >时
2()()())
F y P y P y y y ηηξξ=<=<=<
2
2
2
2
12()t t t dt dt dt ξ--===
2
20
u u y
y
e
-
-=
=⎰
⎰
所以
20
,0()0,0u y y F y y η-⎧>⎪=⎨⎪≤⎩⎰
1
y --⎧
这样平均来说,可以减少40%的工作量.
例4.按规定,某车站每天8:00-9:00,9:00-10:00都恰有一辆客车到站,但到站的时刻是随机的,且两者到站的时间相互独立. 其规律为
一旅客8:20到车站,求他候车时间的数学期望. 解 设旅客的候车时间为X (以分计). X 的分布律为
在上表中,例如
其中A 为事件“第一班车在8:10到站”,B 为“第二班车在9:30到站”. 候车时间的数学期望为
32132
()10+30+ 50+ 70+ 90=27.2266363636
E X =⨯⨯⨯⨯⨯(分).
例5.某商店对某种家用电器的销售采用先使用后付款的方式. 记使用寿命为X (以年计),规定:
1X ≤, 一台付款1500元; 12X <≤ ,一台付款2000元;
23X <≤,一台付款2500元;3X >,一台付款3000元.
设寿命X 服从指数分布,概率密度为
10
1, 0 ()100 , 0x
e x
f x x -⎧>⎪=⎨⎪⎩
≤
试求该商店对上述家电收费(Y 元)的数学期望.
解 先求出寿命X 落在各个时间区间的概率,即有
1
/10
0.10
1{1}d 10.0952,10x P X e x e --==-=⎰
≤ 2
0.20.310
1
1{12}d 0.086110
x P X e x e e ---<==-=⎰
≤,
3/10
0.20.321{23}d 0.077910
x P X e x e e ---<==-=⎰
≤, 0.310
3
1{3}d 0.0740810
x P X e x e ∞
-->===⎰
. 一台收费
得()2732.15E X =,即平均一台收费2732.15元. □
例6 ()max ,M X Y =及()min ,N X Y =的分布 设,X Y 是两个相互独立的随机变量,它们的分布函数分别为()X F x 和()Y F y .现在来求()max ,M X Y =及()min ,N X Y =的分布函数.
由于()max ,M X Y =不大于z 等价与X 和Y 不大于z ,故有
{}{},P M z P X z Y z =≤≤≤.
又由于X 和Y 相互独立,得到()max ,M X Y =的分布函数为
(){}{}{}{}max ,F z P M z P X z Y z P X z P Y z ===≤≤≤≤≤
即有
()()()m a x X Y F z F z F z =.
类似地,可得到()min ,N X Y =的分布函数为
(){}{}{}{}{}min 11,1F z P N z P N z P X z Y z P X z P Y z ==->=->>=->⋅>≤.
即 ()()()m i n 111X Y F z F z F z =---⎡⎤⎡⎤⎣⎦⎣⎦.
例7.有2个相互独立工作的电子装置,它们的寿命 (1,2)k X k = 服从同一指数分布,其概率密度为
1, 0 ()0.0 , 0x e x f x x θθ-⎧>⎪=>⎨⎪⎩
,
≤,
若将这2个电子装置串联联接组成整机,求整机寿命(以小时计)N 的数学期望.
解 (1,2)k X k =的分布函数为
1,0,()0,0.
x e x F x x θ-⎧⎪
->=⎨⎪⎩≤
由第三章§5(5.8)式12min(,)N X X =的分布函数为
22min 1, 0()1[1()] 0, 0
x
e x F x F x x θ-⎧⎪
->=--=⎨⎪⎩≤
因而N 的概率密度为
2min , 0
()2
0, 0x
e x
f x x θθ-⎧>⎪=⎨⎪⎩
≤ 于是N 的数学期望为
2/min 0
2()()d d 2
x x
E N xf x x e x θθ
θ
∞
∞
--∞
=
==
⎰⎰
.
例8.一民航机场的送客车载有20位旅客,自机场开出,旅客有10个站可以下车。
如果到达一个车站没有人下车则不停车。
以X 表示停车的次数,求E X (设每位旅客在各个车站下车是等可能的, 并设各旅客是否下车相互独立)。
解 引人随机变量
0, 1,2,
,10.1,i i X i i ⎧==⎨⎩
在第站没有人下车,在第站有人下车,
易知 1210.X X X X =++
+ 现在来求()E X .
按题意, 任一旅客在第i 站不下车的概率为10
9
, 因此20位旅客都不在第i 站下车的概率为(
109)20,在第i 站有人下车的概率为1-(10
9
)20,也就是 202099
{0}(),{1}1(),1,2,
,10.1010
i i P X P X i ====-=
由此
209
()1(),1,2,
10.10
i E X i =-=
进而 1210()()E X E X X X =+++
121020
()()()
9 10[1()]8.784().
10
E X E X E X =++
=-=次。
