22.1.2二次函数y=ax2图像与性质
22.1.2二次函数y=ax2的图象和性质

知识点三
画二次函数的图象,列表时取的点越多,图象往往越准确,但是 一般采用“五点法”或“七点法”画图,画图时应注意: (1)描点法所画的图象只是整个函数图象的一部分,是近似的, 由于x可取一切实数,所以图象是向两方无限延伸的; (2)点取得越多,图象画得越精确,在限定条件下(即限定自变量 的取值范围)或在实际问题中,函数的图象必须要根据自变量 的取值范围取其中的一部分; (3)所画图象必须平滑(符合点的发展变化的趋势),尤其是顶点 不能画成“尖”形的.
22.1.2
二次函数y=ax2的图象和性质
知识点一
知识点二
知识点三
知识点一二次函数y=x2的图象和性质 二次函数y=ax2+bx+c的图象是抛物线,对称轴与抛物线的交点叫 做顶点,顶点是抛物线的最低点或最高点. 对于特殊的二次函数y=x2,对称轴是y轴,顶点是(0,0),顶点是它的 最低点,在对称轴的左侧,抛物线从左到右下降;在对称轴的右侧,抛 物线从左到右上升.也就是说,当x<0时,y随x的增大而减小;当x>0 时,y随x的增大而增大. 名师解读:理解和记忆二次函数的性质时,可以从y=x2得到启发, 其他二次函数的图象及性质可类比y=x2的图象和性质,主要从开口 方向、对称轴、顶点、增减性等几个方面去进行.
知识点一
知识点二
知识点三
知识点二y=ax2的图象 一般地,抛物线y=ax2的对称轴是y轴,顶点是原点.当a>0时,抛物线 的开口向上,顶点是抛物线的最低点;当a<0时,抛物线的开口向下, 顶点是抛物线的最高点.对于y=ax2,|a|越大,抛物线的开口越小. 名师解读:二次函数y=ax2的图象是抛物线,结合图象可知,二次项 系数a的符号决定了开口方向,|a|决定了开口的大小.
人教版九年级上册数学 22.1.2 二次函数 y=ax2的图象和性质课件

a<0
1 -5-4-3-2-1 -1o1 2 3 4 5 x -2 -3 -4 -5 -6 -7 -8 -9 1 -10 y x2
y
2
y 2 x 2
y x2
总结性质
1.形如二次函数 y=ax2 的图象都是顶点为
( 0 , 0) ______ 的抛物线,反之,顶点在(0,0)
2 y = ax 的抛物线的形式是_________.
体验画图
抛物线的定义:
实际上,二次函数的图象是抛物线,
它们开口向上或向下,一般地,二次
函数 y ax bx c 的图象叫做抛
2 2
物线 y ax bx c .
体验画图
3. 拓展与延伸: 3 个点, (1)画二次函数的图象一般需要___
哪些点比较关键? 抛物线
yx
2
轴 对称图形,对称 是__
y 10 9 8 7 6 5 4 3 2 1 -5-4-3-2-1 O1 2 3 4 5 x
a>0
体验画图
(3)以上都是当a >0时,二次函数 y ax 的图象,
2
那么当 a<0时,试在同一直角坐标系画出二次函数:
1 2 y x ,y x ,y 2 x 2 的图象. 2
2
关于 y 轴对称 原点(0,0)
对称性
顶点
总结提高
2. 二次项系数 a 对形如 y=ax2 的函数值 y 又有
何影响?对图象又有何影响?
y=ax2
开口
a>0 开口向上
a<0 开口向下
增减性 在对称轴左侧递减 在对称轴左侧递增 在对称轴右侧递增 在对称轴右侧递减
LOGO
22.1.2二次函数y=ax2的图象和性质 参考解析
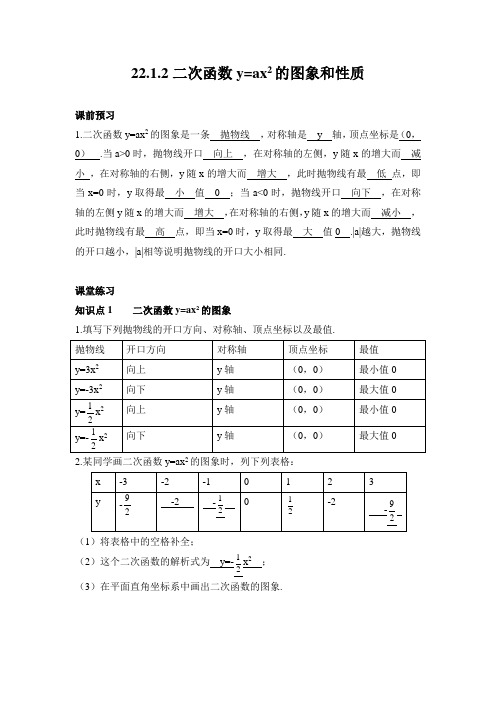
22.1.2二次函数y=ax2的图象和性质课前预习1.二次函数y=ax2的图象是一条抛物线,对称轴是y 轴,顶点坐标是(0,0).当a>0时,抛物线开口向上,在对称轴的左侧,y随x的增大而减小,在对称轴的右侧,y随x的增大而增大,此时抛物线有最低点,即当x=0时,y取得最小值0 ;当a<0时,抛物线开口向下,在对称轴的左侧y随x的增大而增大,在对称轴的右侧,y随x的增大而减小,此时抛物线有最高点,即当x=0时,y取得最大值0 .|a|越大,抛物线的开口越小,|a|相等说明抛物线的开口大小相同.课堂练习知识点1 二次函数y=ax2的图象1.填写下列抛物线的开口方向、对称轴、顶点坐标以及最值.2.某同学画二次函数y=ax2的图象时,列下列表格:(1)将表格中的空格补全;(2)这个二次函数的解析式为y=-1x2;2(3)在平面直角坐标系中画出二次函数的图象.解:(3)函数图象如图所示.知识点2 二次函数y=ax2的性质3.已知二次函数y=(m-2)x2的图象开口向上,则m的取值范围是m>2 .4.下列各点在二次函数y=-2x2图象上的是( B )A.(-1,2)B.(-1,-2)C.(-2,-4)D.(-2,4)5.关于函数y=x2的图象,下列说法错误的是( C )A.它的图象是一条抛物线B.它的开口向上,且关于y轴对称C.它的顶点是抛物线的最高点D.它的顶点在原点处,坐标为(0,0)课时作业1.与二次函数y=x2开口大小相同,方向相反的二次函数是y=-x2.2.二次函数y=-0.2x2的图象是一条开口向下的抛物线,对称轴是y轴,顶点坐标为(0,0).当x= 0 时,函数有最大值0 ;当x >0时,y随x的增大而减小.3.关于函数y=3x2的性质,下列说法正确的是( C )A.无论x为任何实数,y的值总为正B.当x值增大时,y的值也增大C.它的图象关于y轴对称D.它的图象在第一、第三象限内4.已知A (-1,y ₁),B (-2,y ₂)都在二次函数y=x 2上,则y ₁,y ₂之间的大小关系是( C )A.y ₁>y ₂B.y ₁=y ₂C.y ₁<y ₂D.不能确定 5.二次函数y=ax 2(a >0)的图象经过点(3,4),则其图象一定经过点( C ) A.(3,-4) B.(-3,-4) C.(-3,4) D.(4,3)6.如图,当ab >0时,函数y=ax 2与函数y=bx+a 的大致图象是( C )7.二次函数y=2x 2,y=-2x 2,y=12x 2的共同性质是( B ) A.开口向上 B.对称轴是y 轴 C.都有最高点 D.y 随x 的增大而增大 8.已知函数y=(m+2)226m m x +-是关于x 的二次函数. (1)求m 的值;(2)当m 为何值时,函数图象的顶点为最低点? (3)当m 为何值时,函数图象的顶点为最高点? 解:(1)根据二次函数的定义得22026 2.m m m +≠+-=⎧⎨⎩,解得⎩⎨⎧-==.4,221m m ∴m 的值为2或-4;(2)当m=2时,抛物线的开口向上,函数有最小值,函数图象的顶点为最低点; (3)当m=-4时,抛物线的开口向下,函数有最大值,函数图象的顶点为最高点.9.在同一个平面直角坐标系中,画出下列函数的图象:①y=x 2;②y=12x 2;③y=-x 2;④y=-12x 2.从图象上对比,说出解析式中二次项系数a对抛物线的形状有什么影响?解:列表如下描点、连线,函数图象如图所示a的绝对值相同,抛物线的形状相同;a的绝对值越大,开口越小.10.如图,A,B为抛物线y=x2上的两点,且AB∥x轴,与y轴交于点C,以点O为圆心,OC为半径画圆,若2.解:∵AB=22∴BC=122∴点B的横坐标为2代入抛物线的解析式得y=2.∵AB∥x轴,∴点B与点C的纵坐标相同.∴OC=2,即圆的半径为2.由二次函数的对称性得,图中阴影部分的面积等于圆面积的14, 即S 阴影=14π×22=π.11.函数y=ax 2(a ≠0)的图象与直线y=2x-3交于点(1,b ). (1)求a 和b 的值;(2)x 在什么范围时,二次函数y=ax 2中的y 随x 的增大而增大? (3)求抛物线y=ax 2与直线y=-2的两个交点及顶点所围成的三角形的面积. 解:(1)把点(1,b )代入y=2x-3,得b=-1. ∴交点坐标为(1,-1). 把(1,-1)代入y=ax 2,得a=-1. ∴a=-1,b=-1;(2)由(1)得y=-x 2,当x ≤0时,y 随x 的增大而增大; (3)根据题意,得2,2.y x y ⎧=-⎨=-⎩解得2x y ⎧=⎪⎨=-⎪⎩或 2.x y ⎧=⎪⎨=-⎪⎩ ∴两交点坐标分别为(-2),(-2).故S △=12×。
22.1.2二次函数y=ax2的图象和性质教学设计2023—2024学年人教版数学九年级上册

1.学生已经掌握了哪些相关知识:学生在之前的学习中,已经掌握了二次函数的一般形式,有一定的函数图象知识,能够理解函数的性质。他们还学习过一些图形软件,如几何画板,可以用来绘制函数图象,这为学习二次函数图象和性质打下了一定的基础。
2.学生的学习兴趣、能力和学习风格:九年级的学生对数学有着一定的兴趣,他们逻辑思维能力强,喜欢通过探究活动来学习。在学习风格上,他们更倾向于通过实际例子和亲身体验来理解抽象的数学概念。
二、新课讲授(用时10分钟)
1.理论介绍:首先,我们要了解二次函数的基本概念。二次函数是形如y=ax^2的函数,其中a是常数。它广泛应用于生活中的各种问题,如物理学中的抛物线运动、经济学中的成本函数等。
2.案例分析:接下来,我们来看一个具体的案例。这个案例展示了二次函数在实际中的应用,以及它如何帮助我们解决问题。
②二次函数图象的性质:
-开口方向:a>0时,开口向上;a<0时,开口向下。
-顶点:二次函数的顶点坐标为(0,c/a),其中c是常数。
-对称轴:二次函数的对称轴是y轴。
-增减性:当a>0时,函数在顶点左侧递减,在顶点右侧递增;当a<0时,函数在顶点左侧递增,在顶点右侧递减。
③二次函数的性质应用:
-解决实际问题:通过建立二次函数模型,解决抛物线运动、成本函数等问题。
22.1.2二次函数y=ax2的图象和性质教学设计2023—2024学年人教版数学九年级上册
授课内容
授课时数
授课班级
授课人数
授课地点
授课时间
教材分析
“22.1.2二次函数y=ax^2的图象和性质”是人教版数学九年级上册第22章“二次函数”的第二节内容。本节课主要让学生通过探究二次函数y=ax^2的图象和性质,进一步理解二次函数的一般形式,掌握二次函数图象的特点,以及会运用二次函数的性质解决一些实际问题。
二次函数y=ax2的图象和性质ppt课件

例4 如图, 四个二次函数的图象分别对应 ① y=ax2 ;② y=bx2;
③ y=cx2;④ y=dx2,且①与③,②与④分别关于x 轴对称.
(1)比较a,b,c,d 的大小; (2)说明a 与c,b 与d 的数量关系.
解:(1)由抛物线的开口方向,知 a > 0,b > 0,c < 0,d < 0,
由抛物线的开口大小,知 |a| > |b|,|c| > |d|, 因此a > b,c < d. ∴ a > b > d > c. (2)∵①与③,②与④分别关于x 轴对称,
∴①与③,②与④的开口大小相同,方向相反. ∴ a+c=0,b+d=0.
课堂练习
1、下列函数中,y总随x增大而减小的是( B )
归纳总结
位置开 开口向上,在x轴上方 开口向下,在x轴下方
口方向
a的绝对值越大,开口越小
对称性 顶点最值
关于y轴对称,对称轴方程是直线x=0 顶点坐标是原点(0,0)
当x=0时,y最小值=0 当x=0时,y最大值=0
增减性
在对称轴左侧递减 在对称轴左侧递增 在对称轴右侧递增 在对称轴右侧递减
1、如右图,观察函数y=( k-1)x2的图象, 则k的取值范围是 k>1 .
复习引入
1.二次函数的一般形式是怎样的? y=ax²+bx+c(a,b,c是常数,a≠ 0)
2.下列函数中,哪些是二次函数?
①
②
③
④
⑤
3.一次函数的图象是一条 直线.
4.通常怎样画一个函数的图象? 列表、描点、连线
那么,二次函数的图象会是什么样的图形呢?这节课我们 来学习最简单的二次函数y=ax2的图像
不同点: a的值越大,开口越小.
人教版数学九年级上册22.1.2二次函数y=ax2的图像与性质 课件(21张PPT)

二二次次函函数数y的=图x2象的都图是象抛是物一线条,曲线它,们它的的开形口状或类者似向于上投或篮者球向 时下球.在一空般中地所,经二过次的函路数线y,=只ax是2 +这b条x +曲c线(开a≠口0)向的上图,象这叫条做曲抛 线物叫线做y =抛a物x2线+ byx=+xc2 ,
9 6 3
-3
3
实y轴际是上抛,物每线条y抛= 物x 2线的都对有称对轴称,轴抛,物抛线物y 线= x与2 对与称它轴的的对交称点轴 叫的做交抛点物(线0,的0顶)点叫.做顶抛点物是线抛y =物x线2 的的顶最点低,点它或是最抛高物点线.y = x 2 的最低点.
交点坐标
y
求抛物线与直线的 交点坐标的方法: 两解析式联列方程
组
y=4x2 y=3x+1
O
x
1.若抛物线y=ax²与y=4x²的形状及开口方向 均相同,则a= 4
2.下列关于二次函数y=ax²(a≠0)的说法中,错误 的是( C ) A.它的图像的顶点是原点 B.当a<0,在x=0时,y取得最大值
(2)说出函数图象的顶点坐标、对称轴、
开口方向和图象的位置;
在x轴的下方
解: (1)依题意,得 (2)2 a 3
解得
a=
3 4
∴ 该函数的解析式为 y
3 4
x2
例3、y=kx2与y=kx-2(k≠ 0)在同一坐标系中, 可能是( B )
A
B
C
D
例4、求抛物线y=4x2与直线y=3x+1的
描点法
列表、描点、连线
以0为中心 选取7个x值
画最简单的二次函数 y = x2 的图象列表
22.1.2二次函数y=ax2的图象与性质 说课稿 2022—2023学年人教版数学九年级上册

22.1.2 二次函数y=ax²的图象与性质说课稿一、教学目标1.知识与能力:•了解二次函数y=ax²的基本函数图象特点;•掌握二次函数图象的平移、伸缩和翻转变换;•理解二次函数和一次函数的区别。
2.过程与方法:•激发学生对二次函数的兴趣;•引导学生通过观察、探究并总结出二次函数y=ax²的图象特点;•通过实例分析,引导学生掌握二次函数图象的平移、伸缩和翻转变换。
3.情感态度与价值观:•培养学生观察问题、分析问题、解决问题的能力;•引导学生在学习数学的过程中培养耐心和毅力。
二、教学重点和难点1.教学重点:•二次函数y=ax²的基本图象特点;•二次函数图象的平移、伸缩和翻转变换。
2.教学难点:•引导学生通过观察、探究并总结出二次函数y=ax²的图象特点。
三、教学准备1.教学工具:•PowerPoint;•讲师笔记。
2.教学材料:•教材《人教版数学九年级上册》;•预习资料。
四、教学过程第一步:导入新知1.通过展示数学九年级上册预习资料中的图像,激发学生对二次函数的兴趣,并引出本节课的主题。
2.引导学生回顾一次函数y=ax+b的定义和性质,并引出二次函数y=ax²的定义。
第二步:展示二次函数y=x²的图象特点1.在白板上画出二次函数y=x²的图象。
2.通过观察图象,引导学生总结出二次函数y=x²的特点:•对称轴为y轴;•顶点坐标为(0, 0);•图象开口向上。
3.引导学生思考:如果改变a的值,对图象会有什么影响?设置不同的a值进行观察和比较。
第三步:引入二次函数y=ax²的图象变换1.通过展示不同a值的二次函数y=ax²的图象,引导学生观察并比较,总结出不同a值对图象的影响:•a>1时,图象变瘦长;•0<a<1时,图象变胖矮;•a<0时,图象分别在x轴的上方和下方对称。
九年级数学上册二次函数的图象和性质22.1.2二次函数y=ax2的图象和性质课件

图22-1-7
解:(1)填表如上,图象略; (2)a 的符号决定抛物线的开口方向,|a|的大小决定抛物线的开口大小.
6.已知 a≠0,在同一直角坐标系中,函数 y=ax 与 y=ax2 的图象有可能是 (C )
A
B
C
D
【解析】 A 项,函数 y=ax 中,a>0,y=ax2 中,a>0,但当 x=1 时,两 函数图象应有交点(1,a),错误;
下列关系式一定正确的是( C )
A.y1>0>y2
B.y2>0>y1
C.y1>y2>0
D.y2>y1>0
3.函数 y=x2,y=21x2,y=2x2 的图象大致如图 22-1-5 所示,则图中从里
到外的三条抛物线对应的函数依次是( D )
A.y=12x2,y=x2,y=2x2
B.y=x2,y=21x2,y=2x2
类型之二 由二次函数 y=ax2 的图象特征求待定字母的值
已知函数
是关于 x 的二次函数.
(1)求 m 的值;
(2)当 m 为何值时,此函数图象的顶点为最低点?
(3)当 m 为何值时,此函数图象的顶点为最高点?
m+2≠0, 解:(1)由题意,得m2+2m-6=2, 解得 m1=2,m2=-4; (2)若函数图象的顶点为最低点,则 m+2>0, ∴由(1)知,m=2; (3)若函数图象的顶点为最高点,则 m+2<0, ∴由(1)知,m=-4.
分层作业
1.[2016·玉林]抛物线 y=12x2,y=x2,y=-x2 的共同性质是:
①都是开口向上;②都以点(0,0)为顶点;③都以 y 轴为对称轴;④都关于
x 轴对称.其中说法正确的个数有( B )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y=ax2+c (a≠0) 开口方向 顶点坐标 对称轴 增 减 性 极值
a>0 向上 (0 ,c) y轴
当x<0时, y随着x的增大而减小。 当x>0时, y随着x的增大而增大。
a<0 向下 (0 ,c) y轴
当x<0时, y随着x的增大而增大。 当x>0时, y随着x的增大而减小。
x=0时,y最小=c
x y = x2 · · · · · · -3 -2 -1 0 1 2 3 · · · · · ·
9
4
1
0
1
9
4
9
2. 根据表中x,y的数值在 坐标平面中描点(x,y) 3.连线 如图,再用平 滑曲线顺次连接各点, -3 2 就得到y = x 的图象.
y = x2
6
3 3
二次函数 y = x2的图象是一条曲线,它的形状类似 于投篮球时球在空中所经过的路线,只是这条曲线 开口向上,这条曲线叫做抛物线 y = x2 , 二次函数的图象都是抛物线, 它们的开口或者向 上或者向下. 一般地,二次函数 y = ax2 + bx + c (a≠0)的图象叫做抛物线y = ax2 + bx + c y = x2
m2+m
解②得:m1=-2, m2=1 由①得:m>-1 ∴ m=1 此时,二次函数为: y=2x2,
x ….. y=x2 …… y=x2+1 ……
-2 4
-1 1
0 0
y
8
1 1
2 4
…… ……
5
2
0
2
5
y=x2+1
函数y=x2+1的图象与y=x2的 图象的位置有什么关系? 函数y=x2+1的图 象与y=x2的图象 的形状相同吗?
-4
-10 -5
O
-2
x
10
-6
-8
当a>0时,抛物线y=ax2+c的开口 上 ,对称轴 是 y轴 ,顶点坐标是(0,c),在对称轴的左侧,y随x的 增大而 减小,在对称轴的右侧,y随x的增大而 增大, 当x= 0 时,取得最 小 值,这个值等于 c ; 当a<0时,抛物线y=ax2+c的开口 下 ,对称轴 是y轴 ,顶点坐标是(0,c),在对称轴的左侧,y随x的 增大而 增大,在对称轴的右侧,y随x的增大而 减小, 当x= 0 时,取得最 大 值,这个值等于 c 。
(3)将抛物线y=4x2向上平移3个单位,所得的 2+3 y=4x 抛物线的函数式是 。 将抛物线y=-5x2+1向下平移5个单位,所得的 2-4 y=-5x 抛物线的函数式是 。
10
y
8
y=x2+1
y=x2 y=x2-2
5
4
y
2
y=-x2+3
5
6
4
-10
-5
O
-2
x
10
2
y=-x2 y=-x2-2
y轴
向下
|a|越大,抛物线的开口越小;
1、函数y=2x2的图象的开口向上 ,对称 轴 y轴,顶点是 (0,0);
2、函数y=-3x2的图象的开口向下, 对称轴 y轴,顶点是(0,0);
已知 y =(m+1)x 是二次函数且其 图象开口向上,求m的值和函数解析式
解: 依题意有:
m+1>0 ① m2+m=2 ②
(4)抛物线y=-3x2+5的开口 下 ,对称轴是 y轴 , 顶点坐标是 (0,5) ,在对称轴的左侧,y随x的增大 而 增大 ,在对称轴的右侧,y随x的增大而 减小 , 当x= 0 时,取得最 大 值,这个值等于 5 。 (5)抛物线y=7x2-3的开口 上 ,对称轴是 y轴 , 顶点坐标是 (0,-3) ,在对称轴的左侧,y随x的增大 而 减小,在对称轴的右侧,y随x的增大而 增大, 当x= 0 时,取得最 小 值,这个值等于 -3 。 6.二次函数y=ax2+c (a≠0)的图象经过点A(1,-1),B (2,5),则函数y=ax2+c的表达式为 y=2x2-3。若 点C(-2,m),D(n ,7)也在函数的图象上,则点C的坐 标为 (-2,5) 点D的坐标为 ( 5 ,7) 或 ( 5 . ,7)
你画出的图象与图中相同吗? 请找出相同点与不同点:
y x2
-6 -8
1 y x2 2
y 2 x 2
1. 二次函数的图像都是抛物线. 2. 抛物线y=ax2的图像性质: (1) 抛物线y=ax2的对称轴是y轴,顶点是原点.
y
(2)当a>0时,抛物线的开口向 上,顶点是抛物线的最低点;
解:分别填表,再画出它们的图象, 如图
y 1 2 x 2
y 2x2
y x2
8
6 4 2
y 2x2
1 2 y x 2
2 4
-4
-2
1 2 2 函数 y x , y 2 x 的图象与函数 y=x2 2
的图象相比,有什么共同点和不同点?
相同点:开口:向上, 顶点:原点(0,0)——最低点 对称轴: y 轴 增减性:y 轴左侧,y随x增大而减小
o
a>0
当a<0时,抛物线的开口向 下,顶点是抛物线的最高点; |a|越大,抛物线的开口越小;
x
a<0
请同学们把所学的二次函数图象的知识归纳小结。 开口 y=ax2 顶点 对称轴 方向 (0,0) y轴 y轴 左侧 右侧
图象
a>0 最低点
(0,0) a<0 最高点
y轴
向上
x y x y 增 减 增增 大 小 大大 x y x y 增 增 增减 大 大 大小
-8
向 下 平移 |c|个单位得到。
上加下减
(1)函数y=4x2+5的图象可由y=4x2的图象 向 上 平移 5 个单位得到;y=4x2-11的图象 可由 y=4x2的图象向 下平移11 个单位得到。 (2)将函数y=-3x2+4的图象向 下 平移 4 个单位可 得y=-3x2的图象;将y=2x2-7的图象向上 平移 7 个 单位得到y=2x2的图象。将y=x2-7的图象 向上 平移 9 个单位可得到 y=x2+2的图象。
-2
-1
0 0
1 -0.5 0 0.5
2
3
4 -8 2
· · · · · · · · · · · ·
1 2· · y x · -8 2
x · · -2 · ·
-2 -0.5 -1
-2 -4.5 1 1.5
-0.5
· y 2 x 2 · -8 -4.5
-2 -0.5
-4
0
-0.5 -2 -4.5 -8 -2 -2 -4 2 4
10
函数y=-x2-2的图 象可由y=-x2的图 象沿y轴向下平移 2个单位长度得到.
y=-x2 y=-x2-2
-4
-6
图象向上移还是向下移,移多少个 单位长度,有什么规律吗? 函数y=ax2 (a≠0)和函数y=ax2+c (a≠0)的图象形 状相同 ,只是位置不同;当c>0时,函数y=ax2+c 的图象可由y=ax2的图象向 上 平移 c 个单位得到, 当c〈0时,函数y=ax2+c的图象可由y=ax2的图象
直线 (1)一次函数的图象是一条____
(2) 通常怎样画一个函数的图象?
列表、描点、连线
(3) 二次函数的图 象是什么形 状呢?
结合图象讨论性质是数 形结合的研究函数的重要方 法.我们得从最简单的二次 函数开始逐步深入地讨论一 般二次函数的图象和性质.
画最简单的二次函数 y = x2 的图象 1. 列表:在y = x2 中自变量x可以是任 意实数,列表表示几组对应值:
5
函数y=x2+1的图 象可由y=x2的图 象沿y轴向上平移 1个单位长度得到. 形状相同
-10 -5
6
4
2
y=x2
O
-2
x
10
x y=x2 y=x2-2
….. …… ……
-2 4
-1 1
0 0
1 1
2 4
…… ……
2
-1
y
8
0
-1
2
函数y=x2-2的图象 可由y=x2的图象 沿y轴向下平移2 个单位长度得到.
函数y=x2-2的图象与y=x2的 图象的位置有什么关系?
6
4
y=x2
2
形状相同
-10 -5
函数y=x2+1的图 象与y=x2的图象 的形状相同吗?
5
O
-2
x
10
y=x2-2
函数y=-x2+3的图 象可由y=-x2的图 象沿y轴向上平移 3个单位长度得到.
-10 -5
4
y
2
y=-x2+3
5
O
-2
x
x=0时,y最大=c
抛物线y=ax2 +c (a≠0)的图象可由y=ax2的图象通过上 下平移得到.
(4)抛物线y=-3x2+5的开口 下 ,对称轴是 y轴 , 顶点坐标是 (0,5) ,在对称轴的左侧,y随x的增大 而 增大 ,在对称轴的右侧,y随x的增大而 减小 , 当x= 0 时,取得最 大 值,这个值等于 5 。 (5)抛物线y=7x2-3的开口 上 ,对称轴是 y轴 , 顶点坐标是 (0,-3) ,在对称轴的左侧,y随x的增大 而 减小,在对称轴的右侧,y随x的增大而 增大, 当x= 0 时,取得最 小 值,这个值等于 -3 。 6.二次函数y=ax2+c (a≠0)的图象经过点A(1,-1),B (2,5),则函数y=ax2+c的表达式为 y=2x2-3。若 点C(-2,m),D(n ,7)也在函数的图象上,则点C的坐 标为 (-2,5) 点D的坐标为 ( 5 ,7) 或 ( 5 . ,7)
