多边形区域算法

合集下载

扫描线多边形区域填充算法研究

Ｙ）则第ｉ条扫描线Ｙ＋１ｉｉ，＋１ｉ＝Ｙ＋１与ｌ的交点
的Ｘ坐标是： … ＝（ｉ１）ｋ＝（ｉ）ｋ十ＸＹ＋一ｂ／ｙ —ｂ／１ｋ＝ｉ／．／Ｘ＋１ｋ扫描线从ｙ．化到Ｙ＋１时，ｉ变ｉＸ的变化量是ｍ＝１ｋ设计边记录的数据结构：边／．该
扫描线多边形区域填充算科学系，四四川达州６５０）３００
摘要：ＣＤ系统中，在Ａ经常需要对封闭区域进行填充．对于一个功能完善的ＣＤ系统而言，Ａ区域填充算
边表是包含多边形全部边记录的表，按Ｙ它坐标递增（或递减）的顺序存放多边形的所有边，每个Ｙ坐标存放一条或几条边记录．当某条扫描线ｙ遇到多边形边界的新边（ｉ以边的最底端为
１多边形扫描线填充原理
最高点的Ｙ坐标Ｙ该边最低点的Ｘ坐标，扫从描线ｙ变化到Ｙ＋＝Ｙ＋１时，坐标的增量ｍ＝ｉｉ１ｉＸ
１ｋ指向下一条边记录的指针，图１示．／，如所
ＹｘｍａｘｍＹｘｍａＸｎｌ
填充区域按Ｙ向扫描线顺序扫描生成．方其操作
用的内存空间少、何变换容易，不能直接用于几但区域填充．阵表示法是用位于多边形内的像素点集合来表示多边形．ｌ种表示丢失了许多几何＿这信息，但便于进行填充．扫描线多边形区域填充算法的基本思想：待

多边形面积计算公式GPS经纬度计算面积

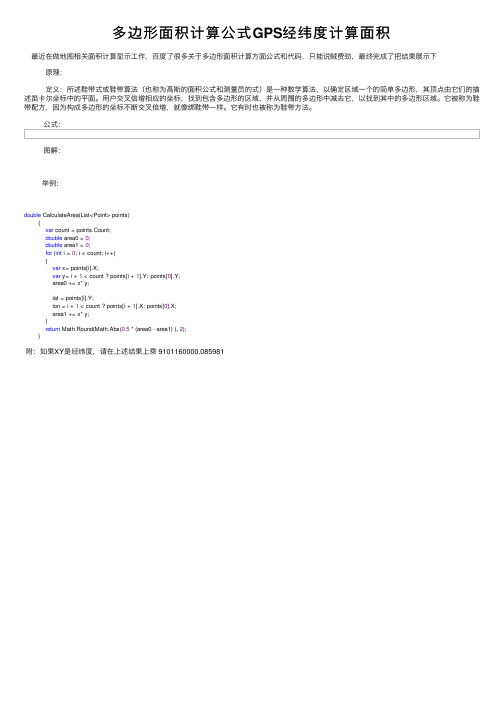
多边形⾯积计算公式GPS经纬度计算⾯积
　最近在做地图相关⾯积计算显⽰⼯作，百度了很多关于多边形⾯积计算⽅⾯公式和代码，只能说贼费劲，最终完成了把结果展⽰下
原理：
定义：所述鞋带式或鞋带算法（也称为⾼斯的⾯积公式和测量员的式）是⼀种数学算法，以确定区域⼀个的简单多边形，其顶点由它们的描述笛卡尔坐标中的平⾯。

⽤户交叉倍增相应的坐标，找到包含多边形的区域，并从周围的多边形中减去它，以找到其中的多边形区域。

它被称为鞋带配⽅，因为构成多边形的坐标不断交叉倍增，就像绑鞋带⼀样。

它有时也被称为鞋带⽅法。

公式：
图解：
举例：
double CalculateArea(List<Point> points)
{
var count = points.Count;
double area0 = 0;
double area1 = 0;
for (int i = 0; i < count; i++)
{
var x= points[i].X;
var y= i + 1 < count ? points[i + 1].Y: points[0].Y;
area0 += x* y;
lat = points[i].Y;
lon = i + 1 < count ? points[i + 1].X: points[0].X;
area1 += x* y;
}
return Math.Round(Math.Abs(0.5 * (area0 - area1) ), 2);
}
附：如果XY是经纬度，请在上述结果上乘 9101160000.085981。

快速多边形区域三角化算法与实现

ｅｇｓｍａｅｆｌｕｅｏＯａｏｒｄｃａｃｌｔｎｔｓｄｅｄｌｓｆｓｔｅｕｅｃｌｕａｉａｋ，ｓｌｙｉｌｍｅｔｔｎａｄｍａｅｉｓｉｂｅｆｒａｙｓｌｒｎｌｕＳｏｉｉｍｐｅｎａｉｎｄｔｕｔｌｎｉｅｔａｇｅｍｐｆｏａｏｍｐｉ
Ｃｉａｈｎ）・
ＡｂｔａｃＴｈｓｃｉａｏｒａｇｌｔｎｆｒｓｍｐｅｔｉｎｌｓｄｓｒｂｄａｏｌｗｓ：ｔｅｐｌｇｎｗａｕｄｉｉｅｎｏｍｏｏｓｒｔ：ｅｂａｉｄｅｆｔｉｎｕａｉｏｉｌｒａｇｅｗａｅｃｉｅｓｆｌｏｏｈｏｙｏｓｓｂｖｄｄｉｔｎ — ｔｎｕｓｐｌｇｎｎｈｅｒａｇｌｔｄ．Ｔｈｅａｇｒｔｍｌｓｉｅｌｈｅｔｘｓｂｔｏａｉｎｃａａｔｒｓｉｓ，ａｄｓｒｅｈｍｏｏｏｙｏｓａｄｔｎｔｎａｅｉｕｌｏｉｈｃａｓｆｄａｌｔｅｖｒｅｅｙｉｓｌｃｔｈｒｃｅｉｔｃｉｏｎｏｔｄｔｅａｏｇｔｅａｏｎｅｘｓｎｈｅｅｅｔｄｔｅｖｒｅｅｒｅｌｏｄｃｄｈｒａｉｎ，ｅｐｎｓｏｒｆｒｔｏｆａｍｏｏｏｕｌｎｈｐｐｉｔｄａｉ，ａｄｔｎｓｌｃｅｈｅｔｘｓｏｄｒｙｔｅｉｅｔｅｃｅｔｏｘａｉｎｏｏｍａｉｎｏｎｔｎｏｓｐｌｇｎｂｔｙｅ，ａａｔｔｉｎｕａｅｈｅｆｒａｉｅｍｏｏｏｏｓｐｏｙｏｏｙｏｙｉｓｔｐｔｌｓｒａｇｌｔｄｔｏｍｔｖｎｔｎｕｌｇｎ．Ｉｈｌｏｉｎｔｅａｇｒｔ，ｔｅｔｐｏｏｙｏｈｅｔｘｓａｈｍｈｏｌｇｆｔｅｖｒｅｅｎｄ

c语言多边形区域填充算法

c语言多边形区域填充算法C语言多边形区域填充算法一、介绍多边形区域填充算法是计算机图形学中的一项重要技术，用于将给定的多边形区域进行填充，使其呈现出丰富的颜色或纹理，增强图形的效果和表现力。

本文将介绍一种常用的C语言多边形区域填充算法——扫描线填充算法。

二、扫描线填充算法原理扫描线填充算法是一种基于扫描线的填充方法，其基本思想是将多边形区域按照水平扫描线的顺序，从上到下逐行扫描，通过判断扫描线与多边形边界的交点个数来确定是否进入多边形区域。

具体步骤如下：1. 首先，确定多边形的边界，将其存储为一个边表。

边表中的每个边都包含起点和终点的坐标。

2. 创建一个活性边表（AET），用于存储当前扫描线与多边形边界的交点。

初始时，AET为空。

3. 从上到下逐行扫描多边形区域，对每一条扫描线，从边表中找出与该扫描线相交的边，并将其加入AET中。

4. 对于AET中的每一对交点，按照从左到右的顺序两两配对，形成水平线段，将其填充为指定的颜色或纹理。

5. 在扫描线的下一行，更新AET中的交点的坐标，然后重复步骤4，直到扫描到多边形区域的底部。

三、代码实现下面是一个简单的C语言实现扫描线填充算法的示例代码：```#include <stdio.h>#include <stdlib.h>#include <stdbool.h>typedef struct {int x;int y;} Point;typedef struct {int yMax;float x;float dx;int next;} Edge;void fillPolygon(int n, Point* points, int color) {// 获取多边形的边界int yMin = points[0].y;int yMax = points[0].y;for (int i = 1; i < n; i++) {if (points[i].y < yMin) {yMin = points[i].y;}if (points[i].y > yMax) {yMax = points[i].y;}}// 创建边表Edge* edges = (Edge*)malloc(sizeof(Edge) * n);int k = n - 1;for (int i = 0; i < n; i++) {if (points[i].y < points[k].y) {edges[i].yMax = points[k].y;edges[i].x = points[i].x;edges[i].dx = (float)(points[k].x - points[i].x) / (points[k].y - points[i].y);edges[i].next = k;} else {edges[i].yMax = points[i].y;edges[i].x = points[k].x;edges[i].dx = (float)(points[i].x - points[k].x) / (points[i].y - points[k].y);edges[i].next = i;}k = i;}// 扫描线填充for (int y = yMin; y < yMax; y++) {int xMin = INT_MAX;int xMax = INT_MIN;for (int i = 0; i < n; i++) {if (y >= edges[i].yMax) {continue;}edges[i].x += edges[i].dx;if (edges[i].x < xMin) {xMin = edges[i].x;}if (edges[i].x > xMax) {xMax = edges[i].x;}int j = edges[i].next;while (j != i) {edges[j].x += edges[j].dx; if (edges[j].x < xMin) {xMin = edges[j].x;}if (edges[j].x > xMax) {xMax = edges[j].x;}j = edges[j].next;}}for (int x = xMin; x < xMax; x++) { drawPixel(x, y, color);}}free(edges);}int main() {// 定义多边形的顶点坐标Point points[] = {{100, 100},{200, 200},{300, 150},{250, 100}};// 填充多边形区域为红色fillPolygon(4, points, RED);return 0;}```四、总结通过扫描线填充算法，我们可以实现对多边形区域的填充，从而提升图形的表现效果。

多边形化算法

多边形化算法
多边形化算法是指将给定的点集或线段组合成封闭的多边形的过程。

这个问题在计算几何学、计算机图形学和地理信息系统等领域中经常遇到。

以下是一些常见的多边形化算法：
1. 凸包算法：凸包算法是最常用的多边形化算法之一。

它的目标是找到包含所有点的最小凸多边形。

常见的凸包算法有Graham扫描算法、Jarvis步进算法和快速凸包算法。

2. 三角剖分算法：三角剖分算法将给定的点集或线段划分为一组互不相交的三角形，从而形成多边形。

常见的三角剖分算法有Delaunay三角剖分算法和Ear Clipping算法。

3. 最小生成树算法：最小生成树算法可以用于生成一个连接给定点集的最小权重树形结构，在某些情况下可以用来构建多边形。

Prim算法和Kruskal算法是两种常用的最小生成树算法。

4. Alpha形算法：Alpha形算法是一种基于给定参数Alpha 的多边形化算法。

它通过连接在给定距离内的点来构建多边形，从而生成不规则的凸多边形。

5. Voronoi图算法：Voronoi图算法将给定的点集划分为一组区域，其中每个区域都由距离最近的点支配。

这些区域可以被视为多边形的一部分。

这些算法在实际应用中根据具体需求和数据特征的不同，选择合适的算法进行多边形化处理。

需要根据具体情况评估算法的效率、精确性和适用性。

多边形面积的算法

多边形面积的算法一、引言多边形是几何学中常见的图形，其面积是计算多边形重要的性质之一。

面积的计算对于建筑、地理学、计算机图形学等领域具有重要意义。

本文将介绍几种常见的多边形面积计算算法，包括三角形面积计算、梯形面积计算和多边形分割法。

二、三角形面积计算算法三角形是最简单的多边形，其面积计算公式为：面积= 底边长× 高 / 2。

其中，底边长是指两个顶点的连线的长度，高是指从底边到顶点的垂直距离。

三、梯形面积计算算法梯形是一个有两条平行边的多边形，其面积计算公式为：面积= (上底 + 下底) × 高/ 2。

其中，上底和下底分别是梯形的两条平行边的长度，高是指两条平行边之间的垂直距离。

四、多边形分割法对于复杂的多边形，可以利用多边形分割法来计算其面积。

该方法将多边形分割成若干个三角形或梯形，然后分别计算每个三角形或梯形的面积，最后将这些面积相加得到多边形的总面积。

具体的步骤如下：1. 将多边形的顶点按照顺时针或逆时针的方向连接起来，形成若干个三角形或梯形。

2. 分别计算每个三角形或梯形的面积，可以使用上述提到的三角形面积计算算法和梯形面积计算算法。

3. 将每个三角形或梯形的面积相加，得到多边形的总面积。

五、应用举例1. 假设有一个三角形，底边长为5，高为3，根据三角形面积计算算法可得其面积为7.5。

2. 假设有一个梯形，上底长为3，下底长为7，高为4，根据梯形面积计算算法可得其面积为20。

3. 假设有一个五边形，顶点依次为A、B、C、D、E，连接顶点后可以得到三个三角形：△ABC、△ACD、△ADE。

假设△ABC的面积为10，△ACD的面积为8，△ADE的面积为6，根据多边形分割法可得五边形的总面积为24。

六、总结多边形面积的计算是几何学中的重要内容，本文介绍了三角形面积计算算法、梯形面积计算算法和多边形分割法。

通过这些算法，可以准确计算出多边形的面积。

在实际应用中，可以根据具体情况选择适合的算法来计算多边形的面积，从而满足不同领域的需求。

割平面算法

割平面算法
割平面算法是一种计算几何的算法，主要用于求解多边形的内部或外部区域。

该算法的基本思想是通过构造一些直线（称为割平面）将多边形划分成一些简单的区域（称为小区域），然后根据小区域的情况确定多边形的内部或外部区域。

具体而言，该算法的步骤如下：首先确定一个多边形和一些割平面，然后将多边形和割平面进行求交，得到一些线段和点。

接着，根据这些线段和点将多边形划分成一些小区域，再根据每个小区域的情况判断其是否在多边形的内部或外部。

最后将所有在多边形内部的小区域合并在一起，就得到了多边形的内部区域。

割平面算法的优点是可以处理一些复杂的多边形，而且算法复杂度比较低。

不过该算法也存在一些缺点，比如对于一些具有孔洞的多边形，需要额外的处理，并且对于一些不规则的多边形，该算法的结果可能不准确。

- 1 -。

任意多边形区域交的有效算法

任意多边形区域交的有效算法
求任意多边形区域交的有效算法
求任意多边形区域交的有效算法是计算机图形学中的一个重要问题。

求任意多边形区域交的有效算法能够精确的计算出多边形之间的交点、交线或者交区域，是多边形运算的基础。

求任意多边形区域交的有效算法必须具有较高的效率。

主要有两种方法来求任意多边形区域交的有效算法，一种是采用极坐标系的基于数学的方法，另一种是基于几何的方法。

极坐标系的基于数学的方法是通过计算极坐标系中多边形的外接圆的极点的坐标，以及极角的大小来判断多边形是否相交。

基于几何的方法是利用线段相交的几何判断算法来判断多边形是否相交，并计算出多边形交点的坐标。

求任意多边形区域交的有效算法在计算机图形学中有着重要的应用，可以应用于计算机游戏开发、动画制作、地理信息系统等多种领域。

因此，求任意多边形区域交的有效算法的研究还有待深入。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

图中，如果用 Alternative 算法，则被多边形包围的那个点被判断为在多边形外部。如果你认为这种定义不符合你的需要，那么有另外一种算法，称为 Winding 算法。 Winding 算法的思路是这样的，将你置身于所给定的点上，然后让你的视线从多边形边界上的一点开始，选择一个方向绕着多边形的边界转一圈，如果你发现你的身体在这个过程中转了360度的非零整数倍，那么你所站在的这个点在多边形的内部，如果你的身体并没有转动（事实上你转动了，只是正向和逆向的转动抵消了），那么就在多边形的外部。这个算法我没有去实现，一般来说它要比 Alternative 算法慢，因为它需要计算每条多边形的边与多给定的点之间的夹角。关于算法实现：程序的界面是用 WTL 写的，如果你想要编译源代码，请在 Visual Studio 中指定 WTL 的 include 文件夹位置。算法核心代码如下，其中 vSelectionPoints 是多边形
7
{
8
CPoint &p1 = vSelectionPoints[j];
9
CPoint &p2 = vSelectionPoints[(j+1)%vSelectionPoints.size()];
10
if (thePoint == p1 || thePoint == p2)
11
{
12
nCrossCount = 0;
候很容易出现射线与多边形的某几条边平行的情况，对于这种情况，我们的算法需要向前多看几个点，以确定射线是确实与多边形相交还是只是“擦过”而已。其二是对于非常靠近多边形边界的点的判定，你可以认为这些点是在多边形外，也可以认为是在多边形内，但你必须在算法中描述这些情况。感兴趣的可以了解一下我的算法实现，附在文末。这个算法在多边形为简单多边形的情况下是没有异议的，但在复杂多边形的情况下会有一些疑问，这涉及到“在多边形内还是多边形外”的定义问题。如下图
if (thePoint.y <= max(p1.y, p3.y) && thePoint.y >= min(p1.y, p3.y)) {
nCrossCount++; } } } } if (nCrossCount % 2 != 0) { return TRUE; } return FALSE;
36 double(p2.y - p1.y) + p1.x;
37Biblioteka if (fabs(fCrossX - thePoint.x) < ESPILON)
38
{
39
nCrossCount = 0;
40
break;
41
}
42
if (fCrossX > thePoint.x)
43
{
44
nCrossCount++;
45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75
}
} } } else { if (thePoint.y != p1.y && thePoint.y == p2.y && thePoint.x < p2.x) {
Lync.in
Link the world.
Home About ProjectsSimpleDark
2009-09-24 / Chris posted in Algorithm / 397 Views / 16 Comments
前些天在考虑一个几何算法，关于如何判断一个点是否在一个给定的多边形内部。这应该是一个比较常规的算法，我以前对几何算法了解的不多，所以既然想到了就稍微研究了一下。查了一下相关的资料，目前有几个 O(N)的算法，其中 N 是多边形的顶点数。第一个叫做交替（Alternative）算法。如下图所示
13
break;
14
}
15
else if (thePoint.y > max(p1.y, p2.y) || thePoint.y < min(p1.y, p2.y))
16
{
17
continue;
18
}
19
else if (thePoint.y < max(p1.y, p2.y) && thePoint.y > min(p1.y, p2.y))
算法检查所给定的点和在该点右边的多边形区域的边界的交点数，若交点数为奇数，则该点在多边形内部，若交点数为偶数，则该点在多边形外部。可以想象成从一个点向右发出一条射线，然后计算这条射线与多边形边界的交点数。从上图中标出的蓝色点向右射出的射线与多边形有1个交点，故判定其在多边形内部，而从标出的白色点向右射出的射线则有偶数个交点，故判定其在多边形外部。这个算法的叙述起来很平常，但实现起来却有两个略带 Tricky 的地方。其一是坐标精度引起的，因为计算机对于坐标的描述是离散的，在计算向右射出的射线与多边形交点的时
20
{
21
if (p2.x == p1.x)
22
{
23
if (thePoint.x == p1.x)
24
{
25
nCrossCount = 0;
26
break;
27
}
28
else if (thePoint.x < p1.x)
29
{
30
nCrossCount++;
31
}
32
}
33
else
34
{
35
double fCrossX = (thePoint.y - p1.y) * double(p2.x - p1.x) /
C1 // thePoint：给定的点
2 // vSelectionPoints：给定的多边形顶点向量
3 BOOL CheckInside(CPoint thePoint, std::vector vSelectionPoints)
4{
5
int nCrossCount = 0;
6
for (size_t j = 0; j < vSelectionPoints.size(); ++j)
while(TRUE) {
j++; CPoint *pp3 = &vSelectionPoints[(j+1)%vSelectionPoints.size()]; if (pp3->y != p2.y) {
break; } }
CPoint &p3 = vSelectionPoints[(j+1)%vSelectionPoints.size()];