实变函数06-07年度_A_(解答)

合集下载

实变函数度(A)(解答)

华中师范大学 2006 –2007 学年第一学期期末考试试卷（A 卷）（解答）课程名称实变函数课程编号 83410014 任课教师判断题（判断正确、错误，请在括号中填“对”或“错”。

共5小题，每题3分，共5×3=15分）1、可数个可数集的并集是可数集。

（对）2、可测集E 上的非负可测函数必Lebesgue 可积。

（错）3、R n 上全体Lebesgue 可测集所组成的集类具有连续势。

（错）4、非空开集的Lebesgue 测度必大于零。

（对）5、若()n f x （1n =，2，）和()f x 都为可测集E 上的可测函数，且lim ()()n n f x f x →∞=，..a e E ，则()()n f x f x ⇒，x E ∈。

（错）二、叙述题 (共5小题 , 每题3分，共5×3 =15分)1、单调收敛定理（即Levi 定理）答：设E 是Lebesgue 可测集，()n f x (1n =，2，)为E 上的非负可测函数，若{()n f x }是单调递增的，记()lim ()n n f x f x →∞=，则lim()()n n EEf x dx f x dx →∞=⎰⎰。

2、R n中开集的结构定理答：R n中的任一非空开集总可表示成R n中至多可数个互不相交的半开半闭区间的并。

（或R n中的任一开集或为空集或可表示成R n中至多可数个互不相交的半开半闭区间的并。

）3、R n中的集合E 是Lebesgue 可测集的卡氏定义（即C .Caratheodory 定义）答：设n E R ⊂，如果对任意nT R ⊂，总有***()()c m T m T E m T E =⋂+⋂则称E 为R n 中的Lebesgue 可测集，或称E 是Lebesgue 可测的。

4、F .Riesz 定理（黎斯定理）答：设E 为Lebesgue 可测集，()n f x (1n =，2，)和()f x 都是E 上的几乎处处有限的可测函数，如果()()n f x f x ⇒ x E ∈，则存在{()n f x }的一个子列{()k n f x }，使得lim ()()k n k f x f x →∞=..a e 于E 。

实变函数习题答案北大版周民强

证: {x : lim fj (x) > 0} =
j →∞ j →∞
∞
∞
∞
k=1 N =1 j =N
1 {x : fj (x) ≥ k } j →∞ 1 , 再由数列上极限的定 k0 ∞ ∞ {x : fj (x) ≥ k10 }, N =1 j =N
事实上, 设 x0 ∈ {x : lim fj (x) > 0}, 则存在 k0 , 使 lim fj (x0 ) ≥ 义, 对于任何正整数 N , 存在 nN ≥ N , 使 fnN (x0 ) ≥ 从而 x0 ∈
∞ −1 } ⊂ {fαm (xm ) 存在; · · · ; 若 E 为有限集, 不妨设元素的个数就为 m, 那么 n=1 , s.t. lim fαm n n n→∞ n→∞
存在极限 lim {fαm (x)}, x ∈ E ; 若 E 为可列集, 利用对角线法则选取子函数列 {fαm }∞ , n m m=1
− + E1 /n ); ∀ n, 取 E1/n 中的 p 个数 x1 , x2 , · · · , xp ,
8. 设 f (x) 是定义在 R1 上的实值函数. 如果对于任意的 x0 ∈ R1 , 必存在 δ > 0, 当 |x − x0 | < δ 时, 有 f (x) ≥ f (x0 ), 试证明集合 E = {y : y = f (x)} 是可数集. 证: 取 y ∈ E , 则 ∃ x ∈ R1 , s.t.f (x) = y ; 由题意, ∃δx > 0, s.t.f (z ) ≥ f (x), z ∈ (x − δx , x + δx ); 取有理数 rx , Rx , 满足 x − δx < rx < x < Rx < x + δx , 如此就建立了 y 与 (rx , Rx ) 的映射 f ; 令 y1 , y2 ∈ E, y1 = y2 , ∃ x1 , x2 ∈ R1 , s.t. f (x1 ) = y1 , f (x2 ) = y2 ; 若 (rx1 , Rx1 ) = (rx2 , Rx2 ), 由题意, f (x1 ) ≥ f (x2 ), f (x2 ) ≥ f (x1 ), 即 f (x1 ) = f (x2 ), 矛盾; 故映射 f 是单射; {(rx , Rx ) : x ∈ R1 , ∃y ∈ E , s.t.f (x) = y } ⊂ Q2 , 因此 E 是可数集. 9. 设 E 是三维欧氏空间 R3 中的点集, 且 E 中任意两点的距离都是有理数, 试证明 E 是可数集. 证: 若 E 中所有的点共线, 记作 l; 固定 l 上一点 P , 到 P 距离为 r ∈ Q+ (Q+ 为正有理数) 的 E 中的点至多有两个, E = {P } {x ∈ E : d(x, P ) = r}, E 可数; 不然,

实变函数A卷(解答).docx

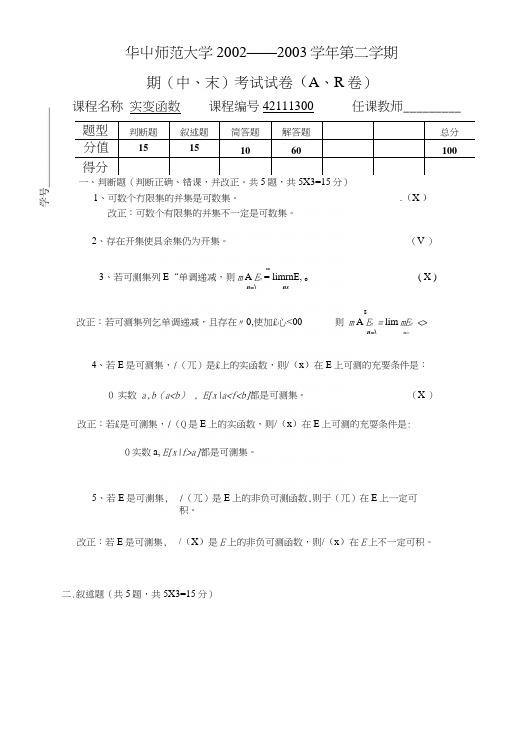
华屮师范大学2002——2003学年第二学期期（中、末）考试试卷（A、R卷）课程名称实变函数课程编号42111300 任课教师_________题型判断题叙述题简答题解答题总分分值151********得分一、判断题（判断正确、错课，并改正。

共5题，共5X3=15分）1、可数个冇限集的并集是可数集。

.（X ）改正：可数个有限集的并集不一定是可数集。

2、存在开集使具余集仍为开集。

（V ）co3、若可测集列E“单调递减，则m A E n = limrnE, o( X )n=\ ns改正：若可测集列乞单调递减，且存在〃0,使加£心<008则m A E n = lim mE n <>n=\n—4、若E是可测集，/（兀）是£上的实函数，则/（x）在E上可测的充要条件是：0 实数a,b（a<b） , E[x\a<f<b]都是可测集。

（X ）改正：若£是可测集，/（Q是E上的实函数，则/（x）在E上可测的充耍条件是: 0实数a, E[x\f>a]都是可测集。

5、若E是可测集, /（兀）是E上的非负可测函数,则于（兀）在E上一定可积。

改正：若E是可测集, /（X）是E上的非负可测函数，则/（x）在E上不一定可积。

二.叙述题（共5题，共5X3=15分）1、集合的对等。

答：设A、B是两个集合，若A、BZ间存在一一对应，则称A与B对等。

2、可测集。

答：设E u R”,如果对任意T uR”,总有mV=/77*（Tn£） + m*（Tn£c）,则称E为可测集。

3、可测集与几型集的关系。

答：设E为可测集，则存在人型集F,使F uE且加E二加F、加（E — F） = O。

4、叶果洛夫定理。

答：设mE < +oo , { f n（x））为E上儿乎处处有限的可测函数列，/（兀）也为E上儿乎处处有限的可测函数，如果AU）^/（x） a.e.于E,则对任意£>0,存在可测了集E£^E 使在E&上,f n （兀）一致收敛于/*（兀），而m{E-E G）< 8 o5、九（兀）在可测集E上依测度收敛于/（兀）的定义。

实变函数课后答案

实变函数课后答案第一章 1.证明：(1) (A -B )-C =A -(B ∪C ); （2）(A ∪B )-C =(A -C )∪(B -C ). 证明：(1) 左=(A ∩B c )∩C c =A ∩(B c ∩C c )= A ∩(B ∪C )c =右；（2）左=(A ∪B )∩C c =(A ∩C c )∪(B ∩C c )=右. 2.证明：(1)();(2)().IIIIA B A B A B A B αααααααα∈∈∈∈-=--=- (1)c c I I A B A B αααα∈∈⎛⎫=== ⎪⎝⎭证明：左（）右；(2)()c c I I A B A B αααα∈∈⎛⎫=== ⎪⎝⎭左右.111111.{},,1.{}1.n n n n n nnA B A B A A n B B A n νννννν-===⎛⎫==- ⎪⎝⎭>=≤≤∞ 3 设是一列集合，作证明：是一列互不相交的集合，而且，证明：用数学归纳法。

当n=2时，B 1=A 1,B 2=A 2-A 1, 显然121212B B B B B B n k =∅== 且，假设当时命题成立，1211,,,kkk B B B B A νννν=== 两两互不相交，而且，111111111kk k k k kk k n k B A A B A B A B νννννννν++=++====+=-==-⇒下证，当时命题成立，因为而，所以11211+1111111111111,,,;kk k k k kk k k k k kk k k B B B B B B B B B B A A A A A A A νννννννννννννννν++=++===+++====⎛⎫=∅ ⎪⎝⎭⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫=-== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ ，于是，两两互不相交;由数学归纳法命题得证。

{}21214.0,,(0,),1,2,,n n n A A n n A n -⎛⎫=== ⎪⎝⎭设求出集列的上限集和下限集。

实变函数题库集答案

实变函数试题库及参考答案本科一、题1．设,A B 为集合，则()\A B B =A B （用描述集合间关系的符号填写）2．设A 是B 的子集，则A ≤B （用描述集合间关系的符号填写）3．如果E 中聚点都属于E ，则称E 是闭集4．有限个开集的交是开集5．设1E 、2E 是可测集，则()12m E E ≤12mE mE +（用描述集合间关系的符号填写） 6．设n E ⊂是可数集，则*m E =07．设()f x 是定义在可测集E 上的实函数，如果1a ∀∈，()E x f x a ⎡⎤≥⎣⎦是可测集，则称()f x 在E 上可测8．可测函数列的上极限也是可测函数 9．设()()n f x f x ⇒，()()n g x g x ⇒，则()()n n f x g x +⇒()()f x g x +10．设()f x 在E 上L 可积，则()f x 在E 上可积11．设,A B 为集合，则()\B A A ⊃A （用描述集合间关系的符号填写） 12．设{}211,2,A k k =-=，则A =a （其中a 表示自然数集N 的基数） 13．设n E ⊂，如果E 中没有不属于E ，则称E 是闭集14．任意个开集的并是开集15．设1E 、2E 是可测集，且12E E ⊂，则1mE ≤2mE16．设E 中只有孤立点，则*m E =0 17．设()f x 是定义在可测集E 上的实函数，如果1a ∀∈，()E x f x a ⎡⎤<⎣⎦是可测，则称()f x 在E 上可测18．可测函数列的下极限也是可测函数 19．设()()n f x f x ⇒，()()n g x g x ⇒，则()()n n f x g x ⇒()()f x g x20．设()n x ϕ是E 上的单调增收敛于()f x 的非负简单函数列，则()E f x dx =⎰()lim nE n x dx ϕ→∞⎰ 21．设,A B 为集合，则()\A B B ⊃B22．设A 为有理数集，则A =a （其中a 表示自然数集N 的基数）23．设n E ⊂，如果E 中的每个点都是内点，则称E 是开集24．有限个闭集的交是闭集25．设n E ⊂，则*m E ≥0 26．设E 是n 中的区间，则*m E =E 的体积27．设()f x 是定义在可测集E 上的实函数，如果1a ∀∈，()E x f x a ⎡⎤≤⎣⎦是可测集，则称()f x 在E 上可测28．可测函数列的极限也是可测函数 29．设()()n f x f x ⇒，()()n g x g x ⇒..a e ，则()n f x ⇒()g x30．设()n f x 是E 上的非负可测函数列，且单调增收敛于()f x ，由勒维定理，有()E f x dx =⎰()lim n E n f x dx →∞⎰31．设,A B 为集合，则()\B A B A =A B32．设A 为无理数集，则A =c （其中c 表示自然数集[]0,1的基数）33．设n E ⊂，如果E 中没有不是内点的点，则称E 是开集34．任意个闭集的交是闭集35．设n E ⊂，称E 是可测集，如果n T ∀⊂，()**m T m TE =+()*c m T E 36．设E 是外测度为零的集合，且F E ⊂，则*m F =037．设()f x 是定义在可测集E 上的实函数，如果1a ∀∈，()E x a f x b ⎡⎤≤<⎣⎦是可测，（a b ≤）则称()f x 在E 上可测38．可测函数列的上确界也是可测函数39．设()()n f x f x ⇒，()()n g x g x ⇒..a e ，则()()n n f x g x ⇒()()f x g x40．设()()n f x f x ⇒，那么由黎斯定理，(){}n f x 有子列()k n f x ，使()()k n f x f x →..a e 于E 41.设,A B 为两个集合,则__c A B AB -.（等于） 42.设n E R ⊂,如果E 满足E E '⊆(其中E '表示E 的导集),则E 是闭.43.若开区间(,)αβ为直线上开集G 的一个构成区间,则(,)αβ满(i)(a,b)G ⊆ (ii),a G b G ∉∉44.设A 为无限集.则A 的基数__A a (其中a 表示自然数集N 的基数) 答案：≥45.设12,E E 为可测集,2mE <+∞,则1212(\)__m E E mE mE -. 答案：≥46.设()f x 是定义在可测集E 上的实函数,若对任意实数a ,都有[()]E xf x a >是可测集E 上的可测函数.47.设x 是E (R ⊆)的内点,则*__0m E . 答案>48.设{}()n f x 为可测集E 上的可测函数列,且()(),n f x f x x E ⇒∈,则由____黎斯__定理可知得,存在{}()n f x 的子列{}()k n f x ,使得.()()()k a e n f x f x x E →∈. 49.设()f x 为可测集E (n R ⊆)上的可测函数,则()f x 在E 上的L 积分值不一定存在且|()|f x 在E 上不一定L 可积.50.若()f x 是[,]a b 上的绝对连续函数,则()f x 是[,]a b 上的有界变差函数.51．设,A B 为集合，则___(\)A B B A A 答案=52．设n E R ⊂，如果E 满足0E E =（其中0E 表示E 的内部），则E 是开集53．设G 为直线上的开集，若开区间(,)a b 满足(,)a b G ⊆且,a G b G ∉∉，则(,)a b 必为G 的构成区间54．设{|2,}A x x n n ==为自然数，则A 的基数=a (其中a 表示自然数集N 的基数)55．设,A B 为可测集，B A ⊆且mB <+∞，则__(\)mA mB m A B - 答案 =56．设()f x 是可测集E 上的可测函数，则对任意实数,()a b a b <，都有[()]E x a f x b <<是可测集57．若()E R ⊆是可数集，则__0mE 答案=58．设{}()n f x 为可测集E 上的可测函数列，()f x 为E 上的可测函数，如果.()()()a e n f x f x x E →∈，则()()n f x f x ⇒x E ∈不一定成立59．设()f x 为可测集()nE R ⊆上的非负可测函数，则()f x 在E 上的L 积分值一定存在 60．若()f x 是[,]a b 上的有界变差函数，则()f x 必可表示成两个递增函数的差（或递减函数的差）多项选择题（每题至少有两个以上的正确答案）1．设[]{}0,1E =中无理数，则（ ACD ）A E 是不可数集B E 是闭集C E 中没有内点D 1mE = 2．设n E ⊂是无限集，则（ AB ）A E 可以和自身的某个真子集对等B E a ≥（a 为自然数集的基数）C E '≠∅D *0mE >3．设()f x 是E 上的可测函数，则（ABD ）A 函数()f x 在E 上可测B ()f x 在E 的可测子集上可测C ()f x 是有界的D ()f x 是简单函数的极限4．设()f x 是[],a b 上的有界函数，且黎曼可积，则（ABC ）A ()f x 在[],a b 上可测B ()f x 在[],a b 上L 可积C ()f x 在[],a b 上几乎处处连续D ()f x 在[],a b 上几乎处处等于某个连续函数5．设n E ⊂，如果E 至少有一个内点，则（ BD ）A *m E 可以等于0B *0m E >C E 可能是可数集DE 不可能是可数集6．设n E ⊂是无限集，则（ AB ）A E 含有可数子集B E 不一定有聚点C E 含有内点DE 是无界的7．设()f x 是E 上的可测函数，则（ BD ）A 函数()f x 在E 上可测B ()f x 是非负简单函数列的极限C ()f x 是有界的D ()f x 在E 的可测子集上可测8．设()f x 是[],a b 上的连续函数，则（ ABD ）A ()f x 在[],a b 上可测B ()f x 在[],a b 上L 可积，且()()()()[],ba ab R f x dx L f x dx =⎰⎰C ()f x 在[],a b 上L 可积，但()()()()[],ba ab R f x dx L f x dx ≠⎰⎰D ()f x 在[],a b 上有界9．设()D x 是狄利克莱函数，即()[][]10,100,1x D x x ⎧⎪=⎨为中有理数为中无理数，则（ BCD ）A ()D x 几乎处处等于1B ()D x 几乎处处等于0C ()D x 是非负可测函数 D ()D x 是L 可积函数10．设n E ⊂，*0m E =，则（ ABD ）A E 是可测集B E 的任何子集是可测集C E 是可数集DE 不一定是可数集11．设n E ⊂，()10E cx Ex x E χ∈⎧=⎨∈⎩，则（ AB ） A 当E 是可测集时，()E x χ是可测函数B 当()E x χ是可测函数时，E 是可测集C 当E 是不可测集时，()E x χ可以是可测函数D 当()E x χ是不是可测函数时，E 不一定是可测集12．设()f x 是(),a b 上的连续函数，则（BD ）A ()f x 在(),a b 上有界B ()f x 在(),a b 上可测C ()f x 在(),a b 上L 可积D ()f x 在(),a b 上不一定L 可积13．设()f x 在可测集E 上L 可积，则（AC ）A ()f x +，()f x -都是E 上的非负可积函数B ()f x +和()f x -有一个在E 上的非负可积C ()f x 在E 上L 可积D ()f x 在E 上不一定L 可积14．设n E ⊂是可测集，则（ AD ）A c E 是可测集B mE <+∞C E 的子集是可测集DE 的可数子集是可测集15．设()()n f x f x ⇒，则（ CD ）A ()f x 几乎处处收敛于()f xB ()n f x 一致收敛于()f xC ()n f x 有子列()n f x ，使()()n f x f x →..a e 于ED ()n f x 可能几乎处处收敛于()f x16．设()f x 是[],a b 上有界函数，且L 可积，则（BD ）A ()f x 在[],a b 上黎曼可积B ()f x 在[],a b 上可测C ()f x 在[],a b 上几乎处处连续D ()f x 在[],a b 上不一定连续17. 设{[0,1]}E =中的无理点,则(CD)（A ）E 是可数集（B ）E 是闭集（C ）E 中的每个点均是聚点（D ）0mE >18. 若E (R ⊆)至少有一个内点，则（BD ）（A ）*m E 可以等于０（B ）*0m E = （C ）E 可能是可数集（D ）E 不可能是可数集19．设[,]E a b ⊆是可测集，则E 的特征函数()E x χ是（ABC ）（A ）[,]a b 上的符号函数（C ）E 上的连续函数（B ）[,]a b 上的可测函数（D ）[,]a b 上的连续函数20．设()f x 是[,]a b 上的单调函数，则（ACD ）（A ）()f x 是[,]a b 上的有界变差函数（B ）()f x 是[,]a b 上的绝对连续函数（C ）()f x 在[,]a b 上几乎处处收敛（D ）()f x 在[,]a b 上几乎处处可导21．设{[0,1]}E =中的有理点，则（ AC ）（A ）E 是可数集（B ）E 是闭集（C ）0mE = （D ）E 中的每一点均为E 的内点22．若()E R ⊆的外测度为0，则（ AB ）（A ）E 是可测集（B ）0mE =（C ）E 一定是可数集（D ）E 一定不是可数集23．设mE <+∞，{}()n f x 为E 上几乎处处有限的可测函数列，()f x 为E 上几乎处处有限的可测函数，如果()(),()f x f x x E ⇒∈，则下列哪些结果不一定成立（ ABCD ）（A ）()E f x dx ⎰存在（B ）()f x 在E 上L -可积（C ）.()()()a en f x f x x E →∈（D ）lim ()()n E E n f x dx f x dx →∞=⎰⎰24．若可测集E 上的可测函数()f x 在E 上有L 积分值，则（ AD ）（A ）()()f x L E +∈与()()f x L E -∈至少有一个成立（B ）()()f x L E +∈且()()f x L E -∈（C ）|()|f x 在E 上也有L -积分值（D ）|()|()f x L E ∈三、单项选择1．下列集合关系成立的是（ A ）A ()\B A A =∅B ()\A B A =∅C ()\A B B A =D ()\B A A B =2．若n R E ⊂是开集，则（ B ）A E E '⊂B 0E E =C E E =DE E '=4．设(){}n f x 是E 上一列非负可测函数，则（ B ） A ()()lim lim n n E E n n f x dx f x dx →∞→∞≤⎰⎰ B ()()lim lim n n E E n n f x dx f x dx →∞→∞≤⎰⎰ C ()()lim lim n n E E n n f x dx f x dx →∞→∞≤⎰⎰ D ()()lim lim n n E E n n f x dx f x →∞→∞≤⎰⎰5．下列集合关系成立的是（ A ）A c c A A αααα∈Λ∈Λ⎛⎫= ⎪⎝⎭B ccA A αααα∈Λ∈Λ⎛⎫= ⎪⎝⎭C c c A A αααα∈Λ∈Λ⎛⎫= ⎪⎝⎭D c cA A αααα∈Λ∈Λ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭6．若n R E ⊂是闭集，则（ C ）A E E '=B E E '⊂C E E '⊂D 0E E =A E 为闭集B E 是不可测集C mE =+∞D 0mE =9．下列集合关系成立的是（B ）A c c A A αααα∈Λ∈Λ⎛⎫= ⎪⎝⎭BccA A αααα∈Λ∈Λ⎛⎫= ⎪⎝⎭C c c A A αααα∈Λ∈Λ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭D cc cA A αααα∈Λ∈Λ⎛⎫=⎪⎝⎭10．设n R E ⊂，则( A ) A E E ⊃B E E '⊂C E E '⊂D E E =11．设P 为康托集，则（ B ）A P 是可数集B 0mP =C P 是不可数集D P 是开集13．下列集合关系成立的是（ A ）A 若AB ⊂则c c B A ⊂B 若A B ⊂则c c A B ⊂C 若A B ⊂则A B B =D 若A B ⊂则A B B =14．设n R E ⊂，则（ A ） A ()E E =B 0E E ⊃C E E '⊂D E E '⊂15．设(){},001E x x =≤≤，则（ B ）A 1mE =B 0mE =C E 是2R 中闭集DE 是2R 中完备集16．设()f x ，()g x 是E 上的可测函数，则（ B ）A ()()E x f x g x ⎡⎤≥⎣⎦不一定是可测集B ()()E x f x g x ⎡⎤≠⎣⎦是可测集C ()()E x f x g x ⎡⎤≤⎣⎦是不可测集D ()()E x f x g x ⎡⎤=⎣⎦不一定是可测集１7．下列集合关系成立的是（A ）（A ）(\)A B B A B = （B ）(\)A B B A =（C ）(\)B A A A ⊆ （D ）\B A A ⊆18. 若()n E R ⊆是开集，则（ B ）（A ）E 的导集E ⊆ （B ）E 的开核E =（C ）E E = （D ）E 的导集E =..19. 设P 的康托集，则(C)（A ）P 为可数集（B ）P 为开集（C ）0mP = （D ）1mP =20、设E 是1R 中的可测集，()x ϕ是E 上的简单函数，则（ D ）（A ）()x ϕ是E 上的连续函数（B ）()x ϕ是E 上的单调函数（C ）()x ϕ在E 上一定不L 可积（D ）()x ϕ是E 上的可测函数21．下列集合关系成立的是（ A ）（A ）()()()A B C A B A C = （B ）(\)A B A =∅（C ）(\)B A A =∅ （D ）A B A B ⊆22. 若()n E R ⊆是闭集，则（ B ）（A ）0E E = （B ）E E =（C ）E E '⊆ （D ）E E '=23. 设Q 的有理数集，则（ C ）（A ）0mQ > （B ）Q 为闭集（C ）0mQ = （D ）Q 为不可测集24.设E 是n R 中的可测集，()f x 为E 上的可测函数，若()0Ef x dx =⎰，则（ A ）（A ）在E 上，()f x 不一定恒为零（B ）在E 上，()0f x ≥（C ）在E 上，()0f x ≡ （D ）在E 上，()0f x ≠四、判断题1. 可数个闭集的并是闭集. （ × ）2. 可数个可测集的并是可测集. （ √ ）3. 相等的集合是对等的. （ √ ）4. 称()(),f x g x 在E 上几乎处处相等是指使()()f x g x ≠的x 全体是可测集. （ √ ）5. 可数个F σ集的交是F σ集. （ × ）6. 可数个可测函数的和使可测函数. （ √ ）7. 对等的集合是相等的. (× )8. 称()(),f x g x 在E 上几乎处处相等是指使()()f x g x =的x 全体是零测集. （ × ）9. 可数个G σ集的并是G σ集. （ √ ）..11. 对等的集合不一定相等. （ √ ）12. 称()(),f x g x 在E 上几乎处处相等是指使()()f x g x ≠的x 全体是零测集.（ √ ）13. 可数个开集的交是开集（ × ）14. 可测函数不一定是连续函数. （ √ ）15. 对等的集合有相同的基数. （ √ ）16. 称()(),f x g x 在E 上几乎处处相等是指使()()f x g x ≠的x 全体的测度大于0 （ × ）17. 可列个闭集的并集仍为闭集（ × ）18. 任何无限集均含有一个可列子集（ √ ）19. 设E 为可测集，则一定存在G σ集G ，使E G ⊆，且()\0m G E =. （ √ ）20. 设E 为零测集，()f x 为E 上的实函数，则()f x 不一定是E 上的可测函数（ × ）21. 设()f x 为可测集E 上的非负可测函数，则()()f x L E ∈ （ × ）22. 可列个开集的交集仍为开集（× ）23. 任何无限集均是可列集（ × ）24. 设E 为可测集，则一定存在F σ集F ，使F E ⊆，且()\0m E F =. （ √ ）25. 设E 为零测集，则()f x 为E 上的可测函数的充要条件是：∀实数a 都有()E xf x a ⎡≥⎤⎣⎦是可测集（ √ ）26. 设()f x 为可测集E 上的可测函数，则()Ef x dx ⎰一定存在. （ × ）五、简答题1. 简述无限集中有基数最小的集合，但没有最大的集合.答：因为任何无限集均含有可数集，所以可数集是无限集中基数最小的，但无限集没有基数最大的，这是由于任何集合A ，A 的幂集2A的基数大于A 的基数. 2. 简述点集的边界点，聚点和内点的关系.答: 内点一定是聚点，边界点不一定是聚点，点集的边界点或为孤立点或为聚点.3. 简单函数、可测函数与连续函数有什么关系？答：连续函数一定是可测函数；简单函数一定是可测函数；简单函数可表示成简单函数或连续函数的极限4. [],a b 上单调函数与有界变差函数有什么关系？答：单调函数是有界变差函数，有界变差函数可表示成两个单调增函数之差.5. 简述集合对等的基本性质.答：A A ；若A B ，则B A ；若A B ，且B C ，则A C .6. 简述点集的内点、聚点、边界点和孤立点之间关系.答：内点一定是聚点，内点不是孤立点，边界点由点集的孤立点和聚点组成.7. 可测集与开集、G σ集有什么关系？答：设E 是可测集，则0ε∀>，∃开集G ，使G E ⊃，使()\m G E ε<，或∃G 集G ，使G E ⊃，且()\0m G E =.8. [],a b 上单调函数、有界变差函数与绝对连续函数有什么关系？答：绝对连续函数是有界变差函数，反之不然；有界变差函数是单调增函数的差，而单调函数是有界变差函数. 9. 简述证明集合对等的伯恩斯坦定理. 答：若AB B *⊂，又B A A *⊂，则A B10. 简述1R 中开集的结构.答: 设G 为1R 中开集，则G 可表示成1R 中至多可数个互不相交的开区间的并. 11. 可测集与闭集、F σ集有什么关系？答：设E 是可测集，则0ε∀>，∃闭集F E ⊂，使()\m E F ε<或∃F σ集F E ⊂，使()\0m E F =.12. 为什么说绝对连续函数几乎处处可微？答：因为绝对连续函数是有界变差，由若当分解定理，它可表示成两个单调增函数的差，而单调函数几乎处处有有限的导数，所以绝对连续函数几乎处处可微.13. 简述连续集的基数大于可数集的基数的理由.答:连续集是无限集，因而包含可数子集，又连续集是不可数集，所以连续集的基数大于可数集的基数. 14. 简述nR 中开集的结构.答：nR 中开集可表示成可数个互不相交的半开半闭区间的并 15. 可测函数列几乎处处收敛、依测度收敛和近一致收敛的关系？答：设()(),n f x f x 是可测集E 上的一列可测函数，那当mE <+∞时，()(),.n f x f x a e →于E ，必有()()n f x f x ⇒.反之不成立，但不论mE <+∞还是mE =+∞，(){}n f x 存在子列(){}k n f x ，使()(),.k n f x f x a e →于E .当mE <+∞时，()(),.n f x f x a e →于E ，由Egoroff 定理可得()n f x 近一致收敛于()f x ，反之，无需条件mE <+∞，结论也成立.16. 为什么说有界变差函数几乎处处可微？答：由若当分解定理，有界变差函数可表示成两个单调增函数的差，而单调函数几乎处处可微，所以有界变差函数几乎处处可微.17. 简述无穷多个开集的交集是否必为开集？答：不一定，如[]1111,11,1n n n +∞=⎛⎫---+=- ⎪⎝⎭18. 可测集E 上的可测函数与简单函数有什么关系？答：简单函数必是可测函数但可测函数不一定是简单函数，可测函数一定可表示成简单函数列的极限形式. 19.[],a b 上的有界变差函数与单调函数有什么关系？答：单调函数必为有界变差函数但有界变差函数不一定为单调函数，有界变差函数可表示成单调函数之差. 20. 简述无穷多个闭集的并集是否必为闭集？答：不一定如()1111,11,1n n n +∞=⎡⎤---+=-⎢⎥⎣⎦ 21. 可测集E 上的可测函数与连续函数有什么关系？答：E 上连续函数必为可测函数但E 上的可测函数不一定时连续函数，E 上可测函数在E 上是“基本上”连续的函数 22.[],a b 上的绝对连续函数与有界变差函数有什么关系？答：绝对连续函数必为有界变差函数但有界变差函数不一定为绝对连续函数六、计算题1. 设()[]230,1\xx E f x xx E⎧∈⎪=⎨∈⎪⎩，其中E 为[]0,1中有理数集，求()[]0,1f x dx ⎰.解：因为0mE =，所以()3,.f x x a e =于[]0,1，于是()[][]30,10,1f x dx x dx =⎰⎰，而3x 在[]0,1上连续，从而黎曼可积，故由黎曼积分与勒贝格积分的关系，[]()41331000,11|44x x dx R x dx ===⎰⎰ 因此()[]0,114f x dx =⎰. 2. 设{}n r 为[]0,1中全体有理数，(){}[]{}12121,,00,1\,,n n n x r r r f x x r r r ∈⎧⎪=⎨∈⎪⎩，求()[]0,1lim n n f x dx →∞⎰.解：显然()n f x 在[]0,1上可测，另外由()n f x 定义知，()0,.n f x a e =于[]0,1()1n ≥ 所以()[][]0,10,100nf x dx dx ==⎰⎰因此()[]0,1lim0nn f x dx →∞=⎰.3. 设()[]2sin 0,1\xx P f x x x P ∈⎧=⎨∈⎩，P 为康托集，求()[]0,1f x dx ⎰.解：因为0mP =，所以()2,.f x x a e =于[]0,1于是()[][]20,10,1f x dx x dx =⎰⎰而2x 在[]0,1上连续，所以[]()31221000,11|33x x dx R x dx ===⎰⎰ 因此()[]0,113f x dx =⎰.4. 设()()[]22sin ,0,11n nx nx f x x n x =∈+，求()[]0,1lim n n f x dx →∞⎰. 解：因为()n f x 在[]0,1上连续，所以可测()1,2,n =又()()[]2222sin 1,0,1,1,2,1122n nx nx nx nx f x x n n x n x nx =≤≤=∈=++而22lim01n nxn x →∞=+，所以()lim 0n n f x →∞=.因此由有界控制收敛定理()[]()[][]0,10,10,1limlim 00nnn n f x dx f x dx dx →∞→∞===⎰⎰⎰5. 设()3cos 0,\2x x E f x x x E π⎧∈⎪=⎨⎡⎤∈⎪⎢⎥⎣⎦⎩，E 为0,2π⎡⎤⎢⎥⎣⎦中有理数集，求()0,2f x dx π⎡⎤⎢⎥⎣⎦⎰. 解：因为0mE =，所以()cos ,.f x x a e =于[]0,1 于是()0,0,22cos f x dx xdx ππ⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦=⎰⎰而cos x 在0,2π⎡⎤⎢⎥⎣⎦上连续，所以黎曼可积，由牛顿莱布尼公式 []()22000,1cos cos sin |1xdx R xdx x ππ===⎰⎰因此()0,21f x dx π⎡⎤⎢⎥⎣⎦=⎰6. 设()()[]22cos ,0,11n nx nx f x x n x =∈+，求()[]0,1lim n n f x dx →∞⎰.解：因为()n f x 在[]0,1上连续，所以可测()1,2,n =又()()[]2222cos 1,0,1,1,2,1122n nx nx nx nx f x x n n x n x nx =≤≤=∈=++而22lim01n nxn x →∞=+，所以()lim 0n n f x →∞=.因此由有界控制收敛定理()[]()[][]0,10,10,1limlim 00nnn n f x dx f x dx dx →∞→∞===⎰⎰⎰7. 设()[]3sin 0,1\xx P f x xx P⎧∈⎪=⎨∈⎪⎩，P 为康托集，求()[]0,1f x dx ⎰.解：因为0mP =，所以(),.f x x a e =于[]0,1 于是()[][]0,10,1f x dx xdx =⎰⎰而x 在[]0,1上连续，所以[]()2121000,11|22x xdx R x dx ===⎰⎰ 因此()[]0,112f x dx =⎰. 8. 求()()0,ln limcos xn n x n e xdx n -→∞+⎰.解：令()()()()0,ln cos xn n x n f x x e x nχ-+= 显然()n f x 在()0,+∞上可测，且()()()()0,0,ln cos xn n x n e xdx f x dx n -+∞+=⎰⎰ 因为()()()()ln ln cos ,0,,1,2,x n x n x n f x e x x n n n-++≤≤∀∈+∞=不难验证()()ln n x n g x n+=，当n 足够大时，是单调递减非负函数，且 ()lim 0n n g x →∞=，所以()()()()()()0,0,0,ln limlim lim n n n n n x n dx g x dx g x n →∞→∞→∞+∞+∞+∞+==⎰⎰⎰()0,00dx +∞==⎰由勒贝格控制收敛定理()()0,lim0n n f x dx →∞+∞=⎰故()()0,ln lim cos 0x n n x n e xdx n -→∞+=⎰. 9. 设()[][]101001x D x x ⎧⎪=⎨⎪⎩为，上的有理点为，上的无理点，求()[]01D x dx ⎰，.证明记1E 是[]0,1中有理数集，2E 是[]0,1中无理数集，则[]12120,1,E E E E ==∅，120,1mE mE ==，且()1210E E D x χχ=+，所以()[]120,1100D x dx mE mE =+=⎰.10 求()0ln limcos xn x n e xdx n+∞-→∞+⎰. 证明易知()ln limcos 0xn x n e x n-→∞+=对任意0,1x n ≥≥，()()ln ln cos x x n x n e x n n-++≤ 设()ln ()x y f y y +=，0y >，则()2ln ()yx y x yf y y -++'=，当3y ≥时，()1ln yx y x y<<++，()0f y '<. 则()ln ()x n f n n+=是单调减函数且非负（3n ≥）；又()ln 1limlim 0n n x n nx n →∞→∞+==+，由Levi 单调收敛定理得()()00ln ln lim lim 00n n x n x n dx dx dx n n+∞+∞+∞→∞→∞++===⎰⎰⎰，即()ln ()x n L E n +∈，再由Lebsgue 控制收敛定理得()()000ln ln lim cos lim cos 00x xn n x n x n e xdx e xdx dx n n+∞+∞+∞--→∞→∞++===⎰⎰⎰11. 设()[]230,1xx Pf x xx P ⎧∈⎪=⎨∈-⎪⎩，其中P 为康托集，求()[]01f x dx ⎰，.解：因为P 为康托集，故0mP =，[]()0,1\1m P = 所以()[]320,1P P f x x x χχ-=+ 所以()[][]()2330,10,1f x dx x mP x m P x=+-=⎰12. 求()[]22,0,11n nxf x E n x ==+，求()lim n n Ef x dx →∞⎰.解：易知：[]()22lim00,11n nxx n x →∞=∈+令()()2221,1n nx f x g x n x x ==+，则()()()22232222222221110111n nx n x nx n x nx g x f x nx nx x n x x x n x n x+-+--=-==≥+++ 所以()()[]()00,1,1n f x g x x n ≤≤∈≥ 又因为()g x 在[]0,1上Lebesgue 可积，所以由控制收敛定理，得 22lim 001n E Enxdx dx n x →∞==+⎰⎰七、证明题1．证明集合等式：(\)A B B A B =证明(\)()c A B B A B B =()()()c c A B A B B A BB B A B ===2．设E 是[0,1]中的无理数集，则E 是可测集，且1mE =证明设F 是[0,1]中的有理数集，则F 是可数集，从而*0m F =，因此F 是可测集，从而cF 可测，又[0,1]\[0,1]c E F F ==，故E 是可测集.由于EF =∅，所以1[0,1]()0m m E F mE mF mF ===+=+，故1mF =3．设(),()f x g x 是E 上的可测函数，则[|()()]E x f x g x >是可测集证明设{}n r 为全体有理数所成之集，则()11[|()()][|()()][|()][|()]n n n n n E x f x g x E x f x r g x E x f x r E x g x r ∞∞==>=≥>=≥<因为(),()f x g x 是E 上的可测函数，所以[|()]n E x f x r ≥，[|()]n E x g x r <是可测集，1,2,n =，于是由可测集性质知[|()()]E x f x g x >是可测集4．设()f x 是E 上的可测函数，则对任何常数0a >，有1[|()|]|()|EmE x f x a f x dx a ≥≤⎰ 证明因为()f x 在E 上可测，所以|()|f x 在E 上非负可测，由非负可测函数积分性质，[|()|][|()|]|()||()|E x f x a E x f x a Eadx f x dx f x dx ≥≥≤≤⎰⎰⎰而[|()|][|()|]E x f x a adx a mE x f x a ≥=⋅≥⎰，所以1[|()|]|()|E mE x f x a f x dx a≥≤⎰ 5．设()f x 是E 上的L -可积函数，{}n E 是E 的一列可测子集，且lim 0n n mE →∞=，则lim ()0nE n f x dx →∞=⎰证明因为lim 0n n mE →∞=，所以0,1N δ∀>∃≥，当n N ≥时，n mE δ<，又()f x 在E 上L -可积，所以由积分的绝对连续性，0,0,εδ∀>∃>当,e E me δ⊂<时|()|ef x dx ε<⎰于是当n N ≥时，n mE δ<，因此|()|nE f x dx ε<⎰，即lim ()0nE n f x dx →∞=⎰6．证明集合等式：\(\)A A B A B =证明 \(\)()(())()c c cc c cA AB AA B A A B A A B ===()()c AA AB A B ==7．设12,A A 是[0,1]的可测子集，且121mA mA +>，则12()0m A A >证明因为12[0,1],[0,1]A A ⊂⊂，所以12[0,1]A A ⊂，于是12()[0,1]1m A A m ≤=另一方面，121122[\()]A A A A A A =，所以()12112211221122()[\()][\()]()m A A m A A A A m A A A mA mA m A A mA ==+=-+ 于是121212()()0m A A mA mA m A A =+->8．设()f x 是定义在可测集nE R ⊂上的实函数，n E 为E 的可测子集（1,2,n =），且1n n E E ∞==，则()f x 在E 上可测的充要条件是()f x 在每个n E 上可测证明对任何实数a ，因为11[|()][|()]([|()])n nn n E x f x a E x f x a E E x f x a ∞∞==>=>=>所以()f x 在E 上可测的充要条件是对每个1,2,n =，()f x 在每个n E 上可测9．设()f x 是E 上的可测函数，则对任何常数0a >，有()[|()]af x EmE x f x a e e dx -≥≤⎰证明因为()f x 在E 上可测，所以()f x e是非负可测函数，于是由非负可测函数积分性质，()()[|()][|()]a f x f x E x f x a E x f x a Ee dx e dx e dx ≥≥≤≤⎰⎰⎰而[|()][|()]a a E x f x a e dx e mE x f x a ≥=⋅≥⎰，所以 ()[|()]af x EmE x f x a ee dx -≥≤⎰10．设()f x 是E 上的可积函数，{}n E 为E 的一列可测子集，mE <+∞，如果lim n n mE mE →∞= 则lim()()nE En f x dx f x dx →∞=⎰⎰证明因()f x 在E 上L -可积，由积分的绝对连续性知，对任意0ε>，存在0δ>，对任何A E ⊆，当mA δ<时有|()|Af x dx ε<⎰，由于lim n n mE mE →∞=<+∞，故对上述的0δ>，存在0k ，当0n k >时n E E ⊆，且有()n n mE mE m E E δ-=-<，于是|()()||()|nnEE E E f x dx f x dx f x dx ε--=<⎰⎰⎰，即 lim()()nE En f x dx f x dx →∞=⎰⎰11．证明集合等式：()\(\)(\)A B C A C B C =证明 ()\()()()(\)(\)c c c AB C A B C A C B C A C B C ===12．设nE R ⊂是零测集，则E 的任何子集F 是可测集，且0mF =证明设F E ⊂，*0m E =，由外测度的单调性和非负性，*00m F mE ≤≤=，所以*0m F =，于是由卡氏条件易知F 是可测集13．设(),(),(),()n n f x g x f x g x 是E 上几乎处处有限的可测函数，且()()n f x f x ⇒，()()n g x g x ⇒，则()()()()n n f x g x f x g x +⇒+.证明对任何正数0σ>，由于|(()())(()())||()()||()()|n n n n f x g x f x g x f x f x g x g x +-+≤-+-所以[|(()())(()())|]n n E x f x g x f x g x σ+-+≥[|()()|][|()()|]22n n E x f x f x E x g x g x σσ⊂-≥-≥于是[|(()())(()())|]n n mE x f x g x f x g x σ+-+≥[|()()|][|()()|]22n n mE x f x f x mE x g x g x σσ≤-≥+-≥0()n →→∞故()()()()n n f xg x f x g x +⇒+ 14．设(),()f x g x 是E 上L -E 上也是L -可积的证明因(),()f x g x 是E 上L -可积，所以|()|,|()|f x gx 在E 上L -可积，从而|()||()|f x g x +L -可积，|()||()|f x g x ≤=+ E 上L -可积15．设()f x 是可测集E 上的非负可测函数，如果()0Ef x dx =⎰，则()0.f x a e =于E证明反证，令[|()0]A E x f x =>，则由()f x 的可测性知，A 是可测集.下证0mA =，若不然，则0mA >由于11[|()0][|()]n A E x f x E x f x n ∞==>=≥，所以存在1N ≥，使1[|()]0mE x f x d N≥=> 于是11[|()][|()]111()()[|()]0EE x f x E x f x NNd f x dx f x dx dx mE x f x N N N N ≥≥≥≥=≥=>⎰⎰⎰因此()0Ef x dx >⎰，矛盾，故()0.f x a e =于E16．证明等式：\()(\)(\)A B C A B A C =证明\()()()()()(\)(\)c cc c c A B C A B C A B C A B A C A B A C ====17．设n E R ⊂是有界集，则*m E <+∞.证明因为E 是有界集，所以存在开区间I ，使E I ⊂由外测度的单调性，**m E m I ≤，而*||m I I =<+∞（其中||I 表示区间I 的体积），所以*m E <+∞18．1R 上的实值连续函数()f x 是可测函数证明因为()f x 连续，所以对任何实数a ，{|()}x f x a >是开集，而开集为可测集，因此()f x 是可测函数 19．设mE <+∞，函数()f x 在E 上有界可测，则()f x 在E 上L -可积，从而[,]a b 上的连续函数是L -可积的证明因为()f x 在E 上有界可测，所以存在0M >，使|()|f x M <，x E ∈，|()|f x 是非负可测函数，由非负可测函数的积分单调性，|()|EEf x dx Mdx M mE <=⋅<+∞⎰⎰故|()|f x 在E 上L -可积，从而()f x 在E 上L -可积因为[,]a b 上的连续函数是有界可测函数，所以L -可积的 20．设()n f x （1,2,n =）是E 上的L -可积函数，如果lim|()|0nn E n f x dx →∞=⎰，则()0n f x ⇒证明对任何常数0σ>，[|()|][|()|]|()|n n n E x f x mE x f x f x dx σσσ≥⋅≥≤⎰所以 [|()|]1[|()|]|()|n n n E x f x mE x f x f x dx σσσ≥≥≤⎰1|()|0()nEfx dx n σ≤→→∞⎰因此 ()0n f x ⇒ 21. 证明集合等式：()()()\\\A B C A C B C =.证明 ()()()()()()\\\c c c A B C A B C A C BC A C B C ===22. 设[]{}00,1E =中的有理点，则0E为可测集且00mE =.证明因为0E 为可数集，记为{}012,,,n E r r r =，0ε∀>，取()11,1,2,22n n n n n I r r n εε++⎛⎫=--= ⎪⎝⎭ 显然 01n n E I +∞=⊂，所以0011102n n n n n n E I m E I εε+∞+∞+∞*===⊂≤≤==∑∑，让0ε→，得00m E *=.n T R ∀∈，由于()()00c T TE T E = 所以()()00c m T m TE m T E ***≤+. 又00,0c T E T m E *⊆=，所以()()()000c c m T m T E m T E m T E ****≥=+.故()()00c m T m T E m T E ***=+故0E 为可测集，且00mE =23. 证明：1R 上的实值连续函数()f x 必为1R 上的可测函数证明 1,a b R ∀∈，不妨假设a b <，因为()f x 是1R 上的连续函数，故()f x 是[],a b 上的连续函数，记[],F a b =，由()f x 在F 上连续，则(),M m m M ∃<，使()m f x M ≤≤，则显然易证，()1,R F f αα∀∈≥是闭集，即()f x 为[],a b 上的可测函数，由,a b 的任意性可知，()f x 是1R 上的可测函数. 24. 设()()f x L E ∈，{}n E 为E 的一列可测子集，mE <+∞ ，如果lim n n mE mE →∞=，则()()lim n n E Ef x dx f x dx →∞=⎰⎰. 证明因()f x 在E 上L 可积，由积分的绝对连续性知，对任意0ε>，存在0δ>，对任何A E ⊆，当mA δ<时有|()|A f x dx ε<⎰，由于lim n n mE mE →∞=<+∞，故对上述的0δ>，存在0k ，当0n k >时n E E ⊆，且有()n n mE mE m E E δ-=-<，于是\|()()||()|nn E E E E f x dx f x dx f x dx ε-=<⎰⎰⎰，即 lim ()()n E En f x dx f x dx →∞=⎰⎰ 25. 证明集合等式：()()()\\\A BC A B A C =.证明()()()()()()()\\\c c c c c A B C AB C A B C A B A C A B A C ====26. 设1E R ⊆，且0m E *=，则E 为可测集. 证明 n T R ∀∈，由于()()n c T R T TE T E ∀∈= 所以()()c m T m TE m T E ***≤+. 又,0c T E T m E *⊆=，所以()()()c c m T m T E m T E m T E ****≥=+.故()()c m T m TE m T E ***=+所以E 为可测集 27. 证明：1R 上的单调函数()f x 必为可测函数.证明 1,a b R ∀∈，不妨假设a b <，因为()f x 是1R 上的单调函数，不妨设()f x 为单调增函数，故()f x 是[],a b 上的单调增函数，即()()121212,,,x x E x x f x f x ∀∈<≤，则1R α∀∈，有1）当()sup x E f x α∈≤时，();E xf x α⎡>⎤=∅⎣⎦2）当()inf x E f x α∈>时，();E x f x E α⎡>⎤=⎣⎦3）当()()inf sup x E x E f x f x α∈∈≤<时，必有10x ER ∈，使 ()()000,f x f x αα+>≤或()()000,0f x f x αα+≥-<.由()f x 的单调增知，()0(),E xf x E x α⎡>⎤=+∞⎣⎦或[)0,E x +∞. 在所有情况下，()E x f x α⎡>⎤⎣⎦都可测.即()f x 是[],a b 上的可测函数.由由,a b 的任意性可知，()f x 是1R 上的可测函数. 28. 设()f x 为可测集nE R ⊆上的可测函数，则()()f x L E ∈的充要条件()()f x L E ∈. 证明必要性若()()f x L E ∈，因为()()()f x fx f x +-=+，且()()f x L E ∈ 所以()(),E E f x dx f x dx +-⎰⎰中至少有一个是有限值，故()()()EE E f x dx f x dx f x dx +-=+⎰⎰⎰即()()f x L E ∈充分性若()()f x L E ∈因为()()()f x f x f x +-=-，且()()f x L E ∈所以()(),E E f x dx f x dx +-⎰⎰中至少有一个是有限值，故()()()E EE f x dx f x dx f x dx +-=-⎰⎰⎰，即()()f x L E ∈.。

《实变函数》习题库参考答案

《实变函数》习题库参考答案《实变函数》习题库参考答案一、判断题 1、( √ )理由:由内点定义知，存在A P U ?),(0δ，从而对任意的)(0P U ，必含有A 中无穷多个点。

满足聚点定义 2、( √ )理由:[法一]:都具有连续基数,故对等 [法二]:可建立一个映射)2tan()(ππ-?--=a b a x x f ,则f(x)为),(b a 到R 的一一映射.3、( √ )理由:由B A ?知, A A B B )(-=,从而由有限可加性知，mA A B m mB +-=)(，又由+∞<="" 4、(="" b="" m="" ma="" p="" √="" 。

从而移项可得结论。

="" 知，+∞<-+∞理由:f(x)在区间[0,5)及[5,10]上均为连续函数，故分别在2个区间上是可测函数，从而再其和集上也是可测函数。

5、( × )理由:例如有理数集Q ，无理数2是Q 的聚点，但不是其内点。

6、( √ )理由:[法一]:都是可数集,故有相同的基数,即对等。

[法二]:可建立一个映射==+==...2,1,1,11,0,1)(n n x n x x f ,则f(x)为集合,1,,31,21,1,0n 到集合 ,1,,31,21,1n 的一一映射。

7、( √ )理由:由B A ?知A A B B )(-=,且φ=-A A B )(，故mA mA A B mmB =+-=)(8、( √ )理由:狄利克莱函数-∈∈=.]1,0[,0]1,0[,1)(Q x Qx x D 是[0,1]上的简单函数，故可测。

9、( √ )理由:由于E E ?Φ='，所以.}3,2,1{为闭集=E 10、( × )理由:如无界。

(完整版)实变函数期末考试卷A及参考答卷

2011—2012学年第1学期数计学院09级数学与应用数学专业(1、2班)《实变函数》期末考试卷（A）考生考试诚信承诺书在我填写考生信息后，表示我已阅读和理解《龙岩学院考试纪律与违纪处分办法》的有关规定，承诺在考试中自觉遵规守纪，如有违反将接受处理；我保证在本科目考试中，本人所提供的个人信息是真实、准确的。

考生签名：实变函数期末考试卷(A )2009级本科1、2班用考试时间2012年01月 04日一填空题（每小题3分，满分24分） 1 我们将定义在可测集qE ⊂上的所有L 可测函数所成的集合记为()M E .任取()f M E ∈，都可以确定两个非负可测函数：()()()(),0,0,0.f x x E f fx x E f +∈>⎧=⎨∈≤⎩当时当时和()()()()0,0,,0.x E f fx f x x E f -∈>⎧=⎨-∈≤⎩当时当时分别称为f 的正部和负部。

请你写出()()(),,f x fx f x +-和()f x 之间的关系：()f x =，()f x =。

2 上题()M E 中有些元素ϕ被称为非负简单函数，指的是：12k E E E E =是有限个互不相交的可测集的并集，在i E 上()i x c ϕ≡（非负常数）（1,2,,i k =）.ϕ在E 上的L 积分定义为：()Ex dx ϕ=⎰，这个积分值可能落在区间中，但只有当时才能说ϕ是L 可积的。

3 若()f M E ∈是非负函数，则它的L 积分定义为：()Ef x dx =⎰，这个积分值可能落在区间中，但只有当时才能说f 是L 可积的。

4 ()M E 中的一般元素f 称为是积分确定的，如果f +和f -，即()Efx dx +⎰和()E f x dx -⎰的值；但只有当时才能说f 是L 可积的，这时将它的积分定义为：()Ef x dx =⎰。

5 从()M E 中取出一个非负函数列(){}n f x ，则法图引理的结论是不等式：；如果再添上条件和就试卷共 8 页第 2 页得到列维定理的结论：。

实变函数测试题与答案

实变函数试题一，填空题1. 设1,2n A n ⎡⎤=⎢⎥⎣⎦,1,2n =,则lim n n A →∞= . 2. ()(),,a b -∞+∞,因为存在两个集合之间的一一映射为3. 设E 是2R 中函数1co s ,00,0x y x x ⎧≠⎪=⎨⎪ =⎩的图形上的点所组成的集合，则E '= ，E ︒= .4. 若集合nE R ⊂满足E E '⊂,则E 为集. 5. 若(),αβ是直线上开集G 的一个构成区间,则(),αβ满足:, .6. 设E 使闭区间[],a b 中的全体无理数集,则mE = .7. 若()n mE f x →()0f x ⎡⎤=⎣⎦,则说{}()n f x 在E 上 . 8. 设nE R ⊂,0nx R ∈,若 ,则称0x 是E 的聚点.9. 设{}()n f x 是E 上几乎处处有限的可测函数列,()f x 是E 上几乎处处有限的可测函数,若0σ∀>,有 ,则称{}()n f x 在E 上依测度收敛于()f x . 10. 设()()n f x f x ⇒,x E ∈,则∃{}()n f x 的子列{}()jn fx ,使得.二,判断题.正确的证明,错误的举反例. 1. 若,A B 可测,A B ⊂且A B ≠,则mA mB <.2. 设E 为点集,P E ∉,则P 是E 的外点.3. 点集11,2,,E n⎧⎫=⎨⎬⎩⎭的闭集. 4. 任意多个闭集的并集是闭集.5. 若nE R ⊂,满足*m E =+∞,则E 为无限集合. 三,计算证明题1.证明:()()()A B C A B A C --=-2.设M 是3R 空间中以有理点(即坐标都是有理数)为中心,有理数为半径的球的全体,证明M 为可数集.3.设nE R ⊂,i E B ⊂且i B 为可测集,1,2i =.根据题意,若有()()*0,i m B E i -→ →∞,证明E 是可测集.4. 设P 是Cantor 集,()[]32ln 1,(),0,1x x P f x x x P⎧+ ∈⎪=⎨ ∈-⎪⎩.求10(L)()f x dx ⎰.5. 设函数()f x 在Cantor 集0P 中点x 上取值为3x ,而在0P 的余集中长为13n的构成区间上取值为16n ,()1,2n =,求1()f x dx ⎰.6. 求极限:13230lim(R)sin 1n nx nxdx n x →∞+⎰.实变函数试题解答一填空题1.[]0,2.2.{}1(,)cos ,0(0,)1x y y x y y x ⎧⎫=≠≤⎨⎬⎩⎭;∅.3.闭集.4.b a -.5.几乎处处收敛于()f x 或a.e.收敛于()f x .6.对000,(,)U x δδ∀> 有{}()0E x -=∅.7.()()n f x f x → a.e.于E . 二判断题1. F .例如,(0,1)A =,[]0,1B =,则A B ⊂且A B ≠,但1mA mB ==.2. F .例如,0(0,1)∉,但0不是(0,1)的外点.3. F .由于{}0E E '=⊄.4. F .例如,在1R 中,11,1n F n n ⎡⎤=-⎢⎥⎣⎦,3,4n =是一系列的闭集,但是3(0,1)n n F ∞==不是闭集.5. T .因为若E 为有界集合,则存在有限区间I ,I <+∞,使得E I ⊂,则**,m E m I I ≤=<+∞ 于*m E =+∞ .三,计算证明题. 1.证明如下:2. M 中任何一个元素可以由球心(,,)x y z ,半径为r 唯一确定,x ,y ,z 跑遍所有的正有理数,r 跑遍所有的有理数.因为有理数集于正有理数集为可数集都是可数集,故M 为可数集.3. 令1i i B B ∞==,则i E B B ⊂⊂且B 为可测集,于是对于i ∀,都有i B E B E -⊂-,故()()**0i m B E m B E ≤-≤-,令i →∞,得到()*0m B E -=,故B E -可测.从而()E B B E =--可测.4. 已知0mP =,令[]0,1G P =-,则()1320221130(L)()(L)ln 1(L)(L)()(L)(L)(R)()133PGGPGf x dx x dx x dxf x dxx dx x dxf x dxx =++ =0+ =+ = ==⎰⎰⎰⎰⎰⎰⎰.5. 将积分区间[]0,1分为两两不相交的集合:0P ,1G ,2G ,其中0P 为Cantor集,n G 是0P 的余集中一切长为13n 的构成区间(共有12n -个)之并.由L 积分的可数可加性,并且注意到题中的00mP =,可得6. 因为323sin 1nx nx n x+在[]0,1上连续,13230(R)sin 1nx nxdx n x +⎰存在且与13230(L)sin 1nx nxdx n x +⎰的值相等.易知由于12x 在()0,1上非负可测，且广义积分1012dx x ⎰收敛，则 12x在()0,1上(L)可积，由于323lim sin 01n nx nx n x →∞=+，()0,1x ∈，于是根据勒贝格控制收敛定理，得到1133232300132301lim(R)sin lim(L)sin 11lim sin 100n n n nx nx nxdx nxdx n x n x nx nx dxn x dx →∞→∞→∞=++⎛⎫ = ⎪+⎝⎭ ==⎰⎰⎰⎰.一、判定下列命题正确与否，简明理由(对正确者予以证明，对错误者举处反例)（15分，每小题3分） 1. 非可数的无限集为c 势集 2. 开集的余集为闭集。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

[0, ]
f ( x)dx 。
解：由题设 f ( x) sin x ， a.e. 于 [0, ] ，而 sin x 在 [0, ] 上连续，于是由积分的惟一性和 L 积分与 R 积分的关系得

[0, ]
f ( x)dx
[0, ]
sin xdx ( R) sin xdx ( cos x)
n n n n n n n
n
m*T m* (T E ) m* (T E c )
则称 E 为 R 中的 Lebesgue 可测集，或称 E 是 Lebesgue 可测的。
n
4、F.Riesz 定理（黎斯定理）答：设 E 为 Lebesgue 可测集， f n ( x ) (n 1 ， 2 ， ) 和 f ( x ) 都是 E 上的几乎处处有限的可测函数，如果 f n ( x ) f ( x)
华中师范大学 2006 –2007 学年第一学期期末考试试卷（A 卷）（解答）
课程名称实变函数课程编号 83410014 任课教师题型分值得分
一、判断题（判断正确、错误，请在括号中填“对”或“错” 。共 5 小题，每题 3 分，共
5×3=15 分） 1、可数个可数集的并集是可数集。 2、可测集 E 上的非负可测函数必 Lebesgue 可积。 3、 R 上全体 Lebesgue 可测集所组成的集类具有连续势。 4、非空开集的 Lebesgue 测度必大于零。
n
（2）由题设 lim Fn ( x) 2 f ( x ) ，再由 Fatou 引理得
2 f ( x)dx lim Fn ( x )dx lim [ f n ( x) f ( x) f n ( x) f ( x) ]dx
E E n n E
2 f ( x ) dx lim f n ( x ) f ( x ) ]dx ，
f ( x)dx
n E E
f n ( x) En ( x)dx
En

f n ( x)dx 可
lim f n ( x) dx lim f n ( x) dx f ( x) dx 。
n En n E E
6、设 E 是 Lebesgue 可测集， f n ( x ) (n 12) ， f ( x ) 都是 E 上的 Lebesgue 可积函数，若
0
dy
y
f ( x, y )dx 。
5、设 E 是 R 中的可测集，若（1） E Ek ，其中 Ek 为可测集， E1 E2 ；
k 1
（2） f ( x ) ， f n ( x ) (n 12) 都是 E 上的可测函数，且 lim f n ( x ) f ( x) a.e. 于 E ；
n
n

E
f n ( x)dx f ( x )dx 。
E
2、 R 中开集的结构定理答： R 中的任一非空开集总可表示成 R 中至多可数个互不相交的半开半闭区间的并。（或 R 中的任一开集或为空集或可表示成 R 中至多可数个互不相交的半开半闭区间的并。） 3、 R 中的集合 E 是 Lebesgue 可测集的卡氏定义（即 C.Caratheodory 定义）答：设 E R ，如果对任意 T R ，总有
E n E
即 lim
n

E
f n ( x) f ( x) ]dx 0 ，
从而 0 lim
n

E
f n ( x) f ( x) ]dx lim f n ( x) f ( x) ]dx 0
n E
故
lim f n ( x ) f ( x) dx 0 。
n E
n
存在 n0 ，当 n n0 时，总有 x En ，从而 En ( x) 1 ，于是 f n ( x ) f n ( x ) En ( x ) f n ( x) 。）又 f n ( x ) f n ( x) En ( x) f n ( x ) F ( x ) ， F ( x) 在 E 上 Lebesgue 可积所以由 Lebesgue 控制收敛定理，并注意到得
n
F F k
k 1

，由闭集的性质知 F 是闭集，且{ F }单调递增取 Fk F i k k
i 1 k 1
k
) F F。 Fk ( F i k
k 1 i 1 k 1

k

2、证明： R 中互不相交的开区间所构成的集族必为至多可数集。证明：记 E 为 R 中互不相交的开区间所构成的集族，对任意 I E ，由有理点的稠密性， I 中必存在有理点，取其中的一个有理点记为 rI I ，并记 B {rI I E} Q n ，于是
n
(
i 1
i
i ) ，总有
n

i 1
f (i ) f ( i ) 。
则称 f ( x ) 是有界闭区间 [a, b] 上绝对连续函数。三、计算题（共 1 题，共 1×10 = 10 分）设 D0 为 [0, ] 中的零测集， f ( x)
sin x , x D0 ，求 x3 e , x D0
由题设易知 F ( x, y ) 也是 R 上的非负可测函数，于是，由非负可测函数的 Fubini 定理
2

0
dx f ( x, y )dy
0
x

dx

F ( x, y )dy

R
F ( x, y )dxdy
2

n

dy

F ( x, y )dx
n
判断题 15
叙述题 15
计算题 10
解答题 60
总分 100
（
对）
（错）（错）（对）
n
5、若 fn ( x) （ n 1， 2，）和 f ( x ) 都为可测集 E 上的可测函数，且 lim f n ( x ) f ( x) ，
a.e. E ，则 f n ( x ) f ( x) ， x E 。
n

E
f n ( x ) f ( x ) dx 0 。
证明：（1）由可测函数的运算性质得 Fn ( x) f n ( x) f ( x) f n ( x ) f ( x) 是 E 上可测函数，又所以
f n ( x ) f ( x) f n ( x ) f ( x) ，从而 Fn ( x) 0 ， Fn ( x) f n ( x) f ( x) f n ( x ) f ( x) 在 E 上非负可测。
证明：记来自 0dx f ( x, y )dy
0
x
0
dy
y
f ( x, y )dx 。
，令
D {( x, y )
0 x 0 y } {( x, y ) } 0 yx y x
f ( x, y ), ( x, y ) D ， F ( x, y ) ( x, y ) D 0,
n
n
B 必为至多可数集。
作 E 到 B 的映射如下：
:EB I ( I ) rI
由于 E 中任意两个不同的 I1 和 I 2 不相交，所以 rI1 rI 2 ，于是是 E 到 B 的单射（实际上还是一一映射），所以 E B Q n ，故 E 也是至多可数集。 3、设 f ( x ) 是 (, ) 上的实值函数，且 f ( x ) 在 (, ) 上的任一有限区间上都可测，则 f ( x ) 在 (, ) 上也可测。

证明：因为 ( , ) [ n, n] ，而 f ( x ) 是 [ n, n] 上的可测函数，
n 1
所以由可测函数的性质得 f ( x ) 在 (, ) 上也可测。 4、用 Fubini 定理证明：若 f ( x, y ) 为 R 2 = ( , + ) ( , + ) 上的非负可测函数，则
lim f n ( x ) f ( x) ( x E ) ，且 lim f n ( x ) dx f ( x ) dx ，
n
n E E
证明：（1） Fn ( x) f n ( x) f ( x) f n ( x ) f ( x) 在 E 上非负可测；（2）用 Fatou 引理证明： lim
n
（3）存在 E 上的 Lebesgue 可积函数 F ( x) ，使得 n ， f n ( x ) F ( x ) ( x E ) 。证明： f ( x ) 在 E 上也 Lebesgue 可积，且 lim
n
En

f n ( x)dx f ( x )dx 。
E
证明：记 f n ( x) f n ( x ) En ( x) ，由题设知 lim f n ( x ) f ( x) a.e. 于 E （事实上 x E ，
0
0
2。
四、解答题（共 6 小题，每题 10 分，共 6×10 = 60 分） 1 、设 F 为 R 中的 F 集，证明：必存在 R 中的一列单调递增的闭集 {Fk } k 1 ，使得

n
n
F Fk 。
k 1
} ，使得证明：因为 F 为 R 中的 F 集，所以一列闭集 {F k k 1
x E ，则存在 { f n ( x ) } 的一个子列 { f nk ( x ) } ，使得