菠萝为何斜着削
方便又快捷的刀切菠萝法--在家如何切菠萝

方便又快捷的刀切菠萝法--在家如何切菠萝
方便又快捷的刀切菠萝法--在家如何切菠萝樱桃好吃树难栽,玫瑰好看刺难去,菠萝好吃皮难切,世间的事物总有其自身的特质,但是聪明至极的人类就会有这样那样的破解方法,一物降一物,物物则通!以前买菠萝,总是买现成的菠萝肉,让水果摊主用其专业的刀具和方法削出完整的菠萝肉,却也少了削菠萝的乐趣,如今有了方便又快捷的刀切菠萝法,在家切菠萝就成了一桩乐事!完整的菠萝方法与过程1,切去菠萝头(带叶的菠萝大头)2,纵着对半切开,一分为二3,对半再切开,再对半切开(一分为二之后再一分为二,共一分为四)
4,刀口向内,削去菠萝心,这部分很硬,一般不食用5,再次刀口向内削菠萝肉
6,在菠萝肉上横切,形成菠萝块
剩下的菠萝皮。
考察“菠萝中的数学”,培育学生数学建模能力

考察“菠萝中的数学”,培育学生数学建模能力作者:纪雪颖来源:《数学教学通讯(教师阅读)》2008年第05期《高中数学课程标准》提出:发展学生的数学应用意识,培养学生的数学建模能力,并单独设立“数学建模”的专题课程,设立“数学与日常生活相联系”的D系列课程.如何将这些课程转化为教学实践?在此我们以“菠萝中的数学”为例,分析“数学建模”教学的实施途径,让学生了解数学建模的方法,培育其数学建模能力.近段时间,有幸进入上海一些实验性、示范性高中,接触到那些通过中考筛选后的优秀学生.不可否认,这些高一、高二学生在学校数学课堂中对于数学课本上的知识学习是优秀的,但大部分学生接触生活场景中的数学问题时,往往感觉陌生而无从下手.学生能熟练掌握并解答课堂课本中设计的问题,却在有意识地发现并使用数学去解决生活中的现实问题方面非常薄弱,这一现象在高中学生中普遍存在.针对这一现象,《高中数学课程标准》提出:发展学生的数学应用意识,培养学生的数学建模能力.为此单独设立“数学建模”的专题课程,设立“数学与日常生活相联系”的D系列课程.如何将这些课程转化为教学实践?在此我们以“菠萝中的数学”为例,分析“数学建模”教学的实施途径,以期打开学生数学应用的眼界,了解数学建模的步骤与方法,引导学生关注生活中的数学.1问题提出菠萝是我们所熟悉的水果,吃菠萝前要削皮去籽几乎是人人皆知.去除菠萝黑籽的方法有许多种,有些人一粒一粒的挖,有些人从菠萝上部削到下部,有些人一圈一圈地削,也有些人采取的是斜着削,削成螺线型.人们在多年的实践和总结后,现在大多数人采取的方法是斜着削.(图1)围绕这一生活现象,我们提出的问题是:人们为什么这样削菠萝?请你从数学角度加以论证.在上海的多所中学里给学生做此问题,拿到问题后,没有老师的任何提示,学生的表现如同我们所设想的一样:新鲜、惊讶.他们从未想过生活中如此小的一个场景都会与数学相关,他们也从未去寻找发掘过生活中的数学.很多学生觉得问题的答案明显而理所当然,如“因为这样削美观”,“因为菠萝就是这么长的”,“因为这种削法是一代一代传下来的”,“因为这样削速度快,损失的果肉少”.无论是从生活常识角度,还是从美学角度提出的想法,学生都觉得很困难再继续从数学角度加以论证.显然很重要的原因之一是,学生还缺少“数学建模”的意识以及能力.我们可以以这个问题为例,给学生介绍“数学建模”的内涵以及实施步骤.2数学建模的五个步骤首先,让学生了解什么是数学建模.数学建模是数学学习的一种新的方式,它为学生提供了自主学习的空间,PISA将“数学建模”定义为5个步骤(如图2):我们可以把世界分为真实世界与数学世界,数学建模的来源是真实世界中的某一问题,通过合理抽象将其转换为数学问题,建立数学模型,利用数学知识与方法技能解决数学问题,再返回到实际生活中,验证该解决方法的可行性与合理度,找寻该模型及其解决方法所存在的局限性,可能的话,再次寻找更合理的模型.如此循环过程便是数学建模.借助“菠萝中的数学”,向学生具体介绍数学建模的五个步骤.第一步,数学建模的来源是现实生活中的一个问题.很显然,在上述例子中,现实生活是饮食中的削皮问题.学生已经想到自己的日常生活常识:当我们购买水果时,希望水果商将皮和籽干净去除的同时,也非常希望保留下来的果肉是最多的(即损失的果肉是最少的).上述问题就与削去的果肉量有关.其关键词是:“损失的果肉最少.第二步,问题解决者尝试用数学来定义并重组问题.这里,学生要理解文字表述中的“损失果肉最少”,既然出现了“最少”这个词,很显然,是将斜向的削法与其他削法进行对比后得出的结论.学生很容易就想到了横向与纵向两种及其他削法,现在要做的是将斜向削法与横向纵向进行比较,并找出这些削法中损失的果肉量在数学上的涵义.这一步的关键是要仔细观察出菠萝籽的排列:交错排列.第三步,逐渐退却现实的外套.我们可以通过不同的方法将问题抽象成一个纯数学的问题,或者说逐渐将问题从现实中剥离.此例中,首先,考虑大多数菠萝的形状,学生不难发现可以将其抽象成圆柱体.在圆柱体这一三维图形上考察菠萝籽的难度显然高于二维平面图形,于是,在如何将立体图形转换成平面图形的提问中,学生想到将圆柱体展开成一矩形.这时,很多学生喜形于色“终于看到出现熟悉的数学内容了.”学生积极地用点表示菠萝黑籽,用连线表示削去的果肉,面对熟悉的平面图形,学生再次为难于如何继续.“从局部到整体,从特殊到一般”的数学思想方法有了用武之地,我们选择化整为零的方法,在已发现的交错排列的菠萝籽中,仅观察虚线框中的四颗菠萝籽,排列方式如图3所示(图中各黑点代表菠萝黑籽):在图中,将四颗菠萝籽看作四个点,分别标记为点A、B、C、D.当横向削除两颗黑籽时,损失的果肉为BD间的距离,当纵向削除两颗黑籽时,损失的果肉为AC间的距离.而斜向则损失AB(AD、DC、CB)间的距离.根据斜向损失果肉最少,我们提出的数学问题是:为什么斜向的距离最短,即为什么AB,AC,BD中,AB最短.这一问题已经是学生非常熟悉而且擅长的较为常规的问题了.通过上述三个步骤我们把问题从真实情境抽象成了一个数学问题.即数学建模首先将实际问题翻译成数学问题,这一过程包括:ν找到与该实际问题相关的数学知识.ν将问题从不同角度表述,包括根据数学概念演绎或做一些理想化的假设.ν理解该问题的语言叙述与数学符号或数学语言之间的关系,以求从数学角度理解问题.ν找寻合适的规则,联系和模型.ν找出该问题与已解决的问题同构的方面.ν将问题译成数学知识,如建立一个数学模型.当学生将一个真实问题转换到数学模型时,整个过程都可能充满着数学.学生会提出诸如“有……可能吗?”,“如果这样,有多少呢?”,“我是如何发现……?”的问题.他们会用已有的技能和概念去解答问题.他们尝试根据实际情况调整所建立的数学模型,建立新的规则,定义他们之间的联系,并提出一个新的数学上的争论点.通常称这一过程为建模中的推理演绎过程.第四步,解决数学问题.由于三条线段(AB,AC,BD)的长短分别代表着三种削法损失的果肉,因此,当前的数学问题是比较三条线段的长短.四边形ABCD可看作一菱形,比较AB、AC、BD的长短即比较该菱形边长,对角线的长短.学生发现要想在菱形中比较边长与对角线的长短,还与菱形的内角大小有关,菱形内角的大小会引起结果的不同,需要对菱形的内角大小进行分类讨论.具体如何分类呢?有学生提出了“从一般回到特殊”,进一步将四边形ABCD理想化为菱形中的特殊情况:正方形.此时,问题就水落石出,迎刃而解了.在正方形ABCD中,设边长AB=x,那么根据勾股定理:AC=BD=根号2x,显然,x<根号2x,即AB<AC且AB<BD.在AB、AC、BD中,AB最短.解决了特殊的正方形的情况后,学生的信心与积极性大增,他们兴致勃勃地回到菱形的情况.对菱形的各内角度数进行探讨,比如:当菱形ABCD的内角为60°和120°时,AB=BD<AC,即此时,只有纵向削籽,损失的果肉最多,横向与斜向削损失的果肉量相等.然后,再将局部的解答拓展到整个矩形.第五步,讲出数学解答在实际生活中的意义.数学问题解决了,但作为数学建模,还必须返回到真实问题中去.对学生来说,只要知道AB、AC、BD三条线段的长短分别代表着三种削法损失的果肉.就不难解释其所表达的意义了.如果横向或纵向削,所损失的果肉为AC与BD,如果斜向削,所损失的果肉为AB,因此,斜向削所损失的果肉为最少.最后学生必须反思,用批判的眼光看结果,并去证实整个过程的合理性.这一反思在建模过程的每一个阶段都要进行,当然,在总结阶段特别重要.反思和证实包括:ν理解数学概念的局域性与局限性.ν反思数学争论,解释并证明结果.ν交流建模过程和解决方案.ν评论所建模型.这一过程是图2中标记为5的那些步骤.这个时候,要求学生把从数学建模中得到的解决方案返回到实际问题中.在菠萝这一问题中,学生认为所建立的这一模型能较合理地解释为什么要这样削菠萝,但还是存在一定的局限性,因为该模型的第一步是将菠萝的形状抽象成圆柱体这一规则图形,但菠萝的形状却不一定是很规则的.学生不知道如何面对这一模型的局限性,担心所建模正确与否,当得知可以将他们所认为的模型的局限与不足写入建模报告后,都热情高涨地探讨、回味、整理.3小结在与学生共同完成“菠萝中的数学”时,学生从最初的新鲜却无从下手,到初步了解如何将生活中的问题转换成数学问题;从感觉毫无数学元素可寻,到惊喜地发现熟悉的数学内容;从茫然不知所措,到喜形于色恍然大悟,再到兴致勃勃热情高涨.学生不仅经历了数学建模的过程,也经历了数学与生活联系的过程.学生感言真切地体会到数学无处不在,生活里蕴涵着如此奇妙的数学,也表示了解了如何运用数学解决实际问题,特别是表面上看并没有任何数学元素呈现的问题,如何进行数学建模.“菠萝中的数学”只是一个比较容易的建模例子,但作为数学建模,它仍然要求学生自己从实际问题中筛选信息,找出问题的本质所在,使问题的数学构成浮出水面.要求学生积极思考,合理想象,动手操作,收集并筛选信息,同时也要求学生从生活语言到其他科学语言,再到数学语言的多阶段转换.在整个建模过程中,学生的数学知识,数学术语,数学事实和数学技能等经历了创造性地融合.这些知识的运用,能力的培养,对学生数学素养的提高有不小的作用.我们生活在一个处处充满数学的世界里:出行的最佳交通路线,火车汽车航班的时刻表,商场举办的各类优惠折扣活动,人体摄入所需的营养成分与比例等等.在这些事件中,需要公民运用数学,解决日常工作与生活所需.通过学习数学建模,引导学生从课本走向生活,关注生活中的数学,落实新课标的要求,培养并提高学生的数学素养.参考文献1 OECD(2006).Assessing Scientific, Reading and Mathematical Literacy: A Framework for PISA 2006,page72-75,page95, 962徐斌艳. Ludwig Matthias.中学生数学建模能力水平的实验分析.中学数学月刊,2007(11)3马晓娟.如何开展中学数学建模活动浅谈.教学参考中学版,2007(1)上。
菠萝削皮方法

菠萝削皮方法
菠萝是一种美味可口的水果,但是它的外皮很难剥离,让很多
人望而却步。
不过,只要掌握正确的方法,削皮菠萝其实并不难。
下面我将分享几种简单易行的菠萝削皮方法,让你轻松享受到新鲜
的菠萝果肉。
第一种方法是使用菠萝刀。
首先,将菠萝的顶部和底部切掉,
使其能够站立在切割板上。
然后,用菠萝刀将菠萝的外皮由上到下
沿着果肉的轮廓切下,确保将外皮和“眼睛”一并削除。
最后,将
削好的菠萝果肉切成片或块,即可食用。
第二种方法是使用菠萝眼睛挖掉器。
首先,将菠萝的顶部和底
部切掉,使其能够站立在切割板上。
然后,用菠萝眼睛挖掉器将菠
萝的眼睛一个个挖掉,再用刀将外皮由上到下沿着果肉的轮廓切下。
最后,将削好的菠萝果肉切成片或块,即可食用。
第三种方法是使用菠萝削皮器。
首先,将菠萝的顶部和底部切掉,使其能够站立在切割板上。
然后,用菠萝削皮器将菠萝的外皮
由上到下沿着果肉的轮廓切下,确保将外皮和“眼睛”一并削除。
最后,将削好的菠萝果肉切成片或块,即可食用。
无论使用哪种方法,削皮菠萝都需要注意以下几点,首先,选择成熟的菠萝,它们的外皮应该是金黄色的,而且有淡淡的菠萝香味。
其次,要小心处理菠萝的“眼睛”,因为它们通常很硬,会影响口感。
最后,削好的菠萝果肉可以直接食用,也可以用来制作菠萝饭、菠萝鸡等美食。
总的来说,削皮菠萝并不难,只要掌握了正确的方法,就能够轻松享受到新鲜的菠萝果肉。
希望以上方法能够帮助到你,让你在削皮菠萝的过程中更加得心应手,享受到美味的菠萝果肉。
省获奖(包河区2013数学小论文)
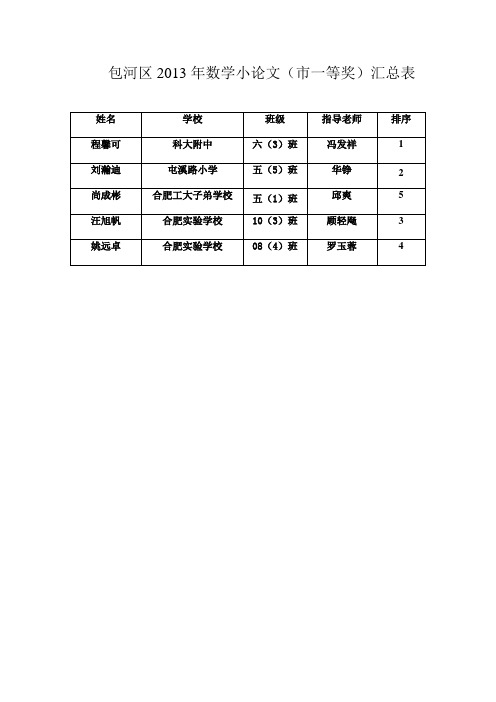
包河区2013年数学小论文(市一等奖)汇总表姓名学校班级指导老师排序程馨可科大附中六(3)班冯发祥 1 刘瀚迪屯溪路小学五(5)班华铮 2 尚成彬合肥工大子弟学校五(1)班邱爽 5 汪旭帆合肥实验学校10(3)班顾轻飏 3 姚远卓合肥实验学校08(4)班罗玉蓉 4程馨可\科大附中\六(3)班\指导老师:冯发祥\序号1菠萝为何斜着削一、缘起今年菠萝大丰收,正值菠萝上市时节,合肥的市面、街头巷尾充斥着这种来自南方价廉物美的热带水果。
我发现,削菠萝100%的都是斜着削的。
每每嚼着甘甜微酸的菠萝肉,心头总是萦绕着一个疑问——菠萝为何斜着削,而不是竖着削或横着削?正逢周末,有必要进行一番仔细考察和研究。
以解开自己的心结。
二、猜测削菠萝之所以都是斜着削或许有如下理由: 1、斜着削是顾客的要求; 2、斜着削店主师傅便于操作; 3、斜着削,削得快,节省削的时间; 4、斜着削成品美观;5、斜着削最经济,少浪费,节省果肉; ……究竟哪种猜测站得住脚,有必要进行一番小考察。
时间:2013年5月5日(星期天),上午10:00——11:00。
地点:科大花园小区门口一固定水果摊点。
记录该时间段来此买菠萝7人次,该时间段此摊主卖菠萝9个。
另外本人亲自挑选了3个形状大小差不多的菠萝,花钱买下,请求摊主师傅,按我的要求,用三种不同削法,且掐好秒表。
菠萝的削法削完的时间横 削 3分15秒 竖 削 2分07秒 斜 削2分50分考察发现:自始至终7名顾客无一人吩咐要求摊主如何如何削,9个菠萝全部是斜削交货。
因此,否定了第一条猜测。
考察发现:摊主竖削时,动作最麻利。
当横削时动作最别扭。
因此否定了第2条猜测。
考察发现:竖削时间最少,菠萝的斜削,并非为了节省削的时间,因此否定了第3条猜测。
考察发现:我花钱买回的,用三种不同方法削好菠萝成品摆在父母的面前,哪种削法削去的最美观?得到的回答是“很难评说”。
看来,第4条猜测也是站不住脚了。
为什么菠萝斜着削?最有可能的答案是——这样削最经济,少浪费,节省果肉。
菠萝怎么削皮 菠萝不削干净能吃吗

菠萝怎么削皮菠萝不削干净能吃吗
今天买了一个菠萝回家吃,菠萝吃之前需要进行削皮,但我之前没有削过菠萝,不知道怎么削好,那么菠萝怎么削皮?菠萝不削干净能吃吗?
一、菠萝怎么削皮
菠萝削皮的方式是比较多的,无论是哪种方式只要将菠萝完整且不浪费的削好,就是不错的,具体如下:
1、首先把菠萝叶子去掉。
2、然后将先沿着四周将表皮去除,厚度大约1厘米。
3、之后取出小水果刀沿着菠萝眼,一般倾斜45度。
4、将菠萝眼剔除后分成几小块。
5、最后侵泡盐水中30分钟左右过清水食用即可。
二、菠萝不削干净能吃吗
不能吃。
菠萝不处理干净是不可以吃的,菠萝的表皮以及菠萝眼上的物质都是不能吃的,具有微毒,不处理干净食用容易加重人体肠胃负担,可能会导致人体出现腹痛、腹泻以及便溏等不适症状发生。
其次不处理干净的菠萝,其中含有一定的过敏物质,食用之后容易诱发或者加重人体过敏现象,所以生活中菠萝不削干净是不建议吃的。
三、菠萝削皮后为什么要用盐水泡
具体原因如下:
菠萝中含有刺激作用的甙类物质和菠萝蛋白酶,这种物质可以分解体内的蛋白质,对口腔粘膜和嘴唇的幼嫩表皮有刺激作用,吃菠萝前不用盐水泡,会让人有一种麻痹刺痛感,而盐水可以浸出甙类,这就是为什么吃菠萝要泡盐水的原因。
四、菠萝要用盐水侵泡多久
半小时左右即可。
菠萝的果肉中含有“菠萝酶”,菠萝酶会分解蛋白质,不用盐水侵泡酶对于口腔粘膜和嘴唇的幼嫩表皮有刺激作用,食盐水能破坏这种酶。
一般使用盐水侵泡菠萝,一般侵泡30分钟左右即可,时间太短菠萝酶不能完全失去活性,依然可能造成过敏,但浸泡时间太长,会造成菠萝的营养过多流失,并且容易滋生细菌导致变质。
菠萝斜着削的数学原理

菠萝斜着削的数学原理宝子们,今天咱们来唠唠菠萝斜着削背后的数学原理,这可老有趣啦。
咱先想想菠萝的形状哈,菠萝它大体上是个圆柱体,不过呢,它身上有那些硬邦邦的疙瘩,就像一个个小堡垒似的。
平常咱们要是直着削菠萝,就会发现,老是会碰到那些疙瘩,削起来可费劲了。
这就好比咱们走直路,但是路上全是小障碍,得一个一个跨过去。
那斜着削呢?这就有大学问啦。
从数学的角度看啊,斜着削其实是在改变切割的角度。
咱们可以把菠萝想象成一个立体的图形,那些疙瘩在菠萝表面是有一定分布规律的。
当我们斜着下刀的时候,就像是找到了这些疙瘩分布的一个“缝隙”。
打个比方,就像一群人站得整整齐齐的,你横着走可能老是撞到人,但是你斜着走呢,就比较容易从人群的间隙里穿过去。
你看啊,斜着削的时候,刀和菠萝表面的接触方式就不一样了。
如果我们把菠萝表面看作是一个平面,直着削的时候,刀和这个平面的相交线就比较短,而且很容易就碰到那些疙瘩代表的“凸起区域”。
但是斜着削呢,刀和这个平面的相交线就变长了。
这就好比同样是一块蛋糕,你横着切一刀,得到的蛋糕块可能就会有很多奶油花在切面上,不太整齐;但是你斜着切一刀,切面上的奶油花就分布得比较均匀,而且切的面积更大。
从角度的角度来说(哈哈,有点绕口呢),斜着削的角度能够让我们避开那些疙瘩的主要受力点。
就像是在打仗的时候,你不正面去冲击敌人防守最严密的地方,而是从侧面找个薄弱环节进攻。
每个疙瘩其实都有它最不容易抵抗外力的方向,斜着削就是利用了这个特点。
这就像是我们做数学题,有时候正面解题特别难,但是换个角度,从侧面去思考,就会发现解题的新思路。
而且呀,斜着削菠萝还能让我们削得更快呢。
因为我们避开了那些难搞的疙瘩,刀在菠萝上滑动得就更顺畅。
这就像汽车在平坦的公路上开得快,要是在坑坑洼洼的路上,就得慢慢开。
咱们削菠萝的时候,刀就像汽车,菠萝表面就像路,斜着削就是找到了那条平坦的“路”。
再说说这个效率的问题哈。
斜着削能在同样的力气下,削掉更多的菠萝皮。
拒绝菠萝好吃皮难剥 课件-2023-2024学年高一上学期劳动技术

劳动创造美好生活!
教学目标:
● 科学观念:通过研究削菠萝皮,知道如何削菠萝皮的具体过程和劳动细节。 ● 科学思维:通过削菠萝皮的过程,知道平时很普通的事情,经过精彩美妙的科学思维,可以创造出炫彩可爱的艺术。 ● 探究实践:通过削菠萝皮,使用并改进自己削菠萝皮的方法,知道可以利用生活中的材料,削菠萝皮,进一步理解削
拓展
● 一种更为便捷的懒人削菠萝的方法,那就是用削菠萝器啦。 ● 先将削菠萝器的手柄和刀体洗净,安装好。 ● 再将菠萝削去头部,以足够将刀体旋入,将刀体插入菠萝头部,开始削皮。 然后稍用力将刀体从头部
逐步旋入菠萝至底部,完成削皮。 ● 最后从刀体上拿出菠萝片,大功告成。削菠萝器市场都有卖,用起来十分地方便呢。
过程
● 二、探究 ● 菠萝酸甜可口,是许多人都很喜欢吃的水果,它营养丰富,既可以生吃,也可以做成菠萝炒饭、
菠萝鸡块、菠萝咕咾肉等,一到菠萝上市的季节,大家都会买上那么几个回家解馋。一般来说, 如果在水果摊购买菠萝,小贩们会帮忙把皮削好,但如果你是在超市买菠萝,那么大概率是没有 帮忙削皮的,那么菠萝怎么削皮呢?
● 3、认真观察下,会发现菠萝身上的菠萝眼的分布规则,所以取小把水果刀以倾斜45°左右的菠萝眼轻 轻剔除菠萝眼。先拿一把小刀斜着向上沿着菠萝眼旁边剃进去,再把另一边也剃进去。这样就可以把有 菠萝眼的地方给拿出来。用同样的方法把剩下的部分都剃干净。
● 4、最后将削好皮的菠萝切成丁,用盐水浸泡一下,就可以抑制菠萝酶对我们口腔粘膜和嘴唇的刺激, 同时也会感到菠萝更加香甜了。
过程
菠萝剥皮的小窍门 方法一 1、菠萝去掉头尾,竖切成四瓣 2、每一瓣菠萝肉用小刀均匀地切成几刀,不要切断菠萝,底部让菠萝皮连着 3、竖刀贴着菠萝皮将菠萝肉与底部菠萝皮分割开,这样就可以切出一块块小三角形的菠萝 方法二 1、先用菜刀将菠萝的底端切掉,使其能竖立在砧板上 2、菠萝正着放好,用刀沿菠萝表皮切下,注意不要切得太厚,差不多1厘米,以免浪费过多的果肉,再用水果刀将没有切除的部分果皮刺掉 3、不多削到剩下一些菠萝眼,然后继续削皮,菠萝身上的菠萝眼的分布规则,所以取小把水果刀以倾斜45°左右的角度轻轻剔除菠萝眼
招待客户时用什么水果最合适

招待客户时用什么水果最合适导读:我根据大家的需要整理了一份关于《招待客户时用什么水果最合适》的内容,具体内容:客户到访,放些水果让客人吃是比较合适的选择,招待客户用的水果有哪些?下面是我搜集整理的一些招待客户用的水果,希望对你有帮助。
招待客户用的水果虽说水果要多吃,但是依照...客户到访,放些水果让客人吃是比较合适的选择,招待客户用的水果有哪些?下面是我搜集整理的一些招待客户用的水果,希望对你有帮助。
招待客户用的水果虽说水果要多吃,但是依照中医的看法,人体质分为寒、热、虚、实。
水果也有水果的性质,一不留神,错吃水果也会让人不舒服。
水果属性和体质确有关,说到食物属性,中医有所谓"四气"。
这是指食物进入体内,会产生"寒、热、温、冷"的作用,如果不温不热,不寒也不凉,则归属于"平"性。
因此,每种水果如果进入了人体,也就有它的"个性"。
中医更强调均衡、阴阳调和,体质偏热的人要多吃寒凉性的食物,体质偏寒的人,自然要多吃温热性的食物,吃水果的原则也一样。
同时,地形、气候也会影响生理与饮食,比如亚热带地区,仲夏暑热难当,受天热、地暑的影响,人们常发生头痛、身热、口渴、心烦等现象,为了达到均衡,最好选择吃些寒、凉性的食物。
春夏日吃水果,注意讲科学,肠胃不好的人,绝对不可以吃冰镇水果,最好是选择多吃一些凉性或温性的水果,不要太甜,也不要太酸,凉性的水果包括:梨(肠胃不好的少吃)、香蕉(不要空腹吃),温性的水果有:苹果(无论什么人都可以吃的一种最好的水果,营养也超好)、柠檬、西红柿(胃酸过多者少吃);容易消化的瓜类、水梨、苹果等也不错。
不过,中医辨证上,虚寒体质以及有慢性肠炎、十二指肠溃疡,或者"胃寒"——也就是胃炎、胃溃疡患者,最好少吃西瓜、香瓜等寒凉食物。
芒果好吃,有人却碰都碰不得,因为一吃就过敏、皮肤痒。
医生指出,芒果皮有组织胺成分,容易引起过敏,理论上芒果属于发物,有感染性疾病、皮肤病、发炎症状的人,吃"发物"就会诱发疾病或者病情加重。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
菠萝为何斜着削一、缘起今年菠萝大丰收,正值菠萝上市时节,合肥的市面、街头巷尾充斥着这种来自南方价廉物美的热带水果。
我发现,削菠萝100%的都是斜着削的。
每每嚼着甘甜微酸的菠萝肉,心头总是萦绕着一个疑问——菠萝为何斜着削,而不是竖着削或横着削?正逢周末,有必要实行一番仔细考察和研究。
以解开自己的心结。
二、猜测削菠萝之所以都是斜着削或许有如下理由:1、斜着削是顾客的要求;2、斜着削店主师傅便于操作;3、斜着削,削得快,节省削的时间;4、斜着削成品美观;5、斜着削最经济,少浪费,节省果肉;……究竟哪种猜测站得住脚,有必要实行一番小考察。
时间:2013年5月5日(星期天),上午10:00——11:00。
地点:科大花园小区门口一固定水果摊点。
记录该时间段来此买菠萝7人次,该时间段此摊主卖菠萝9个。
另外本人亲自挑选了3个形状大小差不多的菠萝,花钱买下,请求摊主师傅,按我的要求,用三种不同削法,且掐好秒表。
菠萝的削法削完的时间横削3分15秒竖削2分07秒斜削2分50分考察发现:自始至终7名顾客无一人吩咐要求摊主如何如何削,9个菠萝全部是斜削交货。
所以,否定了第一条猜测。
考察发现:摊主竖削时,动作最麻利。
当横削时动作最别扭。
所以否定了第2条猜测。
考察发现:竖削时间最少,菠萝的斜削,并非为了节省削的时间,所以否定了第3条猜测。
考察发现:我花钱买回的,用三种不同方法削好菠萝成品摆在父母的面前,哪种削法削去的最美观?得到的回答是“很难评说”。
看来,第4条猜测也是站不住脚了。
为什么菠萝斜着削?最有可能的答案是——这样削最经济,少浪费,节省果肉。
三、验证菠萝斜着削最经济,节省果肉的猜测。
尚需要数学地验证。
事先,有必要实行合理的数学简化:菠萝除皮后当成圆柱体,上下的球面忽略不计。
受圆柱侧面展开的启发,选择6列,12行的点状图数学模型(见下图),同列点距1厘米,同行点距1厘米,因交错布点,列间距0.5厘米。
设定削的沟槽宽度、深度为固定值。
横、竖、斜三种不同削法,削的总沟槽的长短,成了解决问题的焦点。
分别验证如下。
1、竖着削菠萝:见图A,每列5.5厘米,共6列。
6×5.5=33(厘米)图A 图B 图C2、横着削菠萝:见图B ,每行是3厘米12行。
3×12=36(厘米)3、斜着削菠萝:见图C ,33×225.05.0 =33×5.0≈33×0.707=23.33(厘米)36厘米<33厘米<23.33厘米四、结论通过计算得出:斜着削菠萝沟槽总的长度<竖着削菠萝的沟槽总长度<横着削菠萝的沟槽总长度,以此看来,人们之所以斜着削菠萝,是因为斜着削比竖着削与横着削要节省一些果肉,显著的减少浪费。
终于我明白一个道理,解开一个心结。
元旦春节部分商场促销情况调查分析报告一、调查目的与调查方法为了解合肥市部分大中型商场在2013年元旦春节期间促销优惠情况,作者在老师布置和家长指导下,对2012年12月20日至2013年2月1日期间合肥市部分大型商场促销情况实行了调查统计。
通过报纸收集,现场调查,网络查询等方式共收集了合肥市区13家商场元旦春节期间优惠促销信息,重点选择穿着类、鞋类和化妆品三大类商品实行分析比较,并通过建立Excel表格实行统计分析,本报告使用的数据来自于此次调查。
二、合肥市区13家商场2013年元旦春节期间优惠促销信息调查统计(一)穿着类商品优惠促销调查统计表1:合肥市区13家商场穿着类商品促销活动一览从表1统计来看,本次调查的13家商场均对穿着类商品采取各种优惠促销方式扩大元旦春节期间的营业额,优惠促销方式主要采用额满送券、额满立减和额满超值购等。
从表1促销类型能够统计出,13家商场中,采取额满送券方式的有5家,占39%;采取额满立减方式和额满超值购方式的各有4家,分别占31%(见图1)。
从表1计算的实际折扣能够统计出,13家商场中,实际折扣在3—3.5折的商场仅1家,约占8%;实际折扣在3.5—4折的商场有4家,约占31%;实际折扣在4折—4.5折的商场有5家,约占38%;4.5—5折的商场有3家,约占23%(见图2)。
通过图1能够看出,13家商场促销方式在选择上基本均衡,无论是额满送券、额满立减还是额满超值购方式,都能够通过计算得出实际商品折扣额度。
通过图2能够看出,13家商场促销折扣大多在4—4.5折之间,占38%;其次在3.5—4折之间,占31%。
其中,百大集团乐普生商厦实际折扣最高,达到3折;商之都东城店实际折扣最低,达到5折(图3)。
39%31%31%图1 :13家商场促销方式分析8%31%38%23%(二)穿着类商品和化妆品同时优惠促销调查统计本次调查的13家商场中,有7家商场在对穿着类商品采取促销的同时也对化妆类商品实行了优惠促销。
具体见表2。
表2:合肥市区7家商场化妆类商品和穿着类商品促销活动一览图4:7家商场化妆类和穿着类商品同时促销一览表8.118887.897.677.545 4.994.354 4.293化妆品折扣穿着类商品折扣通过图4能够看出,在对穿着类商品和化妆类商品同时实行促销的7家商场中,折扣幅度最高的还是百大乐普生商场。
(三)鞋类商品优惠促销调查统计本次调查的13家商场中,还有部分商场对鞋类商品实行了不同的优惠促销。
具体见表3。
表3:合肥市区部分商场鞋类商品实际折扣一览序号商场名称实际折扣1 金鹰百花井店 3.02 金鹰宿州路店 3.83 百大集团各商场 4.04 大洋百货 4.05 万达百货 4.956 之心城 5.0通过图5对各商场鞋类商品实际折扣分布图能够看出,百大集团各商场、大洋百货和金鹰宿州路店对鞋类商品的折扣基本一致,多为4折左右;万达百货和之心城对鞋类商品的折扣幅度较低,达到5折;折扣幅度最高的商场是金鹰百花井店,达到3折。
三、相关结论和建议(一)关于穿着类商品的结论和购物建议通过图3,能够得出:百大乐普生穿着类商品折扣最高,达到3折;商之都东城店折扣最低,只能达到5折;商之都旗舰店、金鹰宿州路店、大洋百货三家店虽然采取不同的促销方式,但实际折扣都是一样的。
所以建议大家:如果买穿着类商品,最好去百大乐普生,尽量不要去商之都东城店。
(二)关于穿着类和化妆品类商品的结论和购物建议通过图4,能够得出:百大乐普生化妆品和穿着类商品折扣都是最高的;商之都东城店化妆品和穿着类商品折扣都是最低的。
所以建议大家:如果两种商品都要买的话,最好去百大乐普生,尽量不要去商之都东城店。
(三)关于鞋类商品的结论和购物建议通过图5,能够得出:金鹰百花井店鞋类商品折扣最高,达到3折;之心城鞋类商品最低,只有5折。
所以建议大家:如果买鞋类商品,最好去金鹰百花井店,尽量不要去之心城。
从立体停车库想到的我家的后面有一个立体停车库,一共有三层,第一层有十八个车位,每层宽度一样,那应该一共有3×18=54个车位啊?不过,我数来数去发现只有48个,少了6个,这是为什么呢?我仔细观察,这个立体停车库被分成了六组,每9个车位分3层为一组。
要想让所停的车一层一层上升到二层或三层,必须在这组中留一个空位出来,就像我们小时候玩的一种游戏——华容道。
这个空位是非常必要的,因为它给其他车位平移或上升、下降提供了空间。
一组留一个,6组就留了6个空位,怪不得一共会少了6个车位呢。
我觉得这种设计有些浪费资源,可不能够少留些空位呢?思来想去,我认为如果想在这个有限的车库里增加车位的话,唯一的办法就是减少分组。
如果把6组合并成三组,即能够增加三个车位,这样不就好多了?不过新的麻烦又来了:按每辆车重为一吨计算,现在每组车位的承重是8吨,二组合并为一组后,每组的承重量就达到了17吨(因为每组的车位数是2×9-1个),这将会严重地影响车库的坚固度和安全性。
同时,还有一个大的问题:现在存放一辆车,大约要8分钟,合并分组之后,因为车位调整的距离变长,大约要花去现在两倍的时间,也就是16分钟,这很显然将会导致车辆堵塞,也不能适合人们越来越快的生活节奏。
所以看来,从数学和力学的理论出发,现在这种立体停车库的设计,应该是科学的。
“圆”来如此圆是几何图形中最普通不过的了,在我们的日常生活、工农业生产、交通运输、土木建筑等方面被广泛应用。
比如,汽车上方向盘是圆形的,车轮也是圆形的;锅盖、井盖、瓶盖是圆形的;水管、煤气管的横截面也是圆形的……我有时有些疑惑,为什么有这么多的物品都做成圆形的,而不是其他形状,除了美观外,这里面是否还包含着特别的含义和奥秘呢?带着困惑我去问爸爸,爸爸却笑着说,不要着急,先让我们做几个小实验,你可要认真观察呀!就这样我开始了圆的探索之旅。
实验一:爸爸拿来两张大小相同的硬纸,把其中一张折成方柱状,另一张卷成圆筒状,然后爸爸拿来些大米,装进圆筒里,再将米抹平。
又将圆筒中的米倒进方柱中,方柱装满米后,圆筒里还剩一些米。
我看了之后,惊叫道:“原来圆柱比方柱装得更多呀!”爸爸进一步解释,完全一样的两张纸卷成的圆柱比方柱装得米多,说明圆筒的横截面(圆形)比方筒的(方形)面积要大。
实验二:爸爸又取出两块尺寸相同的泡沫塑料板,在中间位置分别挖出面积相同的圆形和方形窗口,然后再分别放上相同重量的字典,我仔细观察后发现:开方形窗口的泡沫塑料板变形水准比开圆形窗口的要大一些。
爸爸说,这是因为圆形的受力特点,圆周上任何一个地方受力,力都能够比较均匀地向圆周分散传递开来,不会产生不均匀受力现象,所以开圆形窗口的塑料板变形小一些。
实验三:爸爸拿出了我小时候玩过的玩具汽车,然后把玩具汽车轮子去掉,安装了四个相同的正方形木块当作车轮,让我推推看,推动时我发现不但费力,而且当方形车轮与地面的接触点分别转动到方形的顶点和四边时,到车轴的距离不相等,这样伴随车轴位置的时上时下,车子就会上下颠簸。
再对比圆形的车轮滚动时,只要路面平整,车轴到离地面的垂直距离保持不变,车子推动时既比较省力有相对平稳。
这时爸爸地对我说,实验做完了,你有什么发现呀?看着我还是一头雾水的样子,爸爸笑眯眯继续说道,上面的三个小实验都是利用圆形的特点,模拟现实生活中的具体应用事例,下面我们一起想一想看看都能得到那些结论。
在爸爸的协助下,我分别把三个实验的结论写了出来:结论一:相同的周长所围成的图形面积,圆形最大。
这也就是说如果使用相同的材料做成面积(容积)最大的东西,圆形是最合适不过的了。
结论二:因为圆形能很好分散和传递受力,从而具有较大的支撑和抗压特性。
结论三:圆是一个轴对称图形且有无数条对称轴,圆心到圆周上任意一点的距离都相等。
写到这里我恍然大悟,这就很好地解释了水管、柱子、硬币、锅盖、可乐罐、茶杯、井盖等做成圆形的原因了。
在相同的条件下,材料既省,又结实耐用,低碳环保。
比如水管的横截面做成圆形既能很好地保证水的流量,又能最大水准的节省原材料,同时能够使水管承受更大的压力,不容易破裂或爆裂,用起来很安全;同样马路上的井盖做成圆形,除了美观、井盖受力均匀,不容易损坏外,还利用“圆上的每个点到圆心的距离都相等”的特性,保证井盖怎么旋转和倾斜都不容易掉进井里去。
