§3 高斯公式与斯托克斯公式 答案
§3高斯公式与斯托克斯公式

§3高斯公式与斯托克斯公式高斯公式和斯托克斯公式都是数学中的重要公式,用于计算曲线、曲面和体积的积分。
本文将对高斯公式和斯托克斯公式进行详细介绍。
一、高斯公式高斯公式是数学中的一个定理,描述了矢量场在一个闭合曲面上的积分与矢量场的散度在整个包围该曲面的体积上的积分之间的关系。
设D为一个封闭的三维空间区域,其边界为S,函数F(x,y,z)=(P(x,y,z),Q(x,y,z),R(x,y,z))为定义在D上的矢量场,其中P,Q和R在D上具有偏导数。
高斯公式的数学表达为:∫∫SF·dS=∭D∇·FdV其中∫∫S表示对曲面S上的面积元素dS进行面积分,∇·F表示矢量场F的散度,∭D表示对区域D进行体积分,dV表示体积元素。
高斯公式提供了计算闭合曲面上矢量场的散度的方法,将曲面S上的面积分转化为闭合区间D内的体积分。
这个公式在电磁学和流体力学等领域中有广泛应用。
例如,在电磁学中,电通量是电场与闭合曲面之间的关系,可以利用高斯公式来计算。
斯托克斯公式是数学中的另一个定理,描述了矢量场环路积分与矢量场旋度在包含该环路的曲面上的面积分之间的关系。
设C为一个平面闭合曲线,其边界为曲线C,函数F(x,y,z)=(P(x,y,z),Q(x,y,z),R(x,y,z))为定义在包含C的曲面S上的矢量场,其中P,Q和R在S上具有偏导数。
斯托克斯公式的数学表达为:∮C F·dr = ∬S (∇×F)·dS其中∮C表示对闭合曲线C进行环路积分,dr表示路径元素,∬S表示对曲面S上的面积元素dS进行面积分,∇×F表示矢量场F的旋度。
斯托克斯公式提供了计算闭合曲线上矢量场的旋度的方法,将闭合曲线上的环路积分转化为包含该曲线的曲面上的面积分。
这个公式在电磁学和流体力学等领域中也有广泛应用。
例如,在电磁学中,安培环路定律描述了磁场与闭合曲线之间的关系,可以利用斯托克斯公式来计算。
数学分析22-3223 高斯公式与斯托克斯公式

如果 S 不能以 z z( x, y) 的形式给出, 则可用一些
光滑曲线把 S 分割为若干小块,使每一小块能用这
种形式来表示. 因而这时 (2) 式也能成立. 为了便于记忆,斯托克斯公式也常写成如下形式:
dydz dzdx dxdy
S
x
y
z
L Pdx Qdy Rdz .
PQ R
例4 计算 L(2 y z)dx ( x z)dy ( y z)dz , 其中
返回
一、高斯公式 二、斯托克斯公式
一、高斯公式
定理22.3 设空间区域 V 由分片光滑的双侧封闭曲 面 S 围成. 若函数 P, Q, R 在 V 上连续, 且有一阶连 续偏导数, 则
V
P x
Q y
R z
dxdydz
Pdydz+Qdzdx+Rdxdy ,
(1)
S
其中 S 取外侧.(1) 式称为高斯公式.
S S1
( x y)dxdydz
V
2
2
5r2
0 d 0 dr 1 (r cos r sin )rdz 0.
而
因此
y( x z)dydz x2dxdz ( y2 xz)dxdy
S1
( y2 x)dxdy 4π.
D
y( x z)dydz x2dzdx ( y2 xz)dxdy 4π.
若S 在 xy 平面上的投影为区域 D( xy), L 在 xy 平面上 的投影为曲线 . 现由第二型曲线积分定义及格林
公式有
L P( x, y, z)dx P( x, y, z( x, y))dx
因为 所以
P( x, y, z( x, y))dxdy .
y D( xy )
高斯公式及斯托克斯公式

Green 公式 一、高斯公式 *二、沿任意闭曲面的曲面积分为零的条件 三、通量与散度
推广
Gauss 公式
一、高斯 ( Gauss ) 公式
定理1. 设空间闭区域 由分片光滑的闭曲
面 所围成, 的方向取外侧, 函数 P, Q, R 在 上有连续的一阶偏导数 , 则有
z
其中 为锥面 x 2 y 2 z 2 介于 z = 0 及
z = h 之间部分的下侧. 解: 作辅助面
1 h h
o x
y
2 2 2 1: z h, ( x, y ) D x y : x y h , 取上侧
记 , 1所围区域为, 则
I (
1 1
2 1 3
Dx y
3 1
y
x
R d x d y R d x d y
R( x, y, z 2 ( x, y ))dxdy R( x, y, z1 ( x, y )) d xdy
Dx y Dx y
R 所以 z d x d y d z R d x d y 若 不是 XY–型区域 , 则可引进辅助面 将其分割成若干个 XY–型区域, 在辅助面 正反两侧面积分正负抵消, 故上式仍成立 . P d x d y d z Pd y d z 类似可证 x Q y d x d y d z Qd z d x 三式相加, 即得所证 Gauss 公式: P Q R x y z d x d ydz P d y d z Q d z d x R d xdy
P d y d z Q d z d x Rdx d y
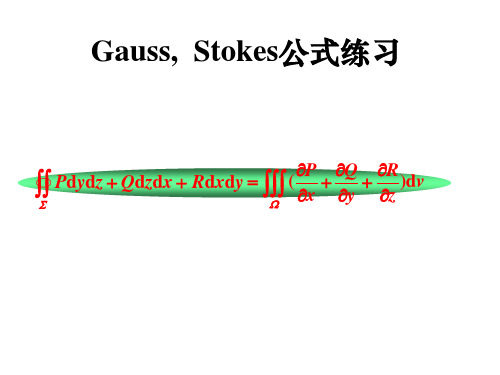
Gauss,Stokes公式练习及内容总结
x , 2 2 x +y y , 2 2 x +y
D
∑
向量点积法
−x −y 2 I = ∫∫ { y, − x, z } ⋅ , ,1dxdy x2 + y 2 x2 + y 2 ∑
= ∫∫ z dxdy
2 ∑
= − ∫∫ ( x + y )dxdy [ Dxy : 1 ≤ x 2 + y 2 ≤ 4 ]
O
x 2 + y 2 + z 2 = 4 所围立体的表面 外侧. 外侧.
如何直接计算 被积函数中有抽象函数, 被积函数中有抽象函数, 故无法直接计算. 高斯公式. 故无法直接计算. 用高斯公式.
分析
x
高斯(Gauss)公式 公式 高斯
解
1 y 3 y 3 f + y , R= f +z , y z z ∂P 1 y 1 y 2 ∂Q 2 ∂R ′ + 3 y , = 3x , = − 2 f ′ + 3 z 2 = 2 f z ∂z ∂y z ∂x z z 故由高斯公式 故由高斯公式
∂u ∂v ∂u ∂v ∂u ∂v = ∫∫∫ u∆vdxdydz + ∫∫∫ + + dxdydz ∂x ∂x ∂y ∂y ∂z ∂z Ω Ω 移项后,即证. 移项后,即证.
高斯(Gauss)公式 公式 高斯
计算曲面积分
1987年研究生考题,计算(10分 1987年研究生考题,计算(10分) 年研究生考题 (10
∂2 ∂2 ∂2 称为拉普拉斯 拉普拉斯( )算子. ∆ = 2 + 2 + 2 ,称为拉普拉斯(Laplace)算子. ∂x ∂y ∂z
高斯公式和斯托克斯公式_681302766

,
a2 − x2 − y2
x
zy =
−y a2 − x2 − y2
∫∫ I = [ a2 − x2 − y2 ⋅
−x
Dxy
a2 − x2 − y2
+ 2 a2 − x2 − y2 ⋅
−y
− y]dxdy
2009-4-3
a2 − x2 − y2
25
z
I = − ∫∫ ( x + 3 y)dxdy
D xy
dz
−
∂Z ∂x
dz^
dx
假设:S : z = z( x, y)二阶偏导连续 , 上侧
S的单位法向量 nv =
1+
1
z
2 x
+
z
2 y
(
−
z
' x
,
−
z
' y
,1)T
= (cos α , cos β , cos γ )T
∂S在 xoy 平面上的投影为 L∗ , L∗所围区域是 D xy
2009-4-3
2009-4-3
3
[证] 先证明第三项
∫∫
S外
Zdx^
dy
=
∫∫∫ Ω
∂Z ∂z
dV
z nv S2 : z = z2(x, y)
•
假设Ω如图所示
nv
∫∫∫ ∫∫ ∫ ∂Z dV= dxdy ∂Z z2 ( x, y) dz
Ω ∂z
D xy
∂z z1 ( x , y ) o
S3
nvS1 : z• = z1(x, y) y
验证斯托克斯公式的正 确性
∫L zdx + xdy + ydz
《电磁场与电磁波》习题参考答案

《电磁场与电磁波》知识点及参考答案第1章 矢量分析1、如果矢量场F 的散度处处为0,即0F∇⋅≡,则矢量场是无散场,由旋涡源所产生,通过任何闭合曲面S 的通量等于0。
2、如果矢量场F 的旋度处处为0,即0F ∇⨯≡,则矢量场是无旋场,由散度源所产生,沿任何闭合路径C 的环流等于0。
3、矢量分析中的两个重要定理分别是散度定理(高斯定理)和斯托克斯定理, 它们的表达式分别是:散度(高斯)定理:SVFdV F dS ∇⋅=⋅⎰⎰和斯托克斯定理:sCF dS F dl∇⨯⋅=⋅⎰⎰。
4、在有限空间V 中,矢量场的性质由其散度、旋度和V 边界上所满足的条件唯一的确定。
( √ )5、描绘物理状态空间分布的标量函数和矢量函数,在时间为一定值的情况下,它们是唯一的。
( √ )6、标量场的梯度运算和矢量场的旋度运算都是矢量。
( √ )7、梯度的方向是等值面的切线方向。
(× )8、标量场梯度的旋度恒等于0。
( √ ) 9、习题1.12, 1.16。
第2章 电磁场的基本规律(电场部分)1、静止电荷所产生的电场,称之为静电场;电场强度的方向与正电荷在电场中受力的方向相同。
2、在国际单位制中,电场强度的单位是V/m(伏特/米)。
3、静电系统在真空中的基本方程的积分形式是:V V sD d S d V Q ρ⋅==⎰⎰和0lE dl ⋅=⎰。
4、静电系统在真空中的基本方程的微分形式是:V D ρ∇⋅=和0E∇⨯=。
5、电荷之间的相互作用力是通过电场发生的,电流与电流之间的相互作用力是通过磁场发生的。
6、在两种媒质分界面的两侧,电场→E 的切向分量E 1t -E 2t =0;而磁场→B 的法向分量B 1n -B 2n =0。
7、在介电常数为e 的均匀各向同性介质中,电位函数为 2211522x y z ϕ=+-,则电场强度E=5x y zxe ye e --+。
8、静电平衡状态下,导体内部电场强度、磁场强度等于零,导体表面为等位面;在导体表面只有电场的法向分量。
高斯公式与斯托克斯公式——习题

证:因为 cos(r, n) = cos(r, x) cos(n, x) + cos(r, y) cos(n, y) + cos(r, z) cos(n, z) ,而
cos(r, x) = x , cos(r, y) = y , cos(r, z) = z ,则由第一、二型曲面积分的关系及奥高公式可得
S
S
由于曲面 S : x = y( y 2 + z 2 ≤ 1) 上任一点 (x, y, z) 处的法向量 n = (cosα , cos β , cosγ ) 中的
∫∫ cosγ = 0 ,从而由定义知 x 2 y 2dxdy = 0 ,因此,原式=0. S (3) ∫L (z − y)dx + (x − z)dy + ( y − x)dz = ∫∫ (1 + 1)dydz + (1 + 1)dzdx + (1 + 1)dxdy S
3S
其中 cosα , cos β , cosγ 为曲面 S 的外法线方向余弦
证:因为 ∫∫ (x cosα + y cos β + z cosγ )dS = ∫∫ xdydz + ydzdx + zdxdy
S
S
=
∫∫∫ V
(
∂ ∂x
x
+
∂ ∂y
y
+
∂ ∂z
z)dxdydz
=
3∫∫∫d V
xdydz
1 1− y
dy ( y − z)dz =
1
[
y(1
−
y)
−
1
(1 −
y
2
)]dy
S
高等数学第22章第3节高斯公式与斯托克斯公式

由斯托克斯公式,可导出空间曲线积分与路线无关的条件. 区域V称为单连通区域,如果V内任一封闭曲线皆可以不经过V以 外的点而连续收缩于属于V的一点。如球体是单连通区域。非单连通区 域称为复连区域。如环状区域不是单连通区域中,而是复连通区域。
与平面曲线积分相仿,空间曲线积分与路线的无关性也有下面相应 的定理。 定理22.5 设为空间单连通区域。若函数P,Q,R在上连续,且有 一阶连续偏导数,则以下四个条件是等价的: (i)对于内任一按段光滑的封闭曲线L有 (ii)对于内任一按段光滑的曲线L,曲线积分 与路线无关; (iii)是内某一函数u的全微分,即 (6) (iv) 在内处处成立。 这个定理的证明与定理21.12相仿,这里不重复了。 例3 验证曲线积分 与路线无关,并求被积表达式的原函数。 解 由于 所以曲线积分与路线无关。
(4) 和
(5) 将(3)、(4)、(5)三式相加即得(2)式。 如果曲面S不能以的形式给出,则可用一些光滑曲线把S分割为若干 小块,使每一小块能用这种形式来表示。因而这时(2)式也能成 立。 ▌ 公式(2)称为斯托克斯公式。 为了便于记忆,斯托克斯公式也常写成如下形式: 例2 计算 其中L为平面x+y+z=1与各坐标面的交线,取逆时针方向为正向(图22 -8)。 解 应用斯托克斯公式推得
, (1) 其中S取外侧。(1)式称为高斯公式。
证 下面只证 读者可类似地证明 这些结果相加便得到了高斯公式(1)。 先设V是一个xy型区域,即其边界曲面S由曲面
①若S为封闭曲面,则曲面积分的积分号用表示。 及以垂直于的边界的柱面组成(图22-6),其中。于是按三重积分的 计算方法有 其中都取上侧。又由于在xy平面上投影区域的面积为零,所以 因此 对于不是xy型区域的情形,则用有限个光滑曲面将它分割成若干个 xy型 区域来讨论。详细的推导与格林公式相似,这里不再细说 了。 ▌ 高斯公式可用来简化某些曲面积分的计算。 例1 计算 其中S是边长为a的正立方体表面并取外侧(即上节习题1(1))。 解 应用高斯公式,所求曲面积分等于
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§3 高斯公式与斯托克斯公式
1.应用高斯公式计算下列曲面积分;
(1),S
yzdydz zxdzdx xydxdy ++⎰⎰其中S 是单位球面2221x y z ++=的外侧;
(2)222,S
x dydz y dzdx z dxdy ++⎰⎰其中S 是立方体0,,x y z a ≤≤表面的外侧;
(3)222,S
x dydz y dzdx z dxdy ++⎰⎰其中S 是锥面222x y z +=与平面z h =所围空
间区域(0z h ≤≤)的表面,方向取外侧;
(4)333,S
x dydz y dzdx z dxdy ++⎰⎰其中S 是单位球面2221x y z ++=的外侧;
(5),S
xdydz ydzdx zdxdy ++⎰⎰其中S 是上半球面z =.
3.应用斯托克斯公式计算下列曲线积分:
(1)222222()()(),L
y z dx x z dy x y dz +++++⎰其中L 为1x y z ++=与三坐标面
的交线,它的走向使所围平面区域上侧在曲线的左侧;
(2)23,L
x y dx dy zdz ++⎰其中L 为221,y z x y +==所交的椭圆的正向;
(3)()()(),L
z y dx x z dy y x dz -+-+-⎰其中L 为以(,0,0),(0,,0),(0,0,)A a B a C a 为
顶点的三角形沿ABCA 的.
4.求下列全微分的原函数:
(1);yzdx xzdy xydz ++
(2)222(2)(2)(2).x yz dx y xz dy z xy dz -+-+-
5.验证下列线积分与路线无关,并计算其值:
(1)(2,3,4)23(1,1,1);xdx y dy z dz -+-⎰
(2)222
111(,,)(,,)
x y z x y z ⎰其中()()111222,,,,x y z x y z 在球面2222x y z a ++=上.。
