仿真实验二 二阶电路响应的三种
电路与信号系统实验报告2-二阶电路的动态响应

二阶电路的动态响应
一、实验内容
1.Multisim仿真
(1)创建电路:
(2)设置=10mH、=22nF,电容的初始电压为5V,电源电压为10V。
利用Transient Analysis观测电容两端的电压。
(3)用Multisim瞬态分析仿真零输入响应(参数欠阻尼、临界阻尼、过阻尼三
种情况);在同一张图中画出三条曲线,标出相应阻值。
(4)用Multisim瞬态分析仿真零响应(参数欠阻尼、临界阻尼、过阻尼三种情况);在同一张图中画出三条曲线,标出相应阻值。
(5)利用Multisim中的函数发生器、示波器和波特仪创建如图所示的电路,观测各种响应。
函数信号发生器设置:方波、频率1kHz、幅度5V、偏置5V。
2.在电路板上按图所示的电路(R1=100Ω、L=10mH、C=47nF)焊接实验电路。
3.调节可变电阻器R2,观察二阶电路的零输入响应和零状态响应由过阻尼过渡到临界阻尼,最后过渡到欠阻尼的变化过渡过程,分别定性地描绘、记录响应的典型变化波形,按表记录所测数据和波形。
欠阻尼:R2=35Ω
临界阻尼:R2=819Ω,衰减时间=100us
过阻尼:R2=1kΩ,衰减时间=160us
4.调节R2使示波器荧光屏上呈现稳定的欠阻尼响应波形,定量测定此时电路的衰减振荡角频率
二、实验结论
电阻越高,响应衰减地越快;电阻越低,响应衰减地越慢。
当电阻为零时,
电路无衰减。
(完成)二阶电路响应的三种状态轨迹及其特点

实验二二阶电路响应的三种(欠阻尼、过阻尼及临界阻尼)状态轨迹及其特点一、实验目的1、熟练掌握二阶电路微分方程的列写及求解过程;2、掌握RLC 二阶电路零输入响应及电路的过阻尼、临界阻尼和欠阻尼状态;3、学会利用MULTISIM 仿真软件熟练分析电路,尤其是电路中各电压电流的变化波形。
二、实验原理用二阶线性常微分方程描述的电路称为二阶电路,二阶电路中至少含有两个储能元件。
二阶电路微分方程式一个含有二次微分的方程,由二阶微分方程描述的电路称为二阶电路。
分析二阶电路的方法仍然是建立二阶微分方程,并利用初始条件求解得到电路的响应。
二阶方程一般都为齐次方程。
齐次方程的通解一般分为三种情况:(RLC 串联时)1、 21S S ≠ 为两个不等的实根(称过阻尼状态)t S t S h e A e A f 211121+= 此时,CL R 2>,二阶电路为过阻尼状态。
2、 σ==21S S 为相等实根(称临界状态)t h e A A f σ)21+=( 此时,CL R 2=,二阶电路为临界状态。
3、 ωσj S ±-=21、为共轭复根(称欠阻尼状态)t h e t f σβω-+=)sin( 此时CL R 2<,二阶电路为欠阻尼状态。
这三个状态在二阶电路中式一个重要的数据,它决定了电路中电流电压关系以及电流电压波形。
三、实验内容电路中开关S 闭合已久。
t=0时将S 打开,并测量。
1、欠阻尼状态(R=10Ω,C=10mF,L=50mH )如图所示,为欠阻尼状态时的二阶电路图。
波形图展示了欠阻尼状态下的C U 和L U 波形(橙色线条为电容电压衰减波形,红色线条为电感电压衰减波形)。
2、临界阻尼(R=10Ω,C=10mF,L=0.25mH )如图所示,为临界状态的二阶电路图。
图展示了临界状态下的C U 的波形。
波形图展示了临界状态下的C U 和L U 波形。
3、过阻尼状态(R=10Ω,C=1mF,L=1mH )如图所示,为过阻尼状态下的二阶电路图。
仿真实验二二阶电路响应
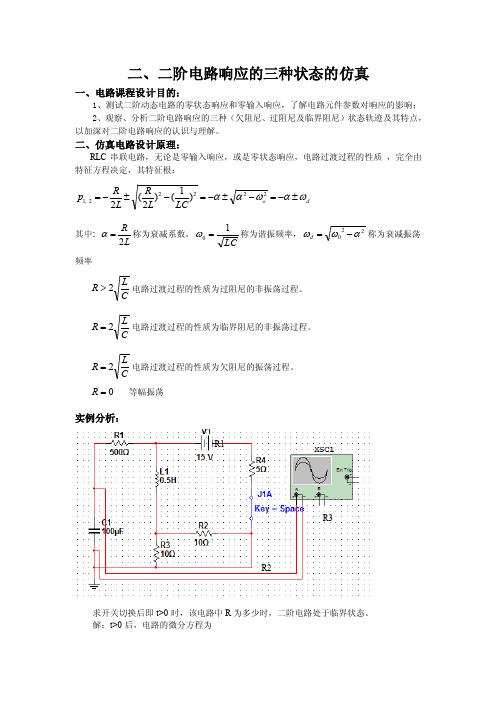
二、二阶电路响应的三种状态的仿真一、电路课程设计目的:1、测试二阶动态电路的零状态响应和零输入响应,了解电路元件参数对响应的影响;2、观察、分析二阶电路响应的三种(欠阻尼、过阻尼及临界阻尼)状态轨迹及其特点,以加深对二阶电路响应的认识与理解。
二、仿真电路设计原理:RLC 串联电路,无论是零输入响应,或是零状态响应,电路过渡过程的性质 ,完全由特征方程决定,其特征根:d o LCL R L R p ωαωαα±-=-±-=-±-=22222,1)1()2(2 其中: L R 2=α称为衰减系数,LC10=ω称为谐振频率,220αωω-=d 称为衰减振荡频率 CL R 2>电路过渡过程的性质为过阻尼的非振荡过程。
CL R 2=电路过渡过程的性质为临界阻尼的非振荡过程。
C L R 2=电路过渡过程的性质为欠阻尼的振荡过程。
0=R 等幅振荡实例分析:求开关切换后即t>0时,该电路中R 为多少时,二阶电路处于临界状态。
解:t>0后,电路的微分方程为R1R2R3Ai i V u u u dtdu C R dt u d LC c c c c c 5)0()0(25)0()0(0'22=-=+=-=+=++ Ate e e te A e A e A C t i Ve t e t A A u A A p p p C L R LC L R L R Cp R LCp t t t t t t t t c )5.5006975.35405.3535(10)()()5.354020()(5.35402542.141,42.14121)(2p 0142.14142.14142.141422142.14142.141212121'2''2,1'2-----------=-+--=+=+=∴==-===Ω==∴-±-==++δδδδδ,为两个相等的实根。
邓 仿真实验2二阶电路响应的三种

四、对比分析与结论
1、分析实验: 本实验这要是观察三种阻态下的波形, 由于引入了可变电阻使电路的转换非常方便。 在 进行波形分析时,由于测的是电感的电压和电流,所以主要从电路的电流变化来看,我们很 容易就能理解电感的充放电过程。 2、实验总结: 通过本次实验的学习, 我熟悉了二阶电路微分方程的列写及求解过程, 了解了 RLC 二阶 电路的响应及电路的过阻尼、 临界阻尼和欠阻尼状态, 更熟练地利用仿真软件分析电路的动 态变化。 在实验中我先是用的并联电路但由于公示用错改用了串联电路, 终于得到正确的波 形,在这个实验上也花费了很多的时间。由此也学会,具体题目具体分析,不要一味的套用 公式。
用二阶线性常微分方程描述的电路称为二阶电路, 二阶电路中至少含有两个不同类型的 储能元件。 二阶电路微分方程式一共含有两个二次微分的方程。 分析二阶电路的方法是建立 二阶微分方程,并利用初始条件求解得到电路的响应。在解二阶方程式时,我们通常是先解 齐次方程。 齐次方程的通解一般分为三种情况: (RLC 串联时) 1、S1 ≠ S2 为两个不等的实根: f = A 1 eS 1 t + A 2 eS 2 t 此时,R > 2
L C
=2
10 −3 1000×10 −12
= 2kΩ
1)欠阻尼状态(R=400Ω ,C=1000pF,L=1mH) 如图所示,为欠阻尼状态时的二阶电路图,以及其在方波激励下的波形。 本次实验的测量值为:电感点电流(蓝色)以及电感电压(红色) 。
单个波形放大为:
由波形图可知在欠阻尼的情况下 (方波激励) , 电感两端电压和电流都是振荡的减小的。
二、二阶电路响应的三种(欠阻尼、过阻尼及临界阻尼)状
态轨迹及其特点
一、仿真实验目的
二阶电路响应的仿真实验报告

二阶电路响应的仿真实验报告一、实验目的本次实验旨在通过仿真实验的方式,探究二阶电路响应的特性,并且了解其在不同频率下的响应情况。
二、实验原理1. 二阶电路的基本概念二阶电路是指带有两个存储元件(电容或电感)的电路,其具有更加复杂的响应特性。
其中,常见的二阶电路包括二阶低通滤波器、二阶高通滤波器以及二阶带通滤波器等。
2. 二阶低通滤波器的特性在二阶低通滤波器中,当输入信号频率很低时,输出信号基本上不会受到影响;而当输入信号频率逐渐升高时,输出信号将会逐渐减小。
当输入信号频率等于截止频率时,输出信号将会下降3dB;而当输入信号频率继续升高时,输出信号将会更加明显地下降。
3. 仿真实验步骤(1)构建一个RC电路,并且设置初始条件和参数值;(2)绘制RC电路的幅度-频率响应曲线;(3)绘制RC电路的相位-频率响应曲线;(4)分析幅度-频率响应曲线和相位-频率响应曲线的特点。
三、实验步骤1. 构建RC电路在Multisim软件中,选择“模拟”选项卡,然后选择“Passive”选项卡,接着选择“R”和“C”元件,并且将它们连接起来。
最终得到的电路图如下所示:2. 设置初始条件和参数值在Multisim软件中,点击“仿真设置”按钮,在弹出的对话框中,将仿真类型设置为“AC Analysis”,并且设置频率范围为1Hz~10MHz。
接着,设置电容C1的值为0.01μF,电阻R1的值为10kΩ。
3. 绘制RC电路的幅度-频率响应曲线在Multisim软件中,点击“仪表”选项卡,并且选择“AC Analysis”仪表。
接着,在弹出的对话框中,将X轴设置为“Frequency”,将Y轴设置为“Magnitude(dB)”,并且勾选上“Decibel Scale”。
最终得到的幅度-频率响应曲线如下图所示:4. 绘制RC电路的相位-频率响应曲线在Multisim软件中,点击“仪表”选项卡,并且选择“AC Analysis”仪表。
二阶电路响应的三种

二阶电路响应的三种(欠阻尼、过阻尼及临界阻尼)动态响应及其特点一、试验目的1、通过RCL电路的放电过程,熟悉二阶电路响应的原理;1、观看分析二阶电路响应的三种轨迹及其特点,深入对二阶电路响应的熟悉与理解;2、娴熟运用multisim分析二阶电路。
二、试验原理及实例1、试验原理如图1,通过RCL串联电路的放电过程来讨论二阶电路的响应。
设开关闭合前电容已带有电荷。
w c(θ-) = u o»⅛(θ-) 二θt = 0时,开关闭合,得出KVL方程:-u c+ U R+U L=0由du r du c di d2u ci = -"u R = Ri =一A,/'应=乙五=TC.微分方程为d2u c R du c 1 八——-+ -------------- -÷—u r = 0dt2 L dt LC c特征方程为p2+]p+1⅛ = 0,特征根为R∕R∖2 1Pl、2 = ^2L i J∖2L∕ ~LC当R > 2J∣时,过阻尼非震荡放电过程;当R = 2j∣时,临界阻尼非震荡放电过程;当RV2^∣时,欠阻尼放电过程。
二、实例如图所示,己知Ri = 100C,& = 100Q,L = 0∙2H,C = 1,254/,在40时开关s打开。
试求先为1。
,7000和400Q时,电容电压〃°的值。
断开开关后,得微分方程d2u c /?3 + 100 du c 1—√÷-l- ------------------------- -^ + -u c = 0dt2 L dt LC%(0_) = %(0_) = 15P(1)当R3 = 1000Q 时,(R3 + IOO)>2Jj 为过阻尼状态。
特征根Pl 2 = -2750 ± √(2750)2 -4 × 106,p1 = -862.541Ω,p2 = -4637.459Ω得∕(t) = 18.43e^862∙541t + 3.427e-4637∙459Ψ(2)当R3= 700∩时,(/?3 + 100) = 2卡为临界阻尼状态。
上海电力 仿真实验八 二阶电路零输入响应的三种状态轨迹
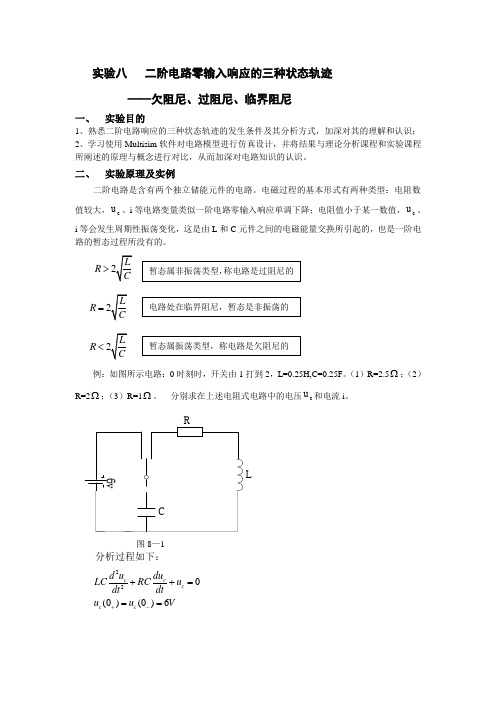
实验八 二阶电路零输入响应的三种状态轨迹——欠阻尼、过阻尼、临界阻尼一、 实验目的1、熟悉二阶电路响应的三种状态轨迹的发生条件及其分析方式,加深对其的理解和认识;2、学习使用Multisim 软件对电路模型进行仿真设计,并将结果与理论分析课程和实验课程所阐述的原理与概念进行对比,从而加深对电路知识的认识。
二、 实验原理及实例二阶电路是含有两个独立储能元件的电路。
电磁过程的基本形式有两种类型:电阻数值较大,c u 、i 等电路变量类似一阶电路零输入响应单调下降;电阻值小于某一数值,c u 、i 等会发生周期性振荡变化,这是由L 和C 元件之间的电磁能量交换所引起的,也是一阶电路的暂态过程所没有的。
R >R=R < 例:如图所示电路:0时刻时,开关由1打到2,L=0.25H,C=0.25F 。
(1)R=2.5Ω;(2)R=2Ω;(3)R=1Ω。
分别求在上述电阻式电路中的电压c u 和电流i 。
L图8—1分析过程如下:220(0)(0)6c c c c c d u du LC RC u dt dtu u V +-++===0(0)(0)0c du i i C dt ++-==-=210LCp RCp ++= 210LCp RCp ++=(1) R=2.5Ω时,过阻尼状态122.5,2,8R R p p =Ω>=-=-2812126t tc u A e A e A A --=++=01212(0)(28)082cdu i C C A A dtA A ++=-=---===-2828()(82),()4()t t t t c c du u t e e v i t Ce e A dt ----=-=-=- (2)R=2Ω,临界阻尼状态。
2,R R =Ω= 124p p ==-412()t c u A A t e -=+ 1(0)6c A u -== 021(0)(4)0c du i C C A A dt++=-=--= 12624A A == 444()6(14)(),()66(14)()t t t c c du u t t e v i t Ce t e A dt ---=+=-=-++(3)R=1Ω,欠阻尼状态,振荡放电过程1201,2 3.46sin(3.46)(0)sin 6(0)(2sin 3.46cos )0t c c cR R p j u Ae t u A du i C C A A dt ββββ+-++=Ω<=-±=+===-=--+=660, 6.93sin A ββ===22() 6.93sin(3.4660)(),() 6.93sin 3.46()t t c c du u t e t v i t C e t A dt --=+=-=三、 仿真设计步骤:1、根据电路设计题目要求设计电路;2、用visio 做出电路原理图并对其进行理论计算分析;3、根据电路模拟图在电路仿真软件上做出仿真模型,通过示波器分析电容电压和电流变化过程,进行电路仿真;4、将测量的结果与理论计算值进行比较,对仿真结果进行分析;5、做出实验小结四、 仿真实验结果如图所示,设计仿真电路图8—2R=2.5Ω时,过阻尼状态波形如下所示:图8—3当将R值换成2Ω时,;临界阻尼波形图如下图8—4当将R值换成1Ω时,欠阻尼振荡放电波形图如下:图8—5图中蓝色为电感电流波形轨迹,红色为电容电压波形轨迹。
完成二阶电路响应的三种欠阻尼、过阻尼及临界阻尼状态轨迹及其特点.docx

实验二二阶电路响应的三种(欠阻尼、过阻尼及临界阻尼)状态轨迹及其特点一、实验目的1、熟练掌握二阶电路微分方程的列写及求解过程;2、掌握 RLC 二阶电路零输入响应及电路的过阻尼、临界阻尼和欠阻尼状态;3、学会利用 MULTISIM 仿真软件熟练分析电路, 尤其是电路中各电压电流的变化波形。
二、实验原理用二阶线性常微分方程描述的电路称为二阶电路, 二阶电路中至少含有两个储能元件。
二阶电路微分方程式一个含有二次微分的方程, 由二阶微分方程描述的电路称为二阶电路。
分析二阶电路的方法仍然是建立二阶微分方程, 并利用初始条件求解得到电路的响应。
二阶方程一般都为齐次方程。
齐次方程的通解一般分为三种情况: ( RLC 串联时)1、S 1 S 2 为两个不等的实根(称过阻尼状态)f hS t S tA 1e 11 A 2 e 12 此时, R 2 L,二阶电路为过阻尼状态。
C2、 S 1 S 2为相等实根(称临界状态) f h ( A 1 A 2 )e t此时, R 2L ,二阶电路为临界状态。
C 3、 S 1、2j 为共轭复根(称欠阻尼状态) f h sin( t)e t此时 R2 L ,二阶电路为欠阻尼状态。
C 这三个状态在二阶电路中式一个重要的数据, 它决定了电路中电流电压关系以及电流电压波形。
三、实验内容电路中开关 S 闭合已久。
t=0 时将 S 打开,并测量。
1、欠阻尼状态( R=10Ω,C=10mF,L=50mH)如图所示,为欠阻尼状态时的二阶电路图。
波形图展示了欠阻尼状态下的U C和 U L波形(橙色线条为电容电压衰减波形,红色线条为电感电压衰减波形) 。
2、临界阻尼( R=10Ω ,C=10mF,L=0.25mH)如图所示,为临界状态的二阶电路图。
图展示了临界状态下的U C的波形。
波形图展示了临界状态下的U C和 U L波形。
3、过阻尼状态( R=10Ω,C=1mF,L=1mH)如图所示,为过阻尼状态下的二阶电路图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
仿真实验二 二阶电路响应的三种(欠阻尼、过阻尼及
临界阻尼)状态轨迹及其特点
实验目的:
(1)、测试二阶动态电路的零状态响应和零输入响应,了解电路元件参数对响应的影响。
(2)、观察、分析二阶电路响应的三种状态轨迹及其特点。
加深对二阶电路响应的认识与 理解。
实验原理:
二阶电路零输入响应:
以电容电压为变量,电路的微分方程为:022=++c t
c c u
d du RC dt u d LC 以上二阶微分方程的特征方程为: 012
=++RCp LCp 方程的特征根为: LC
L R L R p 1)2(2212-±-= (1)p 1和p 2为不相等的负实根(C
L R 2>)应显示过阻尼状态; (2)p 1和p 2为共轭复根 (C L R 2
< )应显示欠阻尼状态; (3)p 1和p 2为相等的负实根 (C
L R 2= )应显示临界阻尼状态。
仿真例题分析:
如图: L=10mH,C=100μF ,R 2为20Ω,电源V=5V 。
理论计算过程:
1、临界状态: 根据公式得: Ω=⨯⨯==--2010
10010102263
C L R 则当R=20Ω时,为临界状态,此时模拟波形为:
2、阻尼状态:
当R=100Ω,即为C L R 2
>时,为过阻尼状态,模拟波形为:
3、欠阻尼状态:
则若R=1Ω,即为C
L R 2
<,应该为欠阻尼状态,此时模拟波形为:
四、结果与误差分析
仿真结果为:在RCL 串联电路中,
当 C
L R 2> 显示过阻尼状态; C L
R 2< 显示欠阻尼状态; C L
R 2= 显示临界阻尼状态。
理论计算结果与仿真测量结果有一定的误差。
主要原因有:
(1)本实验中具体实验值与理论值比较的部分较少,主要通过肉眼观察波形,此时若 在波形上得出数据,则会产生较大误差。
(2)观测误差;我们通过观测得到的数值会受各种因素限制,如在观察示波器时,由于 是肉眼观察,相位差有误差,但是我们只要精心准备仿真试验,尽力减小各种因素 的影响,就可以得到较好的仿真结果。
实验设计总结:
本实验RLC串联电路,示波器波形调节是主要问题,因为只有临界状态才能得到一个具体的阻值,而不是一个范围,所以先确定临界状态的电阻,再在这个值的基础上进行加减,取值最好跨度较大,这样波形才会更加明显。
