2014全国数学竞赛预赛试题分类:概率及期望
2014年全国初中数学联合竞赛试题及答案

2014年全国初中数学联合竞赛预赛试题参考答案(八年级组)第一试一、选择题1.C 2.D 3.A 4.B 5.B (5.由11=x 和1121444k k k k x x -⎛--⎫⎡⎤⎡⎤=+-- ⎪⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭可得11x =,22x =,33x =,44x =,51x =,62x =,73x =,84x =,……因为2014=4×503+2,所以2014x =2) 二、填空题6.20°7.-48.919.5(小正方体个数最少情况如图所示(图中数字表示该位置小正方体的个数)所以最少为5块)10.23(对角四边形的面积之和相等)第二试一、(1)证明:∵2233x x y y =+=+,,∴22x y x y -=-∴ 1 ()x y x y +=≠……………………………………………………6分(2)解:∵2233x x y y =+=+,,∴323233x x x y y y =+=+,, 43243233x x x y y y =+=+,,54354333x x x y y y =+=+,,∴5543433223223339339x y x x y y x x x x y y y y +=+++=++++++3+ 22712712x x y y =+++223()2()1921192119()4261x y x y x y x y =+++=+++=++=.………15分 二、解:方程两边分解因式得 (2x +y )(x +y )=2×19×53.………………………………5分不妨先设x ≥y ≥1,则有2x +y ≥x +2y >x +y >1. 由此,只有三种情况: 253,2106,210238,219,2 2.x y x y x y x y x y x y+=+=+=⎧⎧⎧⎨⎨⎨+=+=+=⎩⎩⎩或或…………………………10分当253,238,x y x y +=⎧⎨+=⎩时,解得15,23,x y =⎧⎨=⎩当2106,21007,219,2 2.x y x y x y x y +=+=⎧⎧⎨⎨+=+=⎩⎩或时,不符合题意.故原方程的正整数解为15,23.x y =⎧⎨=⎩………………………………………………15分俯视图2 12三、解:设本次比赛钓到的鱼的总数是x 条.则钓到3条或3条以上的人共钓到鱼的条数为:()()14+26=16x x -⨯⨯-,钓到()16x -条的人数为165x -;…………………………………………………………5分 类似地,钓到10条或10条以下的人共钓到鱼的条数为:()()114+12213=81x x -⨯⨯+-,钓到这些鱼的人数为815x -;………………10分 根据题意,可知参加本次比赛的总人数得,()167465x -+++=()814215x -+++,解得x =541.因此,本次比赛共钓到541条鱼.……………………………………………………15分四、证明:∵AD 为△ABC 的角平分线,∴12∠=∠.(1)∵CE ∥AD ,∴1E ∠=∠,23∠=∠.∴3E ∠=∠. ∴AC =AE .∵F 为EC 的中点,∴AF ⊥BC . ∴90AFE FAD ∠=∠=︒.∴AF ⊥AD .…………………………………………………………10分(2)延长BA 与MN 延长线于点E ,过B 作BF ∥AC 交NM 延长线于点F .∴3C ∠=∠,4F ∠=∠.∵M 为BC 的中点∴BM =CM . 在△BFM 和△CNM 中,4,3,,F C BM CM ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△BFM ≌△CNM (AAS ). ∴BF =CN . ∵MN ∥AD ,∴1E ∠=∠,245∠=∠=∠. ∴5E F ∠=∠=∠. ∴AE =AN ,BE =BF .设CN =x ,则BF =x , AE =AN =AC -CN =10-x ,BE =AB +AE =6+10-x . ∴6+10-x =x .解得 x =8.∴CN =5.5,AN =2. ………………………………………………25分2014年全国初中数学联合竞赛预赛试题参考答案(九年级组)第一试一、选择题A MDCBNE F35 41 21.B 2.D 3.A 4.D 5.C 6.B 二、填空题7.1792(两边同时乘以a +b +c )8.-8 9.25-=x (提示:[]x ≤x <[]x +1,原方程化为[]x ≤2[]x +27<[]x +1,解得[]x =-3,代入原方程求出x .)10.(1,21)(1011,51-)(提示:除直角三角形ABC 斜边的中点外,直线AB 上与该中点关于斜边上高的垂足对称的点也满足题意)第二试一、解:设甲仓库供应给A 校,B 校,C 校的电脑分别为x 台,y 台,()[]y x -12+台,则乙仓库供应给A 校,B 校,C 校的电脑分别为(9-x )台,(15-y )台,()[]y -15x -9-20+台, 设总运输费为S 元,则S=10x +5y +6()[]y x -12++4(9-x )+8(15-y )+15()[]y -15x -9-20+,得S=15x +6y +48=9x +6(x +y )+48,…………………………………………………………10分 又0≤x ≤9,0≤y ≤15,4≤x +y ≤12,S≥9×0+6×4+48=72,………………………………………………………………………15分 此时,x =0,y =4,又()[]y x -12+=8,故甲仓库供应给A 校,B 校,C 校的电脑分别为0台,4台,8台.……………………20分二、(1)证明:由AB =AD ,知∠ABD =∠ADB =α,由等弧对等圆周角知,∠ACD =∠ACB =α.令∠DFC =β则∠BAD =∠BFC =2β,故∠ABD +∠ADB +∠BAD =α+α+2β=180°,于是α+β=90°,∠CDF =90°.又∠FBC =180°-α-2β=α=∠FCB ,所以FB =FC …………………………10分 (2)解:设边BC 的中点为M ,连接FM . 易知△FCD ≌△FBM ,BC =2CD 又AC 是∠BCD 的角平分线,由角平分线定理,得2==CDBCDE BE …………………25分三、解:点A 的坐标为(-1,0),点B 的坐标为(3,0),点C 坐标为(0,﹣3).∵y =x 2﹣2x ﹣3=(x ﹣1)2﹣4, ∴顶点D 的坐标为(1,﹣4);点E 的坐标为(1,0).………………………………5分 (1)当点M 在对称轴右侧时.①若点N 在射线CD 上,如图,延长MN 交y 轴于点F ,过点M 作MG ⊥y 轴于点G . ∵∠CMN =∠BDE ,∠CNM =∠BED =90°, ∴△MCN ∽△DBE ,∴21==DE BE MN CN , ∴MN =2CN . 设CN =a ,则MN =2a .∵∠CDE =∠DCF =45°,∴△CNF ,△MGF 均为等腰直角三角形, ∴NF =CN =a ,CF =a , ∴MF =MN +NF =3a ,∴MG =FG =223a , ∴CG =FG ﹣FC =22a ,∴M (223a ,﹣3+22a ).代入抛物线解得a =927,∴M (37,﹣920); ………………………………………………………………13分②若点N 在射线DC 上,如图,MN 交y 轴于点F ,过点M 作MG ⊥y 轴于点G . ∵∠CMN =∠BDE ,∠CNM =∠BED =90°, ∴△MCN ∽△DBE ,∴21==DE BE MN CN , ∴MN =2CN .设CN =a ,则MN =2a . ∵∠C DE =45°,∴△CNF ,△MGF 均为等腰直角三角形, ∴NF =CN =a ,CF =a , ∴MF =MN ﹣NF =a ,∴MG =FG =22a , ∴CG =FG +FC =223a ,∴M (22a ,﹣3+223a ).代入抛物线y =(x ﹣3)(x +1),解得a =5, ∴M (5,12);………………………………………………………………………………21分 (2)当点M 在对称轴左侧时. ∵∠CMN =∠BDE <45°, ∴∠MCN >45°,而抛物线左侧任意一点K ,都有∠KCN <45°,∴点M 不存在.…………………………24分综上可知,点M 坐标为(37,﹣920)或(5,12).……………………………………25分2014年全国初中数学联赛(初三组)初赛试卷(3月7日下午4:00—6:00)班级:: 姓名: 成绩:第2题图DACB第4题图DACB考生注意:1、本试卷共五道大题,全卷满分140分;2、用圆珠笔、签字笔或钢笔作答;3、解题书写不要超出装订线;4、不能使用计算器。
2014年中国数学奥林匹克(CMO)试题及其解答

,β =
时,方程x(x + α) = y(y + β)
至少有k组正整数解。引理得证。 下面借助引理证明原命题。
根据引理知,存在正整数α>β,使得方程x(x + α) = y(y + β)至少有k组正整数解,设
这k组正整数解分别为 x ,y 、 x ,y 、 … 、 x ,y 。
令n = x (x + α),1 ≤ i ≤ k,则n = x (x + α) = y (y + β),所以 α,β ⊆ D(n )。于 是知 α,β ⊆ D(n )⋂D(n ) ⋂ … ⋂D(n ),命题得证。
而 p,q = 1,所以μ = 1。于是知u ≡ −1(mod d) ⇒ d|u + 1。
综合两方面知d = u + 1,所以 u + 1,u + 1 = u + 1,引理一得证。
引理二:设v为大于1的正整数,q为v + 1的奇素因子,则2 |q − 1。
交流知识 共享智慧
文武光华
引理二的证明:根据条件知v ≡ −1(mod q) ⇒ v ≡ 1(mod q)。设v关于模q的阶
且1 ≤ f(k) ≤ k,从而根据归纳假设知:
f(k + 2) − f(k + 1) = f f(k + 1) + f k + 2 − f(k + 1) − f f(k) + f k + 1 − f(k)
= f(f(k) + 1) + f k + 1 − f(k) − f f(k) + f k + 1 − f(k)
若 f(k + 1) − f(k) = 0 , 则 f f(k + 1) = f f(k) , f k + 2 − f(k + 1) = f k + 2 − f(k) ,
2009-2014全国大学生数学竞赛试题及答案(最完整版)

。
dx 2
二、(本题满分 5 分)求极限 lim( e x + e2x +
+
e nx
)
e x
,其中
n
是给定的正整数。
x→0
n
∫ 三、(本题满分 15 分)设函数 f (x) 连续, g(x) = 1 f (xt)dt ,且 lim f (x) = A , A 为常
0
x→0 x
数,求 g′(x) 并讨论 g′(x) 在 x = 0 处的连续性。
L
2
五、(本题满分 10 分)已知 y1 = xex + e2x , y2 = xex + e−x , y3 = xe x + e2x − e−x 是某二
阶常系数线性非齐次微分方程的三个解,试求此微分方程。
六、(本题满分 10 分)设抛物线 y = ax2 + bx + 2 ln c 过原点。当 0 ≤ x ≤ 1 时, y ≥ 0 ,又已
六、(本题满分 12 分)设 f (x) 是在 (−∞, +∞) 内的可微函数,且 f ′(x) < mf (x) ,其中
+∞
∑ 0 < m < 1 。任取实数 a0 ,定义 an = ln f (an−1), n = 1, 2, ,证明: (an − an−1) 绝对收敛。 n =1
七、(本题满分 15 分)是否存在区间[0, 2]上的连续可微函数 f (x) ,满足 f (0) = f (2) = 1,
第一届(2009)全国大学生数学竞赛预赛试卷
一、填空题(每小题 5 分,共 20 分)
(x + y) ln(1 + y )
1.计算 ∫∫D
2014全国数学竞赛预赛试题分类:数论

2014数学预赛试题分类:多项式、数论及其它山西6、将1,2,3,4,5,6,7,8,9分别填写于一张3×3的表格中,数,你的填法是: 山西8、若n 个连续正整数之和等于2014,则n 的最大值是 。
山东9、设正整数n 满足31∣(5n + n ),则n 的最小值为 。
福建6.若分数p q (p ,q 为正整数)化成小数为0.198p q= ,则当q 取最小值时,p q += 。
福建9. 23201488889999A ⎡⎤⎡⎤⎡⎤⎡⎤=++++⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦被63除的余数为 。
(符号[]x 表示不超过x 的最大整数。
)江西3.将1,2,3,4,5,6,7,8,9,10这十个数排成一个数列,使得每相邻两项之和皆是质数,并且首尾两项之和也是质数,你的填法是:( ).江西7.已知5025001250(1)x a a x a x a x +=++++ ,则123252325a a a a ++++ 的值为 .江西8.将1,2,3,4,5,6,7,8的每一个全排列皆看成一个八位数,则其中是11倍数的八位数的个数为 .江西12.若整数a ,b 既不互质,又不存在整除关系,则称a ,b 是一个“联盟”数对:设A 是集合{}1,2,,2014M = 的n 元子集,且A 中任两数皆是“联盟”数对,求n 的最大值.河南6、651000-82001的值与零的大小关系为 。
河南7、符号[x]表示不超过x 的最大整数,n 是正整数,则∑=⎪⎭⎫ ⎝⎛++20141]6[]3[]2[n n n n = 。
河南9、求所有这样的正整数n ,使得n222118++是一个正整数的平方。
四川7、设在5╳5的方格表的第i 行第j 列所填的数为ij a ,其中ij a ∈{0,1},ij a =ji a ,1≤i,j ≤5,则表中共有5个1的填表方法总数是 。
(用具体数字作答) 四川10、四川12、陕西10、元素的和为 。
2014年高中数学联赛试题及其解答

加试
一、(本题满分 40 分)设实数a、b、c满足a + b + c = 1,abc>0,求证:ab + bc + ca< √ + 。
证明方法一:因为abc>0,故a、b、c全为正数,或一正两负。 (Ⅰ)若a、b、c中一正两负,不妨设a>0,b、c<0,则ab + bc + ca = a(b + c) + bc = a(b + c) + bc = [1 − (b + c)](b + c) + bc = (b + c) − b − − <0< √ + 。
解答:我们考虑存在复数z 、z ,|z |、|z |<1,z ≠ z ,使得(z + α) + αz =
(z + α) + αz 的充要条件。此时
(z + α) + αz = (z + α) + αz
⇔ α(z − z ) = (z − z )(z + z + 2α)
⇔ α[(z − z ) + 2(z − z )] = (z − z )(z + z )
3、若函数f(x) = x + a|x − 1|在[0, + ∞)上单调递增,则实数a的取值范围是
。
x − ax + a,x ∈ 0,1
解答:根据条件知f(x) =
。f(x)在 0,1 单调递增的充要
x + ax − a,x ∈ 1, + ∞
条件为 ≤ 0 ⇔ a ≤ 0;f(x)在 1, + ∞ 单调递增的充要条件为− ≤ 1 ⇔ a ≥ −2。故实数
2014年全国高中数学联赛甘肃赛区预赛试卷答案
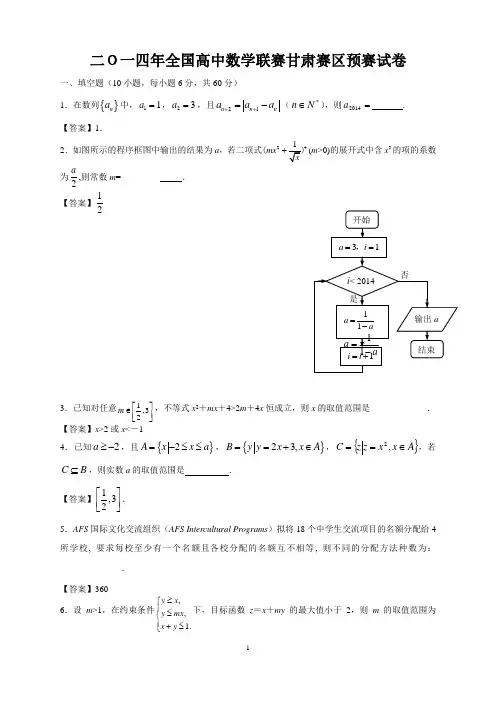
二O一四年全国高中数学联赛甘肃赛区预赛试卷一、填空题(10小题,每小题6分,共60分)1.在数列{}n a 中,11a =,23a =,且21n n n a a a ++=-(*∈N n ),则=2014a .【答案】1.2.如图所示的程序框图中输出的结果为a ,若二项式24mx ((m >0)的展开式中含3x 的项的系数为2a,则常数m =_________ .【答案】123.已知对任意1,32m ⎡⎤∈⎢⎥⎣⎦,不等式x 2+mx +4>2m +4x 恒成立,则x 的取值范围是_____________.【答案】x >2或x <-14.已知2a ≥-,且{}2A x x a =-≤≤,{}23,B y y x x A ==+∈,{}A x x z z C ∈==,2,若C B ⊆,则实数a 的取值范围是 .【答案】1,32⎡⎤⎢⎥⎣⎦.5.AFS 国际文化交流组织(AFS Intercultural Programs )拟将18个中学生交流项目的名额分配给4所学校, 要求每校至少有一个名额且各校分配的名额互不相等, 则不同的分配方法种数为:______________. 【答案】3606.设m >1,在约束条件,,1.y x y mx x y ≥⎧⎪≤⎨⎪+≤⎩下,目标函数z =x +my 的最大值小于2,则m 的取值范围为__________. 【答案】(1,1+2)7.圆锥的轴截面SAB 是边长为2的等边三角形,O 为底面中心,M 为SO 的中点,动点P 在圆锥底面内(包括圆周).若AM ⊥MP ,则P 点形成的轨迹的长度为 . 【答案】27. 8.直角梯形ABCD 中,AD ⊥AB , AB //DC , AB =4,AD =DC =2,设点N 是DC 边的中点,点M 是梯形ABCD 内或边界上的一个动点,则AM AN ⋅的最大值是______________.【答案】69.设实数1a <-,变量x 满足2x ax x +≤-,且2x ax +的最小值为12-,则a = . 【答案】32-10.已知焦点在x 轴上的双曲线的渐近线过椭圆221416x y +=和椭圆221164ax y +=(0<1a ≤)的交点,则双曲线的离心率的取值范围是 . 【答案】)321,2[ 二、解答题(4小题,共60分)11.(本小题满分14分)在数列{}n a 中,11a =,122n n a a n +=-+,n ∈*N .求数列{}n a 的前n项和n S .解:由122n n a a n +=-+得12((1))n n a n a n +-=--,n ∈*N .所以数列{}(1)n a n --是首项为1,且公比为2的等比数列.∴121n n a n -=+-.…………10分所以数列{}n a 的前n 项和(1)212nn n n S -=-+.…………14分 12.(本小题满分14分)已知△ABC 的角A ,B ,C 的对边依次为a ,b ,c ,若满足3tan tan tan 3A B A B ⋅--=(Ⅰ)求∠C 大小;(Ⅱ)若c =2,且△ABC 为锐角三角形,求a 2+b 2取值范围.解:(I 3tan tan tan 3A B A B ⋅--=tan tan 3(tan tan 1)A B A B +=⋅-∴tan tan 1tan tan A BA B+=-⋅tan()A B +=,∴tan C =3C π=…………6分 (II )2262sin sin sin 23A a b c B A A B C A B πππππ⎧<⎪⎪⎪<⇒<<==⎨⎪⎪+=⎪⎩,由正弦定理,2222162[sin sin ()]33168sin(2)336512sin(2)1,6266626a b A A A A A A ππππππππ+=+-=+-<<∴<-<∴<-≤,,22208.3a b <+≤即…………14分13.(本小题满分16分)已知双曲线C :22221x y a b-=(0a >,0b >)的离心率为2,过点(0)P m ,(0m >)斜率为1的直线l 交双曲线C 于A 、B 两点,且3AP PB =,3OA OB ⋅=. (1)求双曲线方程;(2)设Q 为双曲线C 右支上动点,F 为双曲线C 的右焦点,在x 轴负半轴上是否存在定点M 使得2QFM QMF ∠=∠?若存在,求出点M 的坐标;若不存在,请说明理由.解:(1)由双曲线离心率为2知,2c a =,b =,所以双曲线方程可化为222213x y a a-=.又直线l 方程为y x m =+.由222213x y a a y x m ⎧-=⎪⎨⎪=+⎩,得2222230x mx m a ---=. ①设11()A x y ,,22()B x y ,,则12x x m +=,221232m a x x --=.因为 3AP PB =,所以 1122()3()x m y x y m --=-,,,故123x x =-. 结合12x x m +=,解得132x m =,212x m =-. 代入221232m a x x --=,得2223342m a m ---=,化简得226m a =.又1212121222221212()()2()33OA OB x x y y x x x m x m x x m x x m m a a ⋅=+=+++=+++=-=,因为已知3OA OB ⋅=. 所以21a =.此时,m =2290x --=,显然该方程有两个不同的实根.21a =符合要求.故双曲线C 的方程为2213y x -=. …………8分(2)假设点M 存在,设(0)M t ,.由(1)知,双曲线右焦点为(20)F ,.设00()Q x y ,(01x ≥)为双曲线C 右支上一点.当02x ≠时,00tan 2Q F y QFM k x ∠=-=--,00tan Q M y QMF k x t∠==-,因为2QFM QMF ∠=∠,所以 0002000221()y y x ty x x t⨯--=---. 将220033y x =-代入,并整理得,22200002(42)4223x t x t x tx t -++-=--++. 于是 242243t t t t +=-⎧⎨-=+⎩,解得1t =-.当02x =时,090QFM ∠=,而1t =-时,045QMF ∠=,符合2QFM QMF ∠=∠.所以1t =-符合要求.满足条件的点M 存在,其坐标为(10)-,. …………16分 14.(本小题满分16分)已知函数()ln(1)1axf x x x =+++()a ∈R . (Ⅰ)当2a =时,求函数()x f y =的图象在0x =处的切线方程; (Ⅱ)判断函数()f x 的单调性;(Ⅲ)求证:2111ln 1n n n⎛⎫+>- ⎪⎝⎭(*n N ∈).解:(Ⅰ)当2a =时,2()ln(1)1xf x x x =+++,∴22123()1(1)(1)x f x x x x +'=+=+++, ∴ (0)3f '=,所以所求的切线的斜率为3.又∵()00f =,所以切点为()0,0. 故所求的切线方程为:3y x =. …………4分(Ⅱ)∵()ln(1)1axf x x x =+++(1)x >-, ∴221(1)1()1(1)(1)a x ax x af x x x x +-++'=+=+++. ①当0a ≥时,∵1x >-,∴()0f x '>;②当0a <时,由()01f x x '<⎧⎨>-⎩,得11x a -<<--;由()01f x x '>⎧⎨>-⎩,得1x a >--;综上,当0a ≥时,函数()f x 在(1,)-+∞单调递增;当0a <时,函数()f x 在(1,1)a ---单调递减,在(1,)a --+∞上单调递增. …………10分 (Ⅲ)方法一:由(Ⅱ)可知,当1a =-时, ()()ln 11xf x x x =+-+在()0,+∞上单调递增. ∴ 当0x >时,()()00f x f >=,即()ln 11xx x +>+. 令1x n =(*n ∈N ),则111ln 1111n n n n ⎛⎫+>= ⎪+⎝⎭+.另一方面,∵()2111n n n <+,即21111n n n-<+,∴21111n n n>-+. ∴ 2111ln 1n n n⎛⎫+>- ⎪⎝⎭(*n ∈N ).…………16分方法二:构造函数2()ln(1)F x x x x =+-+,(01)x ≤≤ ∴1(21)'()1211x x F x x x x +=-+=++, ∴当01x <≤时,'()0F x >; ∴函数()F x 在(0,1]单调递增. ∴函数()(0)F x F > ,即()0F x >∴(0,1]x ∀∈,2ln(1)0x x x +-+>,即2ln(1)x x x +>- 令1x n =(*n ∈N ),则有2111ln 1n n n⎛⎫+>- ⎪⎝⎭.…………16分 方法三:数学归纳法 酌情给分。
数学竞赛预赛试题及答案
数学竞赛预赛试题及答案试题一:代数问题题目:解下列方程组:\[ \begin{cases}x + y = 5 \\2x - y = 1\end{cases} \]答案:首先将方程①和方程②相加,得到3x = 6,解得x = 2。
将x = 2代入方程①,得到y = 3。
因此,方程组的解为:\[ \begin{cases}x = 2 \\y = 3\end{cases} \]试题二:几何问题题目:已知直角三角形ABC,其中∠A为直角,AB = 6,AC = 8,求斜边BC的长度。
答案:根据勾股定理,直角三角形的斜边长度可以通过以下公式计算:\[ BC = \sqrt{AB^2 + AC^2} = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \]所以,斜边BC的长度为10。
试题三:数列问题题目:数列1, 1, 2, 3, 5, 8, ... 被称为斐波那契数列。
求第10项的值。
答案:斐波那契数列的定义是每一项都是前两项的和。
已知第9项为34,第8项为21,第7项为13,第6项为8,第5项为5,第4项为3,第3项为2,第2项为1,第1项为1。
根据定义,第10项为第8项和第9项的和,即:\[ 34 + 21 = 55 \]所以,斐波那契数列的第10项是55。
试题四:概率问题题目:一个袋子里有5个红球和3个蓝球,随机抽取一个球,求抽到红球的概率。
答案:总共有8个球,其中5个是红球。
抽到红球的概率是红球数量除以总球数,即:\[ P(\text{红球}) = \frac{5}{8} \]试题五:组合问题题目:有7个人参加一个会议,需要选出3个人组成一个委员会。
求不同的委员会组合数。
答案:这是一个组合问题,可以用组合公式计算:\[ C(n, k) = \frac{n!}{k!(n-k)!} \]其中n是总人数,k是委员会的人数。
将数值代入公式,得到:\[ C(7, 3) = \frac{7!}{3!(7-3)!} = \frac{7 \times 6 \times5}{3 \times 2 \times 1} = 35 \]所以,可以组成35种不同的委员会组合。
2014年全国初中数学竞赛精彩试题及问题详解
中国教育学会中学数学教学专业委员会2014年全国初中数学竞赛试题答题时注意:1.用圆珠笔或钢笔作答; 2.解答书写时不要超过装订线; 3.草稿纸不上交.一、选择题(共5小题,每小题7分,共35分.每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的.请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分)1.设非零实数a ,b ,c 满足2302340a b c a b c ++=⎧⎨++=⎩,,则222ab bc caa b c ++++的值为( ). (A )12-(B )0 (C )12(D )12.已知关于x 的不等式组255332x x x t x +⎧->-⎪⎨+⎪-<⎩,恰有5个整数解,则t 的取值范围是( ).(A )6-<t <112-(B )6-≤t <112-(C )6-<t ≤112-(D )6-≤t ≤112-3.如图,在Rt △ABC 中,已知O 是斜边AB 的中点,CD ⊥AB ,垂足为D ,DE ⊥OC ,垂足为E .若AD ,DB ,CD 的长度都是有理数,则线段OD ,OE ,DE ,AC 的长度中,不一定...是有理数的为( ).(A )OD (B )OE (C )DE(D )AC4.如图,已知△ABC 的面积为24,点D 在线段AC 上,点F 在线段BC 的延长线上,且4BC CF =,DCFE 是平行四边形,则图中阴影部分的面积为( ).(A )3 (B )4 (C )6(D )85.对于任意实数x ,y ,z ,定义运算“*”为:()()32233333451160x y x y xy x y x y +++*=+++-,且()x y z x y z **=**,则2013201232****的值为( ). (A )607967(B )1821967(C )5463967(D )16389967二、填空题(共5小题,每小题7分,共35分)6.设a =b 是a 的小数部分,c 是2a 的小数部分,则(4)b b c ++的值为 .7.一个质地均匀的正方体的六个面上分别标有数1,2,3,4,5,6.掷这个正方体三次,则其朝上的面的数和为3的倍数的概率是 .8.已知正整数a ,b ,c 满足2220+--=a b c ,2380-+=a b c ,则abc 的最大值为 .9.实数a ,b ,c ,d 满足:一元二次方程20x cx d ++=的两根为a ,b ,一元二次方程20x ax b ++=的两根为c ,d ,则所有满足条件的数组(),,,a b c d 为 .10.22121+++-…的值为 .三、解答题(共4题,每题20分,共80分)11.如图,抛物线y=23ax bx+-,顶点为E,该抛物线与x轴交于A,B两点,与y轴交于点C,且OB=OC=3OA.直线113y x=-+与y轴交于点D.求∠DBC-∠CBE.12.设△ABC的外心、垂心分别为O H、,若B C H O、、、共圆,对于所有的△ABC,求BAC∠所有可能的度数.13.如图,设点D 在△ABC 外接圆上,且为BC 的中点,点X 在BD 上,E 是AX 的中点,过△ABC 的内心I 作直线R T 平行于DE ,分别与BC ,AX 交于点R ,T ,设直线DR 与ET 交于点S .证明:点S 在△ABC 的外接圆上.14.如果将正整数M 放在正整数m 左侧,所得到的新数可被7整除,那么称M 为m 的“魔术数”(例如,把86放在415的左侧,得到的数86415能被7整除,所以称86为415的魔术数).求正整数n 的最小值,使得存在互不相同的正整数12n a a a ,,…,,满足对任意一个正整数m ,在12n a a a ,,…,中都至少有一个为m 的魔术数.中国教育学会中学数学教学专业委员会2013年全国初中数学竞赛试题参考答案一、选择题 1.A解:由已知得(234)(23)0a b c a b c a b c ++=++-++=,故2()0a b c ++=.于是2221()2ab bc ca a b c ++=-++,所以22212ab bc ca a b c ++=-++. 2.C解:根据题设知不等式组有解,解得,32t -<x <20.由于不等式组恰有5个整数解,这5个整数解只能为15,16,17,18,19,因此14≤32t -<15,解得6-<t ≤112-. 3.D解:因AD ,DB ,CD 的长度都是有理数,所以,OA =OB =OC =2AD BD+是有理数.于是,OD =OA -AD 是有理数.由Rt △DOE ∽Rt △COD ,知2OD OE OC =,·DC DODE OC=都是有理数,而AC=不一定是有理数.4.C解:因为DCFE 是平行四边形,所以DE //CF ,且EF //DC .连接CE ,因为DE //CF ,即DE //BF ,所以S △DEB = S △DEC ,因此原来阴影部分的面积等于△ACE 的面积.连接AF ,因为EF //CD ,即EF //AC ,所以S △ACE = S △ACF .因为4BC CF =,所以S △ABC = 4S △ACF .故阴影部分的面积为6.5.C解:设201320124m ***=,则()20132012433m ****=*32323339274593316460m m m m m m ⨯+⨯+⨯+==++++-, 于是()201320123292****=*3223333923929245546310360967⨯⨯+⨯⨯+⨯+==+-.二、填空题 6.2解:由于2123a a <<<<,故1=-b a ,22=-c a .所以223(4)(1)(124)(1)(1)12b b c a a a a a a a ++=--+-+=-++=-=.7.13解:掷三次正方体,朝上的面的数和为3的倍数的是3,6,9,12,15,18,且3=1+1+1,6=1+1+4=1+2+3=2+2+2,9=1+2+6=1+3+5=1+4+4=2+2+5=2+3+4=3+3+3, 12=1+5+6=2+4+6=2+5+5=3+3+6=3+4+5=4+4+4, 15=3+6+6=4+5+6=5+5+5, 18=6+6+6.记掷三次正方体面朝上的数分别为x ,y ,z .则使x +y +z 为3的倍数的(x ,y ,z )中,3个数都不相等的有8组,恰有两个相等的有6组,3个数都相等的有6组.故所求概率为83263616663⨯⨯+⨯+=⨯⨯.8.2013解:由已知2220+--=a b c ,2380-+=a b c 消去c ,并整理得()228666b a a -++=.由a 为正整数及26a a +≤66,可得1≤a ≤3.若1a =,则()2859b -=,无正整数解; 若2a =,则()2840b -=,无正整数解;若3a =,则()289b -=,于是可解得11=b ,5b =. (i )若11b =,则61c =,从而可得311612013abc =⨯⨯=; (ii )若5b =,则13c =,从而可得3513195abc =⨯⨯=. 综上知abc 的最大值为2013.9.(1212),,,--,(00),,,-t t (t 为任意实数) 解:由韦达定理得,,,.+=-⎧⎪=⎪⎨+=-⎪=⎪⎩a b c ab d c d a cd b 由上式,可知b a c d =--=.若0b d =≠,则1==d a b ,1==bc d ,进而2b d a c ==--=-.若0b d ==,则c a =-,有()(00),,,,,,=-a b c d t t (t 为任意实数). 经检验,数组(1212)--,,,与(00),,,-t t (t 为任意实数)满足条件. 10.200解:设0k >,那么=11111(1)1k k k k ⎤⎫=+=+-⎪⎥++⎝⎭⎣⎦. 上式对1=k ,2,…,99求和,得原式11991100100100⎫⎫=+-=-=⎪⎪⎝⎭⎝⎭.三、解答题11.解:将0x =分别代入y =113x -+,23y ax bx =+-知,D (0,1),C (0,3-),所以B (3,0),A (1-,0).直线y =113x -+过点B .将点C (0,3-)的坐标代入y =(1)(3)a x x +-,得1a =.…………5分抛物线223y x x =--的顶点为E (1,4-).于是由勾股定理得BC=CE,BE=因为BC 2+CE 2=BE 2,所以,△BCE 为直角三角形,90BCE ∠=︒.…………10分因此tan CBE ∠=CE CB =13.又tan ∠DBO =13OD OB =,则∠DBO =CBE ∠.所以,45DBC CBE DBC DBO OBC ∠-∠=∠-∠=∠=︒.…………20分12.解:分三种情况讨论. (i )若△ABC 为锐角三角形.因为1802B HC A B OC A ∠=︒-∠∠=∠,,所以由BHC BOC ∠=∠,可得1802A A ︒-∠=∠,于是60A ∠=︒.…………5分(ii )若△ABC 为钝角三角形.当90A ∠>︒时,因为()1802180BHC A BOC A ∠=︒-∠∠=︒-∠,,所以由180BHC BOC ∠+∠=︒,可得()3180180A ︒-∠=︒,于是120A ∠=︒;当90A ∠<︒时,不妨假设90B ∠>︒,因为2BHC A BOC A ∠=∠∠=∠,,所以由180BHC BOC ∠+∠=︒,可得3180A ∠=︒,于是60A ∠=︒.…………15分(iii )若△ABC 为直角三角形.当90A ∠=︒时,因为O 为边BC 的中点,B C H O ,,,不可能共圆,所以A ∠不可能等于90︒;当90A ∠<︒时,不妨假设90B ∠=︒,此时点B 与H 重合,于是总有B C H O ,,,共圆,因此A ∠可以是满足090A ︒<∠<︒的所有角.综上可得,A ∠所有可能取到的度数为所有锐角及120︒.…………20分13.证明:如图,设DR 与△ABC 的外接圆交于点S ',AX 与S E '交于点T ',连接S C CD S A AE AD '',,,,.由D 为BC 的中点知,A ,I ,D 三点共线,且∠CS D '=∠RCD ,△S CD '∽△CRD ,所以S D CDCD RD'=, ①即2CD S D RD '=⋅. ②…………5分由E 为AX 的中点知,∠AS E '=∠T AE ',△AS E '∽△T AE ',所以S E AEAE T E'=', ③ 即2AE S E T E ''=⋅. ④由IR ∥DE ,知180IRD S'DE S'AE ∠=︒-∠=∠.又因为IDR S DA S EA ''∠=∠=∠,所以△IRD ∽△S AE ',则有ID S ERD AE'=. ⑤ …………10分由I 为△ABC 的内心,连接CI ,由CID CAI ACI DCB BCI ICD ∠=∠+∠=∠+∠=∠知ID CD =.由式①,⑤,得S D S ECD AE''=, 即S D CDS E AE'='. ⑥ 由式②,④,得22CD S D RDAE S E T E'⋅=''⋅. ⑦ 由式⑥,⑦得S D RDS E T E'='', …………15分于是RT '∥DE .又RT ∥DE ,故点T '与T 重合,即点S '在直线ET 上.从而,点S '与S 重合,即点S 在△ABC 的外接圆上.…………20分14.解:若n ≤6,取m =1,2,…,7,根据抽屉原理知,必有12na a a ,,…,中的一个正整数M 是(1i j ,≤i <j ≤7)的公共的魔术数,即7|(10M i +),7|(10M j +).则有7|(j i -),但0<j i -≤6,矛盾.故n ≥7.…………10分又当12n a a a ,,…,为1,2,…,7时,对任意一个正整数m ,设其为k 位数(k 为正整数).则10k i m +(12i =,,…,7)被7除的余数两两不同.若不然,存在正整数i ,(1j ≤i <j ≤7),满足7|[(10)(10)]k k j m i m +-+,即7|10()kj i -,从而7|()j i -,矛盾.故必存在一个正整数i (1≤i ≤7),使得7|(10)k i m +,即i 为m 的魔术数. 所以,n 的最小值为7.…………20分。
2014年全国初中数学竞赛试题及答案
中国教育学会中学数学教学专业委员会2014年全国初中数学竞赛试题答题时注意:1.用圆珠笔或钢笔作答; 2.解答书写时不要超过装订线; 3.草稿纸不上交.一、选择题(共5小题,每小题7分,共35分.每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的.请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分)1.设非零实数a ,b ,c 满足2302340a b c a b c ++=⎧⎨++=⎩,,则222ab bc caa b c ++++的值为( ). (A )12-(B )0 (C )12(D )12.已知关于x 的不等式组255332x x x t x +⎧->-⎪⎨+⎪-<⎩,恰有5个整数解,则t 的取值范围是( ).(A )6-<t <112-(B )6-≤t <112-(C )6-<t ≤112-(D )6-≤t ≤112-3.如图,在Rt △ABC 中,已知O 是斜边AB 的中点,CD ⊥AB ,垂足为D ,DE ⊥OC ,垂足为E .若AD ,DB ,CD 的长度都是有理数,则线段OD ,OE ,DE ,AC 的长度中,不.一定..是有理数的为( ). (A )OD (B )OE (C )DE(D )AC4.如图,已知△ABC 的面积为24,点D 在线段AC 上,点F 在线段BC 的延长线上,且4BC CF =,DCFE 是平行四边形,则图中阴影部分的面积为( ).(A )3 (B )4 (C )6(D )85.对于任意实数x ,y ,z ,定义运算“*”为:()()32233333451160x y x y xy x y x y +++*=+++-,且()x y z x y z **=**,则2013201232****的值为( ). (A )607967(B )1821967(C )5463967(D )16389967二、填空题(共5小题,每小题7分,共35分)6.设33a =,b 是a 的小数部分,c 是2a 的小数部分,则(4)b b c ++的值为 .7.一个质地均匀的正方体的六个面上分别标有数1,2,3,4,5,6.掷这个正方体三次,则其朝上的面的数和为3的倍数的概率是 .8.已知正整数a ,b ,c 满足2220+--=a b c ,2380-+=a b c ,则abc 的最大值为 .9.实数a ,b ,c ,d 满足:一元二次方程20x cx d ++=的两根为a ,b ,一元二次方程20x ax b ++=的两根为c ,d ,则所有满足条件的数组(),,,a b c d 为 .10.444444222222121231991001121231991001++++++++++-+-+-…的值为 .三、解答题(共4题,每题20分,共80分)11.如图,抛物线y=23ax bx+-,顶点为E,该抛物线与x轴交于A,B两点,与y轴交于点C,且OB=OC=3OA.直线113y x=-+与y轴交于点D.求∠DBC ∠CBE.12.设△ABC的外心、垂心分别为O H、,若B C H O、、、共圆,对于所有的△ABC,求BAC∠所有可能的度数.13.如图,设点D 在△ABC 外接圆上,且为BC 的中点,点X 在BD 上,E 是AX 的中点,过△ABC 的内心I 作直线R T 平行于DE ,分别与BC ,AX 交于点R ,T ,设直线DR 与ET 交于点S .证明:点S 在△ABC 的外接圆上.14.如果将正整数M 放在正整数m 左侧,所得到的新数可被7整除,那么称M 为m 的“魔术数”(例如,把86放在415的左侧,得到的数86415能被7整除,所以称86为415的魔术数).求正整数n 的最小值,使得存在互不相同的正整数12n a a a ,,…,,满足对任意一个正整数m ,在12n a a a ,,…,中都至少有一个为m 的魔术数.中国教育学会中学数学教学专业委员会2013年全国初中数学竞赛试题参考答案一、选择题 1.A解:由已知得(234)(23)0a b c a b c a b c ++=++-++=,故2()0a b c ++=.于是2221()2ab bc ca a b c ++=-++,所以22212ab bc ca a b c ++=-++. 2.C解:根据题设知不等式组有解,解得,32t -<x <20.由于不等式组恰有5个整数解,这5个整数解只能为15,16,17,18,19,因此14≤32t -<15,解得6-<t ≤112-. 3.D解:因AD ,DB ,CD 的长度都是有理数,所以,OA =OB =OC =2AD BD+是有理数.于是,OD =OA -AD 是有理数.由Rt △DOE ∽Rt △COD ,知2OD OE OC =,·DC DODE OC =都是有理数,而AC=·AD AB 不一定是有理数. 4.C解:因为DCFE 是平行四边形,所以DE //CF ,且EF //DC .连接CE ,因为DE //CF ,即DE //BF ,所以S △DEB = S △DEC ,因此原来阴影部分的面积等于△ACE 的面积.连接AF ,因为EF //CD ,即EF //AC ,所以S △ACE = S △ACF .因为4BC CF =,所以S △ABC = 4S △ACF .故阴影部分的面积为6.5.C解:设201320124m ***=,则()20132012433m ****=*32323339274593316460m m m m m m ⨯+⨯+⨯+==++++-, 于是()201320123292****=*3223333923929245546310360967⨯⨯+⨯⨯+⨯+==+-.二、填空题 6.2解:由于2123a a <<<<,故1=-b a ,22=-c a .所以223(4)(1)(124)(1)(1)12b b c a a a a a a a ++=--+-+=-++=-=.7.13解:掷三次正方体,朝上的面的数和为3的倍数的是3,6,9,12,15,18,且3=1+1+1,6=1+1+4=1+2+3=2+2+2,9=1+2+6=1+3+5=1+4+4=2+2+5=2+3+4=3+3+3, 12=1+5+6=2+4+6=2+5+5=3+3+6=3+4+5=4+4+4, 15=3+6+6=4+5+6=5+5+5, 18=6+6+6.记掷三次正方体面朝上的数分别为x ,y ,z .则使x +y +z 为3的倍数的(x ,y ,z )中,3个数都不相等的有8组,恰有两个相等的有6组,3个数都相等的有6组.故所求概率为83263616663⨯⨯+⨯+=⨯⨯.8.2013解:由已知2220+--=a b c ,2380-+=a b c 消去c ,并整理得()228666b a a -++=.由a 为正整数及26a a +≤66,可得1≤a ≤3.若1a =,则()2859b -=,无正整数解; 若2a =,则()2840b -=,无正整数解;若3a =,则()289b -=,于是可解得11=b ,5b =. (i )若11b =,则61c =,从而可得311612013abc =⨯⨯=; (ii )若5b =,则13c =,从而可得3513195abc =⨯⨯=. 综上知abc 的最大值为2013.9.(1212),,,--,(00),,,-t t (t 为任意实数) 解:由韦达定理得,,,.+=-⎧⎪=⎪⎨+=-⎪=⎪⎩a b c ab d c d a cd b 由上式,可知b a c d =--=.若0b d =≠,则1==d a b ,1==bc d ,进而2b d a c ==--=-.若0b d ==,则c a =-,有()(00),,,,,,=-a b c d t t (t 为任意实数). 经检验,数组(1212)--,,,与(00),,,-t t (t 为任意实数)满足条件. 10解:设0k >,那么=11111(1)1k k k k ⎤⎫=+=+-⎪⎥++⎝⎭⎣⎦. 上式对1=k ,2,…,99求和,得原式11991100100100⎫⎫=+-=-=⎪⎪⎝⎭⎝⎭.三、解答题11.解:将0x =分别代入y =113x -+,23y ax bx =+-知,D (0,1),C (0,3-),所以B (3,0),A (1-,0).直线y =113x -+过点B .将点C (0,3-)的坐标代入y =(1)(3)a x x +-,得1a =.…………5分抛物线223y x x =--的顶点为E (1,4-).于是由勾股定理得BC =32,CE =2,BE =25. 因为BC 2+CE 2=BE 2,所以,△BCE 为直角三角形,90BCE ∠=︒.…………10分因此tan CBE ∠=CE CB =13.又tan ∠DBO =13OD OB =,则∠DBO =CBE ∠.所以,45DBC CBE DBC DBO OBC ∠-∠=∠-∠=∠=︒.…………20分12.解:分三种情况讨论. (i )若△ABC 为锐角三角形.因为1802BHC A BOC A ∠=︒-∠∠=∠,,所以由BHC BOC ∠=∠,可得1802A A ︒-∠=∠,于是60A ∠=︒.…………5分(ii )若△ABC 为钝角三角形.当90A ∠>︒时,因为()1802180BHC A BOC A ∠=︒-∠∠=︒-∠,,所以由180BHC BOC ∠+∠=︒,可得()3180180A ︒-∠=︒,于是120A ∠=︒;当90A ∠<︒时,不妨假设90B ∠>︒,因为2BHC A BOC A ∠=∠∠=∠,,所以由180BHC BOC ∠+∠=︒,可得3180A ∠=︒,于是60A ∠=︒.…………15分(iii )若△ABC 为直角三角形.当90A ∠=︒时,因为O 为边BC 的中点,B C H O ,,,不可能共圆,所以A ∠不可能等于90︒;当90A ∠<︒时,不妨假设90B ∠=︒,此时点B 与H 重合,于是总有B C H O ,,,共圆,因此A ∠可以是满足090A ︒<∠<︒的所有角.综上可得,A ∠所有可能取到的度数为所有锐角及120︒.…………20分13.证明:如图,设DR 与△ABC 的外接圆交于点S ',AX 与S E '交于点T ',连接S C CD S A AE AD '',,,,.由D 为BC 的中点知,A ,I ,D 三点共线,且∠CS D '=∠RCD ,△S CD '∽△CRD ,所以S D CDCD RD'=, ① 即2CD S D RD '=⋅. ②…………5分由E 为AX 的中点知,∠AS E '=∠T AE ',△AS E '∽△T AE ',所以S E AEAE T E'=', ③ 即2AE S E T E ''=⋅. ④由IR ∥DE ,知180IRD S'DE S'AE ∠=︒-∠=∠.又因为IDR S DA S EA ''∠=∠=∠,所以△IRD ∽△S AE ',则有ID S ERD AE'=. ⑤ …………10分由I 为△ABC 的内心,连接CI ,由CID CAI ACI DCB BCI ICD ∠=∠+∠=∠+∠=∠知ID CD =.由式①,⑤,得S D S ECD AE''=, 即S D CDS E AE'='. ⑥ 由式②,④,得22CD S D RDAE S E T E'⋅=''⋅. ⑦ 由式⑥,⑦得S D RDS E T E'='', …………15分于是RT '∥DE .又RT ∥DE ,故点T '与T 重合,即点S '在直线ET 上.从而,点S '与S 重合,即点S 在△ABC 的外接圆上.…………20分14.解:若n ≤6,取m =1,2,…,7,根据抽屉原理知,必有12na a a ,,…,中的一个正整数M 是(1i j ,≤i <j ≤7)的公共的魔术数,即7|(10M i +),7|(10M j +).则有7|(j i -),但0<j i -≤6,矛盾.故n ≥7.…………10分又当12n a a a ,,…,为1,2,…,7时,对任意一个正整数m ,设其为k 位数(k 为正整数).则10k i m +(12i =,,…,7)被7除的余数两两不同.若不然,存在正整数i ,(1j ≤i <j ≤7),满足7|[(10)(10)]k k j m i m +-+,即7|10()k j i -,从而7|()j i -,矛盾.故必存在一个正整数i (1≤i ≤7),使得7|(10)k i m +,即i 为m 的魔术数. 所以,n 的最小值为7.…………20分。
2014年全国高中数学联赛福建省预赛试题及详解
2014年福建省高中数学竞赛暨2014年全国高中数学联赛(福建省赛区)预赛试卷(考试时间:2014年5月17日上午9:00-11:30,满分160分)一、填空题(共10小题,每小题6分,满分60分。
请直接将答案写在题中的横线上) 1.已知直线1l :260ax y ++=,2l :2(1)10x a y a +-+-=,若12l l ⊥,则a = 。
2.函数2()sin cos 2f x x x x =+-(122x ππ⎡⎤∈⎢⎥⎣⎦,)的值域为 。
3.在三棱锥D ABC -中,2AB BC ==,AB BC ⊥,BC CD ⊥,DA AB ⊥,60CDA ∠=︒。
则三棱锥D ABC -的体积为 。
4.已知1F 、2F 为双曲线C :22124y x -=的左、右焦点,P 为双曲线C 上一点,且点P 在第一象限。
若1243PF PF =,则12PF F △内切圆半径为 。
5.已知集合{}2280A x x x =+->,{}2240B x x ax =-+≤。
若0a >,且A B ⋂中恰有1个整数,则a 的取值范围为 。
6.若分数p q (p ,q 为正整数)化成小数为0.198pq=,则当q 取最小值时,p q += 。
7.随机地投掷3粒骰子,则其中有2粒骰子出现的点数之和为7的概率为 。
8.已知点(11)A -,,(40)B ,,(22)C ,。
平面区域D 由所有满足AP AB AC λμ=+(1a λ<≤,1b μ<≤)的点()P x y ,组成的区域。
若区域D 的面积为8,则a b +的最小值为 。
9. 23201488889999A ⎡⎤⎡⎤⎡⎤⎡⎤=++++⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦被63除的余数为 。
(符号[]x 表示不超过x 的最大整数。
)10.若a ,b ,c 为关于x 的方程320x x x m --+=的三个实根,则m 的最小值为 。
二、解答题(共5小题,每小题20分,满分100分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014数学预赛试题分类:概率与期望
河北3、某植物种子的发芽率为0.8,种子的成苗率为0.6,现有100粒已发芽的种子用来育苗,这些种子
成苗的期望是 。
辽宁9.甲乙两人进行乒乓球比赛,约定每局胜者得1分,负者得0分,比赛进行到有一人比对方多2分
或打满6局时停止.设甲在每局中获胜的概率为
23,乙在每局中获胜的概率为1
3
,且各局胜负相互独立,则比赛停止时已打局数ξ的期望()E ξ为 .
吉林4、某地举行一次民歌大奖赛,六个省各有一对歌手参加决赛,现要选出4名优胜者。
则选出的4名
中恰只有两个人是同一省份的歌手的概率为( )
山东8、甲、乙两人轮流掷一枚骰子,甲先掷,规定:若甲掷到1点,则甲继续掷,否则由乙掷;若乙掷
到3点,则乙继续掷,否则由甲掷。
两人始终按此规则进行。
则第n 次是甲掷的概率P n = 。
福建7.随机地投掷3粒骰子,则其中有2粒骰子出现的点数之和为7的概率为 。
河南8、某次世界杯上,巴西队遇到每个对手获胜的概率为
21,打平的概率为31 ,输的概率为6
1
,获胜一场得3分,平一场得1分,负一场得0分。
已知小组赛每支球队需打三场比赛,获得4分以上(含4分)即可小组出线。
已知淘汰赛双方打平需互罚点球,巴西队点球获胜的概率为5
3
,则巴西队获得最后的冠军且四场淘汰赛中恰有一场点球的概率为 。
湖北8. 三对夫妻排成一排照相,仅有一对夫妻相邻的概率为 陕西6、
甘肃5、AFS 国际文化交流组织拟将18个中学生交流项目的名额分配给4所学校,要求每校至少有一个名
额且各校分配的名额互不相等,则不同的分配方法种数为 。
黑7、身穿红、黄两种颜色衣服的各有两人,身穿蓝颜色衣服的有一人,现将这五人排成一行,要求穿相
同颜色衣服的人不能相邻,则不同的排法共有 种。
A 、24 B 、28 C 、36 D 、48
黑19、在某批次的某种灯泡中,随机地抽取个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于天的灯泡是优
(1)根据频率分布表中的数据,写出、的值;
(2)某人从灯泡样品中随机地购买了个,如果这个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求的最小值;
(3)某人从这个批次的灯泡中随机地购买了个进行使用,若上述频率作为概率,用表示此人所购买的灯泡中次品的个数,求的分布列和数学期望.
江苏5、已知5件产品中有3件合格品,2件次品。
每次任取一个检验,检验后不再放回,恰好经过3次检验找出2件次品的概率为。
贵州4.某种电路开关闭合后,会出现闪动的红灯或绿灯.已知开关第一次闭合,出现红灯和出现绿灯的
概率都是1
2
,从开关第二次闭合起,若前次出现红灯,则下次出现红灯的概率是
1
3
,出现绿灯
的概率是2
3
;若前次出现绿灯,则下次出现红灯的概率是
3
5
,出现绿灯的概率是
2
5
.则开关第3
次闭合后出现红灯的概率是.
安徽8. 从正12边形的顶点中取出4个顶点,它们两两不相邻的概率是___________.
浙江17.有一快递公司承担某地区13个城市之间的快递业务,如果每个快递员最多只能承接4个城市之间的快递业务,要使每两个城市之间至少有1名快递员,那么此快递公司最少需要____名快递员.湖南11.随机挑选一个三位数I,则I含有因子5的概率为.
全国8、。
