Newton迭代法求解非线性方程
求解非线性方程的三种新的迭代法

求解非线性方程的三种新的迭代法
迭代法是一种通过迭代逼近的方式来求解方程的方法。
它的基本思想是通过不断逼近
方程的解,使得逼近值与真实解的差距越来越小,最终得到方程的解。
下面介绍三种新的迭代法:牛顿迭代法,弦截法和切线法。
一、牛顿迭代法
牛顿迭代法是一种通过利用函数导数的信息来逼近方程解的方法。
它的迭代公式为:
x_(n+1) = x_n - f(x_n)/f'(x_n)
x_n表示第n次迭代得到的逼近解,f(x_n)表示在x_n处的函数值,f'(x_n)表示在x_n 处的导数值。
牛顿迭代法的优点是收敛速度快,通常是二阶收敛,但其缺点是需要计算函数的导数,如果导数计算困难或者导数为零的情况下,该方法可能不适用。
二、弦截法
三、切线法
切线法的优点和牛顿迭代法类似,但其缺点是需要计算函数的导数,且对于初始逼近
解的选择比较敏感。
牛顿迭代法、弦截法和切线法都是三种常用的非线性方程迭代法。
它们各自有着优点
和缺点,适用的领域和条件也不尽相同。
在实际问题中,需要根据具体情况选择合适的方
法来求解非线性方程。
非线性方程求根—牛顿迭代法(新)

非线性方程求根——牛顿迭代法一、牛顿迭代法的基本思想基本思想:将非线性方程逐步归结为某种线性方程求解。
设方程f (x )=0有近似根x k (f `(x k )≠0),将f (x )在x k 展开:(ξ在x 和x k 之间)2()()()()()()2!k k k k f f x f x f x x x x x ξ'''=+-+-()()()()k k k f x f x f x x x '≈+-可设记该线性方程的根为x k +1,则()()()0k k k f x f x x x '+-=1()()k k k k f x x x f x +=-'故f (x )=0可近似表示为即为Newton 法迭代格式。
(k =0,1,……)例:用Newton 迭代法求方程310x x --=在x 0=1.5附近的近似实根。
解:32()1,()31f x x x f x x '=--=-迭代公式为312131kk k k k x x x x x +--=--计算步骤如下:(1)取初值x 0=1.5;(2)按照迭代公式计算x 1;(3)若|x 1-x 0|<=0.00001,终止迭代;否则,x 0=x 1;转(2);(4)输出迭代次数和近似根.二、牛顿迭代法的实现MATLAB求解程序设计:方程及一阶导数函数:function[fun,dfun]=fun0(x)fun=x^3-x-1;%求原函数的值dfun=3*x^2-1;%求一阶导数的值计算主程序:clearx0=1.5;[fun,dfun]=fun0(x0);x1=x0-fun/dfun;i=1;while abs(x1-x0)>1e-5x0=x1;[fun,dfun]=fun0(x0);x1=x0-fun/dfun;i=i+1;enddisp('the solution is x1=')x1disp('the iter time is ')i计算结果为:the solution is x1=x1 =1.3247the iter time isi =4可见经过4次迭代即到达要求的精度,原方程的一个近似实数根为1.3247.三、牛顿迭代法的收敛性牛顿迭代法的迭代函数:)()()(x f x f x x '-=ϕ222)]([)()()]([)()()]([1)(x f x f x f x f x f x f x f x '''='''-'-='ϕ设f (x *)=0,f `(x *)≠0,则ϕ`(x *)=0,故Newton 迭代法在x *附近至少平方收敛。
解非线性方程的牛顿迭代法及其应用

解非线性方程的牛顿迭代法及其应用一、本文概述非线性方程是数学领域中的一个重要研究对象,其在实际应用中广泛存在,如物理学、工程学、经济学等领域。
求解非线性方程是一个具有挑战性的问题,因为这类方程往往没有简单的解析解,需要通过数值方法进行求解。
牛顿迭代法作为一种古老而有效的数值求解方法,对于求解非线性方程具有重要的应用价值。
本文旨在介绍牛顿迭代法的基本原理、实现步骤以及在实际问题中的应用。
我们将详细阐述牛顿迭代法的基本思想,包括其历史背景、数学原理以及收敛性分析。
我们将通过具体实例,展示牛顿迭代法的计算步骤和实际操作过程,以便读者能够更好地理解和掌握该方法。
我们将探讨牛顿迭代法在各个领域中的实际应用,包括其在物理学、工程学、经济学等领域中的典型应用案例,以及在实际应用中可能遇到的问题和解决方法。
通过本文的介绍,读者可以深入了解牛顿迭代法的基本原理和应用技巧,掌握其在求解非线性方程中的实际应用方法,为进一步的研究和应用提供有力支持。
二、牛顿迭代法的基本原理牛顿迭代法,又称为牛顿-拉夫森方法,是一种在实数或复数域上近似求解方程的方法。
其基本原理是利用泰勒级数的前几项来寻找方程的根。
如果函数f(x)在x0点的导数f'(x0)不为零,那么函数f(x)在x0点附近可以用一阶泰勒级数来近似表示,即:这就是牛顿迭代法的基本迭代公式。
给定一个初始值x0,我们可以通过不断迭代这个公式来逼近f(x)的根。
每次迭代,我们都用当前的近似值x0来更新x0,即:这个过程一直持续到满足某个停止条件,例如迭代次数达到预设的上限,或者连续两次迭代的结果之间的差小于某个预设的阈值。
牛顿迭代法的收敛速度通常比线性搜索方法快,因为它利用了函数的导数信息。
然而,这种方法也有其局限性。
它要求函数在其迭代点处可导,且导数不为零。
牛顿迭代法可能不收敛,如果初始点选择不当,或者函数有多个根,或者根是重根。
因此,在使用牛顿迭代法时,需要谨慎选择初始点,并对迭代过程进行适当的监控和调整。
牛顿迭代法求解非线性方程组的解

10 简化牛顿法 简化牛顿法又称平行弦法,其迭代公式为
xk1 xk Cf (xk ),C 0, k 0,1,
(4-7)
从不动点迭代法的角度看,简化牛顿法的迭代函数(x) x Cf (x) ,下面讨论简
化牛顿法的收敛性。
若| '(x) ||1 Cf '(x) | 1 ,即取 0 Cf ' (x) 2 .在根 x* 附近成立,则迭代法
x k 的点 Pk 引切线,并将该切线与 x 轴的交点的横坐标 x k1 作为 x* 的新的近似值。 注意到切线方程为
y f (xk ) f '(xk )(x xk )
(4-4)
这样求得的值 x k1 比满足 f (xk ) f '(xk )(x xk ) 0 ,从而就是牛顿公式
x
k 1
| f (xk1) || f (xk ) |
(4-8)
满足此要求的算法称为下山法。
将牛顿法和下山法一起使用时,即在下山法保证函数值稳定下降的前提下,
用牛顿法加快收敛速度。为此,为此将牛顿法的计算结果
xk 1
xk
f (xk ) f ' (xk )
(4-9)
与前一步的近似值 xk 的适当加权平均作为新的改进值
代法中所遇到的 jacobi 矩阵难求的问题。
关键词:非线性方程组、牛顿迭代法、MATLAB、 jacobi 矩阵
一、前言 非线性方程组在实际问题中经常出现,并且在科学与工程计算中的地位越来
越来重要,很多常见的线性模型都是在一定条件下由非线性问题简化得到的,为 得到更符合实际的解答,往往需要直接研究非线性模型,然而从线性到非线性是 一个质的飞跃,方程的性质的不同,所以求解方法也有很大差别。本文主要介绍 关于非线性方程及方程组的数值解法,先分析非线性方程的数值解法,然后再延 伸到方程组的解法。
非线性方程组求解的牛顿迭代法用MATLAB实现

非线性方程组求解的牛顿迭代法用MATLAB实现首先,我们需要定义非线性方程组。
假设我们要求解方程组:```f1(x1,x2)=0f2(x1,x2)=0```其中,`x1`和`x2`是未知数,`f1`和`f2`是非线性函数。
我们可以将这个方程组表示为向量的形式:```F(x)=[f1(x1,x2);f2(x1,x2)]=[0;0]```其中,`F(x)`是一个列向量。
为了实现牛顿迭代法,我们需要计算方程组的雅可比矩阵。
雅可比矩阵是由方程组的偏导数组成的矩阵。
对于方程组中的每个函数,我们可以计算其对每个变量的偏导数,然后将这些偏导数组成一个矩阵。
在MATLAB中,我们可以使用`jacobi`函数来计算雅可比矩阵。
以下是一个示例函数的定义:```matlabfunction J = jacobi(x)x1=x(1);x2=x(2);J = [df1_dx1, df1_dx2; df2_dx1, df2_dx2];end```其中,`x`是一个包含未知数的向量,`df1_dx1`和`df1_dx2`是`f1`对`x1`和`x2`的偏导数,`df2_dx1`和`df2_dx2`是`f2`对`x1`和`x2`的偏导数。
下一步是实现牛顿迭代法。
牛顿迭代法的迭代公式为:```x(k+1)=x(k)-J(x(k))\F(x(k))```其中,`x(k)`是第`k`次迭代的近似解,`\`表示矩阵的求逆操作。
在MATLAB中,我们可以使用如下代码来实现牛顿迭代法:```matlabfunction x = newton_method(x_initial)max_iter = 100; % 最大迭代次数tol = 1e-6; % 收敛阈值x = x_initial; % 初始解for k = 1:max_iterF=[f1(x(1),x(2));f2(x(1),x(2))];%计算F(x)J = jacobi(x); % 计算雅可比矩阵 J(x)delta_x = J \ -F; % 计算增量 delta_xx = x + delta_x; % 更新 xif norm(delta_x) < tolbreak; % 达到收敛条件,停止迭代endendend```其中,`x_initial`是初始解的向量,`max_iter`是最大迭代次数,`tol`是收敛阈值。
用Matlab编写二分法和Newton迭代法求解非线性函数
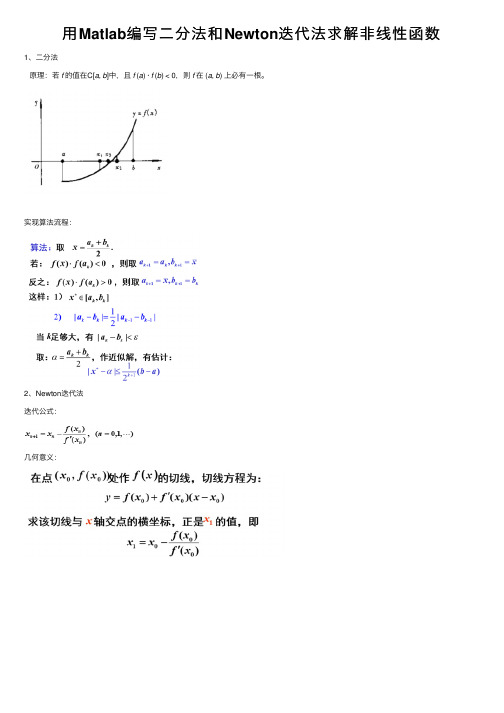
⽤Matlab编写⼆分法和Newton迭代法求解⾮线性函数1、⼆分法原理:若f的值在C[a, b]中,且f (a) · f (b) < 0,则f在 (a, b) 上必有⼀根。
实现算法流程:2、Newton迭代法迭代公式:⼏何意义:3、求解问题⽤Newton法和⼆分法求的解。
4、代码实现1 clear;close;clc2 a=0;b=1;%根区间3 e=10^(-6);%根的容许误差4 [X , N]=dichotomy(e,a,b);%⼆分法5 p0=0.5;%初始值6 N=15;%迭代次数7 [X1]=Newdon(p0,e,N);%Newton迭代法89 function [X , N]=dichotomy(deta,a,b)10 % 函数dichotomy:⼆分法11 %输⼊值:12 %fun:⽅程函数13 %deta:根的容许误差14 %有根区间:[a,b]15 %输出值16 %X:求解到的⽅程的根17 %N:总的迭代次数18 N=1+fix(log2((b-a)/deta));%由公式7.2求得,取整数|X_N-X*|<=(b-a)/2^N<deta,求N19 n=1;20 f1=myfunction(a);21 f2=myfunction(b);22if (f1*f2>0)23 disp('根不在输⼊的区间⾥,请重新输⼊区间');24else25while n <= N26 x=(a+b)/2;27if myfunction(a)*myfunction(x)>028 a=x;29else30 b=x;31 end32 n=n+1;33 end34 X=x;35 fprintf('第%d次⼆分法求出的⽅程的根:\n',N);36 fprintf('X=\n');37 disp(X);38 end39 end4041 function [P]=Newdon(p0,TOL,N)42 %求⽅程组的解43 %输⼊参数44 %初始值:p045 %误差容限:TOL46 %最⼤迭代次数:N47 %输出参数:48 %⽅程近似解:p49 %或失败信息“Method failed”50 format long;51 n=1;%初始迭代次数52 syms x;53while n<=N54if abs(subs(diff(myfunction(x)),x,p0))<TOL55 P=p0;56break;57else58if subs(diff(myfunction(x),2),x,p0)==059 disp('Method failed');60break;61else62 p=p0-myfunction(p0)/subs(diff(myfunction(x)),x,p0);63 p=eval(p);%将exp的值转为⼩数值64if(abs(p-p0)<TOL)65 P=p;66break;67else68 p0=p;69 end70 end71 end72 n=n+1;73 end74 % P=vpa(P,10);%将分数转为⼩数并保留8位⼩数75 fprintf('第%d次NeWton迭代法求出的⽅程的根:\n',N);76 fprintf('P=\n');77 disp(P);78 end7980 function f=myfunction(x)81 f=x*exp(x)-1;82 end5、求解结果。
求解非线性方程组的几种方法及程序实现
求解非线性方程组的几种方法及程序实现
求解非线性方程组一直是理论数学和应用数学研究的重点,并采用不同的方法得到准确的结果。
它们可以分为几种类型:
1. 用以绘图的方法解非线性方程组:该方法充分利用结合几何和数理的原理,给出非线性方程组的解,而不用对系数的解的表达式求解手段。
主要是利用可绘图的几何空间分析,它可以帮助理解问题本身,还可以很容易看出非线性方程组的解。
2. 用迭代法求解非线性方程组:这是一种常用的方法,它通过不断迭代收敛求解非线性方程组。
基本思想是通过构造一个迭代函数,其初始值和原始非线性方程组尽可能接近,然后不断迭代收敛求解非线性方程组。
3. 用强调法求解非线性方程系统:这是基于梯度的一种方法,它利用一个概念,即局部线性化,可以降低维数、转化为一个拐点,最后强化搜索全局解。
4. 用牛顿-拉夫逊方法求解非线性方程组:这是一种准确、快速的非线性方程组求解方法,主要利用牛顿迭代法搜索解的收敛性,加上一些拉夫逊的加速策略得到最终的结果。
5. 用幂法求解非线性方程组:幂法也称为指数序列,是一种重要的求解非线性方程组的方法,基本原理是利用指数的累加和误差的减少,从而最终得到非线性方程组的解。
6. 用逐步逼近法求解非线性方程组:逐步逼近法也称为分步变程法,是一种用于求解非线性方程组的简单方法,其基本思想是用不同的参数,在给定的范围内,逐步逼近目标解。
这些方法的程序实现略有不同,可以利用编程语言比如C、Fortran、Python等,编写程序完成求解。
可以采用函数求解、循环求解、行列式求解或者混合的算法等不同的方式实现,甚至可以用深度学习方法求解有些复杂的非线性方程组。
newton迭代法11-12
若f(a)f(x0)<0 成立,则根必在区间(a, x0)内,取a1=a,b1= x0;否则 必在区间(x0,b)内,取a1= x0,b1=b,
这样,得到新区间(a1,b1),其长度为[a,b]的一半,如此继续下去,进 行k次等分后,得到一组不断缩小的区间,[a,b],[a1,b1],......[ak,bk].
( x*)
2!
( x x*) 2
( p1) ( x*)
( p 1)!
( x x*)p1
( p ) ( x*)
p!
( x x*)p
如果( x*) ( x*) ( p1) ( x*) 0
而 ( p ) ( x*) 0
解三:迭代格式 xk+1=(xk3-5)/2 令x0=2.5,得迭代序列: x1=5.3125, x2=72.46643066, X3=190272.0118, x4=3.444250536 1016, x5=2.042933398 1046, 计算x6时溢出
同样的方程不同的迭代格式有不同的结果 迭代函数的构造有关
L Lk xk x * xk xk 1 x1 x0 1 L 1 L
xk x * x * xk 1 xk xk 1 g'( ) xk x * xk xk+1
因此: 1 xk x * xk xk+1 1 L
证毕.
定理1指出,
例1 用简单迭代法求区间(2,3)内方程x3-2x-5=0的根 lim x 解一 将方程两边同加2x+5,再开三次方,得式同解方程 x= 3 2 x 5 作迭代格式 xk+1= 3 2 xk 5 , k=0,1,
实验五 用Newton法计算方程的根
五. 讨论分析当初始值选取离零点较远时将导致算法无法使用,例如第三题,将初始值改为2就无法计算出结果了,显示如下例如求020sin 35=-+-x x e x 的根,其中控制精度1010-=eps ,最大迭代次数40=M ,在steffensen 加速迭代方法的程序中,我们只需改动:it_max=40; ep=1e-10, 其余不变 。
利用以上程序,我们只需输入:phi=inline('exp(5*x)-sin(x)+(x)^3-20');[x_star,index,it]=steffensen(phi,0.5)可得:x_star = 0.637246094753909index = 0it = 41观察上述结果,index = 0,it = 41表明迭代失败,所以使用以上方法估计的时候,应该尽量估计出解的范围,偏离不应过大,距离增加迭代次数增加,也有可能迭代失败六. 改进实验建议根据上述分析,我认为,应该先对函数作一个简图,方便知道解的大概位置,然后我们才将这个大概值代入Newton 法或者Steffensen 中进行求解。
当然,我们可以用其他数学软件实现Newton 迭代法,我们可以用z-z 超级画板,其操作流程为:牛顿迭代法的公式是:x n+1=x n-f(x n)/f'(x n)。
下面我们就用牛顿迭代法设计程序求方程f(x)=ln(x)+2*x-6的近似解。
(一)观察方程f(x)=0的零点位置(1)显示坐标系的坐标刻度。
(2)作出函数y=ln(x)+2*x-6的图像,如下图所示:可以观察到方程的根在区间[2,3]上,我们可以设定近似解的初始值为2。
(二)设计求方程近似解的程序(1)在程序工作区中输入:f(x){ln(x)+2*x-6;}执行后,返回结果为:>> f(x) #这表示在计算机已经完成了函数f(x)的定义。
(2)定义f(x)的导函数g(x),在程序工作区中输入:Diff(f(x),x);执行后,返回结果为:>> 2+1/x #得到了f(x)的导函数。
解非线性方程组的牛顿迭代法
为克服这两个缺点,通常可用下述方法.
(1) 简化牛顿法,也称平行弦法.
xk 1 xk Cf ( xk )
其迭代公式为 (4.7)
C 0,1 ,.
迭代函数 ( x) x Cf ( x).
若在根 x * 附近成立 ( x) 1 Cf ( x) 1 ,即取 0 Cf ( x) 2,则迭代法(4.7)局部收敛.
8
xk
C 2 C
q2
k
1 q
2k
.
对任意 x0 0,总有 q 1,故由上式推知,当 k 时 xk C ,即迭代过程恒收敛. 例8 解 求 115 .
表7 6 计算结果 k 0 1 2 3 4 xk 10 10.750000 10.723837 10.723805 10.723805
f ( x) , f ( x)
由于
( x)
f ( x) f ( x) . 2 [ f ( x)]
假定 x *是 f ( x) 的一个单根,即 f ( x*) 0, f ( x*) 0 , 则由上式知 ( x*) 0 ,于是依据定理4可以断定,牛顿法 在根 x *的邻近是平方收敛的.
准备 迭代
x0 ,计算 f 0 f ( x0 ), 选定初始近似值
步骤2
按公式
x1 x0 f 0 / f 0
迭代一次,得新的近似值 x1,计算 f1 f ( x1 ), f1 f ( x1 ). 步骤3 控制
x1 满足 1 如果
f1 2 ,则终 或
5
止迭代,以 x1作为所求的根;否则转步骤4. 允许误差,而
3
又因
( x*)
f ( x*) , f ( x*)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Newton迭代法求解非
线性方程
一、 Newton 迭代法概述
构造迭代函数的一条重要途径是用近似方程来代替原方程去求根。
因此,如果能将非线性方程f (x )=0用线性方程去代替,那么,求近似根问题就很容易解决,而且十分方便。
牛顿(Newton)法就是一种将非线性方程线化的一种方法。
设k x 是方程f (x )=0的一个近似根,把如果)(x f 在k x 处作一阶Taylor 展开,即:
)x x )(x ('f )x (f )x (f k k k -+≈ (1-1)
于是我们得到如下近似方程:
0)x x )(x ('f )x (f k k k =-+ (1-2)
设0)('≠k x f ,则方程的解为:
x ̅=x k +f (x k )
f (x k )́
(1-3)
取x ~作为原方程的新近似根1+k x ,即令: )
x ('f )
x (f x x k k k 1k -=+, k=0,1,2,…
(1-4)
上式称为牛顿迭代格式。
用牛顿迭代格式求方程的根的方法就称为牛顿迭代法,简称牛顿法。
牛顿法具有明显的几何意义。
方程:
)x x )(x ('f )x (f y k k k -+= (1-5)
是曲线)x (f y =上点))x (f ,x (k k 处的切线方程。
迭代格式(1-4)就是用切线式(1-5)的零点来代替曲线的零点。
正因为如此,牛顿法也称为切线法。
牛顿迭代法对单根至少是二阶局部收敛的,而对于重根是一阶局部收敛的。
一般来说,牛顿法对初值0x 的要求较高,初值足够靠近*x 时才能保证收敛。
若
要保证初值在较大范围内收敛,则需对)x (f 加一些条件。
如果所加的条件不满足,而导致牛顿法不收敛时,则需对牛顿法作一些改时,即可以采用下面的迭代格式:
)
x ('f )
x (f x x k k k 1k λ
-=+,
⋯=,2,1,0k (1-6)
上式中,10<λ<,称为下山因子。
因此,用这种方法求方程的根,也称为牛顿下山法。
牛顿法对单根收敛速度快,但每迭代一次,除需计算)x (f k 之外,还要计算
)x ('f k 的值。
如果)x (f 比较复杂,计算)x ('f k 的工作量就可能比较大。
为了避免计算导数值,我们可用差商来代替导数。
通常用如下几种方法: 1. 割线法 如果用
1
k k 1k k x x )
x (f )x (f ----代替)x ('f k ,则得到割线法的迭代格式为:
)x (f )
x (f )x (f x x x x k 1k k 1
k k k 1k --+---=
(1-7) 2. 拟牛顿法 如果用
)
x (f ))
x (f x (f )x (f k 1k k k ---代替)x ('f k ,则得到拟牛顿法的迭代格式为:
))
x (f x (f )x (f )
x (f x x 1k k k k 2k 1k -+---
= (1-8)
3. Steffenson 法 如果用
)
x (f )
x (f ))x (f x (f k k k k -+代替)x ('f k ,则得到拟牛顿法的迭代格式为:
)
x (f ))x (f x (f )
x (f x x k k k k 2k 1
k -+-
=+
(1-9)
二、 算法分析
1. 割线法
割线法的迭代公式为:
)x (f )
x (f )x (f x x x x k 1k k 1
k k k 1k --+---
=,k=0,1,2,…
割线法是超线性收敛,其程序流程图为:
2. 拟牛顿法
牛顿拟迭代法迭代公式为:
))
x (f x (f )x (f )
x (f x x 1k k k k 2k 1
k -+---
= (1)对单根条件下,牛顿拟迭代法平方收敛,牛顿拟迭代法程序框图如下所
示:
(2) 对重根条件下,此时
迭代公式修改为:
))
x (f x (f )x (f )
x (f m
x x 1k k k k 2k 1
k -+---=,m 为根的重数 此时,牛顿迭代法至少平方收敛。
3. Steffenson 法
Steffenson 迭代法程序流程图与牛顿拟迭代法类似。
三、 牛顿法的程序
给定初值0p ,用牛顿法格式)
p ('f )
p (f p p 1k 1k 1
k k ---=,⋯=,2,1k ,求解非线性方程
0)x (f =。
*********************************************************************
function [p1,err,k,y] = newton(f1041,df1041,p0,delta,max1) % f1041是非线性函数。
% df1041是f1041的微商。
% p0是初始值。
% delta 是给定允许误差。
% max1是迭代的最大次数。
% p1是牛顿法求得的方程的近似解。
% err 是p0的误差估计。
% k 是迭代次数。
% y = f(p1)
p0, feval('f1041',p0) for k = 1:max1
p1 = p0 - feval('f1041', p0)/feval('df1041', p0); err = abs(p1-p0); p0 = p1;
p1, err, k, y = feval('f1041', p1) if (err < delta) | (y == 0),
break, end
p1, err, k, y = feval('f1041', p1) end
*********************************************************************
四、程序实例与计算结果
例 用上述程序求方程0233=+-x x 的一个近似解,给定初值为,误差界为610-。
解:先用m 文件先定义二个名为和的函数文件。
function y = f1041(x)
y = x^3 – 3*x + 2;
function y=df1041(x)
y=3*x^2-3;
建立一个主程序 clear
newton('f1041','df1041',, 10^(-6), 18)然后在MATLAB命令窗口运行上述主程序,即: >> prog1041
计算结果如下:
p0 = ans = p1 = err = k = 1 y =
p1 = err = k = 1 y =
p1 = err = k = 2 y =
p1 = err = k = 2 y =
p1 = err = k = 3 y =
p1 = err = k = 3 y = p1 = err = k = 4 y =
p1 = err = k = 4 y =
p1 = err = k = 5 y =
p1 = err = k = 5 y =
p1 = err = k = 6 y =
p1 = err = k = 6 y =
p1 = err = k = 7 y =
p1 = err = k = 7 y =
p1 = err = k = 8 y =
p1 = err = k = 8 y =
p1 = err = k = 9 y =
p1 = err = k = 9y =
p1 = err = k = 10 y =
p1 = err = k = 10 y =
p1 = err = k = 11 y =
p1 = err = k = 11 y =
p1 = err = k = 12 y =
p1 = err = k = 12 y =
p1 = err =
k = 13 y =
p1 = err = k = 13 y =
p1 = err = k = 14 y =
p1 = err = k = 14 y =
p1 = err = k = 15 y =
p1 = err = k = 15 y = p1 = err = k = 16 y =
p1 = err = k = 16 y =
p1 = err = k = 17 y =
p1 = err = k = 17 y =
p1 = err = k = 18 y =
ans =
这说明,经过18次迭代得到满足精度要求的值。
以下
是程
序运
行截图:。
