第四章 气体内的输运过程
合集下载
热学 (4 第四章 气体内的输运过程)

设 Q为单位时间内通过的热量简称为热流,则
Q
dT
A
傅立叶定律
dz 若设热流密度为JT,则:
JT
dT dz
20
T2 ( T1 )
B
温度梯度 dT
dz
z0
dS dQ
T T(z)
表示流体中温度沿z
轴方向的空间变化率。
o
T1
Ax
在dt时间内,从温度较高的一侧,通过这一平
面向温度较低的一侧所传递的热量,与这一平面所
在处的温度梯度和面积元成正比
热导率
能量流动方 向与温度梯 度方向相反
恒为正值
dQ κ dT dSdt dz z0
21
三、扩散现象的宏观规律 扩散 (diffusion)
在混合气体内部,当某种气体在各处的密度不均匀时, 这种气体将从密度大的地方向密度小的地方散布,这 种现象叫扩散。
输运过程
扩散:密度 不均匀 m的迁移
热传导:温度T不均均 热的迁移
内摩擦(黏性): 分子定向速度u 不均匀 定向运动动量 p的迁移 22
§ 5-1 气体分子的平均自由程
一、分子的平均自由程和碰撞频率
非平衡态平衡态,碰撞起重要作用。
克劳修斯指出:气体分子的速度虽然很大,但前进中要与其 他分子作频繁的碰撞,每碰一次,分子运动方向就发生改变, 所走的路程非常曲折。
若不均
一种气体
n不均
p不均
生宏 气流
22
我们这里研究的是:纯扩散--仅仅是由于分 子的无规则运动和碰撞引起的扩散过程。
实现纯扩散的条件
Q
dT
A
傅立叶定律
dz 若设热流密度为JT,则:
JT
dT dz
20
T2 ( T1 )
B
温度梯度 dT
dz
z0
dS dQ
T T(z)
表示流体中温度沿z
轴方向的空间变化率。
o
T1
Ax
在dt时间内,从温度较高的一侧,通过这一平
面向温度较低的一侧所传递的热量,与这一平面所
在处的温度梯度和面积元成正比
热导率
能量流动方 向与温度梯 度方向相反
恒为正值
dQ κ dT dSdt dz z0
21
三、扩散现象的宏观规律 扩散 (diffusion)
在混合气体内部,当某种气体在各处的密度不均匀时, 这种气体将从密度大的地方向密度小的地方散布,这 种现象叫扩散。
输运过程
扩散:密度 不均匀 m的迁移
热传导:温度T不均均 热的迁移
内摩擦(黏性): 分子定向速度u 不均匀 定向运动动量 p的迁移 22
§ 5-1 气体分子的平均自由程
一、分子的平均自由程和碰撞频率
非平衡态平衡态,碰撞起重要作用。
克劳修斯指出:气体分子的速度虽然很大,但前进中要与其 他分子作频繁的碰撞,每碰一次,分子运动方向就发生改变, 所走的路程非常曲折。
若不均
一种气体
n不均
p不均
生宏 气流
22
我们这里研究的是:纯扩散--仅仅是由于分 子的无规则运动和碰撞引起的扩散过程。
实现纯扩散的条件
4-气体内的输运现象解析

时气体分子可以从容器的一壁出发,无碰撞地飞到
容器的另一壁。这种气体多处的状态称为真空。 真空是一个相对的概念,随着容器线度的减小,
形成真空态的压强值提高。真空容器中所包含的气
体是高度稀薄的气体,通常称为克努森气体,这种
气体流动称为分子流。
13
6) 单位体积内气体分子相互碰撞次数 假设分子是两两相碰的,单位体积内的分子相 互碰撞的总次数为 1 2 2 2 2 4kT Z AA nZ d v n d n
——分子的有效直径
碰撞时两分子质心距离的平均值称为分子的平均有 效直径d
4
ቤተ መጻሕፍቲ ባይዱ
2、分子的有效碰撞截面 当两分子质心之间垂直距离b<d 时,两分子发生碰撞。 d 2 2 d 4 ( ) 2 这里的σ就是弹性刚球的有效碰撞截面,是一个分 子截面的4倍。
5
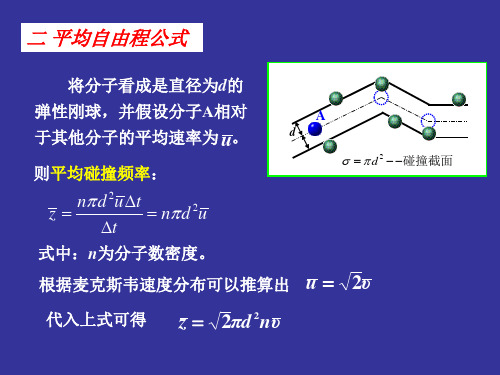
二、平均自由程和平均碰撞频率
热运动分子之间 频繁碰撞,分子的运 动路径曲折复杂 分子在与其它分 子的相邻两次碰撞之 间所经历路程的平均 值为平均自由程 分子在单位时间内 与其它分子的平均碰 撞次数称为平均碰撞 频率
第4章 气体内的输运现象
4.1 气体分子碰撞和平均自由程 4.2 输运过程的宏观规律 4.3 气体输运现象的微观解释
1
§4.1 气体分子碰撞和平均自由程
气体分子之间的碰撞对于气体中发生的过程有
重要的作用,如在气体中建立分子按速率或速度分 布的麦克斯韦分布律,确立能量按自由度均分定理 等,都是通过气体分子的频繁碰撞加以实现并维持 的。因此,分子间的碰撞时气体中建立并维持平衡
Z 2d
2
kT 8kT p 2 4d p 2 2 d p m kT mkT
11
4-气体内的输运现象

N (0 ~ ) P ( ) 0 f ( )d N 物理意义:一个分子在自由飞行了距离后与其他分 子发生碰撞的概率。 N ( ~ ) 1 P ( ) f ( )d N 物理意义:一个分子在自由飞行了距离后仍未与其 他分子发生碰撞的概率。
d u n
2
先假设其它分子静止
2
平均碰撞频率为
Z 2d vn 2vn
10
3、分子的平均自由程 v 1 2 Z 2d n 讨论:
1 2n
1) 分子的平均自由程与分子的有效碰撞截面σ和分 子的数密度n成反比,与平均速率无关。 2) 平衡态下,对确定的气体,平均自由程和平均 碰撞频率有确定的值。 3) 用宏观量 p、T表示的平均碰撞频率和平均自由程:
6
一个分子在单位时间内和其他分子碰撞的次数 是偶然的、不可预测的。 平均自由程 和平均碰撞频率 Z : 反映了分子间碰撞的频繁程度,是对大量分子、 多次碰撞的统计平均值。 二者关系:
v Z
7
1、分子间的相对运动速率 u 设分子运动速度满足麦克斯韦分布律,根据统计 规律,假设所有分子均以平均速率 v 运动。则分子
1 7 2.08 10 m 2 2d n
常温常压下,一个分子在一秒内平均要碰撞几十亿次, 可见气体分子之间的碰撞是多么的频繁!
15
三、有效碰撞截面的概率解释
如图所示的气体层。 一个分子以相对速度u沿x方向 入射气体层,层内其他分子看做 相对静止。问:
A
n
x
入射分子与气层内分子发生碰撞的概率有多大?
26
这也是为什么促使系统从非平衡态过渡到平衡
态的过程称为输运过程或内迁移过程的原因。 输运过程的特点:
(1)描述系统状态的宏观参量在空间的分布不随 时间改变的输运过程,称为稳定的输运过程,相 应系统状态为稳定态。 描述系统状态的宏观参量在空间的分布随时 间改变的输运过程,称为非稳定的输运过程,相 应系统状态为非稳定态。
d u n
2
先假设其它分子静止
2
平均碰撞频率为
Z 2d vn 2vn
10
3、分子的平均自由程 v 1 2 Z 2d n 讨论:
1 2n
1) 分子的平均自由程与分子的有效碰撞截面σ和分 子的数密度n成反比,与平均速率无关。 2) 平衡态下,对确定的气体,平均自由程和平均 碰撞频率有确定的值。 3) 用宏观量 p、T表示的平均碰撞频率和平均自由程:
6
一个分子在单位时间内和其他分子碰撞的次数 是偶然的、不可预测的。 平均自由程 和平均碰撞频率 Z : 反映了分子间碰撞的频繁程度,是对大量分子、 多次碰撞的统计平均值。 二者关系:
v Z
7
1、分子间的相对运动速率 u 设分子运动速度满足麦克斯韦分布律,根据统计 规律,假设所有分子均以平均速率 v 运动。则分子
1 7 2.08 10 m 2 2d n
常温常压下,一个分子在一秒内平均要碰撞几十亿次, 可见气体分子之间的碰撞是多么的频繁!
15
三、有效碰撞截面的概率解释
如图所示的气体层。 一个分子以相对速度u沿x方向 入射气体层,层内其他分子看做 相对静止。问:
A
n
x
入射分子与气层内分子发生碰撞的概率有多大?
26
这也是为什么促使系统从非平衡态过渡到平衡
态的过程称为输运过程或内迁移过程的原因。 输运过程的特点:
(1)描述系统状态的宏观参量在空间的分布不随 时间改变的输运过程,称为稳定的输运过程,相 应系统状态为稳定态。 描述系统状态的宏观参量在空间的分布随时 间改变的输运过程,称为非稳定的输运过程,相 应系统状态为非稳定态。
热力学-4.气体内的输运过程

. 输运系数的数量级 若已知气体分子的质量、有效直径(或碰撞
截面σ), 可以计算出在不同压强和温度条件下的 输运系数。
300K时N2的η =4.2×10-5Pa·s(实验:1.78×10-5Pa·s) 273K时Ar的κ =1.47×10-2W·m-1·K-1
(实验值1.67×10-2W·m-1·K-1)。
dz z0
D为扩散系数;(单位是米2/秒)
气体在非平衡态下的三种典型变化过程:
粘滞现象
——动量的传递
传热
——热量的传递
扩散
——质量的传递
三种输运现象宏观规律共同宏观特征:
它们都是由气体中的某一性质的不均匀分 布而引起的;
为了定量描述这不均匀性,分别采用了定 向流动的速率梯度、温度梯度和密度梯度;
第四章 气体内的输运过程
问题的提出
v 1.6 RT 470 m / s
讲台处的某类气体分子约需多长时间能 运动到你处?
t ~ 0.1秒 ??
矛盾
气体分子热运动平均速率高, 但气体扩散过程进行得相当慢。
设想下课后大家闭着眼睛往外走的情形…
分子速率虽高,但分子在运动中还要和 大量的分子碰撞。
2.69 10 25 m 3
(2)v 1.60 RT /
1.60 8.31 273 / 29 103 448 m s1
(3)Z 2 d 2 nv
1.41 3.14 (3.510 10 )2 2.69 10 25 448 6.54 10 9 s1
)
z0
dS
1 nmv
3
df
(
du dz
)
z0
气体内的输运过程
1 du f ( ) z0 dA,其中 nmv 3 dz 称为牛顿黏性定律. η的单位为泊,以P表示
1P 1N s m 0.1kg m s
2
1
1
考虑到相邻两层流体中相对速度较大的流体总是受到阻力, 即速度较大一层流体受到的黏性力的方向总与速度梯度方向相反,故在式中加上负号
1 υ 平均自由程: λ 2 z 2d n 2d 2 n
式中:d为分子的有效直径,n为分子数密度。
由 p nkT n
p kT
kT λ 2 2πd p
思考 在一封闭容器中装有1mol氦气(视作理想气体),这 时分子无规则运动的平均自由程将决定于什么? (A)压强p (B)体积V (C)温度T (D)平均碰撞频率 z
实验发现,流体在流速较小时将作分层平行流动, 流体质点
轨迹是有规则的光滑曲线, 不同质点轨迹线不相互混杂。 这样的流体流动称为层流。 直圆管中流体流速分布如图 流速箭头的包络面为抛物面, 其平均流速箭头的包络面为 平面
稳恒层流中的黏性 牛顿黏性定律
•流 体 作 层 流 时 , 通过任一平行于流 速的截面两侧的相 邻两层流体上作用 有一对阻止它们相 对“滑动”的切向 作用力与反作用力。
二.热传导现象的宏观规律
当系统与外界之间或系统内部各部分之间存在温度 差时就有热量的传输. 热传递有热传导、对流与辐射 三种方式,本节将讨论热传导
1. 傅里叶定律(Fourier law of heat conduction ) •1822法国科学家傅里叶(Fourier)在热质说思想的指导下 发现了傅里叶定律。 该定律认为热流dQ/dt (单位时间内 通过的热量)与温度梯度 dT /dz 及横截面积dA成正比,
热学 (4 第四章 气体内的输运过程)

速度梯度和面积也可以直接测得; 于是,从公式可以算出
内摩擦系数。
C 小镜 B A
旋转黏度计
17
18
19
二、热传导现象的宏观规律 热传导 (heat conduction)
当系统内各部分的温度不均匀时,就有热量从 温度较高的地方传递到温度较低的地方,由于温差 而产生的热量传递现象。
傅立叶定律
dN
1
N0ex/ dx
13
§5-2 输运过程的宏观规律
一、黏性现象的宏观规律
当气体各层流速不同时,通过任一平行于流速的截面,相 邻两部分气体将沿平行于截面方向互施作用力,结果使得 流动慢的气层加速,使流动快的气层减速。这种相互作用 力称为内摩檫力,也叫做粘滞力。这种现象称为内摩檫现 象,也叫做黏性现象。
5)、采用不同近似程度的各种推导方法的实质是
相同的。
31
理性气体内部压强的微观解释
从微观的角度看来, 理想气体内部的压强 实质上是由于垂直于截面方向的热运动 动量交换引起的
1 n dSdt
2m
6
dK 1 n dSdt2m
6
p dK 2 n(1 m 2 )
dSdt 3 2
32
二、热传导现象的微观解释
并且单位体积中各有 n 的分子沿 + z, - z
方向运动。
6
27
这样,在dt 时间内,从 dS一侧跑到另一侧 的分子数为
dN 1 n v dt dS 6
z
z0
z0
z0
u u0
pz
dS
pz
x
u0
(2)假设分子越过 dS 面之前都是在离 dS 面距离
内摩擦系数。
C 小镜 B A
旋转黏度计
17
18
19
二、热传导现象的宏观规律 热传导 (heat conduction)
当系统内各部分的温度不均匀时,就有热量从 温度较高的地方传递到温度较低的地方,由于温差 而产生的热量传递现象。
傅立叶定律
dN
1
N0ex/ dx
13
§5-2 输运过程的宏观规律
一、黏性现象的宏观规律
当气体各层流速不同时,通过任一平行于流速的截面,相 邻两部分气体将沿平行于截面方向互施作用力,结果使得 流动慢的气层加速,使流动快的气层减速。这种相互作用 力称为内摩檫力,也叫做粘滞力。这种现象称为内摩檫现 象,也叫做黏性现象。
5)、采用不同近似程度的各种推导方法的实质是
相同的。
31
理性气体内部压强的微观解释
从微观的角度看来, 理想气体内部的压强 实质上是由于垂直于截面方向的热运动 动量交换引起的
1 n dSdt
2m
6
dK 1 n dSdt2m
6
p dK 2 n(1 m 2 )
dSdt 3 2
32
二、热传导现象的微观解释
并且单位体积中各有 n 的分子沿 + z, - z
方向运动。
6
27
这样,在dt 时间内,从 dS一侧跑到另一侧 的分子数为
dN 1 n v dt dS 6
z
z0
z0
z0
u u0
pz
dS
pz
x
u0
(2)假设分子越过 dS 面之前都是在离 dS 面距离
第四章 气体内的输运过程补充 大学物理热学部分PPT

3)当任一分子在运动过程中于某地只经受一次碰 撞就会失掉它原来的运动特性,在受碰处被当 地的分子完全“同化”。
1.dt 时间内沿z轴向上和向下穿过ds面的分子数目 dN↑和dN↓
❖气体中处于ds面上方的部分为A,下方的为B,两部
分子的数密度和平均速率分别为nA、nB和 v A 、v B ,于
是
Z
dN
1. 思路与准备
• 模型中的一些假设:
1)把分子看成是彼此无吸引力的刚性小球,都以 平均速率而运动。
2)将系统中的分子等分为三队,各自平行于x轴、 y轴、z轴运动;每一队又等分为两小队,各自 沿坐标轴的正、负方向运动。(输运过程与平衡 态偏离不大 ,平衡态下分子热运动及碰撞的一 些结果都可直接采用)
处的分子热运动平均能量 z0 ;由B部沿z轴向上穿过ds
的分子携带 z0 处的平均能量 z0 。所以,A、B两部
每交换一对分子通过ds沿z轴正方向净输运的热量为:
z0
z0
依据能量按自由度均分定理
z0
i 2kTz0
z0
i
k 2
T
z0
i是分子热运动的自由度。
于是
z0
第四章 气体内的输运过程
补充
输运过程的微观解释
The microscopic explanations of transportation processes
1.思路与准备 2.粘滞现象的微观解释 3. 热传导现象的微观解释 4. 扩散现象的微观解释 5. 输运过程简单微观理论与实验的比较 6. 对简单理论的改进
dkm(u u )
z0 z0
定向流速u的下标表示相应气层的空间位置。利用在z0 处定向流动的速率梯度,可写出
du
1.dt 时间内沿z轴向上和向下穿过ds面的分子数目 dN↑和dN↓
❖气体中处于ds面上方的部分为A,下方的为B,两部
分子的数密度和平均速率分别为nA、nB和 v A 、v B ,于
是
Z
dN
1. 思路与准备
• 模型中的一些假设:
1)把分子看成是彼此无吸引力的刚性小球,都以 平均速率而运动。
2)将系统中的分子等分为三队,各自平行于x轴、 y轴、z轴运动;每一队又等分为两小队,各自 沿坐标轴的正、负方向运动。(输运过程与平衡 态偏离不大 ,平衡态下分子热运动及碰撞的一 些结果都可直接采用)
处的分子热运动平均能量 z0 ;由B部沿z轴向上穿过ds
的分子携带 z0 处的平均能量 z0 。所以,A、B两部
每交换一对分子通过ds沿z轴正方向净输运的热量为:
z0
z0
依据能量按自由度均分定理
z0
i 2kTz0
z0
i
k 2
T
z0
i是分子热运动的自由度。
于是
z0
第四章 气体内的输运过程
补充
输运过程的微观解释
The microscopic explanations of transportation processes
1.思路与准备 2.粘滞现象的微观解释 3. 热传导现象的微观解释 4. 扩散现象的微观解释 5. 输运过程简单微观理论与实验的比较 6. 对简单理论的改进
dkm(u u )
z0 z0
定向流速u的下标表示相应气层的空间位置。利用在z0 处定向流动的速率梯度,可写出
du
热力学第四章气体内的输运过程

2m
du dz
z0
ds vdt
dK 1 nmv du dsdt 1 v du dsdt
3
2019/12/19
dz 崎山z苑0 工作室
3
dz z0 21
二 热传导现象的微观解释
气体动理论认为: a.温度较高的热层分子平均动能大, T1 温度较低的冷层分子平均动能小; b.由于两层分子碰撞和掺和,从热层 到冷层出现热运动能量的净迁移。
2019/12/19
崎山苑工作室
1
第四章 气体内的输运过程
4.1 气体分子的平均自由程 4.2 输运过程的宏观规律 4.3 输运过程的微观解释 *4.4 真空的获得及测量
2019/12/19
崎山苑工作室
2
4.1 气体分子的平均自由程(mean free path)
1. 分子碰撞 分子相互作用的过程。
解:按气体分子算术平均速率公式 算得
v 8RT
v
8RT =
88.31 273 3.14 2 103
m
/
s
1.70
103
m
/
s
按公式 p=nkT 可知单位体积中分子数为
n
p = 1.013105 kT 1.38 1023 273
m
3
2.69 1025 m3
2019/12/19
崎山苑工作室
24
四 理论结果与实验的比较
1.,和D与气体状态参量的关系
mn v 8kT 1
m
2n
1 v 1 4km T1/2
3
3
n p kT
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
z
v
448 6.9 10
8
6.5 10 s
9
1
12
12
二 . 分子按自由程的分布
y P(x) 1/λ
x
z
0 0 N0
x t N
x+dx t+dt N+dN
0
x x+dx
x
经过dx路程分子数的减少量
N x exp( ), N0
dN
1
Ndx
分子行进到 x 出的残存概率。 以 表示的自由程分布。
氮
0.599 10 3.10 10
7
氧
0.647 10
7
空气
7.0 10
8
2.30 10
10
10
例 计算空气分子在标准状态下的平均自由程和平 均碰撞频率。取分子的有效直径d=3.510-10m。已知
空气的平均分子量为29。
解: 已知 T 273K , p 1.0atm 1.013 105 Pa,
0
22
22
三.扩散现象的宏观定律
扩散(diffusion) 在混合气体内部,当某种气体
在各处的密度不均匀时,这种气体将从密度大的地 方向密度小的地方散布,这种现象叫扩散。
若 不 均 匀 则 n不 均 匀 mn 一种气体 p n kT 则 p不 均 匀 则 产 生 宏 观 气 流
v z
v 2 π d vn
1
2
1 2 πd n
2
2 πd n
2
因为P = nkT 所以也可以写成
kT 2 πd P
9
2
9
kT 2 πd P
2
当温度一定时, 压强越小,平均自由程越大。
例. 空气 , t = 0oC,
d 3.510-10m,
在不同压强时对应的 平均自由程 :
π d2
u
n
6
6 — 碰撞截面 (collision cross-section)
中心在 扫过的柱体内的分子都能碰撞
A 2d d
π d2
u
n
u
2
— 碰撞截面 (collision cross-section)
单位时间内扫过的体积
21
若设热流密度为JT,则:
21
T2 ( T1 )
B
温度梯度
dT dz
z0
dS
dQ
T T (z)
表示流体中温度沿z 轴方向的空间变化率。
x
o
T1
A
在dt时间内,从温度较高的一侧,通过这一平 面向温度较低的一侧所传递的热量,与这一平面所 在处的温度梯度和面积元成正比 热导率 恒为正值 能量流动方 dT dQ κ 向与温度梯 dSdt dz z 度方向相反
u0
B
流体沿x 方向作定向流动, 并且流动速率u沿z方向递 增 。 u是z的函数 u u ( z ) 流速梯度
du dz
u u( z )
o
u0
A x
沿z方向所出现的流速空间 变化率。 15
15
z
黏性力的大小与两部分 的接触面dS和截面所在 处的流速梯度成正比。
u0
df dS
L
z0
df
B
u u( z )
o
u0
A x
f (
du dz
) z0 dS
——牛顿黏性定律
——是流体的黏性系数,单位:NSM-2,表示单
位时间、单位面积、单位速度梯度上输运的动量。
( du dz ) z ——是流体定向流动速率梯度在z0处之值
0
16
ds——是在z0处两流体层接触面的面积。
z
2 > 1 2
z0 O x
dM
ΔS
1
y
d dM D dSdt dz z0
——菲克定律
D 为扩散系数,单位m 2s-1,表示单位时间、 26 单位面积、单位密度梯度上所输运的质量。26
§ 4.3 输运过程的微观解释
一 . 黏性现象的微观解释
从分子运动角度看内摩擦现象:
4
4
在相同的t时间内,分子由A到 B的位移大小比它的路程小得多 扩散速率
A
B
(位移量/时间)
(路程/时间)
平均速率
平均碰撞频率(mean collision frequency) z : 单位时间内一个气体分子与其它分子碰撞的 平均次数。 平均自由程(mean free path) :气体分子 在相邻两次碰撞间飞行的平均路程 —
热 学
1
第4章 气体内的输运过程
4.1 气体分子的平均自由程
4.2 输运过程的宏观规律 4.3 输运过程的微观过程
2
2
输运过程(transport process)
非平衡态下气体各部分性质不均匀。
热运动+碰撞 、p、m 的迁移
气体系统由非平衡态向平衡态转变的过程,就 称为输运过程。扩散过程、热传导过程和黏性 性现象都是典型的输运过程。 扩散:密度 不均匀 m的迁移 输运过程 热传导:温度T不均均 热 的迁移 分子定向速度u 不均匀 内摩擦(黏性): 定向运动动量 p的迁移 3
13
dN 1 x exp( )dx, N0
13
§ 4.2 输运过程的宏观规律
(Macroscopic Law of Transport Process )
当气体处于非平衡状态下,气体内部或者各 部分的温度不相等,或者各部分的压强不相 等,或者各气层之间有相对运动,或者这三 者同时存在。在这些非平衡状态下,气体内 部将有能量、质量或动量从一个部分向另一 个部分定向迁移,这种由非平衡态向平衡态 的变化过程就是气体的输运过程。 黏性现象、热传导现象、扩散现象
28
这样,在dt 时间内,从 dS一侧跑到另一侧 的分子数为
dN 1 6 n v dt dS
z
z0
u u0
z0
z0
pz
dS
pz
x
u0
(2)假设分子越过 dS 面之前都是在离 dS 面距离 约为平均自由程处发生最后一次碰撞的, 而且它们带过来的定向动量,就是在那里 的定向动量…… “一次同化论”假设。
u0
因此,在 dt 时间内, 在 dS 下方的流体层 净增加的定向动量为
20
20
二. 热传导现象的宏观定律
热传导(heat conduction)
当系统内各部分的温度不均匀时,就有热量从 温度较高的地方传递到温度较低的地方,由于温差 而产生的热量传递现象。
傅立叶定律
设 Q 为单位时间内通过的热量简称为热流,则
Q
dT dz
A
傅立叶定律
J T dT dz
z u n π d nu
v
v
碰撞夹角 有各种可能(0 — 180)
90 u
u
2v
7
z
2 π d nv
2
7
例.数量级的概念: 氧气O2 ,标准状态下,以 d 310-10m估计
v
n
8 RT πM
P kT
8 8 . 31 273 π 32 10
3
§ 4.1 气体分子的平均自由程
一 . 分子的平均自由程和碰撞频率
气体分子 平均速率
矛盾
v 1.60 RT M mol
氮气分子在270C时的 平均速率为476m.s-1.
气体分子热运动平均速率高, 但气体扩散过程进行得相当慢。
克劳修斯指出:气体分子的速度虽然很大,但前 进中要与其他分子作频繁的碰撞,每碰一次,分 子运动方向就发生改变,所走的路程非常曲折。
分子由上到下携带 的动量是 p z 0 ;
分子由下到上携带 的动量是 p z 0 .
29
29
分子由上到下携带 的动量是 p z ;
0
z
z0
u u0
z0
z0
pz
dS
分子由下到上携带 的动量是 p z .
0
pz
x
14
14
一 . 黏性现象的宏观定律
当气体各层流速不同时,通过任一平行于流速的截 面,相邻两部分气体将沿平行于截面方向互施作用 力,结果使得流动慢的气层加速,使流动快的气层 减速。这种相互作用力称为内摩擦力,也叫做黏性 力。这种现象称为内摩擦现象,也叫做黏性现象。
z
L
z0
df dS df
提示:因δ<<R ,可认为夹层内的 速度梯度处处相等
19
19
解: 外桶的线速度
M
u R u 0
R
2 R L
3
内桶的线速度 夹层流体的速度梯度
A
B
L
R R+δ ω
黏性力对扭丝作用的合力矩:
G 2 RL
R
R
3
所以,气体的黏度为:
G 2 R L
27
27
内摩擦现象的微观本质是: 分子在无序的热运动中输运定向动量的过程。 下面近似地推导关系式:
气体黏性系数
1 3
