2.3幂函数导学案
高中数学 2.3 幂函数导学案(无答案)新人教A版必修1(2021年整理)
湖南省岳阳市平江县高中数学2.3 幂函数导学案（无答案）新人教A版必修1编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（湖南省岳阳市平江县高中数学2.3 幂函数导学案（无答案）新人教A版必修1）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为湖南省岳阳市平江县高中数学2.3 幂函数导学案（无答案）新人教A版必修1的全部内容。
2。
3 幂函数学习目标1.通过具体实例了解幂函数的概念、图象和性质，并能进行简单的应用2.能够类比研究一般函数、指数函数、对数函数的过程与方法，来研究幂函数的图象和性质※学习重点、难点：重点：从五个具体幂函数中认识幂函数的概念和一些性质难点：画五个具体幂函数的图象并由图象概括其性质,体会图象的变化规律学习过程(预习教材P77~ P78,找出疑惑之处）一.课前导学※探索新知探究1:幂函数的概念问题1:实例：(1)如果张红购买了每千克1元的水果W千克,她需要付的钱数为P（元)，试将P表示成W的函数(2)如果正方形的边长为a，面积为S，试将S表示成a的函数(3)如果立方体的边长为a,体积为V,试将V表示成a的函数(4)如果一个正方形场地的面积为S，正方形的边长为a，试将a表示成S的函数(5)如果某人t秒内骑车行进了1k m,他骑车的平均速度为V，试将V表示成t的函数思考1: (1）这五个函数是指数函数么？ （2）指数函数的解析式是_______________ (3)指数函数的特点:底数为 指数为 思考2:这五个函数有什么共同特征?(1） 是常数 （2) 是变量（3)x a系数是 （4)都是 的形式新知：幂函数的概念一般地，形如 的函数称为幂函数，其中 是自变量， 是常数 探究2：常见幂函数的图像和性质问题2：在同一个坐标系中作出下列函数的图象：(1)x y = (2）21x y = （3）2x y = (4）1-=x y (5)3x y =y0 x从图象分析出幂函数所具有的性质: x y = 3x y = 1-=x y定义域值域奇偶性单调性定点讨论:幂函数的性质规律(1)当α为 数时,幂函数为奇函数;当α为数时，幂函数为偶函数(2)α＞0时,幂函数的图象在区间(0,+∞）上是函数α＜0时，幂函数的图象在区间（0，+∞）上是函数(3)所有的幂函数在（0,+∞）都有定义，并且图象都经过点______________二。
2.3幂函数
2.3幂函数【使用说明及学法指导】1.先精读一遍教材P77-P78，用红色笔进行勾画；找出自己的疑惑和需要讨论的问题准备课上讨论质疑。
通过阅读教材，你应该掌握这些：（1）了解幂函数的概念（2）能会画几个简单幂函数的图象精读教材P77完成下列问题（1）以上问题中的五个函数，它们有什么共同特征？（2）一般地，形如的函数称为幂函数，其中α为常数.（3）在同一平面直角坐标系内做出幂函数12312,,,,y x y x y x y x y x-=====的图象观察你的图象,将你发现的结论写在下表内xy=2xy=3xy=21xy=1-=xy 定义域值域奇偶性单调性公共点你现在可以完成以下问题了么？1、下列所给出的函数中，是幂函数的是（）A．3xy-=B．3-=xy C．32xy=D．13-=xy2、下列命题中正确的是（）A．当0=α时函数αxy=的图象是一条直线B．幂函数的图象都经过（0，0）和（1，1）点C．若幂函数αxy=是奇函数，则αxy=是定义域上的增函数D．幂函数的图象不可能出现在第四象限3. 已知幂函数()y f x=的图象过点(2,2)，则它的解析式为.4.比较下列各题中两个值的大小(1) 8.03，7.03（2）321.0，323.0（3）212，318.1做完了上面的那个题，继续努力，能完成这个么？将下列各数按从小到大的顺序排列起来322，31)35(-，32)23(，3)23(-，0)51(，3)32(-，31)34(-教学反思:首先：实例引入，自然引出概念，学生易于接受。
我引导学生从实例出发类比指数函数的定义自己观察、归纳、总结概括出幂函数的定义。
在概念理解上，用步步设问、课堂讨论、练习来加深理解。
我对学生强调了幂函数和指数函数的区别，然后，让学生亲自动手画两个图象，提高学生的动手实践能力，数形结合能力。
引导学生说出图像特征及变化规律，并从而得出幂函数的性质，大部分学生数学基础较差，理解能力，运算能力，思维能力等方面参差不齐；同时学生学好数学的自信心不强，学习积极性不高。
人教版数学高二必修1导学案 2.3幂函数学生版
2.3 幂函数学习目标 1.理解幂函数的概念.2.掌握y ＝x α(α＝－1，12，1,2,3)的图象与性质.3.理解和掌握幂函数在第一象限的分类特征，能运用数形结合的方法处理幂函数的有关问题.学习过程 一、自主学习 1.幂函数的概念阅读教材P 77至倒数第二自然段，完成下列问题．幂函数：一般地，函数 叫做幂函数，其中 是自变量，α是 ． 2.幂函数的图象与性质阅读教材P 77倒数第二自然段至P 78“例1”以上部分，完成下列问题． 幂函数的图象与性质：R R R 问题1 y ＝1x ，y ＝x ，y ＝x 2三个函数有什么共同特征？问题2 类比y ＝x 3的图象和性质，研究y ＝x 5的图象与性质.探究点1：幂函数的概念 例1 已知y ＝(m 2＋2m －2)22m x -＋2n －3是幂函数，求m ，n 的值.探究点2：幂函数的图象及应用例2 若点(2，2)在幂函数f (x )的图象上，点(－2，14)在幂函数g (x )的图象上，问当x为何值时，(1)f (x )>g (x )；(2)f (x )＝g (x )；(3)f (x )<g (x ).变式探究若对于例2中的f (x )，g (x )，定义h (x )＝⎩⎪⎨⎪⎧f x ，f x ≤g x ，g x ，f x >g x ，试画出h (x )的图象.探究点3：幂函数性质的综合应用 命题角度1：比较大小例3 设a ＝2323⎛⎫ ⎪⎝⎭，b ＝1323⎛⎫ ⎪⎝⎭，c ＝2325⎛⎫⎪⎝⎭，则a ，b ，c 的大小关系是( ) A.a >b >c B.b >a >c C.b >c >a D.c >b >a命题角度2：幂函数性质的综合应用例4 已知幂函数y ＝x 3m －9 (m ∈N *)的图象关于y 轴对称且在(0，＋∞)上单调递减，求满足()31m a -+<()332m a --的a 的取值范围.三、当堂检测1.已知幂函数f (x )＝k ·x α的图象过点⎝⎛⎭⎫12，22，则k ＋α等于( )A.12B.1C.32 D.2 2.已知幂函数f (x )的图象经过点(2，22)，则f (4)的值等于( ) A.16 B.116 C.2D.123.设α∈{－1,1，12，3}，则使函数y ＝x α的定义域为R 的所有α的值为( )A.1,3B.－1,1C.－1,3D.－1,1,34.下列是y ＝23x 的图象的是( )5.以下结论正确的是()A.当α＝0时，函数y＝xα的图象是一条直线B.幂函数的图象都经过(0,0)，(1,1)两点C.若幂函数y＝xα的图象关于原点对称，则y＝xα在定义域内y随x的增大而增大D.幂函数的图象不可能在第四象限，但可能在第二象限四、课堂小结本节课我们学习过哪些知识内容?五、学后反思1、我的疑问：2、我的收获：。
高中数学导学案 2.3 幂函数 新人教A版必修1
《2.3 幂函数》导学案主编：段小文 班次 姓名【学习目标】其中2、3是重点和难点1.通过具体实例了解幂函数的图象和性质，体会幂函数的变化规律及蕴含其中的对称性。
2.画五个幂函数的图象并由图象概括其性质。
3.从五个具体幂函数中认识幂函数的一些性质，能利用性质解决数学问题。
【课前导学】预习教材第77-78页，找出疑惑之处，完成新知学习。
1.幂函数的概念：形如 的函数称为幂函数，其中 是自变量， 是常数。
2.幂函数的性质：（1）幂函数的图象都过点 ； （2）当0α>时，幂函数在[0,)+∞上 ；当0α<时，幂函数在(0,)+∞上 ； （3）当2,2α=-时，幂函数是 ；当11,1,3,3α=-时，幂函数是 。
【预习自测】首先完成教材上P79第1、2题，然后做自测题。
1、幂函数()f x的图象过点，则()f x 的解析式是 __ 。
2、下列所给出的函数中，是幂函数的是（ ）A ．3x y -=B ．3-=x yC ．32x y =D ．13-=x y3、如图所示，幂函数αx y =在第一象限的图象， 比较1,,,,,04321αααα的大小（ ） A ．102431<<<<<αααα B ．104321<<<<<αααα C ．134210αααα<<<<< D ．142310αααα<<<<<4、函数2-=x y 在区间]2,21[上的最大值是 （ ）A ．41 B ．1- C ．4 D ．4-【课中导学】首先独立思考探究，然后合作交流展示。
探究一：看教材P77页5个具体的问题，这些函数的解析式结构有何共同特点？其一般形式如何？定义：幂函数的概念。
注意：幂函数与指数函数的区别。
探究二：在同一平面直角坐标系内作出函数12312,,,,y x y x y x y x y x -=====的图象，它们的定义域、值域、奇偶性、单调性、公共点分别如何？ 归纳：幂函数的性质。
幂函数导学案(1)
§2。
3 幂函数1。
通过具体实例了解幂函数的图象和性质；2. 体会幂函数的变化规律及蕴含其中的对称性并能进行简单的应用。
（预习教材P 77～ P 79，找出疑惑之处)复习1：求证3y x =在R 上为奇函数且为增函数。
复习2：1992年底世界人口达到54。
8亿,若人口年平均增长率为x ％，2008年底世界人口数为y （亿），写出：（1）1993年底、1994年底、2000年底世界人口数； (2）2008年底的世界人口数y 与x 的函数解析式．任务二、新课导学探究任务一:幂函数的概念问题:分析以下五个函数,它们有什么共同特征？（1）边长为a 的正方形面积2S a =，S 是a 的函数；(2）面积为S 的正方形边长12a S =，a 是S 的函数； （3）边长为a 的立方体体积3V a =，V 是a 的函数；（4）某人ts 内骑车行进了1km ,则他骑车的平均速度1/v t km s -=,这里v 是t 的函数； （5）购买每本1元的练习本w 本，则需支付p w =元，这里p 是w 的函数。
新知1、幂函数的概念：一般地，形如y x α=()a R ∈的函数称为幂函数，其中α为常数.试一试：判断下列函数哪些是幂函数.① 1y x=;②22y x =；③3y x x =-；④1y =。
探究任务二:幂函数的图象与性质问题:作出下列函数的图象：（1)y x =；（2)12y x =；（3）2y x =；（4）1y x -=；（5）3y x =．说明：② 除函数12y x=外，其余四个幂函数具有奇偶性②在第一象限内，函数1y x -=的图像向上与y 轴无限接近，我们称x 轴y 轴为渐近线 结合以上特殊幂函数的图像得出 一般幂函数的性质（1）所有幂函数在(0,)+∞上都有定义，并且图像都通过点(1,1)（2）若0α>，则幂函数的图像都过原点，并且在区间[0,)+∞上为增函数（3）若0,α<则幂函数的图像在区间(0,)+∞上是减函数，在第一象限内，当x 从右边趋向于原点时，图像在y 轴右方无限地逼近y 轴，当x 趋向于+∞时，图像在x 轴上方无限地逼近x 轴（4）当α为奇数时，幂函数为奇函数；当α为偶数时，幂函数为偶函数从图象分析出幂函数所具有的性质。
幂函数复习导学案(珍藏版)
2.3幂函数复习导学案（珍藏版）一.学习目标：（1）了解幂函数概念。
（2）会画常见幂函数的图象。
（3）结合图象了解幂函数图象的变化情况和简单性质。
（4）会用幂函数的单调性比较两个底数不同而指数相同的幂的大小。
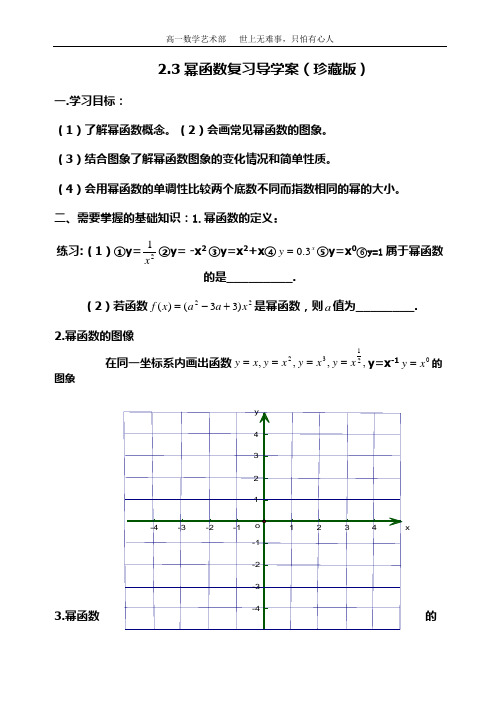
二、需要掌握的基础知识：1.幂函数的定义： 练习:（1）①y=21x②y= -x 2 ③y=x 2+x ④xy 3.0=⑤y=x 0⑥y=1属于幂函数的是_________.（2）若函数22)33()(x a a x f +-=是幂函数，则a 值为________. 2.幂函数的图像在同一坐标系内画出函数,,,,2132x y x y x y x y ====y=x -10x y =的图象3.幂函数的x性质：①所有幂函数在_________都有定义，并且图像都过点________； ②0a >时，幂函数的图像通过_________，并且在区间[)0,+∞上是_________，特别的，当1a >时，幂函数的图像________，当01a <<时，幂函数的图像________。
③0a <时，幂函数的图像在区间()0,+∞上是_________，在第一象限内，当x 从右边趋向原点时，图像在y 轴右方无限地逼近y 轴正半轴，当x 趋向+∞时，图像在x 轴上方无限地逼近x 轴正半轴。
（4）幂函数y x α=的图象，在第一象限内，直线1x =的右侧，图象由下至上，指数 . y 轴和直线1x =之间，图象由上至下，指数α函数,,,,2132x y x y x y x y ====x y =-1的性质4.性质的应用.),0[)(1上是增函数在、证明幂函数+∞=x x f2．比较下列各组中值的大小，并说明理由：(1)1.10.5，1.40.5 (2) (-π)-1, （-3.14）-1 (3)1.40.5，1.433、下列函数中不是幂函数的是 ( )A. B. C. y=2x D.y=x -14、幂函数的如图所示，曲线是幂函数αx y =在第一象限内的图象，已知α分别取2,21,1,1-四个值，则相应图象依次为：________________ 5、幂图像过点，则它的单调递增区间是（ ）Ａ[)1,-+∞Ｂ[)0,+∞Ｃ(),-∞+∞Ｄ(),0-∞6.若幂函数y=f(x)的图像经过点()9,3，则f(25)=______________7.比较下列各组数的大小：（1）0.7521_____0.7621 （2）（-3.14）2_____2π （3）4.06.03.0___2.0（4）3232)6_____()32(----π8. 幂函数y=(m 2-m-1)x m 在区间()+∞,0上是减函数，则 m 的值为________。
2019-2020学年高中数学 2.3 幂函数导学案 新人教A版必修1.doc
2019-2020学年高中数学 2.3 幂函数导学案 新人教A 版必修1【学习目标】1．知识与技能：（1）了解简单幂函数的概念；会利用定义证明简单幂函数的奇偶性（2）了解利用奇偶性画函数图像和研究函数的方法。
2．过程与方法：类比研究一般函数的方法，研究幂函数的图像与性质3．情感、态度、价值观：引导学生发现数学中的对称美，让学生在识图与画图中获得学习的快乐。
【学习重点】幂函数的概念和奇偶函数的概念【学习难点】简单的幂函数的图像性质。
函数奇偶性的判断。
一、【学习过程】知识链接：1.如何画函数图象？2.如何研究一个函数？研究函数性质从那几方面入手？二、预习：1.幂函数的定义： 2.在同一坐标系中画出下列函数图象：y=x 、y ＝x 2、y ＝x 3、y ＝x 21、y ＝x 1-三、新课探究(一)、情景设置：阅读材料并填空：(1) 如果张红购买了每千克1元的蔬菜w 千克,那么她需要支付p = 元(2) 如果正方形的边长为a ,那么正方形的面积 S=(3) 如果立方体的边长为a ,那么立方体的体积V=(4)如果一个正方形场地的面积为S ,那么这个正方形的边长a=(5)如果人t 秒内骑车行进了1 km ,那么他骑车的平均速度v=若将它们的自变量全部用x 来表示,函数值用y 来表示,则它们的函数关系式将是:(二)、新课探究1.幂函数： 强调结构：2.图像与性质○.所有的幂函数在 都有定义,并且函数图象都通过点 ; ○2.如果a>0,则幂函数的图象过点 并在(0,+∞)上为 (增、减)函数;○3.如果a<0,则幂函数的图象过点 ,并在(0,+∞)上为 (增、减)函数; 例1.已知幂函数y ＝f(x)的图像过点(3，1/9)求函数解析式3、奇偶函数的概念一般地，图像关于原点对称的函数叫奇函数，即有 如f(x)=x 3图像关于轴对称的函数叫偶函数，即有 如f(x)=x 2例、判断函数f(x)=-2x 5和f(x)=-x 4+2的奇偶性 练习：1.P80动手实践 完成书中图2-302.求下列幂函数的定义域：（1）y ＝x 52 （2）y ＝x 31 （3）y ＝x 43（4）y ＝x 2-（四）、随堂练习1.如图所示，曲线是幂函数 y = x k在第一象限内的图象，已知 k 分别取 212,1,1-，四个值，则相应图象依次为:________2．比较下列各组中两个值的大小①0.7521，0.7621；②(-0.95)31，(-0.96)31；③0.313.2，0.314.23．通过图像求下列函数的定义域和值域4．(1)y ＝x 23 (2)y ＝x 72 (3)y ＝x 53。
探究式导学案2：2.3幂函数
2.3 幂函数一、三维目标： 知识与技能：(1)理解幂函数概念，会画幂函数x y =，2x y =，3x y =，1-=x y ，21x y = 的图象； (2)结合常见的幂函数图象，理解幂函数图象的变化情况和性质，并能进行简单的应用。
过程与方法：(1)通过观察、总结幂函数的性质，培养学生的识图能力和概括能力； (2)使学生进一步体会数形结合的思想方法。
情感态度与价值观：(1)通过生活实例引出幂函数的概念，使学生体会到数学在实际生活中的应用，激发学生的学习兴趣；(2)了解幂函数图象的变化规律使学生认识到数学美，从而激发学生的学习欲望。
二、学习重、难点：重点：从五个具体幂函数中认识幂函数的一些性质。
难点：画五个具体幂函数的图象并由图象概括其性质，体会图象的变化规律。
三、学法指导：认真阅读教材，体会幂函数与指数函数的不同，在比较过程中进一步掌握指数函数，学习幂函数，认识和掌握五个具体幂函数的图像和性质。
四、知识链接：1.指数函数定义：2.对数函数定义： 五、学习过程： （一）、问题：(1)如果张红购买了每千克1元的蔬菜w 千克，则她需要付款p (元)与w (千克)的函数关 系式为 ；(2)如果正方形的边长为a ，那么正方形的面积s 与a 的函数关系式为 ； (3)如果立方体的边长为a ，那么立方体的体积v 与a 的函数关系式为 ； (4)如果正方形场地的面积为s ，那么这个正方形的边长a 与s 的函数关系式 为 ；(5)如果某人t s 内骑车行进了1km ，那么他骑车的平均速度v (km/s)与t(s)的函数关系式为 。
思考：若这些函数的自变量用x 来表示,函数值用y 来表示,则函数关系式是怎样的？它们有怎样的特点？（二）、幂函数的定义：一般地，函数αx y =叫做幂函数，其中x 为自变量，α为常数。
例1：判断下列函数是否为幂函数？42321(1)(2)2(3)(4)(5) 2.3x y x y x y x y y x===-==探究1：怎么判断一个函数是幂函数还是指数函数？（三）、请在同一坐标系内作出幂函数x y =，2x y =，3x y =，21x y =，1-=x y 的图象。
幂函数导学案
§2.2.3幂函数导学案一、学习目标（1）从五个具体的幂函数中理解幂函数的概念；（2）通过具体实例了解幂函数的图象和性质，并能进行初步的应用. 二、学习内容阅读教材P 77的具体实例（1）~（5），思考下列问题. （1）它们的对应法则分别是什么？（2）以上问题中的函数有什么共同特征？ 答：上述的问题涉及到的函数，都是形如：y x α=，其中x 是自变量，α是常数.探究新知1．幂函数的定义一般地， 的函数称为幂孙函数，其中x 是自变量，α是常数.如 等都是幂函数，幂函数与指数函数，对数函数一样，都是基本初等函数. 2．研究函数的图像（1）y x = （2）12y x = （3）2y x = （4）1y x -= （5）3y x = 思考：如何画出以上五个函数图像通过观察图像，填P 78探究中的表格○1.所有的幂函数在 都有定义,并且函数图象都通过点 ; ○2.如果a>0,则幂函数的图象过点 并在(0,+∞)上为 (增、减)函数; ○3.如果a<0,则幂函数的图象过点 ,并在(0,+∞)上为 (增、减)函数;特别地，当x ＞1，x ＞1时，x ∈（0，1），2y x =的图象都在y x =图象的下方，形状向下凸越大，下凸的程度越大（你能找出原因吗？）当∠α＜1时，x ∈（0，1），2y x =的图象都在y x =的图象上方，形状向上凸，α越小，上凸的程度越大（你能说出原因吗？）（3）α＜0时，幂函数的图象在区间（0，+∞）上是减函数.在第一象限内，当x 向原点靠近时，图象在y 轴的右方无限逼近y 轴正半轴，当x 慢慢地变大时，图象在x 轴上方并无限逼近x 轴的正半轴. 三、学法指导例1.已知幂函数y ＝f(x)的图像过点(3，1/9)求函数解析式例2．证明幂函数()[0,]f x =+∞上是增函数思考：我们知道，若12()()0,1()f x y f x f x =><若得12()()f x f x <，你能否用这种作比的方法来证明()[0,]f x +∞上是增函数，利用这种方法需要注意些什么？例3．利用函数的性质 ，判断下列两个值的大小 （1）11662,3 （2）3322(1),(0)x x x +> （3）22244(4),4a --+【一点通】：利用幂函数的单调性来比较大小.四、归纳、升华、领悟（1）今天学习了哪一类基本函数，它们定义是怎样描述的？（2）你能根据函数图象说出有关幂函数的性质吗？作业与练习【A 组】课本：p79第1、2、3题【B 组】1.下列命题正确的是（ ）A.当 α =0时，函数 y=x α的图象是一条直线B.幂函数的图象都经过（0，0），（1，1）两点C.幂函数的图象不可能出现在第四象限D.若幂函数 y=x α为奇函数，则它是定义域内的增函数2.若幂函数 y=f （x ）的图象经过点（ 2，161)，则 f （4）的值为（ ）A.41B. 161C. 321D. 2561 3.下列函数中，定义域为（0，+∞ ）的是（ ） A. y =61x B. 98-=x y C. 89-=x y D. 25x y = 4.下列函数中，值域为（0，+∞ ）的是（ ）A. 41x y = B. 74-=x y C. 5-=x y D. 25x y =5.若幂函数 ()mnp xy 1-=（m 、n 、p 均为正整数，且 m 、n 互质）的图象在第一、二象限，且不过原点，则（ ）A. p 、n 为奇数，m 为偶数B. p 、m 为奇数，n 为偶数C. p 、n 为偶数，m 为奇数D. p 、m 为偶数，n 为奇数 6.给出四个幂函数和四个图象： （1）21x y = （2）23-=xy （3）32x y = （4）23-=xy下列判断正确的是（ ）A.（1）的图象是甲B.（2）的图象是乙C.（3）的图象是丙 C.（4）的图象是丁7.如图 2 -3 - 7 中的曲线是幂函数 y = x α在第一象限的图象，已知 α 取 ±2和 ±21四个值，则相应于曲线 C 1，C 2，C 3，C 4 的 α 值依次为（ ）8.设 ()21x x f =，若 f （x ）<f -1（x ），则 x 的取值范围为 . 9.已知函数 f （x ）=31a x- 在（ -∞ ，0）上是增函数，在（0，+∞ ）上是减函数，则最小正整数 a 为 .10.若幂函数 y=x α的图象，当 0 <x <1时，在直线 y=x 的上方，当 x >1时，在直线 y=x 的下方，则 α 的取值范围为 .11.已知对任意的 x 1，x 2∈（0，+ ∞ ）且 x 1< x 2，函数 f （x ）= x -p 2 +2p +3（p ∈Z ）满足f （x 1）<f （x 2），且对任意的 x ∈R ，f （x ）- f （ - x ）=0，求 p 值，并写出相应的函数 f （x ）的解析式.12.比较下列每组数的大小：13.分别指出幂函数 y= x α（α∈Z ）的图象具有下列特点时 α 的取值 范围.（1）图象关于 y 轴对称且与坐标轴相交； （2）图象关于 y 轴对称且不与坐标轴相交； （3）图象关于原点对称且不通过原点； （4）图象关于原点对称且通过原点.。
2.3幂函数的学案
2.3 幂函数编写人：王小桃 审评人：邱育明一、重难点：教学重点：从五个具体幂函数中认识幂函数的一些性质 教学难点：幂函数的图像和性质的应用 二、课内研究新知问题一：自主阅读课本P76页的五个具体问题思考问题中的函数具有什么共同特征？通过观察可以发现：上述问题中涉及的函数，都是形如：___________________的函数。
幂函数的概念：一般地，把形如________的函数叫做幂函数，其中x 是 ，α是 。
练习1：已知f(x)=(m+1)x m 是幂函数，则m=_______2、已知幂函数f(x)图像过点（4，2），那么f(9)=__________3、指出下列函数那些是幂函数。
3231(1),(2)2,(3)1,(4)(1)y y x y x y x x ===+=+问题二：对于幂函数，我们只讨论α=1,2,3,0.5,-1时的情形。
在同一平面直角坐标系内作出幂函数y x =，2y x =，3y x =，0.5y x =，1y x -=的图像。
（参照课本77页）画出五个幂函数的图像后，观察图像，将你发现的结论写在下表内。
y x =2y x = 3y x = 0.5y x = 1y x -= 定义域 值域 奇偶性 单调性 公共点幂函数的性质：（在第一象限内）（1） 当α<0时，f(x)=x α是______函数。
（填增或减） （2） 当α>0时，f(x)=x α是______函数。
（填增或减） ①1>α时，α越大，图象越靠近与y 轴。
②10<<α时，α越小，图象越靠近与x 轴。
三、幂函数的应用：例1： 比较下列各题中两个数值的大小。
（1）338.1,7.1 （2）0.8-1 ，0.9-1练习1、(1) 0.50.52.3 2.4， （2）()()0.30.323--，例2：证明幂函数()f x x =在[)0,+∞上是增函数。
练习2、已知函数0.5y x -=,判断该函数在()0,+∞上的单调性，并证明。
幂函数导学案
高一数学《2.3幂函数》导学案[目标展示]（1）掌握幂函数的形式特征，掌握具体幂函数的图象和性质。
（2）能应用幂函数的图象和性质解决有关简单问题。
[重点难点] 重点：从五个具体幂函数图像中认识幂函数的一些性质难点：画五个具体幂函数图像并由图像概况其性质，体会图像的变化和规律。
[课前预习]1、完成下列问题：（1）如果张红购买了每千克1元的蔬菜x 千克，那么她需要支付y=_______元。
（2）如果正方形的边长为x ，那么正方形的面积y=______。
（3）如果立方体的边长为x ，那么立方体的体积y=______。
（4）如果正方形的场地面积为x ，那么正方形的边长y=______。
（5）如果某人x 秒骑车行进了1千米，那么他的速度y=______千米/秒。
讨论：根据函数的定义，以上五个式子都是函数表达式，这五个函数表达式有什么共同特征？如果让你给他们起个名字，你将会给他们起个什么名字呢？2、幂函数的定义：我们把形如的函数称为幂函数，其中是自变量,是常数。
3、幂函数的图象:在同一平面直角坐标系中作出幂函数x y =,2x y =,3x y =,21x y =,1-=x y 的图象。
4、总结规律：幂函数都一定经过第_____象限，一定不经过第_____象限。
在第一象限，幂函数一定过定点__________，当幂指数大于0时，幂函数还过定点____________;当幂指数小于0时，幂函数一定不过点____________;●幂函数的奇偶性：若幂指数是_______，则该幂函数一定是偶函数,反之________成立。
若幂指数是_______，则该幂函数一定是奇函数,反之________成立。
❍幂函数单调性：若幂指数是_________,则幂函数在第一象限一定是____函数；若幂指数是_________,则幂函数在第一象限一定是____函数； 第二或第三象限的单调性，借助函数的________性来理解。
教学设计3：2.3 幂函数
2.3 幂函数幂函数要点导学 一、知识导引1．幂函数定义：形如y ＝x α的函数叫幂函数(α为常数)． 重点掌握α＝1,2,3，12，－1时的幂函数．2．图象：当α＝1,2,3，12，－1时的图象如右图．3．性质(1)当α>0时，幂函数图象都过(0,0)点和(1,1)点，且在第一象限都是增函数；当0<α<1时曲线上凸；当α>1时，曲线下凹：α＝1时为过(0,0)点和(1,1)点的直线．(2)当α<0时，幂函数图象总过(1,1)点，且在第一象限为减函数． (3)当α＝0时，y ＝x α＝x 0，表示过(1,1)点平行于x 轴的直线(除(0,1)点)． (4)当α＝1,2,3，12，－1时的函数的性质同学们可自行研究．二、重点和难点重点：幂函数的定义、图象和性质． 难点：幂函数图象的位置和形状变化． 三、典型例题剖析例1 不论α取何值，函数y ＝(x －1)α－2的图象都通过A 点，求A 点的坐标． 解 因为幂函数y ＝x α的图象恒通过(1,1)点， 所以y ＝(x －1)α的图象恒通过(2,1)点． 所以y ＝(x －1)α－2的图象恒通过(2，－1)点． 一、概念不清例3 下列函数中不能化为幂函数的是( ) A ．y ＝x 0B ．y ＝2x 2C ．y ＝x2D ．y ＝x错解 选A ，或选C ，或选D剖析 错解主要是对幂函数的概念不清，造成错误．由幂函数的定义：y ＝x α(α∈R )称为幂函数，因此，A ，C ，D 中的函数均可化为幂函数，而B 中的函数不能化为幂函数．正解 B例2 作出函数y ＝4log 2x 的图象．错解 y ＝4log 2x ⇒y ＝22log 2x ⇒y ＝2log 2x 2⇒y ＝x 2. 故函数的图象如图所示．剖析 在将函数式y ＝4log 2x 变形为y ＝2log 2x 2，即y ＝x 2时，定义域扩大了． 正解 y ＝4log 2x (x >0)⇒y ＝22log 2x (x >0)⇒y ＝2log 2x 2(x >0)⇒y ＝x 2(x >0)． 作出幂函数y ＝x 2(x >0)的图象，如图所示，即为函数y ＝4log 2x 的图象．例3 若(a ＋1)－1<(3－2a )－1，求实数a 的取值范围． 错解 考查幂函数f (x )＝x －1， 因为该函数为减函数， 所以由(a ＋1)－1<(3－2a )－1， 得a ＋1>3－2a ，解得a >23.故实数a 的取值范围是(23，＋∞)．剖析 函数f (x )＝x－1在(－∞，0)和(0，＋∞)上均为减函数，但在(－∞，0)∪(0，＋∞)上不具有单调性，错解中错用了函数单调性，从而导致错误．正解 考查幂函数f (x )＝x －1，由于该函数在(－∞，0)及(0，＋∞)上均为减函数，所以由(a ＋1)－1<(3－2a )－1，得⎩⎪⎨⎪⎧a ＋1<0，3－2a >0，或a ＋1>3－2a >0， 或3－2a <a ＋1<0， 解得a <－1或23<a <32.故实数a 的取值范围是(－∞，－1)∪(23，32)．例4 如果f (x )＝(m －1)x m^2－4m ＋3是幂函数，则f (x )在其定义域上是( )A ．增函数B ．减函数C ．在(－∞，0)上是增函数，在(0，＋∞)上是减函数D ．在(－∞，0)上是减函数，在(0，＋∞)上也是减函数 解析 要使f (x )为幂函数，则m －1＝1，即m ＝2. 当m ＝2时，m 2－4m ＋3＝－1，∴f (x )＝x －1. ∴f (x )在(－∞，0)上是减函数， 在(0，＋∞)上也是减函数． 答案 D幂函数在第一象限的图象与幂指数α的大小关系从x 轴的正方向按逆时针旋转到y 轴的正方向所经过的幂函数图象所对应的幂指数逐渐增大．如图为y ＝x α在α取－2,2，－12，12四个值时的图象，则对应于曲线C 1，C 2，C 3，C 4的α的值依次为2，12，－12，－2，其规律为在直线x ＝1的右侧“指大图高”．抓住幂函数的奇偶性，利用第一象限图象画出整个幂函数图象，进而利用数形结合进行解题例5 函数y ＝x m ，y ＝x n ，y ＝x p 的图象如图所示，则m ，n ，p 的大小关系是____________． 解析 结合题目给出的幂函数图象，我们可以将其转化成指数问题解决，作直线x ＝a (0<a <1)，可得直线与3个函数图象交点纵坐标的大小关系是a n <a m <a p ，根据指数函数y ＝a x (0<a <1)是单调减函数可得n >m >p .答案 n >m >p点评 以上几例，教同学们学会如何分析问题、转化问题，数形结合使所学知识融会贯通，使所谓的某些“规律”直观地、立体地呈现在函数的图象中，减轻记忆的负担．三种数学思想在幂函数中的应用例6 指出函数f (x )＝x 2＋4x ＋5x 2＋4x ＋4的单调区间，并比较f (－π)与f (－22)的大小．解 因为f (x )＝x 2＋4x ＋4＋1x 2＋4x ＋4＝1＋1(x ＋2)2＝1＋(x ＋2)－2， 所以其图象可由幂函数y ＝x －2向左平移2个单位，再向上平移1个单位得到，如图所示．所以f (x )在(－2，＋∞)上是减函数，在(－∞，－2)上是增函数，且图象关于直线x ＝－2对称．又因为－2－(－π)＝π－2， －22－(－2)＝2－22， 所以π－2<2－22， 故－π距离对称轴更近， 所以f (－π)>f (－22)． 点评 通过化简、变形等，可将复杂的、不熟悉的函数转化为简单的、熟悉的函数形式，进而用其性质来解题．联想加分析“联想”加“分析”是正确求解数学问题的关键．有时面对一道题，从该题的某个条件上看出某一类问题的“影子”，于是“联想”便展开了．很快有了基本思路，再运用“分析”使思路严谨化，解题过程就诞生了，请看下面两例：例7 若(a ＋2)－1>(4－a )－1，求实数a 的取值范围． 联想 这是一道涉及幂函数y ＝x －1的应用问题，我们知道此函数在(－∞，0)及(0，＋∞)上均为减函数，故⎩⎪⎨⎪⎧ a ＋2>0，4－a >0，a ＋2<4－a 或⎩⎪⎨⎪⎧a ＋2<0，4－a <0，a ＋2<4－a . 由⎩⎪⎨⎪⎧a ＋2>0，4－a >0，a ＋2<4－a⇒－2<a <1；由⎩⎪⎨⎪⎧a ＋2<0，4－a <0，a ＋2<4－a ⇒a ∈∅， 则实数a 的取值范围为(－2,1)．分析 此题又不同于幂函数，我们可以看出，当⎩⎪⎨⎪⎧a ＋2>0，4－a <0，即a >4时不等式也成立；于是本题的正确求解要分三种情况．正确的结果是实数a 的取值范围为(－2,1)∪(4，＋∞)．例8 若函数f (x )>0且满足f (xy )＝f (x )·f (y )，若x >1时，f (x )>1，求使f (x －3)<f (2x －5)成立的x 的范围．联想 由于f (x )＝x n 在(0，＋∞)上满足“f (x )>0且f (xy )＝f (x )·f (y )”，于是想到这是一道与幂函数有关的抽象函数问题．令x ＝y ＝1得f (1)＝1. 又f (1)＝f (x ·1x )＝f (x )·f (1x )，所以f (1x )＝1f (x ).则f (x y )＝f (x ·1y )＝f (x )·f (1y )＝f (x )f (y ).设0<x 1<x 2，则x 2x 1>1.由已知得f (x 2x 1)>1，即f (x 2)f (x 1)>1.故f (x 2)>f (x 1)．所以f (x )在(0，＋∞)上单调递增． 因此，由f (x －3)<f (2x －5)⇒⎩⎪⎨⎪⎧x －3>0，2x －5>0，2x －5>x －3⇒x >3.故使f (x －3)<f (2x －5)成立的x 的范围为(3，＋∞)．分析 表面上看没有任何问题，但深入想一下可以发现：条件中并没有x －3>0及2x －5>0的限制，这个是求解时强加的，是片面的，应该这样来解：令x ＝y ＝－1得f (－1)＝1， 则f (－x )＝f (x )·f (－1)＝f (x )． 即f (x )为偶函数．于是由f (x －3)<f (2x －5)及f (x )在(0，＋∞) 上单调递增得|x －3|<|2x －5| ∴(x －3)2<(2x －5)2∴(3x －8)(x －2)>0 ∴x <2或x >83即为所求．可以看出：丰富的联想再加上必要的分析是产生正确结论的保障！但愿这两点你都拥有． 类抽象函数问题的解法大量的抽象函数都是以中学阶段所学的基本初等函数为背景抽象而得．解题时，若能从研究抽象函数的背景入手，通过类比、猜想出它们可能为某种基本初等函数，常可找到解题的切入点，进而加以解决．以正比例函数为模型的抽象函数例9 已知f (x )的定义域为实数集R ，对任意x ，y ∈R ，都有f (x ＋y )＝f (x )＋f (y )，且x >0时，f (x )<0，f (1)＝－2，求f (x )在区间[－3,3]上的最大值和最小值．分析 由条件f (x ＋y )＝f (x )＋f (y )联想正比例函数f (x )＝kx ，其中k <0，满足已知条件．由此猜想函数f (x )是区间[－3,3]上的减函数且又为奇函数，这样问题的解决就有了方向．解 因为对任意x ，y ∈R ，都有f (x ＋y )＝f (x )＋f (y )，于是取x ＝0，可得f (0)＝0，同时设y ＝－x ，得f (x －x )＝f (x )＋f (－x )，所以f (x )＋f (－x )＝0，即f (－x )＝－f (x )，知函数f (x )为奇函数．下面证明它是减函数：任取－3≤x 1<x 2≤3，则x 2－x 1>0， 又x >0时，f (x )<0，即f (x 2－x 1)<0， f (x 2－x 1)＝f (x 2)＋f (－x 1)＝f (x 2)－f (x 1)<0. 所以函数f (x )在区间[－3,3]上是减函数． 当x ＝－3时，函数f (x )取最大值； 当x ＝3时，函数f (x )取最小值． f (x )max ＝f (－3)＝－f (3)＝－f (1＋2) ＝－[f (1)＋f (2)]＝－[f (1)＋f (1)＋f (1)] ＝－3f (1)＝6；f (x )min ＝f (3)＝3f (1)＝－6.点评 本题求解有两个特点：一是赋值；二是在求最值时，反复运用条件．这是求解抽象函数问题时常用的方法．二、以指数函数为模型的抽象函数例10 设函数f (x )的定义域为实数集R ，满足条件：存在x 1≠x 2，使得f (x 1)≠f (x 2)，对任意x 和y ，有f (x ＋y )＝f (x )·f (y )．(1)求f (0)；(2)对任意x ∈R ，判断f (x )值的正负．解 由已知猜想f (x )是指数函数y ＝a x (a >0，且a ≠1)的抽象函数，从而猜想f (0)＝1且f (x )>0.(1)将y ＝0代入f (x ＋y )＝f (x )·f (y )， 得f (x )＝f (x )·f (0)，于是有f (x )[1－f (0)]＝0. 若f (x )＝0，则对任意x 1≠x 2，有f (x 1)＝f (x 2)＝0， 这与已知题设矛盾，所以f (x )≠0，从而f (0)＝1. (2)设x ＝y ≠0，则f (2x )＝f (x )·f (x )＝[f (x )]2≥0， 又由(1)知f (x )≠0，所以f (2x )>0， 由x 为任意实数，知f (x )>0. 故对任意x ∈R ，都有f (x )>0.点评 从已知条件联想到指数函数模型，为问题的解决指出了方向．但在推导过程中，说理的严密性是很重要的，如不能由f (x )[1－f (0)]＝0，直接得出f (0)＝1，这是求解有关抽象函数问题时必须注意的地方．以对数函数为模型的抽象函数例11 设函数f (x )是定义域(0，＋∞)上的增函数，且f (xy )＝f (x )－f (y )．(1)求f (1)的值；(2)若f (6)＝1，求不等式f (x ＋3)＋f (1x)≤2的解集．解 由已知猜想f (x )是对数函数y ＝log a x (a >0，且a ≠1)的抽象函数． (1)将x ＝y ＝1代入f (xy )＝f (x )－f (y )，得f (1)＝f (1)－f (1)，所以f (1)＝0. (2)因为f (6)＝1，所以2＝f (6)＋f (6)，于是f (x ＋3)＋f (1x )≤2等价于f (x ＋3)－f (6)≤f (6)－f (1x )，即f (x ＋36)≤f (6x )，而函数f (x )是定义域(0，＋∞)上的增函数， 所以⎩⎨⎧x ＋36≤6x x ＋36>0，解得x ≥335，因此满足已知条件的不等式解集为[335，＋∞)．点评 (1)对不等式右端的“2”进行变形是本题求解的关键之处；(2)本题是增函数概念“若x 1<x 2，则f (x 1)<f (x 2)”的逆用．利用这个性质可以去掉函数的符号“f ”，从而使问题得以解决．谈函数模型法例12 定义在实数集R 上的函数y ＝f (x )具有下列两条性质：①对于任意x ∈R 都有f (x 3)＝[f (x )]3；②对于任意x 1，x 2∈R ，当x 1≠x 2时，都有f (x 1)≠f (x 2)．则f (－1)＋f (0)＋f (1)的值为( ) A ．1B ．2C ．－1D ．0分析 通过性质①可以看出此函数应为幂函数，性质②则要求这个幂函数必须是一个单调函数．解析 根据题设条件设f (x )＝3x ，则可以求得f (－1)＋f (0)＋f (1)＝0，答案为D. 答案 D例13 已知f (x )是R 上的增函数，且f (x 1＋x 2)＝f (x 1)·f (x 2)，若f (2)＝4，则f (2x ＋1)>8的解集是________．分析 性质f (x 1＋x 2)＝f (x 1)·f (x 2)类似于指数函数的性质a m ＋n ＝a m ·a n ，故可以构建指数函数模型．解析 设f (x )＝a x (a >1)，则由f (2)＝4可得a ＝2， 所以f (x )＝2x .由f (2x ＋1)>8，则22x ＋1>8，解得x >1. 故不等式f (2x ＋1)>8的解集是(1，＋∞)． 答案 (1，＋∞)例15 已知函数f (x )是定义域为R 的增函数，且值域为(0，＋∞)，则下列函数中为减函数的是( )A ．f (x )＋f (－x )B ．f (x )－f (－x )C ．f (x )·f (－x )D.f (－x )f (x )分析 指数函数y ＝a x (a >0，a ≠1)中，在a >1的情况下，函数满足题设的条件①定义域为R ；②增函数；③值域为(0，＋∞)．解析 不妨设f (x )＝2x ，通过观察四个选项，可以得出f (－x )f (x )＝(14)x符合题意，故选D.答案 D幂函数高考考点透视一考情分析本节知识在高考中很少单独出现，一般是与指数函数、对数函数联合命题，因此在学习上要注意知识的结合点．借助y ＝x α(α＝1,2,3，12，－1)的图象和性质研究多项式函数，分式函数、简单的无理函数是高考考查的重点，考试题多以填空题为主．二考题例析1．(陕西高考)函数f (x )＝11＋x 2(x ∈R )的值域为( )A ．[0,1]B ．[0,1)C ．(0,1]D ．(0,1)解析 ∵1＋x 2≥1，∴0<11＋x 2≤1∴f (x )＝11＋x 2的值域是(0,1]．答案 C2．(课标全国高考)下列函数中，既是偶函数又在(0，＋∞)上单调递增的函数是( ) A ．y ＝x 3B ．y ＝|x |＋1C ．y ＝－x 2＋1D ．y ＝2－|x |解析 ∵y ＝x 3在定义域R 上是奇函数，∴A 不对．y ＝－x 2＋1在定义域R 上是偶函数，但在(0，＋∞)上是减函数，故C 不对． D 中y ＝2－|x |＝(12)|x |虽是偶函数，但在(0，＋∞)上是减函数，只有B 对． 答案 B3．(北京高考)函数f (x )＝x ＋1－12－x的定义域为______________． 解析 要使函数f (x )＝1＋x －12－x有意义， 则必须有⎩⎪⎨⎪⎧ x ＋1≥02－x ≠0⇒⎩⎪⎨⎪⎧x ≥－1，x ≠2即x ∈[－1,2)∪(2，＋∞)．答案 [－1,2)∪(2，＋∞)4．(山东高考)设函数f 1(x )＝x 12，f 2(x )＝x －1，f 3(x )＝x 2，则f 3(f 2(f 1(2 007)))＝________.解析 f 3(f 2(f 1(2 007)))＝f 3(f 2(2 00712))＝f 3(2 007－12)＝2 007－1＝12 007.答案 12 007。
幂函数导学案
2.3幂函数导学案一.学习目标：1.通过具体实例了解幂函数的图象和性质，并能进行简单的应用；(重点）2.能够类比研究一般函数、指数函数、对数函数的过程与方法，来研究幂函数的图象和性质；3.通过观察、总结幂函数的性质，培养概括抽象和识图能力；进一步体会数形结合的思想.（难点） 二.新课提问：写出下列y 关于x 的函数解析式1.如果回收旧报纸每公斤１元，某班每年卖旧报纸ｘ公斤，所得价钱ｙ是关于ｘ的函数；2.如果正方形的边长为ｘ，面积为ｙ,这里ｙ是关于ｘ的函数;3.如果正方体的棱长为ｘ, 正方体的体积为ｙ,这里ｙ是关于ｘ的函数;4.如果一个正方形场地的面积为ｘ, 这个正方形的边长为ｙ，这里ｙ是关于ｘ的函数;5.如果某人ｘ秒内骑车行驶了１ｋｍ,他骑车的平均速度是ｙ，这里ｙ是关于ｘ的函数. 探究1：思考 以上各题目的函数关系分别是什么？有什么共同的特征？ （1） （2） （3） （4）1. 幂函数的定义：例1.下列函数中，哪几个函数是幂函数？【变式练习】22x 231(1)y (2)y 2x x (3)y 2 (4)y x 1 (5)y x ====+=-()223f (x)1x+=+-m m m m 幂数已知是函,求的值.探究2：常见幂函数的图像 （1）x y =，2x y =，3x y=，21x y =，1-=x y 的图像（请同学们将五个函数图像画在下面的坐标系中）（2）3x y =的图像（请同学们完成x,y 的对应值表，并用描点法画出它的图像）xx（3）21x y =的图像（请同学们完成x,y 的对应值表，并用描点法画出它的图像）3.常见幂函数的性质观察函数,,,,2132x y x y x y x y ====x y =-1的图象，将你发现的结论写在下表内。
x【提升总结】 1. 2. 3. 4.【课堂训练】1.比较下列各组数的大小.2．已知幂函数y=f(x)的图象过点则f(9)=______.3.如果函数是幂函数，且在区间（0，+∞）内是减函数，则m 的值为 .4.若 ，求实数 的取值范围.课堂小结：作业：证明幂函数 上是增函数.()()1122132a a--+<-1122(1)11.5 1.7，，的大小关系为333555(2)(((，，的大小关系为22m 2m 3f (x)(m m 1)x --=--af (x)=[)0,+∞。
高中数学 2.3 幂函数导学案 北师大版必修1
2.3 幂函数学案课前预习学案一、预习目标预习“五个具体的幂函数”，初步认识幂函数的概念和性质。
二、预习内容1．写出下列函数的定义域，并画出函数图象、指出函数的单调性和奇偶性：12133243252(1)(2)(3)(4)(5)(6)y xy xy x y x y xy x ---= = = = ==2．下列四个命题中正确的为 （ ） A ．幂函数的图象都经过B ．当n<0时，幂函数 的值在定义域内随x 的值增大而减小C ．幂函数的图象不可能出现在第四象限内D ．当n=0时，幂函数图象是一条直线 3．下列各式中正确的是 （ ）A ．－2.4 <(－4.2)B ．(65)21-<(54)21- C ．(－π) >(－2 ) D ．(－π) <54．幂函数的图象过点(2, 4 ), 则它的单调递增区间是。
A ．(0, ＋∞)B ．[0, ＋∞)C ．(－∞, 0)D ．(－∞, ＋∞) 5．已知幂函数 的图象与x 轴、y 轴都无公共点，且关于y 轴对称，则m=__ ___三、提出疑惑同学们，通过你的自主学习，你还有哪些疑惑，请把它填在下面的表格中课内探究学案一、学习目标1．掌握幂函数的形式特征，掌握具体幂函数的图象和性质。
2．能应用幂函数的图象和性质解决有关简单问题。
学习重难点：能应用幂函数的图象和性质解决有关简单问题，概括出幂函数的性质。
二、学习过程探究任务一：幂函数的概念问题：分析以下五个函数，它们有什么共同特征？ （1）边长为a 的正方形面积2S a =，S 是a 的函数； （2）面积为S 的正方形边长12a S =，a 是S 的函数； （3）边长为a 的立方体体积3V a =，V 是a 的函数；（4）某人ts 内骑车行进了1km ，则他骑车的平均速度1/v t km s -=，这里v 是t 的函数； （5）购买每本1元的练习本w 本，则需支付p w =元，这里p 是w 的函数. 新知：一般地，形如y x α=()a R ∈的函数称为幂函数，其中α为常数.试试：判断下列函数哪些是幂函数.①1y x=；②22y x =；③3y x x =-；④1y =.探究任务二：幂函数的图象与性质问题：作出下列函数的图象：（1）y x =；（2）12y x =；（3）2y x =；（4）1y x -=；（5）3y x =． 从图象分析出幂函数所具有的性质.三、 典型例题例1讨论()f x =在[0,)+∞的单调性.变式训练一：讨论()f x =的单调性.例2比较大小：（1） 1.5(1)a+与 1.5(0)a a>；（2）223(2)a-+与232-；（3）121.1-与120.9-.变式训练二练1. 讨论函数23y x=的定义域、奇偶性，作出它的图象，并根据图象说明函数的单调性.练2. 比大小：（1）342.3与342.4；（2）650.31与650.35；（3）32-与32-.四、反思总结幂函数y xα=的图象，在第象限内，直线的右侧，图象由下至上，指数α由小到大. y轴和直线1x=之间，图象由上至下，指数α.五、当堂达标1. 若幂函数()f x x α=在(0,)+∞上是增函数，则（ ）. A ．α>0 B ．α<0 C ．α=0 D ．不能确定2. 函数43y x =的图象是（ ）.A. B. C. D.3. 若11221.1,0.9a b -==，那么下列不等式成立的是（ ）.A ．a <l<bB ．1<a <bC ．b <l<aD ．1<b <a课后练习与提高一、 选择题1、下列所给出的函数中，是幂函数的是（ ）A ．3x y -=B ．3-=xyC ．32x y = D ．13-=x y 2、下列命题中正确的是（ ）A ．当0=α时函数αx y =的图象是一条直线B ．幂函数的图象都经过（0，0）和（1，1）点C ．若幂函数αx y =是奇函数，则αx y =是定义域上的增函数 D ．幂函数的图象不可能出现在第四象限3、如图所示，幂函数αx y =在第一象限的图象，比较1,,,,,04321αααα的大小（ ）A ．102431<<<<<ααααB ．104321<<<<<ααααC ．134210αααα<<<<<D ．142310αααα<<<<<4. 比大小：（1）11221.3_____1.5； （2）225.1______5.09--.5. 已知幂函数()y f x =的图象过点，则它的解析式为 .6.若幂函数xm m m m y )332(22+---=的图象不过原点，求：m 值。
《2.3幂函数》导学案1
《2.3幂函数》导函数1使用说明“自主学习”10分钟完成，出现问题，小组内部讨论完成，展示个人学习成果，教师对重点概念点评.“合作探究”11分钟完成，并进行小组学习成果展示，小组都督互评，教师重点点评. “巩固练习”9分钟完成，组长负责，小组内部点评.“个人收获”5分钟完成，根据个人学习和小组讨论情况，对掌握知识点、方法进行总结.最后5分钟，教师针对本节课中出现的重点问题做总结性点评.通过本节学习应达到如下目标1.了解幂函数的图像和性质，并能进行简单的应用.2.能够类比研究一般函数，指数函数，对数函数的过程与方法，来研究幂函数的图像和性质.3.体会幂函数的变化规律及蕴含其中的对称性.重点与难点幂函数的图像和性质；幂函数的性质学习过程(一)自主探究【问题1】如果张红购买了每千克1元的水果w 千克，那么她需要付的钱数p (元)和购买的水果量w (千克)之间有何关系？【问题2】如果正方形的边长为a ，那么正方形的面积2S a =，这里S 是a 的函数. 【问题3】如果正方体的边长为a ，那么正方体的体积3V a =，这里V 是a 的函数. 【问题4】如果正方形场地面积为S ，那么正方形的边长12a S =，这里a 是S 的函数【问题5】如果某人t s 内骑车行进了1km ，那么他骑车的速度s /km t V 1-=，这里v 是t 的函数.以上是我们生活中经常遇到的几个数学模型，你能发现以上几个函数解析式有什么共同点吗？(从自变量和常数的角度考虑)这只是我们生活中常用到的一类函数的几个具体代表，如果让你给他们起一个名字的话，你将会给他们起个什么名字呢？幂函数的概念如果设变量为x ，函数值为y ，你能根据以上的生活实例得到怎样的一些具体的函数式？这里所得到的函数是幂函数的几个典型代表，你能根据此归纳出幂函数的定义吗？ 幂函数的定义：(二)合作探讨【探究一】幂函数与指数函数有什么区别？试一试：判断下列函数那些是幂函数？(1)0.2xy = (2)15y x = (3)3y x -= (4)2y x -=我们已经对幂函数的概念有了比较深刻的认识，根据我们前面学习指数函数、对数函数的学习经历，你认为我们下面应该研究什么呢？几个常见幂函数的图象和性质在初中我们已经学习了幂函数21,,y x y x y x -===的图象和性质，请同学们在同一坐标系中画出它们的图象.根据你的学习经历，你能在上边的坐标系内画出函数132,y x y x ==的图象吗？【探究二】观察函数12312,,,,y x y x y x y x y x -=====的图象，将你发现的结论写在下表内.【探究三】根据上表的内容并结合图象，试总结函数：1232,,,y x y x y x y x ====的共同性质.归纳：当0>α时，请同学们模仿我们探究幂函数αy x =图象的基本特征0>α的情况探讨0<α时幂函数αy x =图象的基本特征.归纳：当0<α时，.例题剖析【例1】求下列幂函数的定义域，并指出其奇偶性、单调性.(1)23y x = (2)32y x -= (3)2y x -=【例2】比较下列各组数中两个值的大小(在横线上填上“<”或“>”) (1)2114.3________21π(2)3)38.0(-________()339.0-(3)125.1-__________122.1- (4)25.0)31(-____________27.0)31(-(三)巩固练习1、下列函数中，是幂函数的是( )A 、2y x =B 、32y x =C 、1y x= D 、2x y = 2、下列结论正确的是( ) A 、幂函数的图象一定过原点B 、当0<α时，幂函数αy x =是减函数C 、当0>α时，幂函数αy x =是增函数D 、函数2y x =既是二次函数，也是幂函数3、已知某幂函数的图象经过点)2,2(，则这个函数的解析式为_______________________4、写出下列函数的定义域，并指出它们的单调性：(1)4y x = (2)14y x = (3)3y x -= (四)个人收获与问题： 知识： 方法：我的问题：。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2 ，则 f(4)＝________. 2
1 2．如图所示，曲线是幂函数 y＝x 在第一象限内的图象，已知 α 分别取－1,1， ，2 四个 2 值，则相应图象依次为______________．
α
3．写出下列函数的定义域，并指出它们的奇偶性： － (1)f(x)＝x2＋x 2；
1
(2)f(x)＝ x 2 x
【幂函数的概念】 (1)如果张红购买了每千克 1 元的蔬菜 w 千克，那么她需要支付 p 这里 是 的函数． ，这里 ，这里 是 是
(2)如果正方形的边长为 a，那么正方形的面积 S (3)如果立方体的边长为 a，那么立方体的体积 V
的函数． 的函数． ，
(4)如果一个正方形场地的面积为 S，那么这个正方形的边长 a＝ 这里 是 的函数．
－ － －
1 2
1 2
训练 3 比较下列各组数的大小：
(1) 8
7 8
和－ ( ) 8 ；(2)(－2)
1 9
7
－3
和(－2.5) 3；
－
(3)1.1
－0.1
和 1.2
－0.1
；(4) 4.1 ， (3.8)
2 5
2 3
和 (1.9) .
3 5
小结 比较两个幂的大小要仔细观察它们的异同点，指数相同底数不同时，要利用幂函 数的单调性比较，底数相同而指数不同时，要利用指数函数的单调性比较，指数与底数 都不同时，要通过增加一个起桥梁作用的数进行比较． 【当堂训练】 1．已知幂函数 f(x)＝xα 的图象经过点2，
1
yx
定义域 值域 奇偶性
y x2
y x3
y x2
y x 1
单调性
定点 例 2 证明：幂函数 f(x)＝ x在[0，＋∞)上是增函数．
训练 2 证明幂函数 f(x)＝x3 在定义域上是增函数．
1
ห้องสมุดไป่ตู้1.5 2
例 3 比较大小： (1) 1.5 ， 1.7 ；(2)(－1.2)3，(－1.25)3；(3)5.25 1，5.26 1，5.26 2.
例 1 写出下列函数的定义域，并分别指出它们的奇偶性： (1) y x3 ；(2) y x 2
1
；(3 y x 2 .
训练 1
已知 y (m2 2m 2) xm
2
1
2n 3 是定义域为 R 的幂函数，求 m，n 的值．
求幂函数的定义域时，通常要对幂的指数做变形，把负指数变成正指数，把分数指数变 成根式的形式，这样易于看出自变量的受限程度． 【幂函数的图象和性质】 如下图在同一坐标系内作出函数 y x ； y x2 ； y x3 ； y x 2 ； y x 1 的图象， 思考下列问题：
是常数．
【注意】只有满足函数解析式右边的系数为 1 ，底数为自变量 x ，指数为常数这三个条 x 4 件，才是幂函数．如：y＝3x2，y＝(2x)3，y＝ 2 幂函数．
问题 4 观察下列两组函数，说出它们的共同点与不同点： － (1)y＝x2，y＝x3，y＝ ，y＝x 1； 1 (2)y＝2x，y＝3x，y＝( )x，y＝0.3x. 2 共同点：均是幂的形式． 不同点：第一组： 是自变量，第二组： 是自变量．
(5)如果某人 t s 内骑车行进了 1 km，那么他骑车的平均速度 v＝ 这里 问题 1 是 的函数．
km/s，
上面 5 个问题中函数的对应法则分别是什么？
问题 2 上面 5 个问题中的 5 个函数有什么共同特征？ 上面 5 个问题中涉及到的函数，都是形如：y＝xα，其中 是自变量， 【幂函数定义】 一般地，函数 y＝xα 叫做幂函数，其中 x 是自变量， α 是常数．
鸡西市第十九中学学案
2014 年（ ）月（ ）日 班级 姓名
2.3 学习 目标 重点 难点
幂函数
1
1．通过具体实例了解 幂函数的概念 ； 2．会画幂函数 y x ， y x2 ， y x3 ， y x 1 ， y x 2 的图象，并通过其 图象 了解幂函数的图象和性质 ； 会用常见的幂函数的性质解决 比较大小 等问题． 类比研究 一般函数、指数函数、对数函数的方法 元，
；当 0<α<1 时，幂函数的图象 函数．
③α<0 时，幂函数的图象在区间(0，＋∞)上是
在第一象限内，当 x 从右边趋向原点时，图象在 y 轴右方无限地逼近 y 轴正半轴， 当 x 趋于＋∞时，图象在 x 轴上方无限地逼近 x 轴正半轴；
④幂指数互为倒数的幂函数在第一象限内的图象关于直线 y＝x 对称； ⑤在第一象限，作直线 x＝a(a>1)，它同各幂函数图象相交，按交点从下到上的顺序，幂 指数按从小到大的顺序排列． 问题 2 仔细观察这五个函数的图象，你能填写表格的内容吗？
1 2
1
1
(3)f(x)＝ x 2 3( x) 4
y
6 5 4 3 2 1 -6 -5 -4 -3 -2 -1 o -1 -2 -3 -4 -5 -6 1 2 3 4 5 6
1
y
6 5 4 3 2 1
x
-6 -5 -4 -3 -2 -1 o -1 -2 -3 -4 -5 -6
1 2 3
4 5 6
x
问题 1 你能从这五个具体的函数图象中，发现什么规律？ ①所有的幂函数在( ， )上都有定义，并且图象都过定点( ，并且在区间[0，＋∞)上是 , 函数． ； )； ②α>0 时，幂函数的图象通过 特别地，当 α>1 时，幂函数的图象