材料热力学第五章相图热力学
合集下载
材料科学基础 第5章 相 图剖析

dG i dni i dni
由于 所以
dni dni
dG (i i )dni
在 相和 相处于平衡时,dG=0 ,故:
i i
即两相平衡的条件是两相中同一组元的化学 位相等。此时,在两相之间转移趋于平衡。 若多元系中有C个组元,P个相,则它们的相 平衡条件可以写成:
由热力学原理可知,当组元在不同相间转 移时,将引起体系自由能的变化。对于一个多 元系,这种自由能变化可用下式表示:
dG Vdp SdT
dn
i
i
在等温等压条件下,可简化为:
dG
dn
i
i
如果体系中只有 和 两相,当极少量(d n i)的 i 组元从 相转移到 相中,则B
Pb
10
20
30
40
50
60
70
80
90
500 400 tA 300 327.5℃ 231.9℃ M α +L 183℃ 19 α +β F Pb 10 20 30 40 50 60 70 80 90 G Sn E 61.9 L+β N β 97.5 L
200 α 100
tB
W W1 W2
2的质量 Wx W1 x1 体系中相 W21 x 体系中相 的质量 体系中物质的总质量 2
t1 t2 M R P Q
L1
L2 L E x x2 20 40 K S N B 100
由上两式可得:
体系中 相1 相 中 B2 组元的含量 B 中 组元的含量 B组元的含量
W1 (x x1 ) W2 (x 2 x)
1083
时间
Cu 0
30
由于 所以
dni dni
dG (i i )dni
在 相和 相处于平衡时,dG=0 ,故:
i i
即两相平衡的条件是两相中同一组元的化学 位相等。此时,在两相之间转移趋于平衡。 若多元系中有C个组元,P个相,则它们的相 平衡条件可以写成:
由热力学原理可知,当组元在不同相间转 移时,将引起体系自由能的变化。对于一个多 元系,这种自由能变化可用下式表示:
dG Vdp SdT
dn
i
i
在等温等压条件下,可简化为:
dG
dn
i
i
如果体系中只有 和 两相,当极少量(d n i)的 i 组元从 相转移到 相中,则B
Pb
10
20
30
40
50
60
70
80
90
500 400 tA 300 327.5℃ 231.9℃ M α +L 183℃ 19 α +β F Pb 10 20 30 40 50 60 70 80 90 G Sn E 61.9 L+β N β 97.5 L
200 α 100
tB
W W1 W2
2的质量 Wx W1 x1 体系中相 W21 x 体系中相 的质量 体系中物质的总质量 2
t1 t2 M R P Q
L1
L2 L E x x2 20 40 K S N B 100
由上两式可得:
体系中 相1 相 中 B2 组元的含量 B 中 组元的含量 B组元的含量
W1 (x x1 ) W2 (x 2 x)
1083
时间
Cu 0
30
第五章 相图
第三节 二元共晶相图及合金凝固
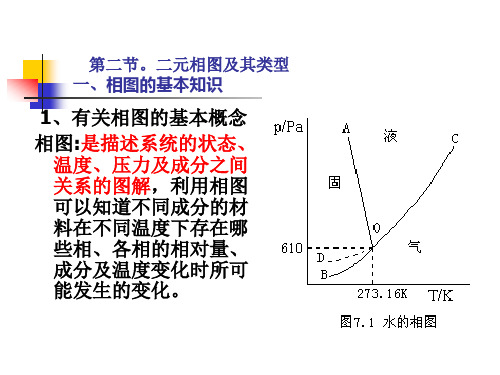
(2)共晶合金(分析要点) ① 凝固过程(冷却曲线、相变、组织示意图)。 ② 共晶线上两相的相对量计算。 ③ 室温组织(α+β)及其相对量计算。
2h
图4-28 Pb-Sn共晶合金平衡凝固过程示意图
1) 在液体中α 和β 同时具有析出条件,都可以析出。
2) 由于α 和β 析出过程在成分上可以互相补充和促进, 共同析出。
二元匀晶相图
一、匀晶相图及其分析 (1)匀晶转变:由液相直接结晶出单相固溶体的 转变。 (2)匀晶相图:具有匀晶转变特征的相图。 Cu-
Ni、 Cu-Au、 Au-Ag、Fe-Cr等
(3)相图分析(以Cu-Ni相图为例) 两点:纯组元的熔点; 两线:L, S相线; 三区:L, α, L+α。
固溶体合金的平衡结晶
金相法
膨胀法 电阻法
热分析法(以Cu-Ni系相图为例):
配制一系列成分不同的Cu-Ni合金; 测定上述合金的冷却曲线 找出各合金的临界点 以温度为纵坐标、以成分为横坐标的图中,将各临 界点连接起来即得到Cu-Ni合金相图
二.相图的建立
名称 晶格类型 熔点 合金1 合金2 合金3 …….. 合金9 合金10 合金11 A金属 fcc 高 100% 90% 80% …….. 20% 10% 0% B金属 fcc 低 0% 10% 20% ……. 80% 90% 100%
二、包晶体转变
过程
成分为P点合金的凝固 β 相的形核在α 相晶体和液体 的边界处,由于β 相的成分介于 液体和α 相之间,所以它是靠消 耗部分已有的α 相和部分液体来 实现。 β 相的生长在液体和α 相的交 界面处最有利,沿边界同时消耗 液体和α 相来长大,形成的β 相 包围在α 相外围,将α 相与液体 分隔开,所以把这种转变称为包 晶转变。
相图热力学

材料科学基础
Fundamentals of Materials Science
相图热力学
6.5 相图热力学
相图:表述物质成分、环境条件与 平衡相之间关系的图形。
✓平衡状态:系统吉布斯自由能处于最低所对应的状态。
相图是相平衡时热力学变量轨迹的几何表达。
实验测定相图
热力学数据
相图的测定: 二元相图:4000个(81%)(4950); 三元相图:8000(5%)(161700)。 四元相图:1000(0.1%)(3921225)
单相平衡
稳定的单相为在某一温度下, 该相的自由能最低,并且在该成分
点出的G(x)~x曲线为“上凹”。
1、在温度T下,AB组元可能形成α、 β两种相,为了降低系统的自由能, 显然将以单一的α存在比β相或α +β两相混合时的自由能低一些。
2、当曲线为“上凹”时,应为均匀成分xB的自由能最低。如果 某一处出现高出xB的成分时,因为物质不灭,必然存在另一处 为低于xB的成分,这时系统的自由能将高于均匀成分时的自由 能,系统未达到平衡,在动力学条件满足时,趋于形成单一均 匀成分。例如枝晶偏析较平衡态的能量高,均匀化退火加热时 通过扩散达到成分均匀的过程是自发的。
计算ΔGm变化。
(1)混合过程中H的变化:
N为原子数 , Z为配位数。
:混合能参量,形成一个A-B键内能的变化。 Ω: 相互作用参数, A,B原子间作用的大小。 • (Ω)0, A-B键稳定,A,B原子一般均匀混合。 • (Ω) 0, A,B原子倾向于偏聚。 • (Ω) =0,原子随机分布,理想固溶体。
(2)混合过程中S的变化: (3)固溶体自由能与成分温度的关系 :2.固溶体自由来自--成分曲线 G(x)为U 形线
• (Ω)0, A-B键稳定,A,B原子均匀混合。 • (Ω) 0, A,B原子倾向于偏聚。 • (Ω) =0,随机分布,理想固溶体。
Fundamentals of Materials Science
相图热力学
6.5 相图热力学
相图:表述物质成分、环境条件与 平衡相之间关系的图形。
✓平衡状态:系统吉布斯自由能处于最低所对应的状态。
相图是相平衡时热力学变量轨迹的几何表达。
实验测定相图
热力学数据
相图的测定: 二元相图:4000个(81%)(4950); 三元相图:8000(5%)(161700)。 四元相图:1000(0.1%)(3921225)
单相平衡
稳定的单相为在某一温度下, 该相的自由能最低,并且在该成分
点出的G(x)~x曲线为“上凹”。
1、在温度T下,AB组元可能形成α、 β两种相,为了降低系统的自由能, 显然将以单一的α存在比β相或α +β两相混合时的自由能低一些。
2、当曲线为“上凹”时,应为均匀成分xB的自由能最低。如果 某一处出现高出xB的成分时,因为物质不灭,必然存在另一处 为低于xB的成分,这时系统的自由能将高于均匀成分时的自由 能,系统未达到平衡,在动力学条件满足时,趋于形成单一均 匀成分。例如枝晶偏析较平衡态的能量高,均匀化退火加热时 通过扩散达到成分均匀的过程是自发的。
计算ΔGm变化。
(1)混合过程中H的变化:
N为原子数 , Z为配位数。
:混合能参量,形成一个A-B键内能的变化。 Ω: 相互作用参数, A,B原子间作用的大小。 • (Ω)0, A-B键稳定,A,B原子一般均匀混合。 • (Ω) 0, A,B原子倾向于偏聚。 • (Ω) =0,原子随机分布,理想固溶体。
(2)混合过程中S的变化: (3)固溶体自由能与成分温度的关系 :2.固溶体自由来自--成分曲线 G(x)为U 形线
• (Ω)0, A-B键稳定,A,B原子均匀混合。 • (Ω) 0, A,B原子倾向于偏聚。 • (Ω) =0,随机分布,理想固溶体。
第五章相图

• .马氏体相变速度极快,高达声速。
• .马氏体相变没有一个特定的温度, 而是在一个温度范围内进行的。
18
五、 有序—无序转变
• 随温度升降而出现低温有序和 高温无序的可逆转变过程称为 有序—无序转变。
19
五、 有序—无序转变
完全有序时 为,完全
无序时 为。 如: 磁铁矿
• 有序参数 ( )( )
• 碰撞频率υ表示为:
原子或分子的跃迁频 率
• υυ(Δ/)
原子或分子跃迁新旧 界面的迁移活化能
38
一、晶核形成过程动力学 均匀成核( )
• 成核速率可以写成:
• υυ(Δ/)
•
(Δ/)
• (Δ/)
•
(Δ/)
•·
常数
受核化位垒影响 的成核率因子
受原子扩散影响 的成核率因子
39
、均匀成核( )
见图
•
,只有在合适的过冷度下,
υ有最大值。
40
图—
41
、非均匀成核( )
• 非均匀成核是指借助于表面、界 面、微粒裂纹、器壁以及各种催 化位置等而形成晶核的过程。
4
图—
5
一、按热力学分类二级相变
• 相变时两相化学势相等,其一级偏微商 也相等,但二级偏微商不等,即:
• µµ • ( µ )( µ ) • ( µ )( µ )
6
一、按热力学分类二级相变
• ( µ )≠( µ ) • ( µ )≠( µ ) • ( µ )≠( µ ) • 即 µµ ≠;≠ ≠ β≠β α≠α • 式中β和α分别为等温压缩系数和等
29
三、晶核()形成条件
新相的 体积
• Δ=ΔΔ=Δγ
新相总 表面积
• .马氏体相变没有一个特定的温度, 而是在一个温度范围内进行的。
18
五、 有序—无序转变
• 随温度升降而出现低温有序和 高温无序的可逆转变过程称为 有序—无序转变。
19
五、 有序—无序转变
完全有序时 为,完全
无序时 为。 如: 磁铁矿
• 有序参数 ( )( )
• 碰撞频率υ表示为:
原子或分子的跃迁频 率
• υυ(Δ/)
原子或分子跃迁新旧 界面的迁移活化能
38
一、晶核形成过程动力学 均匀成核( )
• 成核速率可以写成:
• υυ(Δ/)
•
(Δ/)
• (Δ/)
•
(Δ/)
•·
常数
受核化位垒影响 的成核率因子
受原子扩散影响 的成核率因子
39
、均匀成核( )
见图
•
,只有在合适的过冷度下,
υ有最大值。
40
图—
41
、非均匀成核( )
• 非均匀成核是指借助于表面、界 面、微粒裂纹、器壁以及各种催 化位置等而形成晶核的过程。
4
图—
5
一、按热力学分类二级相变
• 相变时两相化学势相等,其一级偏微商 也相等,但二级偏微商不等,即:
• µµ • ( µ )( µ ) • ( µ )( µ )
6
一、按热力学分类二级相变
• ( µ )≠( µ ) • ( µ )≠( µ ) • ( µ )≠( µ ) • 即 µµ ≠;≠ ≠ β≠β α≠α • 式中β和α分别为等温压缩系数和等
29
三、晶核()形成条件
新相的 体积
• Δ=ΔΔ=Δγ
新相总 表面积
第五章材料的相结构及相图

电子浓度为21/13时,为复杂立方结构,或称γ黄铜结构
电子浓度为21/12时,为密排六方结构,或称ε黄铜结构。 其他影响因数:尺寸因素及组元的电负性差。 例:电子浓度21/14的电子化合物,当组元原子尺寸差较小时,倾向于形成密排六方 结构;当尺寸差较大时,倾向于形成体心立方结构;若电负性差较大,则倾向于形 成复杂立方及密排六方结构。 性能:结合键为金属键,具有明显的金属特性。电子化合物的熔点及硬度较高 ,脆性较大
有些与金属固溶体类似,如原子半径差越小,温度越高,电负性差越小,离子间的 代换越易进行 ,其固溶度也就越大。当两化合物的晶体结构相同,且在其他条件 有利的情况下 ,相同电价的离子间有可能完全互换而形成无限固溶体 。
此外,必须考虑以下情况 (1) 保持晶格的电中性 ,代换前后离子的总电价必须相等 若相互代换的离子间电价相等,称为等价代换, 例 钾 长 石 K [AlSi303]与钠长石Na [AlSi303〕中的K+与Na+的代换及上例中Si4+代 换 Ti4+, Mg2+与Fe2+的互换等。
eC、eA分别为在非电离状态下正离子及负离子的价电子数
类型:一般有AB、A2B(或AB2)等类型 特点:种类繁多,晶体结构十分复杂,包括从离子键、共价键过渡到 金属键为主的一系列化合物 如: Mg2Si 电负性影响大,较强的离子键
Mg2Sn 电负性差减小,共价键为主,呈半导体特征 Mg2Pb 金属键占主导地位
之差超过14%~15%,则固溶度(摩尔分数)极为有限;
原因:点阵畸变导致能量升高,Δ r越大,点阵畸变能越高
2
r
rA rB rA
按弹性力学方法计算
2 3 r rB 3 8 G rB A 8 G rB r rA
材料科学基础I 第五章 (相图)
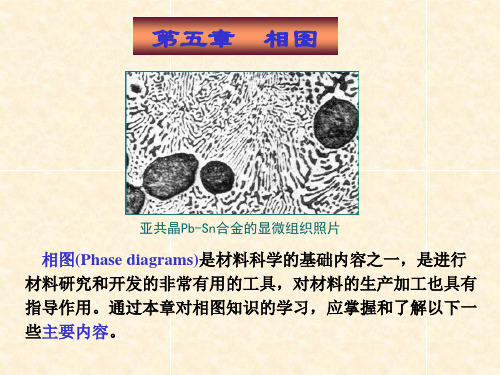
F = 0的含义是:在保持系统平衡状态不变的条件下,没有可以 的含义是:在保持系统平衡状态不变的条件下, 的含义是 独立变化的变量。 独立变化的变量。即,任何变量的变化都会造成系统平衡状态 的变化。 的变化。
纯水的PT相图: 纯水的 相图:在a点,水在 相图 点 水在1 大气压、 ℃ 条件下 保持液(水 条件下, 大气压、(0℃)条件下,保持液 水) –固(冰)二相平衡。温度升高,冰 二相平衡。 固 冰 二相平衡 温度升高, 溶化成水;温度降低, 溶化成水;温度降低,水结晶成 也就是说,此时水的液-固平 冰。也就是说,此时水的液 固平 衡转变是在恒温(0℃ 下进行的 下进行的。 衡转变是在恒温 ℃)下进行的。 b点是气 液二相平衡点,意义与 点是气–液二相平衡点 点是气 液二相平衡点,意义与a 点相似。 之间(0℃ 点相似。在a、b之间 ℃~100℃), 、 之间 ℃, 水是单一的液相(P =1),此时F =1, 水是单一的液相 ,此时 , 这说明在此范围内温度的变化不 会引起状态的改变。 会引起状态的改变。
二、相图的建立
建立相图的方法有两种: 建立相图的方法有两种: 利用已有的热力学参数,通过热力学计算和分析建立相图; 利用已有的热力学参数,通过热力学计算和分析建立相图; 依靠实验的方法建立相图。 依靠实验的方法建立相图。 目前计算法还在发展之中,实际使用的相图都是实验法建立的。 目前计算法还在发展之中,实际使用的相图都是实验法建立的。 实验法建立相图的原理和步骤: 实验法建立相图的原理和步骤: 二元合金相图的建立为例。 以A-B二元合金相图的建立为例。 二元合金相图的建立为例 首先, 首先,将A-B二元合金系分成 二元合金系分成 若干种不同成分的合金。 若干种不同成分的合金。 1) 合金成分间隔越小,合金数目 合金成分间隔越小, 越多,测得的相图越精确; 越多,测得的相图越精确; 2) 合金成分间隔不需要相等。 合金成分间隔不需要相等。
材料科学基础-第五章 材料的相结构及相图
相律在相图中的应用
C
2 二元系
P 1 2
3 1
f 2 1 0
3 2 1 0
含义
单相合金,成分和温度都可变 两相平衡,成分、相对量和温度 等因素中只有一个独立变量 三相平衡,三相的成分、相对 量及温度都确定 单相合金其中两个组元的含量 及温度三个因素均可变 两相平衡,两相的成分、数量 及温度中有两个独立变量 三相平衡,所有变量中只有 一个是独立变量 四相平衡所有因素都确定不变
结构简单的具有极高的硬度及熔点,是合金工具钢和硬 质合金的重要组成相。
I. 间隙化合物
间隙化合物和间隙固溶体的异同点
相同点: 非金属原子以间隙的方式进入晶格。
不同点: 间隙化合物:间隙化合物中的金属组元大多与自 身原来的结构类型不同 间隙固溶体:间隙固溶体中的金属组元仍保持自 身的晶格结构
I. 尺寸因素
II. 晶体结构因素 组元间晶体结构相同时,固溶度一般都较大,而且有可 能形成无限固溶体。若不同只能形成有限固溶体。
III. 电负性差因素
两元素间电负性差越小,越易形成固溶体,且形成的 固溶体的溶解度越大;随两元素间电负性差增大,固 溶度减小。
1)电负性差值ΔX<0.4~0.5时,有利于形成固溶体 2)ΔX>0.4~0.5,倾向于形成稳定的化合物
Mg2Si
Mg—Si相图
(2)电子化合物
由ⅠB族或过渡金属元素与ⅡB,ⅢB,ⅣB族元素 形成的金属化合物。 不遵守化合价规律,晶格类型随化合物电子浓度 而变化。 电子浓度为3/2时: 呈体心立方结构(b相); 电子浓度为21/13时:呈复杂立方结构(g相); 电子浓度为21/12时。呈密排六方结构(e相);
NaCl型 CaF2型 闪锌矿型 硫锌矿型 (面心立方) (面心立方) (立方ZnS) (六方ZnS)
材料科学基础 第五章 5.1-5.4相图
5.2.3 杠杆定律
设成份为 X的合金的总重量为1,液相的相对重量为 QL,其 成份为 X1,固相相对重量为Qα,其成份为X2,则 :
5.2.4 相图的类型和结构 根据组元的多少,可分为单元系、二元系、三元 系 …. 相图。
二元系相图的类型有:
① 液态无限溶解,固态无限溶解 -匀晶相图; ②液态无限溶解,固态有限溶解 -共晶相图和包晶
共晶组织:共晶转变产物。(是两相混合物)
共晶合金的特殊性质: ①比纯组元熔点低,简化了熔化和铸造的操作; ②共晶合金比纯金属有更好的流动性,其在凝固之 中防止了阻碍液体流动的枝晶形成,从而改善铸造 性能; ③恒温转变(无凝固温度范围)减少了铸造缺陷, 例如偏聚和缩孔; ④共晶凝固可获得多种形态的显微组织,尤其是规 则排列的层状或杆状共晶组织可能成为优异性能的 原位复合材料(in-situ composite )。
5.2.2 相律
相律(phase rule)是表示在平衡条件下,系统的自 由度数、组元数和相数之间的关系,是系统的平 衡条件的数学表达式。 相律数学表达式:f = C – P + 2 式中 P—平衡相数 C—体系的组元数 f—体系自由度(degrees of freedom) 数 2-温度和压力 自由度数 f:是指不影响体系平衡状态的独立可 变参数(温度、压力、浓度等)的数目。 在恒压下,相律表达式: f = C – P + 1
相律的应用
① 利用它可以确定系统中可能存在的最多平衡相数 单元系,因f ≥0,故 P≤1-0+1=2,平衡相最大为二个。 注意:这并不是说,单元系中能够出现的相数不能超过二 个,而是说,某一固定 T下,单元系中不同的相只能有两 个同时存在,而其它相则在别的条件下存在。
第五章二元相图资料
f = 总变量数 非独立变量数
[P(C 1) 2] C(P 1) C P 2
5-1 相图的基本知识
对于不含气相的凝聚态体系,压力在通常范围的变化 对平衡状态的影响极小。因此,相律可写成如下形式:
f C P 1
相律给出了平衡状态下多元多相体系中中存在的相数 与组元数及温度、压力之间的关系,对分析和研究相图具 有重要的意义。
合金如CuNi、AuAg、AuP等只发生匀晶转变,其相图
均为匀晶相图。
5-2 二元匀晶相图
临界点:a点—纯Cu的熔点 b点—纯Ni的熔点
临界线:acb线—液相线(凝固 开始线)
adb线—固相线(凝固 终了线)
相区:液相线以上为液相区, 固相线以下为固相区,而液 相线与固相线所包围的区域 为液、固两相平衡共存区。
整理可得:Q QL
wBo wB
wBL wBo
ao ob
L
o
L+
wBL wBo wB
A
wB
B
o
QL
Q
杠杆定律的力学比喻
5-2 二元匀晶相图
杠杆定律:
%
Q Qo
ao ab
wBo wBL wB wBL
100%
L%
QL Qo
ob ab
wB wB
wBO wBL
100%
L
o
L+
wBL wBo wB
wSn /%
PbSn二元共晶相图
成分为e的液相中同时凝固出成分为m的 相和成分为n的 相
Le Te (m n )
5-3 二元共晶相图
单相区:液相L相区
固相 相区
固相 相区
两相区:L + 相区
[P(C 1) 2] C(P 1) C P 2
5-1 相图的基本知识
对于不含气相的凝聚态体系,压力在通常范围的变化 对平衡状态的影响极小。因此,相律可写成如下形式:
f C P 1
相律给出了平衡状态下多元多相体系中中存在的相数 与组元数及温度、压力之间的关系,对分析和研究相图具 有重要的意义。
合金如CuNi、AuAg、AuP等只发生匀晶转变,其相图
均为匀晶相图。
5-2 二元匀晶相图
临界点:a点—纯Cu的熔点 b点—纯Ni的熔点
临界线:acb线—液相线(凝固 开始线)
adb线—固相线(凝固 终了线)
相区:液相线以上为液相区, 固相线以下为固相区,而液 相线与固相线所包围的区域 为液、固两相平衡共存区。
整理可得:Q QL
wBo wB
wBL wBo
ao ob
L
o
L+
wBL wBo wB
A
wB
B
o
QL
Q
杠杆定律的力学比喻
5-2 二元匀晶相图
杠杆定律:
%
Q Qo
ao ab
wBo wBL wB wBL
100%
L%
QL Qo
ob ab
wB wB
wBO wBL
100%
L
o
L+
wBL wBo wB
wSn /%
PbSn二元共晶相图
成分为e的液相中同时凝固出成分为m的 相和成分为n的 相
Le Te (m n )
5-3 二元共晶相图
单相区:液相L相区
固相 相区
固相 相区
两相区:L + 相区
材料热力学 第5章 两相平衡
第五章 两相平衡热力学
二组元材料的热力学理论是材料热力学最基 本的内容,本章主要讨论二组元材料的两相 平衡热力学问题。
某一个温度T下!
5. 二组元两相平衡热力学
以二元系相平衡(Phase equilibrium)为 基础,分析材料学中的一些基本问题,掌握 运用热力学分析材料平衡相成分以及平衡组 织的基本方法。
5.3.1 第二相为纯组元时的溶解度
5.3.2 第二相为化合物时的溶解度
脱溶序列:
各个合计不同成分脱溶序列不一定相同,有些合金不一 定出现G.P区或过渡相;
同一系不同成分的合金,在同一温度下时效,可能有不 同脱溶序列。过饱和度大的合金更易出现G.P区或过渡 相;
同成分合金,时效温度不同,脱溶序列也不一样。一般 情况下,时效温度高,预脱溶阶段或过渡相出现的过渡 结构较少。温度低时,则有可能只停留在偏聚区或过渡 相阶段;
在成分一定(如C3)时,温 度低(T1)三种结构的产物均 可析出,温度稍高(T2)只可 能析出过渡相及平衡相,更 高温度(T3)则只能析出平衡 相。
5.4 固溶体间的两相平衡
5.5 相稳定化参数
如合金固态存在着α及β两相,两相 在某温度T1时的自由能-成分关系曲 线见图。由公切线定律可确定某一 合金(x0) T1时平衡的α及β相成分。 作不同温度下的自由能-成分关系 曲线,则由一系列的平衡α及β相成 分可得β相在α相中的固溶度曲线。 ;
若此合金系可能出现过渡相及G.P区,它们的自由能成分关系曲线分别为G过和GGP区,G.P的结构总与基体 相同,所以其自由能曲线与基体自由能曲线连在一起。
根据公切线定律同样可确定过渡相及G.P区在α相中之 固溶度曲线。
亚稳定相图 1.β相固溶度曲线;2.过渡相(β’) 固溶度曲线;3. G.P区固溶度曲线
二组元材料的热力学理论是材料热力学最基 本的内容,本章主要讨论二组元材料的两相 平衡热力学问题。
某一个温度T下!
5. 二组元两相平衡热力学
以二元系相平衡(Phase equilibrium)为 基础,分析材料学中的一些基本问题,掌握 运用热力学分析材料平衡相成分以及平衡组 织的基本方法。
5.3.1 第二相为纯组元时的溶解度
5.3.2 第二相为化合物时的溶解度
脱溶序列:
各个合计不同成分脱溶序列不一定相同,有些合金不一 定出现G.P区或过渡相;
同一系不同成分的合金,在同一温度下时效,可能有不 同脱溶序列。过饱和度大的合金更易出现G.P区或过渡 相;
同成分合金,时效温度不同,脱溶序列也不一样。一般 情况下,时效温度高,预脱溶阶段或过渡相出现的过渡 结构较少。温度低时,则有可能只停留在偏聚区或过渡 相阶段;
在成分一定(如C3)时,温 度低(T1)三种结构的产物均 可析出,温度稍高(T2)只可 能析出过渡相及平衡相,更 高温度(T3)则只能析出平衡 相。
5.4 固溶体间的两相平衡
5.5 相稳定化参数
如合金固态存在着α及β两相,两相 在某温度T1时的自由能-成分关系曲 线见图。由公切线定律可确定某一 合金(x0) T1时平衡的α及β相成分。 作不同温度下的自由能-成分关系 曲线,则由一系列的平衡α及β相成 分可得β相在α相中的固溶度曲线。 ;
若此合金系可能出现过渡相及G.P区,它们的自由能成分关系曲线分别为G过和GGP区,G.P的结构总与基体 相同,所以其自由能曲线与基体自由能曲线连在一起。
根据公切线定律同样可确定过渡相及G.P区在α相中之 固溶度曲线。
亚稳定相图 1.β相固溶度曲线;2.过渡相(β’) 固溶度曲线;3. G.P区固溶度曲线
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
X
(2) 2 1
(5.13)
敞开系统的 d T V d P i d ni
i
dG SdT VdP i*dni RT ln X i dni RT ln i dni (5.14)
i i i
例氢 关气 系溶 如解 图度 和 所氢 示气 。压 力 的 平 方 根 的 比
5.2
含图 量 的总 变结 化说 对明 于了 氢在 气熔 溶融 解铁 度中 的合 影金 响元 。素
5.1
化学势定义为(2.40)
G i n i T , P , n j
引入活度,如式子(3.77), with
k
(5.23)
将 ei 的定义代入,当X0→1时, 根据3.84式的 定义 % i / X i 100 M i / M 0 得:
j
( j) i
230 M i ( j ) M 0 M j ei M0 M0
(5.24)
相应的5.13式也可以写成:
log
% i
e %j
( j) i j
ai lim i 1 X i 1 X i
如果溶质浓度由重量百分比来表示,上面的式子 可以表示为:(3.81)
a % i RT ln a & lim i 1 X 0 1 % i
i % i
% i
由 X 0 1(下标0表示溶剂)和温度以及压力可以 确定系统的状态 (此时 )。 X 1 0和 X 2 0
(5.25)
对于图5.1中所示的氢溶解在低浓度的铁合金中, 则5.25式可写成:
log
% H
e
(H ) H
%H e % j
( j) H
(5.26)
图5.2表示了氢气在一定压力范围内满足理想状态, 对于这个系统有:
e
(H ) H
log lim X 0 1 % H
% H ( j)
2
zN [2 X a X b w ab 2 X a X c w ac 2 X b X c w bc X a (1 X a ) w aa
(5.33)
因为Xa+Xb+Xc=1
1 U mix zN [ X a X b ( 2 wab waa wbb ) 2 X a X c ( 2 wac waa wcc ) X b X c ( 2 wbc wbb wcc )] H mix
第五章三元相图及溶液模型 潘伟
氢气在铁中的溶解遵循Sieverts定律;气体在金 属中的分解,不管是固态还是液态金属,都是原 子形态的,和在自然界中分子形态的不同。对于 反应:
H 2 (g ) 2H
2 H
(5.4)
给出平衡常数
a (% H ) K pH 2 pH 2
% 2 H
(5.5)
% H
0
因而:
log
eH % j
(5.27)
% 图5.3表示, log H 对于溶质的百分
含量成线性关系,
eH
j
为常数。
5.2 正规溶液的深入讨论
正规溶液相对理想溶液而言在某些性质方面更 接近于实际情况。通过引进非理想混和热熵以 及非最近邻原子之间的相互作用,它的应用可 以得到扩展。混合时总的熵变分两部分:
0 1
0 其中 1 是无限稀溶液为参考态时 1 的值。以无限稀溶
液为参考态时 法近似 :
0 1为1。等号右边的一次微分可以用差分
ln 1 ln 1 X2 X2 X 2 X 2
其中 1 对仅有组分2,浓度为X2的时候 的值,这样忽略高次项得:
( 2) 1 是
(1) ( 2) ( 3) 0 ln 1 ln 1 ln 10 ln 1 0 ln 1 0 1 1 1
一般说来,在二元系统中,确定了温度、压 力以及一个组分的参数,如X1,这个系统的状态 就确定了。 即在常温常压下, a1=a1(X1) (5.1)
然而,在常温常压的三元系统中,要确定这 个系统的状态,除了温度和压力值,还需要两个 组分的参数:
a1=a1(X1,X2)
(5.2)
Wagner指出,图5.1中给出的溶质和溶质之间的
G xs H mix T S t NX a X b z i wi wi'
i
(5.30)
仍然保留4.9式Hildebrand模型的形式,加入一个参量 α后得
reg Gmix X a X b RT X a ln X a X b ln X b
扩展为三元系统的正规溶液时先做了如下的规定,遵 循 Hildebrand 模型且仅讨论最近邻原子的相互作用且
(5.21)
或者表示为:
ln i ln
% i
M k ln ln 1 X k 1 M k 0
0 i
(5.22)
因为
( j) i
0 i 是一个常数,所以:
M0 M j ln i ln i% X j X j M0 Xk M0 Mk
(5.32)
混合前的纯物质中,分别有1/2z na =1/2zNXa 个 A-A对, 1/2z nb =1/2zNXb 个B-B对,1/2z nc =1/2zNXc 个C-C对。则混合后的内能变化为:
U mix 1 2 2 2 X b w bb X c w cc X a w aa X b w bb X c w cc ) 1 2 X b (1 X b ) w bb X c (1 X c ) w cc zN (2 X a X b w ab 2 X a X c w ac 2 X b X c w bc X a w aa
S mix S 0
T
0
C P dT T
(5.28)
其中 S 0是在0K时混合熵的变化,它仅仅和溶液 的构成相关联。第二项是混合时热温熵的改变, 它表示溶液在混合时原子和分子振动能的变化。
对于理想溶液的混合,当溶质是随机分布时,构型 熵的变化表示为:
S
id mix
R X i ln X i
因为有:
ln 1 ln n 2 n1
2
(5.15)
(5.16)
ln 1 X 2 ln 2 X 1 X 2 n 2 X 1 n1
根据摩尔分数的定义可知:
n1 n2 n2 1 X 2 n2 n n n n n 2 n 1 2 3 1 2
对于常用的质量百分比浓度来说,对体系溶质与 溶质之间的相互作用系数定义如下:
e
( 2) 1
log lim X 0 1 % 2
% 1
(5.20)
如果在摩尔分数条件下的参考状态为纯组元, 则(3.86)式为:
% i
M k i Mk i X0 Xk 1 X k 1 0 0 M M k k 0 i 0 i
(5.37)
与理想溶液具有最小自由能相对应,溶液组元随机 分布的结构熵ΔS0是最大的。在真实溶液中,以熵为 驱动力使系统趋向于无序的过程受到化学键能的调 制,趋向于形成低能键,即原子以最小结合能结合
例如,在 A-B 二元系统, w= 1/2(2wab-waa-wbb)<0 时,会 形成 A-B原子团簇,而在w>0时,趋向于形成A的原子团 簇和B的原子团簇。这种团簇的形成可由化学方程式表示
(5.34)
在三元体系中过剩Gibbs函数表示为
G xs ab X a X b ac X a X c bc X b X c
混合Gibbs自由能
reg Gmix ab X a X b ac X a X c bc X b X c
(5.35)
RT X a ln X a X b ln X b X c ln X c
相互作用关系可以用活度系数来表示。在用摩尔
分数表示时,5.2式可以写成如下形式
a1=a1(X1,X2)
对于三元以上系统
1 1 X 1 , X 2 (5.6)
1 1 X 1 , X 2 ,
(5.7)
将lnγ1展开成Maclaurin级数:
ln 1 ln 1 ln 1 ln 1 ln X 1 X2 X3 X 1 X 2 X 3 1 2 2 ln 1 2 ln 1 X1 X1X 2 (5.8) 2 2 X X X 1 1 2
组分1的活度系数 。
0 表示溶质组份i对组分1的活度系数 1
Wagner同时也定义了溶质和溶质之间的相互作 用系数 1( 2 ) :
( 2) 1
ln 1 lim X 0 1 X 2
(5.12)
所以5.11式又可表达为
ln 1 ln 1 X
0
(1) 1 1
(5.36)
这种概念也可以扩展到混和离子熔化物以及间隙固溶体 的按化学计量比组成的多相体系,如(A, B)x, (C, D)y。
5.3 准化学溶液模型
正规溶液模型假定组元在溶液中随机分布,有非零
的混合熵,即形成溶液时化学结合能改变。实际溶
液混合时体系自由能应减小
G mix H mix T S t T S 0
在无限稀薄溶液中对第一项进行近似 : ( 2) 0 ln 1 ln 1 / 1 1( 2 ) (5.9) X2 X2 ln 0 X 2 X2 0 1
