高一数学必修3第二章统计复习题和答案
(完整)高一数学必修三《统计》知识点+练习+答案,推荐文档
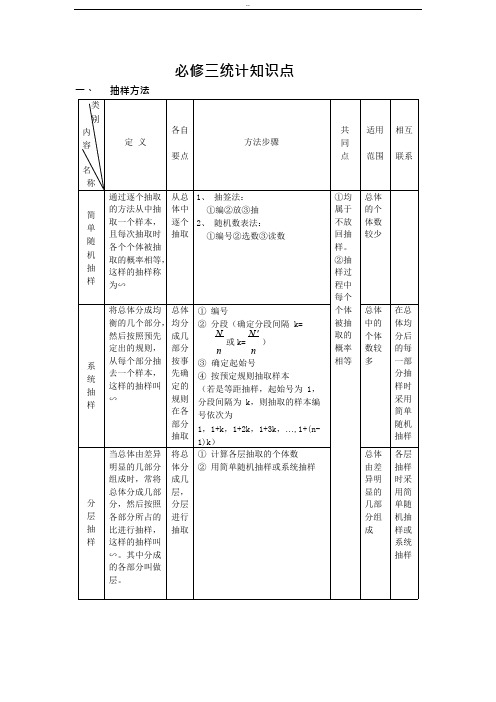
必修三统计知识点二、统计初步有关概念和公式:1、频数——落在各个小组的数据的个数叫~。
2、频率——每一个小组频数与数据的比值叫做这一组的~。
3、总体——所要考察对象的全体叫做~。
4、个体——每一个考察对象~。
5、样本——从总体中所抽取的一部分个体叫做总体的一个样本。
6、样本容量——样本中个体的数目叫做~。
7、众数——在一组数据中,出现次数最多的数据叫做这组数据的众数。
8、中位数——将一组数据按从小到大排列,把处在最中间位置的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数。
9、总体分布——总体取值的概率分布规律通常称为~。
10、连续型总体——可以在实数区间取值的总体叫~。
11、累积频率——样本数据小于某一数值的频率,叫做~。
计算最大值与最小值的差决定组距与数据列法决定分点列表12、频率分布表试验结果频数频率表的行式分组个数累计频数频率累积频率(有时可省略)(有时可省略)横轴——实验结果纵轴频率条形图用高度表示各取值的频率适用于个体取不同值较少横轴——产品尺寸纵轴——频率/组距13、直方图用图形面积的大小表示在各个区间内取值的概率适用于个体在区间内取值横轴——产品尺寸累积频率分布图纵轴——累计频率反映一组数据的分布情况14、总体分布曲线——当样本容量无限增大、分组的组距无缩限小时、频率分布直方图就会无限趋近于一条光滑曲线,这条曲线叫总体密度曲线。
以这条曲线为图象的函数叫做总体的概率密度函数。
总体密度函数反映了总体分布,即反映总体在各个范围内取值的概率。
P(a<ξ<b)的值等于直线 x=a,x=b 与曲线、x 轴围成的图形面积。
15、累积分布曲线——当样本容量无限增大、分组的组距无缩限小时,累积频率分布图就会无限趋近于一条光滑曲线,这条曲线叫累积分布曲线。
它反映了总体的累积分布规律,即曲线上任意一点 P(a,b)纵坐标 b,表示总体取小于 a 的值的概率。
1①正态总体的概率密度函数f(x)-(x - )22 2, ∈R(其中 总体的平均数, 总体的标准差,N(μ,σ2)—正态总体,有时记作 N(μ,σ2)1)曲线在轴上方,并且关于直线 x=对称:②正态曲线的性质2)曲线在x=μ时处于最高点,由这一点向左、右两边延伸时,曲线逐渐下降:3)曲线的对称轴位置由μ确定:直线的形状由σ确定,σ越大,曲线的形状越“矮胖”反过来曲线越“高瘦”③正态曲线在几个区间上的取值:区间取值概率(μ-σ,μ+σ)68.3%(μ-2σ,μ+2σ)95.44%(μ-3σ,μ+3σ)99.7%16、质控图④小概率事件——通常指发生的概率小于5%的事件。
高一数学人教A版必修三练习:第二章统计2.2.1含解析

(本栏目内容,在学生用书中以独立形式分册装订!)一、选择题(每小题5分,共20分)1.对于样本频率分布折线图与总体密度曲线的关系,下列说法中正确的是()A.频率分布折线图与总体密度曲线无关B.频率分布折线图就是总体密度曲线C.样本容量很大的频率分布折线图就是总体密度曲线D.如果样本容量无限增大、分组的组距无限减小,那么频率分布折线图就会无限接近总体密度曲线解析:总体密度曲线通常是用样本频率分布估计出来的.而频率分布折线图在样本容量无限增大,分组的组距无限减小的情况下会无限接近于一条光滑曲线,这条光滑曲线就是总体密度曲线.答案: D2.下面是甲、乙两名运动员某赛季一些场次得分的茎叶图,据图可知()A.甲运动员的成绩好于乙运动员B.乙运动员的成绩好于甲运动员C.甲、乙两名运动员的成绩没有明显的差异D.甲运动员的最低得分为0分解析:从茎叶图可以看出,甲运动员的成绩集中在大茎上的叶多,故成绩好.故选A.答案: A3.某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100].若低于60分的人数是15,则该班的学生人数是( )A .45B .50C .55D .60解析: 设该班人数为n ,则20×(0.005+0.01)n =15,n =50,故选B. 答案: B4.观察新生婴儿的体重,其频率分布直方图如图所示,则新生婴儿体重在[2 700,3 000)内的频率为( )A .0.001B .0.1C .0.2D .0.3解析: 由频率分布直方图的意义可知,各小长方形的面积=组距×频率组距=频率,即各小长方形的面积等于相应各组的频率.在区间[2 700,3 000)内频率的取值为(3 000-2 700)×0.001=0.3.故选D.答案: D二、填空题(每小题5分,共15分)5.一个社会调查机构就某地居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10 000人中再用分层抽样方法抽出100人作进一步调查,则在[2 500,3 000)(元)月收入段应抽出________人.解析:由题意得在[2500,3000)(元)月收入段应抽出的人数为0.0005×500×100=25.答案:256.某省选拔运动员参加2015年的全运会,测得7名选手的身高(单位:cm)分布茎叶图如图所示,记录的平均身高为177 cm,其中有一名候选人的身高记录不清,其末位数为x,那么x的值为________.解析:依题意得180×2+1+170×5+3+x+8+9=177×7,x=8.答案:87.下面是某中学期末考试各分数段的考生人数分布表:则分数在[700,800)的人数为________人.解析:由于在分数段[400,500)内的频数是90,频率是0.075,则该中学共有考生900.075=1 200,则在分数段[600,700)内的频数是1 200×0.425=510,则分数在[700,800)内的频数,即人数为1 200-(5+90+499+510+8)=88.答案:88三、解答题(每小题10分,共20分)8.下表给出了某校500名12岁男孩中用随机抽样得出的120人的身高(单位:cm).(1)列出样本频率分布表;(2)画出频率分布直方图;(3)估计身高小于134 cm的人数占总人数的百分比.解析:(1)样本频率分布表如下:(2)其频率分布直方图如下:(3)由样本频率分布表可知身高小于134 cm 的男孩出现的频率为0.04+0.07+0.08=0.19,所以我们估计身高小于134 cm 的人数占总人数的19%.9.为了调查甲、乙两个交通站的车流量,随机选取了14天,统计每天上午8:00~12:00间各自的车流量(单位:百辆),得如图所示的统计图,试求:(1)甲、乙两个交通站的车流量的极差分别是多少? (2)甲交通站的车流量在[10,40]间的频率是多少? (3)甲、乙两个交通站哪个站更繁忙?并说明理由.解析: (1)甲交通站的车流量的极差为73-8=65(百辆),乙交通站的车流量的极差为71-5=66(百辆).(2)甲交通站的车流量在[10,40]间的频率为414=27.(3)甲交通站的车流量集中在茎叶图的下方,而乙交通站的车流量集中在茎叶图的上方,从数据的分布情况来看,甲交通站更繁忙.。
高中数学必修3第二章:统计2.3变量间的相关关系

Y 研考点·知规律
探究悟道 点拨技法
题型一 相关关系的判断 【例 1】 河北国欣农研会的科研人员在 7 块并排、形状大小 相同的试验田上对某棉花新品种进行施化肥量 x 对产量 y 影响的 试验,得到如下表所示的一组数据(单位:kg): 施化肥量 x 15 20 25 30 35 40 45 棉花产量 y 330 345 365 405 445 450 455
D 读教材·抓基础
回扣教材 扫除盲点
课本导读
1.两个变量的线性相关 (1)在散点图中,点散布在从 左下角 到 右上角的区域,对于 两个变量的这种相关关系,我们将它称为正相关. (2)在散点图中,点散布在从 左上角 到 右下角的区域,两个 变量的这种相关关系称为负相关. (3)如果散点图中点的分布在整体上看大致在一条直线附近 , 就称这两个变量之间具有线性相关关系,这条直线叫做回归直线.
() (A)她儿子10岁时的身高一定是145.83 cm (B)她儿子10岁时的身高在145.83 cm以上 (C)她儿子10岁时的身高在145.83 cm左右 (D)她儿子10岁时的身高在145.83 cm以下
2.经调查知,某品牌汽车的销售量y(辆)与广告费用x(万元)之 间的回归直线方程为 yˆ =250+4x,当广告费用为50万元时,预计 汽车销售量约为 ______辆.
2.回归方程 (1)最小二乘法:使得样本数据的点到回归直线的 距离的平方
和最小的方法叫最小二乘法.
(2)回归方程:两个具有线性相关关系的变量的一组数据:(x1,
^^ ^
y1)、(x2,y2),…,(xn,yn).其回归方程为y=bx+a,则
n
n
xi- x yi- y xiyi-n x y
(完整版)高一数学必修3第二章统计复习题和答案

高一数学必修 3 第二章统计复习题一、选择题1.某机构进行一项市场检查,规定在某商场门口随机抽一个人进行咨询检查,直到检查到预先规定的检查人数为止,这类抽样方式是A .系统抽样B.分层抽样C.简单随机抽样D.非以上三种抽样方法2.一个年级有 12 个班,每个班的同学从 1 至 50 排学号,为了沟通学习经验,要求每班学号为14 的同学留下进行沟通,这里运用的是A. 分层抽样B. 抽签抽样C.随机抽样D. 系统抽样3. 某单位有员工750 人,此中青年员工350 人,中年员工250 人,老年员工150 人,为了认识该单位员工的健康状况,用分层抽样的方法从中抽取样本,若样本的青年员工为7 人,则样本容量为A .7B.15C. 25D. 354.为认识 1200 名学生对学校教改试验的建议,打算从中抽取一个容量为30的样本,考虑采纳系统抽样,则分段的间隔k 为A. 40B. 30C. 20D. 125.在某项体育竞赛中,七位裁判为一选手打出的分数以下:90899095939493去掉一个最高分和一个最低分后,所剩数据的均匀值和方差分别为A . 92,2B. 92, 2.8C. 93, 2 D . 93, 2.86.变量 y 与 x 之间的回归方程A .表示 y 与 x 之间的函数关系B .表示 y 和 x 之间的不确立关系C.反应 y 与 x 之间的真切关系达到最大限度的符合 D .反应 y 和 x 之间真切关系的形式7. 线性回归方程?y bx a 必过点A . (0,0)B. ( x, 0)C. (0,y )D. ( x,y )8.在以下各图中,每个图的两个变量拥有有关关系的图是( 1)( 2)(3)(4)A .( 1)( 2)B.( 1)( 3)C.( 2)( 4)D.( 2)( 3)9.一个容量为 40 的样本数据分组后组数与频数以下:[25, 25.3), 6;[ 25.3, 25.6),4;[ 25.6,25.9), 10;[ 25.9, 26.2), 8;[ 26.2, 26.5), 8;[ 26.5, 26.8), 4;则样本在[25,25.9)上的频次为31C.1D.1A .B .20102410.容量为100的样本数据,按从小到大的次序分为8组,以下表:组号12345678数 10 13x14 1513129第三 的 数和 率分 是()A 14 和 0.14B0.14 和 14C1和 0.14D1 和 114 3 1411. 已知数据 a 1, a 2 ,..., a n 的均匀数 a ,方差 S 2 , 数据 2a 1 ,2a 2 ,..., 2a n 的均匀数和方差 ( )A . a, S 2B . 2a, S 2C . 2a, 2S 2D . 2a, 4S 212、在抽 品尺寸的 程中,将其尺寸分红若干 ,[a ,b ]是此中的一 ,抽 出的个体在 上的 率m , 上的直方 的高h , | a b | ()A .mB . hmC .hD . h mhm二、填空13. 一个 体的60 个个体的 号0,1,2,⋯ ,59, 要从中抽取一个容量 10 的 本,依据 号按被6 除余 3 的方法,取足 本, 抽取的 本号 是.14. 甲、乙两人在 10 天中每日加工部件的个数用茎叶 表示(以下 ),中 一列的数字表示部件个数的十位数,两 的数字表示部件个数的个位数. 10 天甲、乙两人日加工部件的均匀数分和.甲乙9 8 1 9 7 10 1 3 2 0 21 42 41 1 5 3 0 215. 已知 本 9,10,11, x, y 的均匀数是 10 , 准差是2 , xy.16. 假如数据 x 1 , x 2 , ⋯ , x n 的均匀数 4, 方差 0.7, 3x 1 + 5 , 3x 2 + 5 ,⋯, 3x n + 5 的平均数是,方差是.17. 某市居民 2005 ~2009 年家庭年均匀收入 x ( 位: 万元) 与年均匀支出 Y ( 位: 万元)的 料以下表所示:年份 2005 2006 2007 2008 2009 收入 x 11.5 12.1 13 13.3 15支出 Y6.88.89.81012依据 料,居民家庭年均匀收入的中位数是,家庭年均匀收入与年均匀支出有性有关关系.18.从某小学随机抽取 100 名同学,将他 身高( 位:厘米)数据 制成 率散布直方 (如 ).由 中数据0.035可知 a =.a频次组距若要从身高在 [ 120,130 , [ 130, 140 , [ 140, 150 0.020三 内的学生中,用分 抽 的方法 取18 人参加一 0.0100.005活 , 从身高在 [ 140, 150] 内的学生中 取的人数O100 110 120 130 140 150身高.三、解答19.在 2007 全运会上两名射运甲、乙在比中打出以下成:甲: 9.4, 8.7,7.5, 8.4,10.1, 10.5, 10.7, 7.2, 7.8, 10.8;乙: 9.1, 8.7,7.1, 9.8,9.7, 8.5, 10.1,9.2, 10.1, 9.1;( 1)用茎叶表示甲,乙两个成;并依据茎叶剖析甲、乙两人成;( 2)分算两个本的均匀数x 和准差 s ,并依据算果估哪位运的成比定.甲乙频次组距20.“你低碳了?” 是某市倡建型社会而布的公益广告里的一句.活者了认识广告的宣成效,随机抽取了120 名年在0.025 0.020[10 , 20) , [20 , 30) ,⋯, [50 ,60)的市民行0.015卷,由此获得的本的率散布直方如所示.0.005(1)依据直方填写右边率散布表;0102030405060年纪(2)依据直方,估受市民年的中位数(保存整数);分组频数频次(3)按分抽的方法在受市民中抽取n 名市民作本次[10,20)18活的者,若在 [10, 20)的年中随机抽取了 6 人,0.15的 n 多少?[20,30)30[30,40)[40,50)0.2[50,60)60.0521.以下是某地收集到的新房子的销售价钱y 和房子的面积x的数据:房子面积( m2)11511080135105销售价钱(万元)24.821.618.429.222(1)画出数据对应的散点图;(2)求线性回归方程;(3)据( 2)的结果预计当房子面积为150m2时的销售价钱 .(此题建议使用计算器)销售价钱(万元)3530252015105房子面积 (m 2) 70809010011012013014022.为了认识初三学生女生身高状况,某中学对初三女生身高进行了一次丈量,所得数据整理后列出了频次散布表以下:组别频数频次[145.5 ,149.5)10.02[149.5 ,153.5)40.08[153.5 ,157.5)200.40[157.5 ,161.5)150.30[161.5 ,165.5)80.16[165.5 ,169.5)m n合计M N ( 1)求出表中m, n, M , N所表示的数;频次( 2)画出频次散布直方图;组距0.10.090.080.070.060.050.040.030.020.01O145.5 149.5 153.5 157.5 161.5 165.5 169.5身高高一数学必修 3 第二章统计复习题答案一、选择题DDBAB CDDCA DA二、填空题13.3, 9, 15, 21, 27, 33, 39, 45, 51, 5714.24 , 2315.9616.17 , 6.317.13 ,正18.0.0303三、解答题19.( 1)以下图,茎表示成绩的整数环数,叶表示小数点后的数字.甲乙8257147875491872187511011由上图知,甲中位数是 9.05 ,乙中位数是 9.15,乙的成绩大概对称,能够看出乙发挥稳固性好,甲颠簸性大.( 2)解:甲1) =9.11. =′( 9.4+8.7+7.5+8.4+10.1+10.5+10.7+7.2+7.8+10.810s甲=1[(9.49.11) 2(8.7 9.11) 2... (10.89.11) 2 ] =1.3.10x乙=1? (9.1+8.7+7.1+9.8+9.7+8.5+10.1+9.2+10.1+9.1)= 9.14.10s乙 =1(22(2= 0.9.)())[ 9.1-9.14 + 8.7 - 9.14 + 鬃?9.1- 9.1410由 s甲 > s乙,这说了然甲运动员的颠簸大于乙运动员的颠簸,因此我们预计,乙运动员比较稳固.分组 频数 频次[10,20) 18 0.1520.解:( 1)[20,30) 30 0.25[30,40) 42 0.35[40,50) 24 0.2[50,60)60.05( 2)由已知得受访市民年纪的中位数为()0.1= 30+100? 33 (岁);30 + 0.5 - 0.015? 100.025? 10 = 30 +0.035 0.03535(3) 由6=n,解得 n = 40 .18 12021.解:( 1)数据对应的散点图以下图:销售价钱(万元) 3530251 5520 ( 2) xx i 109 , l xx( x i x) 2 1570 ,155 i 1i 11055y 23.2,l xy( x i x)( y i y)308i房子面积 (m 2)170 80 90 100 110 120 130 140设所求回归直线方程为$l xy308 0.1962 ;y = bx + a ,则 b1570lxxa y bx 23.21093081.81661570故所求回归直线方程为 y 0.1962 x 1.8166( 3)据(2),当 x150m 2 时,销售价钱的预计值为:y 0.1962 150 1.816631.2466 (万元)1 50, m 50 (1 4 20 15 8) 222.解:( 1) M0.022频次 N 1,n0.04组距500.1 ( 2)如右图0.09 0.08 0.07 0.06 0.05 0.04 0.03 0.02 0.01O145.5 149.5 153.5 157.5 161.5 165.5 169.5 身高。
高一数学人教A版必修三练习第二章 统计2.1.1 Word版含解析

(本栏目内容,在学生用书中以独立形式分册装订!)一、选择题(每小题分,共分).下面的抽样方法是简单随机抽样的是( ).在某年明信片销售活动中,规定每万张为一个开奖组,通过随机抽取的方式确定号码的后四位为的为三等奖.某车间包装一种产品,在自动包装的传送带上,每隔分钟抽一包产品,检验其质量是否合格.某学校分别从行政人员、教师、后勤人员中抽取人、人、人了解学校机构改革的意见.用抽签法从件产品中选取件进行质量检验解析:对每个选项逐条落实简单随机抽样的特点、不是简单随机抽样,因为抽取的个体间的间隔是固定的;不是简单随机抽样,因为总体的个体有明显的层次;是简单随机抽样.答案:.已知总体容量为,若用随机数表法抽取一个容量为的样本,下面对总体的编号正确的是( ),,…,,,…,,,…,,,…,解析:用随机数表法抽取样本时,样本的编号位数要一致,故选.答案:.从总数为的一批零件中抽取一个容量为的样本,若每个零件被抽取的可能性为,则为( )解析:∵每个个体被抽到机会相等,都是=,∴=.答案:.用简单随机抽样方法从含有个个体的总体中,抽取一个容量为的样本,其中某一个体“第一次被抽到”的可能性,“第二次被抽到”的可能性分别是( ),,,,解析:简单随机抽样中每个个体被抽取的机会均等,都为.答案:二、填空题(每小题分,共分).(·苏州高一期中)某中学高一年级有人,高二年级有人,高三年级有人,以每人被抽取的机会为,从该中学学生中用简单随机抽样的方法抽取一个样本,则样本容量为W.解析:=(++)×=.答案:.关于简单随机抽样,有下列说法:①它要求被抽取样本的总体的个数有限;②它是从总体中逐个地进行抽取;③它是一种不放回抽样;④它是一种等可能性抽样,每次从总体中抽取一个个体时,不仅各个个体被抽取的可能性相等,而且在整个抽样过程中,各个个体被抽取的可能性也相等,从而保证了这种抽样方法的公平性.其中正确的有(请把你认为正确的所有序号都写上).解析:由随机抽样的特征可判断.答案:①②③④.假设要考察某公司生产的克袋装牛奶的质量是否达标,现从袋牛奶中抽取袋进行检验,利用随机数表抽取样本时,先将袋牛奶按,,…,进行编号,如果从随机数表第行第列的数开始向右读,请你依次写出最先检测的袋牛奶的编号W.(下面摘取了随机数表第行至第行)解析:找到第行第列的数开始向右读,第一个符合条件的是,第二个数大于,要舍去,第三个数也要舍去,第四个数符合题意,这样依次读出结果.答案:,,,,。
高中数学必修3(人教B版)第二章统计2.3知识点总结含同步练习题及答案

描述:例题:高中数学必修3(人教B版)知识点总结含同步练习题及答案第二章 统计 2.3 变量的相关性一、学习任务1. 能通过收集现实问题中两个有关联变量的数据作出散点图,并利用散点图直观认识变量间的相关关系.2. 了解线性回归的方法,了解用最小二乘法研究两个变量的线性相关问题的思想方法,会根据给出的线性回归方程系数公式建立线性回归方程(不要求记忆系数公式).二、知识清单变量间的相关关系相关关系 线性相关三、知识讲解1.变量间的相关关系2.相关关系变量与变量之间的关系一类是确定性的函数关系,像正方形的边长 和面积 的关系 .另一类是变量间确实存在关系,但又不具备函数关系所要求的确定性,它们的关系是带有随机性的.例如,人的身高不能确定体重,但一般说来“身高者,体也重”.我们说身高与体重这两个变量具有相关关系.函数关系与相关关系的异同点相同点:是两者均是指两个变量的关系;不同点:①函数关系是一种确定性的关系,相关关系是一种非确定性的关系.②函数关系式一种因果关系,而相关关系不一定是因果关系,其也可能是伴随关系.a S 给出下列关系:①正方形的边长与面积之间的关系;②水稻产量与施肥量之间的关系;③降雪量与交通事故的发生率之间的关系.其中具有相关关系的是______.解:②③两个变量之间的关系有两种:函数关系与相关关系.①正方形的边长和面积之间的关系是函数关系.②水稻产量与施肥量之间的关系不是严格的函数关系,但是具有相关性,因而是相关关系.③降雪量与交通事故的发生率具有相关关系.下图中的两个变量是相关关系的是( )描述:3.线性相关两个变量的线性关系对具有相关关系的两个变量进行统计分析的方法叫回归分析.将样本中的个数据点(,,,)描在平面直角坐标系中,就得到了散点图.如果两个变量的散点图中的点散步在左下角到右上角的区域,即一个变量的值由小变大时,另一个变量的值也由小变大,我们将这种相关称为正相关.如果两个变量的散点图中的点散步的位置是从左上角到右下角的区域,即一个变量的值由小变大是,另一个变量的值由大变小,我们将这种相关称为负相关.如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量具有线性相关关系.回归直线方程“最贴近”已知的数据点的直线方程称之为回归直线方程,简称回归方程,方程为,叫做回归系数.刻画了实际观察值与回归直线上相应点纵坐标之间的偏离程度,个离差构成的总离差越小越好,总离差通常是用离差的平方和来表示,即作为总离差,并使之达到最小.回归直线就是所有直线中取最小的那一条.由于平方又叫二乘方,所以这种使“离差平方和最小”的方法,叫做最小二乘法.A.①② B.①③ C.②④ D.②③解:D①属于函数关系,因为每个 值对应一个 值,这是确定性的关系;②中散点图中各点分布的区域大致为从左下角到右上角,没有确定的函数关系,但是具有相关关系;③中散点图分布的区域大致在一条曲线附近,对于每个 ,其对应的 呈现出一定的规律性,因此这两个变量具有相关关系;④ 中各点的分布比较均匀,但对于每个 , 的分布没有规律,因此不属于相关关系.x y x y x y n (,)x i y i i =12⋯n =a +bx y ^b −y i y ^i y i n Q =(−a −b ∑i =1ny i x i )2Q(),得散点图2.由这两个散点图可以判断( )(,)u i v i i =12⋯10高考不提分,赔付1万元,关注快乐学了解详情。
数学3必修第二章统计基础训练A组及答案

(数学3必修)第二章 统计[基础训练A 组] 一、选择题1 10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a ,中位数为b ,众数为c ,则有( ) A c b a >> B a c b >> C b a c >> D a b c >> 2 下列说法错误的是 ( )A 在统计里,把所需考察对象的全体叫作总体B 一组数据的平均数一定大于这组数据中的每个数据C 平均数、众数与中位数从不同的角度描述了一组数据的集中趋势D 一组数据的方差越大,说明这组数据的波动越大3 某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,那么由此求出的平均数与实际平均数的差是( ) A 3.5 B 3- C 3 D 5.0-4 要了解全市高一学生身高在某一范围的学生所占比例的大小,需知道相应样本的( )A 平均数B 方差C 众数D 频率分布5 要从已编号(160 )的60枚最新研制的某型导弹中随机抽取6枚来进行发射试验,用每部分选取的号码间隔一样的系统抽样方法确定所选取的6枚导弹的编号可能是( )A5,10,15,20,25,30 B3,13,23,33,43,53 C1,2,3,4,5,6 D2,4,8,16,32,486A 14和0.14B 0.14和14 C141和0.14 D31和141二、填空题1 为了了解参加运动会的2000名运动员的年龄情况,从中抽取100名运动员;就这个问题,下列说法中正确的有 ;① 2000名运动员是总体;②每个运动员是个体;③所抽取的100名运动员是一个样本; ④样本容量为100;⑤这个抽样方法可采用按年龄进行分层抽样;⑥每个运动员被抽到的概率相等2 经问卷调查,某班学生对摄影分别执“喜欢”、“不喜欢”和“一般”三种态度,其中执“一般”态度的比“不喜欢”态度的多12人,按分层抽样方法从全班选出部分学生座谈摄影,如果选出的2位“喜欢”摄影的同学、1位“不喜欢”摄影的同学和3位执“一般”态度的同学,那么全班学生中“喜欢”摄影的比全班人数的一半还多 人3 数据70,71,72,73的标准差是______________4 数据123,,,...,n a a a a 的方差为2σ,平均数为μ,则(1)数据123,,,...,,(0)n ka b ka b ka b ka b kb ++++≠的标准差为 ,平均数为(2)数据123(),(),(),...,(),(0)n k a b k a b k a b k a b kb ++++≠的标准差为 ,平均数为5 观察新生婴儿的体重,其频率分布直方图如图所示,则新生婴儿体重在(]2700,3000的三、解答题1 试求全校初二男生俯卧撑的平均成绩2为了了解初三学生女生身高情况,某中学对初三女生身高进行了一次测量,所得数(1)求出表中,,,m n M N所表示的数分别是多少?(2)画出频率分布直方图(3)全体女生中身高在哪组范围内的人数最多?3某校高中部有三个年级,其中高三有学生1000人,现采用分层抽样法抽取一个容量为185的样本,已知在高一年级抽取了75人,高二年级抽取了60人,则高中部共有多少学生?4从两个班中各随机的抽取10名学生,他们的数学成绩如下:画出茎叶图并分析两个班学生的数学学习情况数学3(必修)第二章 统计 [基础训练A 组]参考答案一、选择题1 D 总和为147,14.7a =;样本数据17分布最广,即频率最大,为众数,17c =;从小到大排列,中间一位,或中间二位的平均数,即15b = 2 B 平均数不大于最大值,不小于最小值3 B 少输入9090,3,30=平均数少3,求出的平均数减去实际的平均数等于3-4 D5 B60106=,间隔应为106 A 频数为100(1013141513129)14-++++++=;频率为140.14100=二、填空题1 ④,⑤,⑥ 2000名运动员的年龄情况是总体;每个运动员的年龄是个体;23 3位执“一般”对应1位“不喜欢”,即“一般”是“不喜欢”的3倍,而他们的差为12人,即“一般”有18人,“不喜欢”的有6人,且“喜欢”是“不喜欢”的6倍,即30人,全班有54人,1305432-⨯=327071727371.5,4X +++==2s ==4 (1)k σ,k b μ+(2)k σ,k kb μ+(1)1212......n nka b ka b ka ba a a X kb k b nnμ+++++++++==⋅+=+s kk σ===(2)1212()()...()...n nk a b k a b k a b a a a X k nb k nb nnμ+++++++++==⋅+=+s kk σ===5 0.3 频率/组距0.001=,组距300=,频率0.0013000.3=⨯=三、解答题1解:1089685716645743313607.25050X⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯===2解:(1)150,50(1420158)20.02M m===-++++=21,0.0450N n===(2)…(3)在153.5157.5范围内最多3解:从高三年级抽取的学生人数为185(7560)50-+=而抽取的比例为501100020=,高中部共有的学生为1185370020÷=4解:乙班级总体成绩优于甲班。
(完整版)人教版高一数学必修三第二章统计全部教案和测试题

人教版高一数学必修三第二章统计目录简单随机抽样(新讲课)系统抽样(新讲课)分层抽样(新讲课)2用样本的频次散布预计整体散布(2 课时 ) (新讲课)用样本的数字特色预计整体的数字特色(2 课时 ) (新讲课)变量之间的有关关系(新讲课)两个变量的线性有关(第一课时)(新讲课)两个变量的线性有关(第二课时)(新讲课)生活中线性有关实例(第三课时)(新讲课)第二章统计单元检测题(一)第二章统计单元检测题(一)参照答案第二章统计单元检测题(二)第二章统计单元检测题(二)参照答案第二章统计单元检测题(三)第二章统计单元检测题(三)参照答案第二章统计一、课程目标:本章主要介绍最基本的获得样本数据的方法,以及集中从样本数据中提守信息的统计方法,此中包含用样本预计整体散布、数字特色和线性回归等内容。
本章经过实质问题,进一步介绍随机抽样、样本预计整体、线性回归的基本方法。
二、学习目标:1、随机抽样(1)能从现实生活或其余学科中提出拥有一订价值的统计问题。
(2)联合详细的实质问题情境,理解随机抽样的必需性和重要性。
(3)在参加解决统计问题的过程中,学会用简单随机抽样从整体中抽取样本;经过对实例的剖析,认识分层抽样和系统抽样方法。
(4)经过试验、查阅资料、设计检盘问卷等方法采集数据。
2、用样本预计整体(1)经过实例领会散布的意义和作用,在表示样本数据的过程中,学会列频次散布彪、花频次散布直方图、频次折线图、茎叶土,领会它们各自的特色。
(2)经过实例理解样本数据标准差的意义和作用,学会计算数据样本差。
(3)能依据实质问题的需求合理地选用样本,从样本数据中提取基本的数字特色,并做出合理的解说。
(4)进一步领会用样本预计整体的思想。
(5)会用随机抽样的基本方法和样本预计整体的思想,解决一些简单的实质问题。
(6)形成对数据办理过程进行初步评论的意识。
3、变量的有关性(1)经过采集现实问题中两个有关系变量的数据作出散点图,并利用散点图直观认识变量间的有关关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一数学必修3第二章统计复习题
一、选择题
1.某机构进行一项市场调查,规定在某商场门口随机抽一个人进行询问调查,直到调查到事先规定的调查人数为止,这种抽样方式是 A .系统抽样 B .分层抽样 C .简单随机抽样 D .非以上三种抽样方法 2. 一个年级有12个班,每个班的同学从1至50排学号,为了交流学习经验,要求每班学号为14的同学留下进行交流,这里运用的是 A.分层抽样
B.抽签抽样
C.随机抽样
D.系统抽样
3. 某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本,若样本的青年职工为7人,则样本容量为
A .7
B .15
C .25
D .35
4.为了解1200名学生对学校教改试验的意见,打算从中抽取一个容量为30的样本,考虑采用系统抽样,则分段的间隔k 为
A. 40
B. 30
C. 20
D. 12 5.在某项体育比赛中,七位裁判为一选手打出的分数如下:
90 89 90 95 93 94 93
去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为
A . 92,2
B . 92 ,2.8
C .93,2
D .93,2.8
6. 变量y 与x 之间的回归方程 A .表示y 与x 之间的函数关系 B .表示y 和x 之间的不确定关系 C .反映y 与x 之间的真实关系达到最大限度的吻合 D .反映y 和x 之间真实关系的形式
7. 线性回归方程ˆy
bx a =+必过点 A .(0,0) B .(x ,0) C .(0,y ) D .(x ,y )
8.在下列各图中,每个图的两个变量具有相关关系的图是
(1) (2)(3)(4)
A .(1)(2)
B .(1)(3)
C .(2)(4)
D .(2)(3)
9.一个容量为40的样本数据分组后组数与频数如下:[25,25.3),6;[25.3,25.6),4;[25.6,
25.9),10;[25.9,26.2),8;[26.2,26.5),8;[26.5,26.8),4;则样本在[25,25.9)上的频率为
A .
320
B .
1
10
C .12
D .14
10
第三组的频数和频率分别是 ( )
A 14和0.14
B 0.14和14 C
141和0.14 D 31和14
1
11. 已知数据12,,...,n a a a 的平均数为a ,方差为2
S ,则数据122,2,...,2n a a a 的平均数和方差为( )
A .2,a S
B .2
2,a S C .22,2a S D .22,4a S
12、在抽查产品尺寸的过程中,将其尺寸分成若干组,[a ,b ]是其中的一组,抽查出的个体在该组上的频率为m ,该组上的直方图的高为h ,则=-||b a ( ) A .
h m B .hm C .m
h
D .m h + 二、填空题
13. 一个总体的60个个体的编号为0,1,2,…,59,现要从中抽取一个容量为10的样本,请根据编号按被6除余3的方法,取足样本,则抽取的样本是 . 14. 甲、乙两人在10天中每天加工零件的个数用茎叶图表示(如下图),中间一列的数字
表示零件个数的十位数,两边的数字表示零件个数的个位数.则这10天甲、乙两人日加工零件的平均数分别为 和 .
15. 已知样本9,10,11,,x y 的平均数是1016. 如果数据1x ,2x ,
…,n x 的平均数为4,方差为0.7,则1
35x ,235x , (35)
x 的
平均数是 ,方差是 .
17. 某市居民2005~2009年家庭年平均收入x (单位:万元)与年平均支出
Y (单位:万元)的统计资料如下表所示:
根据统计资料,居民家庭年平均收入的中位数是 ,家庭年平均收入与年平均支出有 线性相关关系.
18.从某小学随机抽取100名同学,将他们身高(单位:厘米) 数据绘制成频率分布直方图(如图).由图中数据 可知a = .
若要从身高在[120,130﹚,[130,140﹚,[140,150﹚
三组的学生中,用分层抽样的方法选取18人参加一 项活动,则从身高在[140,150]的学生中选取的人数 应为 .
三、解答题
19. 在2007全运会上两名射击运动员甲、乙在比赛中打出如下成绩:
a
120
甲:9.4,8.7,7.5,8.4,10.1,10.5,10.7,7.2,7.8,10.8; 乙:9.1,8.7,7.1,9.8,9.7,8.5,10.1,9.2,10.1,9.1; (1)用茎叶图表示甲,乙两个成绩;并根据茎叶图分析甲、乙两人成绩;
(2)分别计算两个样本的平均数x 和标准差s ,并根据计算结果估计哪位运动员的成绩比较稳定.
20. “你低碳了吗?”这是某市为倡导建设节约型 社会而发布的公益广告里的一句话.活动组织者为了
了解这则广告的宣传效果,随机抽取了120名年龄在 [10,20) ,[20,30) ,…, [50,60) 的市民进行问 卷调查,由此得到的样本的频率分布直方图如图所示.
(1) 根据直方图填写右面频率分布统计表;
(2)
(3) 按分层抽样的方法在受访市民中抽取n 名市民作为本次
活动的获奖者,若在[10,20)的年龄组中随机抽取了6人,
则的n 值为多少?
21. 以下是某地搜集到的新房屋的销售价格y 和房屋的面积x 的数据:
(1)画出数据对应的散点图; (2)求线性回归方程;
(3)据(2)的结果估计当房屋面积为2150m 时的销售价格.
(本题建议使用计算器)
22.为了了解初三学生女生身高情况,某中学对初三女生身高进行了一次测量,所得数据整
(1)求出表中,,,m n M N 所表示的数; (2)画出频率分布直方图;
高一数学必修(m 2)
一、选择题
DDBAB CDDCA DA
二、填空题
13. 3,9,15,21,27,33,39,45,51,57 14.24 , 23 15. 96
16. 17 , 6.3 17. 13 ,正 18. 0.030 3
三、解答题
19.(1)如图所示,茎表示成绩的整数环数,叶表示小数点后的数字.
由上图知,甲中位数是9.05,乙中位数是9.15,乙的成绩大致对称, 可以看出乙发挥稳定性好,甲波动性大. (2)解:x 甲
1
10
(9.4+8.7+7.5+8.4+10.1+10.5+10.7+7.2+7.8+10.8)=9.11. s 甲
])11.98.10(...)11.97.8()11.94.9[(10
1
222-++-+-=1.3. 1
10
x 乙(9.1+8.7+7.1+9.8+9.7+8.5+10.1+9.2+10.1+9.1)=9.14. 22
2
1[9.19.148.79.149.19.140.910
s 乙
()()
()
.
由s s 甲
乙,这说明了甲运动员的波动大于乙运动员的波动,所以我们估计,乙运动员比较
稳定.
20.解:(1)
(2)由已知得受访市民年龄的中位数为
0.50.015100.025100.1
10030
30
30
330.0350.035
35
()(岁);
(3) 由618120
n
,解得40n .
21.解:(1)数据对应的散点图如图所示: (2)1095151==∑=i i x x ,1570)(2
5
1
=-=∑=x x l i i xx ,
308))((,2.235
1
=--==∑=y y x x l y i i i xy
设所求回归直线方程为y bx
a ,则1962.01570
308
≈=
=
xx
xy l l b ; 8166.11570
308
1092.23≈⨯
-=-=x b y a 故所求回归直线方程为8166.11962.0+=x y
(3)据(2),当2
150m x =时,销售价格的估计值为:
2466.318166.11501962.0=+⨯=y
(万元)
22.解:(1)1
50,50(1420158)20.02
M m ===-++++= 2
1,0.0450N n === (2)如右图
(m 2)。
