散布图(scatter diagram)
散布图

四、散布图的相关检验
2、符号检验法(中值法)
◆令:n1+n3=n+ ; n2+n4=n- ; s=Min(n+,n-),即s为n+、n-之中的最小值。
◆查符号检验表得判断值Sα。
在符号检验表中查得与n和α相对应的判断值Sα。 其中:n点数的总和(恰好在中位线上的点子不计算): n=n++n-。
α:显著水平α,也称作风险度,是与置信度β相对应的参数α+ β=1。 α:一般取0.01、0.05,意谓着判断错误的风险率是0.01(1%)和0.05(5%)
达。 ②相关关系:变量之间存在密切关系,但又不能由一个(或几 个)变量的数值精确地求另一变量的数值,称这类变量的关系 为相关关系。
③不相关:事物之间没有关系。
一、散布图概述
3、散布图的用途:
①用来发现和确认两组数据之间的关系并确定两组相
关数据之间预期的关系。
②通过确定两组数据、两个因素之间的相关性,有助
四、散布图的相关检验
2、符号检验法(中值法)
散布图中位线 Y (%)
93 92
Ⅱ n2=5
● ●
P
● ● ● ●
Ⅰ n1=10
● ●
91
90 89 88 87 86 85
● ● ● ● ●
●
● ● ●
●
● ● ● ●
Q
● ● ●
●
● ●
n3 =10
8.0 8.5 9.0
Ⅲ
●
Ⅳ n4 =5
9.5
X(g)
异常值
三、作散布图的注意事项
3、分层的必要性
在下图中,从全体座标点看不至相关,然而,从“*”与 “×”将座标点分层,则发现各自皆有相关。 反之,整体好像相关,而分层后层内没有相关的情况存在, 所以作散布图前应考虑分层,且以不同的记号表示分层后的座 标点。
QCC七大手法

QCC七大手法 1何谓特性要因图(Characteristic Diagram):对於结果(特性)与原因(要因)间或所期望之效果(特性)之对策间的关系,以箭头连接,详细分析原因或对策的一种图形。
特性要因图为日本品管权威学者石川馨博士於1952年所发明,故又称[石川图]。
又因其形状似鱼骨,故又称为[鱼骨图]。
再因其在阐明原因与结果之关系,亦又称之为[因果图]。
QCC七大手法 2何谓检查表(Check Sheet):检查表是一种为了便於收集数据,使用简单记号填写并予统计整理,作为进一步分析或作为核对、检查之用而设计的一种表格或图表。
QCC七大手法 3何谓柏拉图(Pareto Diagram):根据所搜集之数据,按不良原因、不良状况、不良发生位置告示不同区分标准,以寻求占最大比率之原因、状况或位置的一种图形。
QCC七大手法 4何谓散布图(Scatter Diagram):在两组数据或原因与结果之间是否有相关及其所相关程度如何,无法层别检讨是何者影响结果时,此时应绘制出两种数据之间是否有相关及其相关程序如何的散布图来探讨其潜在因素。
QCC七大手法 5何谓直方图(Histogram):为了要容易的看出如长度、重量、时间、硬度等计量值的数据之分配情形,所用来表示的图形。
直方图是将所收集的测定值或数据之全距分为几个相等的区间作为横轴,并将各区间内之测定值所出现次数累积而成的面积,用柱子排起来的图形,故我们亦称之为柱状图。
QCC七大手法 6何谓管制图(Control Chart):是一种以实际产品品质特性与根据过去经验所判明的制程能力的管制界限比较,而以时间顺序来表示的一种图形。
一般管制图纵轴为制品的品质特性,以制程变化的数据为分度;横轴为制品的群体号码,或制造年月日等,以时间顺序、制造顺序,将点绘在图上的一种图形。
QCC七大手法7何谓层别法(Stratification):为区别各种不同原因对结果之影响,而以各别原因为主体,分别作统计分析的方法,称为层别法。
什么是QC七打手法

什麽是QC七大手法?1.直方图(Histogram):直方图就是将所收集的数据、质量特性值或结果值,用一定的范围在横轴上加以区分成几个相等的区间,将各区间内的测定值所出现的次数累积起来的面积,用柱形画出图形,直方图可以了解产品在规格标准之下的分布形态。
(1)说明:划分数据(如考试成绩)的分配范围为数个区间,计算各区间内该数据的出现次数,并制作成次数分配表。
(2) 用途:描述数据的分布(平均值、变异、对称),借以判断工序有无异常情形。
并检查该数据是否正常受控,有足够的能力符合客户需求。
步骤:1.收集数据作直方图,数据至少50个以上.一般对于数据个数多少,称为样品大小, 用n 表示.2.整理数据将数据整理,并找出最大值与最大值.3.决定组数分组的组数并没有统一的规定,但太多或太少组皆会使直方图失真.A.分组组数依数据之样本大小n决定B.最大值减最小值的差(R),用2,5,10等相关数值除之.4.决定组距组距h 可由组数k 除以全距R 来决定,如下式。
组距(h)= 全距(R) / 组数(k)一般取h 值为量测单位之整数倍5.决定组界组界即是每一分组之上下界限值,计算方法如下:第一组下组界:=最小值-最小量测单位/2;第一组上组界:=第一组下界+h,依此类推。
6. 计算组中点各组皆以组中点为代表值,其计算方法如下:组中点= ( L1+U1 ) / 27.计算次数并作次数分配表:将组界、组中点填入次数分配表,将原数据依其值归类入某一组并以计票的方式以////字划记各组之次数8.绘制直方图以组界或组中点为X轴,次数为Y轴。
再以各组之组距为底边,次数为高,对每一组绘一长方形,相邻的组其长方形需紧靠在一起,不要有空隙.9.记入必要事项收集数据期间,样本大小,品质特性的单位,测定日期,测定者,必要的批号.2.管制图(Control Chart)(1)说明:把品质特性(如芯片的薄膜厚度)的点以记号标示上去,藉着该点在管制界限内侧或外侧的情形,可以判断工序是否在控制状态中。
7.散布图
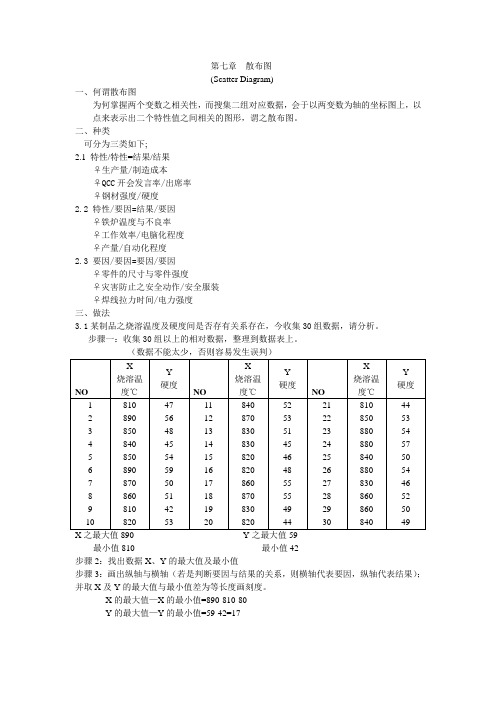
第七章散布图(Scatter Diagram)一、何谓散布图为何掌握两个变数之相关性,而搜集二组对应数据,会于以两变数为轴的坐标图上,以点来表示出二个特性值之间相关的图形,谓之散布图。
二、种类可分为三类如下;2.1 特性/特性=结果/结果♀生产量/制造成本♀QCC开会发言率/出席率♀钢材强度/硬度2.2 特性/要因=结果/要因♀铁炉温度与不良率♀工作效率/电脑化程度♀产量/自动化程度2.3 要因/要因=要因/要因♀零件的尺寸与零件强度♀灾害防止之安全动作/安全服装♀焊线拉力时间/电力强度三、做法3.1某制品之烧溶温度及硬度间是否存有关系存在,今收集30组数据,请分析。
步骤一:收集30组以上的相对数据,整理到数据表上。
(数据不能太少,否则容易发生误判)X之最大值890 Y之最大值59最小值810 最小值42步骤2:找出数据X、Y的最大值及最小值步骤3:画出纵轴与横轴(若是判断要因与结果的关系,则横轴代表要因,纵轴代表结果);并取X及Y的最大值与最小值差为等长度画刻度。
X的最大值—X的最小值=890-810-80Y的最大值—Y的最小值=59-42=17800 810 820 830 840 850 860 870 880 890烧溶温度℃X步骤4:将各组对数据点在坐标上。
横轴与纵轴的数据交汇处点上“·”二组数据重复在同一点上时,划上二重圆记号“◎”三组数据重复在同一点上时,划上三重圆记号“⊙”605856 NO.154 (X=890,Y=58)硬52度50 NO.1Y48 (X=810,Y=47) 图:数据打点法46444240800 810 820 830 840 850 860 870 880 890烧溶温度℃X60 n=3058 时间=9/25~9/29硬56度54Y52 制品名:SA-5050 单位:压延课48 绘图者:林武东46 绘制日:444240800 810 820 830 840 850 860 870 880 890图:钢的烧溶温度与硬度散布图步骤5:记入必要事项数据数、采取时间、目的、制品名、工程名、绘图者、绘制日期、、、、、、、均要说明。
散布图法-详解

散布图法-详解散布图法(Scatter Diagram Method)目录• 1 什么是散布图法• 2 散布图法的步骤• 3 散布图法示例什么是散布图法散布图法(Scatter Diagram Method)是指根据若干时期的历史资料,将其业务量和成本数据逐一在坐标图上标注,形成若干个散布点,再通过目测的方法尽可能画出一条接近所有坐标点的直线,并据以推算出固定成本总额和单位变动成本的一种成本习性分析方法。
散布图法由于将全部成本数据均作为描述成本习性的依据,其准确程度比高低点法高。
但因为其采用目测的方法得出固定成本,因而计算结果也具有一定的不准确性。
在质量管理过程中,经常需要对一些重要因家进行分析和控制这些因素大多错综复杂地交织在一起,它们既相互联系又相互制约既可能存在很强的相关性,也可能不存在相关性。
如何对这些因素进行分析?散布团法便是这样一种直观而有效的好方法,通过做散布图,因素之间繁杂的数据就变成了坐标图上的点,其相关关系使一目了然地呈现出来。
在分析质量事故时,总是希望能够寻找到造成质量事故的主要原因,但影响产品质量的因素往往很多,有时只需要分析具体两个因索之间到底存在着什么关系。
这时可将这两种因素有关的数据列出来,并用一系列点标在直角坐标系上,制作成图形,以观察两种因素之间的关系,这种图就称为散布图,对它进行分析称为相关分析。
散布图法的步骤散布图法的工作步骤为:1)收集历史数据收集以前各期产量与总成本的历史数据。
2)画出散布图将各期总成本数据标入直角坐标系,画出散布图。
3)确定固定成本平均值根据离散的历史成本点目测成本随产量变动的趋势,画出一条能反映成本平均变动趋势的直线,直线与纵轴的交点即固定成本平均值。
4)计算单位变动成本在直线上任取一点,根据的计算公式,计算出单位变动成本。
5)计算总成本按照计算出的固定成本平均值(a)、单位变动成本(b),预测未来某期产量下的总成本,预测公式为:y = a + bx式中:y—未来预测期的总成本;x—产量。
QC七大手法(新)

常用品管手法概要概要:统计是采取“数据与事实发言”的管理方法,除了客观判定事实外,亦应具有相当合理的说服力,而在QC活动中所采取的统计手法,均极为简易。
重要性:94年版ISO9001 4.20中,特别规定应将各项品质改善,用统计的手法来分析,2000版ISO9001中8.1策划中谈到使用统计技术的要求,并且条文8.4资料分析万万离不计分析。
常用品管手法1.根据数据、事实发言-图表(GRAPH),查检表(CHECK LIST),散布图(Scatter diagram);2.整理原因与结果之关系,以探讨潜伏性之问题- 特性要因图(Characteristic Dirgram);3.凡事物不能完全单用平均数来考虑,应了解事物均有变异存在,须从平均数与变异数来考虑- 直方图(Histogram)、管制图(Control Chart)。
4.所有数据不可仅止于平均,须根据数据之来龙去脉,考虑适当分层-曾别法(Stratification)。
5.并非对所有原因采取措施,而是先从影响较大的2-3项采取措施,即所谓管理重点- 排列图(柏拉图)(Pareto Diagram).ISO中应使用统计技术的场合推移图:1、品质目标达成情况控制;2、各阶层不良率控制;查检表:1、内部审核结果不符合点分布判断;2、5S执行情况点检;特性要因图:1、显著问题原因分析;2、潜在问题分析;3、客户抱怨分析;曾别图:1、作业条件之曾别;2、制品之曾别;3、班别等;排列图:1、不良项目排列;2、供应商别合格率排列;3、客户别不良率;直方图:1、制程常态分布情况;管制图:1、制程稳定情况。
在近日ISO旋风席卷全球之际,各企业应依实绩的情况,积极的在各阶层全面事实QC教育训练,提升品质意思,熟用各种品管手法/技术,及以提升系统的品质,在近日ISODE 洪流冲击下,必将成为明日企业的佼佼者。
目 录第一章:查检表---------------------3 第二章:散布图--------------------16 第三章:层别图--------------------19 第四章:直方图--------------------26 第五章:柏拉图--------------------45 第六章:特性要因图----------------55 第七章:管制图--------------------59第一章:查检表(Check Sheet;Check list)一.定义:查检表是使用简单易于了解的标准化表格或图形,人员只需填入规定之查检记号,再加以统计完整其数据,即可提供量化分析或比对检查用者谓之,亦称为点检表或查核表。
散布图(scatter diagram)

散布图(scatter diagram)又名:散点图( scatter plot) ,X-Y图(X-Y graph)概述散布图是分别用横、纵坐标轴表示一对变量,来描述它们之间相互关系的一种工具。
加果这两个变量相关,点的分布呈直线或曲线形状。
相关性越强,这些点的散布形状越接近一条直线。
适用场合·当收集到一组成对数据后;·当因变量的值可能受多个自变量值的综合影响时;·当试图确定两个变量是否相关时,例如:——鉴别问题潜在的根本原因;——采用头脑风暴法列出问题因果关系的鱼骨图后,客观地验证这种因果关系是否真的存在;——判断出现的两种相关结果是否都由相同的原因引起;——构建控制图之前对自相关性的检测。
实施步骤1.为可能存在关联的变量收集成对的数据。
2.画一张坐标图,将自变量标于横轴,因变量标于纵轴。
在每一个数据对应的横坐标值和纵坐标值的相交处画点或记号。
如果有两个点落在一起,就在此处画两个相连的点,确保都可以被看到。
3.通过点的分布特征,查看相关关系是否明显。
如果数据点清晰地形成一条直线,便可以证明变量相关,就可以使用回归分析或关联分析进行进一步的分析研究了。
否则要继续完成步骤4~7的工作。
4将图表中的点分成4个象限。
如果在图中有X个点:从上到下,数出X/2个点,在此位置画一条垂直于纵轴的直线;从左到右,数出X/2个点,在此位置画一条垂直于横轴的直线。
注意:如果点数为奇数,直线会经过一个点。
5数出每一个象限内点的个数.不包括落在直线上的点。
6把对角象限内点的个数加起来,并找到其中的较小者以及算出所有象限内点的个数:A=Ⅰ象限点的个数+Ⅲ象限点的个数B=Ⅱ象限点的个数十Ⅳ象限点的个数Q=A和B中的较小者N =A+B7在趋势检验表(表5. 18)中找出N允许的极值。
·如果Q小于临界值,这两个变量相关;·如果Q大于或等于临界值,表明分布是随机的。
示例这个例子是第4章ZZ-400改进项目的一部分。
QC七大手法

SL
SU
直方图(Histogram) 直方图(
4)离岛型:在左端或右端形成小岛。说明存在测量有错误、工序调节错误或使用 了不同原料等异常原因。
SL
SU
直方图(Histogram) 直方图(
5)双峰型:有两个高峰出现。有2种分配相混合,例如2台机器或2家不同供应商 有差异时,会出现这种形状,因测量值不同的原因影响,应先分层后再作直方 图。
散布图(scatter diagram)
3.1 定义:
将两个可能相关的变量数据用点画在坐标图上,用来表示一组成对 的数据之间是否有相关性,能大概掌握原因和结果之间是否有关联及 关联的程度。 3.2 散布图的判读
3.2.1 完全正(负)关联:点散布 在一条直线上; 3.2.2 高度(中度、低度)正(负) 关联:原因(X)与结果(Y) 的变化近于等比例; 3.2.3 无关联:原因(X)与结果 (Y)变化完全不成比例 3.2.4 曲线关联:原因(X)与结果Y)变化呈曲线变化。
质 的 提 升
P A P A P A
改 善
D
C
D
C
改 保持 善
D
C
保持
改 保持 善
持续转动PDCA就可不断提高管理质量,这称为盘状上升。
QC统计手法概述
1.2.3 改善:
改善就是要打破现状,为一种改变目前的作业方法,使效果更好的活动。 改善活动的具体步骤是: 1)确定问题点; 2)对问题点的现状分析; 3)改善措施实施; 4)实施结果的确认; 5)标准化;
2.4.2 记录用检查表制作方法
1) 决定希望掌握的项目和所要收集的数据; 2)决定检查表的格式; 3)决定记录的符号: a. “正”字记号,运用频率最高,一般较常采用; b. “ ”,多用于质量管理,如:次数分配表;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
散布图(scatter diagram)
又名:散点图( scatter plot) ,X-Y图(X-Y graph)
概述
散布图是分别用横、纵坐标轴表示一对变量,来描述它们之间相互关系的一种工具。
加果这两个变量相关,点的分布呈直线或曲线形状。
相关性越强,这些点的散布形状越接近一条直线。
适用场合
·当收集到一组成对数据后;
·当因变量的值可能受多个自变量值的综合影响时;
·当试图确定两个变量是否相关时,例如:
——鉴别问题潜在的根本原因;
——采用头脑风暴法列出问题因果关系的鱼骨图后,客观地验证这种因果关系是否真的存在;
——判断出现的两种相关结果是否都由相同的原因引起;
——构建控制图之前对自相关性的检测。
实施步骤
1.为可能存在关联的变量收集成对的数据。
2.画一张坐标图,将自变量标于横轴,因变量标于纵轴。
在每一个数据对应的横坐标值和纵坐标值的相交处画点或记号。
如果有两个点落在一起,就在此处画两个相连的点,确保都可以被看到。
3.通过点的分布特征,查看相关关系是否明显。
如果数据点清晰地形成一条直线,便可以证明变量相关,就可以使用回归分析或关联分析进行进一步的分析研究了。
否则要继续完成步骤4~7的工作。
4将图表中的点分成4个象限。
如果在图中有X个点:
从上到下,数出X/2个点,在此位置画一条垂直于纵轴的直线;
从左到右,数出X/2个点,在此位置画一条垂直于横轴的直线。
注意:如果点数为奇数,直线会经过一个点。
5数出每一个象限内点的个数.不包括落在直线上的点。
6把对角象限内点的个数加起来,并找到其中的较小者以及算出所有象限内点的个数:A=Ⅰ象限点的个数+Ⅲ象限点的个数
B=Ⅱ象限点的个数十Ⅳ象限点的个数
Q=A和B中的较小者
N =A+B
7在趋势检验表(表5. 18)中找出N允许的极值。
·如果Q小于临界值,这两个变量相关;
·如果Q大于或等于临界值,表明分布是随机的。
示例
这个例子是第4章ZZ-400改进项目的一部分。
ZZ.-400制造小组怀疑产品纯度(%)和铁含量(10-6)之间存在相关关系。
关于纯度和铁含量的散布图如图表5.172所示。
图表中共有24个数据点。
中位数线(X/2)画出后,各有12个点落在中位数线的两侧。
为检验相关关系,计算如下:
A=Ⅰ象限点的个数+Ⅲ象限点的个数=4+3=7
B=Ⅱ象限点的个数+Ⅳ象限点的个数=8+9 =17
Q=A和B中的较小者=7和17中的较小者=7
N=A+B=7+17=24
在趋势检验表(表5. 18)中找出N的临界值。
当N=24时,临界值是6。
如果Q小于这个临界值,这两个变量相关。
如果Q大于临界值,表明这种分布特征可视为随机出现。
在本例中:
Q=7>6
因此,此分布特征可视为随机出现,没有表现出相关关系。
注意事项
·在什么情况下可以应用散布图?下面是几个例子:
——变量n代表15分钟以后的一个反应的温度。
变量B代表产品颜色的测度。
你认为温度越高可能导致产品越黑。
在散布图中描绘温度和颜色的数据点。
——变量A代表新软件的培训人数,而变量B代表计算机热线服务电话的呼叫次数,你认为培训人数的增加可能会导致呼叫次数的减少。
在散布图中描绘培训人数和呼叫次数的数据点。
——用控制图检验测量数据的自相关性。
在特定的时间测量出变量A的数据,变量B也采用相同的测量方法,但是要用变量A对应数据的前一个时间点的数据。
如果散布图显示出相关性,就再做一张图,变量B采用比变量A提前两个时间段的观测数据。
持续增加散布图中两个变量的时间间隔,直到显示出它们之间没有相关性。
·即使散布图表明了某种相关关系,也不要轻易认为变量之间是因果关系,因为这两个变量可能同时受第三个变量的影响。
·画出数据点后,点的散布形状与直线越相近,这两变量之间的相关性就越强。
参考“相关性分析”中的图表5. 39至图表5.42,以及它们的曲线图类型和相关解释。
·如果直线的趋势不明显,那么由统计量(N和Q)来判断某种相关关系的存在是否具有必然性。
如果由统计量判断相关关系不存在,那么图中的分布情况就可视为随机出现。
·如果散布图表明变量之间不相关,可以考虑数据是否被分层了。
更多的细节请参阅“分层法”。
·如果图中显示两个变量不相关,考虑是否自变量分布范围过宽。
有时是因为数据覆盖的范围不够宽而导致相互之间的关系不够明显。
·充分发挥创造力去思考如何使用散布图去发现问题的根本原因。
·通过“图形方法”了解更多关于图表技术的知识。
通过对决策树图(图表5.68)的研究可以让你更清楚在什么时候使用散布图,以及什么时候附加运用一些其他图表工具对你的工作更有所帮助。
·画出散布图只是分析变量之间关系的第一步。
通过学习“相关性分析”和“回归分析”掌握需要的相关统计方法。
END。
