平面图形及立体图形的计算练习题
第01讲 平面、立体图形综合一(直线型)(解析版)

60cm
3
随练 随练 1、图①的周长大于图②的周长,这种说法对吗?为什么?
随练 2、右边图形的周长是多少?
随练 3、如图,这个多边形任意相邻的两条边都互相垂直,根据图中给出的数(单位:厘米),那么 这个多边形周长是__________厘米.
曲线型图形题
课前小测 1、 阿呆的高斯积分比阿瓜的多 150 分,且阿呆的高斯积分比阿瓜的 4 倍少 30 分,阿呆和阿瓜分别 有多少分?(请用两种方法解答)
2、三块布共长 220 米,第二块布长是第一块的 3 倍,第三块布长是第二块的 2 倍,三块布各有多长? (列方程解答)
3、司机小王身上带有 1 元、2 元、5 元、10 元四种面值的纸币共 82 元,其中 1 元和 2 元纸币共 22 张,5 元和 10 元纸币共 7 张,2 元纸币的张数是 5 元纸币张数的 2.5 倍.问:小王身上有多少张 10 元纸币?
随练 5、如图, AE : EB 3 : 2 , CD : DB 7 : 5 ,三角形 ABC 的 面积是 60 平方厘米,求三角形 AED 的面积为多少平方厘米.
7
知识精讲 一、基本公式
长方体及正方体
二、三视图求表面积 在观察物体的时候,我们往往可以从不同的角度进行观察.角度不同,看到的风景就会不同.比 如:我们可以从正面看,上面看,左面看,看到的图形分别称为正视图,俯视图和左视图.并且 容易发现:正面看和后面看,上面看和下面看,左面看和右面看得到的图形是相同的.对于较复 杂的立体图形,通过三视图法往往可以很方便地计算出表面积.
1、分割法就是把图形切开,但是并不移动,使题目便于解答,组合图形中,如多边形、圆、扇 形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形,为了计算它们的面 积,常常需要用到割补的方法.必要时,我们需要将整个图形切割成最小单元来求解。 2、填补法就是把图形切开,把切下来的那部分移动到其他位置,使题目便于解答;注意:切割 下来的面积和要补上的面积要相等. 二、常见一半模型 下图中阴影部分面积均为长方形面积的一半.其中,A 为长方形长边上任意一点,B 为长方形内 部任意一点.
【湘教版数学(2024年)七年级上册同步练习题】 4.1立体图形与平面图形(含答案)

【湘教版数学(2024年)七年级上册同步练习】4.1立体图形与平面图形一、单选题1.观察下列实物模型,其整体形状给我们以圆柱的形象的是()A.B.C.D.2.如图是某个几何体的展开图,该几何体是()A.三棱柱B.四棱柱C.圆柱D.圆锥3.如图,在正方体的展开图中,与汉字“抗”相对的面上的汉字是()A.共B.同C.疫D.情4.如图,图、图、图均由四个全等的等边三角形组成,其中能够折叠围成一个立体图形的有()A.只有图①B.只有图①、图②C.图①、图②、图③D.只有图②、图③5.如图①所示的是一个正方体的表面展开图,将对应的正方体从如图②所示的位置依次翻过第1格、第2格,到第3格时正方体朝上的一面上的字是()A.亚B.欢C.迎D.您二、填空题6.一个正方体的每个面上都有一个汉字,其平面展开图如图所示,那么该正方体中与“爱”字相对的是.7.如果一个圆柱的侧面展开图是一个正方形,那么这个圆柱的高是底面直径的倍.8.如图所示为8个立体图形.其中,柱体的序号为,锥体的序号为,有曲面的序号为.9.如图是正方体的展开图,那么原正方体中,与“党”字所在面对面上的汉字是.10.圆锥有个面,有个顶点,它的侧面展开图是.11.一个正方体的每个面都写有一个汉字,其平面展开图如图所示,那么在该正方体中,和“超”相对的字是.三、解答题12.如图,上面的图形分别是下面哪个立体图形展开的形状,请你把有对应关系的平面图形与立体图形连接起来.答案解析部分1.【答案】D【知识点】立体图形的初步认识2.【答案】A【知识点】几何体的展开图3.【答案】D【知识点】几何体的展开图4.【答案】B【知识点】几何体的展开图5.【答案】B【知识点】几何体的展开图6.【答案】国【知识点】几何体的展开图7.【答案】【知识点】几何体的展开图8.【答案】①②⑤⑦⑧;④⑥;③④⑧【知识点】立体图形的初步认识9.【答案】年【知识点】几何体的展开图10.【答案】二;一;扇形【知识点】几何体的展开图11.【答案】自【知识点】几何体的展开图12.【答案】解:∵三个长方形和两个三角形如图摆放是三棱柱的展开图,一个扇形和一个圆是圆锥如图摆放的展开图,六个长方形如图摆放是长方体的展开图,一个长方形和两个圆如图摆放是圆柱的展开图,∴连接如图:【知识点】几何体的展开图。
数学中的平面图形和立体图形

数学中的平面图形和立体图形一、平面图形的知识1.1 定义与性质平面图形是平面内的图形,它由线段、射线、直线组成。
平面图形有无数个,如正方形、长方形、三角形、圆形、椭圆形等。
根据边数和角数对平面图形进行分类:(1)三角形:由三条边和三个角组成,分为不等边三角形、等腰三角形、等边三角形;(2)四边形:由四条边和四个角组成,分为矩形、正方形、平行四边形、梯形;(3)五边形、六边形等:根据边数和角数进行分类;(4)圆:由无数条等距的线段组成,圆心到圆上任意一点的距离相等。
1.3 面积计算(1)三角形面积:底×高÷2;(2)矩形面积:长×宽;(3)正方形面积:边长×边长;(4)圆形面积:π×半径²。
二、立体图形的知识2.1 定义与性质立体图形是空间内的图形,它由平面图形组成。
立体图形有无数个,如长方体、正方体、圆柱、圆锥、球等。
根据面、棱、顶点的数量对立体图形进行分类:(1)三棱锥:四个面,六个棱,四个顶点;(2)四棱锥:五个面,七个棱,四个顶点;(3)五棱锥:六个面,十一个棱,五个顶点;(4)长方体:六个面,十二条棱,八个顶点;(5)正方体:六个面,十二条棱,八个顶点;(6)圆柱:两个底面,一个侧面,四个顶点;(7)圆锥:一个底面,一个侧面,两个顶点;(8)球:一个曲面,无数个点。
2.3 体积计算(1)三棱锥体积:底面积×高÷3;(2)四棱锥体积:底面积×高÷3;(3)五棱锥体积:底面积×高÷3;(4)长方体体积:长×宽×高;(5)正方体体积:棱长×棱长×棱长;(6)圆柱体积:底面积×高;(7)圆锥体积:底面积×高÷3;(8)球体积:4/3×π×半径³。
三、平面图形与立体图形的联系与转换平面图形与立体图形之间存在联系,如长方体、正方体的展开图是矩形或正方形,圆柱的侧面展开图是矩形或圆形。
人教版七年级上4.1.1 立体图形与平面图形练习含答案
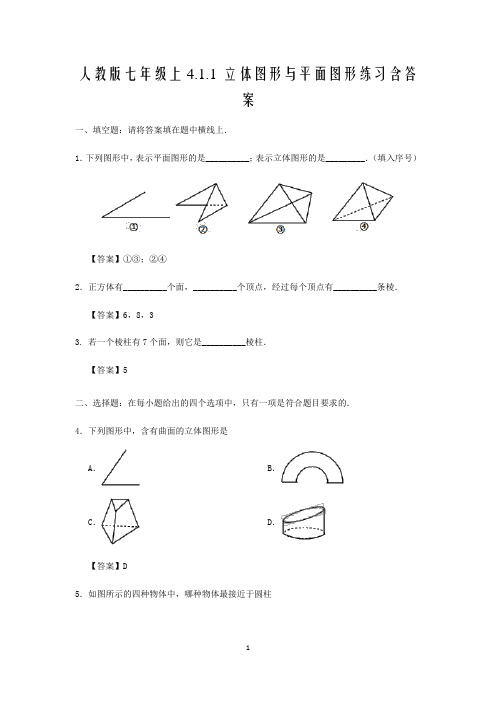
人教版七年级上4.1.1 立体图形与平面图形练习含答案一、填空题:请将答案填在题中横线上.1.下列图形中,表示平面图形的是__________;表示立体图形的是_________.(填入序号)【答案】①③;②④2.正方体有__________个面,__________个顶点,经过每个顶点有__________条棱.【答案】6,8,33. 若一个棱柱有7个面,则它是__________棱柱.【答案】5二、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.4.下列图形中,含有曲面的立体图形是A.B.C.D.【答案】D5.如图所示的四种物体中,哪种物体最接近于圆柱A.B.C.D.生日蛋糕弯管烟囱酒瓶【答案】A6.如图是一块带有圆形空洞和矩形空洞的小木板,则下列物体中最有可能既可以堵住圆形空洞,又可以堵住矩形空洞的是A.正方体B.球C.圆锥D.圆柱体【答案】D7.下面的几何体是棱柱的为A.B.C.D.【答案】C8.下列几何体中,是圆柱的为A.B.C.D.【答案】A三、解答题:解答应写出文字说明、证明过程或演算步骤.9.将下列几何体与它的名称连接起来.【答案】如图:10.如图所示的正方体的六个面分别标着连续的整数,求这六个整数的和.11.一个长方体如图所示.(1)求它的体积和表面积;(用含a、b的代数式表示)(2)当a=10,b=8时,该长方体的表面积是__________.【答案】(1)体积为a⋅b⋅6=6ab,表面积为2(ab+6a+6b)=2ab+12a+12b.(2)当a=10,b=8时,原式=2×10×8+12×10+12×8=376。
故答案为376.。
最新人教版七年级数学上册:立体图形与平面图形课时练习及答案解析.docx

新人教版数学七年级上册4.1.1立体图形与平面图形课时练习一、选择题(共15小题)1.如下图,下列四个几何体中,它们各自的三视图(主视图、左视图、俯视图)有两个相同,而另一个不同的几何体是()A.①②B.②③C.②④D.③④答案:B知识点:简单几何体的三视图解析:解答:运用已学过的简单几何体三视图,分别列出上述四个几何体的三视图。
①长方体:它的主视图、左视图、俯视图均为长方形,主视图是由其长和高组成的长方形,左视图是由其宽和高组成的长方形,俯视图是由其长和宽组成的长方形。
在没有告知长宽高具体数据的情况下,我们一般地认为长宽高是互不相等的。
②圆柱:它的主视图和左视图都是长方形,长方形的长都等于圆柱底面的直径,宽等于圆柱的高。
其俯视图是圆。
③圆锥:它的主视图和左视图都是三角形,三角形的底等于圆锥底面的直径,两腰都是顶点到底面圆边的距离。
其俯视图是圆。
④球:它的三视图都是圆,并且圆的直径相等。
分析:本题容易混淆的是①图和③图,有的学生会默认①图的主视图和俯视图相同,对于③图,有时会记错它的左视图。
本题考查简单几何体的三视图。
2.将下列图形绕直线l 旋转一周, 可以得到右图所示的立体图形的是()答案:C知识点:图形的旋转;主视图解析:解答:图形绕直线旋转一周,得到一个立体图形。
这个立体图形的横切面(俯视图)是圆,圆的半径等于旋转面上的点到直线的距离。
而该立体图形的主视图,则是平面图形以旋转直线为对称轴作出来的轴对称图形。
比如,圆柱是由长方形绕其一边旋转得到的,它的底面半径是该长方形另一边的长,绕其旋转的一边就是它的高。
圆锥是由一个直角三角形绕其一条直角边旋转一周得到的图形,这条直角边就是圆锥的高,另一条直角边就是圆锥的底面半径。
题目中的立体图形是一个等腰梯形,其上底长小于下底长。
由此,可以选出正确答案。
分析:在大脑中构建旋转立体图形,或者将已知立体图形的主视图画出来,按照选项中的直线位置作对称轴,得到的图形就是正确选项。
七年级数学立体图形与平面图形(基础)(含答案)

长方体是柱体,④正确;
正棱柱的侧面一定是长方形,⑤正确
正确的有4个,故选C.
试题难度:三颗星知识点:平面图形
5.下列的立体图形中,有4个面的是( )
A.三棱锥B.三棱柱
C.四棱锥D.四棱柱
答案:A
解题思路:
三棱锥有1个底面,3个侧面,共4个面,A正确;
三棱柱有2个底面,3个侧面,共5个面,B不正确;
四棱锥有1个底面,4个侧面,共5个面,C不正确;
四棱柱有2个底面,4个侧面,共6个面,D不正确.
故选A.
试题难度:三颗星知识点:立体图形
故选B.
试题难度:三颗星知识点:立体图形
4.下列图形全部属于柱体的是( )
A. B.
C. D.
答案:C
解题思路:
柱体包括圆柱和棱柱,C中的三个图形,一个是圆柱,两个是棱柱,
满足题意.
其中A中有一个是三棱锥;B中有一个圆锥,一个不规则多面体;
D中有一个是圆台,选项A,B,D均不符合题意.
故选C.
试题难度:三颗星知识点:立体图形
珍珠的形状类似于球体,火柴盒的形状类似于长方体,故选C.
试题难度:三颗星知识点:立体图形
8.下面图形中,是平面图形的是( )
A. B.
C. D.
答案:D
解题思路:
A是圆锥,B是圆柱,C是长方体,
只有D是三角形,是平面图形,故选D.
试题难度:三颗星知识点:平面图形
9.下列各组图形中都是平面图形的是( )
2.下列几何体中,属于柱体的有( )
A.1个B.2个
C.3个D.4个
答案:B
解题思路:
柱体包括圆柱和棱柱,其中第3图形个是正方体,属于棱柱,第5个图形是圆柱体,有2个属于柱体,故选B.
二年级图形练习题

二年级图形练习题一、认识图形1. 下列哪些是平面图形?- A. 圆- B. 球- C. 三角形- D. 立方体2. 请在下列图形中找出所有的平面图形,并用“√”标记。
- ① 正方形- ② 圆柱- ③ 长方形- ④ 圆锥二、图形分类1. 将下列图形按照平面图形和立体图形分类。
- ① 圆- ② 球- ③ 三角形- ④ 立方体- ⑤ 长方形- ⑥ 圆柱2. 请列举出至少三种平面图形,并说明它们的特点。
三、图形计数1. 观察下面的图形,数一数有几个圆形、几个三角形和几个正方形。
- [图形示例:圆形×3,三角形×2,正方形×1]2. 在下面的图形中,有几个长方形?几个正方形?- [图形示例:长方形×4,正方形×3]四、图形组合1. 用两个三角形可以组成哪些图形?请画出它们。
2. 如果给你一个正方形和一个三角形,你能组成哪些图形?请画出它们。
五、图形变换1. 如果将一个正方形旋转90度,它看起来会有什么变化?2. 一个长方形沿着它的长边或短边对折,会变成什么图形?六、图形对称1. 观察下面的图形,指出哪些图形是轴对称图形。
- [图形示例:圆形、长方形、三角形]2. 如果将一个轴对称图形沿着对称轴对折,两边的形状会完全重合吗?七、图形拼组1. 用四个相同的小正方形可以拼成一个什么图形?2. 如果用三个相同的等边三角形拼成一个图形,会是什么形状?八、图形识别1. 观察下面的图形,判断它是哪种基本图形。
- [图形示例:圆形、正方形、长方形等]2. 观察下面的图形,判断它是由哪些基本图形组成的。
- [图形示例:由两个三角形组成的菱形等]九、图形应用1. 请画出一个由圆形和三角形组成的简单图案。
2. 请用至少两种不同的图形设计一个简单的徽章。
十、图形创意1. 想象一下,如果所有的房子都是由几何图形构成的,你会怎样设计你的梦想小屋?2. 请画出一个由不同图形组合成的动物图案。
立体图形与平面图形练习题(含答案

立体图形与平面图形
1.从下列物体抽象出来的几何图形可以看成圆柱的是( )
2.下列图形不是立体图形的是( )
A.球
B.圆柱
C.圆锥
D.圆
3.下列图形属于棱柱的有( )
A.2个
B.3个
C.4个
D.5个
4.将下列几何体分类:
其中柱体有,锥体有,球体有(填序号).
5.如图所示是用简单的平面图形画出三位携手同行的好朋友,请你仔细观察,图中共有三角形个,圆个.
6.把下列图形与对应的名称用线连起来:
圆柱四棱锥正方体三角形圆
第1课时立体图形与平面图形
1.B
2.D
3.B
4.①①①①①①①
5.44
6.解:如图所示.
第2课时从不同的方向看立体图形和立体图形的展开图1.A 2.B 3.C 4.B 5.A
6.三棱柱五棱柱六棱柱长方体圆柱圆锥。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平面图形及立体图形的计算练习题1、求阴影部分的面积。
(单位:厘米)
2、求阴影部分的面积。
(单位:厘米)
3、求阴影部分的面积。
(单位:厘米)
4、已知直角三角形面积是12平方厘米,求阴影部分的面积。
5、图中圆的半径为5厘米,求阴影部分的面积。
(单位:厘米)
6、正方形边长为2厘米,求阴影部分的面积。
7.把19个边长为2厘米的正方体重叠起来堆成如右图所示的立方体,这个立方体的表面积是多少平方厘米.
8.如图是一个立体图形的侧面展开图,求它的全面积和体积.
参考答案
1.解:把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形, 所以阴影部分面积为:2×3=6平方厘米
2.
解:这种图形称为环形,可以用两个同心圆的面积差或差的一部分来求。
(π -π)×=×3.14=3.66平方厘米
3.解: 连对角线后将"叶形"剪开移到右上面的空白部分,凑成正方形的一半.
所以阴影部分面
积为:8×8÷2=32平方厘米
4.解: 设三角形的直角边长为r ,则
=12,=6 圆面积为:π÷2=3π。
圆内三角形的面积为12÷2=6,
阴影部分面积为:(3π-6)×=5.13平方厘米
5.解:上面的阴影部分以AB 为轴翻转后,整个阴影部分成为梯形减去直角三角形,或两个小直角三角形AED 、BCD 面积和。
所以阴影部分面积为:5×5÷2+5×10÷2=37.5平方厘米
6.解:右半部分上面部分逆时针,下面部分顺时针旋转到左半部分,组成一个矩形。
所以面积为:1×2=2平方厘米
7.这个立方体的表面由3×3×2+8×2+10×2=54个小正方形组成,故表面积为4×54=216(平方厘米).
8.
这个立体图形是一个圆柱的四分之一(如图),圆柱的底面半径为10厘米,高为8厘米. 它的全面积为: 810281014.324
11014.34122⨯⨯+⨯⨯⨯⨯+⨯⨯⨯ 6.4421606.125157=++=(平方厘米). 它的体积为:
62881014.3412=⨯⨯⨯(立方厘米).。
