专训 二次函数图象信息题的四种常见类型
高频题型专题：二次函数的图象信息题压轴题五种模型全攻略(解析版)
高频题型专题：二次函数的图象信息题压轴题五种模型全攻略【考点导航】目录【典型例题】 (1)【考点一 二次函数与一次函数图象共存问题】 ........................................................................................ 1 【考点二 二次函数与反比例函数图象共存问题】 .................................................................................... 5 【考点三 含字母参数的二次函数的图象和性质】 .................................................................................. 10 【考点四 二次函数的图象和性质与系数a ,b ,c 的问题】 ....................................................................... 16 【考点五 二次函数的图象与几何动点问题】 (21)【典型例题】【考点一 二次函数与一次函数图象共存问题】例题：（2023春·福建福州·八年级福建省福州延安中学校考期末）函数||y a x =与()20y ax a a =−≠在同一直角坐标系中的大致图象可能是（ ）． ． ． ． 【答案】C【分析】根据一次函数与二次函数的性质判断即可． 【详解】解：∵a >，∴||y a x =经过一、三象限；当0a >时，二次函数()20y ax a a =−≠开口向上，与y 轴的交点在负半轴上， 当0a <时，二次函数()20y ax a a =−≠开口向下，与y 轴的交点在正半轴上，∴只有选项C 符合题意；故选：C ．【点睛】题目主要考查一次函数与二次函数图象的判断，熟练掌握一次函数与二次函数的性质是解题关键． 【变式训练】1．（2023春·重庆渝中·八年级重庆巴蜀中学校考期末）如图是一次函数y kx b =+的图象，则二次函数22y kx bx =++的图象可能为（ ）A ．B ．C ．D ．【答案】C【分析】先根据一次函数图象确定00k b >>，，进而确定二次函数开口向上，对称轴在y 轴左侧，由此即可得到答案．【详解】解：∵一次函数y kx b =+的图象经过第一、二、三象限且与y 轴交于y 轴的正半轴， ∴00k b >>，，∴二次函数22y kx bx =++的图象的开口向上， ∵二次函数的对称轴为直线02bx k =−<，∴二次函数的对称轴在y 轴左侧，∴四个选项中只有C 选项中的函数图象符合题意， 故选C ．【点睛】本题主要考查了一次函数图象与二次函数图象综合判断，正确求出00k b >>，是解题的关键． 2．（2023春·广西南宁·八年级南宁市天桃实验学校校考期末）在同一坐标系中，一次函数1y mx =−+与二次函数，2y x m =+的图象可能是( )A ．B ．C ．D ．【答案】D【分析】根据一次函数的1b =和二次函数的1a =即可判断出二次函数的开口方向和一次函数经过y 轴正半轴，从而排除A 和C ，分情况探讨m 的情况，即可求出答案.【详解】解：二次函数为2y x m =+ ， 10a ∴=>，∴二次函数的开口方向向上， ∴排除C 选项.一次函数1y mx =−+，1>0b ∴=，一次函数经过y 轴正半轴， ∴排除A 选项.当0m >时，则0m −<，一次函数经过一、二、四象限，二次函数2y x m =+经过y 轴正半轴，∴ 排除B 选项.当0m <时，则0m −>一次函数经过一、二、三象限，二次函数2y x m =+经过y 轴负半轴， ∴D 选项符合题意.故选：D.【点睛】本题考查了一次函数和二次函数的图像性质，解题的关键在于熟练掌握图像性质中系数大小与图像的关系.3．（2023·全国·九年级假期作业）在同一平面直角坐标系中，函数y mx m =+和函数222(0)y mx x m =−++≠的图象可能是（ ）A ．B ．C ．D ．【答案】D【分析】根据函数图象判断两个m 值，函数的图象是否正确即可得到答案．【详解】解：A 、根据函数图象可知：一次函数解析式中0m <，二次函数解析式中0m −<，即0m >，两者符号不相同，故该选项不符合题意；B 、根据函数图象可知：一次函数解析式中0m <，二次函数解析式中0m −>，即0m <，两者符号相同，但根据a m =−，2b =得抛物线的对称轴应在y 轴的左侧，与图象不符，故该选项不符合题意；C 、根据函数图象可知：一次函数解析式中0m >，二次函数解析式中0m −>，即0m <，两者符号不相同，故该选项不符合题意；D 、根据函数图象可知：一次函数解析式中0m <，二次函数解析式中0m −>，即0m <，两者符号相同，根据a m =−，2b =得抛物线的对称轴应在y 轴的左侧，与图象相符，故该选项符合题意； 故选：D ．【点睛】此题考查一次函数与二次函数的图象性质，根据图象判断函数解析式中字母的取值，正确理解函数图象是解题的关键．A ．B ．C ．D ．【答案】C【分析】从二次函数图象的开口方向和对称轴的位置，可以得到a<0，0b >，可知直线y ax b =+经过第一、二、四象限．【详解】解：由二次函数的图象可知，开口向下，对称轴bx 02a =−>，∴a<0，0b >，∴一次函数y ax b =+的图象是经过第一、二、四象限. ∴只有选项C 符号条件， 故选：C ．【点睛】本题考查二次函数及一次函数的图象，解题关键是由二次函数的图象得到,a b 的符号，从而判断直线的位置．【考点二 二次函数与反比例函数图象共存问题】． ． ． ．【答案】D【分析】根据2y ax ax =+可知，二次函数图象与y 轴交点为0y =时，即二次函数图象过原点．再分两种情况即0a ＞，0a ＜时结合二次函数2y ax bx c =++中a ，b 同号对称轴在y 轴左侧，a ，b 异号对称轴在y 轴右侧来判断出二次函数与反比例函数图象所在象限，找到符合题意的即为正确答案．【详解】解：①当0a ＞时，二次函数2y ax ax =+开口向上，过原点，对称轴在y 轴左侧，故二次函数在一、二、三象限，反比例函数在一、三象限；②当0a ＜时，二次函数2y ax ax =+开口向下，过原点，对称轴在y 轴左侧，故二次函数在二、三、四象限，反比例函数在二、四象限， 观察图象可知只有D 符合， 故选：D ．【点睛】本题主要考查了二次函数图象以及反比例函数图象的性质，解题的关键是根据二次函数中a 的取值确定二次函数以及反比例函数的图象． 【变式训练】A ．B ．C ．D ．【答案】D【分析】根据a 的符号变化判断反比例函数和二次函数所在象限即可得出答案． 【详解】解：当0a >时，2y ax =的图像开口向上，过一、二象限；ay x =的图像位于一、三象限，可知，D正确；当a<0时，2y ax =的图像开口向下，过三、四象限；ay x =的图像位于二、四象限，无此选．故选：D【点睛】本题考查反比例函数和二次函数的图像，理解函数表达式中的系数与函数图像的关系是解题的关键．A ．B ．C ．D ．【答案】C【分析】令0x =，求出两个函数图象在y 轴上相交于同一点，再根据抛物线开口方向向上确定出0a >，然后确定出一次函数图象经过第一三象限，从而得解． 【详解】解：0x =时，两个函数的函数值y b =，所以，两个函数图象与y 轴相交于同一点，故B 、D 选项错误； 由A 、C 选项可知，抛物线开口方向向上，所以，0a >，所以，一次函数y ax b =+经过第一三象限， 所以，A 选项错误，C 选项正确． 故选：C ．【点睛】本题考查了二次函数图象，一次函数的图象，应该熟记一次函数y ax b =+在不同情况下所在的象限，以及熟练掌握二次函数的有关性质：开口方向、对称轴、顶点坐标等．A ． ． ． ．【答案】D【分析】由抛物线开口方向，对称轴位置及抛物线与y 轴交点位置判断a ，b ，c 的符号，从而可得直线与反比例函数图象的大致图象． 【详解】解：∵抛物线开口向上， ∴0a >，∵抛物线对称轴在y 轴左侧， ∴0b >， ∴0b −<∵抛物线与y 轴交点在x 轴下方， ∴0c <，∴直线y ax b =−经过第一，三，四象限，反比例函数cy x =图象分布在第二、四象限，故选：D ．【点睛】本题考查二次函数的性质，解题关键是掌握函数图象与系数的关系．A ．B ．C ．D ．【答案】A【分析】由二次函数图象分别判断出,,a b c 的符号，然后根据正比例函数与反比例函数的性质判断即可． 【详解】解：由二次函数图象可得： 开口向下， ∴a<0，对称轴在y 轴右边， ∴02b a −>，∴0b >，图象与y 轴交于正半轴， ∴0c >， ∴0b c +>，∴()y b c x =+图象过一三象限，ay x =图象过二四象限，故选：A ．【点睛】本题考查了函数图象的判断，相关知识点有：一次函数、反比例函数、二次函数的图象与性质，熟悉函数的图象与性质是解题关键．A ．B ．C ．D ．【答案】C【分析】根据二次函数()20y ax bx c a =++≠的图象开口向上，得出0a >，与y 轴交点在y 轴的负半轴，得出0c <，利用对称轴02b x a −>＝，得出0b <，然后对照四个选项中的图象判定即可．【详解】解：因为二次函数2y ax bx c =++的图象开口向上，得出0a >，与y 轴交点在y 轴的负半轴，得出0c <，利用对称轴02b x a −>＝，得出0b <，所以一次函数y bx c =+经过二、三、四象限，反比例函数ay x =经过一、三象限．A. 一次函数y bx c =+经过一、三、四象限，反比例函数ay x =经过二、四象限，不符合题意； B. 一次函数y bx c =+经过一、二、三象限，反比例函数ay x =经过二、四象限，不符合题意； C. 一次函数y bx c =+经过二、三、四象限，反比例函数ay x =经过一、三象限，符合题意； D. 一次函数y bx c =+经过一、三、四象限，反比例函数ay x =经过一、三象限，不符合题意；故选：C ．【点睛】本题考查的是由二次函数的图象判断各项系数的符号，一次函数与反比例函数的图象，熟记一次函数与反比例函数的图象的性质是解本题的关键．右图所示，则二次函数2y ax bx c =++的图象可能是（ ）A ．B ．C ．D ．【答案】C【分析】根据一次函数图象可得0,0a b ><，根据反比例函数可得0c <，据此即可求解． 【详解】解：∵一次函数y x b α=+的图象经过一、三、四象限， ∴0,0a b ><，∵反比例函数cy x =的图象在第二、四象限，∴0c <，∴抛物线的开口向上，对称轴在y y 轴交于负半轴， 故选：C ．【点睛】本题考查了一次函数、反比例函数、二次函数图象综合判断，熟练掌握以上函数图象的性质是解题的关键．【考点三 含字母参数的二次函数的图象和性质】例题：（2023·全国·九年级专题练习）已知二次函数2(31)3(0)y ax a x a =−++≠，下列说法正确的是( ) 【答案】C【分析】根据二次函数的图象和性质，逐一进行判断即可．【详解】解：∵2(31)3(0)y ax a x a =−++≠， 当1x =时：(31)322y a a a =−++=−， ∵0a ≠， ∴222a −≠，即：点(1,2)不在该函数的图象上，故A 选项错误； 当1a =时，()224321y x x x =−+=−−，∴抛物线的开口向上，对称轴为2x =， ∴抛物线上的点离对称轴越远，函数值越大， ∵13x −≤≤，123222−−>−>−，∴当=1x −时，y 有最大值为()21218−−−=，当2x =时，y 有最小值为1−， ∴18y −≤≤，故B 选项错误； ∵[]()222(31)43961310a a a a a ∆=−+−⨯=−+=−≥，∴该函数的图象与x 轴一定有交点，故选项C 正确；当0a >时，抛物线的对称轴为：313132222a x a a +==+>， ∴该函数图象的对称轴一定在直线32x =的右侧，故选项D 错误； 故选C ．【点睛】本题考查二次函数的图象和性质．熟练掌握二次函数的性质，是解题的关键． 【变式训练】A ．①②B ．②③C ．②D ．③④【答案】B【分析】根据二次函数的图象与性质进行逐一分析即可．【详解】解：∵抛物线对称轴为21==022b a a a −−−>，1=02c >，∴二次函数图象必经过第一、二象限，又∵2=4=42b ac a ∆−−，∵0a >， ∴424a −<，当420a −<时，抛物线与x 轴无交点，二次函数图象只经过第一、二象限，当0424a <−<时，抛物线与x 轴有两个交点，二次函数图象经过第一、二、四象限， 故①错误；②正确；∵抛物线对称轴为21==022b a a a −−−>，0a >，∴抛物线开口向上， ∴当1x a <时，y 随x 的增大而减小，故③正确； ∴当1x a >时，y 随x 的增大而增大，故④错误，故选：B ．【点睛】本题考查二次函数的图象与性质，熟练掌握二次函数图象与各项系数符号之间的关系是解题的关键．2．（2023·江苏南京·校考三模）已知整式22M a a =−，下列关于整式M 的值的结论： ①M 的值可能为4；②当1a >时，M 的值随a 的增大而增大； ③当a 为小于0的实数时，M 的值大于0； ④不存在这样的实数a ，使得M 的值小于1−． 其中所有正确结论的序号是（ ） A ．①③ B ．①②④ C ．②③④ D ．①②③④【答案】D【分析】根据一元二次方程的知识，二次函数的图象和性质，依次判断，即可． 【详解】①当4M =，∴224M a a =−=，解得：11a =21a = ∴M 的值可能为4， ∴①正确；②设函数的解析式为：22M a a =−，如图1∴对称轴为：12b x a =−=，函数图象的开口向上，∴当1a >，函数M 随a 的增大而增大， ∴②正确；③同理，当1x <，函数M 随a 的增大而减小，∴当a<0时，函数M 在y 轴是上方，即0M >， ∴③正确；④设函数的解析式为：22M a a =−，如图1∴当1a =时，函数M 有最小值，最小值为：1− ∴无论a 取任何数，1M ≥− ∴④正确；综上所述：正确的为：①②③④ 故选：D ．【点睛】本题考查一元二次方程，二次函数的图象和性质，解题的关键是掌握解一元二次方程，二次函数图象和性质，实数的性质．3．（2023·湖北武汉·统考一模）已知函数()222(y kx k x k =−++为实数)，下列四个结论：①当0k =时，图象与坐标轴所夹的锐角为45︒； ②若0k <，则当1x >时，y 随着x 的增大而减小；③不论k 为何值，若将函数图象向左平移1个单位长度，则图象经过原点； ④当2k <−时，抛物线顶点在第一象限．其中正确的结论是 （填写序号） 【答案】②③④【分析】由一次函数22y x =−+即可判断①；根据二次函数的性质即可判断②；得到平移后的解析式即可判断③；求得顶点坐标即可判断④．【详解】解：①当0k =时，函数为一次函数22y x =−+，由于系数为2−，所以图象与坐标轴所夹的锐角不为45︒，故①错误；②若0k <，抛物线的对称轴为直线()2111222k x kk −+=−=+<，则当1x >时，y 随着x 的增大而减小，故②正确；③当函数图象向左平移1解析式为()()2(1)212y k x k x =+−+++，则其图象过原点，故③正确；④当2k <−时，对称轴直线()211022k x kk −+=−=+>，顶点纵坐标为228(2)(2)044k k k k k −+−=−>，故抛物线顶点在第一象限，故④正确； 故答案为：②③④．【点睛】本题考查了抛物线与x 轴的交点：把求二次函数2(,,y ax bx c a b c =++是常数，0)a ≠与x 轴的交点坐标问题转化为解关于x 的一元二次方程．也考查了二次函数的性质．4．（2023春·福建福州·八年级福建省福州延安中学校考期末）对于二次函数()25144y ax a x a =−+++．有下列说法：①若1a <−，则二次函数的图象与y 轴的负半轴相交； ②若0a >，当12x ≤≤时，y 有最大值3；③若a 为整数，且二次函数的图象与x 轴的两个公共点都为整数点，则a 的值只能等于1； ④若0a <，且()()()1232,,3,,4,A y B y C y 为该函数图象上的三点，则123y y y >>． 其中正确的是 ．（只需填写序号） 【答案】①②④【分析】求出44a +的取值即可判断①；由对称轴方程可判断出当1x =时，函数在12x ≤≤时，y 有最大值3，故可判断②；根据二次函数的图象与x 轴的两个公共点都为整数点可知对称轴也是整数，可求出a ，进而判断③；分别求出A ，B ，C 三点对应的函数值，再进行比较即可判断④． 【详解】解：①对于()25144y ax a x a =−+++，令0x =，得44y a =+，由1a <−可得440y a =+<，即二次函数的图象与y 轴的负半轴相交，故①正确；②二次函数()25144y ax a x a =−+++对称轴方程为直线()512a x a−+=−512a a +=412a a a ++=122a a +=+， ∵0a >， ∴2,x >又抛物线的开口向上， ∴二次函数()25144y ax a x a =−+++的图象在12x ≤≤内，当1x =时，y 有最大值，最大值为：3；故②正确； ③∵二次函数()25144y ax a x a =−+++的图象与x 轴有两个交点，∴()()251444a a a ∆=−+−+⎡⎤⎣⎦22251011616a a a a =++−−2961a a =−+()231a =−， ∵a 为整数， ∴()2310a =−>V ，即a 为任意整数；又二次函数的图象与x 轴的两个公共点都为整数点， ∴对称轴122a x a +=+必为整数，此时a 的值不只能等于1，也可以是1−，故③错误；④∵()()()1232,,3,,4,A y B y C y 为函数()25144y ax a x a =−+++图象上的三点，∴当2x =时，22y a =−+； 当3x =时，21y a =−+；当4x =时，0y =； ∵a<0，∴22210a a −+>−+>，即123y y y >>．故④正确， 所以，正确的结论是①②④， 故答案为：①②④．【点睛】本题主要考查了二次函数图象与系数的关系，利用数形结合，从开口方向、对称轴、与x 轴（y 轴）的交点进行判断是解题的关键．【考点四 二次函数的图象和性质与系数a ,b ,c 的问题】A ．1个B ．2个C ．3个D ．4个【答案】B【分析】由抛物线的开口方向判断a 与0的关系，由抛物线与y 轴的交点判断y 与0的关系，然后根据对称轴及抛物线与x 轴交点情况进行推理，进而对所得结论进行判断．【详解】解：①函数的对称轴在y 轴右侧，则0ab <，抛物线与y 轴交于负半轴，则0c <，则0abc >，故①正确；②函数的对称轴为1x =，函数和x 轴的一个交点是()3,0，则另外一个交点为()1,0−，当=1x −时，0y a b c =−+=，故②错误；③函数的对称轴为12bx a =−=，即12a b =−，故③错误； ④由②③得，2b a =−，0a b c −+=，故30a c +=，而抛物线开口向上，则0a >，即50a >，故80a c +>，故选：B ．【点睛】主要考查图象与二次函数系数之间的关系，会利用对称轴的范围求2a 与b 的关系，以及二次函数与方程之间的转换是解题的关键． 【变式训练】1．（2023·黑龙江齐齐哈尔·统考三模）如图，二次函数()2<0y ax bx c a =++的图象与x 轴交于A 、B 两点，与y 轴交于点C ，对称轴为直线1x =，结合图象给出下列结论：①0abc >；②240ac b −<；③30a c +<；④方程221ax bx c k ++=−−的两根和为1；⑤若()1212,x x x x <是方程20ax bx c ++=的两根，则方程()()1230a x x x x −−+=的两根(),m n m n <满足()()120a m x n x −−>；其中正确结论有（ ）【答案】B【分析】综合二次函数图象与各项系数之间的关系，以及二次函数与方程之间的联系进行逐项分析． 【详解】解：由题意，a<0，对称轴为直线12b x a =−=，∴2b a =−，0b >，抛物线与y 轴相交于正半轴，则0c >， ∴<0abc ，故①错误；∵抛物线与x 轴有两个不同的交点，∴240b ac −>，即：240ac b −<，故②正确；∵由图象可得，当=1x −时，函数值0y <， ∴<0a b c −+，∴30a c +<，故③正确；对于方程221ax bx c k ++=−−，整理得：2210ax bx c k ++++=，∴其两根之和12b x x a +=−，∵2b a =−， ∴122x x +=∴方程221ax bx c k ++=−−的两根和为2，故④错误；∵()1212,x x x x <是方程20ax bx c ++=的两根，∴函数2y ax bx c =++图象与x 轴的两个交点的横坐标为()1212,x x x x <， ∵方程()()1230a x x x x −−+=的两根(),m n m n <，∴抛物线2y ax bx c =++与直线3y =−的交点横坐标为(),m n m n <，∵抛物线开口向下， ∴1m x <，2n x >，∴10m x −<，20n x −>，∵a<0， ∴()()120a m x n x −−>，故⑤正确；∴正确的有②③⑤， 故选：B ．【点睛】本题考查二次函数图象与性质，二次函数与一元二次方程之间的联系，掌握函数的基本性质，理解并熟练运用函数与方程之间的关系是解题关键．2．（2023·黑龙江齐齐哈尔·统考中考真题）如图，二次函数()20y ax bx c a =++≠图像的一部分与x 轴的一个交点坐标为()3,0，对称轴为直线1x =，结合图像给出下列结论：①0abc >；②2b a =；③30a c +=；④关于x 的一元二次方程220(0)ax bx c k a +++=≠有两个不相等的实数根；⑤若点()1,m y ，()22,y m −+均在该二次函数图像上，则12y y =．其中正确结论的个数是（ ）A ．4B ．3C ．2D ．1【答案】B【分析】根据抛物线的对称轴、开口方向、与y 轴的交点确定a 、b 、c 的正负，即可判定①和②；将点()3,0代入抛物线解析式并结合2b a =−即可判定③；运用根的判别式并结合a 、c 的正负，判定判别式是否大于零即可判定④；判定点()1,m y ，()22,y m −+的对称轴为1x =，然后根据抛物线的对称性即可判定⑤．【详解】解：抛物线开口向上，与y 轴交于负半轴， ∴00a c ><，，∵抛物线的对称轴为直线1x =， ∴12ba −=，即20b a =−<，即②错误； ∴0abc >，即①正确， 二次函数()20y ax bx c a =++≠图像的一部分与x 轴的一个交点坐标为()3,0930a b c ∴++=()9320a a c ∴+−+=，即30a c +=，故③正确；∵关于x 的一元二次方程220(0)ax bx c k a +++=≠，()2222444b a c k b ac ak ∆=−+=−−，00a c ><，，∴40ac −>，240ak −≤，∴无法判断2244b ac ak −−的正负，即无法确定关于x 的一元二次方程220(0)ax bx c k a +++=≠的根的情况，故④错误；∵()212m m +−+=∴点()1,m y ，()22,y m −+关于直线1x =对称 ∵点()1,m y ，()22,y m −+均在该二次函数图像上，∴12y y =，即⑤正确；综上，正确的为①③⑤，共3个 故选：B ．【点睛】本题考查了二次函数的()20y ax bx c a =++≠的性质及图像与系数的关系，能够从图像中准确的获取信息是解题的关键．A ．1个B ．2个C ．3个D ．4个【答案】C【分析】根据二次函数的图象和性质一一判断即可． 【详解】∵抛物线对称轴1x =−，经过点()10，，∴12ba −=−，0a b c ++=， ∴23b a c a ==−，， ∵a<0，∴00b c <>，，∴0ab >且0c >，故①错误，∵抛物线对称轴-1x =，经过()10，， ∴()3,0−和()10，关于对称轴对称，∴2x =-时，0y >，∴420a b c −+>，故②正确，∵抛物线与x 轴交于()3,0−，∴4x =-时，0y <，∴1640a b c −+<，∵2b a =，∴1680a a c −+<，即80a c +<，故③错误，∵336c a a a =−=−，2b a =，∴33c a b =−，故④正确，∵直线22y x =+与抛物线2y ax bx c =++两个交点的横坐标分别为12x x ，， ∴方程()2220ax b x c +−+−=的两个根分别为12x x ，， ∴122b x x a −+=−，122=c x x a −⋅ ， ∴1212x x x x ++=2222325b c a a a a a a −−−−−−+=−+=−，故⑤正确，正确的个数为3个． 故选：C ．【点睛】本题考查二次函数与系数的关系，二次函数图象上的点的特征，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．【考点五 二次函数的图象与几何动点问题】例题：（2023·河南周口·河南省淮阳中学校考三模）如图，在Rt ABC △中，908A AC AB ∠=︒==，．动点D从点A 出发，沿线段AB 以1单位长度/秒的速度运动，当点D 与点B 重合时，整个运动停止．以AD 为一边向上作正方形ADEF ，若设运动时间为x 秒()08x <≤，正方形ADEF 与ABC 重合部分的面积为y ，则下列能大致反映y 与x 的函数关系的图象是（ ）A ．B ．C ．D ．【答案】D【分析】根据题目所给条件，分当04x ≤≤时和当48x <≤时，建立函数关系式，利用二次函数的性质，即可得到答案．【详解】解；当04x ≤≤时，正方形ADEF 与ABC 重合部分的面积为正方形ADEF 的面积，∴2y x =，∴当48x <≤时，设DE 与BC 相交于M ，EF 与BC 相交于N ，，此时正方形ADEF 与ABC 重合部分的面积为正方形ADEF 的面积减去三角形EMN 的面积，∵ABC 是等腰直角三角形，8AB AC ==，∴8DM DB FN FC x ====−，∴()828EM EN x x x ==−−=−，∴()222221282163216322MNE ADEF y S S x x x x x x x =−=−−=−+−=−+−正方形△，∵10−<，∴二次函数的图象为开口向下的抛物线，故选：D ．【点睛】本题主要考查二次函数的解析式与图象的关系，正确列出函数关系式和判断二次函数的开口方向是解题的关键．【变式训练】 1．（2023·全国·九年级专题练习）如图，在正方形ABCD 中，4AB =，动点M ，N 分别从点A ，B 同时出发，沿射线AB ，射线BC 的方向匀速运动，且速度的大小相等，连接DM ，MN ，ND ．设点M 运动的路程为()04x x ≤≤，DMN 的面积为S ，下列图像中能反映S 与x 之间函数关系的是（ ）． ． ． ． 【答案】A【分析】先根据ADM DCN BMN ABCD S S S S S =−−−V V V 正方形，求出S 与x 之间函数关系式，再判断即可得出结论． 【详解】解：ADM DCN BMN ABCD S S S S S =−−−V V V 正方形，1114444(4)(4)222x x x x =⨯−⨯−⨯−−−，21282x x =−+， 21(2)62x =−+，故S 与x 之间函数关系为二次函数，图像开口向上，2x =时，函数有最小值6，故选：A ．【点睛】本题考查了正方形的性质，二次函数的图像与性质，本题的关键是求出S 与x 之间函数关系式，再判断S 与x 之间函数类型． 2．（2023·安徽合肥·校考三模）如图，正方形ABCD 中，4cm AB =，动点,P Q 分别从,A D 同时出发，点P 以每秒2cm 的速度沿A B C →→运动，点Q 以每秒1cm 的速度沿→D C 运动，P 点到达点C 时运动停止．设P 点运动x （秒）时，APQ △的面积()2cm y ，则y 关于x 的函数图象大致为：（ ）A ．B ．C ．D ．【答案】B【分析】分两种情况：当点P 在AB 上，即02x ≤≤时，此时APQ y S =，利用三角形面积公式得到y 关于x 的函数关系；当点P 在BC 上，即24x <≤时，此时APQ ABP CPQ ADQABCD S S S S S =−−−△△△△正方形，利用正方形和三角形面积公式得到y 关于x 的函数关系．进而可得y 关于x 的分段函数，根据函数解析式即可判断函数图象．【详解】解：当点P 在AB 上，即02x ≤≤时，如图，此时，2AP x =cm ，211244(cm )22APQ y S AP BC x x ∴==⋅=⋅⋅=△；当点P 在BC 上，即24x <≤时，如图，此时，(24)cm BP x =−，DQ x =cm ，(82)cm CP x ∴=−，(4)cm CQ x =−，2111222APQ ABP CPQ ADQ ABCD S S S S S AB AB BP CP CQ AD DQ =−−−=−⋅−⋅−⋅△△△△正方形，22211144(24)(82)(4)428(cm )222y x x x x x x ∴=−⨯⋅−−−−−⨯⋅=−++；．综上，24(02)28(24)x x y x x x ≤≤⎧=⎨−++<≤⎩． 故选：B ．【点睛】本题主要考查动点问题的函数图象，学会利用分类讨论思想和数形结合思想解决问题是解题关键． ，APQ 的面积为 ． ．C ． ． 【答案】D【分析】先找出运动轨迹几何运动的转折点，据此可分三段进行求解：①当点P 在AD 上运动，点Q 在AB 上运动，即04t ≤≤时；②当点P 在AD 上运动，点Q 在BC 上运动，即48t <≤时；③当点P 在CD 上运动，点Q 在BC 上运动，即812t <≤时．再根据三角形的面积公式分段求出y 关于t 的函数关系式，最后根据关系判断函数图像即可．【详解】解：①当点P 在AD 上运动，点Q 在AB 上运动，即04t ≤≤时，此时cm cm AP t AQ t ==，， ∴()22111cm 222APQ S AP AQ t t t =⋅=⋅=； ②如图：当点P 在AD 上运动，点Q 在BC 上运动，即48t <≤时，cm AP t =，∴()21142cm 22APQ S AP AB t t =⋅=⋅=； ③如图：当点P 在CD 上运动，点Q 在BC 上运动，即812t <≤时，∴()()()()8cm 4cm 12cm 12cm DP t BQ t CQ t CP t =−=−=−=−，，，， ∴APQ ABQ CPQ ADP ABCD S S S S S =−−−矩形1122AB AD CQ CP AD DP =⋅−⋅−⋅,()()()()1114844121288222t t t t =⨯−−⋅−−⋅−−⋅⋅− ＝2162t t ⎛⎫−+ ⎪⎝⎭2cm ； 综上，()()221422(48)168122t x t y t t t t t ⎧<<⎪⎪=<<⎨⎪⎪−+<≤⎩．故选：D ．【点睛】本题主要考查了动点问题的函数图像，理解题意、分段求出函数解析式是解题关键．。
(一)二次函数图象信息题常见的四种类型
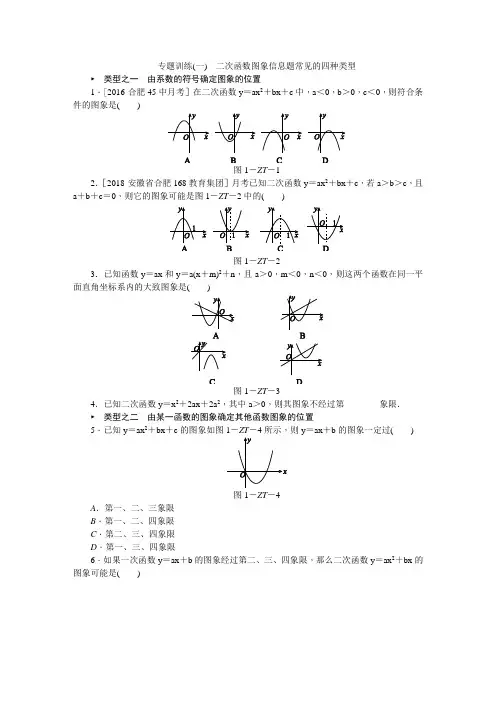
专题训练(一)二次函数图象信息题常见的四种类型►类型之一由系数的符号确定图象的位置1．［2016·合肥45中月考］在二次函数y＝ax2＋bx＋c中，a＜0，b＞0，c＜0，则符合条件的图象是()图1－ZT－12．［2018·安徽省合肥168教育集团］月考已知二次函数y＝ax2＋bx＋c，若a＞b＞c，且a＋b＋c＝0，则它的图象可能是图1－ZT－2中的()图1－ZT－23．已知函数y＝ax和y＝a(x＋m)2＋n，且a＞0，m＜0，n＜0，则这两个函数在同一平面直角坐标系内的大致图象是()图1－ZT－34．已知二次函数y＝x2＋2ax＋2a2，其中a＞0，则其图象不经过第________象限．►类型之二由某一函数的图象确定其他函数图象的位置5．已知y＝ax2＋bx＋c的图象如图1－ZT－4所示，则y＝ax＋b的图象一定过()图1－ZT－4A．第一、二、三象限B．第一、二、四象限C．第二、三、四象限D．第一、三、四象限6．如果一次函数y＝ax＋b的图象经过第二、三、四象限，那么二次函数y＝ax2＋bx的图象可能是()图1－ZT－57．如图1－ZT－6，一次函数y1＝x与二次函数y2＝ax2＋bx＋c的图象相交于P，Q两点，则函数y＝ax2＋(b－1)x＋c的图象可能为()图1－ZT－6图1－ZT－7►类型之三由函数图象确定系数及代数式的符号8．［2017·六盘水］已知二次函数y＝ax2＋bx＋c的图象如图1－ZT－8所示，则() A．b＞0，c＞0 B．b＞0，c＜0C．b＜0，c＜0 D．b＜0，c＞0图1－ZT－89.已知抛物线y＝ax2＋bx＋c如图1－ZT－9所示，对称轴为直线x＝1，则代数式：(1)abc；(2)a＋b＋c；(3)a－b＋c；(4)4a＋2b＋c中，值为正数的个数是()A．1 B．2 C．3 D．4图1－ZT－910．［2017·杭州］设直线x ＝1是函数y ＝ax 2＋bx ＋c(a ，b ，c 是实数，且a ＜0)的图象的对称轴，( )A ．若m ＞1，则(m －1)a ＋b ＞0B ．若m ＞1，则(m －1)a ＋b ＜0C ．若m ＜1，则(m ＋1)a ＋b ＞0D ．若m ＜1，则(m ＋1)a ＋b ＜011．如图1－ZT －10，抛物线y ＝ax 2＋bx ＋c(a>0)的对称轴是过点(1，0)且平行于y 轴的直线．若点P(4，0)在该抛物线上，则4a －2b ＋c 的值为________．图1－ZT －1012．［2017·资阳］如图1－ZT －11，抛物线y ＝ax 2＋bx ＋c 的顶点和该抛物线与y 轴的交点在一次函数y ＝kx ＋1(k ≠0)的图象上，它的对称轴是直线x ＝1，有下列四个结论：①abc＜0，②a ＜－13，③a ＝－k ，④当0＜x ＜1时，ax ＋b ＞k.其中正确结论的个数是( ) A ．4 B ．3 C ．2 D ．1图1－ZT －11► 类型之四 利用二次函数求一元二次方程的根13．小兰画了一个函数y ＝x 2＋ax ＋b 的图象如图1－ZT －12，则关于x 的方程x 2＋ax ＋b ＝0的解是( )A ．无解B ．x ＝1C ．x ＝－4D ．x 1＝－1，x 2＝4图1－ZT －1214．二次函数y ＝ax 2＋bx ＋c 的图象如图1－ZT －13所示，则当函数值y ＞0时，x 的取值范围是( )A ．x ＜－1B ．x ＞3C ．－1＜x ＜3D ．x ＜－1或x ＞3图1－ZT －1315．［2018·马鞍山期中］已知二次函数y ＝ax 2＋2ax －3的部分图象如图1－ZT －14，由图象可知关于x 的一元二次方程ax 2＋2ax －3＝0的两个根分别是x 1＝1.3和x 2＝( )A ．－1.3B ．－2.3C ．－0.3D ．－3.3图1－ZT －1416．［2016·淮南期中］如图1－ZT －15所示，一次函数y 1＝kx ＋n 与二次函数y 2＝ax 2＋bx ＋c 的图象相交于A(－1，5)，B(9，2)两点，则关于x 的不等式kx ＋n ≥ax 2＋bx ＋c 的解集为( )A ．－1≤x ≤9B ．－1≤x ＜9C ．－1＜x ≤9D ．x ≤－1或x ≥9图1－ZT －15 17．［2016·南宁］二次函数y ＝ax 2＋bx ＋c 和正比例函数y ＝23x 的图象如图1－ZT －16所示，则关于x 的一元二次方程ax 2＋(b －23)x ＋c ＝0的两根之和( ) A ．大于0 B ．等于0C ．小于0D ．不能确定图1－ZT －1618．［2017·遂宁］函数y ＝x 2＋bx ＋c 与函数y ＝x 的图象如图1－ZT －17所示，有以下结论：①b 2－4c ＞0；②b ＋c ＝0；③b ＜0；④方程组⎩⎪⎨⎪⎧y ＝x 2＋bx ＋c ，y ＝x 的解为⎩⎨⎧x 1＝1，y 1＝1，⎩⎪⎨⎪⎧x 2＝3，y 2＝3；⑤当1＜x ＜3时，x 2＋(b －1)x ＋c ＞0.其中正确的是( )A ．①②③B ．②③④C ．③④⑤D ．②③⑤图1－ZT－17教师详解详析1．[解析] D∵a＜0，b＞0，c＜0，∴图象开口向下，对称轴在x轴的右侧，交y轴于负半轴．只有D选项中的图象符合题意．故选D.2．[解析] D当x＝1时，a＋b＋c＝0，即抛物线经过点(1，0)．当a＞b＞0＞c时，抛物线的对称轴x＝－b2a＜0，没有图形符合；当a＞0＞b＞c时，则抛物线的对称轴x＝－b2a＞0，选项D符合要求；而a＞b＞c＞0和0＞a＞b＞c都不符合a＋b＋c＝0.综上所述，本题选D.3．[解析] B由函数表达式y＝a(x＋m)2＋n(a>0)可知其图象开口向上，其顶点坐标为(－m，n)．又因为m＜0，n＜0，所以顶点在第四象限，排除A，C，D.故选B.4．[答案] 三、四[解析] ∵二次项系数为1，∴抛物线开口向上．又∵对称轴是直线x＝－a＜0，4a2－8a2＝－4a2<0，故与x轴没有交点，∴其图象不经过第三、四象限．5．[解析] D∵抛物线开口向上，∴a＞0.∵对称轴为直线x＝－b2a＞0，a＞0，∴b＜0，∴y＝ax＋b的图象一定过第一、三、四象限．故选D.6．[解析] C∵一次函数y＝ax＋b的图象经过第二、三、四象限，∴a＜0，b＜0，∴二次函数y＝ax2＋bx的图象开口向下，对称轴为直线x＝－b2a＜0，在y轴左边．故选C.7．[解析] A由于一次函数y1＝x与二次函数y2＝ax2＋bx＋c的图象有两个不同的交点，且这两个交点都位于第一象限，所以方程ax2＋bx＋c＝x，即ax2＋(b－1)x＋c＝0有两个不相等的正实数根，所以函数y＝ax2＋(b－1)x＋c的图象与x轴有两个不同的交点，且两个交点都在x轴的正半轴上．故选A.8．[解析] B∵图象的开口向下，∴a＜0.∵图象的对称轴为直线x＝－b2a＞0，∴b＞0.又∵图象与y轴的交点位于原点的下方，∴c＜0.故选项B符合题意．9．[解析] B∵抛物线开口向上，∴a＞0.∵抛物线的对称轴为直线x＝1，－b2a＝1，∴b＝－2a，∴b<0.∵抛物线与y轴的交点在x轴下方，∴c＜0，∴abc＞0.∵当x＝1时，y＜0，∴a＋b＋c＜0.∵当x＝－1时，y＞0，∴a－b＋c＞0.∵当x＝2时，y＜0，∴4a＋2b＋c＜0.故选B.10．[解析] C∵a＜0，∴函数y有最大值．当x＝1时，函数y的最大值为a＋b＋c①.当m＞1，x＝m时，函数y＝m2a＋mb＋c②.由②－①，得(m2－1)a＋(m－1)b＜0.又∵m－1＞0，∴(m＋1)a＋b＜0，故选项A，B不一定正确．当m＜1，x＝m时，函数y＝m2a＋mb＋c③.由③－①，得(m2－1)a＋(m－1)b＜0.又∵m－1＜0，∴(m＋1)a＋b＞0，故选项C正确，选项D错误．11．[答案] 0[解析] 方法一：∵抛物线的对称轴为直线x＝1，由对称性可知，点P(4，0)和点(－2，0)关于直线x＝1对称，因此点(－2，0)也在抛物线y＝ax2＋bx＋c上，∴4a－2b＋c＝0.方法二：由题意，得方程组⎩⎪⎨⎪⎧－b 2a ＝1，16a ＋4b ＋c ＝0.从而求得⎩⎪⎨⎪⎧b ＝－2a ，c ＝－8a .把b ，c 的值代入4a －2b ＋c 中，得4a －2b ＋c ＝0.12．[解析] A 由抛物线的开口向下，且对称轴为直线x ＝1可知a ＜0，－b 2a＝1，即b ＝－2a ＞0.由抛物线与y 轴的交点在一次函数y ＝kx ＋1(k ≠0)的图象上知c ＝1，则abc ＜0，故结论①正确．由①知y ＝ax 2－2ax ＋1.∵当x ＝－1时，y ＝a ＋2a ＋1＝3a ＋1＜0，∴a ＜－13，故结论②正确；∵抛物线y ＝ax 2＋bx ＋c 的顶点在一次函数y ＝kx ＋1(k ≠0)的图象上，∴a ＋b ＋1＝k ＋1，即a ＋b ＝k .又∵b ＝－2a ，∴a －2a ＝k ，即a ＝－k ，故结论③正确．由函数图象知，当0＜x ＜1时，二次函数图象在一次函数图象上方，∴ax 2＋bx ＋1＞kx ＋1，即ax 2＋bx ＞kx .又∵x ＞0，∴ax ＋b ＞k ，故结论④正确．综上所述，共有4个结论正确，故选A.13．[解析] D ∵二次函数y ＝x 2＋ax ＋b 的图象与x 轴交于点(－1，0)和(4，0)，即当x ＝－1或4时，x 2＋ax ＋b ＝0，∴关于x 的方程x 2＋ax ＋b ＝0的解为x 1＝－1，x 2＝4，故选D.14．D15．[解析] D 二次函数y ＝ax 2＋2ax －3的图象的对称轴是直线x ＝－2a 2a＝－1.又∵x 1与x 2关于对称轴对称，∴1.3－(－1)＝－1－x 2，解得x 2＝－3.3，故选D.16．[解析] A 结合图象可知一次函数图象在二次函数图象上方时，对应的x 的取值范围即本题的答案，由图可知当－1≤x ≤9时，kx ＋n ≥ax 2＋bx ＋c .故选A.17．[解析] A 由图象可知二次函数y ＝ax 2＋bx ＋c 和正比例函数y ＝23x 的图象的交点的横坐标之和大于0，即方程组⎩⎪⎨⎪⎧y ＝ax 2＋bx ＋c ，y ＝23x的解中未知数x 的两个值的和大于0，可得ax 2＋bx ＋c ＝23x 变形为方程ax 2＋(b －23)x ＋c ＝0后，它的两根之和大于0. 18．[解析] B ∵函数y ＝x 2＋bx ＋c 的图象与x 轴无交点，∴b 2－4c ＜0，故结论①错误； 当x ＝1时，y ＝1＋b ＋c ＝1，则b ＋c ＝0，故结论②正确；∵对称轴在y 轴的右侧，∴a ，b 异号．又∵a ＝1＞0，∴b ＜0，故结论③正确；根据抛物线与直线y ＝x 的交点知：方程组⎩⎪⎨⎪⎧y ＝x 2＋bx ＋c ，y ＝x 的解为⎩⎨⎧x 1＝1，y 1＝1，⎩⎨⎧x 2＝3，y 2＝3，故结论④正确；∵当1＜x ＜3时，二次函数值小于一次函数值，∴x 2＋bx ＋c ＜x ，∴x 2＋(b －1)x ＋c ＜0，故结论⑤错误．综上所述，结论②③④正确，故选B.。
专题课堂-四 二次函数图象信息题归类
专题课堂-四 二次函数图象信息题归类（PPT优秀 课件）
专题课堂-四 二次函数图象信息题归类（PPT优秀 课件）
15．如图，已知二次函数y＝ax2＋bx＋c的图象过A(2，0)，B(0， －1)和C(4，5)三点．
(1)求二次函数的解析式； (2)设二次函数的图象与x轴的另一个交点为D，求点D的坐标； (3)在同一坐标系中画出直线y＝x＋1，并写出当x在什么范围内时 ，一次函数的值大于二次函数的值．
第二十二章 二次函数
专题课堂(四) 二次函数图象信息题归类
类型一：确定函数图象的大致位置 1．(2016·泰安)二次函数y＝ax2＋bx＋c的图象如图所示，那么一
次函数y＝ax＋b的图象大致是( A )
2．在同一坐标系中，一次函数y＝－mx＋n2与二次函数y＝x2＋m的图 象可能是( )D
类型二：利用二次函数图象确定系数之间的关系 3．(2016·常德)二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示， 下列结论：①b＜0；②c＞0；③a＋c＜b；④b2－4ac＞0， 其中正确的个数是( C) A．1个 B．2个 C．3个 D．4个
专题课堂-四 二次函数图象信息题归类（PPT优秀 ቤተ መጻሕፍቲ ባይዱ件）
专题课堂-四 二次函数图象信息题归类（PPT优秀 课件）
解：(1)y＝12x2－12x－1 (2)当 y＝0 时，得12x2－12x－1＝0，解得 x1＝2，x2＝－1， ∴点 D 坐标为(－1，0) (3)－1<x<4
专题课堂-四 二次函数图象信息题归类（PPT优秀 课件）
11．(2016·南宁)二次函数 y＝ax2＋bx＋c(a≠0)和正比例函数 y＝23 x 的图象如图所示，则方程 ax2＋(b－32)x＋c＝0(a≠0)的两根之和(A )
典中点二次函数专训3二次函数图像信息题的四种常见类型
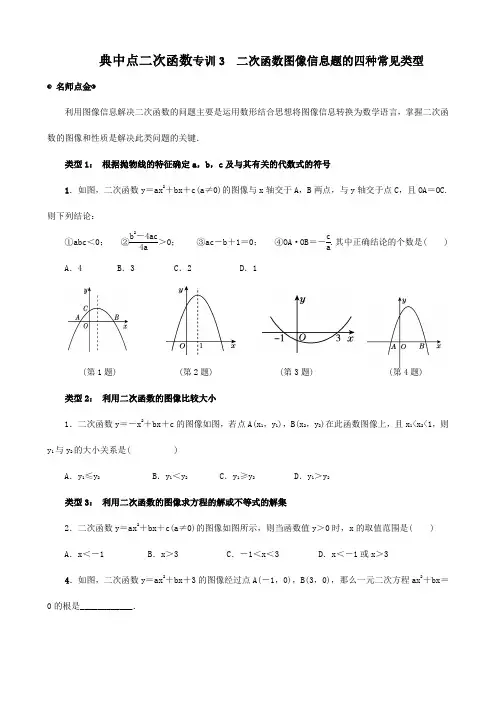
典中点二次函数专训3 二次函数图像信息题的四种常见类型 ◐名师点金◑利用图像信息解决二次函数的问题主要是运用数形结合思想将图像信息转换为数学语言，掌握二次函数的图像和性质是解决此类问题的关键．类型1： 根据抛物线的特征确定a ，b ，c 及与其有关的代数式的符号1．如图，二次函数y ＝ax 2＋bx ＋c(a ≠0)的图像与x 轴交于A ，B 两点，与y 轴交于点C ，且OA ＝OC.则下列结论：①abc ＜0； ②b 2－4ac 4a ＞0； ③ac －b ＋1＝0； ④OA ·OB ＝－c a.其中正确结论的个数是( ) A ．4 B ．3 C ．2 D ．1(第1题) (第2题) (第3题) (第4题) 类型2： 利用二次函数的图像比较大小1．二次函数y ＝－x 2＋bx ＋c 的图像如图，若点A(x 1，y 1)，B(x 2，y 2)在此函数图像上，且x 1<x 2<1，则y 1与y 2的大小关系是( )A ．y 1≤y 2B ．y 1＜y 2C ．y 1≥y 2D ．y 1＞y 2类型3： 利用二次函数的图像求方程的解或不等式的解集2．二次函数y ＝ax 2＋bx ＋c(a ≠0)的图像如图所示，则当函数值y ＞0时，x 的取值范围是( )A ．x ＜－1B ．x ＞3C ．－1＜x ＜3D ．x ＜－1或x ＞34．如图，二次函数y ＝ax 2＋bx ＋3的图像经过点A(－1，0)，B(3，0)，那么一元二次方程ax 2＋bx ＝0的根是____________．类型4：根据抛物线的特征确定其他函数的图像5．二次函数y＝ax2＋bx的图像如左下图所示，那么一次函数y＝ax＋b的图像大致是( )6．如图，A(－1，0)，B(2，－3)两点在一次函数y1＝－x＋m与二次函数y2＝ax2＋bx－3的图像上．(1)求m的值和二次函数的表达式；(2)设二次函数的图像交y轴于点C，求△ABC的面积．。
二次函数图象信息题的四种常见类型
抛物线开口向上的图像
1
特点
图像开口朝上，a>0。
2
性质在抛物ຫໍສະໝຸດ 的中心处，函数取得最小值，也称为“顶点”，坐标为(f(g),-h(f(g)))。
3
例题
如果抛物线y=ax^2+bx+c的顶点是(-1,4)，则方程的形式是什么？
抛物线开口向下的图像
特点
图像开口朝下，a<0。
性质
函数的最大值位于抛物线的中心 处，其坐标为(f(g),-h(f(g)))。
二次函数图象信息题的四 种常见类型
在学习二次函数时，掌握常见的四种图像类型对于学生们是非常重要的。这 个幻灯片将介绍这些类型，以及如何轻松应对与它们相关的信息问题。
什么是二次函数？
1 定义
二次函数是形如y=ax^2+bx+c的函数，其中a，b，c为常数，a不等于零。图像为开口朝 上或朝下的轮廓类似于一个U形。
例题
如果抛物线y=ax^2+bx+c的最大 值点是(2,5)，则a的值是多少？
两个实根的图像
特点
图像与x轴有两个交点（实 根），a>0。
性质
当x趋近于正无穷或负无穷时， 二次函数趋近于无穷大。此 外，抛物线的轴线是根的平 均值。
例题
给定二次函数y=-2(x-4)(x-3)， 求它的零点是多少？
无实根的图像
1
特点
图像可以用a(x-h)^2+k的形式表示，其中a<0。
2
性质
在抛物线的中心处，函数达到最大值。图像完全位于或高于x轴上方。
3
例题
二次方程y=x^2+4x+13有实根吗？如果不是，图像是什么样子的？
最新冀教版初中数学九年级下册精品专训1 二次函数图像信息题的四种常见类型
专训1 二次函数图像信息题的四种常见类型名师点金：利用图像信息解决二次函数的问题主要是运用数形结合思想将图像信息转换为数学语言，掌握二次函数的图像和性质是解决此类问题的关键．根据抛物线的特征确定a ，b ，c 及与其有关的代数式的符号1．【中考·孝感】如图，二次函数y ＝ax 2＋bx ＋c(a ≠0)的图像与x 轴交于A ，B 两点，与y 轴交于点C ，且OA ＝OC.则下列结论：①abc ＜0；②b 2－4ac 4a ＞0；③ac －b ＋1＝0；④OA·OB ＝－c a.其中正确结论的个数是( ) A ．4 B ．3 C ．2 D ．1(第1题)(第2题)利用二次函数的图像比较大小 2．二次函数y ＝－x 2＋bx ＋c 的图像如图，若点A(x 1，y 1)，B(x 2，y 2)在此函数图像上，且x 1<x 2<1，则y 1与y 2的大小关系是( )A ．y 1≤y 2B ．y 1＜y 2C ．y 1≥y 2D ．y 1＞y 2利用二次函数的图像求方程的解或不等式的解集3．【中考·黄石】二次函数y ＝ax 2＋bx ＋c(a ≠0)的图像如图所示，则当函数值y ＞0时，x 的取值范围是( )A ．x ＜－1B ．x ＞3C ．－1＜x ＜3D ．x ＜－1或x ＞3(第3题)(第4题)4．【中考·阜新】如图，二次函数y＝ax2＋bx＋3的图像经过点A(－1，0)，B(3，0)，那么一元二次方程ax2＋bx＝0的根是____________．根据抛物线的特征确定其他函数的图像5．【中考·聊城】二次函数y＝ax2＋bx的图像如图所示，那么一次函数y＝ax＋b的图像大致是()(第5题)6．如图，A(－1，0)，B(2，－3)两点在一次函数y1＝－x＋m与二次函数y2＝ax2＋bx －3的图像上．(1)求m的值和二次函数的表达式；(2)设二次函数的图像交y轴于点C，求△ABC的面积．【导学号：89274029】(第6题)答案1．B 2.B 3.D 4.x 1＝0，x 2＝2 5.C6．解：(1)将点A(－1，0)的坐标代入y 1＝－x ＋m ，得m ＝－1；将点A(－1，0)，B(2，－3)的坐标分别代入y 2＝ax 2＋bx －3，得⎩⎪⎨⎪⎧a －b －3＝0，4a ＋2b －3＝－3.解得⎩⎪⎨⎪⎧a ＝1，b ＝－2. ∴y 2＝x 2－2x －3.(2)易知C 点的坐标为(0，－3)，一次函数的图像与y 轴的交点坐标为(0，－1)．∴S △ABC ＝12×[－1－(－3)]×1＋12×[－1－(－3)]×2＝12×2×1＋12×2×2＝3.。
专题训练(三) 二次函数图象信息题归类
专题训练(三) 二次函数图象信息题归类
4．[2018·安顺] 已知二次函数y＝ax2＋bx＋c(a≠0)的图象如图3－ ZT－5，分析下列四个结论：①abc＜0；②b2－4ac＞0；③3a＋c
＞0；④(a＋c)2＜b2.其中正确的结论有( B )
A．1个
B．2个
C．3个
D．4个
图3－ZT－5
专题训练(三) 二次函数图象信息题归类
0，所以 ac＞0，选项 A 错误；由对称轴直线 x＝－2ba>0，知 b＜0，选项 B 正确； 由抛物线与 x 轴有两个不同的交点，知 b2－4ac＞0，选项 C 错误；当 x＝1 时， y＞0，即 a＋b＋c＞0，选项 D 错误．
专题训练(三) 二次函数图象信息题归类
2．[2018·青岛] 已知一次函数 y＝bax＋c 的图象如图 3－ZT－2，则 二次函数 y＝ax2＋bx＋c 在平面直角坐标系中的图象可能是( A )
特殊 若a－b＋c>0，则x＝－1时，y>0
关系 当对称轴为直线x＝1时，2a＋b＝0；当对称轴为直线x＝－1
时，2a－b＝0；判断2a＋b大于或小于0，看对称轴与直线x＝
1的位置关系；判断2a－b大于或小于0，看对称轴与直线x＝
－1的位置关系
专题训练(三) 二次函数图象信息题归类
类型之一 利用二次函数图象考查以上表格中的问题
专题训练(三) 二次函数图象信息题归类
5．[2017·广安]如图3－ZT－6所示，抛物线y＝ax2＋bx＋c的顶
点为B(－1，3)，与x轴的交点A在点(－3，0)和(－2，0)之间，
以下结论：①b2－4ac＝0；②a＋b＋c>0；③2a－b＝0；④c－a
＝3.其中正确结论的个数是( B )
北师版数学下册2.5.3二次函数图象信息题的四种常见类型(练习题课件)
失量 图标
【提示】下载后此页用户可自行删除！
2．二次函数 y＝－x2＋bx＋c 的图象如图所示，若点 A(x1，y1)， B(x2，y2)在此函数图象上，且 x1<x2<1，则 y1 与 y2 的大小关 系是( B ) A．y1≤y2 B．y1＜y2 C．y1≥y2 D．y1＞y2
3．【中考·黄石】二次函数 y＝ax2＋bx＋c(a≠0)的图象如图所示， 则当函数值 y＞0 时，x 的取值范围是( D ) A．x＜－1 B．x＞3 C．－1＜x＜3 D．x＜－1 或 x＞3
②当 y1＝－x2－2x＋8 时，解－x2－2x＋8＝0，得 x＝－4 或 x＝2， ∴抛物线与 x 轴的交点坐标是(－4，0)和(2，0)．∵y2 随着 x 的增大而增大， 且 y2 过点 A(－1，5)，∴y1 与 y 2 都经过 x 轴上的同一点(－4，0)．
－k＋b＝5， 把点(－1，5)，(－4，0)的坐标分别代入 y2＝kx＋b，得－4k＋b＝0，解得
4．如图，一次函数 y1＝kx＋n 与二次函数 y2＝ax2＋bx＋c 的图 象相交于 A(－1，5)，B(9，2)两点，则关于 x 的不等式 kx＋n≥ax2 ＋bx＋c 的解集为( A ) A．－1≤x≤9 B．－1≤x＜9 C．－1＜x≤9 D．x≤－1 或 x≥9
*5.【中考·阜新】如图，二次函数 y＝ax2＋bx＋3 的图象经过点 A(－1，0)，B(3，0)，那么关于 x 的一元二次方程 ax2＋bx＝ 0 的根是_x_1_＝__0_，__x_2_＝__2____．
kb＝ ＝3253， 0，∴y2＝53x＋230.综上，y2 的表达式为 y2＝5x＋10 或 y2＝53x＋230.
使用 说明
此课件下载后
【二次函数图象信息题的四种常见类型】PPT课件
第二十二章 二次函数
22.2 二次函数与一元二次方程 第3课时 二次函数图象信息题
的四种常见类型
习题链接
提示：点击 进入习题
1D 2B 3D 4A
答案显示
5 x1＝0，x2＝2 6D 7 见习题
类型
1．【2018·毕节】已知二次函数y＝ax2＋bx＋c(a≠0)的图象 如图所示，下列结论：
1、“读”是我们学习语文最基本的方法之一，古人说，读书时应该做到“眼到，口到，心到”。我看，你们今天达到了这个要求。 2、大家自由读书的这段时间里，教室里只听见琅琅书声，大家专注的神情让我感受到什么叫“求知若渴”，我很感动。 3、经过这么一读，这一段文字的意思就明白了，不需要再说明什么了。 4、请你们读一下，将你的感受从声音中表现出来。 5、读得很好，听得出你是将自己的理解读出来了。特别是这一句，请再读一遍。
A．－1≤x≤9 B．－1≤x＜9 C．－1＜x≤9 D．x≤－1或x≥9
探究培优
5．【中考·阜新】如图，二次函数y＝ax2＋bx＋3的图象经 过点A(－1，0)，B(3，0)，那么关于x的一元二次方程 ax2＋bx＝0的根是___x_1＝__0_，__x_2_＝__2___．
夯实基础
6．已知函数y＝(x－a)(x－b)(其中a＞b)的图象如图所示， 则函数y＝ax＋b的图象正确的是( D )
探究培优
3．【中考·黄石】二次函数y＝ax2＋bx＋c(a≠0)的图象如图 所示，则当函数值y＞0时，x的取值范围是( D )
A．x＜－1 B．x＞3 C．－1＜x＜3 D．x＜－1或x＞3
探究培优
4．如图，一次函数y1＝kx＋n与二次函数y2＝ax2＋bx＋c 的图象相交于A(－1，5)，B(9，2)两点，则关于x的不 等式kx＋n≥ax2＋bx＋c的解集为( A )
(完整版)专题训练(一)二次函数图象常见四种信息题
专题训练（一）二次函数图象常见四种信息题►类型之一由系数的符号确定图象的位置1．在二次函数y＝ax2＋bx＋c中，a＜0，b＞0，c＜0，则符合条件的图象是()图1－ZT－12．已知二次函数y＝ax2＋bx＋c，若a＞b＞c，且a＋b＋c＝0，则它的图象可能是图1－ZT－2中的()图1－ZT－23．[2018·德州]如图1－ZT－3，函数y＝ax2－2x＋1和y＝ax－a(a是常数，且a≠0)在同一平面直角坐标系的图象可能是()图1－ZT－34．已知二次函数y＝x2＋2ax＋2a2，其中a＞0，则其图象不经过第________象限．►类型之二由某一函数的图象确定其他函数图象的位置5．2018·宁波如图1－ZT－4，二次函数y＝ax2＋bx的图象开口向下，且经过第三象限的点P.若点P的横坐标为－1，则一次函数y＝(a－b)x＋b的图象大致是()图1－ZT－4 图1－ZT－56．如图1－ZT－6，一次函数y1＝x与二次函数y2＝ax2＋bx＋c的图象相交于P，Q两点，则函数y＝ax2＋(b－1)x＋c的图象可能为()图1－ZT－6图1－ZT－7►类型之三由函数图象确定系数及代数式的符号7．已知二次函数y＝ax2＋bx＋c的图象如图1－ZT－8所示，则()A．b＞0，c＞0B．b＞0，c＜0C．b＜0，c＜0D．b＜0，c＞0图1－ZT－8 图1－ZT－98．[2018·毕节]已知二次函数y＝ax2＋bx＋c(a≠0)的图象如图1－ZT－9所示，有下列结论：①abc＞0；②2a＋b＞0；③b2－4ac＞0；④a－b＋c＞0，其中正确的个数是() A．1B．2C．3D．49．设直线x＝1是函数y＝ax2＋bx＋c(a，b，c是实数，且a＜0)的图象的对称轴，下列说法一定正确的是()A．若m＞1，则(m－1)a＋b＞0B．若m＞1，则(m－1)a＋b＜0C．若m＜1，则(m＋1)a＋b＞0D．若m＜1，则(m＋1)a＋b＜010．如图1－ZT－10，抛物线y＝ax2＋bx＋c的顶点和该抛物线与y轴的交点在一次函数y＝kx＋1(k≠0)的图象上，它的对称轴是直线x＝1，有下列四个结论：①abc＜0；②a＜－13；③a＝－k；④当0＜x＜1时，ax＋b＞k.其中正确结论的个数是()A ．4B ．3C ．2D ．1图1－ZT －10 图1－ZT －1111.如图1－ZT －11，抛物线y ＝ax 2＋bx ＋c(a>0)的对称轴是过点(1，0)且平行于y 轴的直线．若点P(4，0)在该抛物线上，则4a －2b ＋c 的值为________．► 类型之四 利用二次函数求一元二次方程的根12．[2018·孝感]如图1－ZT －12，抛物线y ＝ax 2与直线y ＝bx ＋c 的两个交点坐标分别为A(－2，4)，B(1，1)，则方程ax 2＝bx ＋c 的解是____________．图1－ZT －1213．[2018·襄阳]已知二次函数y ＝x 2－x ＋14m －1的图象与x 轴有交点，则m 的取值范围是( )A ．m ≤5B ．m ≥2C ．m ＜5D ．m ＞214．[2018·马鞍山期中]已知二次函数y ＝ax 2＋2ax －3的部分图象如图1－ZT －13所示，由图象可知关于x 的一元二次方程ax 2＋2ax －3＝0的两个根分别是x 1＝1.3和x 2＝( )A ．－1.3B ．－2.3C ．－0.3D ．－3.3图1－ZT －13 图1－ZT －1415．如图1－ZT －14，一次函数y 1＝kx ＋n 与二次函数y 2＝ax 2＋bx ＋c 的图象相交于A(－1，5)，B(9，2)两点，则关于x 的不等式kx ＋n ≥ax 2＋bx ＋c 的解集为( )A ．－1≤x ≤9B ．－1≤x ＜9C ．－1＜x ≤9D ．x ≤－1或x ≥916．[2018·湖州]在平面直角坐标系xOy 中，已知点M ，N 的坐标分别为(－1，2)，(2，1)，若抛物线y ＝ax 2－x ＋2(a ≠0)与线段MN 有两个不同的交点，则a 的取值范围是( )A ．a ≤－1或14≤a ＜13B .14≤a ＜13 C ．a ≤14或a ＞13D ．a ≤－1或a ≥1417．[2018·贵阳]已知二次函数y ＝－x 2＋x ＋6及一次函数y ＝－x ＋m ，将该二次函数在x 轴上方的图象沿x 轴翻折到x 轴下方，图象的其余部分不变，得到一个新图象(如图1－ZT －15所示)，当直线y ＝－x ＋m 与新图象有4个交点时，m 的取值范围是( )图1－ZT －15A ．－254＜m ＜3B ．－254＜m ＜2C ．－2＜m ＜3D ．－6＜m ＜－2教师详解详析1．[解析]D ∵a ＜0，b ＞0，c ＜0，∴图象开口向下，对称轴在y 轴的右侧，交y 轴于负半轴．只有D 选项中的图象符合题意．故选D.2．[解析]D 当x ＝1时，a ＋b ＋c ＝0，即抛物线经过点(1，0)．当a ＞b ＞0＞c 时，抛物线的对称轴x ＝－b 2a ＜0，没有图形符合；当a ＞0＞b ＞c 时，则抛物线的对称轴x ＝－b2a ＞0，选项D 符合要求；而a ＞b ＞c ＞0和0＞a ＞b ＞c 都不符合a ＋b ＋c ＝0.综上所述，本题选D.3．[解析]B A ．由一次函数y ＝ax －a 的图象可得a ＜0，此时二次函数y ＝ax 2－2x ＋1的图象应该开口向下，故本选项错误；B ．由一次函数y ＝ax －a 的图象可得a ＞0，此时二次函数y ＝ax 2－2x ＋1的图象应该开口向上，对称轴x ＝－－22a＞0，故本选项正确；C ．由一次函数y ＝ax －a 的图象可得a ＞0，此时二次函数y ＝ax 2－2x ＋1的图象应该开口向上，对称轴x ＝－－22a＞0，和x 轴的正半轴相交，故本选项错误；D ．由一次函数y ＝ax －a 的图象可得a ＞0，此时二次函数y ＝ax 2－2x ＋1的图象应该开口向上，故本选项错误．4．[答案]三、四[解析]∵二次项系数为1，∴抛物线开口向上．又∵对称轴是直线x ＝－a ＜0，4a 2－8a 2＝－4a 2<0，故与x 轴没有交点，∴其图象不经过第三、四象限．5．[解析]D 由二次函数的图象可知， a ＜0，b ＜0，当x ＝－1时，y ＝a －b ＜0， ∴y ＝(a －b )x ＋b 的图象在第二、三、四象限．6．[解析]A 由于一次函数y 1＝x 与二次函数y 2＝ax 2＋bx ＋c 的图象有两个不同的交点，且这两个交点都位于第一象限，所以方程ax 2＋bx ＋c ＝x ，即ax 2＋(b －1)x ＋c ＝0有两个不相等的正实数根，所以函数y ＝ax 2＋(b －1)x ＋c 的图象与x 轴有两个不同的交点，且两个交点都在x轴的正半轴上．故选A.7．[解析]B∵图象的开口向下，∴a＜0.∵图象的对称轴为直线x＝－b2a＞0，∴b＞0.又∵图象与y轴的交点位于原点的下方，∴c＜0.故选项B符合题意．8．[解析]D①∵抛物线的对称轴在y轴右侧，∴ab＜0，∵抛物线与y轴交于负半轴，∴c＜0，∴abc＞0，故①正确；②∵a＞0，x＝－b2a＜1，∴－b＜2a，即2a＋b＞0，故②正确；③∵抛物线与x轴有两个交点，∴b2－4ac＞0，故③正确；④当x＝－1时，y＞0，即a－b＋c＞0，故④正确．故选D.9．[解析]C∵a＜0，∴函数y有最大值．当x＝1时，函数y的最大值为a＋b＋c①.当m＞1，x＝m时，函数y＝m2a＋mb＋c②.由②－①，得(m2－1)a＋(m－1)b＜0.又∵m－1＞0，∴(m＋1)a＋b＜0，故选项A，B不一定正确．当m＜1，x＝m时，函数y＝m2a＋mb＋c③.由③－①，得(m2－1)a＋(m－1)b＜0.又∵m－1＜0，∴(m＋1)a＋b＞0，故选项C正确，选项D错误．10．[解析]A由抛物线的开口向下，且对称轴为直线x＝1，可知a＜0，－b2a＝1，即b＝－2a＞0.由抛物线与y轴的交点在一次函数y＝kx＋1(k≠0)的图象上，知c＝1，则abc＜0，故结论①正确．由①知y＝ax2－2ax＋1.当x＝－1时，y＝a＋2a＋1＝3a＋1＜0，∴a ＜－13，故结论②正确；∵抛物线y ＝ax 2＋bx ＋c 的顶点在一次函数y ＝kx ＋1(k ≠0)的图象上，∴a ＋b ＋1＝k ＋1，即a ＋b ＝k .又∵b ＝－2a ，∴a －2a ＝k ，即a ＝－k ，故结论③正确．由函数图象知，当0＜x ＜1时，二次函数图象在一次函数图象上方，∴ax 2＋bx ＋1＞kx ＋1，即ax 2＋bx ＞kx .又∵x ＞0，∴ax ＋b ＞k ，故结论④正确．综上所述，4个结论都正确．故选A.11．[答案]0[解析]方法一：∵抛物线的对称轴为直线x ＝1，由对称性可知，点P (4，0)和点(－2，0)关于直线x ＝1对称，因此点(－2，0)也在抛物线y ＝ax 2＋bx ＋c 上，∴4a －2b ＋c ＝0.方法二：由题意，得方程组⎩⎪⎨⎪⎧－b 2a ＝1，16a ＋4b ＋c ＝0.从而求得⎩⎪⎨⎪⎧b ＝－2a ，c ＝－8a .把b ，c 的值代入4a －2b ＋c 中，得4a －2b ＋c ＝0.12．[答案]x 1＝－2，x 2＝1[解析]∵抛物线y ＝ax 2与直线y ＝bx ＋c 的两个交点坐标分别为A (－2，4)，B (1，1)，∴方程组⎩⎪⎨⎪⎧y ＝ax 2，y ＝bx ＋c 的解为⎩⎨⎧x 1＝－2，y 1＝4，⎩⎨⎧x 2＝1，y 2＝1， 即方程ax 2＝bx ＋c 的解是x 1＝－2，x 2＝1.13．[解析]A ∵二次函数y ＝x 2－x ＋14m －1的图象与x 轴有交点，∴Δ＝(－1)2－4×1×(14m －1)≥0，解得m ≤5.14．[解析]D 二次函数y ＝ax 2＋2ax －3的图象的对称轴是直线x ＝－2a2a ＝－1.又∵x 1与x 2关于对称轴对称，∴1.3－(－1)＝－1－x 2，解得x 2＝－3.3.故选D.15．[解析]A 由图可知当－1≤x ≤9时，kx ＋n ≥ax 2＋bx ＋c .故选A. 16．[解析]A ∵抛物线的表达式为y ＝ax 2－x ＋2.观察图象可知，当a ＜0时，x ＝－1，y ≤2， 且－－12a≥－1时，满足条件，可得a ≤－1；当a ＞0时，x ＝2，y ≥1，且－－12a ≤2时满足条件，∴a ≥14.∵直线MN 的表达式为y ＝－13x ＋53，由⎩⎪⎨⎪⎧y ＝－13x ＋53，y ＝ax 2－x ＋2消去y ，得到3ax 2－2x ＋1＝0. ∵Δ＞0， ∴a ＜13，∴14≤a ＜13满足条件． 综上所述，满足条件的a 的值为a ≤－1或14≤a ＜13.17．[解析]D 如图，当y ＝0时，－x 2＋x ＋6＝0，解得x 1＝－2，x 2＝3，则A (－2，0)，B (3，0)，将该二次函数在x轴上方的图象沿x轴翻折到x轴下方的部分图象的表达式为y＝(x＋2)·(x－3)，即y＝x2－x－6(－2≤x≤3)，当直线y＝－x＋m经过点A(－2，0)时，2＋m＝0，解得m＝－2；当直线y＝－x＋m与抛物线y＝x2－x－6(－2≤x≤3)有唯一公共点时，方程x2－x－6＝－x＋m有相等的实数解，解得m＝－6，所以当直线y＝－x＋m与新图象有4个交点时，m的取值范围为－6＜m＜－2.故选D.。
二次函数图像中的信息
经典题型题型1 从二次函数的图像中获取信息神归纳：1、根的判别式：△=ac b 42-△0>，一元二次方程有2个不相等的实数根，二次函数图像与x 轴有两个交点。
△0=，一元二次方程有2个相等的实数根，二次函数图像与x 轴有一个交点。
△0<.一元二次方程没有实数根，二次函数图像与x 轴没有交点。
二次函数的对称轴与顶点坐标：对称轴:ab x 2-=，顶点坐标：)44,2(2a b ac a b -- a 决定二次函数图像的开口：0>a ，图像开口向上，a 0<，图像开口向下。
c 决定二次函数图像与纵坐标的交点：0>c ，与y 轴上半轴相交，0=c ，与原点相交，0<c ，与y 轴下半轴相交。
记做几组特殊值：1=x 时，c b a y ++= 或 1-=x 时，c b a y +-=2=x 时，c b a y ++=24或2-=x 时，c b a y +-=243=x 时，c b a y ++=39或3-=x 时，c b a y +-=39二次函数的图象与各项系数之间的关系（1） 二次项系数a二次函数)0(2≠++=a c bx ax y 中，a 作为二次项系数，显然a ≠0．⑴ 当a 0>时，抛物线开口向上，a 的值越大，开口越小，反之a 的值越小，开口越大；⑵ 当a 0<时，抛物线开口向下，a 的值越小，开口越小，反之a 的值越大，开口越大．总结起来，a 决定了抛物线开口的大小和方向，a 的正负决定开口方向，a 的大小决定开口的大小．（2）一次项系数b在二次项系数a 确定的前提下，b 决定了抛物线的对称轴．⑴ 在a 0>的前提下，当0>b 时，02<-ab ，即抛物线的对称轴在y 轴左侧； 当0=b 时，02=-a b ，即抛物线的对称轴就是y 轴；当0<b 时，02>-ab ，即抛物线对称轴在y 轴的右侧． ⑵ 在a 0<的前提下，结论刚好与上述相反，即当b 0>时，02>-ab ，即抛物线的对称轴在y 轴右侧； 当b 0=时，02=-ab ，即抛物线的对称轴就是y 轴； 当b 0<时，02<-a b ，即抛物线对称轴在y 轴的左侧． 总结起来，在a 确定的前提下，b 决定了抛物线对称轴的位置．ab 的符号的判定：对称轴ab x 2-=在y 轴左边则ab 0>，在y 轴的右侧则ab 0<， 概括的说就是“左同右异”总结：（3） 常数项c⑴ 当c 0>时，抛物线与y 轴的交点在x 轴上方，即抛物线与y 轴交点的纵坐标为正；⑵ 当c =0时，抛物线与y 轴的交点为坐标原点，即抛物线与y 轴交点的纵坐标为0；⑶ 当c 0<时，抛物线与y 轴的交点在x 轴下方，即抛物线与y 轴交点的纵坐标为负．总结起来，c 决定了抛物线与y 轴交点的位置．总之，只要a 、b 、c 都确定，那么这条抛物线就是唯一确定的．1、二次函数)0(2≠++=a c bx ax y 的图象如图，给出下列四个结论：①042>-ac b ；②024<+-c b a ；③02=-b a ；④)1(2-≠-<+m b a bm am ，其中正确结论的个数是（ ）A.4个B.3个C.2个D.1个2、二次函数)0(2≠++=a c bx ax y 的图象如图，给出下列四个结论：①042<-b ac ； ②b c a 24<+； ③023<+c b ； ④)1()(-≠<++m a b b am m ，其中正确结论的个数是（ ）A.4个B.3个C.2个D.1个1、二次函数)0(2≠++=a c bx ax y 的图象如图所示，给出下列四个结论：①042<-b ac ； ②当2-<x 时，y 随x 的减小而减小； ③0<c ； ④a b 2=.其中正确结论的个数是（ ）A.4个B.3个C.2个D.1个2、已知：如图，关于x 的二次函数)0(2≠++=a c bx ax y 的图象与x 轴交于A 、B 两点，与y 轴交于C 点，且对称轴为直线1=x ，点B 坐标为)0,1(-．则下面的四个结论：①02=+b a ；②024<+-c b a ；③0>ac ；④1=x 是关于x 的方程)0(02≠=++a c bx ax 的一个根．其中正确的个数是（ ）A.4个B.3个C.2个D.1个3、如图，二次函数)0(2≠++=a c bx ax y 的图象与x 轴交于A 、B 两点，与y 轴交于点C ，点B 坐标)0,1(-，且对称轴是1=x ．下面的四个结论：①3=OA ；②0<++c b a ；③0>ac ；④042>-ac b ．其中正确的结论是（ ）。
专训 二次函数图象信息题的四种常见类型(4)
专训二次函数图象信息题的四种常见类型名师点金：利用图象信息解决二次函数的问题主要是运用数形结合思想将图象信息转换为数学语言，掌握二次函数的图象和性质是解决此类问题的关键．根据抛物线的特征确定a，b，c及与其有关的代数式的符号1．【2015·孝感】如图，二次函数y＝2＋＋c(a≠0)的图象与x轴交于A，B两点，与y轴交于点C，且＝.则下列结论：①＜0；②＞0；③－b＋1＝0；④·＝－.其中正确结论的个数是( )A．4 B．3 C．2 D．1(第1题)(第2题)利用二次函数的图象比较大小2．二次函数y＝－x2＋＋c的图象如图，若点A(x1，y1)，B(x2，y2)在此函数图象上，且x1<x2<1，则y1与y2的大小关系是( )A．y1≤y2B．y1＜y2C．y1≥y2D．y1＞y2利用二次函数的图象求方程的解或不等式的解集3．【中考·黄石】二次函数y＝2＋＋c(a≠0)的图象如图所示，则当函数值y＞0时，x的取值范围是( ) A．x＜－1 B．x＞3C．－1＜x＜3 D．x＜－1或x＞3(第3题)(第4题)4．【中考·阜新】如图，二次函数y＝2＋＋3的图象经过点A(－1，0)，B(3，0)，那么一元二次方程2＋＝0的根是．根据抛物线的特征确定其他函数的图象5．【中考·聊城】二次函数y＝2＋的图象如图所示，那么一次函数y＝＋b的图象大致是( )(第5题)6．如图，A(－1，0)，B(2，－3)两点在一次函数y1＝－x＋m与二次函数y2＝2＋－3的图象上．(1)求m的值和二次函数的解析式．(2)设二次函数的图象交y轴于点C，求△的面积．(第6题)答案1．B2341＝0，x2＝2 56．解：(1)将点A(－1，0)的坐标代入y1＝－x＋m，得m＝－1；将点A(－1，0)，B(2，－3)的坐标分别代入y2＝2＋－3，得解得∴y2＝x2－2x－3.(2)易知C点的坐标为(0，－3)，一次函数的图象与y轴的交点坐标为(0，－1)．∴S△＝×[－1－(－3)]×1＋×[－1－(－3)]×2＝×2×1＋×2×2＝3.。
二次函数图象信息题的四种常见类型
类型 4 根据抛物线的特征确定其他函数的图象
5．【中考·聊城】二次函数y＝ax2＋bx的图象如图所 示，那么一次函数y＝ax＋b的图象大致是( C)
同类变式
6．如图，A(－1，0)，B(2，－3)两 点在一次函数y1
＝－x＋m与二次函数y2＝ax2＋bx －3的图象上．
(1)求m的值和二次函数的解析式． (2)设二次函数的图象交y 轴于点C，求△ABC的 面积．
类型 3 利用二次函数的图象求方程的解或不等式的解集
3．【中考·黄石】二次函数y＝ax2＋bx＋c(a≠0)的图 象如图所示，则当函数值y＞0时，x的3 C．－1＜x＜3 D．x＜－1或x＞3
同类变式
4．【中考·阜新】如图，二次函数y＝ax2＋bx＋3 的图象经过点A(－1，0)，B(3，0)，那么一元 二次方程ax2＋bx＝0的根是____________．
习题课
专训 二次函数图象信息题 的四种常见类型
阶段方法技巧训练（一）
汇报人姓名
利用图象信息解决二次函数的问题主要是运 用数形结合思想将图象信息转换为数学语言，掌 握二次函数的图象和性质是解决此类问题的关键．
类型
1 根据抛物线的特征确定a，b，c及与其有关的代数式的符号
1.【2015·孝感】如图，二次函数y＝ax2＋bx＋c(a≠0)的
单击添加大标 题
单击此处添加正文，文字是您思想的提炼，为了演示发布的良好效果，请言简意赅地阐述您的观 点。您的内容已经简明扼要，字字珠玑，但信息却千丝万缕、错综复杂，需要用更多的文字来表 述；但请您尽可能提炼思想的精髓，否则容易造成观者的阅读压力，适得其反。正如我们都希望 改变世界，希望给别人带去光明，但更多时候我们只需要播下一颗种子，自然有微风吹拂，雨露 滋养。恰如其分地表达观点，往往事半功倍。当您的内容到达这个限度时，或许已经不纯粹作用 于演示，极大可能运用于阅读领域；无论是传播观点、知识分享还是汇报工作，内容的详尽固然 重要，但请一定注意信息框架的清晰，这样才能使内容层次分明，页面简洁易读。如果您的内容 确实非常重要又难以精简，也请使用分段处理，对内容进行简单的梳理和提炼，这样会使逻辑框 架相对清晰。为了能让您有更直观的字数感受，并进一步方便使用，我们设置了文本的最大限度， 当您输入的文字到这里时，已濒临页面容纳内容的上限，若还有更多内容，请酌情缩小字号，但 我们不建议您的文本字号小于14磅，请您务必注意。
冀教版九年级下册数学第30章 二次函数 集训课堂 练素养 二次函数图像信息题的四种常见类型
(2)若y2随着x的增大而增大，且抛物线与直线都经过x轴 上的同一点，求直线的表达式.
解：①当y1＝－x2－2x时，－x2－2x＝0， 得x＝0或－2， ∴抛物线与x轴的交点是(0，0)和(－2，0)． ∵y2随着x的增大而增大，且直线过点A(－1，5)， ∴抛物线与直线都经过x轴上的同一点(－2，0)．
把点(－1，5)，(－2，0)的坐标分别 代入 y2＝kx＋b，得－－k2＋k＋b＝b＝5，0， 解得kb＝＝51，0， ∴y2＝5x＋10.
②当y1＝－x2－2x＋8时，－x2－2x＋8＝0， 得x＝－4或2， ∴抛物线与x轴的交点是(－4，0)和(2，0)． ∵y2随着x的增大而增大，且直线过点A(－1，5)， ∴抛物线与直线都经过x轴上的同一点(－4，0)．
6 【中考·广州】已知抛物线y1＝－x2＋mx＋n，直线y2 ＝kx＋b，抛物线的对称轴与直线交于点A(－1，5)， 点A与抛物线的顶点B的距离是4.
(1)求抛物线的表达式；
解：由题意得 B(－1，1)或(－1，9)， ∴－2×（m－1）＝－1，4×（4×－（1－）1·n）－m2＝1 或 9. 解得 m＝－2，n＝0 或 8. ∴抛物线的表达式为 y1＝－x2－2x 或 y1＝－x2－2x＋8.
③当 x＝－1 时，y＝a－b＋c＝0， ∴(a＋c)2－b2＝(a＋b＋c)(a－b＋c)＝0，正确． ④当 x＝1 时，y＝a＋b＋c＝n. ∵a＝－b2，c＝32b， ∴n＝2b，2c－a＝72b.∵b<0， ∴72b>4b，即 2c－a>2n，错误．
4 【2021·凉山州】二次函数y＝ax2＋bx＋c(a≠0)的图像 如图所示，则下列结论中不正确的是( ) D A．abc>0
∵二次函数 y2＝2x2＋x＋m 的图像的对称轴为直线 x＝ －14，且 2＞0， ∴当 0≤x≤1 时，y 随 x 的增大而增大，且最小值为 m. ∵当 0≤x≤1 时，总有 y2≥y1， ∴m≥4，即 m 的最小值为 4.
二次函数的图像与性质【十大题型】(原卷版)—2024年中考数学一轮复习【举一反三】系列(全国通用)
二次函数的图像与性质【十大题型】【题型1 根据二次函数解析式判断其性质】 (3)【题型2 二次函数y=ax 2+bx+c 的图象和性质】 (4)【题型3 二次函数平移变换问题】 (5)【题型4 根据二次函数的对称性求字母的取值范围】 (6)【题型5 根据二次函数的性质求最值】 (6)【题型6 根据二次函数的最值求字母的取值范围】 (7)【题型7 根据二次函数自变量的情况求函数值的取值范围】 (7)【题型8 根据二次函数的增减性求字母的取值范围】 (8)【题型9 二次函数图象与各项系数符号】 (8)【题型10 二次函数与三角形相结合的应用方法】 (11)【知识点 二次函数的图像与性质】1.定义：一般的，形如y =ax 2+bx +c (a .b .c 是常数，a ≠0)的函数叫做二次函数。
其中x 是自变量，a .b .c 分别是函数解析式的二次项系数.一次项系数.常数项。
二次函数解析式的表示方法(1)一般式：y ＝ax 2＋bx ＋c (其中a ，b ，c 是常数，a ≠0)；(2)顶点式：y ＝a (x －h )2＋k (a ≠0)，它直接显示二次函数的顶点坐标是(h ，k )；(3)交点式：y ＝a (x －x 1)(x －x 2)(a ≠0)，其中x 1，x 2是图象与x 轴交点的横坐标 ．注意：任何二次函数的解析式都可以化成一般式或顶点式，但并非所有的二次函数都可以写成交点式，只有抛物线与x 轴有交点，即240b ac -³时，抛物线的解析式才可以用交点式表示．二次函数解析式的这三种形式可以互化.2.二次函数的图象是一条抛物线。
当a ＞0时，抛物线开口向上；当a ＜0时，抛物线开口向下。
|a |越大，抛物线的开口越小；|a |越小，抛物线的开口越大。
y =ax 2y =ax 2+k y =a (x -h )2y =a (x -h )2+k y =ax 2+bx +c 对称轴y 轴y 轴x =h x =h abx 2-=(0，0)(0，k )(h ，0)(h ，k )⎪⎪⎭⎫ ⎝⎛--a b ac a b 44,22顶点a >0时，顶点是最低点，此时y 有最小值；a <0时，顶点是最高点，此时y 有最大值。
2021春北师版九年级数学下册 第2章 2.5.3 二次函数图像信息题的四种常见类型
类型 4 根据二次函数图象的特征确定其他函数的图象
6．已知函数y＝(x－a)(x－b)(其中a＞b)的图象如图所示， 则函数y＝ax＋b的图象正确的是( D )
返回பைடு நூலகம்
7．如图，A(－1，0)，B(2，－3)两点在一次函数y1＝－x＋m
与二次函数y2＝ax2＋bx－3的图象上．
(1)求m的值和二次函数的表达式； 解：将点A(－1，0)的坐标代入y1＝－x＋m，
其中正确的个数为( )C
A．1 B．2
C．3
D．4
返回
类型 2 利用二次函数的图象比较大小
2 ． 二 次 函 数 y ＝ － x2 ＋ bx ＋ c 的 图 象 如 图 所 示 ， 若 点
A(x1，y1)，B(x2，y2)在此函数图象上，且x1<x2<1，
则y1与y2的大小关系是( B )
A．y1≤y2
等式kx＋n≥ax2＋bx＋c的解集为( A )
A．－1≤x≤9
B．－1≤x＜9
C．－1＜x≤9
D．x≤－1或x≥9
返回
5．(中考·阜新)如图，二次函数y＝ax2＋bx＋3的图象 经过点A(－1，0)，B(3，0)，那么关于x的一元二 次方程ax2＋bx＝0的根是___x_1_＝__0_，__x_2＝__2___．
∴BC∥x轴．
∴S△ABC＝
1 2
×(2－0)×[0－(－3)]＝
12×2×3＝3.
返回
第二章 二次函数与一元二次方程
2.5 二次函数与一元二次方程 第3课时 二次函数图像信息题的四
种常见类型
1
2
3
4
5
6
7
类型
1
根据二次函数图像的特征确定 a,b,c及与其有关的代数式的符号
涉及二次函数的图象的五种类型(解析版)—九年级数学上册(人教版)
涉及二次函数图象的五类题型类型一：二次函数中的图象共存问题类型二：二次函数图象与系数的关系类型三：利用二次函数图象信息求二次函数表达式类型四：利用二次函数图象解决一元二次方程的问题类型五：利用二次函数图象解决一元二次不等式的问题类型一：二次函数中的图象共存问题1．一次函数y＝x+a与二次函数y＝ax2﹣a在同一坐标系中的大致图象可能是（ ）A．B．C．D．【分析】根据二次函数的图象和一次函数与x轴，与y轴的交点可得相关图象进行判断．【解答】解：由一次函数y＝x+a可知，一次函数的图象与x轴交于（﹣a，0），与y轴交于点（0，a），由二次函数y＝ax2﹣a可知，抛物线与x轴交于（﹣1，0）和（1，0），与y轴交于点（0，﹣a），∵两个函数的图象与x轴交于不同的两点，与y轴交于不同的两点，∴A、B、D不可能，选项C中，由直线经过一、三、四象限可知a＜0，由抛物线可知开口向下，交y轴的正半轴，则a＜0，故C有可能；故选：C．2．函数y＝ax+1与y＝ax2+bx+1（a，b是常数，且a≠0）在同一坐标系中的图象可能是（ ）A．B．C．D．【分析】本题可先由一次函数y＝ax+1图象得到字母系数的正负，再与二次函数y＝ax2+bx+1的图象相比较看是否一致．【解答】解：A．由一次函数的图象可知a＜0，由抛物线图象可知，开口向下，a＜0，但是一次函数与y 轴的交点和二次函数与y轴的交点，不是同一点（0，1），故A选项错误；B．由一次函数的图象可知a＞0，由抛物线图象可知，开口向下，a＜0，两者相矛盾，故B选项不正确，不符合题意；C．由一次函数的图象可知a＞0，由抛物线图象可知，开口向上，a＞0，且两函数相交y轴于同一点（0，1），故C选项正确，符合题意；D．由一次函数的图象可知a＜0，由抛物线图象可知，开口向上，a＞0两者相矛盾，故D选项不正确，不符合题意．故选：C．3．二次函数y＝ax2+bx+c（a≠0）的图象如图所示，则一次函数y＝ax与一次函数y＝bx﹣c在同一坐标系内的图象大致是（ ）A．B．C．D．【分析】根据二次函数y＝ax2+bx+c（a≠0）的图象可以得到a、b、c的正负，从而可以得到一次函数y ＝ax与一次函数y＝bx﹣c的图象，本题得以解决．【解答】解：由二次函数y＝ax2+bx+c（a≠0）的图象可得，a＞0，b＜0，c＞0，∴一次函数y＝ax的图象经过第一、三象限，一次函数y＝bx﹣c的图象经过第二、三、四象限，故选：A．4．一次函数y＝bx+a与二次函数y＝ax2+bx+c（a≠0）在同一坐标系中的图象大致是（ ）A．B．C．D．【分析】观察A、C、D中二次函数图象，可得出a＜0、b＜0，利用一次函数图象与系数的关系可排除A、D选项；观察B选项中二次函数图象，可得出a＞0、b＜0，利用一次函数图象与系数的关系可排除B选项．此题得解．【解答】解：观察A、C、D中二次函数图象，可知：a＜0，b＜0，∴一次函数y＝bx+a的图象经过二、三、四象限，A、D不符合题意，C符合题意；观察B中二次函数图象，可知：a＞0，b＜0，∴一次函数y＝bx+a的图象经过一、二、四象限，B不符合题意．故选：C．5．在同一直角坐标系中，函数y＝mx+m和y＝﹣mx2+2x+2的图象可能是（ ）A．B．C．D．【分析】根据直线y＝mx+m求得m的符号，然后根据二次函数的性质即可判断．【解答】解：A．由函数y＝mx+m的图象可知m＜0，即函数y＝﹣mx2+2x+2开口方向朝上，与图象不符，故A选项错误；B．由函数y＝mx+m的图象可知m＜0，即函数y＝﹣mx2+2x+2开口方向朝上，称轴为x＝﹣＝＝＜0，则对称轴应在y轴左侧与图象不符，故B选项错误；C．由函数y＝mx+m的图象可知m＞0，即函数y＝﹣mx2+2x+2开口方向朝下，故C选项错误；D．由函数y＝mx+m的图象可知m＜0，即函数y＝﹣mx2+2x+2开口方向朝上，对称轴为x＝﹣＝＝＜0则对称轴应在y轴左侧，与图象相符，故D选项正确．故选：D．6．二次函数y＝a（x﹣2）2+c与一次函数y＝cx+a在同一坐标系中的大致图象是（ ）A．B．C．D．【分析】可先根据一次函数的图象判断a、b的符号，再判断二次函数图象与实际是否相符，判断正误．【解答】解：A、一次函数y＝cx+a的图象与y轴交于负半轴，a＜0，与二次函数y＝a（x﹣2）2+c的图象开口向上，即a＞0相矛盾，故A错误；B、一次函数y＝cx+a的图象过一、二、四象限，a＞0，c＜0，二次函数y＝a（x﹣2）2+c的图象开口向上，顶点为（2，c）在第四象限，a＞0，c＜0，故B正确；C、二次函数y＝a（x﹣2）2+c的对称轴直线x＝2，在y轴右侧，故C错误；D、一次函数y＝cx+a的图象过一、二、三象限，c＞0，与抛物线y＝a（x﹣2）2+c的顶点（2，c）在第四象限，c＜0相矛盾，故D错误；故选：B．7．在同一直角坐标系中，函数y＝ax+a和函数y＝ax2+x+2（a是常数，且a≠0）的图象可能是（ ）A．B．C．D．【分析】根据a的正负判断一次函数经过的象限和二次函数的开口方向和对称轴的正负，然后逐个分析即可．【解答】解：当a＞0时，一次函数过一二三象限，抛物线开口向上，对称轴x＝＜0，故B、C不符合题意，当a＜0时，一次函数过二三四象限，抛物线开口向下，对称轴x＝＞0，故A不符合题意．故选：D．类型二：二次函数图象与系数的关系8．如图为二次函数y＝ax2+bx+c（a≠0）的图象，对称轴是直线x＝1，则下列说法：①b＞0；②2a+b＝0；③4a﹣2b+c＞0；④3a+c＞0；⑤m（ma+b）＜a+b（常数m≠1）．其中正确的个数为（ ）A．2B．3C．4D．5【分析】由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴x＝1计算2a+b与0的关系；再由根的判别式与根的关系，进而对所得结论进行判断．【解答】解：①由抛物线的开口向下知a＜0，对称轴为直线x＝﹣＞0，则b＞0，故本选项正确；②由对称轴为直线x＝1，∴﹣＝1，∴b＝﹣2a，则2a+b＝0，故本选项正确；③由图象可知，当x＝﹣2时，y＜0，则4a﹣2b+c＜0，故本选项错误；④从图象知，当x＝﹣1时，y＝0，则a﹣b+c＝0，∵b＝﹣2a，∴a+2a+c＝0，即3a+c＝0，故本选项错误；⑤∵对称轴为直线x＝1，∴当x＝1时，抛物线有最大值，∴a+b+c＞m2a+mb+c，∴m（ma+b）＜a+b（常数m≠1），故本选项正确；故选：B．9．已知二次函数y＝ax2+bx+c的图象如图所示，有以下结论：①a+b+c＜0；②a﹣b+c＞1；③abc＞0；④4a﹣2b+c＜0．正确结论的个数是（ ）A．1B．2C．3D．4【分析】该函数开口方向向下，则a＜0，由对称轴可知，b＝2a＜0，与y轴交点在y轴正半轴，则c＞0，再根据一些特殊点，比如x＝1，x＝0，顶点等进行判断即可．【解答】解：∵函数开口方向向下，a＜0，∵对称轴为x＝﹣1，则﹣＝﹣1，∴b＝2a＜0，∵与y轴交点在y轴正半轴，∴c＞0，∴abc＞0，故③正确；当x＝﹣1时，y＝a﹣b+c＞1，即a﹣b+c＞1，故②正确；当x＝1时，y＝a+b+c＜0，故①正确；由抛物线的对称性可知，当x＝﹣2与x＝0时y值相同，此时y＝4a﹣2b+c＞0，故④错误．综上，正确的个数有三个．故选：C．10．在平面直角坐标系xOy中，二次函数y＝ax2+bx+c（a≠0）的图象如图所示，以下结论中正确的是（ ）A．abc＞0B．2a+c＜0C．9a﹣3b+c＜0D．若m为任意实数，则a﹣b≥m（am+b）【分析】根据二次函数的图象判断a，b，c的符号，根据抛物线与x轴的交点即可判断B，C选项，根据抛物线开口向上，对称轴为直线x＝﹣1，得出最小值为a﹣b+c，进而即可求解．【解答】解：由图象可得，a＞0，b＞0，c＜0，则abc＜0，故选项A错误，不符合题意；对称轴为直线x＝﹣＝﹣1，∴b＝2a，∵当x＝1时，a+b+c＝0，∴c＝﹣a﹣b＝﹣a﹣2a＝﹣3a，∴2a+c＝2a﹣3a＝﹣a＜0，故B正确，符合题意；∵抛物线的对称轴为直线x＝﹣1，x＝1和x＝﹣3时，y＝0，∴9a﹣3b+c＝0，故C错误，不符合题意；∵a＞0，对称轴为直线x＝﹣1，∴若m为任意实数，则a﹣b+c≤am2+bm+c，即a﹣b≤m（am+b），故D错误，不符合题意；故选：B．11．在平面直角坐标系xOy中，二次函数y＝ax2+bx+c（a≠0）的大致图象如图所示，则下列结论：①abc＞0；②0＜c＜2；③a+b+c＝1；④x1＜﹣1；⑤b2＜4ac．其中正确的有（ ）A．5个B．4个C．3个D．2个【分析】由抛物线开口方向得到a＜0，然后利用抛物线的对称轴得到b的符号，根据抛物线与y轴的交点可得c的符号，则可选项①②进行判断；利用x＝1时，y＝0可对选项③进行判断，利用抛物线的对称性可对选项④进行判断；根据抛物线与x轴的交点可对选项⑤进行判断．【解答】解：∵抛物线开口向下，∴a＜0，∵抛物线的对称轴为直线x＝﹣＜0，∴b＜0，∵抛物线与y轴的交点在x轴的上方，∴0＜c＜2，∴abc＞0，故选项①②正确；∵x＝1时，y＝0，即a+b+c＝0，∴选项③错误．∵（1，0）关于y轴的对称轴为（﹣1，0），而的对称轴在y轴的左侧，∴x1＜﹣1，∴选项④正确；∵抛物线与x轴有两个交点，∴b2﹣4ac＞0，∴b2＞4ac∴选项⑤错误．结论正确的是①②④共3个．故选：C．12．如图是二次函数y＝ax2+bx+c图象的一部分，与x轴的交点A在点（2，0）和（3，0）之间，对称轴是直线x＝1．对于下列说法：①abc＜0；②2a﹣b＝0；③4a﹣2b+c＜0；④b2＜4ac；⑤3b＜2c；⑥若两点（﹣2，y1）（3，y2）在二次函数图象上，则y1＞y2，其中正确的有（ ）A．1个B．2个C．3个D．4个【分析】根据二次函数的图象与性质即可求出答案．【解答】解：①由二次函数的图象可知：a＜0，c＞0，由对称轴可知：x＝﹣＞0，∴b＞0，∴abc＜0，故①正确；②由对称轴可知：﹣＝1，∴2a+b＝0，故②错误；③由图象可知，x＝3时，y＜0，而（3，0）关于直线x＝1的对称点为（﹣1，0），当x≤1时，随x的增大而增大，∴当x＝﹣2时，y＜0，∴4a﹣2b+c＜0，故③正确；④由图象可知抛物线与x轴有两个交点，故Δ＝b2﹣4ac＞0，∴b2＞4ac，故④错误；⑤∵﹣＝1，∴a＝﹣，∵（3，0）关于直线x＝1的对称点为（﹣1，0），且x＝3时，y＜0，∴x＝﹣1时，y＜0，∴a﹣b+c＜0，∴﹣，∴3b＞2c，故⑤错误；⑥∵抛物线开口向下，且点（﹣2，y1）到直线x＝1的距离大于点（3，y2）到直线x＝1的距离，∴y1＜y2，故⑥错误；故选：B．13．已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，有下列5个结论：①abc＞0；②b2＜4ac；③2c＜3b；④a+b＞m（am+b）（m≠1）；⑤若方程|ax2+bx+c|＝1有四个根，则这四个根的和为2．其中正确的结论有（ ）A．2个B．3个C．4个D．5个【分析】①由二次函数图象性质知，开口向下，则a＜0．再结合对称轴﹣＞0，得b＞0．据二次函数图象与y轴正半轴相交得c＞0；②由于二次函数图象与x轴交于不同两点，则b2﹣4ac＞0，即b2＞4ac；③由＝1，得b＝﹣2a，当x＝﹣1时，y＜0，即a﹣b+c＜0，所以2a﹣2b+2c＜0，把b替换成a计算；④x＝1时函数有最大值，所以当x＝1时的y值大于当x＝m（m≠1）时的y值，即a+b+c＞m（am+b）+c，所以a+b＞m（am+b）（m≠1）成立；⑤将x轴下方二次函数图象翻折到x轴上方，则与直线y＝1有四个交点即可，由二次函数图象的轴对称性知：关于对称轴对称的两个根的和为2，四个根的和为4．【解答】解：∵图象开口向下，∴a＜0，∵对称轴在y轴的右侧，a与b异号，∴b＞0，∵与y轴交于正半轴，∴c＞0，∴abc＜0，故①错误；∵二次函数图象与x轴交于不同两点，则Δ＝b2﹣4ac＞0．∴b2＞4ac．故②错误；∵＝1，∴b＝﹣2a．又∵当x＝﹣1时，y＜0．即a﹣b+c＜0．∴2a﹣2b+2c＜0．∴﹣3b+2c＜0．∴2c＜3b．故③正确；∵x＝1时函数有最大值，∴当x＝1时的y值大于当x＝m（m≠1）时的y值，即a+b+c＞m（am+b）+c∴a+b＞m（am+b）（m≠1）成立，故④正确．将x轴下方二次函数图象翻折到x轴上方，则与直线y＝1有四个交点即可，由二次函数图象的轴对称性知：关于对称轴对称的两个根的和为2，四个根的和为4，故⑤错误．综上：③④正确，故选：A．14．如图是二次函数y＝ax2+bx+c（a≠0）图象的一部分，对称轴为，且经过点（2，0）．下列说法：①abc＜0；②﹣2b+c＝0；③4a+2b+c＜0；④若，是抛物线上的两点，则y1＜y2；⑤（其中）．其中结论正确的有（ ）A．1个B．2个C．3个D．4个【分析】根据所给函数图象，可得出a，b，c的正负，再根据抛物线的对称性和增减性，依次对所给说法进行判断即可解决问题．【解答】解：由函数图象可知，a＜0，b＞0，c＞0，所以abc＜0．故①正确．因为抛物线的对称轴为直线x＝，所以，即b＝﹣a．因为抛物线与x轴的一个交点坐标为（2，0），所以抛物线与x轴的另一个交点坐标为（﹣1，0），所以a﹣b+c＝0，则﹣b﹣b+c＝0，即﹣2b+c＝0．故②正确．因为抛物线经过点（2，0），所以4a+2b＝c＝0．故③错误．因为抛物线开口向下，所以抛物线上的点，离对称轴越远，其纵坐标越小．因为，，且3＞2，所以y1＜y2．故④正确．因为抛物线的对称轴为直线x＝，且开口向下，所以当x＝时，函数有最大值为，则对于抛物线上任意一点（顶点除外），其纵坐标小于，即am2+bm+c＜，又因为a＝﹣b，所以m（am+b）＜，即（m≠）．故⑤正确．故选：D．15．如图，已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，有下列5个结论：①abc＜0；②b＜a+c；③4a+2b+c＞0；④2c＜3b；⑤a+b＜m（am+b）（m≠1的实数）．其中正确结论的有（ ）A．①②③B．①③④C．③④⑤D．②③⑤【分析】由抛物线的开口方向判断a的符号，由抛物线与y轴的交点判断c的符号，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．【解答】解：①由图象可知：a＜0，c＞0，∵﹣＞0，∴b＞0，∴abc＜0，故此选项正确；②当x＝﹣1时，y＝a﹣b+c＜0，故a﹣b+c＞0，错误；③由对称知，当x＝2时，函数值大于0，即y＝4a+2b+c＞0，故此选项正确；④当x＝3时函数值小于0，y＝9a+3b+c＜0，且x＝﹣＝1，即a＝﹣，代入得9（﹣）+3b+c＜0，得2c＜3b，故此选项正确；⑤当x＝1时，y的值最大．此时，y＝a+b+c，而当x＝m（m≠1）时，y＝am2+bm+c，所以a+b+c＞am2+bm+c，故a+b＞am2+bm，即a+b＞m（am+b），故此选项错误．故①③④正确．故选：B．16．如图，二次函数y＝ax2+bx+c（a≠0）图象的对称轴是直线x＝1，下列结论中：①abc＜0；②b2＞4ac；③3a+c＞0；④若m为任意实数，则am2+a+b．正确的个数为（ ）A．4个B．3个C．2个D．1个【分析】分别判a、b、c的符号，即可判断①；根据图象与x轴交点可以判断②；根据对称轴是直线x ＝1，得到b＝﹣2a，结合a﹣b+c＜0，即可判断③；根据二次函数的对称轴得出最值，即可判断④．【解答】解：∵图象开口向下，与y轴交点再x轴上方，∴a＜0，c＞0，∵，∴b＝﹣2a＞0，∴abc＜0，故①正确；∵函数图象与x轴有2个交点，∴b2﹣4ac＞0，即b2＞4ac，故②正确；∵函数图象的对称轴是直线x＝1，∵函数图象与x轴的另一个交点在﹣1和0之间，∴当x＝﹣1时，a﹣b+c＜0，∴a﹣（﹣2a）+c＜0，即3a+c＜0，故③错误；当x＝1时，y的值最大．此时，y＝a+b+c，而当x＝m时，y＝am2+bm+c，∴a+b+c≥am2+bm+c，即a+b≥am2+bm，故④正确；综上所述，①②④正确，共3个，故选：B．17．如图，已知二次函数y＝ax2+bx+c（a，b，c是常数）的图象关于直线x＝﹣1对称，则下列五个结论：①abc＞0；②2a﹣b＝0；③9a﹣3b+c＜0；④a（m2﹣1）+b（m+1）≤0（m为任意实数）；⑤3a+c＜0．其中结论正确的个数为（ ）A．2个B．3个C．4个D．5个【分析】根据所给函数图象可得出a，b，c的正负，再结合抛物线的对称性及增减性，利用数形结合的思想对所给结论依次进行判断即可．【解答】解：由函数图象可知，a＜0，b＜0，c＞0，所以abc＞0．故①正确．因为抛物线的对称轴为直线x＝﹣1，所以﹣＝﹣1，即2a﹣b＝0．故②正确．因为抛物线的对称轴为直线x＝﹣1，且x＝1时，函数值小于零，所以x＝﹣3时，函数值小于零，则9a﹣3b+c＜0．故③正确．因为抛物线的对称轴为直线x＝﹣1，且开口向下，所以当x＝m时，am2+bm+c≤a﹣b+c，即am2﹣a+bm+b≤0，所以a（m2﹣1）+b（m+1）≤0．故④正确．由函数图象可知，当x＝1时，函数值小于零，则a+b+c＜0，又因为b＝2a，所以3a+c＜0．故⑤正确．故选：D．类型三：利用二次函数图象信息求二次函数解析式18．已知二次函数的图象如图所示，则其抛物线的表达式可能为（ ）A．y＝﹣3x2﹣1B．y32+1C．y＝3x2+1D．y＝3x2﹣1【分析】依据题意，结合图象可得，抛物线的开口向下，顶点是（0，1），对称轴是y轴，从而可以判断得解．【解答】解：由题意，抛物线的开口向下，顶点是（0，1），对称轴是y轴，∴B选项正确，A、C、D错误．故选：B．19．如图的抛物线的解析式为（ ）A．y＝x2﹣1B．y＝x2+1C．y＝（x﹣1）2D．y＝（x+1）2【分析】由图知抛物线顶点：（1，0），故设y＝a（x﹣1）2，又因为交y轴于（0，1），代入解析式即可．【解答】解：图知抛物线顶点：（1，0），故设y＝a（x﹣1）2，又∵抛物线交y轴于（0，1），∴1＝a（0﹣1）2，解得：a＝1，∴抛物线的解析式为：y＝（x﹣1）2，故选：C．20．已知二次函数的图象如图所示，则它的表达式可能是（ ）A．y＝﹣4（x﹣m）2﹣m2﹣2B．y＝﹣（x+a）（x﹣a+1）C．y＝﹣x2﹣（a+3）x+（）D．y＝ax2﹣bx+b﹣a【分析】根据二次函数图象与系数的关系判断．【解答】解：抛物线y＝﹣4（x﹣m）2﹣m2﹣2顶点为（m，﹣m2﹣2），而﹣m2﹣2＜0，顶点在x轴下方，故A不符合题意；在y＝﹣（x+a）（x﹣a+1）中，令y＝0得x1＝﹣a，x2＝a﹣1，则抛物线对称轴为直线x＝＝﹣，故B不符合题意；图中抛物线可能是y＝﹣x2﹣（a+3）x+（），故C符合题意；在y＝ax2﹣bx+b﹣a＝（ax﹣b+（x﹣1）中，令y＝0得x1＝，x2＝1，故抛物线与x轴有一个交点横坐标为1，故D不符合题意；故选：C．21．如图是某个二次函数的图象，根据图象可知，该二次函数的表达式是（ ）A．y＝x2﹣x﹣2B．C．D．y＝﹣x2+x+2【分析】根据图象知，可设该二次函数为顶点式y＝a（x﹣）2+，然后把（2，0）代入求出a即可．【解答】解：设抛物线解析式为y＝a（x﹣）2+，把（2，0）代入得a+＝0，解得a＝﹣1，所以抛物线解析式为y＝﹣（x﹣）2+．即y＝﹣x2+x+2，故选：D．22．如图，已知抛物线y＝﹣3x与直线y＝2x交于O，A两点．点B是抛物线上O，A之间的一个动点，过点B分别作两条坐标轴的平行线，与直线OA交于点C，E，以BC，BE为边构造矩形BCDE，设点D 的坐标为（m，n），则m关于n的函数关系式是 m＝n2﹣n ．【分析】根据点D的坐标，可得出点E的坐标，点C的坐标，继而确定点B的坐标，将点B的坐标代入抛物线解析式可求出m，n之间的关系式．【解答】解：如图，∵直线OA的解析式为：y＝2x，点D的坐标为（m，n），∴点E的坐标为（n，n），点C的坐标为（m，2m），∴点B的坐标为（n，2m），把点B（n，2m）代入y＝x2﹣3x，可得m＝n2﹣n，∴m、n之间的关系式为m＝n2﹣n，故答案为：m＝n2﹣n．23．抛物线的图象如图所示，其中点A为顶点．（1）写出点A，B的坐标；（2）求出抛物线的解析式．【分析】（1）观察图象即可写出点A ，B 的坐标；（2）利用待定系数法即可求解．【解答】解：（1）观察图象可知，A （2，﹣4），B （0，4）；（2）∵A 为顶点，A （2，﹣4），∴设抛物线的解析式为y ＝a （x ﹣2）2﹣4，把B （0，4）代入得，4a ﹣4＝4，解得a ＝2，∴抛物线的解析式为y ＝2（x ﹣2）2﹣4．24．如图，抛物线y ＝ax 2+bx +c （a ≠0）与x 轴交于点A ，B ，与y 轴交于点C ，OA ＝OC ＝2OB ＝2．（1）求抛物线的解析式；（2）若P 为线段AC 上方抛物线上的一个动点，求四边形BCPA 面积的最大值．【分析】（1）根据题意可求出A 、B 、C 三点的坐标，代入抛物线表达式，解方程组，即可得出抛物线的解析式；（2）因为S 四边形BCPA ＝S △BCA +S △ACP ，先求出S △BCA ，再过C 作CD //AB 交AP 于点D ，设P （t ，y t ），y AP ＝k x +b （k ≠0），将P ，A 代入，得出y AP 的解析式，用t 表示出D 点坐标，再得到CD 的长度，根据S △ACP ＝S △PCD +S △ACD ，得到S 四边形BCPA 的二次函数表达式，解出最大值即可．【解答】解：（1）∵OA ＝OC ＝2OB ＝2，∴A （2，0），B （﹣1，0），C （0，2），将点A （2，0），B （﹣1，0），C （0，2），分别代入y ＝ax 2+bx +c 中，可得解得∴抛物线的解析式为y ＝﹣x 2+x +2；（2）∵S 四边形BCPA ＝S △BCA +S △ACP ，，∴S △A C P 最大时，S 四边形BCPA 最大，过C 作CD //AB 交AP 于点D设P （t ，y t ），设y A P ＝k x +b （k ≠0），将P ，A 代入得，解得：∴∵CD ∥AB∴y D ＝y C ＝2∵D 在上，∴，即∵S △ACP ＝S △PCD +S △ACD ，，易知y1+y2＝y t，∴，∴，∴t＝1时，∴四边形BCPA面积的最大值为4．类型四：利用二次函数图象解决一元二次方程问题25．如图，以（1，﹣4）为顶点的二次函数y＝ax2+bx+c的图象与x轴负半轴交于A点，则一元二次方程ax2+bx+c＝0的正数解的范围是（ ）A．2＜x＜3B．3＜x＜4C．4＜x＜5D．5＜x＜6【分析】先根据图象得出对称轴左侧图象与x轴交点横坐标的取值范围，再利用对称轴x＝1，可以算出右侧交点横坐标的取值范围．【解答】解：∵二次函数y＝ax2+bx+c的顶点为（1，﹣4），∴对称轴为x＝1，而对称轴左侧图象与x轴交点横坐标的取值范围是﹣3＜x＜﹣2，∴右侧交点横坐标的取值范围是4＜x＜5．故选：C．26．二次函数y＝ax2+bx+c的图象如图所示，则关于x的一元二次方程x2﹣bx+a＝0的根的情况是（ ）A．只有一个实数根B．没有实数根C．有两个不相等的实数根D．有两个相等的实数根【分析】首先根据二次函数的图象得到a＜0，b＞0，然后判断一元二次方程的判别式求解即可．【解答】解：∵二次函数图象开口向下，对称轴大于零，∴a＜0，，∴b＞0，∴x2﹣bx+a＝0，Δ＝b2﹣4ac＝（﹣b）2﹣4×1×a＝b2﹣4a＞0，∴关于x的一元二次方程x2﹣bx+a＝0的根的情况是有两个不相等的实数根．故选：C．27．如图，在平面直角坐标系xOy中，画出了函数y＝x2﹣4|x|+3的部分图象，若关于x的方程x2﹣4|x|+3＝kx有3个不相等的实数根，则k的值为（ ）A．或B．或C．或D．﹣4﹣2或﹣4+2【分析】依据题意，由函数y＝x2﹣4|x|+3可知，x＞0和x＜0时的函数图象关于y轴对称，进而画出图象，再由关于x的方程x2﹣4|x|+3＝kx有3个不相等的实数根，可以看作函数y＝x2﹣4|x|+3与y＝kx的图象有三个交点，进而利用数形结合可以判断得解．【解答】解：由函数y＝x2﹣4|x|+3可知，x＞0和x＜0时的函数图象关于y轴对称，函数图象如图所示：当k＞0时，x2+4x+3＝kx，即x2+（4﹣k）x+3＝0，当直线y＝kx与函数y＝x2﹣4|x|+3的图象有三个交点时，∴Δ＝（4﹣k）2﹣12＝0，∴k＝4﹣2或k＝4+2（不符合题意，舍去），∴k＝4﹣2．当k＜0时，x2﹣4x+3＝kx，即x2﹣（4+k）x+3＝0，当直线y＝kx与函数y＝x2﹣4|x|+3的图象有三个交点时，∴Δ＝（4+k）2﹣12＝0，∴k＝﹣4+2或k＝﹣4﹣2（不符合题意，舍去），∴k＝﹣4+2．综上所述，关于x的方程x2﹣4|x|+3＝kx有3个不相等的实数根，则k的值为4﹣2或﹣4+2．故选：C．28．已知二次函数y＝x2+2x+m的部分图象如图所示，则关于x的一元二次方程x2+2x+m＝0的解为（ ）A．x1＝3，x2＝1B．x1＝﹣3，x2＝1C．x1＝﹣3，x2＝3D．x1＝﹣3，x2＝﹣1【分析】由函数图象可以得出二次函数y＝x2+2x+m经过（﹣3，0）这一点，就可以求出函数的解析式，当y＝0时求出x的值就可以求出结论．【解答】解：由函数图象，得二次函数y＝x2+2x+m经过（﹣3，0）这一点，把（﹣3，0）代入y＝x2+2x+m，得：0＝9﹣6+m，解得：m＝﹣3，∴y＝x2+2x﹣3，∴x2+2x﹣3＝0，解得：x1＝﹣3，x2＝1．故选：B．29．若二次函数y＝ax2+bx+c的部分图象如图所示，则关于x的方程ax2+bx+c＝0的解为（ ）A．x1＝﹣2，x2＝3B．x1＝﹣1，x2＝3C．x1＝0，x2＝3D．x1＝1，x2＝3【分析】先利用抛物线的对称性写出抛物线与x轴的一个交点坐标为（﹣1，0），然后根据抛物线与x轴的交点问题可得到关于x的方程ax2+bx+c＝0（a≠0）的解．【解答】解：抛物线的对称轴为直线x＝1，抛物线与x轴的一个交点坐标为（3，0），所以抛物线与x轴的一个交点坐标为（﹣1，0），即x＝﹣1或3时，函数值y＝0，所以关于x的方程ax2+bx+c＝0（a≠0）的解为x1＝3，x2＝﹣1．故选：B．30．二次函数y＝ax2+bx+c的图象如图所示，下列说法错误的是（ ）A．函数的最大值为4B．函数图象关于直线x＝﹣1对称C．当x＜﹣1时，y随x的增大而减小D．x＝1或x＝﹣3是方程ax2+bx+c＝0的两个根【分析】根据函数图象确定对称轴、最大值、增减性、二次函数与一元二次方程的关系判断即可．【解答】解：由图象知，函数最大值为4；对称轴为直线x＝﹣1；当x＜﹣1时，y随x的增大而增大；故A，B正确；C错误；∵抛物线与x轴交于点（1，0），对称轴为直线x＝﹣1，∴抛物线与x轴的另一交点为（﹣3，0），∴方程ax2+bx+c＝0的解是x1＝1，x2＝﹣3，故D正确．故选：C．31．如图是二次函数y＝ax2+bx+c的图象，图象上有两点分别为A（2.18，﹣0.51），B（2.68，0.54），则方程a（x﹣1）2+b（x﹣1）+c＝0的一个解只可能是（ ）A．1.59B．2.68C．3.45D．3.72【分析】根据自变量两个取值所对应的函数值是﹣0.51和0.54，可得当函数值为0时，x的取值应在所给的自变量两个值之间，再根据平移的性质得出结论．【解答】解：∵图象上有两点分别为A（2.18，﹣0.51）、B（2.68，0.54），∴当x＝2.18时，y＝﹣0.51；x＝2.68时，y＝0.54，∴当y＝0时，2.18＜x＜2.68，∵二次函数y＝a（x﹣1）2+b（x﹣1）+c是由二次函数y＝ax2+bx+c向右平移1个单位得到，∴二次函数y＝a（x﹣1）2+b（x﹣1）+c的图象与x轴交点是由二次函数y＝ax2+bx+c图象与x轴交点右平移1个单位得到∴当y＝0时，3.18＜x＜3.68，∴只有选项C符合，故选：C．类型五：利用二次函数图象解决一元二次不等式问题32．抛物线y＝ax2+bx+c的部分图象如图所示，对称轴为直线x＝﹣1，则当y＜0，x的取值范围是（ ）A．x＜1B．x＞﹣1C．﹣3＜x＜1D．﹣4≤x≤1【分析】则根据函数的对称性，另外一个交点坐标为（﹣3，0），进而求解．【解答】解：∵抛物线与x轴的一个交点为（1，0），函数的对称轴为x＝﹣1，则根据函数的对称性，函数与x轴另外一个交点坐标为（﹣3，0），故当y＜0时，x的取值范围是﹣3＜x＜1，故选：C．33．抛物线的部分图象如图所示，其与x轴时的一个交点为（﹣3，0），对称轴为直线x＝﹣1，将抛物线y1沿着x轴的正方向平移2个单位长度得到新的抛物线y2，则当y2＜0时，x的取值范围是（ ）A．﹣3＜x＜﹣1B．﹣1＜x＜1C．﹣1＜x＜3D．1＜x＜3【分析】依据题意，由y1与x轴时的一个交点为（﹣3，0），对称轴为直线x＝﹣1，从而与x轴的另一个交点为（﹣1+2，0），即（1，0），又抛物线的开口向上，故当y1＜0时，﹣3＜x＜1，进而当将抛物线y1沿着x轴的正方向平移2个单位长度得到新的抛物线y2，则抛物线y2与x轴的交点为（﹣1，0），（3，0），进而可以判断得解．【解答】解：由题意，∵y1与x轴时的一个交点为（﹣3，0），对称轴为直线x＝﹣1，∴与x轴的另一个交点为（﹣1+2，0），即（1，0）．抛物线的开口向上，∴当y1＜0时，﹣3＜x＜1．将抛物线y1沿着x轴的正方向平移2个单位长度得到新的抛物线y2，∴抛物线y2与x轴的交点为（﹣1，0），（3，0）．∴当y2＜0时，﹣1＜x＜3．故选：C．34．二次函数y＝x2+x﹣2的图象如图所示，则函数值y＞0时，x的取值范围是（ ）A．x＜﹣2B．x＞1C．﹣2＜x＜1D．x＜﹣2或x＞1【分析】先解方程x2+x﹣2＝0得抛物线与x轴的交点坐标为（﹣2，0），（1，0），然后利用函数图象写出抛物线在x轴上方所对应的自变量的取值范围即可．【解答】解：当y＝0时，x2+x﹣2＝0，解得x1＝﹣2，x2＝1，∴抛物线与x轴的交点坐标为（﹣2，0），（1，0），当﹣2＜x＜1时，y＞0，即函数值y＜0时，x的取值范围是x＜﹣2或x＞1．故选：D．35．抛物线y＝ax2+bx+c的部分图象如图所示，则当y＞0时，x的取值范围是（ ）A．x＞﹣1B．x＜﹣1C．﹣1＜x＜3D．x＞3【分析】利用抛物线的对称性确定抛物线与x轴的另一个交点坐标为（3，0），然后结合二次函数图象，写出抛物线在x轴上方所对应的自变量的范围即可．【解答】解：∵抛物线与x轴的一个交点坐标为（﹣1，0），对称轴是直线x＝1，∴抛物线与x轴的另一个交点坐标为（3，0），∵抛物线开口向下，∴当﹣1＜x＜3时，y＞0．故选：C．36．如图，抛物线y＝x2﹣14x+45与x轴交于点A、B，把抛物线在x轴及其下方的部分记作C1，将C1向左平移得到C2，C2与x轴交于点B、D，若直线y＝x+k与C1、C2共有3个不同的交点，则k的取值范围是（ ）A．B．﹣5≤k＜﹣1C．﹣9≤k＜﹣5D．【分析】依据题意，首先求出点A和点B的坐标，然后求出C2解析式，分别求出直线y＝x+k与抛物线C2相切时k的值以及直线y＝x+k过点B时k的值，结合图形即可得到答案【解答】解：∵抛物线y＝x2﹣14x+45与x轴交于点A、B，∴B（5，0），A（9，0）．又抛物线为y＝x2﹣14x+45＝（x﹣7）2﹣4，∴抛物线向左平移4个单位长度∴平移后解析式y＝（x﹣3）2﹣4．当直线y＝x+k过B点，有2个交点∴0＝5+k．∴k＝﹣5．当直线y＝x+k与抛物线C2相切时，有2个交点∴x+k＝（x﹣3）2﹣4，即x2﹣7x+5﹣k＝0．∵相切，∴Δ＝49﹣20+4k＝0∴k＝﹣．如图，∵若直线y＝x+k与C1、C2共有3个不同的交点，∴﹣＜m＜﹣5．故选：D．。
(一)二次函数图象信息题常见的四种类型-教育文档
专题训练(一)二次函数图象信息题常见的四种类型►类型之一由系数的符号确定图象的位置1．［2019·合肥45中月考］在二次函数y＝ax2＋bx＋c中，a＜0，b＞0，c＜0，则符合条件的图象是()图1－ZT－12．［2019·安徽省合肥168教育集团］月考已知二次函数y＝ax2＋bx＋c，若a＞b＞c，且a＋b＋c＝0，则它的图象可能是图1－ZT－2中的()图1－ZT－23．已知函数y＝ax和y＝a(x＋m)2＋n，且a＞0，m＜0，n＜0，则这两个函数在同一平面直角坐标系内的大致图象是()图1－ZT－34．已知二次函数y＝x2＋2ax＋2a2，其中a＞0，则其图象不经过第________象限．►类型之二由某一函数的图象确定其他函数图象的位置5．已知y＝ax2＋bx＋c的图象如图1－ZT－4所示，则y＝ax＋b的图象一定过()图1－ZT－4A．第一、二、三象限B．第一、二、四象限C．第二、三、四象限D．第一、三、四象限6．如果一次函数y＝ax＋b的图象经过第二、三、四象限，那么二次函数y＝ax2＋bx的图象可能是()图1－ZT－57．如图1－ZT－6，一次函数y1＝x与二次函数y2＝ax2＋bx＋c的图象相交于P，Q两点，则函数y＝ax2＋(b－1)x＋c的图象可能为()图1－ZT－6图1－ZT－7►类型之三由函数图象确定系数及代数式的符号8．［2019·六盘水］已知二次函数y＝ax2＋bx＋c的图象如图1－ZT－8所示，则() A．b＞0，c＞0 B．b＞0，c＜0C．b＜0，c＜0 D．b＜0，c＞0图1－ZT－89.已知抛物线y＝ax2＋bx＋c如图1－ZT－9所示，对称轴为直线x＝1，则代数式：(1)abc；(2)a＋b＋c；(3)a－b＋c；(4)4a＋2b＋c中，值为正数的个数是()A．1 B．2 C．3 D．4图1－ZT－910．［2019·杭州］设直线x＝1是函数y＝ax2＋bx＋c(a，b，c是实数，且a＜0)的图象的对称轴，()A．若m＞1，则(m－1)a＋b＞0B．若m＞1，则(m－1)a＋b＜0C．若m＜1，则(m＋1)a＋b＞0D．若m＜1，则(m＋1)a＋b＜011．如图1－ZT－10，抛物线y＝ax2＋bx＋c(a>0)的对称轴是过点(1，0)且平行于y轴的直线．若点P(4，0)在该抛物线上，则4a－2b＋c的值为________．图1－ZT－1012．［2019·资阳］如图1－ZT －11，抛物线y ＝ax 2＋bx ＋c 的顶点和该抛物线与y 轴的交点在一次函数y ＝kx ＋1(k ≠0)的图象上，它的对称轴是直线x ＝1，有下列四个结论：①abc＜0，②a ＜－13，③a ＝－k ，④当0＜x ＜1时，ax ＋b ＞k.其中正确结论的个数是( ) A ．4 B ．3 C ．2 D ．1图1－ZT －11► 类型之四 利用二次函数求一元二次方程的根13．小兰画了一个函数y ＝x 2＋ax ＋b 的图象如图1－ZT －12，则关于x 的方程x 2＋ax ＋b ＝0的解是( )A ．无解B ．x ＝1C ．x ＝－4D ．x 1＝－1，x 2＝4图1－ZT －1214．二次函数y ＝ax 2＋bx ＋c 的图象如图1－ZT －13所示，则当函数值y ＞0时，x 的取值范围是( )A ．x ＜－1B ．x ＞3C ．－1＜x ＜3D ．x ＜－1或x ＞3图1－ZT －1315．［2019·马鞍山期中］已知二次函数y ＝ax 2＋2ax －3的部分图象如图1－ZT －14，由图象可知关于x 的一元二次方程ax 2＋2ax －3＝0的两个根分别是x 1＝1.3和x 2＝( )A ．－1.3B ．－2.3C ．－0.3D ．－3.3图1－ZT －1416．［2019·淮南期中］如图1－ZT －15所示，一次函数y 1＝kx ＋n 与二次函数y 2＝ax 2＋bx ＋c 的图象相交于A(－1，5)，B(9，2)两点，则关于x 的不等式kx ＋n ≥ax 2＋bx ＋c 的解集为( )A ．－1≤x ≤9B ．－1≤x ＜9C ．－1＜x ≤9D ．x ≤－1或x ≥9图1－ZT －1517．［2019·南宁］二次函数y ＝ax 2＋bx ＋c 和正比例函数y ＝23x 的图象如图1－ZT －16所示，则关于x 的一元二次方程ax 2＋(b －23)x ＋c ＝0的两根之和( ) A ．大于0 B ．等于0C ．小于0D ．不能确定图1－ZT －1618．［2019·遂宁］函数y ＝x 2＋bx ＋c 与函数y ＝x 的图象如图1－ZT －17所示，有以下结论：①b 2－4c ＞0；②b ＋c ＝0；③b ＜0；④方程组⎩⎪⎨⎪⎧y ＝x 2＋bx ＋c ，y ＝x 的解为⎩⎨⎧x 1＝1，y 1＝1，⎩⎪⎨⎪⎧x 2＝3，y 2＝3；⑤当1＜x ＜3时，x 2＋(b －1)x ＋c ＞0.其中正确的是( )A ．①②③B ．②③④C ．③④⑤D ．②③⑤图1－ZT －17教师详解详析1．[解析] D∵a＜0，b＞0，c＜0，∴图象开口向下，对称轴在x轴的右侧，交y轴于负半轴．只有D选项中的图象符合题意．故选D.2．[解析] D当x＝1时，a＋b＋c＝0，即抛物线经过点(1，0)．当a＞b＞0＞c时，抛物线的对称轴x＝－b2a＜0，没有图形符合；当a＞0＞b＞c时，则抛物线的对称轴x＝－b2a＞0，选项D符合要求；而a＞b＞c＞0和0＞a＞b＞c都不符合a＋b＋c＝0.综上所述，本题选D.3．[解析] B由函数表达式y＝a(x＋m)2＋n(a>0)可知其图象开口向上，其顶点坐标为(－m，n)．又因为m＜0，n＜0，所以顶点在第四象限，排除A，C，D.故选B.4．[答案] 三、四[解析] ∵二次项系数为1，∴抛物线开口向上．又∵对称轴是直线x＝－a＜0，4a2－8a2＝－4a2<0，故与x轴没有交点，∴其图象不经过第三、四象限．5．[解析] D∵抛物线开口向上，∴a＞0.∵对称轴为直线x＝－b2a＞0，a＞0，∴b＜0，∴y＝ax＋b的图象一定过第一、三、四象限．故选D.6．[解析] C∵一次函数y＝ax＋b的图象经过第二、三、四象限，∴a＜0，b＜0，∴二次函数y＝ax2＋bx的图象开口向下，对称轴为直线x＝－b2a＜0，在y轴左边．故选C.7．[解析] A由于一次函数y1＝x与二次函数y2＝ax2＋bx＋c的图象有两个不同的交点，且这两个交点都位于第一象限，所以方程ax2＋bx＋c＝x，即ax2＋(b－1)x＋c＝0有两个不相等的正实数根，所以函数y＝ax2＋(b－1)x＋c的图象与x轴有两个不同的交点，且两个交点都在x轴的正半轴上．故选A.8．[解析] B∵图象的开口向下，∴a＜0.∵图象的对称轴为直线x＝－b2a＞0，∴b＞0.又∵图象与y轴的交点位于原点的下方，∴c＜0.故选项B符合题意．9．[解析] B∵抛物线开口向上，∴a＞0.∵抛物线的对称轴为直线x＝1，－b2a＝1，∴b＝－2a，∴b<0.∵抛物线与y轴的交点在x轴下方，∴c＜0，∴abc＞0.∵当x＝1时，y＜0，∴a＋b＋c＜0.∵当x＝－1时，y＞0，∴a－b＋c＞0.∵当x＝2时，y＜0，∴4a＋2b＋c＜0.故选B.10．[解析] C∵a＜0，∴函数y有最大值．当x＝1时，函数y的最大值为a＋b＋c①.当m＞1，x＝m时，函数y＝m2a＋mb＋c②.由②－①，得(m2－1)a＋(m－1)b＜0.又∵m－1＞0，∴(m＋1)a＋b＜0，故选项A，B不一定正确．当m＜1，x＝m时，函数y＝m2a＋mb＋c③.由③－①，得(m2－1)a＋(m－1)b＜0.又∵m－1＜0，∴(m＋1)a＋b＞0，故选项C正确，选项D错误．11．[答案] 0[解析] 方法一：∵抛物线的对称轴为直线x＝1，由对称性可知，点P(4，0)和点(－2，0)关于直线x＝1对称，因此点(－2，0)也在抛物线y＝ax2＋bx＋c上，∴4a－2b＋c＝0.方法二：由题意，得方程组⎩⎪⎨⎪⎧－b 2a ＝1，16a ＋4b ＋c ＝0.从而求得⎩⎪⎨⎪⎧b ＝－2a ，c ＝－8a .把b ，c 的值代入4a －2b ＋c 中，得4a －2b ＋c ＝0.12．[解析] A 由抛物线的开口向下，且对称轴为直线x ＝1可知a ＜0，－b 2a＝1，即b ＝－2a ＞0.由抛物线与y 轴的交点在一次函数y ＝kx ＋1(k ≠0)的图象上知c ＝1，则abc ＜0，故结论①正确．由①知y ＝ax 2－2ax ＋1.∵当x ＝－1时，y ＝a ＋2a ＋1＝3a ＋1＜0，∴a ＜－13，故结论②正确；∵抛物线y ＝ax 2＋bx ＋c 的顶点在一次函数y ＝kx ＋1(k ≠0)的图象上，∴a ＋b ＋1＝k ＋1，即a ＋b ＝k .又∵b ＝－2a ，∴a －2a ＝k ，即a ＝－k ，故结论③正确．由函数图象知，当0＜x ＜1时，二次函数图象在一次函数图象上方，∴ax 2＋bx ＋1＞kx ＋1，即ax 2＋bx ＞kx .又∵x ＞0，∴ax ＋b ＞k ，故结论④正确．综上所述，共有4个结论正确，故选A.13．[解析] D ∵二次函数y ＝x 2＋ax ＋b 的图象与x 轴交于点(－1，0)和(4，0)，即当x ＝－1或4时，x 2＋ax ＋b ＝0，∴关于x 的方程x 2＋ax ＋b ＝0的解为x 1＝－1，x 2＝4，故选D.14．D15．[解析] D 二次函数y ＝ax 2＋2ax －3的图象的对称轴是直线x ＝－2a 2a＝－1.又∵x 1与x 2关于对称轴对称，∴1.3－(－1)＝－1－x 2，解得x 2＝－3.3，故选D.16．[解析] A 结合图象可知一次函数图象在二次函数图象上方时，对应的x 的取值范围即本题的答案，由图可知当－1≤x ≤9时，kx ＋n ≥ax 2＋bx ＋c .故选A.17．[解析] A 由图象可知二次函数y ＝ax 2＋bx ＋c 和正比例函数y ＝23x 的图象的交点的横坐标之和大于0，即方程组⎩⎪⎨⎪⎧y ＝ax 2＋bx ＋c ，y ＝23x的解中未知数x 的两个值的和大于0，可得ax 2＋bx ＋c ＝23x 变形为方程ax 2＋(b －23)x ＋c ＝0后，它的两根之和大于0. 18．[解析] B ∵函数y ＝x 2＋bx ＋c 的图象与x 轴无交点，∴b 2－4c ＜0，故结论①错误； 当x ＝1时，y ＝1＋b ＋c ＝1，则b ＋c ＝0，故结论②正确；∵对称轴在y 轴的右侧，∴a ，b 异号．又∵a ＝1＞0，∴b ＜0，故结论③正确；根据抛物线与直线y ＝x 的交点知：方程组⎩⎪⎨⎪⎧y ＝x 2＋bx ＋c ，y ＝x 的解为⎩⎨⎧x 1＝1，y 1＝1，⎩⎨⎧x 2＝3，y 2＝3，故结论④正确；∵当1＜x ＜3时，二次函数值小于一次函数值，∴x 2＋bx ＋c ＜x ，∴x 2＋(b －1)x ＋c ＜0，故结论⑤错误．综上所述，结论②③④正确，故选B.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
专训二次函数图象信息题的四种常见类型
名师点金：利用图象信息解决二次函数的问题主要是运用数形结合思想将图象信息转换为数学语言，掌握二次函数的图象和性质是解决此类问题的关键．
根据抛物线的特征确定a ，b ，c 及与其有关的代数式的符号
1．【2015·孝感】如图，二次函数y ＝ax 2＋bx ＋c(a ≠0)的图象与x 轴交于A ，B 两点，与y 轴交于点C ，且OA ＝OC.则下列结论：
①abc ＜0；②b 2－4ac 4a
＞0；③ac －b ＋1＝0；④OA·OB ＝－c a .其中正确结论的个数是()
A ．4
B ．3
C ．2
D ．1(第1题)
(第2题)
利用二次函数的图象比较大小
2．二次函数y ＝－x 2＋bx ＋c 的图象如图，若点A(x 1，y 1)，B(x 2，y 2)在此函数图象上，且x 1<x 2<1，则y 1与y 2的大小关系是(
)
A ．y 1≤y 2
B ．y 1＜y 2
C ．y 1≥y 2
D ．y 1＞y 2
利用二次函数的图象求方程的解或不等式的解集
3．【中考·黄石】二次函数y ＝ax 2＋bx ＋c(a ≠0)的图象如图所示，则当函数值y ＞0时，x 的取值范围是(
)A ．x ＜－1
B ．x ＞3
C ．－1＜x ＜3
D ．x ＜－1或x ＞3
(第3题)
(第4题)
4．【中考·阜新】如图，二次函数y＝ax2＋bx＋3的图象经过点A(－1，0)，B(3，0)，那么一元二次方程ax2＋bx＝0的根是____________．
根据抛物线的特征确定其他函数的图象
5．【中考·聊城】二次函数y＝ax2＋bx的图象如图所示，那么一次函数y＝ax＋b的图象大致是()
(第5题)
6．如图，A(－1，0)，B(2，－3)两点在一次函数y1＝－x＋m与二次函数y2＝ax2＋bx －3的图象上．
(1)求m的值和二次函数的解析式．
(2)设二次函数的图象交y轴于点C，求△ABC的面积．
(第6题)
答案
1．B 2.B 3.D 4.x 1＝0，x 2＝2 5.C
6．解：(1)将点A(－1，0)的坐标代入y 1＝－x ＋m ，得m ＝－1；
将点A(－1，0)，B(2，－3)的坐标分别代入y 2＝ax 2＋bx －3－b －3＝0，＋2b －3＝－3.解得＝1，
＝－2.
∴y 2＝x 2－2x －3.
(2)易知C 点的坐标为(0，－3)，一次函数的图象与y 轴的交点坐标为(0，－1)．
∴S △ABC ＝12×[－1－(－3)]×1＋12×[－1－(－3)]×2＝12×2×1＋12×2×2＝3.。