2012年数学全真模拟试题测试题一及答案
2012年中考数学模拟试题(一)及答案

2012年中考数学模拟试题(一)注意事项:1.本试卷共8页,三大题,满分120分,考试时间120分钟.2. 第Ⅰ卷上选择题和填空题在第Ⅱ卷的答题栏上答题,在第Ⅰ卷上答题无效.第Ⅰ卷一、选择题(每小题3 分,共24分) 1.下列计算中,正确的是A.2x+3y=5xyB.x ·x 4=x 4C.x 8÷x 2=x 4D.(x 2y )3=x 6y 32.如图是由6个相同的小立方块搭成的几何体,那么这个几何体的俯视图是ABCD3.平面直角坐标系中,某点在第二象限且它的横坐标、纵坐标之和为2,则该点的坐标是 A .(-1,2) B.(-1,3) C.(4,-2) D.(0,2)4.如图,有反比例函数1y x =,1y x=-的图象和一个圆,则图中阴影部分的面积是A .πB .2πC .4πD .条件不足,无法求5.正比例函数(1)y a x =+的图象经过第二、四象限,若a 同时满足方程22(12)0x a x a +-+=,则此方程的根的情况是A.有两个不相等的实数根B.有两个相等的实数根 C.没有实数根D.不能确定6.当五个数从小到大排列后,其中位数是4,如果这组数据唯一的众数是6,那么这5个数可能的最大和是( )A .21B .22C .23D .247.如图,在△ABC 中,,23tan ,30=︒=∠B A AC=32,则AB 等于 A .4B .5C .6D .78. A 是半径为5的⊙O 内的一点,且OA =3,则过点A 且长小于10的整数弦的条数是 A.1条 B.2条 C.3条 D.4条 二、填空题(每空3分,共18分)9.分解因式2x 2-4xy +2y 2= .10.如图,直线MA ∥NB ,∠A =70°,∠B =40°,则∠P = .第10题图 第11题图 第13题图11. 如图是由8块相同的等腰直角三角形黑白瓷砖镶嵌而成的正方形地面示意图,一只蚂蚁在上面自由爬动,并随机停留在某块瓷砖上,尉蚂蚁停留在黑色瓷砖上的概率是 . 12.关于x 的分式方程442212-=++-x x k x 有增根x=-2,则k 的值是 . 13.如图,B 是线段AC 的中点,过点C 的直线l 与AC 成600的角,在直线上取一点P ,使∠APB =300,则满足条件的点P 有 个.14.如图,已知平面直角坐标系,A 、B 两点的坐标分别为A (2,-3),B (4,-1).若C (a ,0),D (a+3,0)是x 轴上的两个动点,则当a=____时,四边形ABDC 的周长最短.湖北洪湖市2012年中考数学模拟试题(一)请把第Ⅰ卷填空题答案填在下面相对应的位置上9. ;10.; 11. ; 12. ;13. ; 14. .第Ⅱ卷PBM A N三、解答题:15.(5分)计算:1011)|1|4-⎛⎫+--- ⎪⎝⎭16.(5分),并求出它的正整数解解不等式3722xx -≤-17.(5分)先化简,再求值:222112()2442x x x x x x-÷--+-,其中2x =(tan45°-cos30°)18.( 6分)用四块如图①所示的正方形瓷砖拼成一个新的正方形,使拼成的图案是一个轴对称图形。
2012年新课标数学仿真模拟试卷一(文理合卷)
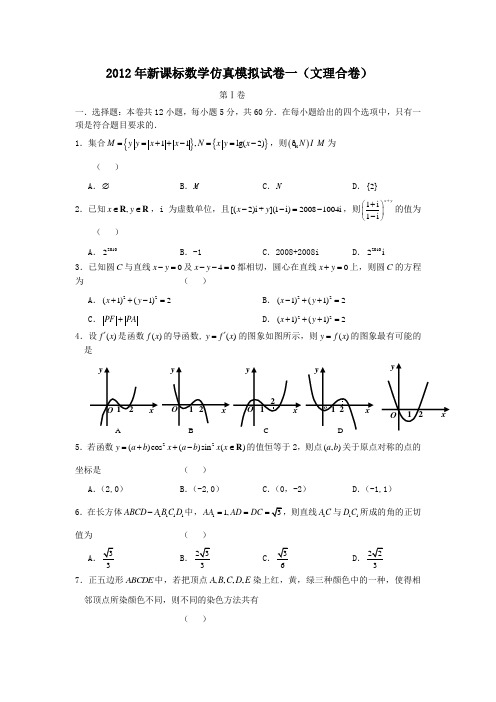
2012年新课标数学仿真模拟试卷一(文理合卷)第Ⅰ卷一.选择题:本卷共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.集合{}{}11,lg(2)M y y x x N x y x ==++-==-,则()N M ðR 为( )A .∅B .MC .ND .{2}2.已知,x y ∈∈R R ,i 为虚数单位,且[(2)i +](1i)20081004i x y --=-,则1i 1i x y++⎛⎫⎪-⎝⎭的值为( )A .20102B .-1C .2008+2008iD .20102i3.已知圆C 与直线0x y -=及40x y --=都相切,圆心在直线0x y +=上,则圆C 的方程为( )A .22(1)(1)2x y ++-=B .22(1)(1)2x y -++=C .PF PA +D .22(1)(1)2x y +++= 4.设()f x '是函数()f x 的导函数,()y f x '=的图象如图所示,则()y f x =的图象最有可能的是5.若函数22()cos ()sin ()y a b x a b x x =++-∈R 的值恒等于2,则点(,)a b 关于原点对称的点的坐标是 ( ) A .(2,0)B .(-2,0)C .(0,-2)D .(-1,1)6.在长方体1111ABCD A B C D -中,11,AA AD DC ===1AC 与11D C 所成的角的正切值为 ( ) ABCD7.正五边形ABCDE 中,若把顶点,,,,A B C D E 染上红,黄,绿三种颜色中的一种,使得相邻顶点所染颜色不同,则不同的染色方法共有( )BA .30种B .27种C .24种D .21种8.已知,,A B C 是平面上不共线的三点,O 为平面ABC 内任一点,动点P 满足等式1[(1)(1)3OP OA OB λλ=-+-(12)](OC λλ++∈ R 且0)λ≠,则P 的轨迹一定通过ABC ∆的( ) A .内心 B .垂心C .重心D .AB 边的中点9.右图所示的算法流程图中,输出的S 表达式为 A .112399++++B .1123100++++C .123.....99++++D .123.....100++++10.(理)定义:若数列{}n a 为任意的正整数n ,都有1(n n a a d d ++=为常数),则称{}n a 为“绝对和数列”,d 叫做“绝对公和” .已知“绝对和数列”{}n a 中,12a =,绝对公和为3,则其前2009项的和2009S 的最小值为A .-2009B .-3010C .-3014(文)已知数列{}n a 的前n 项和是(0n n S a m a =-≠且1)a ≠,那么“数列{}n a 是等比数列”的充要条件是( ) A .1m =B .1m ≥C .1m ≤D .m 为任意实数11.已知12,F F 分别为双曲线22221(0,0)x y a b a b-=>>的左,右焦点,M 为双曲线上除顶点外的任意一点,且12F MF ∆的内切圆交实轴于点N ,则12||||F N NF 的值为( )A .2b B .2a C .2c D 12.函数()f x 的定义域为D ,若对于任意12,x x D ∈,当12x x <时,都有12()()f x f x ≤,则称函数()f x 在D 上为非减函数.设函数()f x 在[0,1]上为非减函数,且满足以下三个条件:①(0)0f = ②1()()32x f f x = ③(1)1()f x f x -=-则11()()38f f +等于 ( )A .34B .12C .1D .23第Ⅱ卷二.填空题:本题共4小题,每小题5分,共20分.把答案填在题中横线上.13.31nx ⎛⎫ ⎪⎝⎭的展开式中第二项与第三项的系数之和等于27,则n 等于 ;系数最大的项是第 项.14.若数列{}n a 满足112,(1)2n n a na n a +=-+=,则数列{}n a 的通项公式n a = . 15.一个多面体的直观图和三视图(正视图、左视图、俯视图)如图所示,则三棱锥C A ABV -的体积为 .16.(理)已知s 表示的区域内存在一个半径为1为 .(文)tan18tan 42tan120tan18tan 42tan 60++三.解答题:本题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分) 设ABC ∆的内角,,A B C 所对的边分别为,,,a b c 且1cos 2a C cb +=.(Ⅰ)求角A 的大小;(Ⅱ)若1a =,求ABC ∆的周长l 的取值范围.18.(本小题满分12分)某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置. 若指针停在A 区域返券60元;停在B 区域返券30元;停在C 区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.(Ⅰ)若某位顾客消费128元,求返券金额不低于30元的概率;(Ⅱ)若某位顾客恰好消费280元,并按规则参与了活动,他获得返券的金额记为X(元).求随机变量X 的分布列和数学期望.19.(本小题满分12分)如图,三棱柱111ABC A B C -中,侧面11AAC C ⊥底面ABC ,112,AA AC AC AB BC ====, 且AB BC ⊥,O 为AC 中点. (Ⅰ)证明:1AO ⊥平面ABC ; (Ⅱ)求直线1AC 与平面1A AB 所成角的正弦值; (Ⅲ)在1BC 上是否存在一点E ,使得//OE 平面1A AB ,若不存在,说明理由;若存在,确定点E 的位置. 20.(本小题满分12分)如图,设抛物线21:4(0)C y mx m =>的准线与x 轴交于1F ,焦点为2F ;以12,F F 为焦点,离心率12e =的椭圆第18题图1A BCO A 1B 1第19题图第22题图ECADB2C 与抛物线1C 在x 轴上方的交点为P ,延长2PF 交抛物线于点Q ,M 是抛物线1C 上一动点,且M 在P 与Q 之间运动.(Ⅰ)当1m =时,求椭圆2C 的方程; (Ⅱ)当12PF F ∆的边长恰好是三个连续的自然数时,求MPQ ∆面积的最大值.21.(本小题满分12分) 已知函数1ln ()xf x x+=. (Ⅰ)若函数在区间1(,)2a a +(其中0a >)上存在极值,求实数a 的取值范围;(Ⅱ)如果当1x ≥时,不等式()1kf x x ≥+恒成立,求实数k 的取值范围;(Ⅲ)求证[]22(1)(1)()n n n e n -*+>+⋅∈!N .请考生在第(22),(23),(24)三题中任选一题做答,如果多做,则按所做的第一题记分. 22.(本小题满分10分)选修4-1:几何证明选讲如图,在Rt△AB C 中,90C ∠= ,BE 平分∠ABC 交AC 于点E ,点D 在AB 上,DE EB ⊥. (Ⅰ)求证:AC 是△BDE 的外接圆的切线;(Ⅱ)若6AD AE ==,求EC 的长.23.(本小题满分10分)选修4-4:坐标系与参数方程PyxQ第20题图已知曲线C 的极坐标方程是4cos ρθ=.以极点为平面直角 坐标系的原点,极轴为x 轴的正半轴,建立平面直角坐标系,直线l的参数方程是:1x y ⎧=+⎪⎪⎨⎪=⎪⎩,求直线l 与曲线C 相交所成的弦的弦长.24.(本小题满分10分)选修4-5:不等式选讲,,a b c +∈R ,求证:32a b c b c c a a b ++≥+++ 参考答案一:1-5 DBBCB 6-10 BADA (理)B (文)A 11-12 AA 二: 13.【答案】:9 5 14.【答案】:4n -2 15.【答案】:316a ;16.【答案】:(理)2+ (文)-1 三:17.解:(Ⅰ)由1cos 2a C c b +=得1sin cos sin sin 2A C CB += …1分又()sin sin sin cos cos sin B A C A C A C =+=+ …3分 1sin cos sin 2C A C ∴=,sin 0C ≠ ,1cos 2A ∴=, 又0A <<π 3A π∴=…6分(Ⅱ)由正弦定理得:sin sin a B b B A ==,c C =…7分)())1sin sin 1sin sin l a b c B C B A B =++=+=++112cos 2B B ⎫=++⎪⎪⎝⎭12sin 6B π⎛⎫=++ ⎪⎝⎭,3A π=20,,3B π⎛⎫∴∈ ⎪⎝⎭5,666B πππ⎛⎫∴+∈ ⎪⎝⎭1sin ,162B π⎛⎫⎛⎤∴+∈ ⎪ ⎥⎝⎭⎝⎦故ABC ∆的周长l 的取值范围为(]2,3.…12分(Ⅱ)另解:周长l 1a b c b c =++=++ 由(Ⅰ)及余弦定理2222cos a b c bc A =+-221b c bc ∴+=+22()1313()2b c b c bc +∴+=+≤+ 2b c +≤又12b c a l a b c +>=∴=++> 即ABC ∆的周长l 的取值范围为(]2,3.…12分18.解:设指针落在A ,B ,C 区域分别记为事件A ,B ,C . 则111(),(),()632P A P B P C ===.…3分(Ⅰ)若返券金额不低于30元,则指针落在A 或B 区域. 111()()632P P A P B ∴=+=+=…6分即消费128元的顾客,返券金额不低于30元的概率是12.(Ⅱ)由题意得,该顾客可转动转盘2次. 随机变量X 的可能值为0,30,60,90,120.…7分111(0)224P X ==⨯=;111(30)2233P X ==⨯⨯=;11115(60)2263318P X ==⨯⨯+⨯=;111(90)2369P X ==⨯⨯=;111(120)6636P X ==⨯=.…10分所以,随机变量X 的分布列为:其数学期望115110306090120404318936EX =⨯+⨯+⨯+⨯+⨯= . …12分19.解:(Ⅰ)证明:因为11A A AC =,且O 为AC 的中点, 所以1AO AC ⊥.…1分 又由题意可知,平面11AAC C ⊥平面ABC ,交线为AC ,且1AO ⊂平面11AAC C , 所以1AO ⊥平面ABC .…4分(Ⅱ)如图,以O 为原点,1,,OB OC OA 所在直线分别为x ,y ,z 轴建立空间直角坐标系. 由题意可知,112,A A AC AC ===又,AB BC AB BC =⊥; 112OB AC ∴==.所以得:11(0,0,0),(0,1,0),(0,1,0),(1,0,0)O A A C C B -则有:11(0,1,(1,1,0).AC AA AB ===设平面1AA B 的一个法向量为(,,)x y z =n ,则有10000AA y x y AB ⎧⎧⋅==⎪⎪⇔⎨⎨+=⎪⋅=⎪⎩⎩n n ,令1y =,得1,x z =-= 所以(1,1,=-n .…6分111cos ,|||A C A C A C ⋅<>==n n |n因为直线1AC 与平面1A AB 所成角θ和向量n 与1A C所成锐角互余,所以sin θ=.…8分(Ⅲ)设0001(,,),,E x y z BE BC λ==即000(1,,)(x y z λ-=-,得00012x y z λλ⎧=-⎪=⎨⎪=⎩所以(1,2),E λλ=-得(1,2),OE λλ=-…10分令//OE 平面1A AB ,得=0OE ⋅n ,即120,λλλ-++-=得1,2λ=即存在这样的点E ,E 为1BC 的中点.…12分20.解:(Ⅰ)当1m =时, 24y x =,则12(1,0),(1,0)F F -设椭圆方程为22221(0x y a b a b +=>>),则1,c =又12c e a ==,所以22,3a b ==所以椭圆C 2方程为22143x y +=1…4分(Ⅱ)因为c m =,12c e a ==,则2a m =,223b m =,设椭圆方程为2222143x y m m +=由222221434x y m m y mx ⎧+=⎪⎨⎪=⎩,得22316120x mx m +-=…6分即(6)(32)0x m x m +-=,得23P mx =代入抛物线方程得p y =,即2(3m P 212557,24333p m m m PF x m PF a PF m =+==-=-=,12623mF F m ==, 因为12PF F ∆的边长恰好是三个连续的自然数,所以3m =…8分此时抛物线方程为212y x =,(2,P ,直线PQ方程为:3)y x =--.联立23)12y x y x⎧=--⎪⎨=⎪⎩,得2213180x x -+=,即(2)(29)0x x --=,所以92Q x =,代入抛物线方程得Q y =-,即9(,2Q -∴252PQ =. 设2(,)12t M t 到直线PQ 的距离为d,(t ∈-则2752d t ==-…10分当t =max 752d =, 即MPQ ∆面积的最大值为156125216⨯.…12分21.解:(Ⅰ)因为1ln ()xf x x+=,0x > ,则ln ()xf x x'=-, … 1分当01x <<时,()0f x '>;当1x >时,()0f x '<.所以()f x 在(0,1)上单调递增;在(1,)+∞上单调递减,所以函数()f x 在1x =处取得极大值.… 2分因为函数()f x 在区间1(,)2a a +(其中0a >)上存在极值,所以1,112a a <⎧⎪⎨+>⎪⎩ 解得1 1.2a <<… 4分 (Ⅱ)不等式()1kf x x ≥+, 即为(1)(1ln ),x x k x ++≥ 记(1)(1ln )(),x x g x x++=所以22[(1)(1ln )](1)(1ln )ln (),x x x x x x xg x x x '++-++-'==… 6分令()ln ,h x x x =-则1()1h x x'=-,1,()0.x h x '≥∴≥()h x ∴在[1,)+∞上单调递增,min [()](1)10h x h ∴==>, 从而()0g x '>故()g x 在[1,)+∞上也单调递增,min [()](1)2g x g ∴==,所以2k ≤…8分(Ⅲ)由(Ⅱ)知:2()1f x x >+恒成立,即122ln 11,11x x x x x-≥=->-++ 令(1)x n n =+,则2ln[(1)]1(1)n n n n +>-+,所以 2ln(12)1,12⨯>-⨯ 2ln(23)1,23⨯>-⨯ 2ln(34)1,34⨯>-⨯ ………… ……2ln[(1)]1(1)n n n n +>-+.叠加得:22ln[123⨯⨯⨯ (211)(1)]2[1223n n n ⨯+>-++⨯⨯…1](1)n n + 112(1)2211n n n n n =-->-+>-++… 10分则22123⨯⨯⨯…22(1)n n n e -⨯+>,所以[]22(1)(1)()n n n e n -*+>+⋅∈!N …12分22.解(Ⅰ)取BD 的中点O ,连接OE .∵BE 平分∠ABC ,∴∠CBE =∠OBE .又∵OB =OE ,∴∠OBE =∠BEO ,∴∠CBE =∠BEO ,∴BC ∥OE .…3分∵∠C =90°,∴OE ⊥AC ,∴AC 是△BDE 的外接圆的切线.…5分(Ⅱ)设⊙O 的半径为r ,则在△AOE 中,222AE OE OA +=,即2226(r r +=+,解得r =…7分∴OA =2OE ,∴∠A =30°,∠AOE =60°.∴∠CBE =∠OBE =30°.∴EC=1113222BE ==.…10分23.解:曲线C 的极坐标方程是4cos ρθ=化为直角坐标方程为2240x y x +-=,即()2224x y -+=,直线l的参数方程1x y ⎧=+⎪⎪⎨⎪=⎪⎩,化为普通方程为x -y -1=0,…5分曲线C 的圆心(2,0)到直线l,所以直线l 与曲线C 相交所成的弦的弦长.…10分24.解:左端变形111a b c b c c a a b++++++++ 111()()a b c b c c a a b =+++++++, ∴只需证此式92≥即可。
人教版2012年中考数学模拟题(一)含答案

2012年中考数学模拟题(含答案)(试卷满分 120分,考试时间120分钟)一.选择题 (每小题4分,共40分)1. 下列图形中,不是中心对称图形是( )A.矩形B.菱形C.正五边形D.正八边形2. 函数y =中,自变量x 的取值范围是( )A.x ≥0 B .x >0且x ≠1 C .x >0 D.x ≥0且x ≠1 3. -5的相反数是( )A.-5B.5C.D.-4. 如果一个角是36°,那么 ( )A.它的余角是64° B .它的补角是64° C .它的余角是144° D .它的补角是144°5. 若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有( )A.2对B.3对C.4对D.6对 6. 棱长是1cm 的小立方体组成如图所示的几何体,那么这个几何体的表面积是( )A.36cm 2B.33cm 2C.30cm 2D.27cm 27. 在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下( )A.小明的影子比小强的影子长B.小明的影长比小强的影子短C.小明的影子和小强的影子一样长D.无法判断谁的影子长 8. 已知点P (3,-2)与点Q 关于x 轴对称,则Q 点的坐标为( )A.(-3,2)B.(-3,-2)C.(3,2)D.(3,-2) 9. “比a 的23大1的数”用代数式表示是( ) A. 23a +1 B. 32a +1 C. 25a D. 23a -1 10. 下列命题中错误的命题是 ( ) A.的平方根是B.平行四边形是中心对称图形C.单项式与是同类项 D.近似数有三个有效数字二.填空题 (每小题3分,共24分)11. 两个同心圆的圆心为点O ,半径分别为3cm 和5cm ,一直线l 与小圆相切于点C ,交大圆于两点A 、B ,则AB 的长为_________cm.12. 在Rt ΔABC 中 ,∠C = 90°,AC = 3 , BC = 4 ,若⊙A .⊙B .⊙C 两两外切 ,则⊙C 的半径为 ____________13.用计算器计算:。
2012年中考数学仿真模拟试卷1 OK

2012年中考数学仿真模拟试卷1考生须知:1、本试卷满分120分, 考试时间100分钟。
2、答题前,在答题纸上写姓名和准考证号3、必须在答题纸的对应答题位置上答题,写在其他地方无效,答题方式详见答题纸上的说明。
4、考试结束后,试题卷和答题纸一并上交。
一、仔细选一选: (本题有10小题,每小题3分,共30分)下面每小题给出四个选项中,只有一个是正确的,注意用多种不同方法来选取正确答案。
1、下列各数中,相反数最大的是( ) A 、-1B 、0C 、1D 、-2.12、我国云南大部分地区滴雨未降,正在经历严峻的干旱形势,云南省气象台为此发布全省干旱“红色预警”,干旱一周导致损失20亿。
截至到六月份,云南全省作物受旱面积1755万亩,因旱饮水困难的有385万人.其中受灾人数用科学记数法表示(保留两个有效数字)正确的是( )A 、0.385×107B 、7109.3⨯ C 、61085.3⨯ D 、6109.3⨯ 3、视力表对我们来说并不陌生.如图是视力表的一部分,五个不同方向的“E ”之间存在的变换有( ) A 、平移、旋转B 、旋转、相似 、平移C 、轴对称、平移、相似D 、相似、平移4、两个大小不同的球在水平面上靠在一起,组成如图所示的几何体,则该几何体的左视图是( ) A 、两个外离的圆 B 、两个外切的圆 C 、两个相交的圆 D 、两个内切的圆5、函一个圆形人工湖如图所示,弦是湖上的一座桥,已知桥长100m ,测得圆周角水平面主视方向(第4标准对数视040404AOBCD(第5题45ACB ∠=︒,则这个人工湖的直径AD 为( )A 、502mB 、1002mC 、1502mD 、2002m6、在不大于100的自然数中,既不是完全平方数(平方根是整数)也不是完全立方数(立方根是整数)的数的概率有( )A 、253 B 、10187 C 、10087 D 、 10188 7、如图,在平面直角坐标系中,过格点A ,B ,C 作一圆弧,点B 与图中4×7方格中的格点的连线中,能够与该圆弧相切的格点个数有( )xy110B CAA 、1个B 、2个C 、3个D 、4个8、如果0)1)(2(2=-+-x m x x 方程的三根,可作为一个三角形的三边长,则m 的取值范围是( ) A 、43≥m B 、43﹤1≤m C 、143≤≤m D 、43≤m9、已知:如图,三个半圆彼此相外切,它们的圆心都在x 轴的正半轴上并与直线y =3x 相切,设半圆C 1、半圆C 2、半圆C 3…的半径分别是r 1、r 2、r 3….,则当r 1=1时,则2012r =( )A 、20113 B 、20123C 、20103D 、310、若},,,max{21n s s s 表示实数n s s s ,,,21 中的最大者.设),,(321a a a A =,⎪⎪⎪⎭⎫ ⎝⎛=321b b b B ,记}.,,max{332211b a b a b a B A =⊗设,1(-=x A )1,1+x ,⎪⎪⎪⎭⎫ ⎝⎛--=|1|21x x B ,若1-=⊗x B A ,则x 的取值范E围为( )A 、131≤≤-xB 、211+≤≤x C 、121≤≤-x D 、311+≤≤x二、认真填一填: (本题有6小题,每小题4分,共24分)要注意认真看清题目的条件和要填写的内容,尽量完整的填写答案。
2012年深圳市中考数学模拟卷1评分标准与参考答案

2012年深圳市中考模拟卷一评分标准与参考答案选择题:题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 A D B A B D B D C C B B填空题:题号 1314 15 16 答案2(a +2)(a -2)1/41701,或3解答题:17.解:原式=53413232212111322=++--=⨯+⎪⎭⎫ ⎝⎛-+--;……2+2+2=6分 18.解:原式=()()()()x x x x x x x x x x 412121121111=--+=-+⋅⎪⎭⎫⎝⎛+--,……4分 当2=x 时,原式=2224=。
…………6分 19.解:(1)调查的人数为:300%50150=(人); …………1分 补全的统计图见下图:……5(1+1+1+1)分(2)随手乱扔垃圾的人约为:2400×10%=240(人)。
…………7分20.证明:(1)∵CF 平分∠BCD ,∴∠BCF=∠DCF , …………1分∵BC=DC ,CF=CF ,∴△BFC ≌△DFC 。
…………2分(2)过点F 作FG ∥AD 交AB 于点G, …………3分由(1)△BFC ≌△DFC ,∴∠EDF=∠CBF ,DF=BF , …………4分又∵DF ∥AB ,∴∠DFE=∠GBF ,∠GFB=∠FBC=∠EDF , …………5分 ∴△BFG ≌△FDE ,∴DE=GF , …………6分又∵AD ∥FG ,AG ∥DF ,∴AD=GF=DE 。
…………7分21.解:(1)设订购甲款运动服x 套,则乙款运动服订购(30-x )套,依题意,得: 7600≤350x +200(30-x )≤8000, …………3分 解得:340332≤≤x , …………4分 又∵x 是整数,∴x =11,12,13。
答:共有三种方案,第一种方案是:订购甲款运动服11套,乙款运动服19套;第二种方案是:订购甲款运动服12套,乙款运动服18套;第三种方案是:订购甲款运动服13套,乙款运动服17套。
2012大连市数学中考一模试题及答案

2012年大连市数学中考模拟一一、选择题(本题共8小题,每小题3分,共24分。
在每小题给出的四个选项中。
只有一个选项正确) 1、23-的绝对值是 ( )A .32-B .23- C .23 D .322、图1是由四个完全相同的正方体组成的几何体,这个几何体的俯视图是 ( )3、下列计算结果正确的是 ( )A .224222+=B .33222÷=C =D =4、袋中有3个红球和4个白球,这些球除颜色不同外其余均相同,在看不到球的条件下,随机从袋中摸出1个球,则摸出白球的概率是 ( ) A .17B .37C .47D .345、在平面直角坐标系中,将点P (-2,3)向下平移4个单位得到点P ′,则点P ′所在象限为 ( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限6、我市某一周的最大风力情况如下表所示:则这周最大风力的众数与中位数分别是( )A .7 ,5B .5 ,5C .5 ,1.75D .5 ,47、矩形和菱形都具有的特征是 ( )A .对角线相等B .对角线互相平分C .对角线互相垂直D .对角线平分一组对角8、如图2,一条抛物线与x 轴相交于A 、B 两点(点A 在点B 的左侧),其顶点P 在线段MN 上移动.若点M 、 N 的坐标分别为(-1,-2)、(1,-2),点B 的横坐标的最大值为3,则点A 的横坐标的最小值为( ) A .-3 B .-1 C . 1 D . 3 二、填空题(本题共8小题,每小题3分,共24分) 9、sin30°= .10、因式分解:24a -= . 11、当x=11时,221x x -+= .12、从小刚等7名合唱队员中任选1名作为领奖者,则小刚被选中的概率是 . 13、如图3,AB ∥CD ,CE 与AB 交于点A ,BE ⊥CE ,垂足为E .若∠C=37°,则∠B= °.14、如果关于x 的方程230x x k -+=(k 为常数)有两个不相等的实数根,那么k 应满足的条件为 . 15.如图4,在平面直角坐标系中,线段OA 与线段OA ′关于直线:l y x =对称.已知点A 的坐标为(2,1),则点A′的坐标为 .16、如图5,为了测量某建筑物CD 的高度,测量人员先在地面上用测角仪AE 自A 处测得建筑物顶部C 的仰角是30°,然后在水平地面上向建筑物前进42米,此时自B 处测得建筑物顶部C 的仰角是60°.已知测角仪的高度始终是1.5米,则该建筑物CD 的高度约为米(结果保留到1米,参考数据:2 1.43 1.7≈,)三、解答题(本题共4小题。
2012年浙江省初中模拟考试数学试卷(1)及答案

2012年浙江省初中模拟考试1九年级 数学试题卷(满分150分,考试用时120分钟)一、选择题:(本大题共10小题,每小题4分,满分40分,请选出各题中一个符合题意的正确选项,不选、多选、错选,均不不给分)1.-2的绝对值是( ) A . -2 B . 2 C .12 D . 12- 2.如图,直线AB 、CD 被直线EF 所截,则∠3的同旁内角是( ) A .∠1 B .∠2 C .∠4 D .∠5 3.小明的讲义夹里放了大小相同的试卷共10页,其中语文4页、数学3页、英语5页,他随机地从讲义夹中抽出1页,抽出的试卷恰好是数学试卷的概率为( ) A .21 B .103C .52D .101 4.抛物线2y x =先向右平移1个单位,再向上平移3个单位,得到新的抛物线解析式是( )A .()213y x =++ B .()213y x =+-C .()213y x =-- D .()213y x =-+5.如图,下列水平放置的几何体中,左视图不是..长方形的是( ) 12354A B C D EF(第2题图)6.如右图,已知圆的半径是5,弦AB 的长是6,则弦AB 的弦心距是( )A .3B .4C .5D .8 7.同学们玩过滚铁环吗?当铁环的半径是30cm ,手柄长40cm .当手柄的一端勾在环上,另一端到铁环的圆心的距离为50cm 时,铁环所在的圆与手柄所在的直线的位置关系为( )A .相离B .相交C .相切D .不能确定 8.在数-1,1,2中任取两个数作为点坐标,那么该点刚好在一次函数2y x =-图象上的概率是( ) A .12B .13 C .14 D .169.如图,在ABC ∆中,AB =10,AC =8,BC =6,经过点C 且与边AB 相切的动圆与CA ,CB 分别相交于点P ,Q ,则线段PQ 长度的最小值是( )A .B .C .D .QPCBAOABMP O A . 4.8 B .4.75 C .5 D .210.如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下次沿顺时针方向跳两个点;若停在偶数点上,则下次沿逆时针方向跳一个点.若青蛙从5这点开始跳,则经过2012次后它停在哪个数对应的点上 ( ) A .1 B .2 C .3 D .5 二、填空题(本题共6小题,每小题5分,共30分) 11.因式分解22x x -= .12.如图,已知点P 为反比例函数4y x=的图象上的一点,过点P 作横轴的垂线,垂足为M ,则OPM ∆的面积为 .13.已知关于x 的方程2220x x k -+=的一个根是1,则k = . 14.如图,点A 、B 、C 在圆O 上,且040BAC ∠=,则BOC ∠= . 15.小明的圆锥形玩具的高为12cm ,母线长为13cm ,则其侧面积是 2cm .16.一个长方形的长与宽分别为163cm 和16cm ,绕它的对称中心134O C BA旋转一周所扫过的面积是 2cm ;旋转90度时,扫过的面积是2cm .三、解答题:(本题共8小题,第17~20题每题8分,第21题10分,第22、23题每题12分,第24题14分,共80分) 17.(1)计算:002012124sin 60+-⨯; (2)解不等式()()21331x x -+≤+.18.求代数式的值:2222(2)42x x x x x x -÷++-+,其中12x =.19.为了解某校九年级学生体育测试成绩情况,现从中随机抽取部分学生的体育成绩统计如右表:根据上面提供的信息,回答下列问题: (1)求随机抽取学生的人数 ; (2)统计表中b = ;(3)已知该校九年级共有500名学生,如果体育成绩达28分以上(含28分)为优秀,请估计该校九年级学生体育成绩达到优秀的总人数.体育成绩(分) 人数(人) 百分比(%) 26 8 1627 a 2428 15 d 29 b e 30 c 1020.已知:如图,在□ABCD 中,E 是CA 延长线上的点,F 是AC 延长线上的点,且AE = CF .求证:(1)△ABE ≌△CDF ; (2)BE ∥DF .21.我市某服装厂主要做外贸服装,由于技术改良,2011年全年每月的产量y (单位:万件)与月份x 之间可以用一次函数10y x =+表示,但由于“欧债危机”的影响,销售受困,为了不使货积压,老板只能是降低利润销售,原来每件可赚10元,从1月开始每月每件降低0.5元。
2012年安徽中考数学模拟试题(一)(word版及答案免费)

(2)甲的票数是:200×34%=68(票) 乙的票数是:200×30%=60(票) 丙的票数是:200×28%=56(票) (3)甲的平均成绩: 乙的平均成绩: 丙的平均成绩: ∵乙的平均成绩最高 ∴应该录取乙。 20、(7分)(2012安徽)如图,AB是⊙O的直径,AM和BN是它的两条切 线,DE切⊙O于点E,交AM与于点D,交BN于点C,F是CD的中点,连接OF。 A
济宁市2011年高中阶段学校招生考试 数学试题参考答案
一、选择题
题号 答案
1 C
2 D
3 D
4 C
5 A
6 B
7 C
8 B
9 A
10 D
二、填空题: 11、m>1 12、y=(x-2)2+1 13、相交 14、 100 15、 三、解答题: 16、解:原式=…………………2分 = …………………4分 = …………………5分 17、证明:∵四边形ABCD是平行四边形 ∴AD∥BC,OB=OD …………………1分 ∵∠EDO=∠FBO, ∠OED=∠OFB …………………2分 ∴△OED≌△OFB ∴DE=BF …………………3分 又∵ED∥BF ∴四边形BEDF是平行四边形 …………………4分 ∵EF⊥BD ∴平行四边形BEDF是菱形。 …………………5分 18、解:过点P作PC⊥AB,垂足为C,设PC=x海里 在Rt△APC中,∵tan∠A= ∴AC= = ……………2分 在Rt△PCB中,∵tan∠B= ∴BC= = ……………4分
23、(10分)(2012安徽)如图,第一象限内半径为2的⊙C与y轴相切于点 A,作直径AD,过点D作⊙C的切线l交x轴于点B,P为直线l上一动点,已知直 线PA的解析式为:y=kx+3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012年中考数学预测试题一
(总分:120分 时间:100分钟)
一、选择题:(每小题3分,共30分.在每小题给出的四个选项中,只有一个是正确的) 1.一个数的相反数是3,则这个数是( )
A. 3
1
-
B. 3
1
C. 3-
D. 3
2.在“2008北京”奥运会国家体育场的“鸟巢”钢结构工程施工建设中,首次使用了我国科研人员自主研制的强度为84.610⨯帕的钢材,那么84.610⨯的原数为( ) A .4 600 000 B .46 000 000 C .460 000 000 D .4 600 000 000
3.下列命题中真命题是————————————————————————( ) (A )任意两个等边三角形必相似; (B )对角线相等的四边形是矩形;
(C )以400
角为内角的两个等腰三角形必相似;
(D )一组对边平行,另一组对边相等的四边形是平行四边形
4.抛物线2)8(2+--=a y 的顶点坐标是——————————————-——( ) A 、(2,8) B 、(8,2) C 、(—8,2) D 、(—8,—2)
5. 如图,△ABC 和△DEF 是两个形状大小完全相同的等腰直角三角形,∠B=∠DEF=90°,点B 、C 、
E 、
F 在同一直线上.现从点C 、E 重合的位置出发,让△ABC 在直线EF 上向右作匀速运动,而△DEF 的位置不动.设两个三角形重合部分的面积为y ,运动的距离为x .下面表示y 与x 的函数关系式的图象大致是——————————( )
6.若不等式组⎩⎨⎧>-<+m
x x x 148 的解集是x >3,则m 的取值范围是————————
( )
A
B
C
D
O
(A)m >3 (B)m ≥3 (C)m ≤3 (D)m <3
7.把长为8cm 的矩形按虚线对折,按图中的虚线剪出一个直角梯形,
打开得到一个等腰梯形,剪掉部分的面积为6cm 2
,则打开后梯形的周长是—————( )
A .(10+213)cm
B .(10+13)cm
C .22cm
D .18cm
8.在平面内有线段AB 和直线l,点A 、B 到直线l 的距离分别是4㎝、6㎝.则线段AB 的中点C 到直线l 的距离是————————————————————————( ) (A)1 或 5 (B)3 或 5 (C)4 (D)5
9.在Rt △ABC 的直角边AC 边上有一动点P(点P 与点A 、C 不重合),过点P 作直线截得的三角形与△ABC 相似,满足条件的直线最多有 ————————————————( ) (A)1条 (B)2条 (C)3条 (D)4条
10.如图,在ΔABC 中,∠C =90°,AC =8,AB =10,点P 在AC 上,AP =2,若⊙O 的圆心在线段BP 上,且⊙O 与AB 、AC 都相切,则⊙O 的半径是——( )
A. 1
B. 4
5
C. 7
12
D. 9
4
二、填空题(每小题4分,共24分) 11. 函数1
24
y x =
-中,自变量x 的取值范围是 . 12.方程x x 22
=的解是 。
13.如图,点A 在函数=y x
6
-
)0(<x 的图象上,过点 A 作AE 垂直x 轴,垂足为E ,过点A 作AF 垂直y
轴,垂足为F ,则矩形AEOF 的面积是____________ 14.如图,A 、B 、C 为⊙0上三点,∠ACB =20○
,则∠BAO 的度数
3cm
3cm
第7题图
第10题 y
x
O
A F E
(第13题图)
为 __________○。
15.从1-,1,2这三个数中,任取两个不同的数作为一次函数y kx b =+的系数k ,b ,则一次函数y kx b =+的图象不经过第四象限的概率是 .
16.如图,E 、F 分别是 ABCD 的边AB 、CD 上 的点,AF 与DE 相交于点P ,BF 与CE 相交于 点Q ,若S
△APD
15=2cm ,S
△BQC
25=2cm ,
则阴影部分的面积为 2
cm . 三、解答题(本大题共有8小题,共66分.) 17(本小题满分6分)计算:2330tan 3)2(0
----
18.(本小题满分6分)先化简,再求值:⎪⎭⎫ ⎝⎛
--+2122x x ÷
2
4--x x
,其中42-=x .
19.(本小题满分6分)
九年级一班的两位学生对本班的一次数学成绩(分数取整数,满分为100分)进行了一次初步统
P
A B
C
D
E
F
Q
(第16题图)
计,看到80分以上(含80分)有17人,但没有满分,也没有低于30分的.为更清楚了解本班的考试情况,他们分别用两种方式进行了统计分析,如图1和图2所示.请根据图中提供的信息回答下列问题:
(1)班级共有多少名学生参加了考试? (2)填上两个图中三个空缺的部分; (3)问85分到89分的学生有多少人?
20.(本小题满分8分)某乡薄铁社厂的王师傅要在长为25cm ,宽为18cm 的薄铁板上裁出一个最大的圆和两个尽可能大的小圆.他先画出了如图所示的草图,但他在求小圆半径时遇到了困难,请你帮助王师傅计算出这两个小圆的半径.
人数
分数
2
3 5 10
11 29.5 39.5 49.5 59.5 69.5 79.5 89.5 99.5
(第19题图1)
(第19题图2)
85分 ~100分
60分以下
60分~85分
62%
20%
%
图中的各部分都只 含最低分不含最高分
21.(本小题满分8分)为配合我市“创卫”工作,某中学选派部分学生到若干处公共场所参加义务劳动.若每处安排10人,则还剩15人;若每处安排14人,则有一处的人数不足14人,但不少于10人.求这所学校选派学生的人数和学生所参加义务劳动的公共场所个数.
22.(本小题满分10分)如图,在ABC △中,2C B ∠=∠,D 是BC 上的一点,且AD AB ⊥,点E 是BD 的中点,连结AE . (1)求证:AEC C ∠=∠ (2)求证:2BD AC =
(3)若 6.5AE =,5AD =,那么ABE △的周长是多少?
23. (本小题满分10分)
先阅读下列材料,再解答后面的问题
材料:一般地,n 个相同的因数a 相乘:a.a.a …..a=a n。
如23
=8,此时,3叫做以2为底8
的对数,记为()38log 8log 22=即。
一般地,若()0,10>≠>=b a a b a n 且,则n 叫做以a 为底b 的对数,记为()813.log log 4
==如即n b b a a ,则4叫做以3为底81的对数,记为
)481log (81log 33=即。
问题:(1)计算以下各对数的值:
=
==64log 16log 4log 222.
A
C
D E
B
(2)观察(1)中三数4、16、64之间满足怎样的关系式?64log 16log 4log 222、、 之
间又满足怎样的关系式?
(3)由(2)的结果,你能归纳出一个一般性的结论吗? ()0,0,10log log >>≠>=
+N M a a N M a a
且
根据幂的运算法则:m n m
n
a a a +=⋅以及对数的含义证明上述结论。
24.(本小题满分12分)如图,抛物线的顶点坐标是⎪⎭
⎫ ⎝⎛8925
,-,且经过点) 14 , 8 (A .
(1)求该抛物线的解析式;
(2)设该抛物线与y 轴相交于点B ,与x 轴相交于C 、D 两点(点C 在点D 的左边), 试求点B 、C 、D 的坐标;
(3)设点P 是x 轴上的任意一点,分别连结AC 、BC . 试判断:PB PA +与BC AC +的大小关系,并说明理由.
D
A
O x
y
C
B . (第24题图)。
