有限元第二次作业

合集下载

2016年秋国科大有限元作业答案

∴ u(x) = ui +
1
有限元作业答案 smartsrh 2016 年秋季中国科学院大学张年梅教授
图 2: 题图 2
2. 利用梁单元计算以下结构的应力。
解：将此梁划分为两个单元 AB 和 BC 。首先计算节点等效载荷阵列 { } [ ]T P = RyA + FyA RθA + MθA FyB MθB RyC RθC [ ]T = RyA − P /2 RθA − P l/8 −P /2 9P l/8 RyC RθC 计算各个单元刚度矩阵如下 12 6l −12 6l [ ](AB ) 2EI 6l 4l2 −6l 2l2 = 3 K l −12 −6l 12 −6l 2 2 6l 2l −6l 4l
6l 4l2 2EI −12 −6l = 3 l 6l 2l2 0 0
12
6l−126l Nhomakorabea2
有限元作业答案 smartsrh 2016 年秋季中国科学院大学张年梅教授
[ ]AB [ ]AB [ ]AB { }AB ∴ σ =E ε =E B δ [

3
= Ey (6l − 12x)/l
3
有限元作业答案 smartsrh 2016 年秋季中国科学院大学张年梅教授
4. 证明三结点三角形单元的插值函数满足 Ni (xj , yj ) = δij 及 Ni + Nj + Nk = 1
证明：假设三节点 i、j 、m 逆时针方向编号，不妨考虑横向位移，纵向位移与此同理 β1 β1 1 xi yi u ui xj ym − xm yj yi xm − xi ym xi yj − xj yi i uj = 1 xj yj β2 =⇒ β2 = 1 yj − ym ym − yi yi − yj uj 2∆ β3 β3 1 xm ym um um xm − xj xi − xm xj − xi β x y − x y y x − x y x y − x y u 1 j m m j i m i m i j j i [ ] ] i 1 [ ∴u= 1 x y = ym − yi yi − yj uj β2 2∆ 1 x y yj − ym β3 xm − xj xi − xm xj − xi um x y − x y y x − x y x y − x y j m m j i m i m i j j i [ ] ] 1 [ ∴ Ni Nj Nm = 1 x y yj − ym ym − yi yi − yj 2∆ xm − xj xi − xm xj − xi x y − x y 1 x y m j i i ] j m 1 1 [ det = ∴ Ni (xi , yi ) = 1 xi yi y − y 1 x y j m j j = 1 2∆ 2∆ xm − xj 1 xm ym xj ym − xm yj 1 yj − ym = 0 = Ni (xm , ym ) ∴ Ni (xj , yj ) = 2∆ xm − xj [ ] xj ym − xm yj 1 xi yi yi xm − xi ym xi yj − xj yi 1 x y yj − ym + ym − yi + yi − yj = 1 det 1 xj yj = 1 Ni +Nj +Nm = 2∆ 2∆ xm − xj 1 xm ym xi − xm xj − xi Ni + Nj + Nm = 1 ∴ Ni (xj , yj ) = δij

(完整版)有限元第二章课后题答案

2 弹性力学问题的有限单元法思考题2.1 有限元法离散结构时为什么要在应力变化复杂的地方采用较密网格，而在其他地方采用较稀疏网格？答：在应力变化复杂的地方每一结点与相邻结点的应力都变化较大，若网格划分较稀疏，则在应力突变处没有设置结点，而使得所求解的误差很大，若网格划分较密时，则应力变化复杂的地方可以设置更多的结点，从而使得所求解的精度更高一些。

2.2 因为应力边界条件就是边界上的平衡方程，所以引用虚功原理必然满足应力边界条件，对吗？答：对。

2.3 为什么有限元只能求解位移边值问题和混合边值问题？弹性力学中受内压和外压作用的圆环能用有限元方法求解吗？为什么？答：有限元法是一种位移解法，故只能求解位移边值问题和混合边值问题。

而应力边值问题没有确定的位移约束，不能用位移法求解，所以也不能用有限元法求解。

2.4 矩形单元旋转一个角度后还能够保持在单元边界上的位移协调吗？答：能。

矩形单元的插值函数满足单元内部和单元边界上的连续性要求，是一个协调元。

矩形的插值函数只与坐标差有关，旋转一个角度后各个结点的坐标差保持不变，所以插值函数保持不变。

因此矩形单元旋转一个角度后还能够保持在单元边界上的位移协调。

2.5 总体刚度矩阵呈带状分布，与哪些因素有关？如何计算半带宽？答：因素：总体刚度矩阵呈带状分布与单元内最大结点号与最小结点号的差有关。

计算：设半带宽为B ，每个结点的自由度为n ，各单元中结点整体码的最大差值为D ，则B=n(D+1)，在平面问题中n=2。

2.6 为什么单元尺寸不要相差太大，如果这样，会导致什么结果？答：由于实际工程是一个二维或三维的连续体，将其分为具有简单而规则的几何单元，这样便于网格计算，还可以通过增加结点数提高单元精度。

在几何形状上等于或近似与原来形状，减小由于形状差异过大带来的误差。

若形状相差过大，使结构应力分析困难加大，误差同时也加大。

2.7 剖分网格时，在边界出现突变和有集中力作用的地方要设置结点或单元边界，试说明理由。

《有限元分析》课程作业

《有限元分析》课程作业任课教师：徐亚兰学生姓名：陈新杰学号：班级：1304012时间：2016-01-05一、问题描述及分析问题：如图1所示，有一矩形平板，在右侧受到P=10KN/m 的分布力，材料常数为：弹性模量Pa E 7101⨯=；泊松比3/1=μ；板的厚度为t=；试按平面应力问题利用三角形与矩形单元分别计算各个节点位移及支座反力。

图1 平面矩形结构的有限元分析分析：使用两种方案：一、基于3节点三角形单元的有限元建模，将矩形划分为两个3节点三角形单元；二、基于4节点矩形单元的有限元建模，使用一个4节点矩形单元。

利用MATLAB 软件计算出各要求量，再将两种方案的计算结果进行比较、分析、得出结论。

二、有限元建模及分析1、基于3节点三角形单元的有限元建模及分析（1）结构的离散化与编号如图2所示，将平面矩形结构分为两个3节点三角形单P=10KN/m1m1m元。

单元①三个节点的编号为1，2，4，单元②三个节点的编号为3，4，2，各个节点的位置坐标为(),,1,2,3,4i i x y i =，各个节点的位移（分别沿x 方向和y 方向）为(),,1,2,3,4i i u v i =。

图2 方案一：使用两个3节点三角形单元（2）各单元的刚度矩阵及刚度方程 a.单元的几何和节点描述单元①有6个节点位移自由度（DOF ）。

将所有节点上的位移组成一个列阵，记作(1)q ；同样，将所有节点上的各个力也组成一个列阵，记作(1)F ，则有(1)112244,,,,,)q u v u v u v =（(1)112244(,,,,,)x y x y x y F F F F F F F =同理，对于单元②，有(2)334422,,,,,)q u v u v u v =（1234X y ①②(2)334422(,,,,,)x y x y x y F F F F F F F =b.单元的位移场描述对于单元①，设位移函数012012(,)(,)u x y a a x a y v x y b b x b y ⎫=++⎪⎬=++⎪⎭(1-1)由节点条件，在,i i x x y y ==处，有(,)(,)i i i i i i u x y u v x y v =⎫⎬=⎭1,2,4i = (1-2) 将式(1-1)代入节点条件式(1-2)中，可求出式（1-1）中待定系数，即011122211223444411()22u x y a u x y a u a u a u AAu x y ==++ (1-3) 11122112234441111()221u y a u y b u b u b u AAu y ==++ (1-4) 21122112234441111()221x u a x u c u c u c u AAx u ==++ (1-5) 01122341()2b a v a v a v A =++(1-6) 11122341()2b b v b v b v A =++(1-7) 21122341()2b c v c v c v A =++(1-8)在式(1-3)~式(1-8)中1122123441111()221x y A x y a a a x y ==++ (1-9)2212442442124421244(1,2,3)1111x y a x y x y x y y b y y y x c x x x ⎫==-⎪⎪⎪⎪=-=-⎬⎪⎪⎪==-+⎪⎭ (1-10) 上式中的符号(1,2,3)表示下标轮换，如12,23,31→→→同时更换。

有限元习题及答案ppt课件

病原体侵入机体，消弱机体防御机能，破坏机体内环境的相对稳定性，且在一定部位生长繁殖，引起不同程度的病理生理过程
病原体侵入机体，消弱机体防御机能，破坏机体内环境的相对稳定性，且在一定部位生长繁殖，引起不同程度的病理生理过程
病原体侵入机体，消弱机体防御机能，破坏机体内环境的相对稳定性，且在一定部位生长繁殖，引起不同程度的病理生理过程
病原体侵入机体，消弱机体防御机能，破坏机体内环境的相对稳定性，且在一定部位生长繁殖，引起不同程度的病理生理过程
病原体侵入机体，消弱机体防御机能，破坏机体内环境的相对稳定性，且在一定部位生长繁殖，引起不同程度的病理生理过程
病原体侵入机体，消弱机体防御机能，破坏机体内环境的相对稳定性，且在一定部位生长繁殖，引起不同程度的病理生理过程
病原体侵入机体，消弱机体防御机能，破坏机体内环境的相对稳定性，且在一定部位生长繁殖，引起不同程度的病理生理过程
病原体侵入机体，消弱机体防御机能，破坏机体内环境的相对稳定性，且在一定部位生长繁殖，引起不同程度的病理生理过程
病原体侵入机体，消弱机体防御机能，破坏机体内环境的相对稳定性，且在一定部位生长繁殖，引起不同程度的病理生理过程
病原体侵入机体，消弱机体防御机能，破坏机体内环境的相对稳定性，且在一定部位生长繁殖，引起不同程度的病理生理过程
病原体侵入机体，消弱机体防御机能，破坏机体内环境的相对稳定性，且在一定部位生长繁殖，引起不同程度的病理生理过程

(完整word版)有限元分析大作业报告要点

有限元分析大作业报告试题1：一、问题描述及数学建模图示无限长刚性地基上的三角形大坝，受齐顶的水压力作用，试用三节点常应变单元和六节点三角形单元对坝体进行有限元分析，并对以下几种计算方案进行比较：（1）分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算；（2）分别采用不同数量的三节点常应变单元计算；（3）当选常应变三角单元时，分别采用不同划分方案计算。

该问题属于平面应变问题，大坝所受的载荷为面载荷，分布情况及方向如图所示。

二、采用相同单元数目的三节点常应变单元和六节点三角形单元计算1、有限元建模（1）设置计算类型：两者因几何条件和载荷条件均满足平面应变问题，故均取Preferences 为Structural（2）选择单元类型：三节点常应变单元选择的类型是Solid Quad 4 node182；六节点三角形单元选择的类型是Solid Quad 8 node183。

因研究的问题为平面应变问题，故对Element behavior（K3）设置为plane strain。

（3）定义材料参数：弹性模量E=2.1e11，泊松比σ=0.3（4）建几何模型：生成特征点；生成坝体截面（5）网格化分：划分网格时，拾取lineAB和lineBC，设定input NDIV 为15；拾取lineAC，设定input NDIV 为20，选择网格划分方式为Tri+Mapped，最后得到600个单元。

（6)模型施加约束：约束采用的是对底面BC 全约束。

大坝所受载荷形式为Pressure ，作用在AB 面上，分析时施加在L AB 上，方向水平向右，载荷大小沿L AB 由小到大均匀分布。

以B 为坐标原点，BA 方向为纵轴y ，则沿着y 方向的受力大小可表示为：}{*980098000)10(Y y g gh P -=-==ρρ2、计算结果及结果分析（1）三节点常应变单元三节点常应变单元的位移分布图三节点常应变单元的应力分布图（2）六节点三角形单元六节点三角形单元的变形分布图六节点三角形单元的应力分布图①最大位移都发生在A点，即大坝顶端，最大应力发生在B点附近，即坝底和水的交界处，且整体应力和位移变化分布趋势相似，符合实际情况；②结果显示三节点和六节点单元分析出来的最大应力值相差较大，原因可能是B点产生了虚假应力，造成了最大应力值的不准确性。

有限元方法例题解答

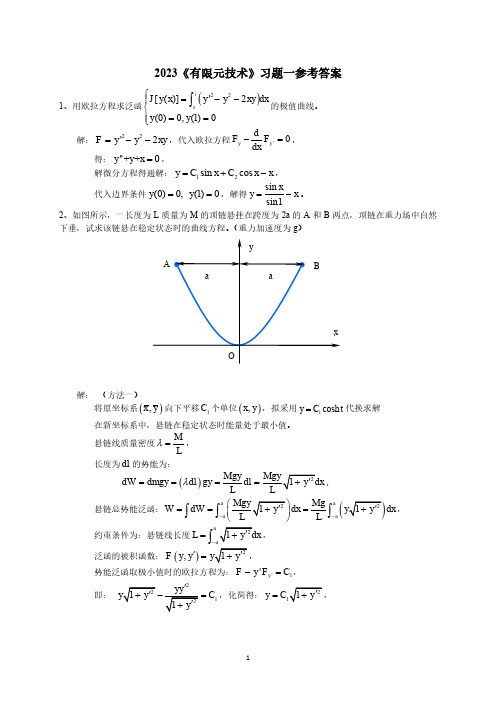
2023《有限元技术》习题一参考答案1、用欧拉方程求泛函()1022[()]'2(0)0,(1)0J y x y y xy dx y y ⎧=--⎪⎨⎪==⎩⎰的极值曲线。

解：22'2F y y xy =--，代入欧拉方程'0y y dF F dx-=，得：''++0y y x =，解微分方程得通解：12sin cos y C x C x x =+-，代入边界条件(0)0,(1)0y y ==，解得sin sin1xy x =-。

2、如图所示，一长度为L 质量为M 的项链悬挂在跨度为2a 的A 和B 两点，项链在重力场中自然下垂，试求该链悬在稳定状态时的曲线方程。

（重力加速度为g ）解：（方法一）将原坐标系(),x y 向下平移1C 个单位(),x y ，拟采用1cosh y C t =代换求解在新坐标系中，悬链在稳定状态时能量处于最小值。

悬链线质量密度MLλ=，长度为dl 的势能为：()Mgy dW dmgy dl gy dl L λ====，悬链总势能泛函：(a a a a Mg W dW dx dx L --===⎰⎰⎰，约束条件为：悬链线长度aL -=⎰，泛函的被积函数：(),F y y '=，势能泛函取极小值时的欧拉方程为：'1'y F y F C -=，即：21C -=，化简得：y C =于是：dx =x =，令1cosh y C t =（在新坐标系下才能作此代换），得：1sinh sinh dy C tdt t =⎧=，代入x =，得112x C dt C t C ==+⎰所以，21x C t C -=，21cosh cosh x C t C ⎛⎫-= ⎪⎝⎭回代1cosh y C t =得：211cosh x C y C C ⎛⎫-= ⎪⎝⎭，曲线关于y 轴对称得20C =，1C由悬链线长度112sinhaaL C C -==⎰给出，故新坐标系下所求曲线方程为11cosh x y C C ⎛⎫=⎪⎝⎭， 1C 由11sinh 2L aC C =确定。

有限元作业试题及答案.doc

E引入约束，求解整体平衡方程
2
答：一般选用三角形或四边形单元，在满足一定精度情况,
有限元划分网格的基本原则是:
1、拓朴正确性原则。即单元间是靠单元顶点、或单元边、或单元面连接
2、几何保形原则。即网格划分后，单元的集合为原结构近似
3、特性一致原则。即材料相同，厚度相同
4、单元形状优良原则。单元边、角相差尽可能小
c j二elcm= —a
Ni = l/a2 • a x = x/a
同理可得：Nj二y/a
有限元方法及应用试题
1
答：单元离散（划分、剖分）一单元分析一整体分析
有限元分析的主要步骤主要有：
A结构的离散化
B单元分析。选择位移函数、根据几何方程建立应变与位移的关系、根据物理方程建立应力
与位移的关系、根据虚功原理建立节点力与节点位移的关系（单元刚度方程）
C等效节点载荷计算
D整体分析，建立整体刚度方程
7、图示三角形ijni为等边三角形单元，边长为1,单位面积材料密度位P,集中力F垂直作用于nij边的中点，集度为q的均布载荷垂直作用于im边。写出三角形单元的节点载荷向量。
q:移到m, i点F:移到m, j点重力：移到m, I, j点
要证{8}=0
只需证，Nm = 0
Nm= 1/2A (am+bmx +cmy)
(d)平面三角形单元，29个节点，38个自由度
4、什么是等参数单元？。
如果坐标变换和位移插值采用相同的节点，并且单元的形状变换函数与位移插值的形函
数一样，则称这种变换为等参变换，这样的单元称为等参单元。
5பைடு நூலகம்
v(x, y)=
答：不能取这样的位移模式，因为在平面三节点三角形单元中，位移模式应该是呈线性的。

有限元试卷和答案

3 a 1
a
图1
1、解：设图 1 所示的各点坐标为点 1（ a， 0），点 2（a，a），点 3（0，0）于是，可得单元的面积为 (1) 形函数矩阵 N 为
1 (0 + ax − ay ) a2 1 N1 = 2 (0 + 0gx + ay ) a 1 N1 = 2 (a 2 − ax + 0gy ) a N1 =
判断正误（×）1. 节点的位置依赖于形态，而并不依赖于载荷的位置（√）2. 对于高压电线的铁塔那样的框架结构的模型化处理使用梁单元（×）3. 不能把梁单元、壳单元和实体单元混合在一起作成模型（√）4. 四边形的平面单元尽可能作成接近正方形形状的单元（×）5. 平面应变单元也好，平面应力单元也好，如果以单位厚来作模型化处理的话会得到一样的答案（×）6. 用有限元法不可以对运动的物体的结构进行静力分析（√）7. 一般应力变化大的地方单元尺寸要划的小才好（×）8. 所谓全约束只要将位移自由度约束住，而不必约束转动自由度（×）9. 线性应力分析也可以得到极大的变形（√）10. 同一载荷作用下的结构，所给材料的弹性模量越大则变形值越小（1）用加权余量法求解微分方程，其权函数 V 和场函数 u 的选择没有任何限制。（ × ）（2）四结点四边形等参单元的位移插值函数是坐标 x、y 的一次函数。（√ ）（3）在三角形单元中，其面积坐标的值与三结点三角形单元的结点形函数值相等。续。（√ ）（× ）（× ）（6）等参单元中 Jacobi 行列式的值不能等于零。（√）（7）在位移型有限元中，单元交界面上的应力是严格满足平衡条件的。（× ）（4）二维弹性力学问题的有限元法求解，其收敛准则要求试探位移函数 C1 连（5）有限元位移法求得的应力结果通常比应变结果精度低。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2-2图示悬臂板，属于平面应力问题，其网格图及单元、节点编号见图2-1，E=×1011，u=，演算其单刚阵到总刚阵的组集过程，并用MATLAB软件计算总刚阵。

图2-1答：根据图2-1所示列出单元节点列表：i j k1354225332654162（1）计算单元刚度阵单元1的刚度矩阵：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=15,514,513,515,414,413,415,314,313,31kkkkkkkkkk，[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=14,514,513,515,414,413,415,314,313,31kkkkkkkkkk；单元2的刚度矩阵：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=25,523,522,525,323,322,325,223,222,22kkkkkkkkkk，[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=24,523,522,525,323,322,325,223,222,22kkkkkkkkkk；节点单元单元3的刚度矩阵：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=36,635,632,636,535,532,536,235,232,23k kk k k kk k k k ，[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=36,635,632,636,535,532,536,235.232,2300000000000000000000000000k k k k k k k k k k ；单元4的刚度矩阵：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=46,642,641,646,242,241,246,142,141,14k k k k k k k k k k ，[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=46,641,646,242,241.246,142,141,140000000000000000000000000000k k k k k k k k k ；总刚度矩阵：[][][][][][]432141k k k k kK ee +++=∑==[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡++++++++++++=46,636,635,642,632,641,636,535,525,515,514,523,513,532,522,515,414,413,425,315,314,323,313,322,346,236,235,225,223,242,232,222,241,246,142,141,100000000000k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k K Matlab 程序语言的编写：function Idexglobal gNode gElement gMaterial gNode=[]%gNode 同样是一个矩阵，每一行表示一个结点，第1 列是结点的x 坐标，第2 列是结点的y坐标gElement=[3 4 52 3 52 5 61 2 6 ];%gElement 是一个矩阵，每一行表示一个单元，第1 行是单元的第1 个结点号，第2 行是单元的第2个结点号。

Returnfunction k=StiffnessMatrix(ie)%计算单元刚度矩阵函数global gNode gElementk=zeros(6,6); %6x6单元刚阵E=*10^11; %材料特性u= ; %材料特性t=; %材料特性xi=gNode(gElement(ie,1),1);yi=gNode(gElement(ie,1),2);xj=gNode(gElement(ie,2),1);yj=gNode(gElement(ie,2),2);xm=gNode(gElement(ie,3),1);ym=gNode(gElement(ie,3),2); %计算节点坐标分量ai=xj*ym-xm*yj;aj=xm*yi-xi*ym;am=xi*yj-xj*yi;bi=yj-ym;bj=ym-yi;bm=yi-yj;ci=-(xj-xm);cj=-(xm-xi);cm=-(xi-xj);d=[1,xi,yi;1,xj,yj;1,xm,ym];area=det(d); %计算单元面积B=[bi 0 bj 0 bm 0 ;0 ci 0 cj 0 cm;ci bi cj bj cm bm];B=B/2/area;D=[1 u 0;u 1 0;0 0 (1-u)/2];D=D*E/(1-u^2);k=transpose(B)*D*B*t*abs(area); %计算单元刚度矩阵Returnfunction gK=AssembleStiffnessMatrix% 计算总刚阵global gElement gK iegK=zeros(12,12);for ie =1:1:4 %单元循环k=StiffnessMatrix(ie);for i=1:1:3 %节点循环for j=1:1:3 %节点循环for p=1:1:2 %自由度循环for q=1:1:2 %自由度循环m=(i-1)*2+p; %每个节点有2个自由度，i节点的第p个自由度为（i-1)*2+pn=(j-1)*2+q; %每个节点有2个自由度，i节点的第p个自由度为（i-1)*2+pM=(gElement(ie,i)-1)*2+p;N=(gElement(ie,j)-1)*2+q;gK(M,N)=gK(M,N)+k(m,n);endendendendendReturn则单元1的刚度矩阵为>> StiffnessMatrix(1)ans =+010 *0 00 00 0单元2的刚度矩阵>> StiffnessMatrix(2)ans =+010 *0 0 0 0 0 0 0 0单元3的刚度矩阵为>> StiffnessMatrix(3)ans =+010 *0 00 0 0 0单元4的刚度矩阵>> StiffnessMatrix(4)ans =+010 *0 0 0 0 0 0 0 0总刚度矩阵为ans =+011 *Columns 1 through 80 0 0 00 0 0 00 00 00 0 00 0 00 0 0 00 0 0 00 0 00 0 00 0 0 0 0 0 0 0 0 0Columns 9 through 120 00 00 0 00 0 00 0 0 0 0 02-3 在平面问题有限元分析中，（1）用到了哪些弹性力学中的基本方程答：平衡微分方程、几何方程、相容方程（形变协调方程）。

（2）力的平衡条件是如何满足的答：根据能量守恒原理，有外力所作虚功应该等于内力虚功。

也就是结构在外载荷作用下处于平衡状态则在结构上的力在任意虚功位移上所作的虚功之和等于零。

以下是用到的方程：000=+∂∂+∂∂+∂∂=+∂∂+∂∂+∂∂=+∂∂+∂∂+∂∂Z zy x Y zy x X z y x zzy zx yz y yx xzxy x στττστττσ z u x w z w y wz v y v x v y u x u zx z yz y xy x ∂∂+∂∂=∂∂=∂∂+∂∂=∂∂=∂∂+∂∂=∂∂=γεγεγε,,, （3）变形协调条件是如何满足的答：对材料进行线弹性和各向同性的假设，用弹性力学中应力-应变之间的关系得到变形协调条件。

下面是形变协调方程。

y x z y x z x z x x x z y x z y z y y z z y x z y x y x xy zxy zx yz zx y z y zx yz xy yz z y xyz xy zx xy y x ∂∂∂=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂∂∂∂∂∂=∂∂+∂∂∂∂∂=⎪⎪⎭⎫⎝⎛∂∂+∂∂+∂∂∂∂∂∂∂=∂∂+∂∂∂∂∂=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂∂∂∂∂∂=∂∂+∂∂εγγγγεεεγγγγεεεγγγγεε2222222222222222222,2,2,2-4 在平面三角形单元中的位移、应变、应力具有什么特征位移特征：(1)必须包含单元的刚体位移；(2)必须包含单元的常应变状态；(3)必须保证不偏惠各坐标轴；(4)必须保证单元内位移连续。

应力特征：(1)三角形单元其应力仅与单元材料和几何尺寸有关，与节点位移有关，而与单元内位置坐标无关，也即这类单元内的应力是常量。

(2)三角形单元内应力连续，但在公共边界上应力有突变，密布网格可以减少这种冲突的不合理性。

应变特征：由于简单三角形单元取线性位移模式，其应变矩阵为常数矩阵，即在这样的位移模式下，三角形单元内的应变为某一常量。

2-5 在平面三角形单元中，当尺寸逐步缩小，单元中的位移、应变、应力具有什么特征当单元尺寸逐步减小时，单元各点的应变趋于相等，这时常量应变成为主要成分，因此，位移应能反应这种常应变状态，由于应力矩阵也是常数矩阵，单元应力也是常量。

但是相邻单元一般具有不同的力，在单元的公共边上会有应力突变，随着单元尺寸的逐步减小，这种突变会急剧降低，从而不会妨碍有线单元法的简答收敛于精确解。