方程思想及其应用
方程思想在小学数学教学中的应用
方程思想在小学数学教学中的应用一、引导学生树立符号思维在小学数学教学中渗透方程思想的第一步是引导学生树立符号思维，即要求学生明确数学符号的意义和应用情况。
这不仅是小学数学教材知识点编排要求，更是符合学生思维发展过程的教学方式。
利用数学符号表示未知数，对小学生来说是一个全新的内容且具有一定的抽象性，所以小学数学教师一方面要用贴近生活、直观性强的例子帮助学生理解数学符号的意义和树立符号思维；另一方面要关注数学教学的趣味性，防止学生因为觉得教学内容枯燥乏味、不好理解而发生走神、开小差的情况。
首先，小学数学教师可以通过列举贴近现实生活的例子，帮助学生理解符号的意义，例如，教师可以利用幻灯片为学生呈现红十字符号、麦当劳黄“M”符号等，并要求学生说出符号代表的意义，以此让学生理解符号的作用就是代指某些事物，在数学世界中，人们常用英文字母来代指某些量或非确定性数值。
其次，教师可以利用学过的旧知识帮助学生进一步理解数学符号的意义，例如，教师利用正方形、长方形和三角形的面积计算公式，帮助学生理解用数学符号代指非确定性数值。
在此过程中，教师可以提供加法交换律公式帮助学生理解：利用英文字母表示非确定性数值是惯例，但理论上任意图形、字母都可以用于指代非确定数值，且没有硬性规定某一个字母只能用来固定表示某一个量，此举是为了防止学生在做题时出现混淆。
最后，教师还可以通过游戏帮助学生了解符号能用来表示未知数的作用，例如，教师以填空题为例，将填空题“若一个长方形的长为3cm，宽为2cm，则该长方形的面积为cm”中的横线改为字母x，则填空题变成了“若一个长方形的长为3cm，宽为2cm，则该长方形的面积为xcm”，以此让学生体会字符在表示未知数上的作用。
二、帮助学生掌握利用符号表述数学规律的能力具备利用符号表述数学规律的能力是学生能根据题干内容写出对应方程的前提，所以小学数学教师要通过充足的训练帮助学生学会并有效巩固这一能力。
为了提升学生的学习兴趣和帮助学生掌握利用符号表述数学规律的能力，小学数学教师可以利用“数青蛙”这一传统游戏并创新游戏方式，帮助学生在游戏中不知不觉掌握利用符号表述数学规律的能力。
方程思想思维方式在教学实践中的探索与应用
方程思想思维方式在教学实践中的探索与应用方程思想是数学中的重要思维方式，通过把问题转化为方程的形式，用方程来描述和解决问题。
在教学实践中，探索和应用方程思想具有重要意义。
方程思想能够培养学生的抽象思维能力。
在解决实际问题时，往往需要将问题抽象成数学模型，然后用方程来描述。
这样的思维过程要求学生能够在具体问题中抓住其中的关键要素，并能够把问题抽象成一般性的表达式。
通过反复练习和应用，学生的抽象思维能力得到了锻炼和提升。
方程思想培养了学生的逻辑思维能力。
在解决方程问题时，需要进行推理和演绎，从已知条件出发，通过逻辑推理找到未知数的值。
这要求学生具备良好的逻辑思维能力，能够进行合理的推理和推断。
通过方程思想培养的逻辑思维能力，可以使学生在其他学科和实际生活中也能够运用较高水平的逻辑思维解决问题。
方程思想还有助于提高学生的解决问题的能力。
在现实生活中，很多问题都可以转化为方程问题，而方程问题又可以通过方程思想来解决。
通过练习和应用方程思想，学生可以掌握解决问题的方法和技巧，能够迅速准确地找到问题的解决办法。
这有助于培养学生独立思考和解决问题的能力，提高他们的综合素质。
方程思想还培养了学生的数学建模能力。
数学建模是将实际问题抽象为数学模型，然后用数学方法进行分析和求解的过程。
方程是数学建模的重要工具，通过运用方程思想，学生可以将实际问题转化为数学模型，然后用方程解决问题。
通过方程思想的应用，学生不仅能够解决具体的问题，还可以培养他们的数学建模能力，使其对实际问题的分析和解决具备了一定的能力。
方程思想思维方式在教学实践中的探索和应用具有重要意义。
它不仅能够培养学生的抽象思维能力、逻辑思维能力和解决问题的能力，还有助于提高学生的数学建模能力。
教师在教学中应重视方程思想的培养和应用，通过激发学生的兴趣和动手实践，使他们能够灵活运用方程思想解决实际问题。
方程思想思维方式在教学实践中的探索与应用
方程思想思维方式在教学实践中的探索与应用“方程思想”是一种解决问题的思维方式，它通过建立和解决方程来分析和解决各种实际问题。
在教学实践中，方程思想能够培养学生的逻辑思维、数学运算和问题解决能力，提高他们的综合素质和学习能力。
下面将结合实际教学实践，探讨方程思想在教学中的应用。
方程思想可以帮助学生理解和运用数学知识。
数学是一门抽象的学科，很多学生在学习过程中难以理解其中的概念和运算规则。
通过方程思想，将问题转化为代数方程式，让学生从具体的实例中提取问题的本质，并通过数学符号和变量的运算，解决与问题相关的数学运算。
在解决关于线性方程组的问题时，学生常常难以理解其中的平行和相交等概念。
通过引入平面坐标系和方程思想，将问题转化为线性方程组，并通过解方程组来求解问题，可以帮助学生更好地理解和运用线性方程组的概念和解法。
在解决关于速度的问题时，学生需要将速度、时间和距离之间的关系建立为一个方程，并通过方程推导出未知量。
这个过程需要学生分析问题的条件和要求，确定未知量，并运用数学知识进行推导和计算。
这样的思维方式可以培养学生的逻辑思维和问题解决能力，使他们能够独立思考和解决各种问题。
方程思想可以帮助学生理解实际问题和建立数学模型。
实际问题往往是复杂的，通过方程思想，可以将问题简化为数学模型，从而更好地理解和分析问题。
在解决关于比例问题时，学生常常难以理解比例和比例关系的概念。
通过方程思想，我们可以将比例问题建立为一个等比例方程，通过解方程求解比例关系。
这样的思维方式可以帮助学生理解比例问题的本质，建立数学模型，并通过数学运算解决问题。
运用方程思想解决几何问题“六法”_
１
６
所以２
S△ABC ＝３．
x２ －１
２
x＋１
５＝０,解 得 x１ ＝３－ ,
２
２
x２ ＝３＋
３＋
６
６
(舍去),此时Байду номын сангаас 求 出 AF ＝６－ ３－
＝
２
２
(
)
６
所 以 存 在 直 线 EF 将 Rt△ABC 的 周 长 与
＜５．
２
解法探究
２０２４ 年 １ 月下半月
面积同时平分,且 AE 的长为３－
解 x１ ＝ ３,
又 ３＋x１ ＝３＋ ３＞４,所
x２ ＝－ ３(舍去)．
６
．
２
１
(ⅱ )若点 F 与 B 重合,如图 ９,由 S△AEB ＝ S△ABC
２
可知 E 为 AC 的 中 点,由 于 BC ＜AB ,故 BC ＋CE ＜
AE ＋AB ,所以不存在满足题设要求的直线 EF ．
分线,
已知 BD ＝２
０,
EF＝１
５,求
EF 平 分 Rt△ABC 的 周 长,设
解:设矩 形 的 长 AB ＝x,
图５
宽 BC ＝y．在 Rt△BAD 中,
BD２ ＝ AD２ ＋ AB２ ,即
２
因为 EF 是 BD 的垂直平分线,则有 BO＝
x２ ＋y２ ＝２
０．
所以 △OFD≌△OEB．
所以 OE＝OF＝７．
°,所 以 可 得
７１
解法探究
２０２４ 年 １ 月下半月
△BED ∽△BCA ．
DE BD
k
９＋k
第一讲：方程思想在三角形和四边形中的应用
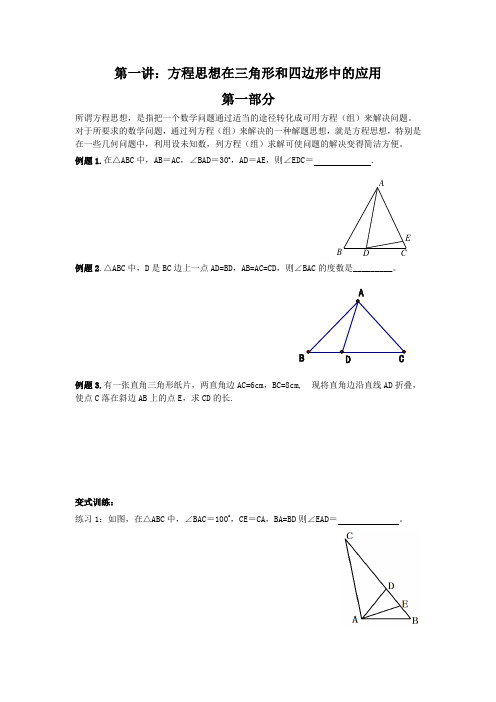
第一讲：方程思想在三角形和四边形中的应用第一部分所谓方程思想，是指把一个数学问题通过适当的途径转化成可用方程（组）来解决问题。
对于所要求的数学问题，通过列方程（组）来解决的一种解题思想，就是方程思想，特别是在一些几何问题中，利用设未知数，列方程（组）求解可使问题的解决变得简洁方便。
例题1.在△ABC 中，AB ＝AC ，∠BAD ＝30o ，AD ＝AE ，则∠EDC ＝ ． ED C BA例题2.△ABC 中，D 是BC 边上一点AD=BD ，AB=AC=CD ，则∠BAC 的度数是_________。
B D C A例题3.有一张直角三角形纸片，两直角边AC=6cm ，BC=8cm, 现将直角边沿直线AD 折叠，使点C 落在斜边AB 上的点E ，求CD 的长.变式训练：练习1：如图，在△ABC 中，∠BAC ＝100o ，CE ＝CA，BA=BD 则∠EAD ＝ 。
2：如图P,Q是⊿ABC的边上的两点,且BP=PQ=QC=AP=AQ,则∠BAC的大小等于_________度.3：如图，∆A B C中，A=，求∠E D C的度数。
=∠=︒D，40且A E A DBAC BA4：如图，△ABC中，AB=AC,BC=BD,AD=DE=EB,求∠A的度数。
5：如图，CA=CB,DF=DB,AE=AD,求∠A的度数。
6：△ABC中，AB=BC，M、N分别BC边上两点，且∠BAM=∠CAN，MN=AN,求∠MAC的度数。
7：如图，在△ABC中，∠ABC=∠BAC，∠BAC的外角线交BC的延长线于点D若∠ADC=1/2∠CAD，求∠ABC的度数．8：如图，在△ABC中，∠B＜∠C＜∠A，∠BAC和∠ABC的外角平分线AE、BD分别与BC、CA 的延长线交于E、D．若∠ABC=∠AEB，∠D=∠BAD．求∠BAC的度数．9：在Rt△ABC中，∠C=90°, AC=1，BC=3. AB的中垂线DE交BC于点D, 连结AD，求AD 的长.10：如左图所示，有一张直角三角形纸片，两直角边AC=5cm，BC=10cm，将△ABC折叠，使点B与点A重合，折痕为DE，求CD的长。
方程思想及应用
方程思想及应用————————————————————————————————作者：————————————————————————————————日期：目录摘要 (2)Abstract (3)引言 (3)1.方程思想的涵义 (4)1.1方程................................................................... 错误!未定义书签。
1.2方程思想 (5)1.3方程思想的步骤 (5)1.4方程思想的两个重要方面 (5)1.5方程思想是一种源于解决应用问题的思想 (6)2.方程思想的应用 (6)2.1方程思想数学学科中的应用 (9)2.2方程思想在物理学科中的应用 (9)2.3方程思想在配平化学方程式中的应用 (12)3.方程思想的学习和教学 (13)3.1方程思想的学习 (14)3.2方程思想的教学 (14)参考文献 (17)方程思想的应用与教学摘要:方程思想是一种重要的数学思想，是指在分析问题的数量关系时，将问题中的已知量和未知量之间的数量关系通过适当设元建立起方程(组)，然后通过解方程(组)使问题得到解决的思维方式。
重点就是化未知为已知的思想，关键是利用已知条件或公式、定理中的已知结论构造方程(组)。
它在多门学科中都有广泛的应用，因此我们要让学生逐步掌握这种数学思想方法，就必须在数学教学中逐步进行有目的的引导和培养。
关键词：方程思想；应用；教学The Equation of the Application of the Thought and teachingAbstract：Equation thinking is a kind of important mathematical ideas, which means in its analysis of the question of the quantitative relationships, the issue of the known and unknown quantities of the quantitative relationships between the amount established by the appropriate setting element equation or equation group, and then solve the equation (group) so that the problems can be resolved by such a way of thinking. Focus on the translation of the unknown to the known, and the key is to use a known conditions or formula, theorem, known conclusions structure equations (group). It has a wide range of applications in several disciplines, and therefore we want to have the students gradually master this mathematical thinking, it must be in Math Teaching, step-by-step with the aim of the boot and training.Key Words: Equation thinking; Adhibition; Teaching引言数学家笛卡尔曾设想一个解决所有问题的通用方法：第一步：将任何问题转化为数学问题；第二步：将任何数学问题转化为代数问题；第三步：将任何代数问题化归为单个方程的求解；第四步：讨论方程（组）的问题，得到解之后再对解解释。
高中数学基本数学思想：函数与方程思想在数列中的应用
高中数学基本数学思想：函数与方程思想在数列中的应用函数思想和方程思想是学习数列的两大精髓.“从基本量出发，知三求二.”这是方程思想的体现.而“将数列看成一种特殊的函数，等差、等比数列的通项公式和前n项和公式都是关于n的函数.”则蕴含了数列中的函数思想.借助有关函数、方程的性质来解决数列问题，常能起到化难为易的功效。
以下是小编给大家带来的方程思想在数列上的应用，仅供考生阅读。
函数与方程思想在数列中的应用(含具体案例)本文列举几例分类剖析：一、方程思想1.知三求二等差(或等比)数列{an}的通项公式，前n项和公式集中了等差(或等比)数列的五个基本元素a1、d(或q)、n、an、Sn.“知三求二”是等差(或等比)数列最基本的题型，通过解方程的方法达到解决问题的目的.例1等差数列{an}的前n项和为Sn，已知a10=30，a20=50，(1)求数列{an}的通项公式;(2)若Sn=242，求n的值.解(1)由a10=a1+9d=30，a20=a1+19d=50，解得a1=12，因为n∈N*，所以n=11.2.转化为基本量在等差(等比)数列中，如果求得a1和d(q)，那么其它的量立即可得.例2在等比数列{an}中，已知a6―a4=24，a3a5=64，求{an}的前8项的和S8.解a6―a4=a1q3(q2―1)=24.(1)由a3a5=(a1q3)2=64，得a1q3=±8.将a1q3=―8代入(1)，得q2=―2(舍去);将a1q3=8代入(1)，得q=±2.当q=2时，a1=1，S8=255;当q=―2时，a1=―1，S8=85.3.加减消元法利用Sn求an利用Sn求an是求通项公式的一种重要方法，其实这种方法就是方程思想中加减消元法的运用.例3(2011年佛山二模)已知数列{an}、{bn}中，对任何正整数n都有：a1b1+a2b2+a3b3+…+an―1bn―1+anbn=(n―1)?2n+1.若数列{bn}是首项为1、公比为2的等比数列，求数列{an}的通项公式.解将等式左边看成Sn，令Sn=a1b1+a2b2+a3b3+…+an―1bn―1+anbn.依题意Sn=(n―1)?2n+1，(1)又构造Sn―1=a1b1+a2b2+a3b3+…+an―1bn―1=(n―2)?2n―1+1，(2)两式相减可得Sn―Sn―1=an?bn=n?2n―1(n≥2).又因为数列{bn}的通项公式为bn=2n―1，所以an=n (n≥2).当n=1，由题设式子可得a1=1，符合an=n.从而对一切n∈N*，都有an=n.所以数列{an}的通项公式是an=n.4.等差、等比的综合问题这一类的综合问题往往还是回归到数列的基本量去建立方程组.例4设{an}是公比大于1的等比数列，Sn为数列{an}的前n项和.已知S3=7，且a1+3，3a2，a3+4构成等差数列，求数列{an}的通项公式.解根据求和定义和等差中项建立关于a1，a2，a3的方程组.由已知得a1+a2+a3=7，(a1+3)+(a3+4)2=3a2.解得a2=2.设数列{an}的公比为q，由a2=2，可得a1=2q，a3=2q.又S3=7，可知2q+2+2q=7，即2q2―5q+2=0，解得q1=2，q2=12.由题意得q>1，所以q=2.可得a1=1，从而数列{an}的通项为an=2n―1.二、函数思想数列是一类定义在正整数或它的有限子集上的特殊函数.可见，任何数列问题都蕴含着函数的本质及意义，具有函数的一些固有特征.如一次、二次函数的性质、函数的单调性、周期性等在数列中有广泛的应用.如等差数列{an}的通项公式an=a1+(n―1)d=dn+(a1―d)，前n项和的公式Sn=na1+n(n―1)2d=d2n2+(a1―d2)n，当d≠0时，可以看作自变量n的一次和二次函数.因此我们在解决数列问题时，应充分利用函数有关知识，以它的概念、图象、性质为纽带，架起函数与数列间的桥梁，揭示了它们间的内在联系，从而有效地分解数列问题.1.运用函数解析式解数列问题在等差数列中，Sn是关于n的二次函数，故可用研究二次函数的方法进行解题.例5等差数列{an}的前n项的和为Sn，且S10=100，S100=10，求S110，并求出当n为何值时Sn有最大值.分析显然公差d≠0，所以Sn是n的二次函数且无常数项.解设Sn=an2+bn(a≠0)，则a×102+b×10=100，a×1002+b×100=10.解得a=―11100，b=11110.所以Sn=―11100n2+11110n.从而S110=―11100×1102+11110×110=―110.函数Sn=―11100n2+11110n的对称轴为n=111102×11100=55211=50211.因为n∈N*，所以n=50时Sn有最大值.2.利用函数单调性解数列问题通过构造函数，求导判断函数的单调性，从而证明数列的单调性.例6已知数列{an}中an=ln(1+n)n (n≥2)，求证an>an+1.解设f(x)=ln(1+x)x(x≥2)，则f ′(x)=x1+x―ln(1+x)x2. 因为x≥2，所以x1+x<1，ln(1+x)>1，所以f ′(x)<0.即f(x)在[2，+∞)上是单调减函数.故当n≥2时，an>an+1.例7已知数列{an}是公差为1的等差数列，bn=1+anan.(1)若a1=―52，求数列{bn}中的最大项和最小项的值;(2)若对任意的n∈N*，都有bn≤b8成立，求a1的取值范围.(1)分析最大、最小是函数的一个特征，一般可以从研究函数的单调性入手，用来研究函数最大值或最小值的方法同样适用于研究数列的最大项或最小项.解由题设易得an=n―72，所以bn=2n―52n―7.由bn=2n―52n―7=1+22n―7，可考察函数f(x)=1+22x―7的单调性.当x<72时，f(x)为减函数，且f(x)<1;当x>72时，f(x)为减函数，且f(x)>1.所以数列{bn}的最大项为b4=3，最小项为b3=―1.(2)分析由于对任意的n∈N*，都有bn≤b8成立，本题实际上就是求数列{bn}中的最大项.由于bn=1+1n―1+a1，故可以考察函数f(x)=1+1x―1+a1的形态.解由题，得an=n―1+a1，所以bn=1+1n―1+a1.考察函数f(x)=1+1x―1+a1，当x<1―a1时，f(x)为减函数，且f(x)<1;当x>1―a1时，f(x)为减函数，且f(x)>1.所以要使b8是最大项，当且仅当7<1―a1<8，所以a1的取值范围是―73.利用函数周期性解数列问题例8数列{an}中a1=a2=1，a3=2，anan+1an+2an+3=an+an+1+an+2+an+3且anan+1an+2≠1成立.试求S100=a1+a2+…+a100的值.分析从递推式不易直接求通项，观察前几项a1=1，a2=1，a3=2，a4=4，a5=1，a6=1，a7=2，a8=4，a9=1，…可猜测该数列是以4为周期的周期数列.解由已知两式相减得通过上述实例的分析与说明，我们可以发现，在数列的教学中，应重视方程函数思想的渗透，应该把函数概念、图象、性质有机地融入到数列中，通过数列与函数知识的相互交汇，使学生的知识网络得以不断优化与完善，同时也使学生的思维能力得以不断发展与提高.高中数学思想方法介绍，高中数学解题思想方法与讲解数学思想，是指现实世界的空间形式和数量关系反映到人们的意识之中，经过思维活动而产生的结果。
方程思想的解题中的应用
方程思想的解题中的应用数学思想是数学的灵魂，任何数学问题的解决都是数学思想作用的结果，因此正确理解和掌握数学思想是数学学习的关键。
今天所说的方程思想就是一种十分重要的数学思想。
方程模型是研究现实世界数量关系的最基本的数学模型，它可以使人们从数量关系的角度来认识事物。
下面笔者就从以下几个角度阐述方程思想在解题中的运用。
一、通过构造方程，解决与定义、性质、规律相关的问题数学中的很多定义、性质、规律等理论性知识本身就直接或间接地体现着方程关系，如，单项式与同类二次根式的定义、各种类型的方程的定义、非负数的性质、平方根的特点等等。
若遇到此类问题，可以运用其所隐含的数学关系，通过建立方程加以解决。
二、通过几何定理体现的数量关系，将与几何图形相关的问题转化为方程问题解决几何中的许多定理都反映了图形数量上的相等关系，例如勾股定理、相交弦定理、切割线定理等等。
在很多情况下，若能根据这些定理反映数量关系，合理设出未知数并建立方程，可以使复杂几何问题的解答变得相对简单。
三、通过寻找等量关系，用方程思想解决实际问题例，《中华人民共和国道路交通安全法实施条例》中规定：超速行驶属违法行为。
为确保行车安全，一段高速公路全程限速110千米/时（即任一时刻的车速都不能超过110千米/时）。
以下是张师傅和李师傅行驶完这段全程为400千米的高速公路时的对话片断。
张：“你的车速太快了，平均每小时比我多跑20千米，少用我1小时就跑完了全程，还是慢点。
”李：“虽然我的时速快，但最大时速也不超过我平均时速的10%，可没有超速违法啊。
”李师傅超速违法吗？为什么？分析：此题是一道判断说理题，解题的关键是求出李师傅的平均速度，而实际上在张师傅和李师傅的对话中隐藏着一个等量关系，即李师傅所用的时间-张师傅所用的时间=1小时。
于是可设出未知数，列方程解决。
说明：运用方程思想解答应用题的关键是寻找等量关系，在实际问题中等量关系是多样化的，需要我们认真审题，打开思路，深入挖掘。
方程思想在解题教学中应用案例
方程思想在解题教学中应用的案例方程思想是指将所研究的教学问题的已知量与未知量之间的数量关系转化为方程(组),从而使得问题解决。
方程思想应用非常广泛,而许多同学在学习中往往见到了方程才想到用方程的思想来解决,事实上,许多题目表面上看是非方程的问题,有的甚至是几何问题,但运用方程的思想来求解,也可以使问题迎刃而解。
下面笔者结合多年的教学经验谈一点粗浅看法。
一、方程思想在代数中的应用案例1.已知:当x=2时,代数式x2+3ax的值为2008,当x=-1,求(a2x2+334)/a-1674x代数式的值.分析:本案例通过条件建立方程模型求出a,即可解决。
解:因为当x=2时,所以22+3a×2=2008 即a=334.∴原式=(3342×12+334)/334-1674×(-1)=2009.案例2.若■和■是同类根式,求(a+b)ab的值.分析:已知条件中,没有方程,由同类根式的定义构造出关于a、b 的方程组,求出方程组的解便是问题解决。
解:由同类根式的定义得a+b=23a+b=4b解得a=1,b=1∴(a+b)ab=2评注:在求代数式的值时,要审清题意,构建方程(组)模型,如案例1构建方程模型,案例2构建方程组模型。
因此在分析题意时,应引导学生层层分析,逐步寻求关系,从而发现解题思路。
二、方程思想在函数中的应用案例3.已知抛物线y=x2+(1-2a)x+a2(a≠0)与x轴交于两点a(x1,0)、b(x2,0)(x1≠x2).(1)求a的取值范围,并证明a、b两点都在原点0的左侧;(2)若抛物线与y轴交于点c,且oa+ob=oc-2,求a的值.分析:(1)二次函数图象与x轴有两个不同的交点时,根的判别式大于0,从而可确定a的取值范围,对(2)运用方程思想来求a的值. 解:(1)∵抛物线与x轴交于两点a(x1,0)、b(x2,0)且(x1≠x2) ∴?驻=(1-2a)2-4a2>0,∴a0,即x1,x2必为同号.而x1+x2=-(1-2a)=2a-1<1/2-1=-1/2<0∴x1,x2必为负数.∴点a(x1,0)、b(x2,0)都在原点o的左侧.(2)∵x1,x2同为负数,∴由oa+ob=oc-2得-x1-x2=a2-2∴a2+2a-3=0∴a1=-3,a2=1∵a<1/4且a≠0∴a的值为-3.评注:本案例综合了二次函数、韦达定理、一元二次方程根的判别式等相关知识,解题时应抓住二次函数与一元二次方程之间的关系。
方程思想在初中数学中应用
课 改 前 沿都市家教 156笛卡尔的方程思想是：实际问题→数学问题→代数问题→方程问题。
我们知道，哪里有等式，哪里就有方程；哪里有公式，哪里就有方程；求值问题是通过解方程来实现的；不等式问题也与方程密切相关的。
方程思想，是从问题的数量关系入手，运用数学语言将问题中的条件转化为数学模型（方程、不等式、或方程与不等式的混合组），将问题中的已知量和未知量之间的数量关系通过适当设元建立起方程(组)，然后通过解方程（组）或不等式（组）来使问题获解的思维方式。
有时，还实现函数与方程的互相转化。
这种思想在代数、几何中有着广泛的应用。
一、方程思想在代数中的应用1.方程思想与整式的结合【典例分析】若最简根式343b a b −+23226ab b b −+a,b.分析：利用同类二次根式的定义可以得到根指数相等和被开方数相等的信息。
从而列出一个关于a 、b 的二元一次方程组解得a 、b 。
2.方程思想与勾股定理的结合【典例分析】小宇手里有一张直角三角形纸片ABC ，他无意中将直角边AC 折叠了一下，恰好使AC 落在斜边AB 上，且C 点与E 点重合,（如图）小宇经过测量得知两直角边AC =6cm,BC =8cm,他想用所学知识求出CD 的长，你能帮他吗？B 分析：此题以△BED 为直角三角形作为隐含条件，先由勾股定理求得AB=10cm，设CD=x cm，则DE=x cm，在Rt △BED 中，借助勾股定理建立方程。
∵BD=(8-x )cm，BE=4cm，∴，解得x =3，即CD=3cm。
3.方程思想与函数的结合方程与函数本身就有必然的联系，函数本身就可以看成一个方程，因此方程与函数有着相同的思路和解题方法，都是通过建立相等关系，求出未知数的值，因此函数问题的关键就是找出相等关系，建立变量之间的等量关系求解，要求对变量所涉及的相关知识要比较熟练，这是轻松求解函数问题的必要基础。
【典例分析】如图，A、B 分别是x 轴上位于原点左右两侧的点，点P（2，p）在第一象限，直线PA 交y 轴于点C（0,2），直线PB 交y 轴于点D，△AOP 的面积为6；求△COP 的面积；求点A 的坐标及p 的值；△BOP 与△DOP 的面积相等，求直线BD 的函数解析式。
方程思想思维方式在教学实践中的探索与应用
方程思想思维方式在教学实践中的探索与应用1. 引言1.1 引言内容方程思想是数学中重要的概念之一，它代表了一种对问题进行分析和解决的思维方式。
在教育教学实践中，方程思想的运用具有非常重要的意义，可以帮助学生更好地理解数学知识，提高解决问题的能力，培养逻辑思维和创新能力，提高学生的学习成绩和综合素质。
通过对方程思维在教学中的重要性的探讨，可以更深入地了解其在教学实践中的作用和意义。
方程思维在教学实践中的具体应用是指将方程思想融入教学内容和教学方法中，通过实际的案例分析和教学实践，让学生在解决问题过程中通过构建方程式进行思考和分析，从而提高解决问题的能力。
在教学实践中，方程思维也会遇到各种挑战，如学生对数学知识的理解不到位，解题思路不清晰等。
针对这些挑战，我们需要采取有效的解决方法，如设置巩固性练习，引导学生建立正确的解题思维，提高学生的问题解决能力。
通过对方程思维在教学实践中的探索与应用进行案例分析，可以更具体地了解其实际效果和意义，为进一步推广方程思维的教学方式提供参考。
未来，我们可以将方程思维进一步融入数学教学中，探索更多创新的教学方法和手段，为学生提供更好的数学学习体验，促进学生全面发展。
【引言内容】2. 正文2.1 方程思想在教学中的重要性方程思想在教学中扮演着重要的角色，它不仅是数学学科的基础，更是培养学生逻辑思维能力和问题解决能力的利器。
通过学习方程思想，学生可以掌握抽象化和符号化的思维方式，能够将问题进行数学建模，并通过代数运算找到问题的解。
这种思维方式有助于培养学生的逻辑思维能力，锻炼学生的解决问题的能力，同时也能帮助学生理解抽象的数学概念，提高数学学科的学习质量。
方程思想在教学中还有助于激发学生的学习兴趣和提高学习动力。
通过解决实际问题的过程中，学生能够体会到数学知识的实用性和重要性，从而增加对数学学科的兴趣。
方程思维也有助于培养学生的自主学习能力和团队合作精神，通过合作解决复杂的方程问题，学生们能够相互学习、探讨，共同进步。
方程思想及应用
目录摘要 (2)Abstract (3)引言 (3)1.方程思想的涵义 (4)1.1方程.............................................................................. 错误！未定义书签。
1.2方程思想 (5)1.3方程思想的步骤 (5)1.4方程思想的两个重要方面 (5)1.5方程思想是一种源于解决应用问题的思想 (6)2.方程思想的应用 (6)2.1方程思想数学学科中的应用 (9)2.2方程思想在物理学科中的应用 (9)2.3方程思想在配平化学方程式中的应用 (12)3.方程思想的学习和教学 (13)3.1方程思想的学习 (13)3.2方程思想的教学 (14)参考文献 (17)方程思想的应用与教学摘要:方程思想是一种重要的数学思想，是指在分析问题的数量关系时，将问题中的已知量和未知量之间的数量关系通过适当设元建立起方程(组)，然后通过解方程(组)使问题得到解决的思维方式。
重点就是化未知为已知的思想，关键是利用已知条件或公式、定理中的已知结论构造方程(组)。
它在多门学科中都有广泛的应用，因此我们要让学生逐步掌握这种数学思想方法，就必须在数学教学中逐步进行有目的的引导和培养。
关键词：方程思想；应用；教学The Equation of the Application of the Thought and teachingAbstract：Equation thinking is a kind of important mathematical ideas, which means in its analysis of the question of the quantitative relationships, the issue of the known and unknown quantities of the quantitative relationships between the amount established by the appropriate setting element equation or equation group, and then solve the equation (group) so that the problems can be resolved by such a way of thinking. Focus on the translation of the unknown to the known, and the key is to use a known conditions or formula, theorem, known conclusions structure equations (group). It has a wide range of applications in several disciplines, and therefore we want to have the students gradually master this mathematical thinking, it must be in Math Teaching, step-by-step with the aim of the boot and training.Key Words: Equation thinking; Adhibition; Teaching引言数学家笛卡尔曾设想一个解决所有问题的通用方法：第一步：将任何问题转化为数学问题；第二步：将任何数学问题转化为代数问题；第三步：将任何代数问题化归为单个方程的求解；第四步：讨论方程（组）的问题，得到解之后再对解解释。
方程思想在初中数学教学中的应用
方程思想在初中数学教学中的应用摘要：在数学教学中，教师不仅仅要教授学生做对题目，更重要的是要教会学生数学思想方法。
方程是初中数学教学中的重要内容，教师在教学中要立足教材挖掘内容，启发学生对思想方法的转化，通过问题让学生体验思想，在实践中巩固所学的知识，以此将函数与方程思想渗透于数学教学中，提高学生的解题能力以及学习效率。
关键词：方程思想数学教学应用研究一、方程思想的应用意义方程思想是指从问题中的未知量入手，探求未知量和已知量之间的数量关系，运用数学语言，将问题中的条件转化为数学模型，适当设元建立相应个数的方程（组），实现问题与方程的相互联系，进而达到解决问题的目的。
教师在教学中要有意识地渗透方程思想，让学生学会初步应用。
方程思想既是解决现实生活中数量关系和变化规律的重要思维方式，也是初中数学教学的核心内容之一。
但有些教师在教学中却采取“知识点—典型题—解题方法”的教学模式，反复操练各种题型，这种题海战术式的解题训练有时虽然可以提高形式推导的能力，但容易束缚学生思维。
新课程理念下的数学教学强调要重视数学思想方法的渗透，构建良好认知结构，培养和发展学生的数学思维能力。
方程思想是学生学习数学知识和解决数学问题的一种重要思想，在初中数学教学中，不断提升学生的函数与方程思想，对于培养学生数学知识学习能力与解决问题的能力具有积极的意义。
因此，要有目的、有意识地将函数与方程思想渗透到课堂教学中，提升学生运用函数与方程思想解决问题的能力，让函数与方程思想贯穿于学生整个数学学习过程中，以指导学生更好地学习数学。
二、方程思想在初中数学教学中的应用1.立足教材，挖掘函数与方程思想的教学内容当前的初中数学课程内容中，函数与方程则占据了很大部分，是整个初中数学教学中的核心与重点。
因此，教师要想将函数与方程思想有效地渗透到初中数学教学中，首先就需要从初中数学教材出发，认真研读教材，挖掘函数与方程相关的内容，并在这些内容的教学中向学生渗透。
专题 方程思想在勾股定理中的应用(四大题型)(解析版)
（苏科版）八年级上册数学《第3章 勾股定理》专题 方程思想在勾股定理中的应用【例题1】（2022春•赣州月考）在Rt △ABC 中，∠C ＝90°，∠A 、∠B 、∠C 所对的边分别为a 、b 、c ，已知a ：b ＝5：12，c ＝26，则△ABC 的面积为（ ）A ．96B ．98C ．108D ．120【分析】根据勾股定理和三角形的面积求解即可．【解答】解：∵c＝26，a：b＝5：12，∴设a＝5x，则b＝12x，∵a2+b2＝c2，即（5x）2+（12x）2＝262，解得x＝2，∴a＝10，b＝24．∴12ab=12×10×24=120，故选：D．【点评】本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．【变式1-1】在Rt△ABC中，∠C＝90°，已知a：b＝3：4，c＝10，其中a，b，c分别为∠A，∠B，∠C的对边，则a的长为（ ）A．3B．6C．8D．12【分析】由a与b的比值，设a＝3k，b＝4k，再由c的长，利用勾股定理列出关于k的方程，求出方程的解得到k的值，即可确定出a的长．【解答】解：由a：b＝3：4，设a＝3k，b＝4k，在Rt△ABC中，a＝3k，b＝4k，c＝10，根据勾股定理得：a2+b2＝c2，即9k2+16k2＝100，解得：k＝2或k＝﹣2（舍去），则a＝3k＝6．故选：B．【点评】此题考查了勾股定理，以及比例的性质，熟练掌握勾股定理是解本题的关键．【变式1-2】直角三角形的斜边为20cm，两直角边之比为3：4，那么这个直角三角形的周长为（ ）A．27cm B．30cm C．40cm D．48cm【分析】根据两直角边之比，设出两直角边，再由已知的斜边，利用勾股定理求出两直角边，即可得到三角形的周长．【解答】解：根据题意设直角边分别为3xcm与4xcm，由斜边为20cm，根据勾股定理得：（3x）2+（4x）2＝202，整理得：x2＝16，解得：x＝4，∴两直角边分别为12cm，16cm，则这个直角三角形的周长为12+16+20＝48cm．故选：D．【点评】此题考查了勾股定理，利用了方程的思想，熟练掌握勾股定理是解本题的关键．【变式1-3】在△ABC中，∠C＝90°，a+c＝32，a：c＝3：5，则△ABC的周长为 ．【分析】根据a+c＝32和a：c＝3：5可以准确计算a、c的长度，根据a、c的长度计算b的长度，即可求得a+b+c．【解答】解：△ABC中，∠C＝90°，∴△ABC为直角三角形，即c2＝b2+a2，∵a+c=32 a：c=3：5，∴a＝12，c＝20，∵c2＝b2+a2，∴b＝16．∴a+b+c＝12+16＝20＝48．故答案为：48．【点评】本题考查了勾股定理的灵活运用，本题中根据a、c的两个等量关系式计算a、c的长度是解题的关键．【变式1-4】（2022春•天门校级月考）一直角三角形的一直角边长为6，斜边长比另一直角边长大2，则该三角形的面积为（ ）A．8B．10C．24D．48【分析】设另一直角边长为x，根据勾股定理列出方程，解方程求出x，根据三角形的面积公式计算，得到答案．【解答】解：设另一直角边长为x，则斜边长为（x+2），由勾股定理得，x 2+62＝（x +2）2，解得，x ＝8，∴该三角形的面积=12×6×8＝24，故选：C ．【点评】本题考查的是勾股定理，如果直角三角形的两条直角边长分别是a ，b ，斜边长为c ，那么a 2+b 2＝c 2．【变式1-5】已知直角三角形的斜边为2，周长为2A ．12B ．1CD ．2【分析】根据已知可得到两直角边的和，根据完全平方公式即可求得两直角边的乘积，从而不难求得其面积．【解答】解：设两直角边分别为：a ，b ，斜边为c ，∵直角三角形的斜边为2，周长为2+∴a +b ∵（a +b ）2＝a 2+b 2+2ab ＝c 2+2ab ＝4+2ab ＝6，∴ab ＝1，∵三角形有面积=12ab =12，故选：A ．【点评】此题主要考查学生对勾股定理及完全平方和公式的运用．【变式1-6】（2021秋•重庆期中）如图，Rt △ABC 中，∠CAB ＝90°，△ABD 是等腰三角形，AB ＝BD ＝4，CB ⊥BD ，交AD 于E ，BE ＝1，则AC ＝ ．【分析】根据等腰三角形的性质得到∠BAE ＝∠BDE ，根据等式的性质得到∠CAE ＝∠DEB ，求得AC ＝EC ，根据勾股定理列方程即可得到结论．【解答】解：∵AB＝BD＝4，∴∠BAE＝∠BDE，∵CB⊥BD，∴∠DBE＝∠CAB＝90°，∴∠DEB＝90°﹣∠D，∠CAE＝90°﹣∠BAD，∴∠CAE＝∠DEB，∵∠AEC＝∠DEB，∴∠CAE＝∠CEA，∴AC＝EC，∵BE＝1，∴BC＝AC+1，∵AC2+AB2＝BC2，∴AC2+42＝（AC+1）2，∴AC=15 2，故答案为：15 2．【点评】本题考查了直角三角形的性质，等腰三角形的性质，勾股定理，证得AC＝CE是解题的关键．【变式1-7】（2021春•盘龙区期末）如图，在矩形ABCD中，AB＝4，BC＝8，对角线AC、BD相交于点O，过点O作OE垂直AC交AD于点E，则DE的长是（ ）A．3B．5C．2.4D．2.5【分析】连接CE，由矩形的性质可得∠CDE＝90°，AD＝BC＝8，AB＝DC＝4，AO＝OC，由OE⊥AC，AO＝OC，可知OE垂直平分AC，则可得AE＝CE；设DE＝x，则AE＝CE＝8﹣x，在Rt△CDE中，由勾股定理得关于x的方程，求解即可．【解答】解：连接CE，如图：在矩形ABCD中，AB＝4，BC＝8，∴∠CDE＝90°，AD＝BC＝8，AB＝DC＝4，AO＝OC，∵OE⊥AC，∴AE＝CE，设DE＝x，则AE＝CE＝8﹣x，在Rt△CDE中，由勾股定理得：DE2+DC2＝CE2，∴x2+42＝（8﹣x）2，解得x＝3．∴DE的长为3．故选：A．【点评】本题考查了矩形的性质、线段垂直平分线的性质及勾股定理等知识点，数形结合、熟练掌握相相关性质及定理是解题的关键．【变式1-8】如图，在Rt△ABC中，∠ACB＝90°，∠A、∠B、∠C所对的边分别为a、b、c．（1）若a：b＝3：4，c＝15，求b；（2）若a＝6，b＝8，求c的长及斜边上的高．【分析】（1）根据已知的比用x表示边长，然后利用勾股定理列出方程求解即可；（2）根据勾股定理求出斜边，并用三角形的面积公式求斜边上的高即可．【解答】解：（1）∵a：b＝3：4，∴设b＝4x，a＝3x，∴c＝5x，又∵c＝15，∴5x＝15，∴x＝3，∴b＝4×3＝12．（2）∵b＝8，a＝6，∴c＝10，由三角形的面积公式得，ab＝c•CD，∴CD=abc=6×810=4.8．【点评】本题考查的是勾股定理即三角形的面积公式，解题关键是掌握勾股定理并灵活应用．【变式1-9】（2023春•荔城区期末）如图，在Rt△ABC中，∠C＝90°，AC＝8，AB＝10，AB的垂直平分线分别交AB、AC于点D、E．求AE的长．【分析】由勾股定理先求出BC＝6，连接BE，根据中垂线的性质设AE＝BE＝x，知CE＝8﹣x，在Rt△BCE 中由BC2+CE2＝BE2列出关于x的方程，解之可得答案．【解答】解：在Rt△ABC中，∠C＝90°，AC＝8，AB＝10，∴BC==6，连接BE，∵DE垂直平分AB，∴AE＝BE，设AE＝BE＝x，则CE＝8﹣x，在Rt△BCE中，∵BC2+CE2＝BE2，∴62+（8﹣x）2＝x2，解得x=25 4，∴AE=25 4．【点评】本题主要考查勾股定理，解题的关键是掌握勾股定理及线段中垂线的性质．【变式1-10】（2022秋•建湖县期末）如图，在△ABC中；AB＝AC，BC＝13，D是AB上一点，BD＝5，CD＝12．（1）求证：CD⊥AB；（2）求AC长．【分析】（1）根据勾股定理的逆定理即可得到结论；（2）根据勾股定理列方程即可得到结论．【解答】（1）证明：∵BC＝13，BD＝5，CD＝12，∴BD2+CD2＝52+122＝132＝BC2，∴△CDB是直角三角形，∠CDB＝90°，∴CD⊥AB；（2）解：∵AB＝AC，∴AC＝AB＝AD+BD＝AD+5，∵∠ADC＝90°，∴AC2＝AD2+CD2，∴（AD+5）2＝AD2+122，∴AD=119 10，∴AC=11910+5=16910．【点评】本题考查了勾股定理的逆定理，勾股定理，正确的识别图形是解题的关键．关性质及定理是解题的关键．【变式1-11】（2023春•沂水县期中）如图，在△ABC中，∠ACB＝90°，以B为圆心，BC为半径画弧，交线段AB于点D，以A为圆心，AD为半径画弧，交线段AC于点E，连接CD．（1）若∠A＝25°，求∠ACD的度数；（2）若BC＝4，CE＝3，求AD的长．【分析】（1）根据三角形内角和定理求出∠B，根据等腰三角形的性质求出∠BCD，计算即可；（2）根据线段的和差以及勾股定理可得结论．【解答】解：（1）根据作图可知BD＝BC．∵∠ACB＝90°，∠A＝25°，∴∠B＝65°．∵BD＝BC，∴∠BCD=∠BDC=180°65°2=57.5°，∴∠ACD＝90°﹣∠BCD＝90°﹣57.5°＝32.5°；（2）根据作图可知AD＝AE，BD＝BC．∵∠ACB＝90°，BC＝4，CE＝3，∴BD＝BC＝4∵AE＝AD，∴AC＝AD+3，AB＝AD+4．在Rt△ACB中，由勾股定理得：AB2＝AC2+BC2．即（AD+4）2＝（AD+3）2+42．解得：AD＝4.5．【点评】本题考查的是勾股定理，三角形的内角和定理，掌握勾股定理是解题的关键．【例题2】（2022秋•南京期末）如图，在△ABC中，AD⊥BC，交BC于点D，AB＝17，AC＝10．（1）若CD＝6，则AD＝ ，BD＝ ；（2）若BC＝20，求CD的长．【分析】（1）由勾股定理可得出答案；（2）设CD＝x，则BD＝20﹣x，由勾股定理可得出102﹣x2＝172﹣（20﹣x）2，则可得出答案．【解答】解：（1）∵AD⊥BC，∴∠ADB＝∠ADC＝90°，∵AB＝17，AC＝10，CD＝6，∴AD==8，∴BD=15．故答案为：8，15；（2）设CD＝x，则BD＝20﹣x，∵AC2﹣CD2＝AD2，AB2﹣BD2＝AD2，∴AC2﹣CD2＝AB2﹣BD2，∴102﹣x2＝172﹣（20﹣x）2，解得x=211 40，∴CD=211 40．【点评】本题考查了勾股定理的应用，熟练掌握勾股定理是解题关键．【变式2-1】如图，在锐角△ABC中，已知AB＝15，BC＝14，AC＝13，AD⊥BC于D点，求AD的长．【分析】设BD＝x，则CD＝14﹣x，根据勾股定理得出方程，解方程求出x的值，再由勾股定理即可求出AD的长．【解答】解：设BD＝x，则CD＝14﹣x，∵AD⊥BC，∴∠ADB＝∠ADC＝90°，∵△ADB与△ACD均为直角三角形，∴AD2＝AB2﹣BD2＝AC2﹣CD2，即152﹣x2＝132﹣（14﹣x）2，解得x＝9，∴BD＝9，∴AD==12．【点评】本题考查了勾股定理；熟练掌握勾股定理，由勾股定理得出方程求出BD是解决问题的关键．【变式2-2】已知在△ABC中，D是BC的中点，DE⊥BC，垂足为D，交AB于点E，且BE2﹣AE2＝AC2．（1）求∠A的度数；（2）若DE＝3，BD＝4，求AE的长．【分析】（1）连接CE，根据线段垂直平分线的性质转化线段BE到△AEC中，利用勾股定理的逆定理可求∠A度数；（2）设AE＝x，则AC可用x表示，在Rt△ABC中利用勾股定理得到关于x的方程求解AE值．【解答】解：（1）连接CE，∵D是BC的中点，DE⊥BC，∴CE＝BE．∵BE2﹣AE2＝AC2，∴AE2+AC2＝CE2．∴△AEC是直角三角形，∠A＝90°；（2）在Rt△BDE中，BE=5．所以CE＝BE＝5．设AE＝x，则在Rt△AEC中，AC2＝CE2﹣AE2，所以AC2＝25﹣x2．∵BD＝4，∴BC＝2BD＝8．在Rt△ABC中，根据BC2＝AB2+AC2，即64＝（5+x）2+25﹣x2，解得x＝1.4．即AE＝1.4．【点评】本题主要考查了勾股定理及其逆定理，解题的关键是利用勾股定理求解线段长度，选择直角三角形借助勾股定理构造方程是解这类问题通用方法．【变式2-3】如图，在△ABC中，AC BC＝13，AD、CE分别是△ABC的高线与中线，点F是线段CE的中点，连接DF，若DF⊥CE，则AB＝（ ）A．10B．11C．12D．13【分析】连接DE，根据直角三角形的性质得到AB＝2DE，根据线段垂直平分线的性质得到DE＝DC，得到AB＝2CD，根据勾股定理列式计算得到得到答案．【解答】解：连接DE，∵AD⊥BC，点E是AB的中点，∴AB＝2DE，∵DF⊥CE，点F是线段CE的中点，∴DE＝DC，∴AB＝2CD，在Rt△ABD中，AD2＝AB2﹣BD2，在Rt△ACD中，AD2＝AC2﹣DC2，∴AB2﹣BD2＝AC2﹣DC2，即（2CD）2﹣（13﹣CD）22﹣DC2，解得，CD＝5，∴AB＝2CD＝10，故选：A．【点评】本题考查的是勾股定理、直角三角形的性质，如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2+b2＝c2．【变式2-4】如图，∠ABC＝90°，AB＝6cm，AD＝24cm，BC+CD＝34cm，C是直线l上一动点，请你探索当C离B多远时，△ACD是一个以CD为斜边的直角三角形？【分析】设BC＝xcm，则CD＝（34﹣x）cm，再根据勾股定理及勾股定理的逆定理列出方程，求出x的值即可．【解答】解：设BC＝xcm时，三角形ACD是以DC为斜边的直角三角形，∵BC+CD＝34，∴CD＝34﹣x，在Rt△ABC中，AC2＝AB2+BC2＝36+x2，在Rt△ACD中，AC2＝CD2﹣AD2＝（34﹣x）2﹣576，∴36+x2＝（34﹣x）2﹣576，解得x＝8．∴当C离点B8cm时，△ACD是以DC为斜边的直角三角形．【点评】本题考查的是勾股定理的逆定理，熟知如果三角形的三边长a，b，c满足a2+b2＝c2，那么这个三角形就是直角三角形是解答此题的关键．【变式2-5】（2022秋•南海区期末）如图，在△ABC中，AB＝BC＝10，AC＝AD⊥BC，垂足为D．（1）求证：∠B＝2∠CAD．（2）求BD的长度；（3）点P是边BC上一点，且点P到边AB和AC的距离相等，求点P到边AB距离．【分析】（1）由等腰三角形的性质，三角形内角和定理，即可证明；（2）设CD ＝x （x ＞0），由勾股定理得到AB 2﹣BD 2＝AC 2﹣DC 2，列出关于x 的方程，求出x 的值，即可得到答案；（3）由三角形面积公式得到12BC •AD =12AB •PM +12AC •PN ，即可解决问题．【解答】（1）证明：∵AB ＝AC ，∴∠BAC ＝∠C ，∵∠BAC +∠C +∠B ＝180°，∴∠B +2∠C ＝180°，∵AD ⊥BC ，∴∠CAD +∠C ＝90°，∴2∠C +2∠CAD ＝180°，∴∠B ＝2∠CAD ，（2）解：设CD ＝x （x ＞0），在Rt △ABD 和Rt △ACD 中，∵AB 2﹣BD 2＝AC 2﹣DC 2＝AD 2，∴102﹣（10﹣x ）2=―x 2，∴x ＝2，∴BD ＝BC ﹣CD ＝10﹣2＝8；（3）解：作PM ⊥AB 于M ，PN ⊥AC 于N ，且PM ＝PN ，连接AP ，在Rt △ABD 中，AD 6，∵△ABC 的面积＝△PAB 的面积+△PAC 的面积，∴12BC •AD =12AB •PM +12AC •PN ，∴10×6＝（PM ，∴PM ＝10﹣∴P到AB的距离是10﹣【点评】本题考查等腰三角形的性质，勾股定理，三角形的面积，关键是掌握由勾股定理列出关于CD的方程；由三角形面积公式得到12BC•AD=12AB•PM+12AC•PN．【变式2-6】（2023春•金安区校级期末）如图，在△ABC中，AB＝15，BC＝14，AC＝13，求△ABC的面积．某学习小组经过合作交流，给出了下面的解题思路，请你按照他们的解题思路，完成解答过程．（1）作AD⊥BC于D，设BD＝x，用含x的代数式表示CD，则CD＝ ；（2）请根据勾股定理，利用AD作为“桥梁”建立方程，并求出x的值；（3）利用勾股定理求出AD的长，再计算三角形的面积．【分析】（1）直接利用BC的长表示出DC的长；（2）直接利用勾股定理进而得出x的值；（3）利用三角形面积求法得出答案．【解答】解：（1）∵BC＝14，BD＝x，∴DC＝14﹣x，故答案为：14﹣x；（2）∵AD⊥BC，∴AD2＝AC2﹣CD2，AD2＝AB2﹣BD2，∴132﹣（14﹣x）2＝152﹣x2，解得：x＝9；（3）由（2）得：AD==12，∴S△ABC =12•BC•AD=12×14×12＝84．【点评】此题主要考查了勾股定理以及三角形面积求法，正确得出AD的长是解题关键．【例题3】（2022秋•卧龙区校级月考）如图，在长方形ABCD 中，BC ＝4，CD ＝3，现将该长方形沿对角线BD 折叠，使点C 落在对点C '处，BC '交AD 于点E ．（1）试说明DE ＝BE ；（2）求AE 的长．【分析】（1）利用等角对等边解决问题即可；（2）设BE ＝DE ＝x ，在Rt △ABE 中，利用勾股定理构建方程求解，再根据AE ＝AD ﹣DE 即可解决问题．【解答】解：（1）∵四边形ABCD 是矩形，∴AD ∥BC ，∴∠ADB ＝∠DBC ，由翻折的性质可知∠DBE ＝∠DBC ，∴∠DBE ＝∠ADB ，∴DE ＝BE ．（2）设BE ＝DE ＝x ，在Rt △ABE 中，∵∠A ＝90°，∴BE2＝AB2+AE2，∴32+（4﹣x）2＝x2，解得x=25 8，∴BE=DE=25 8，∴AE=AD―DE=4―258=78．【点评】本题考查翻折变换，矩形的性质，等腰三角形的判定和性质，勾股定理，解题的关键是熟练掌握翻折的性质．【变式3-1】如图是一张直角三角形的纸片，两直角边AC＝6cm、BC＝8cm，现将△ABC折叠，使点B 与点A重合，折痕为DE，则CD的长为（ ）A．154cm B．254cm C．74cm D．无法确定【分析】设CD＝xcm，则BD＝BC﹣CD＝（8﹣x）cm，再根据折叠的性质得AD＝BD＝8﹣x，然后在△ACD中根据勾股定理得到（8﹣x）2＝62+x2，再解方程即可．【解答】解：设CD＝xcm，则BD＝BC﹣CD＝（8﹣x）cm，∵△ABC折叠，使点B与点A重合，折痕为DE，∴AD＝BD＝8﹣x，在△ACD中，∠C＝90°，∴AD2＝AC2+CD2，∴（8﹣x）2＝62+x2，解得x=7 4，即CD的长为74 cm．故选：C．【点评】本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了勾股定理．【变式3-2】如图，在Rt△ABC中，∠B＝90°，AB＝4，BC＝3，延长BC至E，使得CE＝BC，将△ABC 沿AC翻折，使点B落点D处，连接DE，则DE的长为（ ）A．95B．125C．165D．185【分析】连接BD交AC于点F，由折叠的性质得出AB＝AD，∠BAC＝∠DAC，由勾股定理求出CF的长，则可由中位线定理求出DE的长．【解答】解：连接BD交AC于点F，∵将△ABC沿AC翻折，使点B落点D处，∴AB＝AD，∠BAC＝∠DAC，∴BF＝DF，∠BFC＝90°，∵AB＝4，BC＝3，∴AC=5，设CF＝x，则AF＝5﹣x，∵AB2﹣AF2＝BF2，BC2﹣CF2＝BF2，∴42﹣（5﹣x）2＝32﹣x2，∴x=9 5，∴CF=9 5，∵CE＝BC，∴CF=12 DE，∴DE=18 5．故选：D．【点评】本题考查了折叠的性质，勾股定理，中位线定理，熟练掌握折叠的性质是解题的关键．【变式3-3】（2023春•米东区期末）如图，将矩形ABCD沿对角线BD所在直线折叠，点C落在同一平面内，落点记为F，BF与AD交于点E，若BC＝2AB＝8，求DE的长．【分析】设DE＝x，则AE＝8﹣x，依据∠EBD＝∠EDB，即可得到ED＝BE＝x．Rt△ABE中，利用勾股定理即可得到DE的长．【解答】解：∵BC＝2AB＝8，∴AB＝4，设DE＝x，则AE＝8﹣x，由题可得，∠CBD＝∠EBD，∠CBD＝∠EDB，∴∠EBD＝∠EDB，∴ED＝BE＝x，Rt△ABE中，AB2+AE2＝BE2，即42+（8﹣x）2＝x2，解得x＝5，∴DE＝5．【点评】本题主要考查了矩形的性质、勾股定理的运用，解题时，常常设要求的线段长为x，然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度，选择适当的直角三角形，运用勾股定理列出方程求出答案．【变式3-4】（2022秋•沙坪坝区期末）如图，△AB'C是将长方形ABCD沿着AC折叠得到的．若AB＝4，BC＝6，则OD的长为 ．【分析】由矩形的性质可得AB＝CD＝4，AD＝BC＝6，AD∥BC，根据平行线的性质和折叠的性质可得∠EAC＝∠ACE＝∠ACB，即AE＝EC，根据勾股定理可求AE的长．【解答】解：∵四边形ABCD是矩形，∴AB＝CD＝4，AD＝BC＝8，AD∥BC，∴∠OAC＝∠ACB，由折叠可得∠ACO＝∠ACB，∴∠OAC＝∠ACO，∴AO＝CO，在Rt△DOC中，CO2＝DO2+CD2，即（6﹣OD）2＝DO2+16，解得OD=5 3，故答案为：5 3．【点评】本题考查了翻折变换，解题时常常设要求的线段长为x，然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度，选择适当的直角三角形，运用勾股定理列出方程求出答案．【变式3-5】（2023春•东莞市校级月考）如图，矩形纸片ABCD中，已知AD＝8，折叠纸片使AB边与对角线AC重合，点B落在点F处，折痕为AE，且BE＝3．（1）求CF的长；（2）求AB的长．【分析】（1）根据题意可得CE＝5，根据折叠的性质可得，∠B＝∠AFE＝90°，BE＝EF＝3，AB＝AF，在Rt△CEF中，利用勾股定理即可求出CF；（2）设AB ＝AF ＝x ，则AC ＝x +4，在Rt △ABC 中，利用勾股定理建立方程求解即可．【解答】解：（1）∵四边形ABCD 为矩形，AD ＝8，∴∠B ＝90°，AD ＝BC ＝8，∵BE ＝3，∴CE ＝BC ﹣BE ＝8﹣3＝5，根据折叠的性质可得，∠B ＝∠AFE ＝90°，BE ＝EF ＝3，AB ＝AF ，∴∠CFE ＝90°，在Rt △CEF 中，CF ==4；（2）设AB ＝AF ＝x ，则AC ＝AF +CF ＝x +4，在Rt △ABC 中，AB 2+BC 2＝AC 2，∴x 2+82＝（x +4）2，解得：x ＝6，∴AB ＝6．【点评】本题主要考查折叠的性质、矩形的性质、勾股定理，熟练掌握折叠的性质，利用勾股定理解决问题是解题关键．【变式3-6】（2022秋•卧龙区校级月考）将矩形ABCD 沿直线AE 折叠，顶点D 恰好落在BC 边上的F 点处，若AD ＝10cm ，AB ＝8cm ，求图中阴影部分的面积．【分析】由折叠的性质得AF ＝AD ＝10cm ，EF ＝DE ，由勾股定理求出BF ＝6cm ，则CF ＝4cm ，设CE ＝x ，则DE ＝EF ＝8﹣x ，由勾股定理得CE 2+FC 2＝EF 2，代入求出x ＝3cm ，由S 阴影＝S △ABF +S △CEF =12AB •BF +12CF •CE 即可得出结果．【解答】解：∵四边形ABCD 为矩形，∴AD ＝BC ＝10cm ，AB ＝CD ＝8cm ，∠B ＝∠C ＝90°，∵矩形ABCD沿直线AE折叠，顶点D恰好落在BC边上的F处，∴AF＝AD＝10cm，EF＝DE，在Rt△ABF中，由勾股定理得：BF==6（cm），∴CF＝BC﹣BF＝10﹣6＝4（cm），设CE＝xcm，则DE＝EF＝（8﹣x）cm，在Rt△ECF中，由勾股定理得：CE2+FC2＝EF2，即：x2+42＝（8﹣x）2，解得：x＝3，∴CE＝3cm，∴S阴影＝S△ABF+S△CEF=12AB•BF+12CF•CE=12×8×6+12×4×3＝30（cm2）．【点评】本题考查了折叠的性质、矩形的性质、勾股定理、三角形面积的计算等知识；熟练掌握折叠的性质是解题的关键．【变式3-7】（2022春•平邑县校级期中）在Rt△ABC中，∠C＝90°，AC＝6，BC＝8，D，E分别是AB和CB上的点，把△ABC沿着直线DE折叠，顶点B的对应点是点B'．（1）如图1，如果点B'恰好与顶点A重合，求CE的长；（2）如图2，如果点B'恰好落在直角边AC的中点上，求CE的长．【分析】（1）利用勾股定理求出AB的长，再利用翻折得到AE＝BE，在Rt△ACE中利用勾股定理即可求出CE的长；（2）点B'是直角边AC的中点，可以得到B'C的长度，再利用翻折得到B′E＝BE，在Rt△B'CE中利用勾股定理即可求出CE的长．【解答】解：（1）在Rt△ABC中，∠C＝90°，AC＝6，BC＝8，∴AB=10，根据折叠的性质，∴△ADE ≌△BDE ，∴AE ＝BE ，设CE 为x ，则：AE ＝BE ＝8﹣x ，在Rt △ACE 中：x 2+62＝（8﹣x ）2，解得：x =74，即CE 的长为：74；（2）∵点B '是直角边AC 的中点，∴B 'C =12AC =3，根据折叠的性质，∴△B 'DE ≌△BDE ，∴B ′E ＝BE ，设CE 为x ，则：B ′E ＝BE ＝8﹣x ，在Rt △B 'CE 中：x 2+32＝（8﹣x ）2，解得：x =5516，即CE 的长为：5516．【点评】本题考查勾股定理以及图形的变换中的折叠问题．在折叠过程中，对应角和对应边相等是解题的关键；在直角三角形中，知道一条边长以及另外两条边的关系时，通常采用方程思想来解题．【例题4】（2023秋•文山市月考）如图，有一个池塘，其底边长为10尺，一根芦苇AB 生长在它的中央，高出水面部分BC 为1尺．如果把该芦苇沿与水池边垂直的方向拉向岸边，那么芦苇的顶部B 恰好碰到岸边的B '．请你计算这个池塘水的深度和这根芦苇的长度各是多少？【分析】设池塘水的深度是x尺，则这根芦苇的长度是（x+1）尺，在Rt△CAB′中，由勾股定理得得出方程，解方程即可．【解答】解：设池塘水的深度是x尺，则这根芦苇的长度是（x+1）尺，由题意得：∠ACB'＝90°，B'C=102=5（尺），在Rt△CAB′中，由勾股定理得：AC2+B′C2＝AB′2，即x2+52＝（x+1）2，解得：x＝12，∴x+1＝12+1＝13，答：池塘水的深度是12尺，这根芦苇的长度是13尺．【点评】此题主要考查了勾股定理的应用，由勾股定理得出方程是解题的关键．【变式4-1】（2023春•余干县期中）如图是某小区为迎接十四运，方便群众活动健身设计的秋千示意图，秋千AB在静止位置时，下端B离地面0.6m，当秋千到AB′的位置时，下端B′距静止位置的水平距离DB′等于1.2m，距地面1m，求秋千AB的长．【分析】利用已知表示出AD的长，再利用勾股定理得出即可．【解答】解：设AB＝xm，则AB′＝xm，由题意可得出：DB＝1﹣0.6＝0.4（m），则AD＝AB﹣DB＝（x﹣0.4）m，在Rt△AB′D中，AD2+B′D2＝AB′2，则（x﹣0.4）2+1.22＝x2，解得：x＝2．答：秋千AB的长为2m．【点评】本题考查了勾股定理的应用，善于观察题目的信息是解题以及学好数学的关键．【变式4-2】（2022秋•运城期末）如图，∠AOB=90°，OA＝18cm，OB＝6cm，一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O，机器人立即从点B出发，沿直线匀速前进拦截小球，恰好在点C处截住了小球．如果小球滚动的速度与机器人行走的速度相等，那么机器人行走的路程BC 是多少？【分析】由题意可知，若设BC＝xcm，则AC＝xcm，OC＝OA﹣AC＝（18﹣x）cm，这样在Rt△BOC中，利用勾股定理就可建立一个关于“x”的方程，解方程即可求得结果．【解答】解：小球滚动的速度与机器人行走的速度相等，运动时间相等，即BC＝CA，设BC＝xcm，则AC＝xcm，OC＝OA﹣AC＝（18﹣x）cm，∵∠AOB＝90°，∴由勾股定理可知OB2+OC2＝BC2，又∵OC＝（18﹣x）cm，OB＝6cm，∴62+（18﹣x）2＝x2，解方程得出x＝10（cm）．答：机器人行走的路程BC是10cm．【点评】本题考查了勾股定理，解题的关键是，抓住“机器人与小球同时出发，速度相等”这两个条件，得到BC＝AC，从而将已知量和未知量集中到Rt△BOC中，就可利用勾股定理建立方程来求解．【变式4-3】（2021春•绥宁县期末）如图，AB为一棵大树，在树上距地面10m的D处有两只猴子，它们同时发现地面上C处有一筐水果，一只猴子从D处向上爬到树顶A处，然后利用拉在A处的滑绳AC滑到C处，另一只猴子从D处先滑到地面B，再由B跑到C，已知两猴子所经过的路程都是15m，求树高AB．【分析】Rt△ABC中，∠B＝90°，则满足AB2+BC2＝AC2，BC＝a（m），AC＝b（m），AD＝x（m），根据两只猴子经过的路程一样可得10+a＝x+b＝15解方程组可以求x的值，即可计算树高＝10+x．【解答】解：Rt△ABC中，∠B＝90°，设BC＝a（m），AC＝b（m），AD＝x（m）则10+a＝x+b＝15（m）．∴a＝5（m），b＝15﹣x（m）又在Rt△ABC中，由勾股定理得：（10+x）2+a2＝b2，∴（10+x）2+52＝（15﹣x）2，解得，x＝2，即AD＝2（米）∴AB＝AD+DB＝2+10＝12（米）答：树高AB为12米．【点评】本题考查了勾股定理在实际生活中的应用，本题中找到两只猴子行走路程相等的等量关系，并且正确地运用勾股定理求AD的值是解题的关键．【变式4-4】（2023•湘乡市校级开学）如图，有两棵树，一棵高10米，另一棵高4米，一只小鸟从一棵树的树梢飞到另一棵树的树梢的直线距离是10米，求两树相隔的距离．【分析】由题意知，AB＝10米，CD＝4米，AD＝10米，在Rt△AED中，利用勾股定理求出DE的长即可．【解答】解：如图，由题意知，AB＝10米，CD＝4米，AD＝10米，∴AE＝10﹣4＝6（米），在Rt△AED中，由勾股定理得，DE==8（米），∴BC＝DE＝8米，即两树相隔的距离为8米．【点评】本题考查了勾股定理的应用，熟练掌握勾股定理是解题的关键．【变式4-5】（2022秋•双塔区校级期中）如图所示的是一个拉箱的示意图，箱体长AB＝65cm，拉杆最大伸长距离BC＝35cm，在箱体的底端装有一圆形滚轮，其直径为6cm．当拉杆拉到最长时，滚轮的圆心在图中的A处，当拉杆全部缩进箱体时，滚轮圆心水平向右平移55cm到A′处．请求点C离地面的距离（假设点C的位置保持不变）【分析】过C作CE⊥DN于E，延长AA'交CE于F，根据勾股定理即可得到方程652﹣x2＝1002﹣（55+x）2，求得A'F的长，即可利用勾股定理得到CF的长，进而得出CE的长．【解答】解：如图所示，过点C作CE⊥DN于点E，延长AA′交CE于F，则∠AFC＝90°．设A′F＝xcm，则AF＝（55+x）cm，由题可得，AC＝AB+BC＝65+35＝100（cm），A′C＝65cm．∵Rt△A′CF中，CF2＝652﹣x2，Rt△ACF中，CF2＝1002﹣（55+x）2，∴652﹣x2＝1002﹣（55+x）2，解得x＝25，∴A'F＝25（cm），∴CF=60（cm）．又∵EF＝AD＝3cm，∴CE＝60+3＝63（cm），∴点C离地面的距离为63cm．【点评】本题主要考查了勾股定理的应用，在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法，关键是从题中抽象出勾股定理这一数学模型，画出准确的示意图．【变式4-6】（2023春•德州期末）如图1，同学们想测量旗杆的高度．他们发现系在旗杆顶端的绳子垂到了地面，并多出了一段，但这条绳子的长度未知．小明和小亮同学应用勾股定理分别提出解决这个问题的方案如下：小明：①测量出绳子垂直落地后还剩余1.5米，如图1；②把绳子拉直，绳子末端在地面上离旗杆底部6米，如图2．小亮：先在旗杆底端的绳子上打了一个结，然后举起绳结拉到如图3点D处．（1）请你按小明的方案求出旗杆的高度；（2）已知小亮举起绳结离旗杆6.75米远，此时绳结离地面多高？【分析】（1）由题可知，旗杆，绳子与地面构成直角三角形，根据题中数据，用勾股定理即可解答；（2）由题可知，BD＝BC＝11.25米，DE＝6.75米．在Rt△BDE中根据勾股定理列出方程BE2+6.752＝11.252，求出BE＝9，进而求解即可．【解答】解：（1）如图2，设旗杆的长度为x米，则绳子的长度为（x+1.5）米，在Rt△ABC中，由勾股定理得：x2+62＝（x+1.5）2，解得：x＝11.25，故旗杆的高度为11.25米；（2）由题可知，BD＝BC＝11.25米，DE＝6.75米．在Rt△BDE中，由勾股定理得：BE2+6.752＝11.252，解得：BE＝9，∴EC＝BC﹣BE＝11.25﹣9＝2.25（米），∴DF＝EC＝2.25米．故绳结离地面2.25米高．【点评】本题考查的是勾股定理的应用，根据题意得出直角三角形是解答此题的关键．【变式4-7】（2022秋•抚州期末）长清的园博园广场视野开阔，阻挡物少，成为不少市民放风筝的最佳场所，某校七年级（1）班的小明和小亮学习了“勾股定理”之后，为了测得风筝的垂直高度CE，他们进行了如下操作：①测得水平距离BD的长为15米；②根据手中剩余线的长度计算出风筝线BC的长为25米；③牵线放风筝的小明的身高为1.6米．（1）求风筝的垂直高度CE；（2）如果小明想风筝沿CD方向下降12米，则他应该往回收线多少米？【分析】（1）利用勾股定理求出CD的长，再加上DE的长度，即可求出CE的高度；（2）根据勾股定理即可得到结论．【解答】解：（1）在Rt△CDB中，由勾股定理得，CD2＝BC2﹣BD2＝252﹣152＝400，所以，CD＝20（负值舍去），所以，CE＝CD+DE＝20+1.6＝21.6（米），答：风筝的高度CE为21.6米；（2）由题意得，CM＝12米，∴DM＝8米，∴BM=17（米），∴BC﹣BM＝25﹣17＝8（米），∴他应该往回收线8米．【点评】本题考查了勾股定理的应用，熟悉勾股定理，能从实际问题中抽象出勾股定理是解题的关键．【变式4-8】（2022秋•佛山校级期末）铁路上A，B两站（视为直线上的两点）相距25km，C，D为两村庄（视为两个点），DA⊥AB于点A，CB⊥AB于点B（如图），已知DA＝10km，CB＝15km，现在要在铁路AB上建一个土特产收购站E，使得C，D两村庄到收购站E的直线距离相等，请求出收购站E到A站的距离．【分析】由勾股定理两直角边的平方和等于斜边的平方即可求，即在直角三角形DAE和直角三角形CBE 中，DE2＝AD2+AE2，CE2＝BE2+BC2，得出AD2+AE2＝BE2+BC2，设AE为xkm，则BE＝（25﹣x）km，将BC＝10代入关系式即可求得．【解答】解：∵C、D两村到E站距离相等，∴CE＝DE，在Rt△DAE和Rt△CBE中，DE2＝AD2+AE2，CE2＝BE2+BC2，∴AD2+AE2＝BE2+BC2．设AE为xkm，则BE＝（25﹣x）km，将BC＝10，DA＝15代入关系式为x2+102＝（25﹣x）2+152，解得x＝15，∴E站应建在距A站15km处．【点评】此题考查勾股定理的应用，基础知识要熟练掌握．【变式4-9】（2022秋•叙州区期末）“村村通”公路是我国的一项重要的民生工程，如图，A，B，C三个村都分别修建了一条互通公路，其中AB＝BC，现要在公路BC边修建一个景点M（B，C，M在同一条直线上），为方便A村村民到达景点M，又修建了一条公路AM，测得AC＝13千米，CM＝5千米，AM＝12千米．（1）判断△ACM的形状，并说明理由；（2）求公路AB的长．【分析】（1）由勾股定理的逆定理即可得出结论；（2）设AB＝BC＝x千米，则BM＝（x﹣5）千米，在Rt△ABM中，由勾股定理得出方程，解方程即可．【解答】解：（1）△ACM是直角三角形，理由如下：∵AC＝13千米，CM＝5千米，AM＝12千米，∴CM2+AM2＝AC2，∴△ACM是直角三角形，∠AMC＝90°；（2）设AB＝BC＝x千米，则BM＝（x﹣5）千米，由（1）可知，∠AMC＝90°，∴∠AMB＝180°﹣∠AMC＝90°，在Rt△ABM中，由勾股定理得：122+（x﹣5）2＝x2，解得：x＝16.9，答：公路AB的长为16.9千米．【点评】本题考查了勾股定理的应用以及勾股定理的逆定理等知识，熟练掌握勾股定理和勾股定理的逆定理是解题的关键．【变式4-10】（2022春•江津区期中）中菲黄岩岛争端持续，我海监船加大黄岩岛附近海域的巡航维权力度．如图，OA⊥OB，OA＝36海里，OB＝12海里，黄岩岛位于O点，我国海监船在点B处发现有一不明国籍的渔船，自A点出发沿着AO方向匀速驶向黄岩岛所在地点O，我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船，结果在点C处截住了渔船．（1）请用直尺和圆规作出C处的位置；（2）求我国海监船行驶的航程BC的长．【分析】（1）由题意得，我海监船与不明渔船行驶距离相等，即在OA上找到一点，使其到A点与B点的距离相等，所以连接AB，作AB的垂直平分线即可．（2）连接BC，利用第（1）题中作图，可得BC＝AC．在直角三角形BOC中，利用勾股定理列出方程122+（36﹣BC）2＝BC2，解方程即可．【解答】解：（1）作AB的垂直平分线与OA交于点C；（2）连接BC，由作图可得：CD为AB的中垂线，则CB＝CA．由题意可得：OC＝36﹣CA＝36﹣CB．∵OA⊥OB，∴在Rt△BOC中，BO2+OC2＝BC2，即：122+（36﹣BC）2＝BC2，解得BC＝20．答：我国海监船行驶的航程BC的长为20海里．【点评】本题考查了勾股定理的应用以及线段垂直平分线的性质，利用勾股定理不仅仅能求直角三角形的边长，而且它也是直角三角形中一个重要的等量关系．【变式4-11】（2022秋•广陵区校级期末）如图，有一架秋千，当它静止在AD的位置时，踏板离地的垂直高度为0.6m，将秋千AD往前推送3m，到达AB的位置，此时，秋千的踏板离地的垂直高度为。
方程思想的应用
方程思想的应用1 定义方程方程是数学中的一种结构，是一种数学式，表达由未知量构成的有关关系。
一般来说，方程可以以等式的形式表达，左边的表达式称为“方程的左端”，右边的表达式称为“方程的右端”。
一般来说，方程有两个或多个变量，这些变量之间应该是结构上相等的。
2 方程的应用方程在日常生活和复杂应用中都具有重要的意义。
在日常生活中，方程往往用于表达一些量与量之间的关系，例如体积与体积的关系，还有财务计算的方程等。
在工程学校的学习中，方程也得到广泛使用，用于解决一些数学模型，如力学模型，电子模型，气体传输模型等等。
3 线性方程和非线性方程方程通常分为两类：线性方程和非线性方程。
线性方程是指其变量之间是线性相关的方程，这种方程中有一对或多对变量之间是线性关系，而非线性方程则是其变量之间不是线性相关的方程。
一般来说，线性方程的解往往比较容易，而非线性方程的解非常复杂，往往需要利用若干数学工具来完成。
4 方程的特殊问题方程也存在一些特殊的问题，例如方程没有实根，或者方程没有唯一解，这些问题也是需要充分考虑到的。
这些特殊的问题往往需要在理论和实践中共同探讨解决，以求系统的解决方案，以完成解方程的任务。
5 方程的数学思想方程本质上是一种数学思想，是一种利用数学结构来解决问题的思想。
根据它可以更好地理解、建立和解决实际问题。
方程的重要性不仅在于解决问题，而且还可以将问题抽象化，这一抽象方面的重要性往往被其他数学问题所忽视，但它也是方程解决问题的基础。
6 方程的总结方程是数学中的一种重要结构，是表达变量之间的关系的重要数学有机体。
方程在日常生活和工程应用中都发挥着重要作用，例如在财务计算中，以及工程学校的数学建模中都有着广泛的应用。
在方程的解题过程中，除了解决问题，还需要更深入的理解，以便更好地利用方程的数学思想解决问题。
方程思想在初中几何题中的应用
教法研究离是20，求AB、CD的长解：设BD=x，则AB=3x,CD=4x2解：设∠AOE=x，∠BOF=y，则∠DOE=3x，∠COF=3yAED.求∠EDC的度数.解：设∠EDC=xDBF相等的角？请说明理由.解：（1）∵BE平分∠ABC交，BD平分∠EBC2019年21期┆99教法研究代数式表示出来，可以简化计算过程。
例5：如图，⊙O为△ABC的内切圆，切点分别为D，解：连结OE，OD，OF.四、落实“八项规定精神”，持续推进廉政建设。
中央“八项规定”的出台，公司党委一直严格执行其精神，以整治形式主义、官僚主义为基础，坚定推进公司党风廉政建设。
每到重大节日，公司党委书记都要集中对各级党员干部集体谈话，各分管领导、部门负责人都要对所属人员进行集中谈话，公司纪委也将对每个关键岗位人员发送廉洁提醒短信进行警示，并要求开展专项监督检查节日后，将对发现的问题进行查处。
同时，在每个季度，对主管及中层管理人员，每月都要进行自查自评，看有没有违纪违规情况发生。
即使自己自评没有，但一旦发现，就将从重处罚。
在涉及收受红包礼金、公款吃喝、违规接待、红白喜事上都予以了重点监管，确保这些环节中不出现违规不守纪律事件。
五、努力提升监督执纪能力，强化纪检队伍建设作为反腐倡廉的首要部门，纪委、纪检人员担子不轻，压力巨大。
随着企业的发展，腐败可能会出新的变化，或许更加隐秘，更加难于查到。
这就需要我们的纪检队伍中专、兼职人员，不仅要有极高的政治素养，还要有更多的专业知专门拟定了具体的措施。
首先，必须强化纪检监察人员的政治思想建设，对执纪违纪的情况坚决查处，失职失责的坚决问责，严防、严控“灯下黑”现象发生；其次对纪检监察工作不断提出新要求，通过各种学习、培训、轮训、考试，以案例教学，努力提升他们的政治素养和办案能力，努力打造一支忠诚、干净、担当的纪检监察队伍，为企业发展作出重要贡献。
参考文献：[1]刘征文.强化反腐倡廉建设培育廉洁企业文化[J].现代国企研究,2018(20):237.[2]谢鑫建.反腐风暴契机下大学生廉洁教育体系的构建与强化[J].高教学刊,2015(23):247-248.[3]宋婷.传承核电企业廉洁文化强化反腐倡廉思想教育机制[J].东方企业文化,2015(06):23-24.（作者单位：中国五冶集团有限公司第四工程分公司）100┆好日子。
方程思想在圆中的应用
方程思想在圆中的应用方程思想是初中数学的重要思想方法，初中数学中有许多问题可以通过列方程、解方程的方法得到快速有效的解决。
在求圆中有关线段的长度问题时，需要运用方程思想来求解.下面我们通过几道例题来看一看方程思想在圆中的应用.一、利用勾股定理列方程例题1、如图，AB为⊙O的直径，AD、BD是⊙O的弦，BC是⊙O的切线，切点为B，OC//AD，BA、CD的延长线相交于点E．(1)求证：CD是⊙O的切线;(2)若AE=1，ED=3，求⊙O的半径．【分析】本题考查了切线的判定与性质，掌握切线的判定与性质是解决问题的关键．(1)首选连接OD，易证得△COD≌△COB(SAS)，然后由全等三角形的对应角相等，求得∠CDO=90°，即可证得直线CD是⊙O的切线；(2)设⊙O的半径为r，则OE=r+1，在Rt△ODE中，利用勾股定理列出方程，求解即可．【解答】证明：(1)连接DO．∵AD//OC，∴∠DAO=∠COB，∠ADO=∠COD．∵OA=OD，∴∠ADO=∠DAO．∴∠COD=∠COB．又∵OD=OB，OC=OC，∴△COD≅△COB，∴∠CDO=∠CBO．∵BC是⊙O的切线，∴OB⊥CB，即∠CBO=90∘．∴∠CDO=90∘，即OD⊥CD.∴CD是⊙O的切线；(2)设⊙O的半径为r，则OD=r，OE=r+1．∵CD是⊙O的切线，∴∠EDO=90∘．∴在Rt△EDO中，ED2+OD2=OE2．∴32+r2=(r+1)2，解得r=4．所以⊙O的半径为4.本题第二问利用勾股定理在单个Rt△EDO列方程求出⊙O的半径，有时还会遇到在双Rt△利用勾股定理列方程.我们一起来看下面一道例题.例题2、如图，在Rt△ABC中，∠C=90°，以BC为直径的⊙O交AB于点D，切线DE交AC于点E．(1)求证：∠A=∠ADE;(2)若AD=16，DE=10，求BC的长．【分析】本题考查圆的切线的性质、勾股定理、等腰三角形的判定和性质等知识，综合性较强．(1)只要证明∠A+∠B=90°，∠ADE+∠B=90°即可解决问题；(2)首先证明AC=2DE=20，在Rt△ADC中，DC=12，设BD=x，在Rt△BDC中，BC2=x2+122，在Rt△ABC中，BC2=(x+16)2−202，可得x2+122=(x+ 16)2−202，解方程即可解决问题．【解答】(1)证明：连接OD ，∵DE 是切线，∴∠ODE =90°，∴∠ADE +∠BDO =90°，∵∠ACB =90°，∴∠A +∠B =90°，∵OD =OB ，∴∠B =∠BDO ，∴∠ADE =∠A ．(2)解：连接CD ．∵∠ADE =∠A ，∴AE =DE ，∵BC 是⊙O 的直径，∠ACB =90°，∴EC 是⊙O 的切线， ∴ED =EC ，∴AE =EC ，∵DE =10，∴AC =2DE =20，在Rt △ADC 中，DC =√202−162=12，设BD =x ，在Rt △BDC 中，BC 2=x 2+122，在Rt △ABC 中，BC 2=(x +16)2−202，∴x 2+122=(x +16)2−202，解得x =9，∴BC =√122+92=15．本题第二问双直角三角形BDC 和ABC 有公共边BC ，分别用勾股定理表示出BC 的平方后列方程求解.二、利用相似列方程例题3、如图，已知△ABC 内接于⊙O ，且AB =AC ，直径AD 交BC 于点E ，F 是OE 上的一点，使CF// BD ．(1)求证：BE =CE ；(2)试判断四边形BFCD 的形状，并说明理由；(3)若BC =8，AD =10，求CD 的长．【分析】本题主要考查了圆的有关性质：垂径定理、圆周角定理，三角形全等的判定与性质，菱形的判定与性质，勾股定理，三角形相似的判定与性质，熟悉圆的有关性质是解决问题的关键．(1)证明△ABD≌△ACD ，得到∠BAD =∠CAD ，根据等腰三角形的性质即可证明；(2)菱形，证明△BFE≌△CDE ，得到BF =DC ，可知四边形BFCD 是平行四边形，易证BD =CD ，可证明结论；(3)设DE =x ，则根据CE 2=DE ⋅AE 列方程求出DE ，再用勾股定理求出CD ．【解答】(1)证明：∵AD 是直径，∴∠ABD =∠ACD =90°，在Rt △ABD 和Rt △ACD 中，{AB =AC AD =AD,∴Rt △ABD≌Rt △ACD ， ∴∠BAD =∠CAD ，∵AB =AC ，∴BE =CE ；(2)四边形BFCD 是菱形．证明：∵AD 是直径，AB =AC ，∴AD ⊥BC ，BE =CE ，∵CF//BD ，∴∠FCE =∠DBE ，在△BED 和△CEF 中，∴△BED≌△CEF ，∴CF =BD ，∴四边形BFCD 是平行四边形，∵∠BAD =∠CAD ，∴BD =CD ，∴四边形BFCD 是菱形；(3)解：∵AD 是直径，AD ⊥BC ，BE =CE ，∵∠AEC =∠CED ，∠CAE =∠ECD ，∴△AEC∽△CED ，∴AECD =ECED，∴CE2=DE⋅AE，设DE=x，∵BC=8，AD=10，∴42=x(10−x)，解得：x=2或x=8(舍去)在Rt△CED中，CD=√CE2+DE2=√42+22=2√5．三、利用等面积法列方程例题4、如图，△ABC内接于⊙O，AB是直径，⊙O的切线PC交BA的延长线于点P，OF//BC交AC于点E，交PC于点F，连接AF．(1)判断AF与⊙O的位置关系，并说明理由；(2)若⊙O的半径为8，AF=6，求AC的长．【分析】(1)AF为为圆O的切线，利用SAS得出三角形AOF与三角形COF全等，由全等三角形的对应角相等及垂直定义得到AF垂直于OA，即可得证；(2)根据平行线的性质可知：OE垂直于AC，利用面积法列方程求出AE的长，即可确定出AC的长．【解答】解：(1)AF为圆O的切线，理由是：连接OC，∵PC为圆O切线，∴CP⊥OC，∴∠OCP=90°，∵OF//BC，∴∠AOF=∠B，∠COF=∠OCB，∵OC=OB，∴∠OCB=∠B，∴∠AOF=∠COF，∵在△AOF和△COF中，{OA=OC∠AOF=∠COF OF=OF，∴△AOF≌△COF(SAS)，∴∠OAF=∠OCF=90°，∴AF⊥OA，OA为⊙O的半径，则AF为⊙O的切线；(2)∵AB是⊙O的直径，∴∠ACB=90°∵OF//BC∴∠AEO=∠ACB=90°∴AE=CE=12AC，∵OA⊥AF，∴在Rt△AOF中，OA=8，AF=6，根据勾股定理得：OF=10，设AE=x,∴S△AOF=12×8×6=12×10⋅x，∴AE=245，则AC=2AE=485．方程思想是非常重要的数学思想方法，在圆这一章中特别是在求有关线段长度的时候往往要用到方程思想。
浅谈方程思想在初中数学中的应用
浅谈方程思想在初中数学中的应用
方程思想是数学中一个重要的思维方式，它在初中数学中的应
用非常广泛，包括以下几个方面：
1. 解决实际问题。
在初中数学中，很多实际问题都可以转化为方程来求解。
例如，求两个数的平均数是某个值，可以用方程表达出来，然后解出这个
方程得到答案。
通过这种方式，方程思想可以帮助学生学会把实际
问题抽象化，从而更好地理解和解决问题。
2. 建立数学模型。
方程思想可以帮助学生建立数学模型，将实际问题抽象化为一
个或多个方程，从而进行数学求解。
例如，求两个数的和是某个值，可以建立方程来求解。
通过这种方式，方程思想可以帮助学生把问
题形式化，从而更好地理解和掌握数学知识。
3. 培养逻辑思维能力。
通过解方程的过程，学生需要运用逻辑思维能力进行推理，例如：如何把方程变形、化简；如何用等式的性质进行变形等等。
这
样不仅能够提高学生的逻辑思维能力，还能够培养学生解决问题的
能力。
总之，方程思想在初中数学中是一个非常重要的思维方式，它
不仅能够帮助学生解决实际问题，还能够培养学生的逻辑思维能力
和解决问题的能力。
勾股定理及方程思想的综合应用
典型问题分析与解决策略
典型问题一
已知直角三角形两条直角边，求 斜边。
解决策略
直接应用勾股定理，建立方程并 求解。
典型问题二
已知直角三角形一条直角边和斜 边，求另一条直角边。
解决策略
验证三边是否满足勾股定理条件 。
典型问题三
判断一个三角形是否为直角三角 形。
解决策略
通过勾股定理建立方程，并化简 求解。
XX
PART 02
方程思想在勾股定理中应 用
REPORTING
方程建模与求解过程
勾股定理描述
求解过程
在直角三角形中，直角边的平方和等 于斜边的平方，即$a^2 + b^2 = c^2$。
通过代入已知数值，解三角形两条边时，可建立 方程求解第三边。例如，已知直角边 $a$和$b$，求斜边$c$，则方程为 $a^2 + b^2 = c^2$。
• 方程思想在复杂问题中的应用：对于更复杂的数学问题，如多元函数、微分方 程等，方程思想仍然具有重要的应用价值。通过建立适当的方程或方程组，可 以将复杂问题转化为相对简单的求解问题。
• 勾股定理与方程思想的跨学科应用：除了在数学领域中的应用外，勾股定理和 方程思想还可以在其他学科中找到广泛的应用。例如，在物理学中，勾股定理 可以用于计算物体的位移、速度等；在化学中，方程思想可以用于解决化学反 应中的平衡问题；在经济学中，方程思想可以用于分析市场供需关系等。因此 ，掌握勾股定理和方程思想对于提高跨学科解决问题的能力具有重要意义。
结合勾股定理和方程思想，可以建立化学反应中物质质量、 物质的量和反应速率等物理量之间的关系式，进而进行化学 计算。
经济问题中价格、数量和总收入关系分析
价格与数量关系
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（文科）中档题复习（一）
方程思想及其应用
学习目标：（1）熟悉不同知识模块中方程建立的常见知识与方法；
（2）优化方程的算法；
（3）理解方程与函数、不等式之间的联系与转化； （4）逐步建立不同知识之间的联系与转化。
一、填空题
1、已知锐角3πα⎛⎫
+
⎪⎝
⎭
的终边经过点(1,P ,则cos α= 2、在等比数列{}n a 中，已知13118a a a =，那么28a a =__________ 3、在△ABC 中，若4=•=•，则边AB 的长等于
4、以双曲线22
163
x y -
=的右焦点为圆心且与双曲线的渐近线相切的圆的方程是
5、已知椭圆C 的离心率为
2
，焦点12,F F 在x 轴上，椭圆上一点(),2P t 满足120PF PF ⋅=,
点M (),x y 是椭圆上任意一点，若m x =，则m 的取值范围是 6、已知实数,,a b c 满足9a b c ++=，24ab bc ca ++=，则b 的取值范围是 7、方程2
2sin (1)sin 10x x λ-++=在[0,2)π上恰有两解，则实数λ的取值范围是 变式1：关于x 的方程2
2(1)10x x λ-++=有整数解，则所有整数λ的集合为
综合应用：在平面直角坐标系xOy 中，设直线
2m y =+和圆222x y n +=相切，其
中m ，*
0||1n m n ∈<-≤N ，
，若函数1
()x f x m n +=- 的零点0(,1),x k k k ∈+∈Z ，则
k =
二、例题
例题1：在ABC △中，已知角,,A B C 的对边分别为,,a b c （1）若
()()3a b c b c a bc +++-=，90,4B C c -=︒=，求b ；
（2）若2
2
8a c b -=，且sin cos 3cos sin 0A C A C +=，求b 。
例题2：设函数2()ln f x x a x =-
与1
()g x x a
=
1x =于点A ，B ，且曲线()y f x =在点A 处的切线与曲线()y g x =在点B 处的切线平行。
求函数(),()f x g x 的表达式；
例题:3：在平面直角坐标系xOy 中，已知圆B ：22(1)16x y -+=与点(1,0)A -，P 为圆B 上
的动点，线段PA 的垂直平分线交直线PB 于点R ，点R 的轨迹记为曲线C 。
（1）求曲线C 的方程；
（2）曲线C 与x 轴正半轴交点记为Q ，过原点O 且不与x 轴重合的直线与曲线C 的交点
记为M ，N ，连结QM ，QN ，分别交直线(x t t =为常数，且2x ≠）于点E ，F ，设E ，F 的纵坐标分别为12,y y ，求12y y ⋅的值（用t 表示）。
例题4：已知点()1,0C ，点,A B 是⊙O ：2
2
9x y +=上任意两个不同的点，且满足
0AC BC ⋅=，设P 为弦AB 的中点．
（1）求点P 的轨迹T 的方程；
（2）试探究在轨迹T 上是否存在这样的点： 它到直线1x =-的距离恰好等于到点C 的距离？ 若存在，求出这样的点的坐标；若不存在，说明理由．
(1)连接RA ，由题意得，RA RP =，4RP RB +=，
所以42RA RB AB +=>=，…………………………………………………2分
由椭圆定义得，点R 的轨迹方程是22
143
x y +=.……………………………4分
(2)设M 00(,)x y ，则00(,)N x y --，,QM QN 的斜率分别为,QM QN k k ，
x
则002QM y k x =
-，0
02
NQ y k x =+，……………………………………………6分 所以直线QM 的方程为00(2)2y y x x =
--，直线QN 的方程0
0(2)2
y y x x =-+，8分 令(2)x t t =≠，则001200(2),(2)22
y y y t y t x x =
-=--+，……………………10分 又因为00(,)x y 在椭圆2200143x y +=，所以2
200
334
y x =-， 所以2
22
022********(3)(2)34(2)(2)444
x t y y y t t x x --⋅=-==----，其中t 为常数.…14分 （1）法一：连结CP ，由0AC BC ⋅=，知AC ⊥BC ∴|CP |＝|AP |＝|BP |＝
1
||2
AB ，由垂径定理知22||||OP AP +即22||||9OP CP +=，………………………………………4分 设点(),P x y ，则有2222()[(1)]9x y x y ++-+=，
化简，得到22
4x x y -+=；………………………………8分 法二：设11(,)A x y ，22(,)B x y ，P (,)x y ，
根据题意，知2222
11229,9x y x y +=+=，12122,2x x x y y y =+=+， ∴222222
1122112242,42x x x x x y y y y y =++=++
故222222
11121222121244()(22)()182()x y x y x x y y x y x x y y +=+++++=++ ……
① ………4分
又0AC BC ⋅=，有1122(1,)(1,)0x y x y --⋅--=，即1212(1)(1)0x x y y -⨯-+=， ∴121212()121x x y y x x x +=+-=-，代入①式，得到2
2
44182(21)x y x +=+-， 化
简
，
得
到
224x x y -+=； …………………………………………………………………………8分
（2）根据抛物线的定义，到直线1x =-的距离等于到点()1,0C 的距离的点都在抛物线
22y px =上，其中
12
p =，
∴2p =，故抛物线方程为2
4y x =，………………………………10分 由
方
程
组22244
y x x x y ⎧=⎪⎨-+=⎪⎩得
2340
x x +-=，解得
121,4x x ==-， …………………………12分
由于0x ≥，故1x =，此时2y =±， 故
满
足
条
件
的
点
存
在
，
其
坐
标
为
(1,2)
-和
(1,2)． ………………………………………………14分
如有侵权请联系告知删除，感谢你们的配合！。