三视图识图练习
三视图习题50道(含答案).

三视图练习题1、若某空间几何体的三视图如图所示,则该几何体的体积是( (A2 (B1 (C23(D132、一个几何体的三视图如图,该几何体的表面积是((A372 (B360 (C292 (D2803、若某几何体的三视图(单位:cm如图所示,则此几何体的体积是(A3523cm3(B3203cm3 (C2243cm3(D1603cm34、一个长方体去掉一个小长方体,所得几何体的正(主视图与侧(左视图分别如右图所示,则该几何体的俯视图为: (5、若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积...等于 (A.2 C..66、图2中的三个直角三角形是一个体积为20cm2的几何体的三视图,则h= cm第2题第5题7、一个几何体的三视图如图所示,则这个几何体的体积为。
8、如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为______.9、如图1,△ ABC 为正三角形,AA '//BB ' //CC ' , CC ' ⊥平面ABC 且3AA '=32BB '=CC '=AB,则多面体△ABC -A B C '''的正视图(也称主视图是(10、一空间几何体的三视图如图所示,则该几何体的体积为( .A.2π+B. 4π+C. 2π+D. 4π 11、上图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是(A .9πB .10πC .11πD .12π第7题侧(左视图正(主视图俯视图俯视图正(主视图侧(左视图12、一个棱锥的三视图如图,则该棱锥的全面积(单位:c2m为((A(B(C(D13、若某几何体的三视图(单位:cm如图所示,则此几何体的体积是3cm.14、设某几何体的三视图如上图所示。
则该几何体的体积为3m15、已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm,可得这个几何体的体积是(A.3 4000 cm3B.3 8000 cm3C.3 2000cmD.34000cm16、一个几何体的三视图如上图所示,其中正视图与侧视图都是边长为2的正三角形,则这个几何体的侧面积为(A.33π B.2πC.3π D.4π第14题正视图侧视图俯视图第17题17、如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积为(A .32πB .16πC .12πD .8π18、下图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是A.9πB.10πC.11π D .12π19、右图是一个多面体的三视图,则其全面积为( AB6C6 D4 20、如图所示,一个空间几何体的正视图和侧视图都是底为1,高为2的矩形,俯视图是一个圆,那么这个几何体的表面积为(A .2πB .52πC .4πD .5π21、一个几何体的三视图及其尺寸(单位:cm如图所示,则该几何体的侧面积为_ ______cm 2.22、如果一个几何体的三视图如图所示(单位长度: cm, 则此几何体的表面积是(A. 2(20cm + B.212cmC. 2(24cm + D. 242cm俯视图左视图俯视图图2723. 如右图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的表面积为A .π3 B .π2 C .π23D .π424. 如下图,某几何体的正视图与侧视图都是边长为1的正方形,且体积为12。
新员工培训课程三视图及基础识图01

新员工入门培训课程---《三视图及基础识图》
五、练一练(1)
分别画出下列立体图形的三视图
新员工入门培训课程---《三视图及基础识图》
五、练一练(2)
你能说出下面这个几何体的三视图吗?
正视图
侧视图
俯视图
新员工入门培训课程---《三视图及基础识图》
六、考考你(1)
题 西 林 苏壁
轼
新员工入门培训课程---《三视图及基础识图》
5、三视图的绘制
常用工具
图
比
板
例
尺
丁字尺
圆
分
规
规
除此之外还有三角板、曲线板、铅笔(硬度:H/HB/B) 分规是用来截取线段和尺寸、等分直线段或圆周。
ቤተ መጻሕፍቲ ባይዱ
新员工入门培训课程---《三视图及基础识图》
5、三视图的绘制
常见的图线说明
图线名称 粗实线 细实线 虚线
3、三视图的展开
大家发现三个视图展开后的方位关系吗?
V
W
高
高
平
平
齐
齐
长对正
H
宽相等 宽相等
任何物体均有前后、左右、上下六个方位,方 位关系是用于分析每一视图如何反映物体的这 些方位。
三视图的展开 以V面为基准,沿 Y 轴剪开,然后 H 面 绕X轴向下转90° W面绕Z轴向右转 90°
三视图的位置 主视图在图纸的左上角 左视图在主视图的正右方 俯视图在主视图的正下方
且投 倾射 斜线 于互 投相 影平 面行
正投影法
斜投影法
工程图样一般都是采用正投影
新员工入门培训课程---《三视图及基础识图》
二、正投影的基本特征 真实性 积聚性 收缩性
三视图识图练习题.docx

三视图1•将长方体截去一个四棱锥后,得到的几何体的直观图如图所示,则该几何体的俯视图为()2.如图,甲、乙、丙是三个立体图形的三视图,与甲、乙、丙相对应的标号是()①长方体;②圆锥;③三棱锥;④圆柱.3.如图所示,下列几何体各自的三视图中,有且仅有两个视图相同的是()4.某几何体的正视图和侧视图均如图所示,则该几何体的俯视图不可能是(15.—个几何体的三视图如右图,则组成该组合体的简单几何体为()A.圆柱与圆台B.四棱柱与四棱台C.圆柱与四棱台D.四棱柱与圆台5.一个长方体截去两个三棱锥,得到的几何体如图所示,则该几何体的三视图为()正视图A.③①②B. ①②③C.③②④D.④②③AD.②④Mr视图6. 将正方体(如图(1)所示)截去两个三棱锥,得到如图(2)所示的几何体,则该几何体的侧视图为7. 如图所示为一个简单几何体的三视图,则其对应的几何体是()&某几何体的直观图如图所示,下列给出的四个俯视图中正确的是()9•一个几何体的三视图如图所示,则该几何体的直观图可以是()俯觇图iE 觇图侧视图 W 8 ® A B C D10.如果用口表示1个立方体,用勿表示2个立方体叠加,用■表示3个立方体叠 A BAB正觇图 韵视图A CBC11 .一个几何体的三视图如图所示,则该几何体的直观图可以是()B.12.下列三视图所对应的直观图是()A.13.下面的三视图对应的物体是()WWW14.如图是哪一个物体的三视图(16.如图是一个物体的三视图,则此三视图所描述物体的直观图是()17.某几何体的三视图如图所示,则这个几何体的直观图是图中的()正视图績视图1&空间几何体的三视图如图所示,则此空间几何体的直观图为(19.某建筑物的三视图如图所示,则此建筑物结构的形状是(A.圆锥B.四棱柱C.从上往下分别是圆锥和四棱柱D.从上往下分别是圆锥和圆柱20.如图所示为一个简单几何体的三视图,则其对应的几何体是()21.已知一个几何体的三视图如图所示,则此几何体的组成为()A.上面为棱台,下面为棱柱B.上面为圆台,下面为棱柱C.上面为圆台,下面为圆柱D.上面为棱台,下面为圆柱22.如图所示为长方体木块堆成的几何体的三视图,此几何体共由 ________ 块木块堆成.23.己知某组合体的正视图与侧视图相同(其中AB=AC,四边形BCDE为矩形),则该组合体的俯视图可以是图中的_________.(把你认为所有正确图象的序号都填上)24._____ 若一个正三棱柱的三视图如图所示,则这个三棱柱的高(两底面之间的距离)和底面边长分别是_____ 和_______ .4—侧觇图VWWW答案解析1.【答案】C【解析】俯视图从图形的上边向下边看,看到一个正方形的底面,在底面上有一条对角线,对角线是由左上角到右下角的线,故选C.2.【答案】D【解析】3.【答案】D【解析】在各自的三视图中①正方体的三个视图都相同;②圆锥有两个视图相同;③三棱台的三个视图都不同;④正四棱锥有两个视图相同.4.【答案】D【解析】根据几何体的三视图知识求解.由于该几何体的正视图和侧视图相同,且上部分是一个矩形,矩形中间无实线和虚线,因此俯视图不可能是D.5.【答案】C【解析】从该几何体可以看出,正视图是一个矩形内有一斜向上的对角线;俯视图是一个矩形內有一斜向下的对角线,没有斜向上的对角线,故排除B、D项;侧视图是一个矩形内有一斜向下的对角线,且都是实线,因为没有看不到的轮廓线,所以排除A项.6.【答案】B【解析】还原正方体后,将6, D, A三点分别向正方体右侧面作垂线.DiA的射影为CiB,且为实线,BiC 被遮挡应为虚线.7.【答案】A【解析】对于A,该几何体的三视图恰好与已知图形相符,故A符合题意;对于B,该几何体的正视图的矩形中,对角线应该是虚线,故不符合题意;对于C,该几何体的正视图的矩形中,对角线应该是从左上到右下的方向,故不符合题意;对于D,该几何体的侧视图的矩形中,对角线应该是虚线,故不符合题意.故选A.&【答案】B【解析】几何体的俯视图,轮廓是矩形,几何体的上部的棱都是可以看见的线段,所以C, D不正确;几何体的上部中间的棱与正视图方向垂直,所以A不正确.故选B.9.【答案】D【解析】由俯视图是圆环可排除A, B, C,进一步将三视图还原为几何体,可得选项D.10.【答案】B【解析】结合已知条件易知B正确.11.【答案】D【解析】由俯视图可知,原几何体的上底面应该是圆面,由此排除选项A和选项C.而俯视图内部只有一个虚圆,所以排除B.故选D.12.【答案】C【解析】从俯视图可以看出直观图的下面部分为长方体,上面部分为圆柱,且与下面的长方体的顶面的两边相切,由侧视图可以看出上下部分高度相同.只有C满足这两点,故选C.13.【答案】D【解析】从俯视图可以看出直观图的下面部分为三个长方体,且三个长方体的宽度相同.只有D 满足这两点,故选D.14.【答案】C【解析】经分析可知,该物体应该是一个圆柱竖直放在一个长方体上,A中的不是一个圆柱,故排除.B 中的圆柱直径小于长方体的宽.D项中上面不是一个圆柱体.故选C.15.【答案】B【解析】由己知中的三视图可得该几何体是一个组合体,由几何体上部的三视图均为矩形可知上部是四棱柱,由下部的三视图中有两个梯形可得下部为四棱台,故组成该组合体的简单几何体为四棱柱与四棱台,故选B.16.【答案】D【解析】正视图和侧视图相同,说明组合体上面是锥体,下面是正四棱柱或圆柱,由俯视图可知下面是圆柱.故选D.17.【答案】B【解析】由正视图可排除A, C选项;由侧视图可排除D选项,综合三视图可得,B选项正确.故选B.18.【答案】A【解析】由已知中三视图的上部分是锥体,是三棱锥,满足条件的正视图的选项是A与D,由侧视图可知,选项D不正确,由三视图可知该几何体下部分是一个四棱柱,选项都正确,故选A.19.【答案】C【解析】由图可得该几何体是一个组合体,其上部的三视图有两个三角形,一个圆,故上部是一个圆锥,其下部的三视图均为矩形,故下部是一个四棱柱.故选C.20.【答案】A【解析】对于A,该几何体的三视图恰好与已知图形相符,故A符合题意;对于B,该几何体的正视图的矩形中,对角线应该是虚线,故不符合题意;对于C,该几何体的正视图的矩形中,对角线应该是从左上到右下的方向,故不符合题意;对于D,该几何体的侧视图的矩形中,对角线应该是虚线,故不符合题意.故选A.21.【答案】C【解析】结合图形分析知上为圆台,下为圆柱.故选C.22.【答案】4【解析】由三视图知,由4块木块组成.如图.23.【答案】①②③④【解析】由正视图和侧视图可知几何体为锥体和柱体的组合体.(1)若几何体为圆柱与圆锥的组合体,则俯视图为③;(2)若几何体为棱柱与圆锥的组合体,则俯视图为④;(3)若几何体为棱柱与棱锥的组合体,则俯视图为①;(4)若几何体为圆柱与棱锥的组合体,则俯视图为②.24.【答案】2陋3【解析】25.【答案】三视图对应的几何体如下图所示.“长方体【解析】。
工程制图三视图习题集

6-44 求作俯视图。
圆球
圆柱孔
圆柱
东南大学 交通学院 制图教研室
6-45 求作左视图。
东南大学 交通学院 制图教研室
6-46 求作左视图。
东南大学 交通学院 制图教研室
6-47 求作俯视图。
东南大学 交通学院 制图教研室
6-48 求作俯视图。
东南大学 交通学院 制图教研室
6-26 作左视图。
东南大学 交通学院 制图教研室
6-27 求作左视图。
东南大学 交通学院 制图教研室
6-27 求作左视图。
东南大学 交通学院 制图教研室
6-28 求作俯视 图。
东南大学 交通学院 制图教研室
6-28 求作俯视 图。
东南大学 交通学院 制图教研室
6-29 求作俯视 图。
东南大学 交通学院 制图教研室
6-23 求作俯视 图。
东南大学 交通学院 制图教研室
6-24 求作俯视图。
东南大学 交通学院 制图教研室
6-24 求作俯视图。
东南大学 交通学院 制图教研室
6-25 求作俯视图。
东南大学 交通学院 制图教研室
6-25 求作俯视图。
东南大学 交通学院 制图教研室
6-26 作左视图。
东南大学 交通学院 制图教研室
⑴
⑵
⑶
⑷
正确旳左视图是 ⑷
东南大学 交通学院 制图教研室
6-40已知主视图和俯视图,选择正确旳左视图。
⑴
⑵
⑶
⑷
正确旳左视图是 ⑷
东南大学 交通学院 制图教研室
6-41 求作俯视图。
东南大学 交通学院 制图教研室
6-42 补全主视图和俯视图中所缺旳线。
三视图练习题及答案

三视图练习题及答案三视图是工程设计、制图等领域中常用的表达方式之一,它能够以三个不同的视角展示一个物体的外观和内部结构,帮助人们更好地理解和分析物体的形状和构造。
为了提高对三视图的理解和应用能力,下面将给出一些三视图练习题及答案,希望对读者有所帮助。
1. 请根据给出的三视图,画出物体的立体图。
答案:根据三视图,我们可以确定物体的形状和尺寸,然后利用透视法将其转化为立体图。
在绘制过程中,需要注意比例和透视关系,以保证立体图的准确性。
2. 给出一个物体的立体图,请根据立体图绘制出相应的三视图。
答案:在绘制三视图时,我们需要观察立体图中的各个面,然后根据其相对位置和大小来绘制对应的正视图、俯视图和侧视图。
在绘制过程中,需要注意比例和尺寸的准确性,以确保三视图能够准确地表达立体图的形状和结构。
3. 请根据给出的三视图,判断物体的形状是什么?答案:通过观察三视图中的线条和面,我们可以判断物体的形状。
例如,如果正视图中的线条是直的,侧视图中的线条是弯曲的,那么物体可能是一个圆柱体。
通过观察三视图中的特征,我们可以逐步推断出物体的形状。
4. 给出一个物体的形状,请根据形状绘制出相应的三视图。
答案:在绘制三视图时,我们需要观察物体的形状和结构,然后根据其特征来绘制对应的正视图、俯视图和侧视图。
在绘制过程中,需要注意线条的粗细和长度,以确保三视图能够准确地表达物体的形状和结构。
通过以上的练习题和答案,我们可以提高对三视图的理解和应用能力。
练习三视图不仅可以帮助我们更好地理解和分析物体的形状和结构,还可以提高我们的制图能力和空间想象力。
在实际工程设计和制图中,三视图是非常重要的表达方式,掌握好三视图的绘制和解读技巧对于工程师和设计师来说是非常必要的。
总之,通过不断地练习和应用,我们可以提高对三视图的掌握程度,为工程设计和制图提供更准确、更有效的表达方式。
希望以上的练习题和答案能够对读者有所帮助,进一步提高对三视图的理解和应用能力。
机械制图-三视图练习
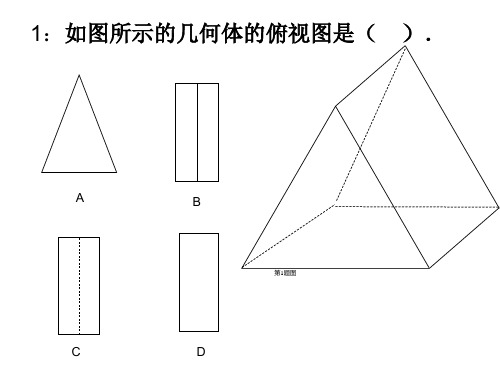
A
B
C.
D
A.圆锥 柱
主视图
左视图
C.长方体 俯视图 D. 球体
23. 如图,空心圆柱的左视图是( )
B.圆
24. 如图所示的几何体的俯视图是 () 25. 如图所示的几何体的正视图是( )
(第6题图)
A.
B.
C.
D.
26. 如图,是由两个相同的小正方体和一个圆锥 体组成的立体图形,其俯视图是( )
A.
B.
12. 如图所示的物体的俯视图是( )
13. 由5个相同的正方体搭成的几何体如图所示, 则它的左视图是( )
主视方向
A.
B.
C.
D.
14. 下列四个几何体中,主视图是三角形的是( )
15. 如图所示的物体由两个紧靠在一起的圆柱体组 成,它的主视图是( )
16. 如图,下列水平放置的几何体中,主视图不是 长方形的是( )
9:骰子是一种特A 别的数字B 立方体C ,它符D 合 规则:相对两面的点数之和总是7.下面四 幅图中可以折成符合规则的骰子的是 ()
10:画下面几何体的三视图
从上面看
主视图
从左面看
左视图
从正面看
俯视图
11:由一些大小相同的小正方体组成的几何体的主 视图和俯视图
(1)请你画出这个几何体的一种左视图;
B.5 D.3
19. 将两个大小完全相同的杯子(如图甲)叠放在一起( 如图乙),则图乙中实物的俯视图是( ).
20. 如图3,是由四个相同的小正方形组成的立体 图形,它的左视图是( )
图3
主视方
A
B
C
D
向
21. 下列所给的几何体中,主视图是三角形的是( )
三视图练习题有答案
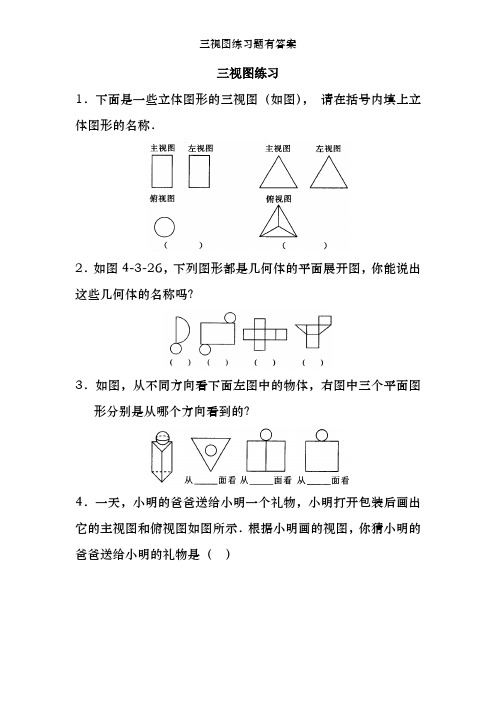
三视图练习1.下面是一些立体图形的三视图(如图),•请在括号内填上立体图形的名称.2.如图4-3-26,下列图形都是几何体的平面展开图,你能说出这些几何体的名称吗?3.如图,从不同方向看下面左图中的物体,右图中三个平面图形分别是从哪个方向看到的?4.一天,小明的爸爸送给小明一个礼物,小明打开包装后画出它的主视图和俯视图如图所示.根据小明画的视图,你猜小明的爸爸送给小明的礼物是()A.钢笔B.生日蛋糕C.光盘D.一套衣服5.一个几何体的主视图和左视图如图所示,它是什么几何体?请你补画出这个几何体的俯视图.6.一个物体的三视图如图所示,试举例说明物体的形状.7.已知一个几何体的三视图如图所示,则该几何体的体积为多少?8.已知几何体的主视图和俯视图如图所示.(1)画出该几何体的左视图;(2)该几何体是几面体?它有多少条棱?多少个顶点?(3)该几何体的表面有哪些你熟悉的平面图形?9.小刚的桌上放着两个物品,它的三视图如图所示,你知道这两个物品是什么吗?10.一个由几个相同的小立方体搭成的几何体的俯视图如图所示,方格里的数字表示该位置的小立方体的个数,请你画出这个几何体的主视图和左视图.11.如图所示,下列三视图所表示的几何体存在吗?如果存在,请你说出相应的几何体的名称.12.由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图所示,俯视图的方格中的字母和数字表示该位置上小立方体的个数,求x,y的值.13.马小虎准备制作一个封闭的正方体盒子,他先用5•个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在下图中的每个图形上再接一个正方形,•使新拼接成的图形经过折叠能成为一个封闭的正方体盒子.(注:添加的正方形用阴影表示)14.由几个小立方体叠成的几何体的主视图和左视图如图,求组成几何体的小立方体个数的最大值与最小值.参考答案:1.圆柱,正三棱锥2.圆锥圆柱正方体三棱柱3.上正侧4.B 5.略6.如粉笔,灯罩等7.1208.(1)略(2)六面体,12条,8个(3)等腰梯形,•正方形9.长方体木板的正前方放置了一个圆柱体10.略11.不存在12.1或2,3 13.略14.12个,7个。
(完整word版)三视图练习 (2)

三视图练习1.一个几何体的三视图如右图所示,它的正视图和侧视图均为半圆,俯视图为圆,则这个空间几何体的体积是( ) A .32π B .34π C .π4 D .π32.有一个几何体的三视图及其尺寸如下图(单位:cm),则该几何体的表面积为( )A .12πcm 2B .15πcm 2C .24πcm 2D .36πcm 23.某几何体的三视图如图所示,根据图中标出的数据.可得这个几何体的表面积为( )A.错误!未找到引用源。
B.错误!未找到引用源。
C.错误!未找到引用源。
D.124.如图,网格纸上小正方形边长为1,粗线是一个棱锥的三视图,则此棱锥的体积为( ). (A )38 (B )34(C )34 (D)325.一个简单几何体的三视图如图所示,其正视图和俯视图均为正三角形,侧视图为腰长是2的等腰直角三角形则该几何体的体积为( )A .B .1C .D .36.某几何体的三视图如图所示(单位:cm ),则该几何体的侧面PAB 的面积是( ) A .7B .2C .1D .37.说出下列三视图(依次为主视图、左视图、俯视图)表示的几何体是( )A .六棱柱B .六棱锥C .六棱台D .六边形8.一个空间几何体的三视图如图所示,则该几何体的体积为( )A .56πcm 3 B .3πcm 3 B .C .32πcm 3 D .37πcm 3 9.右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( ) (A)9π (B )10π (C)11π (D)12π10.用若干单位正方体搭一个几何体,使它的正视图和俯视图如图所示,则它的体积的最大值和最小值分别为( )A. 9,14B.7,13C. 8,14D. 9,13 11.已知某几何体的三视图如上图所示,其中正视图,侧视图均是由三角形与半圆构成,视图由圆与内接三角形构成,根据图中的数据可得此几何体的体积为( ) (A)2132π+(B)4136π+ (C)132+(D) 166+12.一个几何体的三视图如图所示,则该几何体的体积为( )(A)92 (B)72(C)3 (D)4 13.右图是一个几何体的三视图,根据图中数据,可得该几何体的体积是( )(A) 9π (B)1333π- (C )103π (D)133π 14.一个几何体的三视图如图所示,则该几何体的体积是( ) (A )64 (B )72 (C )80(D )11215.一个几何体的三视图如图所示,则该几何体的体积是( )A .64B .72C .80D .11216.已知一个几何体的三视图如下图所示(单位:cm),其中正视图是直角梯形,侧视图和俯视图都是矩形,则这个几何体的体积是________cm 3.17.如图为一个几何体的三视图,其中俯视为正三角形,A 1B 1=2,AA 1=4,则该几何体的表面积为_______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
10.如果用□表示1个立方体,用 表示2个立方体叠加,用■表示3个立方体叠加,那么图中由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是()
11.一个几何体的三视图如图所示,则该几何体的直观图可以是()
A. B. C. D.
12.下列三视图所对应的直观图是()
17.【答案】B
【解析】由正视图可排除A,C选项;由侧视图可排除D选项,综合三视图可得,B选项正确.故选B.
18.【答案】A
【解析】由已知中三视图的上部分是锥体,是三棱锥,满足条件的正视图的选项是A与D,由侧视图可知,选项D不正确,由三视图可知该几何体下部分是一个四棱柱,选项都正确,故选A.
6.【答案】B
【解析】还原正方体后,将D1,D,A三点分别向正方体右侧面作垂线.D1A的射影为C1B,且为实线,B1C被遮挡应为虚线.
7.【答案】A
【解析】对于A,该几何体的三视图恰好与已知图形相符,故A符合题意;对于B,该几何体的正视图的矩形中,对角线应该是虚线,故不符合题意;对于C,该几何体的正视图的矩形中,对角线应该是从左上到右下的方向,故不符合题意;对于D,该几何体的侧视图的矩形中,对角线应该是虚线,故不符合题意.故选A.
A.圆柱与圆台B.四棱柱与四棱台
C.圆柱与四棱台D.四棱柱与圆台
5.一个长方体截去两个三棱锥,得到的几何体如图所示,则该几何体的三视图为()
6.将正方体(如图(1)所示)截去两个三棱锥,得到如图(2)所示的几何体,则该几何体的侧视图为()
7.如图所示为一个简单几何体的三视图,则其对应的几何体是()
8.某几何体的直观图如图所示,下列给出的四个俯视图中正确的是()
【解析】由已知中的三视图可得该几何体是一个组合体,由几何体上部的三视图均为矩形可知上部是四棱柱,由下部的三视图中有两个梯形可得下部为四棱台,故组成该组合体的简单几何体为四棱柱与四棱台,故选B.
16.【答案】D
【解析】正视图和侧视图相同,说明组合体上面是锥体,下面是正四棱柱或圆柱,由俯视图可知下面是圆柱.故选D.
11.【答案】D
【解析】由俯视图可知,原几何体的上底面应该是圆面,由此排除选项A和选项C.而俯视图内部只有一个虚圆,所以排除B.故选D.
12.【答案】C
【解析】从俯视图可以看出直观图的下面部分为长方体,上面部分为圆柱,且与下面的长方体的顶面的两边相切,由侧视图可以看出上下部分高度相同.只有C满足这两点,故选C.
13.【答案】D
【解析】从俯视图可以看出直观图的下面部分为三个长方体,且三个长方体的宽度相同.只有D满足这两点,故选D.
14.【答案】C
【解析】经分析可知,该物体应该是一个圆柱竖直放在一个长方体上,A中的不是一个圆柱,故排除.B中的圆柱直径小于长方体的宽.D项中上面不是一个圆柱体.故选C.
15.【答案】B
①长方体;②圆锥;③三棱锥;④圆柱.
A.③①②B. ①②③C.③②④D.④②③
3.如图所示,下列几何体各自的三视图中,有且仅有两个视图相同的是( )
A.①②B.①③C. ①④D.②④
4.某几何体的正视图和侧视图均如图所示,则该几何体的俯视图不可能是( )
15.一个几何体的三视图如右图,则组成该组合体的简单几何体为()
【解析】在各自的三视图中①正方体的三个视图都相同;②圆锥有两个视图相同;③三棱台的三个视图都不同;④正四棱锥有两个视图相同.
4.【答案】D
【解析】根据几何体的三视图知识求解.
由于该几何体的正视图和侧视图相同,且上部分是一个矩形,矩形中间无实线和虚线,因此俯视图不可能是D.
5答案】C
【解析】从该几何体可以看出,正视图是一个矩形内有一斜向上的对角线;俯视图是一个矩形内有一斜向下的对角线,没有斜向上的对角线,故排除B、D项;侧视图是一个矩形内有一斜向下的对角线,且都是实线,因为没有看不到的轮廓线,所以排除A项.
三视图识图练习
———————————————————————————————— 作者:
———————————————————————————————— 日期:
三视图
1.将长方体截去一个四棱锥后,得到的几何体的直观图如图所示,则该几何体的俯视图为()
2.如图,甲、乙、丙是三个立体图形的三视图,与甲、乙、丙相对应的标号是()
8.【答案】B
【解析】几何体的俯视图,轮廓是矩形,几何体的上部的棱都是可以看见的线段,所以C,D不正确;几何体的上部中间的棱与正视图方向垂直,所以A不正确.故选B.
9.【答案】D
【解析】由俯视图是圆环可排除A,B,C,进一步将三视图还原为几何体,可得选项D.
10.【答案】B
【解析】结合已知条件易知B正确.
18.空间几何体的三视图如图所示,则此空间几何体的直观图为()
A. B. C. D.
19.某建筑物的三视图如图所示,则此建筑物结构的形状是()
A.圆锥B.四棱柱
C.从上往下分别是圆锥和四棱柱D.从上往下分别是圆锥和圆柱
20.如图所示为一个简单几何体的三视图,则其对应的几何体是( )
A. B. C. D.
24.若一个正三棱柱的三视图如图所示,则这个三棱柱的高(两底面之间的距离)和底面边长分别是________和________.
答案解析
1.【答案】C
【解析】俯视图从图形的上边向下边看,看到一个正方形的底面,在底面上有一条对角线,对角线是由左上角到右下角的线,故选C.
2.【答案】D
【解析】
3.【答案】D
21.已知一个几何体的三视图如图所示,则此几何体的组成为()
A.上面为棱台,下面为棱柱B.上面为圆台,下面为棱柱
C.上面为圆台,下面为圆柱D.上面为棱台,下面为圆柱
22.如图所示为长方体木块堆成的几何体的三视图,
此几何体共由________块木块堆成.
23.已知某组合体的正视图与侧视图相同(其中AB=AC,四边形BCDE为矩形),则该组合体的俯视图可以是图中的________.(把你认为所有正确图象的序号都填上)
A. B. C. D.
13.下面的三视图对应的物体是()
A. B. C. D.
14.如图是哪一个物体的三视图()
A. B. C. D.
16.如图是一个物体的三视图,则此三视图所描述物体的直观图是()
A. B. C. D.
17.某几何体的三视图如图所示,则这个几何体的直观图是图中的()
A. B. C. D.
