消费者理论：对偶与显示偏好

合集下载

01消费者理论：偏好、效用、约束与选择.

Consumer’s Theory
Ranking也意味着，无差异曲线不能相交
1.1.2
偏好关系与理性
14
人并不总是理性的过于自信
• 中彩者（中彩的金额平均为$479545）与没有中彩的人之间的幸福感没有显著的差异，中彩后，中彩者的生活幸福水平并没有提高！！！那为什么还去买彩票？
Consumer’s Theory
R
n +
9
考虑定义在消费集 X
x1 x2：
上的二元关系“ ”
• “x1 至少与x2一样好” • 或 “x1 不比x2差”
Consumer’s Theory
1.1.1
偏好关系三个公理
10
Axiom 1：完备性(Completeness) x1,x2X，有x1 x2或x2 x1。
消费者理论
版权所有，仅供复旦大学学生学习使用，未经允许请勿擅自引用或传播
Consumer’s Theory
2
一、偏好、效用、约束、选择二、需求三、比较静态分析
Consumer’s Theory
四、显示偏好
一、偏好、效用、约束与选择
Preference, Utility, Constraint and Choice
22
偏好关系具有何种性质才能用一个连续的实值函数来表示？即效用函数的存在性问题。 Debreu(1954)：任意满足公理1、2与连续性的二元关系都可以用连续的实值函数来代表。(MWG) 这说明，存在性并不依赖于对“tastes”的假设为了简化数学证明、增强直感性，严格单调性也被引入“存在性定理” 效用函数的存在性定理：如果二元关系满足完备性、传递性、连续性和严格单调性，那么就存在 n u ( ) : R R 来连续的实值函数（效用函数）：表示偏好关系

7显示偏好理论

图形表示。
2.2、显示偏好原理直接显示偏好：（x1，x2）是在价格（p1，
p2）下选择的消费束，（y1，y2）是使 p1x1+p2x2≥p1y1+p2y2
成立的另一个消费束。
同时假设消费者总是在他能够购买的消费束中选择他最偏好的消费束。
那么，有偏好关系（x1，x2）}（y1，y2）。
原因：第二个价格下第一个消费束是可选择的，假设第一个消费束的福利更高，消费者就选择第一个。事实相反，表明假设错误。
4.2、不同时间消费状况的福利比较数量指数：(w1x1t+w2x2t)/(w1x1b+w2x2b)
拉氏数量指数Lq、帕氏数量指数Pq。 Lq =(p1bx1t+p2bx2t)/(p1bx1b+p2bx2b) Pq =(p1tx1t+p2tx2t)/(p1tx1b+p2tx2b) 帕氏数量指数大于1，t时期福利较好。
价格为（p1，p2）购买的消费束。对另一个消费束（y1，y2），如果有：
p1x1+p2x2≥p1y1+p2y2
那么（x1，x2）比（y1，y2）先被选择。
注释: 通常人们使用“显示偏好”，考虑到后面显
示偏好原理也是用类似的词，所以使用“先被选择”。
所以，（x1，x2）比（y1，y2）先被选择。也就是说，（x1，x2）被直接显示偏好于（y1，y2）。
场的资源配置。这与通常的需求分析相对应。
消费者行为分析集中体现理性原理。
主要有两种方法：效用最大化模型、显示偏好模型。
1.2、效用最大化模型基本思想：假设消费者心中存在一个偏好，
消费者是按照自己的偏好配置资源。给定偏好和资源约束，用效用函数描述偏好，把消费者资源配置问题归纳为效用最大化模型。

第三章显示偏好理论..

瓦尔拉斯律是说消费者花费掉她的所有财富，从广义上理解，消费者在生命期内花费掉她的所有资源。
，对所

经济管理学院
经济系
中级微观经济学
瓦尔拉斯需求函数实际上是给出了一个选择
规则，进而给出了一个选择结构。这样一个选择
结构满足显示偏好弱公理用瓦尔拉斯需求函数可
表述为：（为简单见，假设x（p，m）是单值的并且假设它是连续可微的）
假设某个人在消费集X上有一个理性偏好关系义可产生一个选择结构，对于X 中的一个非空子集族B，定，由此，我们说这个
选择结构是由理性偏好关系
产生的。
经济管理学院
经济系
中级微观经济学

命题 3.1: 假设
产生的选择结构
是理性偏好关系，那么由
满足显示偏好弱公理。
这个命题表明，如果消费者行为是为了追求效用最大化，那么她的行为一定满足显示偏好弱公理。从这个意义上说，显示偏好理论是偏好理论的一般化。
中级微观经济学
第三章显示偏好理论
显示偏好理论是模型消费者选择行为
的另一种方法，它是直接对消费者行为强
加一个显示偏好弱公理，这类似于偏好理
论对消费者偏好强加一个理性假设，显示
偏好理论是偏好理论的一般化。
经济管理学院
经济系
中级微观经济学
一、选择规则
消费者选择行为用选择结构来表示，一个选
择结构由两部分组成：

命题3.2: 如果是一个选择结构满足（1）显示偏好弱公理，
（2）B中包含X中的所有元素个数小于或
等于2的子集。
那么存在一个理性化偏好关系
而言理性化选择规则化偏好关系是唯一的。
相对于B
，并且这样的理性

中级微观经济学讲义-2

第二讲消费者理论
四、显示偏好简介
（一）显示偏好弱公理
与古典的从偏好关系到效用函数再到需求函数的逻辑思路不同，求函数的逻辑思路不同，萨缪尔森从行为结果本身推导人的行为准则，抛却了效用理论果本身推导人的行为准则，中的许多主管假定，而仅需要一些隐含的、中的许多主管假定，而仅需要一些隐含的、弱的要求，比如一致性。弱的要求，比如一致性。
第二讲消费者理论
二、效用最大化与支出最小化
（二）效用最大化－续（2）效用最大化－
罗伊恒等式】【罗伊恒等式】构造拉格朗日函数 L( x , λ ) = u( x ) + λ ( y − px )， ∂v ( p, y ) ∂L( x * , λ* ) 根据包络定理，根据包络定理， = = λ*以及 ∂y ∂y ∂v ( p, y ) ∂L( x * , λ* ) = = − λ* x i*，可以得到 ∂ pi ∂p i ∂v ( p , y ) − ∂ pi x i* = x i ( p, y ) = ∂v ( p , y ) ∂y
x 2 f x1 , ∀t ∈ [0,1] ⇒ x t = tx 2 + (1 − t )x1 ~ x1 f ~ 公理 7 : 严格凸性 x 2 ≠ x1 , x 2 f x1 ⇒ x t f x1 ~ (排除了无差异集凹向原点 < 多元化消费 > )
第二讲消费者理论
一、偏好、效用与预算偏好、
第二讲消费者理论
一、偏好、效用与预算偏好、
（一）偏好关系－续（1）偏好关系－
偏好公理：偏好公理：公理 4 : 局部非饱和性公理 5 : 严格单调性公理 6 : 凸性 ∀x 0 ∈ R n , ∃ε > 0 , ∃x ∈ B ε ( x 0 ) I R n ⇒ x f x 0 + + (排除了无差异区域的存在 ) ∀x 0， x1 ∈ R n ， x1 ≥ x 0 ⇒ x1 f x 0 + ~ (排除了无差异集向上弯曲)

北大高微讲义第3章显示偏好理论

所以,有(x1j − x0j ) = (x2j − x0j ) + (x1j − x2j )
两边同除以∆pj
,得:
(x1j − x0j ) ∆p j
=
(x2j − x0j ) ∆p j
+
(x1j − x2j ) ∆p j
(2)
以(1)替代(2)中最后一项的∆pj ,有:
(x1j − x0j ) ∆p j
设 x t 是价格 p t时被选择的商品束 , x是使得pt xt > pt x 的另一个商品束, 则称 x t 直接地显示出严格优于 x。记为：xt P D x
4
3.1 显示偏好公理
3、间接显示偏好( indirectly revealed preference) 亦称：传递闭包关系（transitive closure）
即: ∆p∆x ≤ 0
22
3.4 希克斯补偿和斯拉茨基补偿
二、显示偏好和两种补偿的符号：
结论：
对于两种不同定义的补偿效应的符
号来说，均有
∆p∆x ≤ 0
23
3.4 希克斯补偿和斯拉茨基补偿
三、希克斯补偿需求曲线和斯拉茨基补偿需求曲线
24
第3章显示偏好理论
• 3.1 显示偏好公理 • 3.2 显示偏好和无差异曲线 • 3.3 显示偏好和斯拉茨基方程 • 3.4 希克斯补偿和斯拉茨基补偿 • 3.5 显示偏好和生活水平比较
第1部分消费者行为理论
• 第1章消费者的最优决策 • 第2章比较静态分析 • 第3章显示偏好理论 • 第4章需求 • 第5章消费者的福利变化 • 第6章库恩 --- 塔克条件 • 第7章不确定条件下的个人选择

7、消费者行为理论_显示偏好

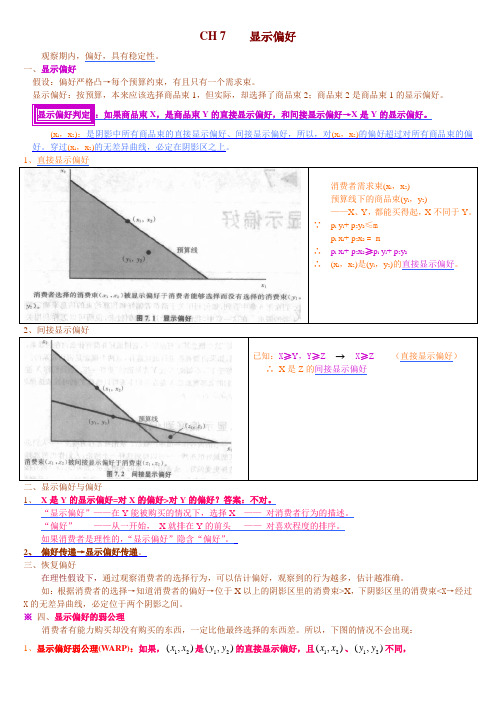
CH 7 显示偏好观察期内，偏好，具有稳定性。

一、显示偏好假设：偏好严格凸→每个预算约束，有且只有一个需求束。

显示偏好：按预算，本来应该选择商品束1，但实际，却选择了商品束2；商品束2是商品束1的显示偏好。

(x l ，x 2)：是阴影中所有商品束的直接显示偏好、间接显示偏好，所以，对(x l ，x 2)的偏好超过对所有商品束的偏好。

穿过(x l ，x 2)的无差异曲线，必定在阴影区之上。

2、间接显示偏好已知：X ≥Y ，∴ X 是Z 二、显示偏好与偏好1、 X 是Y 的显示偏好=对X 的偏好>对Y 的偏好？答案：不对。

“显示偏好”——在Y 能被购买的情况下，选择X —— 对消费者行为的描述。

“偏好” ——从一开始， X 就排在Y 的前头 —— 对喜欢程度的排序。

如果消费者是理性的，“显示偏好”隐含“偏好”。

2、偏好传递→显示偏好传递。

三、恢复偏好在理性假设下，通过观察消费者的选择行为，可以估计偏好，观察到的行为越多，估计越准确。

如：根据消费者的选择→知道消费者的偏好→位于X 以上的阴影区里的消费束>X ，下阴影区里的消费束<X →经过X 的无差异曲线，必定位于两个阴影之间。

※ 四、显示偏好的弱公理消费者有能力购买却没有购买的东西，一定比他最终选择的东西差。

所以，下图的情况不会出现： 1、显示偏好弱公理(W ARP)：如果，12(,)x x 是12(,)y y 的直接显示偏好，且12(,)x x 、12(,)y y 不同，那么，12(,)y y 不可能是12(,)x x 的直接显示偏好。

换言之：如果，商品束12(,)x x 的价格12(,)p p ，商品束12(,)y y 的价格12(,)q q ，那么，只要 p l x l + p 2x 2≥p l y l + p 2y 2（价格相同），就不可能有 q l y l + q 2y 2≥q l x l + q 2x 2。

第07章-显示偏好

x2
x2*
在凸性、单调良性偏好下，在凸性、单调良性偏好下，在预算约束下，在预算约束下，存在一个最优消费束。最优消费束。
x1*
x1
1. 直接显示偏好 Direct Preference Revelation
x2
消费束X 消费束X*和Y都满足预算约束，但消费者选择了约束，
x* y
消费束 x*，而没有选择说明什么？消费束 y。说明什么？
C
B 与B
A B C D
I
D
A
B
B
C D
A
D
C, B
D
A ，且 C
有C
I
A，A ，
I
B, B
I
违反显示偏好强公理
≺ ≺ ≺ ≺
D
≺ ≺ ≺ ≺
≺ ≺ ≺ ≺
≺ ≺ ≺ ≺
≺ ≺ ≺ ≺
≺ ≺ ≺ ≺
A
C
B C
D D
恢复偏好（无差异曲线） Recovering Indifference Curves
(10, 1) $22 $21 $12
(5, 5) $20 $15 $15
(5, 4) $18 $14 $13
圈中的消费束消费者能支付，但他没有选择。圈中的消费束消费者能支付，但他没有选择。
C hoices ( 10, 1) ( 5, 5) ( 5, 4) Prices ( $2, $2) $22 ( $2, $1) $21 ( $1, $2) $12 $20 $15 $15 $18 $14 $13
第六讲
第七章显示偏好
Revealed Preference
第七章显示偏好－－主要要点
显示偏好的概念 – 直接显示偏好和间接显示偏好显示偏好弱公理和显示偏好强公理检验消费者的行为是否效用最大化行为恢复偏好

02消费者理论：需求

2.4.3 补偿需求函数的性质
32
PubliCcoFnsinuamnecre’s Theory
❖Prop. 1：h(p,u)在
n
上是连续函数
❖Prop. 2：h(p,u)是p的零次齐次函数
h(tp,u)=h(p,u), t>0
证明：Shephard’s Lemma
❖Prop. 3：The Compensated Law of
e(pt,u)=ptxt=tp1xt+(1-t)p2xt≥tp1x1+(1-t)p2x2，即e(pt,u)≥te(p1,u)+(1-t)e(p2,u)，从而e(p,u)对
p凹。
PubliCcoFnsinuamnecre’s Theory
支出函数的性质
20
PubliCcoFnsinuamnecre’s Theory
29
(Substitution Effect & Income Effect)
x2 m/p2
o
x0 xh
x0=x(p0,m) x1=x(p1,m)
xh=h(p1,u0)
x1
=x(p1,m+m)
u1 u0
x1
PubliCcoFnsinuamnecre’s Theory
Hicks补偿
Substitution Effect & Income Effect 30
❖ 在现代理论中，效用函数仅仅是一个归纳消费者偏好所包含的信息的方便工具
偏好关系
“Represent”
PubliCcoFnsinuamnecre’s Theory
无差异曲线
效用函数
补充说明
4
❖偏好假设（or理性偏好or一致偏好）对于现代消费者理论是必需的吗？

显示性偏好理论

显示性偏好理论（Revealed Preference Theory）显示性偏好的概述显示性偏好理论（Revealed Preference Theory）是由美国经济学家保罗·萨默尔森（P.Samuelson）提出来的，其基本精神是：消费者在一定价格条件下的购买行为暴露了或显示了他内在的偏好倾向。

因此我们可以根据消费者的购买行为来推测消费者的偏好。

这是一种不基于“偏好关系（效用函数）—消费者选择”的逻辑思路，而是一个相反的过程，即“消费者选择—偏好关系”。

该理论可以从消费者行为分辨最好的可能选择。

换句话说，消费者的消费习惯可以显示他们的喜好。

理论的出现，是基于消费者需求理论以边际替代率作为依归。

而边际替代率的假设，就是消费者是为了把功用极大化而作消费决定。

虽然公用极大化的假设不受争议，但需求理论隐含着的功用函数就难以被准确计算。

显示行偏好理论就能弥补需求理论的不足，借观察行为来界定功用函数。

假设某甲有两个消费选择：买两个苹果和三条香蕉，或者买三条香蕉和两个苹果。

如果两个选择的费用一样，而他选了前者，那就表示某甲喜欢前者多于后者。

然后，这显示前者永远都较后者受欢迎。

如果该消费者买后者，就一定是他负担不起买前者的费用。

该理论进一步显示，偏好是带有传递关系的。

如果我们有A、B、C 到Z 多个选择，而偏好 A 多于 B 、B 多于 C ，如此类推。

那结论就显示出，我们对 A 的偏好多于 C ，一直数下去，多于Z 。

有了这套理论，经济学家就可以规划与消费者理论的模组一致的无差异曲线。

显示性偏好的内容一、显示偏好原理设消费者在价格为（p1,p2）时购买的商品束为（x1,x2），如果另一个商品组合（y1,y2）满足如下条件：方程1在这种情况下，若消费者总是在他能够购买的商品束中选择他最偏好的商品束，则一定有对（x1,x2）的偏好大于（y1,y2），即（x1,x2）是（y1,y2）的直接显示偏好。

二、间接显示性偏好和无差异曲线1．间接显示性偏好如果（x1,x2）是（y1,y2）的直接显示偏好，同时（y1,y2）是（z1,z2）的直接显示偏好，则（x1,x2）是（z1,z2）的间接显示偏好。

第一讲消费者行为理论(6)显示偏好

p 1 x1 p 2 x 2 m p1 y1 p 2 y 2 m
p 1 x1 p 2 x 2 p 1 y1 p 2 y
( x 1 , x 2 ) ( y1 , y 2 )
如果在(y1,y2)支付得起的条件下，消费者没有选择(y1,y2)而选择(x1,x2) ，那么对(x1,x2)的偏好就一定超过对(y1,y2)的偏好。
当 Pq p1 x 1 p 2 x 2
t t t t
p1 x 1 p 2 x 2
t b t
b
1
这表明在时期t消费者的境况改善了，并且（x1t,x2t）是（x1b,x2b）的显示偏好。
当 Pq p1 x 1 p 2 x 2
t t t t
p1 x 1 p 2 x 2
t b t
消费者的境况在时期b要比时期t好。
拉氏价格指数、总支出指数和显示偏好及消费者福利之间的关系
Lp
消费者的境况在时期t要比时期b好。
利用各种指数判断消费者福利
判断条件
拉氏数量指数小于1 帕氏数量指数大于1 拉氏价格指数小于M 帕氏价格指数大于M
T时期的消费者福利状况（相对于基期）变差
变好变好变差
（二）显示偏好强公理
对于一个理性消费者来说，如果(x1,x2)被直接或间接显示偏好于(y1,y2) ，且(x1,x2)和 (y1,y2)不同，那么(y1,y2)就不可能被直接或间接显示偏好于(x1,x2) 。强公理是最优化行为的充分条件。
三、显示性弱偏好公理的应用：指数和消费者福利
1．数量指数、显示偏好及消费者福利的关系数量指数：以价格为权重计算的一种衡量消费量变动情况的指数设在初始期（即基期）b，价格水平为（p1b,p2b ），消费者的选择为（ x1b,x2b ），而在时期 t ，价格水平为（p1t,p2t），消费者的选择为（x1t,x2t）。帕氏数量指数----以t的价格为权重

中级微观经济学讲义-对偶性质和劳动供给

v( p , y )) e( p , v( p , y ))
0 1 0 0
这个支出还是等于原来的名义收入y 吗？
第二讲消费者理论
五、消费者福利
X2
v( p0 , y EV ) v( p1 , y )
EV
X1
等价变化示意图
第二讲消费者理论
五、消费者福利
（四）斯克斯需求与福利效应
E1 A C
E2
第二讲消费者理论
三、需求定律
（三）需求定律（续）
修正
限制所有商品都是正常商品限制偏好是拟线性偏好。限制需求为市场需求。
“吉芬之谜”
思考：“数学是数学，经济学是经济学”【把抽象的数学运用到具体的经济现象需要附加假设条件】。
第二讲消费者理论
四、显示偏好简介
Tips
第二讲消费者理论
三、需求定律
（三）价格效应（续）【例子】
1 拟线性偏好（对第二种商品线性）
2
完全替代、完全互补偏好
第二讲消费者理论
三、需求定律
（三）价格效应（续）
1 x2 拟线性偏好：u（x1,x2）=x2+f（x1）
2 1
3
x1
第二讲消费者理论
三、需求定律
（三）需求定律
内容
正常商品自身价格的下降会引致其需求量的增加，如果一种物品其自身价格的下降引致需求量的下降，这种物品必为劣质品。
X1
第二讲消费者理论
三、需求定律
引子
在前面的模型中，需求行为呈现了可以观察的特征，比如在其他条件不变，某商品自身价格变动时，其需求数量随之变化。我们已经了解价格和收入【环境参量】对于效用和支出的影响【这似乎是消费者最为关系的东西】。恰好，我们在分析的过程中暂时忽略了数量因素【或者说包络定理恰好起到了

中级微观经济学第1讲消费者理论

33
效用最大化
效用最大化在建立起效用函数之后，消费者选择最优商品束的问题就转化为在预算约束下选择使其效用最大化的最优商品束

严格凸性（strict convexity）：平均消费束严格偏好于端点消费束
x 1 x 3 , x 2 x 3 , x 1 x 2 ,0 t 1, 那么tx1 (1 t ) x 2 x 3 特别地， 1 ~ x 2 , x 1 x 2， t 1, 那么tx1 (1 t ) x 2 x 1 x 0
两种商品已足够

在实际分析中，可将除了我们所关注的商品视为商品1，除此之外的其他商品都视为商品2，或者简单地将购买其他商品的货币看作商品2
5
预算线
计价物（numeraire）
p1 m x1 x2 p2 p2
6
预算线的变动
预算线的变动：四种情况

价格不变，预算变化
预算不变，只有一种商品价格变化
30
边际效用
边际效用（marginal utility, MU）保持其他商品的消费量不变，从某一商品的微小增量中获得的效用改变量
u( x1 , x 2 ) 商品1的边际效用： MU1 x1 商品1的边际效用： MU 2 u( x1 , x 2 ) x 2
15
关于偏好的假定

满足假定1-4的偏好称为良好性状偏好（well-behaved preference）
关于假设的讨论

单调性假设：是goods而不是bads 凸性假设：消费者愿意消费多种商品
16
关于偏好的假定
良好性状偏好的无差异曲线
a.
根据偏好的完备性和传递性，表示不同偏好水平的无差异曲线不 x2 能相交根据偏好的单调性，无差异曲线斜率为负，且越往右上方的无差异曲线代表的偏好水平越高根据偏好的凸性，无差异曲线的斜率非递减；若偏好是严格凸的，则无差异曲线斜率递增

消费者偏好理论定义及应用

消费者偏好理论定义及应用消费者偏好理论是指研究消费者在选择商品或服务时所偏好的特定属性或特征的一种学科理论。

它通过研究消费者选择行为的心理和行为原因，揭示了消费者偏好的形成机制和影响因素，为企业制定市场策略提供了重要的参考依据。

消费者偏好理论主要涉及两个方面的内容：一是消费者的个体偏好，即消费者对不同产品或服务的需求倾向；二是消费者的社会偏好，即消费者在社会环境中通过其他人的评价和行为来确定自己的偏好。

个体偏好主要包括商品属性偏好、价格偏好和品牌偏好。

商品属性偏好指的是消费者对商品的某些特定属性或特征的喜好程度，比如颜色、款式、功能等；价格偏好指的是消费者对商品价格的接受程度，包括对高价和低价的喜好程度和收入水平对价格敏感程度；品牌偏好指的是消费者对某个品牌的信任和忠诚度程度，往往受到品牌声誉、品牌认知度和品牌形象等因素的影响。

社会偏好主要包括社会影响和社会比较。

社会影响指的是消费者在选择商品或服务时会受到他人的评价和意见的影响，比如通过亲友、专家或媒体的建议来做出决策；社会比较指的是消费者在购买决策中会参考他人的行为和使用情况，以确认自己的购买决策是否与他人一致。

消费者偏好理论具有广泛的应用价值。

首先，企业可以通过研究消费者偏好来调整产品设计，提高产品的市场竞争力。

比如，通过研究消费者对产品属性的喜好程度，企业可以针对消费者需求开发更符合市场需求的新产品，从而提高产品的销售量和市场份额。

其次，企业可以通过研究消费者偏好来制定差异化竞争策略。

通过深入了解消费者对品牌的偏好程度，企业可以通过强化品牌形象、提高品牌认知度和提升品牌声誉来提高消费者对品牌的忠诚度；同时，通过研究社会影响因素，企业可以通过明星代言、社交媒体广告等方式来增强消费者对产品或服务的信任感和认可度。

最后，企业可以通过研究消费者偏好来制定定价策略。

通过研究消费者对价格的敏感程度和对高价和低价的偏好程度，企业可以根据市场需求合理定价，从而提高产品的市场竞争力。

【免费下载】显示性偏好理论

三、显示偏好弱公理（WARP）
1.WARP 的含义：
如果（x1,x2）直接显示偏好于（y1,y2），且（x1,x2）和（y1,y2）是两个不同的商品束，则（y1,y2）就不可能直接显示偏好于（x1,x2）。
显示偏好弱公理表明：若消费者在价格（p1,p1）下选择（x1,x2），在价格（q1,q2）下选择（y1,y2），只要：
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，系电，力根通保据过护生管高产线中工敷资艺设料高技试中术卷资，配料不置试仅技卷可术要以是求解指，决机对吊组电顶在气层进设配行备置继进不电行规保空范护载高与中带资负料荷试下卷高问总中题体资，配料而置试且时卷可，调保需控障要试各在验类最；管大对路限设习度备题内进到来行位确调。保整在机使管组其路高在敷中正设资常过料工程试况中卷下，安与要全过加，度强并工看且作护尽下关可都于能可管地以路缩正高小常中故工资障作料高；试中对卷资于连料继接试电管卷保口破护处坏进理范行高围整中，核资或对料者定试对值卷某，弯些审扁异核度常与固高校定中对盒资图位料纸置试，.卷保编工护写况层复进防杂行腐设自跨备动接与处地装理线置，弯高尤曲中其半资要径料避标试免高卷错等调误，试高要方中求案资技，料术编试交写5、卷底重电保。要气护管设设装线备备置敷4高、调动设中电试作技资气高，术料课中并3中试、件资且包卷管中料拒含试路调试绝线验敷试卷动槽方设技作、案技术，管以术来架及避等系免多统不项启必方动要式方高，案中为；资解对料决整试高套卷中启突语动然文过停电程机气中。课高因件中此中资，管料电壁试力薄卷高、电中接气资口设料不备试严进卷等行保问调护题试装，工置合作调理并试利且技用进术管行，线过要敷关求设运电技行力术高保。中护线资装缆料置敷试做设卷到原技准则术确：指灵在导活分。。线对对盒于于处调差，试动当过保不程护同中装电高置压中高回资中路料资交试料叉卷试时技卷，术调应问试采题技用，术金作是属为指隔调发板试电进人机行员一隔，变开需压处要器理在组；事在同前发一掌生线握内槽图部内纸故，资障强料时电、，回设需路备要须制进同造行时厂外切家部断出电习具源题高高电中中源资资，料料线试试缆卷卷敷试切设验除完报从毕告而，与采要相用进关高行技中检术资查资料和料试检，卷测并主处且要理了保。解护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。

ch04 偏好显示分析

在哪里呢？
发现无差异曲线
X2
E B
A CD
X1
发现无差异曲线
X2
E
B A CD
可能的无差异曲线
X1
好或无差异曲线
直接显示性偏好
X2
(x1,x2)
预算线
(y1,y2)
X1
• p1x1+ p2x2 =m,
实际购买商品束（x1,x2)
• p1y1+ p2y2 ≤ m
有能力购买商品束（y1,y2)
• p1x1+ p2x2 p1y1+ p2y2
如消费者选择A (x1, x2 )，而不是B (y1, y2 )， (x1,x2) 是 (y1,y2) 的直接显示偏好
x2
)
偏好显示的两个定理
如果消费选择违反了弱偏好显示定理（WARP），这个消费者就不是经济理性的。
WARP是用经济理性解释所观察到的消费选择的必要条件。
偏好显示的两个定理
偏好显示的强公理（SARP）：如果 (x1,x2)是（y1,y2)的显示偏好（直接或间接），且（y1,y2)与（x1,x2)不同，则（y1,y2)不可能是（x1,x2)的直接或间接显示偏好。
Part 1 消费者理论 Theory of Consumer
Lecture 4 偏好显示分析 Revealed Preference
Analysis
Revealed Preference
• 偏好显示的概念 • 从显示偏好到偏好 • 显示偏好的两个公理 • 如何发现无差异曲线？
偏好显示的概念
正推法： • 支付能力：预算线 • 消费组合的选择：偏好和效用 • 最优选择：需求或消费行为反推法：偏好显示 • 由观察到的消费者行为来评估消费者偏

03消费者理论：对偶与显示偏好

p x x x ) 2( 1 2
* 2
1
1
25
显示偏好
显示偏好
偏好假设（or理性偏好or一致偏好）对于现代消费者理论是必需的吗？
No
26
显示偏好
从消费者的选择行为出发研究消费者的需求规律
显示偏好
古典需求理论
对不可观察的偏好进行公理化假设最优化行为
应用：货币测度的效用函数
11
应用：几个重要的恒等式&货币测度的效用函数例1：已知两商品经济下的支出函数为 e(p1,p2,u) = Kp1ap21-au 求相应的间接效用函数、直接效用函数、货币测度的效用函数、需求函数 m = e(p, u)；v(p,m)=u，则有： v(p,m) = m/(Kp1ap21-a) 又由货币测度的间接效用函数的定义，有： u(p;q,m) ≡ e(p,v(q,m)) = p1ap21-a m/(q1aq21-a) 直接效用函数？ m(p, x) ≡ e(p,u(x))=Kp1ap21-ax1ax21-a
对偶与显示偏好
Duality and Revealed Preferences
Questions
如何从间接效用函数得到直接效用函数？
消费者行为理论中的对偶性
6
理性偏好假设是必须的吗？
显示偏好
货币测度的效用函数
若偏好满足严格单调性，则e(p,u) 对u严格递增 u(· )对正单调变换具有不变性
21
pi

j
u / xi x ju / x j
反需求函数
pi pi (x)
22
Hotelling’s Lemma：
设 u(x) 是消费者的效用函数，那么商品i 的反需求函数为

第二章显示偏好理论总结

• choice-based approach的优点：
– 与偏好方法相比，能够包容更为一般化的选择行为。
– 直接对可观察的行为，而不是对不可观察的偏好作出假设。
– 更为重要的是，它说明个人决策理论并不一定要建立在内生过程（偏好）基础上，而是存在一个坚实的行为基础。
• 问题：两种方法之间的等价性
p1x1 p2 x2 p1 y1 p2 y
q1 y1 q2 y2 q1z1 q2z2
( x1, x2 ) ( y1, y2 ) (x1, x2 ) (z1, z2 ) ( y1, y2 ) (z1, z2 )
商品2
(x1,x2)
(y1,y2) (z1,z2)
商品1
• choice-based approach的核心假设： • 显示偏好弱公理
• 问题2：两种方法之间的关系
– 如果选择行为满足显示偏好弱公理，是否存在一个理性的偏好与这些行为相一致（相容）？
• 不一定！！！
( x1 , x2 ) ( y1, y2 )
如果在(y1,y2)支付得起的条件下，消费者没有选择(y1,y2)而选择(x1,x2) ，那么对(x1,x2)的偏好就一定超过对(y1,y2)的偏好。
商品 2
(x1, x2 )
( y1, y2 )
商品1
间接显示偏好
• 假定存在三个实际消费束(x1,x2)、(y1,y2)和(z1,z2)，如果给定价格(p1,p2)在支付得起的条件下消费者选择了(x1,x2) ，即 p1x1+p2x2≥p1y1+p2y2,给定价格(q1,q2)在支付得起(z1,z2)的条件下消费者选择了(y1,y2) ，即p1y1+p2y2≥p1z1+p2z2，那我们就说 (x1,x2)是(z1,z2)的间接显示偏好。

7第七章显示偏好理论

例子：
P1t=1, P2t=2
x1t =2 x 2t=1； x1b =1 x 2b=2
P1t *x1t+ P2t *x
2 t
< P1t *x1b+ P2t *x
显示偏好概念直接显示偏好

设（x1,x2）是消费者在收入为m时按价格（p1,p2）购买的消费束，按照这种价格和收入，（y1,y2）是有能力购买但是没有购买的商品束。这意味着： p1 y1 p2 y2 m

p1 x1 p2 x2 =m p1 x1 p2 x2 p1 y1 p2 y2

如果我们观察的选择满足显示偏好强公理，那么我们总能找出使观察到的行为是最优化行为的那种偏好。
即满足显示偏好强公理→最优化行为的偏好
20
指数

考察不同时期的消费束时，需要考察比较消费从一个时期到另一个时期所发生的变化。
t t t t 假设在时期t,价格是，消费者的选择是（x1 ，x2 ），在（p1 ，p2 ） b 基期b,消费价格是（p1b , p2 ），消费者选择是（xb，xb）

现在假设恰好（y1,y2）是价格（q1,q2）上的需求束，且（y1,y2）本身又是（z1,z2）的显示偏好，即 q1*y1+q2*y2≥q1*z1+q2*z2 由此我们得到， x
y, y
z
，根据传递性假设，有 x
z

显示偏好弱公理

我们假定，消费者有偏好，总是在他能买得起的商品束中选择最好的商品束。我们怎样判定消费者的行为是否遵循最大化模型？或者说，哪种观察结果会使我们得出消费者并未追求效用最大化的结论？