最新材料力学习题解答(组合变形)文件.doc
组合变形(例题)

A
P 450
A
0.12
103
6.37MPa
T Wn
16700.1030
35
.7MPa
3
24 2
故,安全。
6.372435.72
71.7MPa
p.8
例题
习题6.
例题
图示皮带轮传动轴传递功率N=7kW,转速n=200r/min。皮带轮重量Q=1.8kN。左端齿轮
上的啮合力Pn与齿轮节圆切线的夹角(压力角)为20o。轴的材料为45钢, [] =80MPa。
例题
b
P
25 e
a
P
5
解:(1)将外力向轴线简化,如图所示;
b
其中:M=Pe,这属于拉弯组合变形;
P
a
P
(2)求出a、b点的应力;
a
P A
Pe W
,
b
P A
Pe W
(3)二点均属单向应力状态,求出二点的轴向应变;
a
a E
P 1 e EA W
b
b E
P E
1 A
e W
(4)解方程组得 P EAa b 18.4kN
力是水平方向,B轮上胶带的张力是垂直方向,大小如图示;圆轴的许用应力[σ]=80MPa;试按
第三强度理论求轴所需的直径。
5kN
(3)求可能危险截面C和B上的合成弯矩:
AC
B
D
2kN
MC
M
2 yC
M zC 2
1.52 2.12 2.58kNm
2kN
5kN
300
500
500
MB
M
2 yB
M zB2
xz平面的弯矩图为 代入第三强度理论的强度条件得
材料力学组合变形习题

材料力学组合变形习题L1AL101ADB (3)偏心压缩时,截面的中性轴与外力作用点位于截面形心的两侧,则外力作用点 到形心之距离e和中性轴到形心距离d之间的关系有四种答案:(A ) e=d; (B ) e>d;(C ) e越小,d越大; (D ) e越大,d越小。
正确答案是______。
答案(C )1BL102ADB (3)三种受压杆件如图。
设杆1、杆2和杆3中的最大压应力(绝对值)分别用 max1σ、max 2σ和max3σ表示,现有下列四种答案:(A )max1σ=max 2σ=max3σ; (B )max1σ>max 2σ=max3σ;(C )max 2σ>max1σ=max3σ; (D )max 2σ<max1σ=max3σ。
正确答案是______。
答案(C )1BL103ADD (1)在图示杆件中,最大压应力发生在截面上的哪一点,现有四种答案:(A )A点; (B )B点; (C )C点; (D )D点。
正确答案是______。
答案(C )1AL104ADC (2)一空心立柱,横截面外边界为正方形, 内边界为等边三角形(二图形形心重 合)。
当立柱受沿图示a-a线的压力时,此立柱变形形态有四种答案:(A )斜弯曲与中心压缩组合; (B )平面弯曲与中心压缩组合;(C )斜弯曲; (D )平面弯曲。
正确答案是______。
答案(B )1BL105ADC (2)铸铁构件受力如图所示,其危险点的位置有四种答案:(A )①点; (B )②点; (C )③点; (D )④点。
正确答案是______。
答案(D )1BL106ADC (2)图示矩形截面拉杆中间开一深度为h/2的缺口,与不开口的拉杆相比,开口处的最大应力的增大倍数有四种答案:(A )2倍; (B )4倍; (C )8倍; (D )16倍。
正确答案是______。
答案(C )1BL107ADB (3)三种受压杆件如图,设杆1、杆2和杆3中的最大压应力(绝对值)分别用 max1σ、max 2σ和max3σ表示,它们之间的关系有四种答案:(A )max1σ<max 2σ<max3σ; (B )max1σ<max 2σ=max3σ;(C )max1σ<max3σ<max 2σ; (D )max1σ=max3σ<max 2σ。
组合变形习题解答
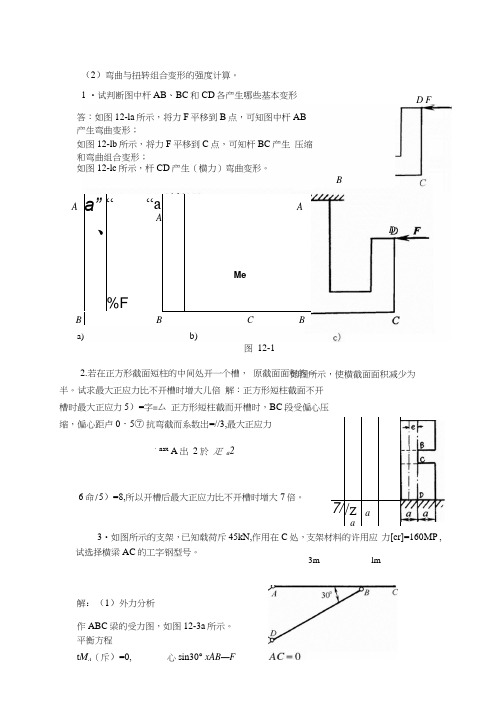
(2)弯曲与扭转组合变形的强度计算。
Aa”、““aAA%FMeBBCB2.若在正方形截面短柱的中间处开一个槽, 原截面面积的一半。
试求最大正应力比不开槽时增大儿倍 解:正方形短柱截面不开槽时最大正应力5)=字=厶 正方形短柱截而开槽时,BC 段受偏心压缩,偏心距卢0・5⑦ 抗弯截而系数出=//3,最大正应力,naxA 出 2於 疋 a 2如图所示,使横截面面积减少为6命/5)=8,所以开槽后最大正应力比不开槽时增大7倍。
7/ /z aa3•如图所示的支架,已知载荷斥45kN,作用在C 处,支架材料的许用应 力[cr]=160MP ,试选择横梁AC 的工字钢型号。
解:(1)外力分析作ABC 梁的受力图,如图12-3a 所示。
平衡方程t M A (斥)=0,心sin30° xAB —FBDb)图 12-1答:如图12-la 所示,将力F 平移到B 点,可知图中杆AB 产生弯曲变形;如图12-lb 所示,将力F 平移到C 点,可知杆BC 产生 压缩和弯曲组合变形;如图12-lc 所示,杆CD 产生(横力)弯曲变形。
D F1 •试判断图中杆AB 、BC 和CD 各产生哪些基本变形a)lm3m第12章组合变形的强度计算主要知识点:(1)弯曲与拉伸(压缩)组合变形的强度计算;z/Z解得心=120kAL 变形。
(2) 内力分析,确定危险截面的位置AB 段受到拉力,F v = F R cos30° = 104RN ,作出图12-3b 所示轴力图。
梁的AB 段、BC 段剪力均为常数,弯矩图均为斜直线,算得M l{ = -45kN ・m,作出图12-3c 所示弯矩图。
故危险截而是B-截而,即B 截而左侧。
危险截而上的轴力F v = 1(MRN 、弯矩M” = -45kN-m(3) 应力分析,确定危险点的位置危险截而上拉伸正应力6= 乌,弯曲正应力6=纬竺),(见图12-3d)。
根据危险截A而上的应力分布规律可知,危险点在危险截而的上侧边缘。
中南大学材料力学--组合变形答案

组合变形答案一、概念题1.A ;2.A ;3.D ;4.C ;5.B ;6.A ;7.C ;8.D ;9.C ;10.C11.略12. 13σσσ=-=二、计算题1截面形心和惯性矩计算:126459.5240.484.8810z z mmz mm I mm ===⨯1-1 截面上的内力:28857.6.12N M Py N mF P kN ====2max 1max 26.8[]32.3[]t Nt Zc Nc ZF Mz MPa A I F Mz MPa A I σσσσ=+=<=-+=< 安全2设切口深度为x ,则偏心距为:x /23112100.005(0.04)P t F A x σ⨯==-322121020.005(0.04)6t xMx W σ⨯⨯==⨯-61210010t t σσσ=+≤⨯ 得 212864000.00521x x x m -+== 3 2642()()P A hP F M PP A W bh bh bh σ⨯=-+=-+=-A 点的应力状态为单向压缩应力状态 454522AP bh σσσ-===-4545451122()()P P E E bh bh εσυσυ-=-=+2(1)Ebh P αευ=-4 过O 点横截面上的应力232324202()()P hP F M P P A W d d d σπππ⨯=+=+= 28T P M P W d τπ== O 点的应力状态为二向应力状态:0x y y σσσττ===220xa P E d E σεπ== 2452452454518cos 90sin 90222cos90sin 902214()x yx y xy x y x yxy b P d Pd P E d Eσσσσστπσσσσστπεσυσπ--+-=+---=+-=+-==-=- 5a 点的应力状态为二向应力状态:32412.710P P P F F F A d σπ===⨯ 3216 5.1010e T P P M M F W dτπ===⨯33031203593030120cos 60sin 6013.91022cos 240sin 240 1.24102211()(13.90.3 1.24)1014.331020010x y x y xy P x y x yxy P P F F F E σσσσστσσσσστεσυσ-+-=+-=⨯+-=+-=-⨯=-=+⨯⨯=⨯⨯2107 2.107.P e F N M N m ==采用第三强度理论校核强度31334.33[]r MPa σσσσ=-==< 安全 61) 计算954920.46.163.68491.1408.9293.75252.3488.66Pz Py Ay By Az Bz P m N m nF N F NF NF NF N F N =====-===-2) 作计算简图3) 作内力图4) 危险截面为A 截面: max max max 20.46.28.08.21.28.T z y M N mM N m M N m===-5)危险点于A 截面的边缘a 点,a 点的应力状态为二向应力状态:2.87MPa σ==2160.83eTP M M MPa W dτπ===max 3.1min 0.2212313max 23.100.22 1.662x yMPaMPaMPaMPaMPaMPaσσσσσσσστ-+=±====--== 6)采用第三强度理论校核强度313 3.32[]r MPa σσσσ=-==< 安全。
材料力学习题组合变形

组合变形基 本 概 念 题一、选择题1. 偏心压缩时,截面的中性轴与外力作用点位于截面形心的两侧,则外力作用点到形心的距离e 和中性轴到形心距离d 之间的关系是( )。
A .e = dB .e >dC .e 越小,d 越大D .e 越大,d 越小2.三种受压杆件如图所示,设杆1、杆2和杆3中的最大压应力(绝对值)分别用1max σ、2max σ、3max σ表示,则( )。
A .1max σ=2max σ=3max σB .1max σ>2max σ=3max σC .2max σ>1max σ=3max σD .2max σ<1max σ=3max σ 题2图3.在图示杆件中,最大压应力发生在截面上的( )。
A .A 点B .B 点C .C 点D .D 点题3图 题4图4. 铸铁杆件受力如图4所示,危险点的位置是( )。
A .①点B .②点C .⑧点D .④点5. 图示正方形截面直柱,受纵向力P 的压缩作用。
则当P 力作用点由A 点移至B 点时柱内最大压应力的比值()max A σ﹕()max B σ为( )。
A .1﹕2B .2﹕5C .4﹕7D .5﹕26. 图示矩形截面偏心受压杆件发生的变形为( )。
A .轴向压缩和平面弯曲组合B .轴向压缩,平面弯曲和扭转组合C.轴向压缩,斜弯曲和扭转组合D.轴向压缩和斜弯曲组合-41-题5图题6图7.图所示悬臂梁的横截面为等边角钢,外力P垂直于梁轴,其作用线与形心轴y垂直,那么该梁所发生的变形是()。
A.平面弯曲B.扭转和斜弯曲C.斜弯曲D.两个相互垂直平面(xoy平面和xoz平面)内的平面弯曲题7图8.图示正方形截面杆受弯扭组合变形,在进行强度计算时,其任一截面的危险点位置有四种答案,正确的是( )。
A.截面形心B.竖边中点A点C.横边中点B点D.横截面的角点D 点题8图题9图9.图示正方形截面钢杆,受弯扭组合作用,若已知危险截面上弯矩为M,扭矩为T,截面上A点具有最大弯曲正应力σ和最大剪应力τ,其抗弯截面模量为W。
结构力学 第八章
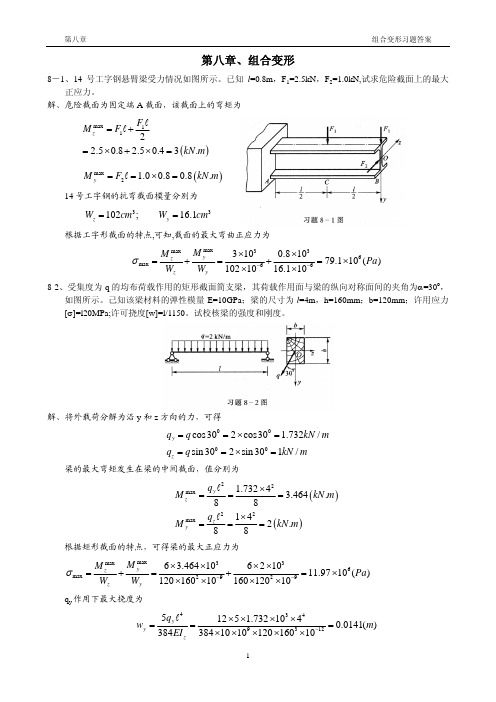
wmax 0.0202 0.76 1 = = < l 4 150 150
解、将均布载荷分解为沿轴线方向和垂直于轴线方向的两个分力,可得: qx = q sin α ; 距离 B 端为 x 的截面上的轴力和弯矩分别为
q y = q cos α
M=
该截面的最大压应力为
q y lx 2
−
qy x2 2
=
q ( lx − x 2 ) cos α 2
σ
所以该点最大切应力为: τ max =
8-16、铁道路标圆信号板,装在外径 D=60mm 的空心圆柱上,所受的最大风载 p=2kN/m2,[σ]=60MPa。试 按第三强度理论选定空心柱的厚度。
解、结构的危险截面为空心柱的固定端,截面的弯矩和扭矩分别为
M = 2×
π × 0.52
4
× 0.8 = 0.314(kN .m);
当中性轴为①时,中性轴的截矩为: 偏心力作用点的位置为:
a y = −0.3; az → ∞ ;
z
②
iz2 0.019333 ey = − = − = 0.0644(m), ay −0.3
当中性轴为②时,中性轴的截矩为: 偏心力作用点的位置为:
iz2 ez = − = 0 az
①
a y = 0.4; az = −0.4 ;
解、将外载荷分解为沿 y 和 z 方向的力,可得
q y = q cos 300 = 2 × cos 300 = 1.732kN / m qz = q sin 300 = 2 × sin 300 = 1kN / m
梁的最大弯矩发生在梁的中间截面,值分别为
M zmax =
max My
1.732 × 42 = 3.464 ( kN .m ) 8 8 q z l 2 1× 4 2 = = = 2 ( kN .m ) 8 8 =
组合变形习题
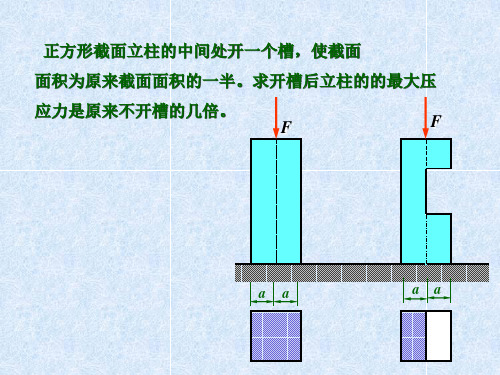
解:作内力图如图 查附录可得 Wz=309cm3,Wy=40.9 cm3 对A截面,由强度条件有
1.2F z l y y A l 1.2F B l x
Mz 0.5Fl Fl Mys maxM z M y Fl 0.4Fl [s ] Wz Wy Wz Wy
F 10.8kN
B截面,由强度条件有
0.4Fl
0.8Fl
s max
M z M y 0.5Fl 0.8Fl [s ] Wz Wy Wz Wy
取梁的许用荷载[F]=6KN
F 6.6kN
解: 未开槽前立柱为轴向压缩
FN F F F s1 2 A A ( 2a ) 4a 2
开槽后1-1是危险截面 危险截面为偏心压缩 将力 F 向1-1形心简化
正方形截面立柱的中间处开一个槽,使截面
面积为原来截面面积的一半。求开槽后立柱的的最大压 应力是原来不开槽的几倍。 F F
a
a
a
a
图示偏心受压杆。试求该杆中不 出现拉应力时的最大偏心距。
图所示简支梁由22a工字钢构成,许用应力[s ]=140MPa,长度l =1m。 1.5F 求该梁的许用荷载[F]。 1.5F
F F
1
Fa/2
1
FN M F Fa / 2 2F s2 2 A W 2a a 1 2a a 2 a 6 开槽后立柱的最大压应力 2F / a 2 2 8 未开槽前立柱的最大压应力 F / 4a
a
a
材料力学 第十章组合变形(1,2,3)

1.2m
解:求支反力,由平衡方程
FB B
FA
' FA
F ' A 0,
FA FB 5kN
A
1.6m 1.6m
m g f A
10kN C
m FAy
作折杆的受力图,折杆及 受力对称,只需分析一半 即杆AC 将FA分解, 得杆的轴力 FN、弯矩M (x)
B
FAx
FN FAx 3kN
3 10 8 10 t 81.1 2 3 c d / 4 d / 32 81.9
3 3
M W
[例10-2]圆截面杆的偏心压缩时不产生拉 力的载荷作用范围
P
y
P
y
Pa
a
z
z
CL11TU12
P
y
Pa
y
P
y
Pa
z
z
z
P
y y
Pa
y
P
z
Pa
z P
y y
z
Pa
y
P
CL11TU10
解: X A 3kN, A 4kN Y
任意横截面x上的内力:
FN X A 3kN FS YA 4kN M ( x) YA x 4 x
1 1截面上危险截面, 其上:FN 3kN,M 8kN m
FN A
M W
t FN M c A W
CL11TU5
y0 Iz tg tg z0 Iz
为中性轴与z轴夹角
3.强度计算:
1)危险截面:当x=0时 M Z , M y 同时取最大,固定端处为危险面 2)危险点:危险面上 D1 , D2点 3)最大应力
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
9.3. 图示起重架的最大起吊重量(包括行走小车等)为P=40 kN ,横梁AC 由两根No18 槽钢组成,材料为Q235 钢,许用应力[ ]=120MPa 。
试校核梁的强度。
Bzo30A yCPNo18× 23.5m解:(1) 受力分析当小车行走至横梁中间时最危险,此时梁AC 的受力为X C Y C S Ao30 AC D P由平衡方程求得oM 0 S sin 30 3.5 P 1.75 0 S P 40kNC A Ao oX 0 X S cos30 0 X S cos30 34.64 kNC A C A1M 0 Y 3.5 P 1.75 0 Y P 20kNA C C2(2) 作梁的弯矩图和轴力图M35kNm(+)xN(-) x—34.64kN此时横梁发生压弯组合变形, D 截面为危险截面,N 34.64 kN M 35 kN .mmax(3) 由型钢表查得No.18 工字钢Wy3 29.2992 152cm A cm(4) 强度校核3 3MN 34.64 10 35 10maxmax c max 4 62A 2W 2 29.299 10 2 152 10y5.9 115.1 121 MPa 1.05[ ] 故梁AC 满足强度要求。
注:对塑性材料,最大应力超出许用应力在5%以内是允许的。
9.5. 单臂液压机架及其立柱的横截面尺寸如图所示。
P=1600 kN ,材料的许用应力[ ]=160MPa。
试校核立柱的强度。
y c890A DP3800 I I P 50ad16b 16 c16860 B C900 14001400截面I-I2760解:(1) 计算截面几何性2A A 1.4 0.86 1.204 m1 ABCD2A A 1.4 0.05 0.016 0.86 2 0.016 1.105m2 abcd2A A A 0.099m1 2截面形心坐标y cA y A y1 1c2 2cA1.204 0.7 1.105 0.051.4 0.05 0.01620.51 m0.099截面对形心轴的惯性矩12I 3 4I 0.86 1.4 0.7 0.51 1.204 0.24 mzc12I II zc1120.86 2 0.016 1.4 0.05 0.016 31.4 0.05 0.016220.05 0.51 1.105 0.2114mI II 4I I I 0.24 0.211 0.029 mzc zc zc(2) 内力分析截开立柱横截面I-I ,取上半部分PI IMNy c900由静力平衡方程可得上海理工大学力学教研室1N P 1600kN M P 0.9 y c 2256kNm 所以立柱发生压弯变形。
(3) 最大正应力发生在立柱左侧t max My NCI Azc3 32256 10 0.51 1600 100.029 0.099 39.67 16.16 55.83 MPa 160 MPa力柱满足强度要求。
9.6. 图示钻床的立柱为铸铁制成,P=15 kN ,许用拉应力为[ t]=35 MPa。
试确定立柱所需要的直径d。
400Pd P解:(1) 内力分析400PMN如图作截面取上半部分,由静力平衡方程可得N P 15kN M 0.4P 6kNm所以立柱发生拉弯变形。
(2) 强度计算先考虑弯曲应力M 32Mt tmax 3W d332M 32 6 10d 3 120.4 mm3 635 10t取立柱的直径 d = 122 mm ,校核其强度上海理工大学力学教研室23 3NM 4N32M4 15 1032 6 10t m ax2323A W d d 0.122 0.1221.28 33.66 34.94MPa[ ]t立柱满足强度要求。
注:在组合变形的截面几何尺寸设计问题中, 先根据主要变形设计, 然后适当放宽尺寸进行强度校核,这是经常使用的方法。
9.7. 在力 P 和 H 联合作用下的短柱如图所示。
试求固定端截面上角点A 、B 、C 、D 的正应力。
PP =25kNH =5kN75MH5025600 zA yB DC z Ay MyBND M zCQ150100解:(1) 将力 P 和 H 向截面形心简化3M25 10 0.025 625 N .m(2) 截面 ABCD 上的内力N P 25 kN MM625 N .myMH 0.6 3 kN .mz(3) 截面几何性质2A 0.15 0.1 0.015 m1243W0.1 0.15 3.75 10 mz6 124 3W0.15 0.1 2.5 10 my6(4) A 点的正应力NMMy z325 106253000AA W Wyz440.015 2.5 10 3.75 106 6 61.67 102.5 10 8 10 8.83 M PaB 点的正应力BM MNy zA W Wy z61.672.5 8 103.83 MPaC 点的正应力上海理工大学力学教研室3CM MNy zA W Wy z61.672.5 8 10 12.17 MPaD 点的正应力DM MNy zA W Wy z61.672.5 8 10 7.17 MPa9.8. 作用于悬臂木梁上的载荷为:xy 平面内的P1=800 N,xz 平面内的P2=1650 N。
若木材的许用应力[ ]=10 MPa ,矩形截面边长之比为h/b =2,试确定截面的尺寸。
P2aO hxP1b1m 1mbyz解:(1) 求内力固定端弯矩最大M max P1 2 1600 Nm M max P2 1 1650 Nmz y(2) 求应力木梁在xy 平面弯曲而引起的固定端截面上的最大应力为M M3Mz max z max z maxmax 2 3W hb/ 6 bz木梁在xz 平面弯曲而引起的固定端截面上的最大应力为M M 1.5My max y max y maxmax 2 3W bh/ 6 by(3) 强度计算固定端截面上 a 点是最大拉应力点, b 点是最大压应力点,应力数值大小是3M z M y1.5max maxσσσσσmax max max 3 3b b3M 1.5M 3 1600 1.5 1650z max y maxb mm3 9036σ10 10h2b180mm9.10. 图示手摇铰车的轴的直径d=30 mm ,材料为Q235 钢,[ ]=80 MPa 。
试按第三强度理论求铰车的最大起重量P。
上海理工大学力学教研室4400 400180PP解:(1) 轴的计算简图0.18PP画出铰车梁的内力图M0.2PxT0.18Px危险截面在梁中间截面左侧M max 0.2P T 0.18 P(2) 强度计算第三强度理论2 2M T 32 r3 3W d2 2 (0.2P) (0.18 P)3 3 6d0.03 80 10P 788N2 2 2 232 (0.2) (0.18) 32 (0.2) (0.18)所以铰车的最大起重量为788N9.12. 操纵装置水平杆如图所示。
杆的截面为空心圆,内径d=24 mm,外径D=30 mm。
材料为Q235 钢,[ ]=100 MPa 。
控制片受力P=600 N 。
试用第三强度理论校核杆的强度。
P1=600N300P2o 80200至控制舵DB CA100250上海理工大学力学教研室 5150解:(1) 水平杆的受力简图y M 1 Z CM 2D xZ AA P1oP2sin80CoB P2cos80Y CzY AM P 0.2 600 0.2 120 N .m1 1sin80 o 0.3 0.295M P P2 2 2列平衡方程M 0 M M 120 0.295P P =406.8 N.mx 1 2 2 2oM 0 Y 0.4 P cos80 0.5 0 Y 88.3 Nz C 2 CoY 0 Y Y P cos80 0 Y 17.66 NC A 2 AoM 0 P 0.15 Z 0.4 P sin80 0.5 0 Z 275.8 N y 1 C 2 CoZ 0 Z P Z P sin 80 0 Z 475.2 NA 1 C 2 A画出内力图M y 71.28N.m M z40.06N.mx2.649N.m7.064N.mxxz 平面内xy 平面内T 120N.mxB 截面是危险截面2 2 71.282 2.6492 71.32 .M M M N mB By Bz(2) 按第三强度理论计算r2 2 2 232 M T 32 71.32 120B3 34 4 3 4 4D 1 d / D 0.03 1 24 / 3089.2 MPa [ ]杆的强度足够.9.14. 图示带轮传动轴传递功率P=7 kW ,转速n=200 r/min 。
皮轮重量Q=1.8 kN 。
左端齿轮o上的啮合力P n 与齿轮节圆切线的夹角(压力角)为20 。
轴的材料为Q255 钢,许用应力[ ]=80 MPa。
试分别在忽略和考虑带轮重量的两种情况下,按第三强度理论估算轴的直径。
T1=2T2A Bφ500φ300上海理工大学力学教研室 6Q 200 400 200o20 T2 P n解:(1) 传动轴的计算简图zy0.15P n cos200.25T2xo P n cos20oP n sin20 3T 2Q求传动轴的外力偶矩及传动力P 7o m 9549 9549 334.2Nm m 0.25T 0.15P cos 202 nn 200mT 1337 N T 2T 2674 N2 1 20.25mP 2371 Nn o0.15cos 20(2) 强度计算a) 忽略皮带轮的重量(Q=0)轴的扭矩图为Tx334.2N m在xz 平面内弯曲的弯矩图为M y162.2Nmx在xy 平面内弯曲的弯矩图为M z802.2N445.6Nmx求合成弯矩2 2 162.22 445.62 472.2 .M M M N mA Ay AzM M 802 N .m MB Bz AB 截面是危险截面上海理工大学力学教研室7M802.2 Nm T334.2NmB B第三强度理论32 2 2M TB Br3 3d2 2 2 232 M T32 802 334.2B B3d48mm3680 10b) 考虑皮带轮的重量xz 平面的弯矩图为M y162.2Nmx360Nmxy 平面的弯矩图不变, B 截面仍是危险截面2 2 3602 802.22 879.3M M M NmB By BzT334.3NmB根据第三强度理论2 2 2 232 32 879.3 334.2M TB B3d 3 49.3 mm680 10上海理工大学力学教研室8。
