电路基础第四章
合集下载
电路分析基础第四章(李瀚荪)
一、陈述 对任意含源单口网络N，都可以用一个电压源 与一个电阻相串联来等效。 R0 i i + + 即 + 等效 u N u u oc _ _ _
电压源的电压等于该网络的开路电压uoc， 这个电阻等于从此单口网络两端看进去，当网 络内部所有独立源均置零(No)时的等效电阻R0 i =0
+
4.6 戴维南定理
7Ω
10Ω
例（2） a 44 b
20 60 60
20
20 60
22
结论 只含电阻单口网络 等效为一个电阻
只含 电阻
R
2.含独立源电路 1V 例(1)
+
_
2
3
0.5A
0.2A 5
0.5A
5
5 0.3A
+ 1.5V _
结论 含独立源单口网络 等效为实际电压源 或实际电流源 含独立 源和电 阻电路
试用电压源与电流源等效变换的方 法计算2电阻中的电流。
1 2A
解:
I
1 3 2A 2A 6
1
3 + 6V –
6 + – 12V (a)
1 2
(b)
– 2V 2
I + +
由图(d)可得
82 I A 1A 2 2 2
2 2 +
2 2 4A
–
8V (d)
(c)
+
– 2V 2
第四章
分解方法及单口网络
——用等效化简的方法分析电路
本章的主要内容： 1、分解、等效的概念； 2、二端网络的等效化简，实际电源 的等效变换 ; 3、置换、戴维南、诺顿定理， 最大功率传递定理； 4、三端网络T形和形的等效变换。
电路分析基础第4章 相量法(2h)
Im
U 2
U
U 1
41.9
60 30
Re
U
Im
U 2
首
U 1
60 尾
41.9
相 接
30
Re
/38 章目录 上一页 下一页 返回 退出
第4章 正弦稳态电路分析
4.3 基尔霍夫定律的相量形式和基本
元件伏安关系的相量形式
一. 电阻 i(t)
+
uR(t) R -
•
I
+
•
UR
R
-
相量模型
已知 i(t) 2I cos(wt y i )
设 i(t)=Imcos(w t+ )
I
1 T
T 0
I
2 m
cos2
(
wt
Ψ
) dt
def
I
1 T i 2 (t )dt
T0
cos2 ( wt Ψ ) 1 cos2(wt Ψ )
2
I 0.707Im Im 2I
i(t) Im cos(wt Ψ ) 2I cos(wt Ψ )
10/38 章目录 上一页 下一页 返回 退出
u2 (t) 4 2cos(314t 60o ) V
U1 630o V U 2 460o V
U U1 U 2 630 460 5.19 j3 2 j3.46
7.19 j6.46 9.6441.9o V
u(t) u1(t) u2 (t) 9.64 2cos(314 t 41.9o ) V
dt
C 相量形式：
•
U Uy u
•
IC
wCUy u
π 2
1 相量关系：
电路分析基础第5版第4章 分解方法及单、双口网络
+ 2
9V
4Ω 3
I1
应用举例
例1：求图示电路中各支路电流。
解： 将3Ω电阻用电流源置换
I3 = 2.7
I1
9 4
1 2
0.9
2.7
A
I2
9 4
1 2
0.9
1.8
A
I4
I5
1 2
I3
0.45
A
I1
2
+
9V
I3 3
2
2
I2
I4
4- 3
2 I5
I1
0.9A I3
2
+
9V
2
I2
2 2
I4
I5
结论：置换后对其他支路没有任何影响。
电压u =α和端口电流i =β，则N2 (或N1)可用一个电压为 α 的电
压源或用一个电流为 β 的电流源置换 ，置换后对 N1 (或N2 ) 内各支路电压、电流没有影响。
i=β
N1
+
u=α
N2
i=β
+
N1
α
N1
+ u=α
β
置换定理适用于线性和非线性电路。
二. 置换的实质
置换：如果一个网络N由两个单口网络组成，且已
联立(1)、(2)，解得 u=12V， i=－1A
用12V电压源置换N1，可求得 i1
用－1A电流源置换N2，可求得 u2=12V
[例]求上一例题中N1和N2的等效电路
0.5i1
6Ω
i
5Ω i1
+
+ 10Ω 1A
12V u
- -2
+
9V
4Ω 3
I1
应用举例
例1：求图示电路中各支路电流。
解： 将3Ω电阻用电流源置换
I3 = 2.7
I1
9 4
1 2
0.9
2.7
A
I2
9 4
1 2
0.9
1.8
A
I4
I5
1 2
I3
0.45
A
I1
2
+
9V
I3 3
2
2
I2
I4
4- 3
2 I5
I1
0.9A I3
2
+
9V
2
I2
2 2
I4
I5
结论：置换后对其他支路没有任何影响。
电压u =α和端口电流i =β，则N2 (或N1)可用一个电压为 α 的电
压源或用一个电流为 β 的电流源置换 ，置换后对 N1 (或N2 ) 内各支路电压、电流没有影响。
i=β
N1
+
u=α
N2
i=β
+
N1
α
N1
+ u=α
β
置换定理适用于线性和非线性电路。
二. 置换的实质
置换：如果一个网络N由两个单口网络组成，且已
联立(1)、(2)，解得 u=12V， i=－1A
用12V电压源置换N1，可求得 i1
用－1A电流源置换N2，可求得 u2=12V
[例]求上一例题中N1和N2的等效电路
0.5i1
6Ω
i
5Ω i1
+
+ 10Ω 1A
12V u
- -2
+
第四章电路基础
Us'= -10I1'+4= -10×1+4= -6V 10×
共同作用： 共同作用： Us= Us'
Us"= -10I1"+(6//4)×4 +(6//4
=-10×(-1.6)+9.6=25.6V 10× )+9 25. +Us"= -6+25.6=19.6V
如图， (a)中 (b)中 6A， 如图，N为线性含源电阻网络 (a)中I1=4A (b)中I2= –6A， 6A 例：求 (c)中I =? (c)中 3 R2 R2 R2 N I1 (a) R1 N I2 (b) I1=4A I2= –6A 6 R1 + 4V N I3 (c) + R1 6V
解： (a)中仅由N内独立源单独作用时 (a)中仅由 中仅由N
(b)中由N内独立源和4V电源共同作用时 (b)中由N内独立源和4V电源共同作用时 中由 4V
4V电源单独作用时 电源单独作用时R 故仅由 4V电源单独作用时R1支路电流 I2′= –6-4= –10A 6 10A
′
若仅由(c)中6V电源单独作用时R 若仅由(c)中6V电源单独作用时R1支路电流 (c) 电源单独作用时
+ x(t) -
电路
+ y(t) -
+ Kx(t) -
+ 电路 Ky(t) -
2、叠加性superposition 、叠加性superposition
若输入x (t)(单独作用 单独作用） 若输入x1(t) → y1(t)(单独作用） , x2(t) → y2(t) … xn(t) → yn(t) 则x1(t) 、x2(t) … xn(t) 同时作用时响 应y(t)= y1(t)+ y2(t)+ … +yn(t)
电气基础知识：第四章 线性电路基本定理
i 52 2.6A 12 8
+
- UocRo
16
例4：图示电路，用戴维南定理求电流I。
+ Uoc -
解：移去待求支路求：Uoc 40V
Ro
除去独立电源求： Ro =7
I 40 10 A 75 3
画出戴维南等效电路，并接入待求支路求响应。 17
3、含受控源电路分析
例5：图示电路，用戴维南定理求电流I2。
Us
I0
Us R1
Is
R0
R1R2 R1 R2
R1 R2
Is Isc
Ro Io
Uo
Ro
Us R1
U0
Io Ro
(U s
/ R1 ( R1
I s )R1R2 R2 )
(Ro :除源输入电阻)
+
R1
Uoc
-
(Io : 短路电流Isc )
(Uo : 开路电压Uoc )
10
二、定理：
1、线性含源单口网络对外电路作用可等效为一
30
三、定理应用： 例1：求图示电路中电流I。
I
I4
I0
解：I0 =1A I4 = -0.25A
I1
I3
I2
I1 =0.5A
I2 =0.5A
I= -Io -I4 = -0.75A
31
例2：已知条件如图所示，求图（b)的电压源电压us。
4A
us
(a)
10A ++
U2o0cV --
4A
us
(b)
Ro = 2 Uoc = 20V us = 100V
Ro
u i
=6
画出等效电路，有 R=Ro =6
第四章 电路分析基础分解(1)分解步骤
R
由元件的VCR得： u=Us u=Ri 联立后解得： u=Us i =Us /R
（4-1） （4-2）
（4-3） （4-4）
求解目标
从这个例子不难得到启发：如果在端钮11‘处相连接的是两 个内部结构复杂或是内部情况不明的单口网络，也可按此 思路求得这两个网络的端口电压和端口电流。所不同者， 需要的是这两个单口网络的VCR而不是元件的VCR。 求解策略
图解法求两个网络的端口电压和端口电流
u
Us Q 2 1
绘出这两元件的伏安特性曲 线后，用曲线相交法求得解 答，求交点Q。
坐标为： u=Us i =Us /R （4-3） （4-4）
O
Us/R 图4-2 （b）
i
（b）伏安特性曲线相交法求解图
单口网络及其VCR
重要概念
单口网络：只有两个端钮与其它电路相连接的网络，称为二 端网络。当强调二端网络的端口特性，而不关心网络内部的情况 时，称二端网络为单口网络，简称为单口(One-port)。 电阻单口网络的特性由端口电压电流关系(简称为VCR)来表 征(它是u-i平面上的一条曲线)。
一个元件的电压电流关系是由这个元件本身所确定的，与 外接的电路无关，例如，电阻元件的VCR总是u=Ri （在u、i为 关联参考方向的前提下），这一关系不会因外接电路不同而不 同。 同样，一个单口网络的VCR也是由这个单口网络本身所确 定，与外接电路无关，只要这个单口网络除了通过它的两个端 钮与外界相连外，别无其他联系。
分解的一般规则：
下列情况，划分就不是随意的。 ⑴当N1是N2的负载，而我们只对负载所得到的电压、 电流、功率感兴趣时； ⑵或当N2（N1）内部情况不明（黑箱）或是一个不可 分割的整体（如某种器件的模型），而我们只需了解它的外 部性能时；性质不同网络相连处的电压、电流易于首先求解 时； ⑶或电路中有非线性电路时。
电路理论基础第四章习题解答西安电子科技大学出版社
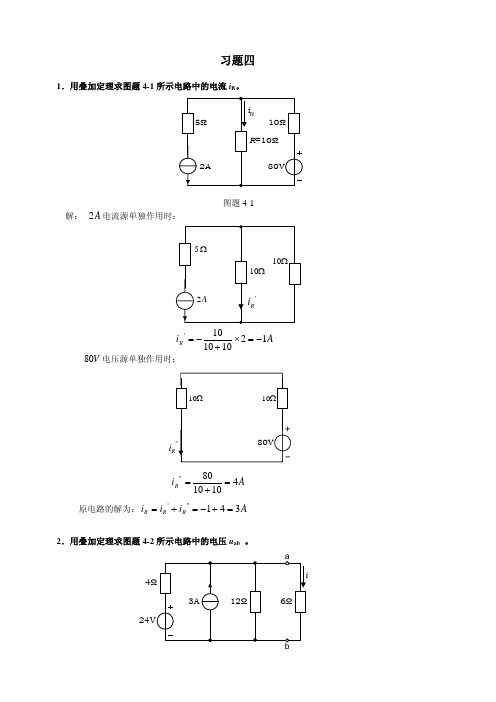
习题四1．用叠加定理求图题4-1所示电路中的电流i R 。
图题4-1解： A 2电流源单独作用时：A i R 12101010'−=×+−=V 80电压源单独作用时：i A i R 4101080''=+=原电路的解为：A i i i R R R 341'''=+−=+=2．用叠加定理求图题4-2所示电路中的电压u ab 。
4图题4-2解：V 24电压源单独作用时：Ω6Ω=+×==46126126//121RV R R u ab 1224411'=×+=A 3电流源单独作用时：Ω4Ω6''A i 13623611214161''=×=×++=V i u ab 6616''''=×=×= 原电路的解为：V u u u ab ab ab 18612'''=+=+=3．用叠加定理求图题4-3所示电路中的电流i 。
6A图题4-3解： A 6电流源单独作用时：ΩΩ6A i 4612612'−=×+−= V 36电压源单独作用时：Ω6Ω6ΩΩA i 261236''−=+−=原电路的解为：()()A i i i 624'''−=−+−=+=4．图题4-4所示电路中，R =6Ω，求R 消耗的功率。
图题4-4解： 将R 支路以外的部分看作一个二端电路。
可采用叠加原理求oc u ：12⎟⎠⎞⎜⎝⎛++××+×+=26363212636oc u V 1688=+=求其等效电阻：eqRΩ=++×=426363eq R 原电路简化为：Ri=eq R u oc =RA R R u i eq oc R 6.14616=+=+=W R i P R R 36.1566.122=×=×=5．图题4-5所示电路中， R 1=1.5Ω R 2=2Ω，求（a ）从a、b 端看进去的等效电阻；（b ）i 1与i s 的函数关系。
第四章BJT及放大电路基础
7、三极管组成电路如左图所示，试分析 （1）当Vi=0V时 （2）当Vi=3V时 电路中三极管的工作状态。 解：（1）当Vi=0V时 ∵Vbe=0V,Ib≈0 ∴三极管处于截止状态, Vo=Vcc=12V （2）当Vi=3V时 三极管Je结处于正偏， Jc结处于反偏状态
∴此时三极管处于放大状态。
8、设某三极管的极限参数PCM＝150mW，ICM＝ 100mA，V（BR）CEO＝30V。试问：
（2）掌握BJT放大、饱和、截止三种工作状态条件及特点。
（3）了解BJT主要参数。
（4）掌握放大电路组成原则、工作原理及基本分析方法。
（5）熟悉放大电路三种基本组态及特点。
（6）了解频响的概念。
主要内容 §4.1 §4.2 §4.3 §4.4 双极结型三极管（BJT） 基本共射极放大电路 放大电路的分析方法 放大电路静态工作点的稳定问题
N EC
二、内部载流子传输过程（以NPN型为例）
BJT处于放大状态外加电压条件：
（发射结正偏） uBE U on 放大的条件 （集电结反偏） uCB 0，即uCE uBE
IE ＝ IEN+IEP
IE
IC ＝ INC + ICBO
IE = IC+ IB
IC
Re
Rc IB
VEE
IB= IEP+IB’－ICBO
5. 集-射极反向击穿电压 U(BR)CEO (重点)
当集—射极之间的电压 UCE 超过一定的数值时，三极管 就会被击穿。
6. 集电极最大允许耗散功耗PCM (重点)
PCM取决于三极管允许的温升，消耗功率过大，温升过高
会烧坏三极管。
PC PCM =IC UCE
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
解(a)开路电压
短路电流
等效戴维宁电阻为
(b)用叠加法求开路电压 及短路电流 。1A电流源作用时，有
20V电压源作用时，有
则
等效戴维宁电阻为
图(a)所示电路的戴维宁和诺顿等效电路如图(c)、(d)所示，为一个电阻。图(b)所示电路的戴维宁和诺顿等效电路如图(e)、(f)所示。
4-18求图(a)、(b)所示两电路的戴维宁等效电路和诺顿等效电路。
解设 ，则
则
即各支路电流及各结电电压为假定值的4倍，所以
4-6题4-6图所示电路中，N为有源线性网络。当 , 时， ；当 , 时， ；当 , 时, 。当 , 时，求
解设N内部独立源作用时产生的 的分量为 ，由叠加定理得
将题给的条件代入，得
解之得
， ，
即有
当 ， 时，有
4-7在图示电路中，当3A的电流源断开时，2A的电流源输出功率为28W，这时 。当2A的电流源断开时，3A的电流源输出功率为54W，这时 。试求两个电流源同时作用时，每个电流源的输出功率。
整理得
即端口 的电压恒为5V，其等效电路为一电压源，如图(c)所示，所以不存在诺顿等效电路。
(b)设 端口电压为 ，电流为 ，应用KCL及KVL得
整理得
即端口 的电流恒为7.5A，其等效电路为一电流源，如图(d)所示，所以不存在戴维宁等效电路。
4-20图(a)电路是一个电桥测量电路。求电阻 分别是 、 和 时的电流 。
式中 为N内部独立源产生的 的分量。将题给条件代入上式，得
求出
， ，
则 和 为任意值时，电压 的计算公式为
4-9图示电路为一非平面电路，电路参数及电源值如图所示。试求电流 。
解当 A单独作用时，可求出
当 单独作用时，可求出
当 单独作用时，可求出
由叠加定理得
4-10应用叠加定理求题4-10图所示电路中的 。欲使 ，电压源不变，电流源电流应为多少？若电流源取12A，则电压源取何值？
解图(b)为10V电压源单独作用的分电路，图(c)为5A电流源单独作用的分电路。由图(b)所示电路得
由图(c)得
由叠加定理得
4-4应用叠加定理求图示电路中的电压 及受控源的功率。
解2A电流源单独作用时，有
求得
4V电压源单独作用时，有
求得
由叠加定理得
受控源的功率为
4-5试求图示梯形电路中各支路电流、结点电压和 。已知 。
解用结点法可求得开路电压 为
短路电流为
等效戴维宁电阻为
等效电路如图(b)、(c)所示。
4-16求图(a)所示电路的戴维宁等效电路和诺顿等效电路。
解用结点法可求得
开路电压为
当 短路时，应用结点法有
短路电流为
等效戴维宁电阻为
等效电路如图(b)、(c)所示。
4-17求图(a)、(b)两电路的戴维宁等效电路和诺顿等效电路。
解R所在支路的电流 已知，根据替代定理可用一个电流源 替代之，设
式中 为N内部独立源所产生的 的分量。将已知条件代入上式，得
解得
，
即有
当 时，由上式可得
4-12图示电路中NS为线性有源电路，已知当 时， ， ；当 时， ， 。如果电流 ，则 为何值？
解 中的电流为已知，由替代定理， 支路可用电流源 替代，设
求得
其开路电压为
用外加电源法可求得
当 时， 获得最大功率，其值为
4-24图(a)所示电路中，当S打开时， ；当S闭合时， 。求含源一端口N的戴维宁等效电路。
解画出图(a)所示电路的等效电路，见图(b)。由图(b)按题给条件得
解得
，
4-25试求题4-25图(a)所示电路中N的戴维宁等效电路。已知端口 的伏安特性如图(b)所示。
解将 拿掉，形成含源一端口，其开路电压为
等效戴维宁电阻为
其等效电路见图(b)。当 时，有
当 时，有
当 时，有
4-21用戴维宁定理求3V电压源中的电流 和该电源吸收的功率。
解将3V电压源拿掉，形成含源一端口，其等效戴维宁参数求解如下：应用KCL、KVL得
求出
开路电压为
用外加电源法可求出
等效电路如图(b)所示。则
解3A电流源单独作用时，应用KCL、KVL可得
求出
8V电压源单独作用时，应用KCL、KVL可得
得
由叠加定理得
电压源不变，则 不变，欲使 ，则电流源产生的分量 应满足下式
得
则电流源应为
若电流源取值 ，则其产生的 分量为
此时电压源产生的分量为
则电压源应为
4-11图示电路中，N为含源线性网络，当改变电阻R的值时，电路中各处电压和电流都随之改变。已知 时， ； 时， ；求当 时，
第四章 电路的基本定理
习题解答
4-1应用叠加定理求图示电路中的电流 、 和 。
解 单独作用时，有
单独作用时，有
单独作用时，有
由叠加定理得
4-2应用叠加定理求图示电路中的电压 。
解6V、5V电压源作用时，有
8V电压源作用时，有
2A电流源作用时，有
由叠加定理得
4-3应用叠加定理求图(a)所示电路中的电流 和电压 。
解应用特勒根定理2，得
代入图示条件得
整理得
得
应用互易定理3，得
4-28图示(a)、(b)两电路中，NR为一互易网络，已知图(b)电路中的 电阻吸收的功率为125W。求 。
解应用特勒根定理2，得
代入图示条件得
由题给条件得 ， ，将其代入上式得
解由题意知，当2A电流源单独作用时，有
当3A电流源单独作用时，有
由叠加定理，2A电流源和3A电流源同时作用时，有
2A电流源和3A电流源发出的功率分别为
4-8图示电路为一线性电阻电路，已知
(1)当 ， 时， ；
(2)当 ， 时， ；
(3)当 ， 时， 。
试给出 和 为任意值时电压 的计算公式。
解由条件(1)可知网络N是含源的，设
短路电流为
等效戴维宁电阻为
图(c)为戴维宁等效电路，图(d)为诺顿等效电路。
4-14求图(a)所示电路的戴维宁等效电路和诺顿等效电路。
解用叠加法求开路电压 和短路电流 。1A电流源单独作用时，有
4V、6V电压源共同作用时，有
则
等效戴维宁电阻为
图(b)为戴维宁等效电路，图(c)为诺顿等效电路。
4-15求图(a)所示电路的戴维宁等效电路和诺顿等效电路。
3V电压源吸收的功率为
(实际发出功率3W)
4-22图示电路中，当 时， 可获得最大功率，并求出最大功率 。
解将 拿掉，形成含源一端口，其开路电压为
等效戴维宁电阻为
则当 时，可获得最大功率，其值为
4-23在图示电路中，求当 为多大时， 获得最大功率？此最大功率是多少？
解将 拿掉，形成含源一端口，应用KCL、KVL可得
解图(c)为图(a)所示电路的等效电路， 、 为N的戴维宁参数。由图(c)得
整理得
(1)
由图(b)得
(2)
比较(1)、(2)两式得
求出
，
4-26在图示(a)、(b)两个电路中，NR为线性无源电阻网络，求 。
解应用特勒根定理2，得
代入已知条件得
求出
4-27在图示(a)、(b)两个电路中，NR为线性无源电阻网络，试分别用特勒根定理和互易定理求图(b)中的电压 。
上式中 为NS内部独立源产生的 的分量，将题给条件代入，得
解得
K=9，
故得
(1)
又设 ，式中 为NS内部独立源产生的 的分量。由电路知 。代入已知条件，得
解得
，
故得
(2)
当 时，由式(1)得
将 代入式(2)得
则此时的 为
4-13求图(a)所示电路的戴维宁等效电路和诺顿等效电路。
解可将1A与 的并联组合等效变成电压源3V与 的串联组合，见图(b)。则开路电压为
解(a)设 端口电压为 ，电流为 ，应用KCL及KVL得
整理得
即得
， ，
(c)、(d)为其等效戴维宁电路和诺顿电路。
(b)设 端口电压为 ，电流为 ，应用KCL及KVL得Fra bibliotek整理得
即得
， ，
(e)、(f)为其等效戴维宁电路和诺顿电路。
4-19求图(a)、(b)所示两个含源一端口的戴维宁或诺顿等效电路。
解(a)设 端口电压为 ，电流为 ，应用KCL及KVL，得
短路电流
等效戴维宁电阻为
(b)用叠加法求开路电压 及短路电流 。1A电流源作用时，有
20V电压源作用时，有
则
等效戴维宁电阻为
图(a)所示电路的戴维宁和诺顿等效电路如图(c)、(d)所示，为一个电阻。图(b)所示电路的戴维宁和诺顿等效电路如图(e)、(f)所示。
4-18求图(a)、(b)所示两电路的戴维宁等效电路和诺顿等效电路。
解设 ，则
则
即各支路电流及各结电电压为假定值的4倍，所以
4-6题4-6图所示电路中，N为有源线性网络。当 , 时， ；当 , 时， ；当 , 时, 。当 , 时，求
解设N内部独立源作用时产生的 的分量为 ，由叠加定理得
将题给的条件代入，得
解之得
， ，
即有
当 ， 时，有
4-7在图示电路中，当3A的电流源断开时，2A的电流源输出功率为28W，这时 。当2A的电流源断开时，3A的电流源输出功率为54W，这时 。试求两个电流源同时作用时，每个电流源的输出功率。
整理得
即端口 的电压恒为5V，其等效电路为一电压源，如图(c)所示，所以不存在诺顿等效电路。
(b)设 端口电压为 ，电流为 ，应用KCL及KVL得
整理得
即端口 的电流恒为7.5A，其等效电路为一电流源，如图(d)所示，所以不存在戴维宁等效电路。
4-20图(a)电路是一个电桥测量电路。求电阻 分别是 、 和 时的电流 。
式中 为N内部独立源产生的 的分量。将题给条件代入上式，得
求出
， ，
则 和 为任意值时，电压 的计算公式为
4-9图示电路为一非平面电路，电路参数及电源值如图所示。试求电流 。
解当 A单独作用时，可求出
当 单独作用时，可求出
当 单独作用时，可求出
由叠加定理得
4-10应用叠加定理求题4-10图所示电路中的 。欲使 ，电压源不变，电流源电流应为多少？若电流源取12A，则电压源取何值？
解图(b)为10V电压源单独作用的分电路，图(c)为5A电流源单独作用的分电路。由图(b)所示电路得
由图(c)得
由叠加定理得
4-4应用叠加定理求图示电路中的电压 及受控源的功率。
解2A电流源单独作用时，有
求得
4V电压源单独作用时，有
求得
由叠加定理得
受控源的功率为
4-5试求图示梯形电路中各支路电流、结点电压和 。已知 。
解用结点法可求得开路电压 为
短路电流为
等效戴维宁电阻为
等效电路如图(b)、(c)所示。
4-16求图(a)所示电路的戴维宁等效电路和诺顿等效电路。
解用结点法可求得
开路电压为
当 短路时，应用结点法有
短路电流为
等效戴维宁电阻为
等效电路如图(b)、(c)所示。
4-17求图(a)、(b)两电路的戴维宁等效电路和诺顿等效电路。
解R所在支路的电流 已知，根据替代定理可用一个电流源 替代之，设
式中 为N内部独立源所产生的 的分量。将已知条件代入上式，得
解得
，
即有
当 时，由上式可得
4-12图示电路中NS为线性有源电路，已知当 时， ， ；当 时， ， 。如果电流 ，则 为何值？
解 中的电流为已知，由替代定理， 支路可用电流源 替代，设
求得
其开路电压为
用外加电源法可求得
当 时， 获得最大功率，其值为
4-24图(a)所示电路中，当S打开时， ；当S闭合时， 。求含源一端口N的戴维宁等效电路。
解画出图(a)所示电路的等效电路，见图(b)。由图(b)按题给条件得
解得
，
4-25试求题4-25图(a)所示电路中N的戴维宁等效电路。已知端口 的伏安特性如图(b)所示。
解将 拿掉，形成含源一端口，其开路电压为
等效戴维宁电阻为
其等效电路见图(b)。当 时，有
当 时，有
当 时，有
4-21用戴维宁定理求3V电压源中的电流 和该电源吸收的功率。
解将3V电压源拿掉，形成含源一端口，其等效戴维宁参数求解如下：应用KCL、KVL得
求出
开路电压为
用外加电源法可求出
等效电路如图(b)所示。则
解3A电流源单独作用时，应用KCL、KVL可得
求出
8V电压源单独作用时，应用KCL、KVL可得
得
由叠加定理得
电压源不变，则 不变，欲使 ，则电流源产生的分量 应满足下式
得
则电流源应为
若电流源取值 ，则其产生的 分量为
此时电压源产生的分量为
则电压源应为
4-11图示电路中，N为含源线性网络，当改变电阻R的值时，电路中各处电压和电流都随之改变。已知 时， ； 时， ；求当 时，
第四章 电路的基本定理
习题解答
4-1应用叠加定理求图示电路中的电流 、 和 。
解 单独作用时，有
单独作用时，有
单独作用时，有
由叠加定理得
4-2应用叠加定理求图示电路中的电压 。
解6V、5V电压源作用时，有
8V电压源作用时，有
2A电流源作用时，有
由叠加定理得
4-3应用叠加定理求图(a)所示电路中的电流 和电压 。
解应用特勒根定理2，得
代入图示条件得
整理得
得
应用互易定理3，得
4-28图示(a)、(b)两电路中，NR为一互易网络，已知图(b)电路中的 电阻吸收的功率为125W。求 。
解应用特勒根定理2，得
代入图示条件得
由题给条件得 ， ，将其代入上式得
解由题意知，当2A电流源单独作用时，有
当3A电流源单独作用时，有
由叠加定理，2A电流源和3A电流源同时作用时，有
2A电流源和3A电流源发出的功率分别为
4-8图示电路为一线性电阻电路，已知
(1)当 ， 时， ；
(2)当 ， 时， ；
(3)当 ， 时， 。
试给出 和 为任意值时电压 的计算公式。
解由条件(1)可知网络N是含源的，设
短路电流为
等效戴维宁电阻为
图(c)为戴维宁等效电路，图(d)为诺顿等效电路。
4-14求图(a)所示电路的戴维宁等效电路和诺顿等效电路。
解用叠加法求开路电压 和短路电流 。1A电流源单独作用时，有
4V、6V电压源共同作用时，有
则
等效戴维宁电阻为
图(b)为戴维宁等效电路，图(c)为诺顿等效电路。
4-15求图(a)所示电路的戴维宁等效电路和诺顿等效电路。
3V电压源吸收的功率为
(实际发出功率3W)
4-22图示电路中，当 时， 可获得最大功率，并求出最大功率 。
解将 拿掉，形成含源一端口，其开路电压为
等效戴维宁电阻为
则当 时，可获得最大功率，其值为
4-23在图示电路中，求当 为多大时， 获得最大功率？此最大功率是多少？
解将 拿掉，形成含源一端口，应用KCL、KVL可得
解图(c)为图(a)所示电路的等效电路， 、 为N的戴维宁参数。由图(c)得
整理得
(1)
由图(b)得
(2)
比较(1)、(2)两式得
求出
，
4-26在图示(a)、(b)两个电路中，NR为线性无源电阻网络，求 。
解应用特勒根定理2，得
代入已知条件得
求出
4-27在图示(a)、(b)两个电路中，NR为线性无源电阻网络，试分别用特勒根定理和互易定理求图(b)中的电压 。
上式中 为NS内部独立源产生的 的分量，将题给条件代入，得
解得
K=9，
故得
(1)
又设 ，式中 为NS内部独立源产生的 的分量。由电路知 。代入已知条件，得
解得
，
故得
(2)
当 时，由式(1)得
将 代入式(2)得
则此时的 为
4-13求图(a)所示电路的戴维宁等效电路和诺顿等效电路。
解可将1A与 的并联组合等效变成电压源3V与 的串联组合，见图(b)。则开路电压为
解(a)设 端口电压为 ，电流为 ，应用KCL及KVL得
整理得
即得
， ，
(c)、(d)为其等效戴维宁电路和诺顿电路。
(b)设 端口电压为 ，电流为 ，应用KCL及KVL得Fra bibliotek整理得
即得
， ，
(e)、(f)为其等效戴维宁电路和诺顿电路。
4-19求图(a)、(b)所示两个含源一端口的戴维宁或诺顿等效电路。
解(a)设 端口电压为 ，电流为 ，应用KCL及KVL，得