电路分析基础第五版第4章
电路分析基础第4章习题答案
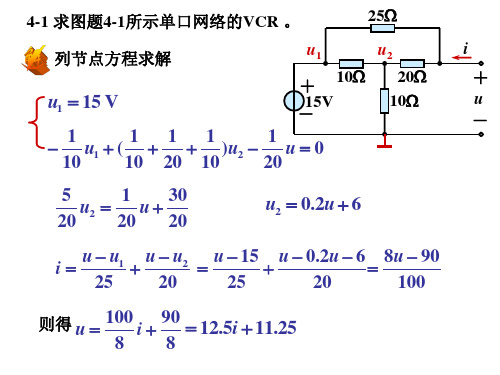
得 u 1.2i 2
5u 4i 5
解方程组
u 1.2i 2
得 u 1.4 V i 0.5 A
4-4 在图题4-4 电路中已知N的VCR为5u = 4i + 5。试求电路中
各支路电流。
i4 i
u 1.4 V i 0.5 A
则可得:
+i1
3 +
5V 1 -
2 u
N
i2
i3 -
i2
5 1
2R 2R R
a
b
(4)8R/3
4-11 R-2R电阻阵列组件如第章图题3-18(a)所示,如何联接端钮以 得到R/2、2R/3、R、8R/3,5R/3、2R、3R及4R的等效电阻?
2R 2R R
2R 2R R (5)5R/3 a
2R 2R R b
2R 2R R
a
b
(6)2R
2R 2R R
a
b
(6)2R
i/mA
R
i
6
5
+ -uS R
+ uN -
4 3
2 1
(a)
1 2 3 4 5 6 7 8 9 10 11 u/V
左边网络端口的伏安关系为:
(b)
i uS u u uS 2u 12 2u
RR R
2000
可画出其伏安特性曲线,如图(b)所示
则端口的电压和电流为: u 4 V i 2 mA
5
A
i3
1.4 2
0.7
A
i4
5
1.4 3
1.2
A
i1 i2 i4 5 1.2 6.2 A
4-5 试设法利用置换定理求解图题4-5所示电路中的电压uO 。 何处划分为好?置换时用电压源还是电流源为好?
电路分析基础第5版第4章 分解方法及单、双口网络

9V
4Ω 3
I1
应用举例
例1:求图示电路中各支路电流。
解: 将3Ω电阻用电流源置换
I3 = 2.7
I1
9 4
1 2
0.9
2.7
A
I2
9 4
1 2
0.9
1.8
A
I4
I5
1 2
I3
0.45
A
I1
2
+
9V
I3 3
2
2
I2
I4
4- 3
2 I5
I1
0.9A I3
2
+
9V
2
I2
2 2
I4
I5
结论:置换后对其他支路没有任何影响。
电压u =α和端口电流i =β,则N2 (或N1)可用一个电压为 α 的电
压源或用一个电流为 β 的电流源置换 ,置换后对 N1 (或N2 ) 内各支路电压、电流没有影响。
i=β
N1
+
u=α
N2
i=β
+
N1
α
N1
+ u=α
β
置换定理适用于线性和非线性电路。
二. 置换的实质
置换:如果一个网络N由两个单口网络组成,且已
联立(1)、(2),解得 u=12V, i=-1A
用12V电压源置换N1,可求得 i1
用-1A电流源置换N2,可求得 u2=12V
[例]求上一例题中N1和N2的等效电路
0.5i1
6Ω
i
5Ω i1
+
+ 10Ω 1A
12V u
- -2
+
电路分析基础第04章电路定理

Pmax
uo2c 4 Req
•最大功率匹配条件
RL Req
最大功率 匹配条件
Pmax
uo2c 4 Req
匹配:RL=Req时,P达到最大值, 称负载电阻与一端口的输入电阻匹配
扩音机为例
Ri
变
压
R=8Ω
ui
器
信号源的内阻Ri为 1kΩ, 扬声器上不可能得到最大功率。 为了使阻抗匹配,在信号源和扬声器之间连上一个变 压器。
第四章 电路定理
§4.1 叠加定理** §4.2 替代定理 §4.3 戴维宁定理** §4.4 特勒根定理 §4.5 互易定理 §4.6 对偶原理
§4.1 叠加定理
一、内容
在线性电阻电路中,任一支路电流(或支路电 压)都是电路中各个独立电源单独作用时在该 支路产生的电流(或电压)之叠加。
i i(1) i(2)+ uu(1)u(2)+
pmax
uo2c 4Req
0.2mW
注
(1) 最大功率传输定理用于一端口电路给定,
(2)
负载电阻可调的情况;
(2) 一端口等效电阻消耗的功率一般并不等于
(3) 大
端口内部消耗的功率,因此当负载获取最
(4)
功率时,电路的传输效率并不一定是50%;
(3) 计算最大功率问题结合应用戴维宁定理
(4) 或诺顿定理最方便.
4、恢复原电路
a
R0
+ Uabo
-
I b
I = U abo 9 R 0 10
例. 求U0 。
解
6
+ 9V 3
–
– 6I + a
+
I
《电路分析基础》_第4章

RO
+
– B
40 RO 8 // 10 4.44 9
A
10 280 uoc 10 ( 20 10) 15.6V 10 8 18
此例从一个侧面证明了戴维南定 理的正确性。也反映了其简便性。
RO
4.44
15.6V B
uoc
+
–
戴维南定理也可以在单口外加电流源i ,用叠加定理计算端 口电压表达式的方法证明。
—
i NS
+ –
a
+
RO
u
b 含源单口网络的VCR表达式:
uoc
–
b
u =K1+K2i = uoc+ Roi
其中:
uoc等于该网络NS的端口开路电压;
a + u
—
i RO
+ –
i
NS
a
+
端口开路时: i =0 u = uoc
u
uoc
–
b
b
RO等于该网络中所有独立源置零时所得网络NR 的等效电阻Rab。 独立源置零
I
+ +
I
º +
5V _
5V _
º
5V _
与电压源并联的元件称为多余元件,多余元件的存在与否并 不影响端口电压的大小,端口电压总等于电压源电压。
us
is
提示:多余元件的存在会使电压源的电流有所改变,但电压源 的电流可为任意值。
总结:一个理想电压源与任何一条支路并联后,对外 等效为理想电压源。 i
(3)外加电压源,求入端电流:
网孔法列方程
( R1+R2 )I + R1IS = - US - U
电路分析基础 第4章 一阶电路的时域分析

时域模型:
电路模型中,元件用R、L、C等参数表征,激励 用电压源电压、电流源电流的时间t的函数表征。
成都信息工程学院-控制工程学院
《电路分析基础》
第四章 一阶电路的时域分析
第4章 一阶电路的时域分析
知识
能力
建立并深刻理解电路的暂态和稳态、 根据给定电路问题合理选择分析方
电路的换路、电路的零输入响应、
线性时不变电容:库伏特性曲线为q-u平面上一条过
原点的直线,且不随时间而变的电容元件。 q(t)=Cu(t)
(2) 符号: q(t) C
i(t) + u(t)
关联参考方向 系数C :电容;
单位:法[拉], F; μF 10-6F ; pF 10-12F;
成都信息工程学院-控制工程学院
《电路分析基础》
《电路分析基础》
第四章 一阶电路的时域分析
动态电路的时域分析
集总电路分:电阻电路和动态电路。 动态电路:至少含有一个动态元件的电路。 动态元件:元件的VCR关系均要用微分或积分来表示的元件。
时域分析: 在时域模型中,以时间为主变量列写电路的 微分方程并确定初始条件,通过求解微分方 程获得电压、电流的时间函数(变化规律)。
即:仅以电场方式存储能量,并可将此能量释放出去,电容本身并不消耗 能量;电容电压反映了电容的储能状态,称电容电压为状态变量。
成都信息工程学院-控制工程学院
《电路分析基础》 5、电容电路的分析 第四章 一阶电路的时域分析
例1 设0.2F电容流过的电流波形如图a所示,
i
5A
已知 u(0) 3。0V试计算电容电压的
C uc(t0)=U0
uc(t) U0
uc1(t) u1(t0)=0
电路分析基础第四章答案

4-2.5μF 电容的端电压如图示。
(1)绘出电流波形图。
(2)确定2μs t =和10μs t =时电容的储能。
解:(1)由电压波形图写出电容端电压的表达式:10 0μs 1μs10 1μs 3μs ()1040 3μs 4μs 0 4μs t t t u t t t t≤≤⎧⎪≤≤⎪=⎨-+≤≤⎪⎪≤⎩ 式中时间t 的单位为微秒;电压的单位为毫伏。
电容伏安关系的微分形式:50 0μs 1μs 0 1μs 3μs()()50 3μs 4μs 0 4μs t t du t i t C t dt t<<⎧⎪<<⎪==⎨-<<⎪⎪<⎩上式中时间的单位为微秒;电压的单位为毫伏;电容的单位为微法拉;电流的单位为毫安。
电容电流的波形如右图所示。
(2)电容的储能21()()2w t Cu t =,即电容储能与电容端电压的平方成正比。
当2μs t =时,电容端电压为10毫伏,故:()()22631010μs 11()5101010 2.510J 22t w t Cu ---===⨯⨯⨯⨯=⨯当10μs t =时,电容的端电压为0,故当10μs t =时电容的储能为0。
4-3.定值电流4A 从t=0开始对2F 电容充电,问:(1)10秒后电容的储能是多少?100秒后电容的储能是多少?设电容初始电压为0。
解:电容端电压:()()()00110422t tC C u t u i d d t C τττ+++=+==⎰⎰;()1021020V C u =⨯=; ()1002100200V C u =⨯=()()211010400J 2C w Cu ==; ()()2110010040000J 2C w Cu ==4-6.通过3mH 电感的电流波形如图示。
(1)试求电感端电压()L u t ,并绘出波形图;(2)试求电感功率()L p t ,并绘出波形图;(3)试求电感储能()L w t ,并绘出波形图。
电路分析基础第4章分解方法及单口网络

is
is is1 is2 isK
5.电流源的串联 电流值相等的电流源可作方向相同的串联,电 流值不相等的电流源不允许串联。
a is1 is2 b
a
is b
is is1 is2
17
6.电流源与二端网络的串联 N1的等效网络不是理想电流源支路。
a
is N1 b
a is b
3
4-2 单口网络的电压电流关系
单口网络的描述方式:
• 详尽的电路图; • VCR(表现为特性曲线或数学公式); • 等效电路。
VCR只取决于单口本身的性质,与外接电路无关。
因而:
• 可以孤立出单口,而用外施电源法求它的VCR; • 求解单口(例如N2)内各电压、电流时,其外部 (例如N1)可 用适当的电路代替。
a
10
10
-
4
2 24V
I +-
+
b 12V
Isc
-
2 24V
+-
+
12V 图(a)
解:把原电路除4电阻以外的部分化简为诺顿等效电 路。为此先把拟化简的单口网络短路,如图(a)所示:
根据叠加原理求短路电流Isc,可得:
Isc
24 10
12 10 // 2
2.4
7.2
9.6 A
35
N a iK
N' uK NK
b
已知:
uk ,或 ik
a
a
N' isk
N'
usk
b
b
isk
usk
11
例:已知电路中U=1.5V,试用置换定理求U1
《电路》第五版-第4章答案

第四章 电路定理4-1应用叠加定理求图示电路中电压ab u 。
2Ω1Ω+-ab u a b 题4-1图解:画出两个电源单独作用时的分电路如题解4-1图所示。
对(a)图应用结点电压法可得:1115sin 13211n t u ⎛⎫++= ⎪+⎝⎭解得:13sin n u tV =()111sin 21n ab u u tV =⨯=+题解4-1图+-(a)()1ab u +-(b)()2ab u对(b)图,应用电阻分流公式有1111351321t t e i e A --=⨯=+++ 所以()2115t ab u i e V -=⨯=()()121sin 5t ab ab ab u u u t e V -=+=+4-2应用叠加定理求图示电路中电压u 。
题4-2图-V解:画出电源分别作用的分电路图①(a)(b)题解4-2图-V u对(a)图应用结点电压法有1111136508240108210n u ⎛⎫++=+ ⎪++⎝⎭解得:()1182.667n u u V ==对(b)图,应用电阻串并联化简方法,可得:104028161040310403821040si u V ⨯⎛⎫⨯+ ⎪+⎝⎭=⨯=⨯⎛⎫++ ⎪+⎝⎭()2823si u u V -==- 所以,由叠加定理得原电路的u 为()()1280u u u V =+=4-3应用叠加定理求图示电路中电压2u 。
3Ω题4-3图2u解:根据叠加定理,作出电压源和电流源单独作用时的分电路,受控源均保留在分电路中。
(a)(b)3Ω题解4-3图()123ΩA(a) 图中()1120.54i A == 所以根据KVL 有()()11213221u i V =-⨯+=-(b) 图中()210i =()22339u V =⨯=故原电路电压()()122228u u u V =+=4-4图示电路中,当电流源1s i 和电压源1s u 反向时(2s u 不变),电压ab u 是原来的0.5倍;当电流源1s i 和电压源1s u 反向时(1s u 不变),电压ab u 是原来的0.3倍。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中产生的电流;
产生的电流。
即:由两个激励产生的响应可表示为每一个激 励单独作用时产生的响应之和。这就是电路理 论中的“叠加性”。
叠加定理:在线性电路中,求某支路(元件)的电压 或电流(响应)等于每个独立源(激励)分别单独作用 时,在该支路产生电压或电流的代数和。
适用范围:多电源激励线性电路。
分析方法: (1)设电压、电流的参考方向。 (2)画子图:每个独立源单独作用时的电路图。 电压源不作用视为短路,电流源不作用视为开路, 其它线性元件照搬。
6
先求出ab支路( 电流ix 所流经的支路)以外电
a ix
b
18V 20
路其余部分就端口ab而
6
3
言的戴维宁等效电路。
c
o (a)
3
6
+
a + uoc - b
18V
6
3
(1)求开路电压uoc, 即断开ab支路后,求 ab之间的电压,如图 (b)所示。
o (b)
uoc = uab=uao- ubo
设想音频放大器(功放)提供恒定功率,
思考
若同时外接多个扬声器,那么以不同的方
式连接,会有什么样的音响效果?
另外,当人们在收听音乐时,偶尔会发生
生失真现象.这又是什么引起的,该如何遭
免呢?
§4-1 叠加定理
线性电路— 由线性元件和独立源构成的电路。
1、线性电路的齐次性 齐次定理:线性电路中所有激励(独立源) 都增大或缩小K倍(K为实常数),响应也将 同样增大或缩小K倍。
利用叠加定理分别求出 1
电压源和电流源单独作
用时的短路电流 isc和isc
如图(b)、(c)所示。
a
1 1
2
1
2 0.2V
i sc
b
1 1
(b)
1A 2
1
(a)
i1
1A i2 2
1
(c)
a
2 isc 0.2V b
a
2 isc
b
图(b)中
isc
0.2 2
若Req 为无限大,则NS不存在戴维宁(南)等效电路。
ia
NS
+
u-
外 电 路
b
(a)
a
N0
Req
b
(c)
a
NS
uoc
b
(b)
ia
Req
+
uoc
u
-
外 电 路
b
(d)
三、诺顿定理(并联型等效电路定理) :
线性含源单口网络NS,对于外电路而言,可 等效为一个电流源并联电阻。电流源的电流等于 该网络NS的短路电流isc ;并联电阻等于该网络中 所有独立源不作用时(即电压源短路,电流源断 路)所得无源网络N0的等效电阻Req。
任何一个二端网络也可以根据该网络端 口电压u和电流i ,用电压源 u 或电流源 i 或 电阻 u/i 来代替。
例1、电路如图所示,求ix 解: 受控源端电压为u,所以
其等效电阻为:
u/2u=0.5
受控源可以用一个0.5电阻 的代替,如图。
分流公式求得:
ix
0.5 3 0.5 1
1A
a
1 10
A
图(c)中
isc
i1
i2
(1 1
1
1
1 1
2
1)
1 6
A
所以:isc
isc
isc
1 10
1 6
4 15
A
(2)再求Req,把图(a)中电流源断开,电压源短
路,如图(d)
a
1
111 4
2 2
Req
Geq 2 3 2 3 S 1 1
6
U
U
(a)
图 2.10 例 2.5 图
(b)
(c)
解:电压源单独作用如图(b)
U 6 9 6V 36
电流源单独作用如图(c) U 6 ( 3 3) 6V
36
所求电压 U U U 12V
例4、电路如图(a)所示,求电压U。
解:电压源单独作用如图(a)
(2)网络N0为含有受控源网络时,可采用外施激励 法;
(3)短路开路法:分别求得原网络短路电流isc和开
路电压uoc, 则
Re q
uoc i sc
3、应用
(1)戴维宁定理和诺顿定理适用于求某一支 路(元件)的电压、电流。
(2)方法:将待求支路当成外电路,其余均视 为含源单口网络化为戴维宁等效电路或诺顿等 效电路。
根据电阻分压公式:
c
6 uao 3 6 18 12V
3 ubo 3 6 18 6V uoc uab uao ubo 12 6 6V
(2)求Req。
3
6
+
a + uoc - b
18V
6
3
o (b)
c
3
6
电压源用短路代替,如图(c)。 a
U1=(0.5/2)2=0.5V
§4-3 戴维宁定理和诺顿定理 一、线性含源单口网络参数 (1) 开路电压:uoc (2)短路电流:isc (3) 等效电阻:Req 含源单口网络内所有独立源为零时,即电压源短 路,电流源开路,由端口处得到的等效电阻。
Req = uoc / isc
+
uoc
isc
Req
3i
2
ia
3
+
u
2
u 13i
(2) b
Req
u i
13
+
3V i
+
u
13
戴维宁等效电路图如图(3)所示。 (3)
例4、电路如图所示,当R = 4 时,I = 2 A,求
当R = 9 时,I =?
2
解:用戴维南宁理求解。
2 2
I
Is
+
U1
-
-R
U2
2 +
求Req。
Req 2 // 2 1
3A
ix
1
+
u
2u
3A 0.5
ix +
1 u
例2、在图示电路中,已知U=1.5V,试用替代定
理求U1。 解: 由于U=1.5V 故:
I=1.5/3=0.5A
+U -
+
3 I
+
2
U1
-
2 -
因此3电阻可以用一
个0.5A的电流源代替,
如图,而不必考虑左
N
侧未知元件。
0.5A +
2
U1
2 -
-
二、戴维宁(南)定理(串联型等效电路定理)
线性含源单口网络NS,对于外电路而言,可 等效为一个电压源串联电阻支路。电压源的电压 等于该网络NS的开路电压uoc;串联电阻等于该网 络中所有独立源不作用时(即电压源短路,电流 源断路)所得无源网络N0的等效电阻Req。
这一电压源串联电阻支路称为线性含源单口 网络NS的戴维宁(南)等效电路。
6
8 5A
2
(a)
(b)
总结: 1、叠加定理适用于线性电路,求支路的电压或电 流响应,但求功率不适用,功率需要用总图响应 求之。
2、在应用叠加定理时,受控源不能作为独立源 (等同于电阻处理) 。
3、总图响应应为子图响应的代数和。
§4-2 替代定理
当电路中的响应为唯一确定值时,电路中 任意支路(网络)电压响应为 u , 电流响应为 i, 则该支路可用电压源 u 或电流源 i 或电阻 u/i 来 代替,不影响电路中其它支路的响应。
U 2 10 8 10 25 V
62
48
6
电流源单独作用如图(a)
U 4 8 6 2 5 125 V
48 62
6
4
8
U 6
5A 2
10V
U U U 25V
4
8
U
6
2
10V
4
U
G
5Ω I L 10Ω
20Ω 20A
G
例2、2Ω求Ix 1Ω
2Ω 1Ω
2Ω a 1Ω I
+ Ix
3A I + + I x
+
I x 3A
+
10V 2I x
2 I x
10V
2Ix
m1
G
G´
G´´
解: 画出子图,受控源视为电阻处理
G : KVL (2 1)Ix 2Ix 10 Ix 2A
特别地,在单激励的线性电路中,任何一个响 应(电压或电流)对激励都存在比例关系。
2、线性电路的叠加性
例:图示电路,求i2 利用KCL和KVL可求得
i2
R1
1
R2
us
R1 R1 R2
is
i1 + R1 uS
a
is i2 R2
(1)第一项是该电路is=0 (2)第二项是该电路us=0
时,us单独作用时在R2 时,is单独作用时在R2中
原电路等效为:
2 2 2
2
Req
uoc ( R Req )I
由R = 4,I = 2 A
+
uoc
I
R
Req
uoc (4 1) 2 10V
