垂直于弦的直径导学案
九年级数学上册 24.1.2 垂直于弦的直径 精品导学案 新人教版

垂直于弦的直径 课题:24.1.2垂直于弦的直径 序号:学习目标:1、知识与技能(1)理解圆的轴对称性;(2)了解拱高、弦心距等概念;(3)使学生掌握垂径定理,并能应用它解决有关弦的计算和证明问题;2、过程与方法:通过研究圆的轴对称性,得到垂径定理的有关结论,并学会运用这些结论解决一些有关证明。
计算和作图问题。
3、情感.态度与价值观:引导学生对图形的观察,发现,激发学生的好奇心和求知欲,并在运用数学知识解答问题的活动中获取成功的体验,建立学习的自信心。
学习重点:“垂径定理”及其应用学习难点:垂径定理的题设和结论以及垂径定理的证明导学过程:. 一、课前预习:阅读课本P80---81的有关内容,完成《导学》教材导读中的问题及自主测评。
. 二、课堂导学:1.情境导入.阅读《导学案》83页的问题导学2. 出示任务,自主学习阅读教材80.81页的有关内容,尝试解决下面的问题:(1)同学们能不能找到下面这个圆的圆心?动手试一试,有方法的同学请举手。
问题:①在找圆心的过程中,把圆纸片折叠时,两个半圆 _______②刚才的实验说明圆是____________,对称轴是经过圆心的每一条_________(2)在找圆心的过程中,折叠的两条相交直径可以是哪样一些位置关系呢?垂直是特殊情况,你能得出哪些等量关系?(3)若把AB 向下平移到任意位置,变成非直径的弦,观察一下,还有与刚才相类似的结论吗?(4)要求学生在圆纸片上画出图形,并沿CD 折叠,实验后提出猜想。
(5)猜想结论是否正确,要加以理论证明引导学生写出已知, 然后让学生阅读课本P81证明,并回答下列问题:①书中证明利用了圆的什么性质?②若只证AE=BE ,还有什么方法?3.合作探究《导学》难点探究和展题设计三、展示 与反馈检查预习情况,解决学生疑惑。
四、课堂小结:垂径定理:分析:给出定理的推理格式A B C DO A B C D O A B C D O E推论:平分弦( )的直径垂直于弦,并且五、达标检测:1.辨析题:下列各图,能否得到AE=BE 的结论?为什么?2. 83页《导学案》.自主测评1—4题课后作业:1、必做题:教材88页习题24.1 5-8题板书设计:24.1.2垂直于弦的直径1.圆的轴对称性:圆是轴对称图形,有无数条对称轴,经过圆心的每一条直线都是它的对称轴。
垂直于弦的直径_导学案.docx

垂直于弦的直径导学案一、知识点回顾:1.圆上各点到圆心的距离都等于__________ ,到圆心的距离等于半径的点都在.2.女口右图_________ 是弓玄, __________ 是劣弧,________ 是优弧。
3.确定一个圆的两个条件是___________ 和__________ o4.圆心到弦的距离叫做_______________5.弦AB所对的弧分为两段______________ 和______________ 。
二、新知学习:1、动手实验,集体研究;活动(一):用纸剪一个圆,并沿着圆的任意一条直径对折问题1:你发现了什么?问题2:由此你得到什么结论?结论为:活动(二):再把圆折一次,使前后两条折痕垂直,请画出可能情况的图形。
其中一种情形如右图:问题1:图中AE=BE吗,为什么?问题2:图中有哪些弧相等?问题3:由此你得到什么结论?1、答2、答3、答所得结论的题设为: ____________________________________________________________________ 所得结论的结论为: ____________________________________________________________________ 结合上面图形,可转化为已知、求证。
已知:求证:证明:垂径定理:垂直于弦的直径平分这条弦,并平分弦所对的两条弧. 几何语言:•••下列图形是否具备垂径定理的条件?应用垂径定理的几个基本图特别注意:_______________________________________________________________________ 三、学以致用:1.在直径是20cm的OO中,AB的长度是16cm,那么弦AB的弦心距OD长为______________ .2.弓形的弦长(弓的跨度为AB)为6cm,弓形的高(弓高为CD)为lcm,则这弓形祈在的圆的半径为________ •例题解析:例1.在OO中,弦AB的长为8cm,圆心O到AB的距离为3cm,求OO的半径.大显身手:你能利用垂径定理解决求赵州桥拱半径的问题吗?[问题:它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m,拱高(弧的中点到弦的距离)为7.2m,你能求出赵州桥主桥拱的半径吗?趁热打铁:1、如图,在直径为100毫米的圆柱形油槽内装入一些油后,截面如图所示。
新人教版九年级数学上册《垂直于弦的直径》导学案

OA B新人教版九年级数学上册《垂直于弦的直径》导学案课 题 垂直于弦的直径 课 型展示课 执笔人审核人级部审核学习时间第 周第 导学稿教师寄语学习目标1、理解圆的轴对称性;了解拱高、弦心距等概念。
2、掌握垂径定理,并能应用它解决有关弦的计算。
(重点)3、垂径定理的题设和结论以及垂径定理的证明。
(难点)学生自主活动材料一.前置性自学1、自学课本80-81页2、怎样找到右边这个圆的圆心?问题:①在找圆心的过程中,把圆纸片折叠时,两个半圆 _______②刚才的实验说明圆是____________,对称轴是经过圆心的每一条_________。
3、在找圆心的过程中,折叠的两条相交直径可以是怎样一些位置关系呢? 垂直是特殊情况,你能得出哪些等量关系?二.小组反馈1、若把AB 向下平移到任意位置,变成非直径的弦,观察一下,还有与刚才类似的结论吗?2、在纸片上画出图形,并沿CD 折叠,实验后提出猜想。
①书中证明利用了圆的什么性质? ②若只证AE=BE ,还有什么方法?3、垂径定理:推论:平分弦( )的直径垂直于弦,并且 4、下列各图,能否得到AE=BE 的结论?为什么?三合作探究1、已知:在圆O 中,弦AB=8,O 到AB 的距离等于3,求圆O 的半径。
2、已知直径是1000mm 的圆柱形水管截面如图所示,若水面宽800 AB mm ,求水的最大深度、四.展示交流AB CDO A B C D O A B C D O E A B C D O E A B O EA B O E D A B OE DB A OMO ABP1、如图,已知AB 是⊙O 的弦,P 是AB 上一点,若AB=10,PB=4,OP=5, 求⊙O 的半径的长。
2、⊙O 的半径是5,P 是圆内一点,且OP =3,过点P 最短弦长为 . 最长弦长为_______.五.拓展提升1、已知一段弧AB ,请作出弧AB 所在圆的圆心。
2、已知线段AB 和CD 是圆O 的两条平行弦,且与圆心的距离分别为3和4,求此二平行弦之间的距离。
24.1.2垂直于弦的直径导学案
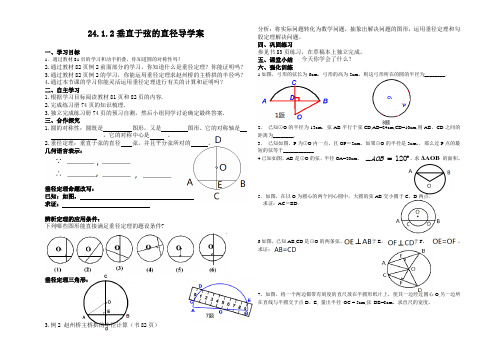
︒=∠120AOB 24.1.2垂直于弦的直径导学案一、学习目标1.通过教材81页的学习和动手折叠,你知道圆的对称性吗?2.通过教材82页例2前面部分的学习,你知道什么是垂径定理?你能证明吗?3.通过教材82页例2的学习,你能运用垂径定理求赵州桥的主桥拱的半径吗?4.通过本节课的学习你能灵活运用垂径定理进行有关的计算和证明吗?二、自主学习1.根据学习目标阅读教材81页和82页的内容.2.完成练习册74页的知识梳理.3.独立完成练习册74页的预习自测,然后小组同学讨论确定最终答案.三、合作探究1.圆的对称性:圆既是 图形,又是 图形。
它的对称轴是,它的对称中心是 。
2.垂径定理:垂直于弦的直径 弦,并且平分弦所对的 。
几何语言表示:垂径定理命题改写:已知:如图,求证:辨析定理的应用条件:下列哪些图形能直接满足垂径定理的题设条件?垂径定理三角形:3.例2 赵州桥主桥拱的半径计算(书82页)分析:将实际问题转化为数学问题,抽象出解决问题的图形,运用垂径定理和勾股定理解决问题。
四、巩固练习参见书83页练习,在草稿本上独立完成。
五、课堂小结 今天你学会了什么? 六、强化训练1.如图,弓形的弦长为6cm ,弓形的高为2cm ,则这弓形所在的圆的半径为________. 2. 已知⊙O 的半径为13cm ,弦AB 平行于弦CD,AB=24cm,CD=10cm,则AB ,CD 之间的距离为________. 3. 已知如图,P 为⊙O 内一点,且OP =2cm ,如果⊙O 的半径是3cm ,,那么过P 点的最短的弦等于____________ 4.已知如图,AB 是⊙O 的弦,半径OA=20cm , ,求 的面积。
5.如图,在以O 为圆心的两个同心圆中,大圆的弦AB 交小圆于C ,D 两点. 求证:AC =BD .6.如图,已知AB,CD 是⊙O 的两条弦, 于E , 于F , 。
求证:7、如图,将一个两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆交于点D 、E, 量出半径 OC = 5cm,弦 DE=8cm 。
人教版数学九年级上册24 垂直于弦的直径(导学案)

24.1.2垂直于弦的直径路漫漫其修远兮,吾将上下而求索。
屈原《离骚》江南学校李友峰——垂径定理及其推论一、新课导入1.导入课题:圆是轴对称图形吗?这节课我们从圆的轴对称性出发探究圆的相关性质.(板书课题)2.学习目标:(1)能通过折纸探究圆的轴对称性,能证明圆是轴对称图形.(2)能由圆的轴对称性推导垂径定理及其推论.(3)能利用垂径定理解决相应问题.3.学习重、难点:重点:圆的轴对称性、垂径定理及其推论.难点:利用垂径定理进行计算或证明.二、分层学习1.自学指导:(1)自学内容:教材第81页“探究”——圆的轴对称性.(2)自学时间:2分钟.(3)自学方法:完成探究提纲.(4)探究参考提纲:①操作:用纸剪一个圆形纸片,沿着圆的任意一条直径所在直线对折,重复几次.a. 通过上面的折纸,圆是轴对称图形吗?有几条对称轴?是轴对称图形,有无数条对称轴.b. “圆的任意一条直径都是它的对称轴”这种说法对吗?若不对,应该怎样说?不对,应该说圆的任意一条直径所在的直线都是它的对称轴.②猜想:圆是轴对称图形,任何一条直径所在的直线都是圆的对称轴.③证明:怎样证明圆是轴对称图形呢?a. 要证圆是轴对称图形,只需证明圆上任意一点关于直径所在直线的对称点也在圆上.b. 怎样证明两点关于已知直线对称?两点的连线被已知直线垂直平分.c. 如图,设CD是⊙O的任意一条直径,A为⊙O上异于点C,D的任意一点,过A作AA′⊥CD,垂足为M.交⊙O于点A′,下面只需证明A′是点A关于直线CD的对称点.如图,连接OA,OA′.在△OAA′中,∵OA=OA′,∴△OAA′是等腰三角形.又AA′⊥CD,∴AM=MA′.即CD是AA′的垂直平分线.∴点A′、A关于直径所在的直线对称即圆是轴对称图形,任何一条直径所在的直线都是圆的对称轴.2.自学:学生可结合探究提纲,相互研讨学习.3.助学:(1)师助生:①明了学情:关注证明过程的逻辑性与规范性.②差异指导:指导学生探究证明思路.(2)生助生:小组内相互交流、研讨.4.强化:(1)圆是轴对称图形,任何一条直径所在的直线都是圆的对称轴.(2)要证某图形是轴对称图形,只需证明该图上任意一点关于对称轴的对称点也在这个图形上.1.自学指导:(1)自学内容:教材第82页例2之前的部分.(2)自学时间:8分钟.(3)自学方法:完成探究提纲.(4)探究参考提纲:①垂径定理:b.归纳:垂直于弦的直径平分弦,并且平分弦所对的两条弧.②垂径定理的推论:b. 反例:当弦AA′为直径时,结论还成立吗?为什么?不成立,因为任意两条直径都互相平分,但不一定垂直.c. 限定:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.2.自学:学生可结合自学导相互研讨学习.3.助学:(1)师助生:①明了学情:了解学生由数学现象概括数学结论时出现的困惑和错误.②差异指导:依据学情进行个别指导或分类指导.(2)生助生:小组内相互交流研讨、订正结论.4.强化:(1)从图形、文字和式子三个方面对垂径定理及其推论进行解读.(2)垂径定理的条件:过圆心,垂直于弦;结论:平分弦,平分弦所对的两条弧.(1)自学内容教材第83页“练习”第1题.(2)自学时间:4分钟.(3)自学方法:完成探究提纲.(4)探究提纲:①线段E满足垂径定理的题设条件:条件1:AB是弦;条件2:OE⊥AB.②依据垂径定理得, AE=12AB=BE.③要求⊙O的半径,只需连接OA,在Rt△AOE中,由勾股定理,就可求得⊙O的半径为5.④给出你的解答过程:2.自学:同学们可结合自学指导进自学.3.助学:1)师助生:①明了学情:观察学生是否会构造直角三角形,书写过程是否规范.②差异指导:从解题思路的探究、辅助线的添加和解题过程的书写等方面给予指导.(2)生助生:生生互动交流、研讨、订正.4.强化:(1)常规辅助线:过圆心作弦的垂线段.(2)设圆的半径为r,弦长为a,圆心到弦的距离为d,则有因此,在这三个量中已知其中两个量就可以求出第三个量(3)练习:如图,已知⊙O的半径为1,弦AB的长为错误!未找到引用源。
人教版九年级上册数学《垂直于弦的直径》导学案

《圆》第一节垂直于弦的直径导教案主编人:主审人:班级:学号:姓名:学习目标:【知识与技术】1理解圆的轴对称性,掌握垂径定理及其余结论2学会运用垂径定理及其推论解决一些相关证明、计算和作图问题3认识拱高、弦心距等观点【过程与方法】经历研究发现圆的对称性,证明垂径定理及其余结论的过程,锻炼思想质量,学习证明的方法【感情、态度与价值观】在学生经过察看、操作、变换、研究出图形的性质后,还要求对发现的性质进行证明,培育学生的新意识,优秀的运用数学【要点】垂径定理及其推论【难点】垂径定理及其推论学习过程 :一、自主学习(一)复习稳固判断:1、直径是弦,弦是直径。
()2、半圆是弧,弧是半圆。
()3、周长相等的两个圆是等圆。
()4、长度相等的两条弧是等弧。
()5、同一条弦所对的两条弧是等弧。
()6、在同圆中,优弧必定比劣弧长。
()7、请在图上画出弦CD,直径 AB. 并说明 ___________________________ 叫做弦;_________________________________叫做直径.8、在图上画出弧、半圆、优弧与劣弧并填出观点及表示方法. 弧: ____半圆: _________________________优弧:________________ _表示方法:__劣弧: _______________________________,表示方法:______9、齐心圆 : ___________________ _等圆: ___________________________.10、同圆或等圆的半径_______. 等弧 : _______________________(二)自主研究请同学按下边要求达成下题:如图, AB 是⊙ O 的一条弦,作直径CD,使 CD⊥ AB,垂足为M.( 1)如图是轴对称图形吗?假如是,其对称轴是什么?圆是对称图形,其对称轴是随意一条过的直线.( 2)你能发现图中有哪些相等的线段和弧?为何?C 相等的线段:A BM 相等的弧:O这样,我们就获得垂径定理:D垂直于的直径均分弦,并且均分弦所对的两条.表达式:下边我们用逻辑思想给它证明一下:已知:直径 CD、弦 AB 且 CD⊥AB 垂足为 M求证: AM=BM ,弧 AC=BC,弧 AD=BD.剖析:要证 AM=BM ,只需证 AM 、 BM 组成的两个三角形全等.所以,只需连接OA、?OB 或 AC、 BC 即可.证明:如图,连接 OA、 OB,则 OA=OB在 Rt△ OAM 和 Rt△ OBM 中CA BM ∴ Rt△OAM≌ Rt△ OBM()O∴ AM=∴点和点∵⊙ O 对于 CD对称对于CD 对称D∴当圆沿着直线CD对折时,点A 与点 B 重合,弧AC与BC重合,AD 与CD重合.∴,,进一步,我们还能够获得结论:均分弦()的直径垂直于,并且均分弦所对的两条.表达式:(三)、归纳总结:1.圆是图形,任何一条所在直线都是它的对称轴.2.垂径定理推论.(四)自我试试:1、辨析题:以下各图,可否获得AE=BE的结论?为何?COO O OA EB A E B A E B A E BD D D2、赵州桥的桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4m,拱高(弧的中点到弦的距离)为7.2m ,你能求出赵州桥的主桥拱的半径吗?CEA BRD注:在半径r,弦 a,弦心距d,拱高 h 四个量中,随意知道此中的个量中,利用定理,就能够求出其余的量。
人教版数学九年级上册同步导学案-24.1.2垂直于弦的直径导学案
《24.1.2垂直于弦的直径》导学案课题垂直于弦的直径数学年级九年级上册知识目标1.掌握垂径定理及其推导过程。
2. 利用垂径定理解决圆的一般问题。
重点难点重点:垂径定理及其运用难点:垂径定理及其运用教学过程知识链接什么是轴对称图形?我们学过哪些轴对称图形?圆也是轴对称图形吗?怎样验证一个图形是轴对称图形,是否圆也具有轴对称的性质呢?今天这节课我们一起来探索相关知识,板书课题。
合作探究活动一、拿出一张圆形纸片,沿着圆的任意一条直径对折,重复做几次,你发现了什么?结论:圆是轴对称图形。
有无数条对称轴,任何一条直径所在的直线都是它的对称轴.活动二、如图,AB是⊙O的一条弦,做直径CD,使CD⊥AB,垂足为E.你能发现图中有那些相等的线段和弧?为什么?结论:AE=BE,即直径CD平分弦AB,并且平分弧AB、弧ADB,即=,=.试一试证明你的发现!已知:在⊙O中,CD是直径,AB是弦CD⊥AB,垂足为E.求证:AE=BE,证明:连结OA、OB,则OA=OB.∵垂直于弦AB的直径CD所在的直线既是等腰三角形OAB的对称轴又是⊙O的对称轴.∴当把圆沿着直径CD折叠时,CD两侧的两个半圆重合,A点和B点重合,AE和BE重合,、分别和、重合.∴AE=BE,你能用文字语言、符号语言归纳出上述结论吗?(1)垂径定理:(2)符号语言:∵AB是⊙O的又∵CDAB⊥∴DECE= = ; =_________我们把这个定理分成几个结论分别有:①CD是直径、AB是弦,②CD⊥AB③AE=BE④=⑤我们知道①②可以推出结论③④⑤,那么如果交换符号结论是否有更多的结论成立?试一试:例如:①直径过圆心③平分弦推出②垂直于弦④平分弦所对优弧⑤平分弦所对的劣弧证明这个结论。
(这个证明方法类似上面的证法,教师点评)形成推论1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.为什么强调这里的弦不是直径?一个圆的任意两条直径总是互相平分,但它们不一定互相垂直.因此这里的弦如果是直径,结论不一定成立.类比推论1你可以写出相应的命题吗?相信自己是最棒的!小组之间讨论,最后教师归纳总结:垂径定理及推论小结:垂径定理的几个基本图形,教师展示ppt,垂径定理中出现的常见三角形,用于计算:在a,d,r,h中,已知其中任意两个量,可以求出其它两个量.例、我是赵州桥,我历史悠久,是世界上现存最早、保存最好的巨大石拱桥。
初中数学九年级上册《垂直于弦的直径》名师精品导学案
《24.1.2垂直于弦的直径》导学案 NO : 35班级 ________ 姓名 _______ 小组 _______ 评价 _____一、 学习目标1、 理解圆的轴对称性,掌握垂径定理及其推论;2、 运用垂径定理及其推论解决一些有关证明、计算与作图的问题。
二、 自主学习1、用纸剪一个圆,沿着圆的任意一条直径对折,重复做几次,你发现了什么?(想一想)由此你能得到什么结论? b5E2RGbCAP圆是 _______ 图形,任何一条 ___________________ 都是圆的对称轴,圆有 _______ 条对称轴(读三遍)。
圆 的直径是圆的对称轴吗? plEanqFDPw 2、阅读教材,总结垂径定理及其推论。
(1) 垂径定理:垂直于弦的直径 _______ 弦,并且平分 __________________ 。
(2) 推论:平分弦(不是直径)的直径 ______ 于弦,并且 ________ 弦所对的两条弧。
(以上读三遍),为什么这里的“弦不是直径”? DXDiTa9E3d3、拓展:若一条直线满足下列五个条件中的任意两个,一定能得出其他三个吗?①经过圆心,②垂直于 弦(非直径),③平分弦,④平分弦所对的优弧⑤平分弦所对的劣弧(请与同学交流你的体会) 。
RTCrpUDGiT 4、自学检测(1) _______________________ 下列命题正确的是A 、弦的垂线平分弦所对的弧C 、过弦的中点的直线必过圆心(2) 如图1, AB 为O O 的直径,弦 A 、/ EOC= / EOD B 、CE=DE C OE=BE D 、BC = BD⑶如图2的O O 中,弦 AB 丄AC 于A , OD 丄AB 于D , OE 丄AC 于 E ,AB=8cm , AC=6cmo 则O O 的半径 OA 长 _____________A 、4cmB 、5cmC 、6cmD 、8cm ⑷点P 是O O 内一点,OP=3cm ,O O 的半径为 5cm ,则经过点________ 5PCzVD7HxA三、合作探究1、如图3,直线l 交以O 为圆心的两个同心圆于 A 、B C 、D 四点,求证:AC=BDbB 、平分弦的直径垂直于这条弦 D 、垂直于弦的直径平分这条弦 CD 丄AB ,垂足为E ,则下列结论不 A最长弦长 图3D C A3、已知O O 的半径为 13cm ,弦 AB//弦 CD, AB=10cm , CD=24cm,求 AB 与 CD 之间的距离。
《24.1.2 垂直于弦的直径》教案、导学案
《24.1.2 垂直于弦的直径》教案【教学目标】1.进一步认识圆是轴对称图形.2.能利用圆的轴对称性,通过探索、归纳、验证得出垂直于弦的直径的性质和推论,并能应用它解决一些简单的计算、证明和作图问题.3.认识垂径定理及推论在实际中的应用,会用添加辅助线的方法解决问题.【教学过程】一、情境导入你知道赵州桥吗?它又名“安济桥”,位于河北省赵县,是我国现存的著名的古代石拱桥,距今已有1400多年了,是隋代开皇大业年间(605~618)由著名将师李春建造的,是我国古代人民勤劳和智慧的结晶.它的主桥拱是圆弧形,全长50.82米,桥宽约10米,跨度37.4米,拱高7.2米,是当今世界上跨径最大、建造最早的单孔敞肩石拱桥.你知道主桥拱的圆弧所在圆的半径吗?二、合作探究探究点一:垂径定理【类型一】垂径定理的理解如图所示,⊙O的直径AB垂直弦CD于点P,且P是半径OB的中点,CD =6cm,则直径AB的长是( )A.23cm B.32cmC .42cmD .43cm解析:∵直径AB ⊥DC ,CD =6,∴DP =3.连接OD ,∵P 是OB 的中点,设OP 为x ,则OD 为2x ,在Rt △DOP 中,根据勾股定理列方程32+x 2=(2x )2,解得x = 3.∴OD =23,∴AB =4 3.故选D.方法总结:我们常常连接半径,利用半径、弦、垂直于弦的直径造出直角三角形,然后应用勾股定理解决问题.【类型二】垂径定理的实际应用如图,一条公路的转弯处是一段圆弧(图中的AB ︵),点O 是这段弧的圆心,C 是AB ︵上一点,OC ⊥AB ,垂足为D ,AB =300m ,CD =50m ,则这段弯路的半径是________m.解析:本题考查垂径定理,∵OC ⊥AB ,AB =300m ,∴AD =150m.设半径为R ,根据勾股定理可列方程R 2=(R -50)2+1502,解得R =250.故答案为250.方法总结:将实际问题转化为数学问题,再利用我们学过的垂径定理、勾股定理等知识进行解答.探究点二:垂径定理的推论 【类型一】利用垂径定理的推论求角如图所示,⊙O 的弦AB 、AC 的夹角为50°,M 、N 分别是AB ︵、AC ︵的中点,则∠MON 的度数是( )A .100°B .110°C .120°D .130°解析:已知M 、N 分别是AB ︵、AC ︵的中点,由“平分弧的直径垂直平分弧所对的弦”得OM ⊥AB 、ON ⊥AC ,所以∠AEO =∠AFO =90°,而∠BAC =50°,由四边形内角和定理得∠MON =360°-∠AEO -∠AFO -∠BAC =360°-90°-90°-50°=130°.故选D.【类型二】利用垂径定理的推论求边如图,点A 、B 是⊙O 上两点,AB =10cm ,点P 是⊙O 上的动点(与A 、B不重合),连接AP 、BP ,过点O 分别作OE ⊥AP 于E ,OF ⊥PB 于F ,求EF 的长.解析:运用垂径定理先证出EF 是△ABP 的中位线,然后运用三角形中位线性质把要求的EF 与AB 建立关系,从而解决问题.解:在⊙O 中,∵OE ⊥AP ,OF ⊥PB ,∴AE =PE ,BF =PF ,∴EF 是△ABP 的中位线,∴EF =12AB =12×10=5cm.方法总结:垂径定理虽是圆的知识,但也不是孤立的,它常和三角形等知识综合来解决问题,我们一定要把知识融会贯通,在解决问题时才能得心应手.【类型三】动点问题如图,⊙O 的直径为10cm ,弦AB =8cm ,P 是弦AB 上的一个动点,求OP 的长度范围.解析:当点P 处于弦AB 的端点时,OP 最长,此时OP 为半径的长;当OP ⊥AB 时,OP 最短,利用垂径定理及勾股定理可求得此时OP 的长.解:作直径MN ⊥弦AB ,交AB 于点D ,由垂径定理,得AD =DB =12AB =4cm.又∵⊙O的直径为10cm,连接OA,∴OA=5cm.在Rt△AOD中,由勾股定理,得OD=OA2-AD2=3cm.∵垂线段最短,半径最长,∴OP的长度范围是3≤OP≤5(单位:cm).方法总结:解题的关键是明确OP最长、最短时的情况,灵活利用垂径定理求解.容易出错的地方是不能确定最值时的情况.三、板书设计【教学反思】教学过程中,强调垂径定理的得出跟圆的轴对称密切相关.在圆中求有关线段长时,可考虑垂径定理的应用.《24.1.2 垂直于弦的直径》教案【教学目标】1、知识目标:(1)充分认识圆的轴对称性。
垂径定理1导学案
24.1.2 垂直于弦的直径(垂径定理第一课时)【学习目标】1.根据圆的对称性探究垂径定理,掌握垂径定理.2.利用垂径定理解决一些实际问题.【导学过程】一.自主学习(一)回顾复习:(独立完成下列各题)1.如图:AB是⊙O______;CD是⊙O______;⊙O中优弧有__________;劣弧有__________。
2.在___圆或____圆中,能够____________叫等弧。
(二)自主探究(一)自主探究一:用纸剪一个圆,沿着圆的任意一条直径所在的直线对折,你发现了什么?结论:圆是_____对称图形,_______________是它的对称轴。
(二)自主探究二:如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为M.(1)如图是轴对称图形吗?如果是,其对称轴是什么?(2)你能发现图中有哪些相等的线段和弧?为什么?相等的线段:______________相等的弧: _____=______;_____=______。
二、合作交流(一)你还能用其他的方法给出证明吗?垂径定理:文字叙述是:垂直于弦的直径_______,并且__________________。
符号语言:∵CD是⊙O_____,AB是⊙O______,且CD__AB于M∴____=_____,_____=______,_____=______。
(二)合作探究二:用垂径定理解决问题已知:⊙O的直径为10cm,圆心O到AB的距离为3cm,求:弦AB的长。
归纳:圆中常用辅助线——作弦心距(圆心到弦的距离),构造Rt△.弦(a)半径(r)弦心距(d),三个量关系为。
简“半径半弦弦心距”。
(三)巩固练习1.已知:AB为⊙O的直径,弦CD⊥AB,垂足为E,则BC =____,AC =____ ;CE=______2.已知:AB为⊙O的弦,AB=24cm, 圆心O到AB的距离为5cm, 求⊙O的直径3.已知:⊙O的直径AB=20cm,∠B=30°,求:弦BC的长三、展示提升:(1)如图,两圆都以点O为圆心,求证:AC=BD(2)圆中有两条互相平行的弦长分别为6cm、8cm,圆的半径为5cm, 求平行两弦之间的距离四、盘点收获OBCA。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4
鸡西市第十九中学初四数学组
5
1
鸡西市第十九中学初四数学组
例 1. 你知道赵州桥吗?它是 1300 多年前我国隋代建造的石拱桥,是我国古代人民勤劳 与智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为 37.4 m ,拱高(弧 的中点到弦的距离)为 7.2 m ,你能求出赵州桥主桥拱的半径吗?
例 2. 如图,一条公路的转弯处是一段圆弦(即图中 CD ,点 O 是 CD 的圆心,• 其中 CD=600m,E 为 CD 上一点,且 OE⊥CD,垂足为 F,EF=90m,求这段弯路的半径.
C E F O D
【当堂训练】
1.圆是______对称图形,它的对称轴是______________________;圆又是 ______对称图形,它的对称中心是____________________. 2.垂直于弦的直径的性质定理是_________________________________. 3.平分________的直径________于弦,并且平分___________________. 4.圆的半径为 5cm,圆心到弦 AB 的距离为 4cm,则 AB=______cm. 5. 如图, CD 为⊙O 的直径, AB⊥CD 于 E, DE=8cm, CE=2cm, 则 AB=______cm.
O A E B
D 反过来:CD 为⊙O 的直径,AB 为⊙O 的弦(不是直径)且 AE=BE, 求证:CD⊥AB, 证明:
AC BC, AD BD 。
归纳总结: ★垂径定理: 弦的直径 这条弦,并平分弦所对的 . 几何符号语言:∵CD 是⊙ O 的直径 又∵ CD AB ∴ , , 。 推论: (不是直径)的直径 于弦,并 弦所对的两条弧 几何符号语言:∵ CD 是⊙ O 的直径 又∵ AE BE (AB 不是直径) ∴ , , 。
16. 已知: 如图,A,B 是半圆 O 上的两点,CD 是⊙O 的直径,∠AOD=80°,B 是 的中点. (1)在 CD 上求作一点 P,使得 AP+PB 最短; (2)若 CD=4cm,求 AP+PB 的最小值.
17.如图,有一圆弧形的拱桥,桥下水面宽度为 7.2m,拱顶高出水面 2.4m,现有一 竹排运送一货箱从桥下经过,已知货箱长 10m,宽 3m,高 2m(竹排与水面持平).问: 该货箱能否顺利通过该桥?
10. 如图, ⊙O 的弦 AB 垂直于 AC, AB=6cm, AC=4cm, 则⊙O 的半径等于______cm. 11. 已知: 如图, AB 是⊙O 的直径, 弦 CD 交 AB 于 E 点, BE=1, AE=5, ∠AEC=30°, 求 CD 的长.
12.已知:如图
,试用尺规将它四等分.
鸡西市第十九中学初四数学组
鸡西市第十九中学学案
2014 年( )月( )日 班级 姓名
垂直于弦的直径 学习 目标 重点 难点
1.圆的对称性。2.通过圆的轴对称性质的学习,理解垂直于弦的直径的 性质。3.能运用垂径定理计算和证明实际问题。 1.通过圆的轴对称性质的学习,理解垂直于弦的直径的性质; 2.能运用垂径定理计算和证明实际问题。 (一)课前预习: 1.什么是轴对称图形?我们学过的图形哪些是轴对称图形?圆是轴对称图形吗? ★ 圆是_________图形,其对称轴是_________________的直线,有 条。 (二)探究新知: 问题:如图, CD 为⊙O 的直径,AB 为⊙O 的弦,且 CD⊥AB,垂足为 E , 观察并猜测:⑴相等的线段: =______(除半径外) ⑵相等的弧_______ =_______, _______=_______。 C 证明:
13.今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何.(选 自《九章算术》卷第九“句股”中的第九题,1 尺=10 寸).
3
鸡西市第十九中学初四数学组
14.已知:⊙O 的半径 OA=1,弦 AB、AC 的长分别为 2 , 3 ,求∠BAC 的度数.
15.已知:⊙O 的半径为 25cm,弦 AB=40cm,弦 CD=48cm,AB∥CD. 求这两条平行弦 AB,CD 之间的距离.
2
鸡西市第十九中学初四数学组
6.如图,⊙O 的半径 OC 为 6cm,弦 AB 垂直平分 OC,则 AB=______cm,∠ AOB=______. 7.如图,AB 为⊙O 的弦,∠AOB=90°,AB=a,则 OA=______,O 点到 AB 的距 离=______.
8.如图,⊙O 的弦 AB 垂直于 CD,E 为垂足,AE=3,BE=7,且 AB=CD,则圆心 O 到 CD 的距离是______. 9. 如图, P 为⊙O 的弦 AB 上的点, PA=6, PB=2, ⊙O 的半径为 5, 则 OP=______.
