测量不确定度评定示例.docx
测量不确定度评定记录-单次1
设备的特性值:
U
=
%
k
=
B类不确定度ub
=
U
=
%
k
3. 环境温度、相对湿度引入的不确定度分量ut,RH:
4. 人员操作引入的不确定度分量uo:
合成标准不确定度uc评定
uc =
ua2 ub2
=
%
扩展不确定度(U)评定
U = kuc =
%
测量不确定度报告
w
=(
±
被检定电能表最大允许误差
±
%
允许测量不确定度U (k=2)
≤
%
改进建议
制表/日期:
(k
=
)
)% 判定
(k
=
)
■ 合格 □ 不合格 □ 待改进
审核/日期:
测量不确定度评定记录
评定日期
测量过程 名称
测量设备 名称
被测量
数学模型:Δ = W - W0
1. 测量结果的重复性ua
a) 仪器设备重复性引入的不确定度分量:
记录序号
测量过程编号 测量设备编号/
型号规格 评定场所
表格编号:
数值(x) (%)
n=
s
n
(xi x)2
u(x)
=
=
i1
=
%
m=
m
m (n 1)
n
xi
x i1
=
%
n
b) 当仪器设备重复性引入的不确定度分量小于由分辨力引入的不确定度分量时,应以分辨力引入的不确定度分量u(δwd)代替 由重复性引入的不确定度分量u(wa)。分辨力d值由仪器说明书给出。
由分辨力引入的不确定度分量u(δwd)
测量不确定度评定的方法以及实例

测量不确定度评定的方法以及实例1.标准不确定度方法:U =sqrt(∑(xi-x̅)^2/(n-1))其中,xi表示测量值,x̅表示测量值的平均值,n表示测量次数。
标准不确定度包含随机误差和系统误差等。
例如,对一组长度进行测量,测得的数据为10.2、10.3、10.1、10.2、10.3,计算平均值为10.22,标准差为0.069、则标准不确定度为0.069/√5≈0.031,即U=0.0312.扩展不确定度方法:扩展不确定度是在标准不确定度的基础上,考虑到误差的正态分布,对标准不确定度进行扩展得到的结果,通常以U'表示。
其计算公式如下:U'=kU其中,k表示不确定度的覆盖因子,代表了误差分布的概率密度曲线下的面积,一般取k=2例如,对上述例子中的长度进行测量,标准不确定度为0.031,取k=2,则扩展不确定度为0.031×2=0.062,即U'=0.0623.组合不确定度方法:4.直接测量法:直接测量法是通过多次测量同一物理量,统计测得值的离散程度来评估测量的不确定度。
该方法适用于一些简单的测量,如长度、质量等物理量的测量。
例如,对一些小球的直径进行测量,测得的数据为2.51 cm、2.49 cm、2.52 cm、2.50 cm,计算平均值为2.505 cm,标准差为0.013 cm。
则标准不确定度为0.013/√4≈0.007 cm,即U=0.0075.间接测量法:间接测量法是通过已知物理量之间的数学关系,求解未知物理量的方法来评估测量的不确定度。
该方法适用于一些复杂的测量,如测量速度、加速度等物理量的测量。
例如,测量物体的速度v,则有v=S/t,其中S为位移,t为时间。
若S的不确定度为U_S,t的不确定度为U_t,则根据误差传递法则,计算得到v的不确定度为U_v = sqrt(U_S^2 + (U_t * (∂v/∂t))^2 )。
总之,测量不确定度评定的方法包括标准不确定度方法、扩展不确定度方法、组合不确定度方法、直接测量法和间接测量法。
测量不确定度案例分析
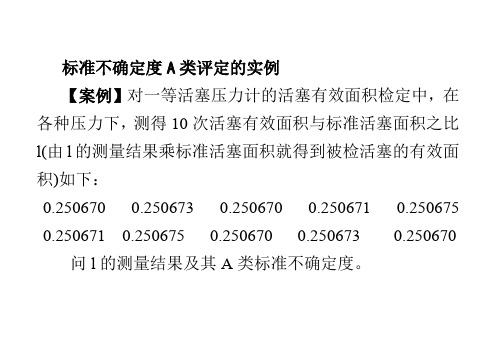
标准不确定度A类评定的实例【案例】对一等活塞压力计的活塞有效面积检定中,在各种压力下,测得10次活塞有效面积与标准活塞面积之比l(由l的测量结果乘标准活塞面积就得到被检活塞的有效面积)如下:0.250670 0.250673 0.250670 0.250671 0.250675 0.250671 0.250675 0.250670 0.250673 0.250670问l的测量结果及其A类标准不确定度。
【案例分析】由于n =10, l 的测量结果为l ,计算如下∑===ni i .l n l 125067201由贝塞尔公式求单次测量值的实验标准差()612100521-=⨯=--=∑.n l l )l (s ni i由于测量结果以10次测量值的平均值给出,由测量重复性导致的测量结果l 的A 类标准不确定度为610630-=⨯=.)l (u n )l (s A 【案例】对某一几何量进行连续4次测量,得到测量值:0.250mm 0.236mm 0.213mm0.220mm ,求单次测量值的实验标准差。
【案例分析】由于测量次数较少,用极差法求实验标准差。
)()(i i x u C Rx s ==式中,R——重复测量中最大值与最小值之差;极差系数c及自由度ν可查表3-2表3-2极差系数c及自由度ν查表得c n =2.06mm ../mm )..()x (u CR )x (s i i 018006221302500=-=== 2)测量过程的A 类标准不确定度评定对一个测量过程或计量标准,如果采用核查标准进行长期核查,使测量过程处于统计控制状态,则该测量过程的实验标准偏差为合并样本标准偏差S P 。
若每次核查时测量次数n 相同,每次核查时的样本标准偏差为Si ,共核查k 次,则合并样本标准偏差S P 为k s s ki ip ∑==12此时S P 的自由度ν=(n -1)k 。
则在此测量过程中,测量结果的A 类标准不确定度为 n S A P u '=式中的n '为本次获得测量结果时的测量次数。
不确定度评定举例

4 不确定度评定举例 (一) 端度规校准1. 概述在比较仪上,对标准端度规和受校准的端度规进行比较,求出两端度规的长度差值,考虑到长度的温度修正,由标准端度规的已知长度,求出受校准端度规的长度。
2. 原理一个名义值50mm 的被校准端度规,将它与同名义长度的已知标准端度规比较,就可求出被校准端度规的长度。
两端度规直接比较的输出是长度差式中:l :受校端度规在20~C 时的长度;ls :标准度规在20~C 时的长度(由标准端度规的校准证书给出): α、αs :受校与标准规的温度热膨胀系数; θ、θs :受校与标准规的温度与20℃的温度偏差。
于是:记受校与标准端度规温差sθθδθ-=。
记受校与标准端度热膨胀系数差s ααδα-=则3.不确定度评定:注意到ls ,d ,α,θ,δα,δθ无关,且δα,δθ期望为0。
而于是:(1)标准的校准不确定度校准证书中给出,标准的展伸不确定度U=0.075um ,并说它按包含因子k=3而得,故标准不确定度校准证书指出,它的自由度18)( s l v于是:(2)测量长度差的不确定度测量两规长度差的实验标准差,通过独立重覆观测25次的变化性而得为13nm ,其自由度为25-1=24。
本例比较中,作5次重复观测并采用平均值,平均值的标准不确定度及自由度于是:(3)比较仪偶然效应比较仪检定证书说明,由偶然误差引起的不确定度为0.01um,它由6次重复测量,置水准95%而得,由t分布临界值,t0.95(5)=2.57,故于是:(4)比较仪系统效应比较仪检定证书给出,由系统误差引起的不确定度为0.02um(3水准),故它可以认为具25%可靠,于是其自由度8%)25(2/1)(2==v d v于是:(5)膨胀系统差的不确定度按均匀分布变化,故它具10%可靠,于是:因(6)规间温差的不确定度标准及被校规应有相同温度,但温差却以等概率落于估计区间-0.05℃至+0.05内任何处,由均匀分布知标准不确定度它具50%可靠,故又不确定度表如下:以上分量无关,合成标准不确定度其自由度在置信水准P=0.99时t0.99(16)=2.92。
测量不确定度评定实例

置上(见图 5—1)
2019/6/14
18
五、测量不确定度应用实 例
2019/6/14
19
其五分、度测头量的示 不值确分定别度为1应、2 用。实则转动
角
例
1 2 1
锥角的第一次测得值为:
1 180 0 1
末位正好对齐。 l = (50.000 838 ±0.000 093)mm 式中,正负号后的值为扩展不确定度U99 k99uc (l) ,而合成标准不确定度
uc (l) =32nm,自由度 = 16,包含因子k99 (16) 2.92 ,从而具有约为 99%的置信水
准。
2019/6/14
17
2019/6/14
20
方(向五2)旋在、转进,行测使第锥量二体次母不检线测再确时次,处定夹于具水度仍平按应位第置一用,次其实检分测度旋头转示
值为1' 。则有:
例
2
2
' 1
2 180 0 2
那么,锥角的实际值为:
1 2 2
2019/6/14
21
(2) B 类不确定度
k=3。故标准量块的标准不确定度u1 为
u1 u(ls ) U / k 0.075 m / 3 0.025 m
证书还指出,它的自由度1 18 。于是
u1 0.025 m,1 18
2019/6/14
10
② 测量长度差的不确定度
量块长度差的实际标准差,通过(以往)独立重复观测 25 次而
五、测量不确定度应用实 u( ) 0.05 ℃/ 3 =0.028 9℃(注意单位)
测量不确定度评估实例M
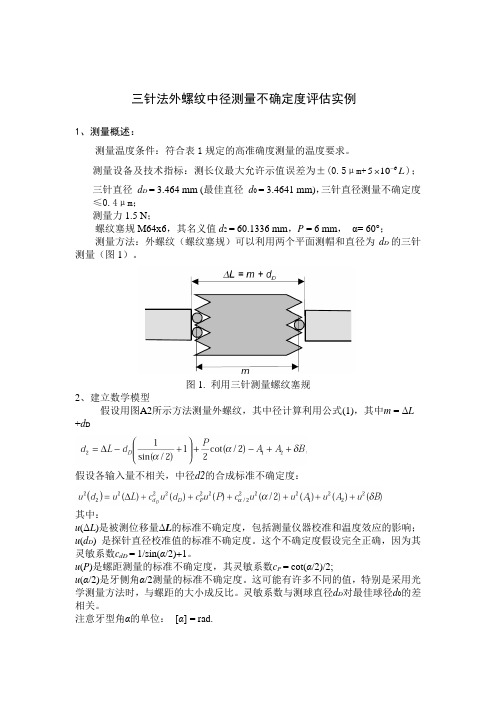
三针法外螺纹中径测量不确定度评估实例1、测量概述:测量温度条件:符合表1规定的高准确度测量的温度要求。
测量设备及技术指标:测长仪最大允许示值误差为±(0.5μm+L 6105-⨯);三针直径 d D = 3.464 mm (最佳直径 d 0 = 3.4641 mm),三针直径测量不确定度≤0.4μm ; 测量力1.5 N ;螺纹塞规M64x6,其名义值d 2 = 60.1336 mm ,P = 6 mm , α= 60°;测量方法:外螺纹(螺纹塞规)可以利用两个平面测帽和直径为d D 的三针测量(图1)。
图1. 利用三针测量螺纹塞规2、建立数学模型假设用图A2所示方法测量外螺纹,其中径计算利用公式(1),其中m = ΔL +d D假设各输入量不相关,中径d2的合成标准不确定度:其中:u (ΔL )是被测位移量ΔL 的标准不确定度,包括测量仪器校准和温度效应的影响; u (d D ) 是探针直径校准值的标准不确定度。
这个不确定度假设完全正确,因为其灵敏系数c dD = 1/sin(α/2)+1。
u (P )是螺距测量的标准不确定度,其灵敏系数c P = cot(α/2)/2;u (α/2)是牙侧角α/2测量的标准不确定度。
这可能有许多不同的值,特别是采用光学测量方法时,与螺距的大小成反比。
灵敏系数与测球直径d D 对最佳球径d 0的差相关。
注意牙型角α的单位: [α] = rad.d D cos(a/2)/sin2(a/2)-P/2sin2(a/2) ;P/2=d0*cos(a/2) (B8)u(A1) 是进行升角修正时采用近似公式引入的不确定度;u(A2) 是测量力修正引入的不确定度;u(δB)是被校螺纹量规不完善、校准程序等所有未明确分离的因素引入的不确定度。
B4.4 不确定度报告的数字示例按照组合3校准螺纹塞规M64x6,其名义值d2 = 60.1336 mm,P = 6 mm,α= 60°。
检定结果不确定度评价示例

电导率仪检定结果不确定度分析以0.2级电导率仪为例,进行分析 一、电子单元引用误差检定的不确定度根据“电导率仪检定规程(修订稿)”的规定,使用电导率仪检定装置(标准电导)评价电子单元的引用误差。
1 数学模型:FS FFSκκκκκκκ-=-=∆式中:Κ — 仪器示值 ΚS — 标准电导率 ΚF — 满量程2 不确定度源及其不确定度: 1) 仪器示值 Κ满量程为200μS/cm ,显示位数占满量程的百分比为0.05%(F.S.);由于显示位数(示值分辨率)造成的不确定度服从均匀分布:029.0320005.0200=⨯ μS/cm按“规程要求”示值重复性上限值为0.07%,引入的不确定度:081.030007.0200=⨯ μS/cm电导率示值Κ的不确定度:086.0081.0029.0)(u 22=+=κ μS/cm005.020011)(===FC κκ cm/μS2) 标准电导率 ΚS标准值相对误差的上限值为0.07%,选用该量程中最大电导率200μS/cm 评价,由于未对标准值修正引入的不确定度:108.030007.0200=⨯ μS/cm根据检定证书知道标准电导率的定值不确定度为0.02%,对于200μS/cm 电导,其标准值的不确定度为:04.00002.0200=⨯ μS/cm标准电导ΚS 的不确定度为900.004.0180.0)(u 22S =+=κ μS/cm005.020011)(===FC κκ cm/μS3 不确定度合成及结论: 检定结果的标准不确定度为:%06.00006.0)()(u )()(u )(u 2222==∙+∙=∆S S C C κκκκ二、 配套检定的不确定度 1、数学模型:FS FFR))25t (02.01(κκκκκκκ-⨯+⋅-=-=∆式中:κ— 仪器示值κS — 标准溶液在参考温度下的标准值 2、不确定度源及其不确定度: 1)仪器示值 κ由于显示位数造成的不确定度服从均匀分布:29.0320005.02000=⨯ μS/cm单次测量的重复性为0.2%,由于测量结果为3次测量的平均值,故而重复性引入的不确定度:33.133002.02000=⋅⨯ μS/cm电导率示值κ的不确定度为33.133.1029.0)(u 22=+=κ μS/cmC(κ)=1/2000=0.0005 cm/μS2)标准溶液标准值k s由标准物质证书知标准物质量值的相对不确定度为0.25% (k=2)96.12%25.01410)u(S =⨯=κμS/cmC(κS )= 1/2000=0.0005 cm/μS3) 温度t标准温度计读数显示位数为0.01℃,由于温度计显示位数引入的不确定度:0029.03201.0= ℃恒温槽温度波动符合正态分布,0255.01.9605.0= ℃026.00255.00029.0)t (u 22=+=℃0.014141002.002.0)t (C =⨯=⨯=FFS κκκ℃-1不确定度合成及结论:配套检定结果的不确定度为:%11.00011.0014.0026.00005.069.10005.033.1)()()()()()()(u 222222222222==⨯+⨯+⨯=∙+∙+∙=∆t C t u C u C u S S κκκκ结论:三、 温度计检定的不确定度 1 数学模型:S t t t -=∆式中:t — 仪器温度示值 t S — 标准温度计示值2 不确定度源及其不确定度: 1)仪器温度示值t温度计示值分度为0.1℃,由于分度引入的不确定度为:029.0321.0=℃ 902.0)(=t u ℃C(t)=12)标准温度计示值t S标准温度计分度为0.01℃,用于温度计分度引入的不确定度为:0029.03201.0=℃标准温度计示值误差引入的不确定度:0289.0305.0=℃029.0029.00029.0)t (u 22S =+=℃C(t S )=13 不确定度合成及结论:)()t (u )()t (u )t (u 2S 222S t C t C ∙+∙=∆温度检定的不确定度:0.041029.0029.0)t (u 22=+=∆℃。
测量结果不确定度

样件球心距测量结果不确定度评定1.概述1.1测量依据: Q/GS-JL-21《 洛氏硬度计操作和保养规程》。
1.2测量环境:温度:(20±2)℃ ;湿度:≤80%1.3测量仪器:三座标测量机动 (600×500×400) mm 最大允许误差:±0.05mm 1.4测量对象:操作件球心距测量 允差: ±0.008mm1.5测量过程:将样件放在测量机中心位置,先测量基准面,再测量球心尺寸. 2.数字模型y=x3.标准不确定度评定3.1由测量机显示值重复性引起的标准不确定度u 1n x xs u ni i1)(121=--==∑-3.2由测量机最大允许误差引起的标准不确定度u 2MPE: ±0.017mm 32=k a u4.合成标准不确评定2221=+=u u u c 5.扩展不确定度评定取k =2 22==c u U ×0.0014=0.0028≈0.003mm6.报告与表示当球心距为18.732mm 时,其扩展不确定度为U=0.03mm ,(k=2)。
报告表示(18.732±0.003)mm编制/日期: 审批/日期:钢件洛氏硬度测量结果不确定度评定1.概述1.1测量依据: Q/GS-JL-27 《洛氏硬度计操作和保养规程》。
1.2测量环境:温度:(10~30)℃;湿度:≤85%1.3测量仪器:洛氏硬度计(20~70)HRC 最大允许误差:±1.0HRC 1.4测量对象:钢管硬度 允差:±2.0HRC1.5测量过程:将V 型试台装在洛氏硬计上,将被测钢件稳定地放在“V ”型词台上,垂直施加规定试验力,(初试力+主试力)在试件上,然后卸除主试力,保压后从表盘读出被测值。
2.数字模型y=x3.标准不确定度评定3.1由硬度计上显示值重复性引起的标准不确定度u 11.19101)(121==--==∑-n x xs u ni i3.2由洛氏硬度计最大允许误差引起的标准不确定度u 2 MPE2==k a u4.合成标准不确评定6.01.1222221=+=+=u u u c 5.扩展不确定度评定取k =2 22==c u U ×1.25=2.5HRC6.报告与表示当测量硬度为40HRC 时,其扩展不确定度为U=2.5HRC ,(k=2)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
— 1 —
定量包装秤测量结果不确定度分析
1、概述
在定量包装中,散料由仪表传感器、仪表显示器、可编程控制器控制粗细料**缸开关及放袋**缸,达到要求的重量。
所用测量设备为DCS -50A -Ⅲ定量自动称重包装秤,○
Ⅲ级秤,在常温下测量,测量过程控制在40kg±200g 。
2、建立数学模型
F=X
F -实际测量结果;
X -定量包装秤显示的结果。
3、标准不确定度
3.1 定量包装秤最大允许误差引入的不确定度u 1
定量包装秤为○
Ⅲ级秤,查相应检定规程得知其最大允许误差为±15g ,区间半宽
a =15g ,均匀分布3=k
g k a u 66.83/15/1===
3.2 仪表分辨力引入的不确定度u 2
仪表分辨力为10g ,区间半宽a =5g ,均匀分布,3=k g k a u 88.23/5/2===
3.3 尿素附粘在包装秤上,影响结果的准确性,根据经验一般估计影响量为30g ,区间半宽a =15g ,均匀分布3=k
g k a u 66.83/15/3===
4、合成标准不确定度
— 2 — 引入不确定度的各个因素彼此独立不相关,所以
g u u u u c 51.1266.888.266.8222232221=++=++=
5、扩展不确定度
c ku U = 取k=2
g U 2551.122=⨯=
6、结果报告
F =40kg U =25g k=2
7、应用分析
测量结果的不确定度为25g ,控制范围为40kg±200g ,25< 2003
1⨯,测量结果的不确定度满足控制要求。
