理论力学第七版答案
理论力学(I)第七版答案

FN = (m+ m + m2 )g +α(−m r + m2r2 ) 1 11 (3) 研究 m ) 1
F 2 − m2 g = m2a2 = m2r2α T F 2 = m2 (g + r2α) T
3.动量矩守恒定律 . 常矢量; 若 ∑MO(F(e) ) ≡ 0,则 LO =常矢量; 常量。 若 ∑Mz (F (e) ) ≡ 0,则 Lz =常量。
J。
6. 查表法 物体 的形 状 细直 杆
均质物体的转动惯量 简 图 转动惯量 惯性半 径
m 2 JzC = l 12 m Jz = l 2 3
体积
ρz =
C
l 2 3
l ρz = 3
薄壁 圆筒
Jz = mR2
ρz = R
2R π lh
圆柱
1 JZ = mR2 2 Jx = Jy =
ρz =
R 2
2
(2) 均质细直杆对一端的 ) ml2 转动惯量
3
(3) 均质细直杆对中心轴 ) ml2 的转动惯量
12
4.组合法 . 例10:已知杆长为 质量为1 ,圆盘半径为 : l m d 质量为 m 。 2 求: JO。
解: JO = JO杆 + JO盘
1 2 JO杆 = ml 3
1 d 2 d 2 JO盘 = m ( ) + m (l + ) 2 2 2 2 2 3 2 2 = m2 ( d + l + ld) 8 1 2 3 2 2 JO = ml + m2 ( d +l +ld) 1 3 8
J z = J zC + md2
例11-9:均质细直杆,已知 :均质细直杆, 求:对过质心且垂直于杆的 解:对一端的 z 轴,有
哈尔滨工业大学 第7版 理论力学 第4章 课后习题答案

解 (1)方法 1,如图 4-6b 所示,由已知得
Fxy = F cos 60° , Fz = F cos 30°
F = F cos 60°cos 30°i − F cos 60°sin 30° j − F sin 60°k = 3 i − 1 Fj − 3 Fk 44 2
41
理论力学(第七版)课后题答案 哈工大.高等教育出版社
A
F
β
MA
C
MB
F
10 N
β M θ − 90° C
MB
(a)
(b)
(c)
图 4-11
解 画出 3 个力偶的力偶矩矢如图 4-11b 所示,由力偶矩矢三角形图 4-11c 可见
MC =
M
2 A
+
M
2 B
=
3 0002 + 4 0002 = 5 000 N ⋅ mm
由图 4-11a、图 4-11b 可得
3 = 250 N 13
FRz = 100 − 200 ×
1 = 10.6 N 5
M x = −300 ×
3 × 0.1 − 200 × 1 × 0.3 = −51.8 N ⋅ m
13
5
M y = −100 × 0.20 + 200 ×
2 × 0.1 = −36.6 N ⋅ m 13
M z = 300 ×
z
F45° F3 F3′ B
F2A
E
F1
C
F5
F6
F F4 45°
D
y
K x
M
(a)
(b)
图 4-9
解 (1) 节点 A 为研究对象,受力及坐标如图 4-9b 所示
理论力学(哈工第七版) 课后练习答案 第三部分
A
ϕ
O
r ϕ
M
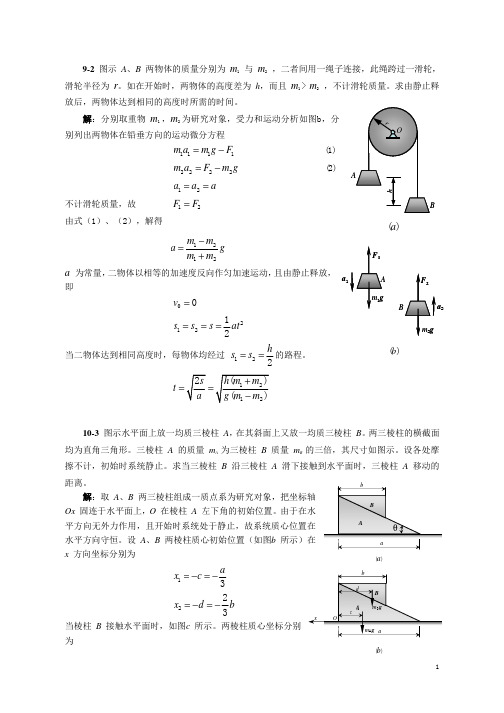
W=
2π
∫ 4ϕ dϕ + (m
0
− mB ) g ⋅ 2π r
A B
A mAg
= 8π 2 + (mA − mB ) g ⋅ 2π r = 8π 2 + 1× 9.8 × 2π × 0.5 = 110 (J)
B
mBg
(a)
(b)
7
12-4 图示坦克的履带质量为 m,两个车轮的质量均为 m1。车轮被看成均质圆盘,半径为 R, 两车轮间的距离为 πR。设坦克前进速度为 v,计算此质点系的动能。 解:系统的动能为履带动能和车轮动能之和。将履带分为四部 分,如图b 所示。履带动能:
O
P2 P aB − 1 a A = FN − P 1−P 2 g g
其中, a A = a , aB = 解得
A
a 2 1 (2 P 1−P 2 )a 2g
B
(a)
FN = P 1+P 2 −
v FN
O
v P 1
A
v aA
v aB B
v P2
(b)
11-1 质量为 m 的点在平面 Oxy 内运动,其运动方程为
得
G1
320
B C
SB
S A = 170 mm S B = 90 mm
(b)
2
10-12 图示滑轮中,两重物 A 和 B 的重量分别为 P1 和 P2。如物体 A 以加速度 a 下降, 不计滑轮质量,求支座 O 的约束力。 解:对整体进行分析,两重物的加速度和支座 O 的约束力如图b 所示。由 动量定理知:
整体受力和运动分析如图b因为0xf所以x方向系统守恒有21cos0brbmvmvv??解得121cosbrmmvvm1所以该系统动能为设此时三棱柱a沿三棱柱b下滑的距离为s则其重力作的功为1sinwmgs??系统动能22b211221sin12cosmmtmmvm由系统动能定理tw即1sinwmgs??上式对时间求导并注意到rdsdtv整理后得22112121sinsincosbbrmmmmvamgvm?????得2b2a212b2b2r2122b21122
哈尔滨工业大学 第七版 理论力学.13
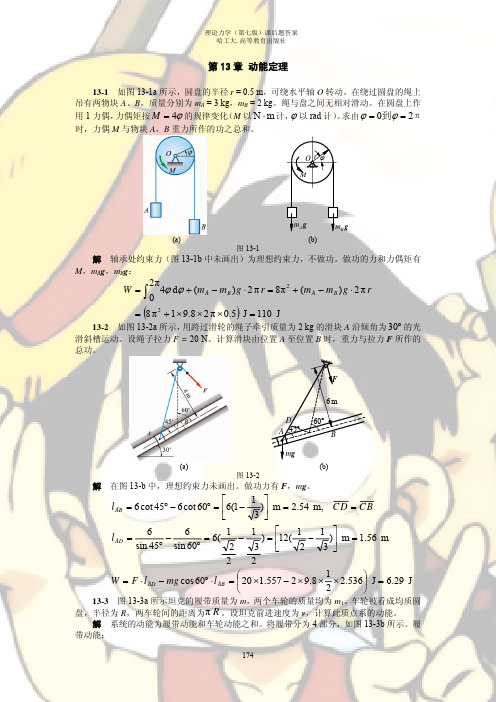
1 2 T履 = ∑ mi vi = TI + TII + TIII + TIV 2
D II A
(a) 图 13-3
IV
2v
C
ω
v
III
Iv=0
(b)
B
由于 v1 = 0, vIV = 2v ,且由于每部分履带长度均为π R ,因此
mI = mII = mIII = mIV = TI =
m 4
1 2 mI vI = 0 2 1 1 m m 2 TIV = mIV v IV = × (2v) 2 = v 2 2 2 4 2 m m 2 II、III 段可合并看作 1 滚环,其质量为 ,转动惯量为 J = R ,质心速度为 v,角速度 2 2 v 为 ω = ,则 R 1 m 1 mv 2 1 m 2 v 2 m 2 TII + TIII = ⋅ v 2 + Jω 2 = + ⋅ R ⋅ 2 = v 2 2 2 4 2 2 2 R m m T履 = 0 + v 2 + v 2 = mv 2 2 2
理论力学(第七版)课后题答案 哈工大.高等教育出版社
第 13 章 动能定理
13-1 如图 13-1a 所示,圆盘的半径 r = 0.5 m,可绕水平轴 O 转动。在绕过圆盘的绳上 吊有两物块 A、B,质量分别为 mA = 3 kg,mB = 2 kg。绳与盘之间无相对滑动。在圆盘上作 用 1 力偶, 力偶矩按 M = 4ϕ 的规律变化 (M 以 N ⋅ m 计, ϕ 以 rad 计) 。 求由 ϕ = 0到ϕ = 2π 时,力偶 M 与物块 A,B 重力所作的功之总和。
第 2 阶段 :系统通过搁板继续运动 x2 距离后静止。由动能定理
理论力学第七版课后习题答案

理论力学第七版课后习题答案第一章: 引言习题1-11.问题描述:给定物体的质量m=2kg,加速度a=3m/s^2,求引力F。
2.解答:根据牛顿第二定律F=ma,其中m表示物体的质量,a表示物体的加速度。
代入已知值,可求得F=6N。
习题1-21.问题描述:给定物体的质量m=5kg,引力F=20N,求加速度a。
2.解答:根据牛顿第二定律F=ma,将已知值代入,可求得a=4m/s^2。
第二章: 运动的描述习题2-11.问题描述:一个物体以恒定速度v=10m/s匀速直线运动,经过t=5s,求物体的位移。
2.解答:位移等于速度乘以时间,即s=vt。
代入已知值,可得s=50m。
习题2-21.问题描述:一个物体以初始速度v0=5m/s匀加速直线运动,加速度a=2m/s^2,经过t=3s,求物体的位移。
2.解答:由于物体是匀加速直线运动,位移可以通过公式s=v0t+0.5at^2计算。
代入已知值,可得s=(53)+(0.52*3^2)=45m。
第三章: 动力学基础习题3-11.问题描述:一个物体质量为m=4kg,受到的力F=10N,求物体的加速度。
2.解答:根据牛顿第二定律F=ma,将已知值代入,可求得a=2.5m/s^2。
习题3-21.问题描述:一个物体质量为m=3kg,受到的力F=6N,求物体的加速度。
2.解答:根据牛顿第二定律F=ma,将已知值代入,可求得a=2m/s^2。
第四章: 动力学基本定理习题4-11.问题描述:一个物体质量为m=8kg,受到的力F=16N,求物体的加速度。
2.解答:根据牛顿第二定律F=ma,将已知值代入,可求得a=2m/s^2。
习题4-21.问题描述:一个物体质量为m=6kg,受到的力F=12N,求物体的加速度。
2.解答:根据牛顿第二定律F=ma,将已知值代入,可求得a=2m/s^2。
以上是理论力学第七版课后习题的答案。
希望能对你的学习有所帮助!。
哈尔滨工业大学 第七版 理论力学 第7章 课后习题答案

tan θ =
r sin ϕ h − r cos ϕ
sin ω 0 t h − cos ω 0 t r ]
图 7-5
注意到 ϕ = ω 0 t ,得
θ = tan −1 [
(2)
自 B 作直线 BD 垂直相交 CO 于 D,则
tan θ =
r sin ω 0 t BD = DO h − r cos ω 0 t
80
理论力学(第七版)课后题答案 哈工大.高等教育出版社
7-6 如图 7-6 所示,摩擦传动机构的主动轴 I 的转速为 n = 600 r/min 。轴 I 的轮盘与轴Ⅱ的轮 盘接触,接触点按箭头 A 所示的方向移动。距离 d 的变化规律为 d = 100 − 5t ,其中 d 以 mm 计, t 以 s 计。已知 r = 50 mm , R = 150 mm 。求: (1)以距离 d 表示轴 II 的角加速度; (2)当 d = r 时,轮 B 边缘上 1 点的全加速度。 解 (1)两轮接触点的速度以及切向加速度相同
∠CBO =
π , x B = 2 R cos ϕ 2 & B = 2 R + vt (↓) x B (0) = 2 R , x
(2 R) 2 − x B
2
vt vt 1 2 − 2 2 − ( )2 R R 2R 2 v v , vC = 2 Rω = − ω =− 2 R sin ϕ sin ϕ sin ϕ = =
两边对时间 t 求导:
vt l
& sec 2 ϕ = , ϕ & = cos 2 ϕ , ϕ && = − ϕ
当ϕ =
v l
v l
2v & cos ϕ sin ϕ ⋅ ϕ l
理论力学(百度文库)-第七版答案-哈工大

哈工大理论力学(I)第7版部分习题答案1-2两个老师都有布置的题目2-3 2-6 2-14 2- 20 2-30 6-2 6-4 7-9 7-10 7-17 7-21 8-5 8-8 8-16 8-24 10-4 10-6 11-5 11-15 10-3以下题为老师布置必做题目1-1(i,j), 1-2(e,k)2-3, 2-6, 2-14,2-20, 2-30 6-2, 6-47-9, 7-10, 7-17, 7-21, 7-268-5, 8-8(瞬心后留), 8-16, 8-24 10-3, 10-4 10-611-5, 11-1512-10, 12-15, 综4,15,16,18 13-11,13-15,13-166-2 图6-2示为把工件送入干燥炉内的机构,叉杆OA=1.5 m在铅垂面内转动,杆AB=0.8 m,A端为铰链,B端有放置工件的框架。
在机构运动时,工件的速度恒为0.05 m/s,杆AB始终铅垂。
设运动开始时,角0=?。
求运动过程中角?与时间的关系,以及点B的轨迹方程。
10-3 如图所示水平面上放1 均质三棱柱A,在其斜面上又放1 均质三棱柱B。
两三棱柱的横截面均为直角三角形。
三棱柱A 的质量为mA三棱柱B 质量mB的 3 倍,其尺寸如图所示。
设各处摩擦不计,初始时系统静止。
求当三棱柱B 沿三棱柱A 滑下接触到水平面时,三棱柱A 移动的距离。
11-4解取A、B 两三棱柱组成1 质点系为研究对象,把坐标轴Ox 固连于水平面上,O 在棱柱A 左下角的初始位置。
由于在水平方向无外力作用,且开始时系统处于静止,故系统质心位置在水平方向守恒。
设A、B 两棱柱质心初始位置(如图b 所示)在x 方向坐标分别为当棱柱B 接触水平面时,如图c所示。
两棱柱质心坐标分别为系统初始时质心坐标棱柱B 接触水平面时系统质心坐标因并注意到得10-4 如图所示,均质杆AB,长l,直立在光滑的水平面上。
求它从铅直位无初速地倒下时,端点A相对图b所示坐标系的轨迹。
哈尔滨工业大学理论力学课后习题答案

----------------------------------------理论力学(第七版)课后题答案哈工大 . 高等教育出版社--------------------------------第 1章静力学公理和物体的受力分析1-1 画出下列各图中物体 A ,ABC 或构件 AB ,AC 的受力图。
未画重力的各物体的自重不计,所有接触处均为光滑接触。
FN1 APFN 2(a)(a1)FTAPFN(b)(b1)A FN1P BFN 3FN 2(c)(c1)FTBFAyP1AP2F Ax(d) (d1)FA FBFA B (e) (e1)1理论力学(第七版)课后题答案哈工大 . 高等教育出版社qFFAy F BA FAxB(f) (f1)FBC F CF A A(g)(g1)FAy FCCA FAx BP1 P2(h)(h1)BFCF CDFAxAF Ay(i) (i 1)(j)(j1)BF B FCPF AyF AxA(k)(k1) 2理论力学(第七版)课后题答案哈工大 . 高等教育出版社FCA FABCF ACAF ABFACBA PFBA(l) (l1)(l2) (l3) 图1-11-2 画出下列每个标注字符的物体的受力图。
题图中未画重力的各物体的自重不计,所有接触处均为光滑接触。
B F N1C FN 2F N P2(a)(a1)F N1BFN1C F N 2FNP2PP1FAyF Ay1FAxFAxA A(a2)(a3)FN1APBFN31P2FN 2 (b)(b1)F NA B FN3P2PF N F N 21(b2) (b3)3理论力学(第七版)课后题答案哈工大 . 高等教育出版社(c)FTDFN2 BP1F N1(c2)(d)F AyA FAxCD FN2B P2P1FN1(c1)F AyA FAxF TP 2(c3)F AyFBqAF Ax C DBFC(d1)FAy FDyqqF BDB F FDxDy (d3)(e)FC(d2)F AyqFAxA BFCyPC FCx(e1)(f)F AyFAxAF1FAyA FBqBxB FBx FCxC PFByFBy FCy(e2) (e3)CF2 FByFAx FBxB(f1)4理论力学(第七版)课后题答案哈工大 . 高等教育出版社F1FAyAFAyF AxAFCxCFCyF Ax(f2)(g)FTD CFCx(g2)CFCyFAyA FAxF BBDF 1FCxF2F ByFBxB(f3)F BCBP(g1)F CyF TC FCxP(g3)F Cy FB(h)FAyAF BBFAx(h1)AF AxFAyCF2FCx B(h2)(i)FCyFCx CF CyA F EFOyF FOxC DFCx EO B(i1) (i2)5理论力学(第七版)课后题答案 哈工大 . 高等教育出版社A AF AxFF AyF E E C DFOyFBy FB yO FOxFBx F BxB B(i3) (i4)FAyD EFCxA F Ax CC FBy F TH FBy FCy BPBFBxFB x(j )(j1) (j2)FAy F DyFDF T2F T 2 E FAx CF C x EyF Dx F Ex A D FDx E FF T1F Ey F T3ExF Dy F (j3)(j4)(j5)CyEF F B D CEF CxB F CyF(k1)DE(k)FF BFCBFCxE CFCy90FD D DEFAy AyFA FAx A FAx(k2) (k3)6理论力学(第七版)课后题答案哈工大 . 高等教育出版社AF A(l)(l1) F2F D DEFE(l3)或F 1 F B FDy F Dy F 2F DxB D F Dx DC EF ExFC F Ey(l2) ’(l3) ’F AD(m)F ADDE HF B F1FF DBBB DCF C(l2)F1 F2DBA C EFA FC FE(l4)F1F2DBAC E FExF A F C F Ey(l4) ’AFCyFCxCF1B(m1)FADF2AF E FH D FAD(m2) (m3)7理论力学(第七版)课后题答案哈工大 . 高等教育出版社A FN AF kFOyO (n)FN1B D qF BF N 2FN3(n2)BF AA(o)BFN B FOx B(n1)FD FFCFEF GG C E(o1)FB DF BD FA FA F BF CFD C(o2) (o3)图 1-2F ED F F F(o4)E8理论力学(第七版)课后题答案 哈工大 . 高等教育出版社 第2章 平面汇交力系与平面力偶系2-1 铆接薄板在孔心 A , B 和 C 处受 3 个力作用,如图 2-1a 所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3-4 在图示刚架中,已知q =3kN/m ,F 可=62kN ,M =10kN ⋅m ,不计刚架自重。
求固
定端A 处的约束反力。
【知识要点】 平面的任意力系的平衡方程及应用,单个物体的平衡问题
【解题分析】 本题应注意固定端A 处的受力分析,初学者很容易丢掉约束力偶。
【解答】 以刚架为研究对象,受力如图。
题3-4图
∑=-⨯+=045cos 42
1,00F q F F Ax x ∑=-=045sin ,00F F F Ay y
∑=⨯+⨯--⨯⨯-
=0445cos 345sin 3
4421,0)(00F F M q M F M A A 解得 F A x =0, F A y =6kN, M A =m kN ⋅12 3-8 如图所示,行动式起重机不计平衡锤的重为P =500kN ,其重心在离右轨1.5m 处。
起
重机的起重量为P 1=250kN ,突臂伸出离右轨10m 。
跑车本身重量略去不计,欲使跑车满载或空载时起重机均不致翻倒,求平衡锤的最小重量P 2以及平衡锤到左轨的最大距离x 。
题3-8图
【知识要点】 平面平行力系的平衡方程及应用,单个物体的平衡问题。
【解题分析】 本题仍为翻倒问题,存在两种临界状态。
【解答】 以起重机为研究对象,受力如图。
若满载不翻倒
0105.13)3(,0)(12=---+=∑P P F x P F M
NA B 由 F NA ≥0,得P 2(x+3)≥3250 (1) 若空载不翻倒 05.43,0)(2∑=-+=P F x P F M NB A
由 F NB ≥0得22502≤x P (2) 由式(1)、(2)得kN P P 3.3331000322≥≥即
把kN P 3.3332=代入(2)得x ≤6.75m
3-11 如图所示,组合梁由AC 和DC 两段铰接构成,起重机放在梁上。
已知起重机重P 1=50kN ,重心在铅直线EC 上,起重载荷P 2=10kN ,如不计梁重,求支座A 、B 和D 三处的约束反力。
【知识要点】 平面任意力系得平衡方程及应用,物体系得平衡问题。
【解题分析】 先研究起重机,再研究连续梁。
连续梁一般先研究附梁最后研究主梁。
【解答】 以起重机为研究对象,受力如图。
题3-11图
0512,0)(21=⨯-⨯-⨯=∑P P F F M NG F
解得 F NG =50kN
以梁CD 为研究对象,受力如图。
016,0)(=⨯'-⨯=∑H G ND C F F F M
解得 F ND =8.33kN 以整体为研究对象,受力如图。
0,0==∑Ax x F F
∑=+--+=0,021ND NB AY y F P P F F F
∑=0)(F M A
036101212=⨯+⨯-⨯-⨯NB ND F P P F
解得 F A x =0, F A y =-48.33kN , F NB =100kN
3-21 图示构架中,物体P 重1200N ,由细绳跨过滑轮E 而水平系于墙上,尺寸如图。
不计杆和滑轮的重量,求支承A 和B 处的约束反力,以及杆BC 的内力FR 。
【知识要点】 平面任意力系得平衡方程,构架得平衡问题
【解题分析】 在求解二力杆BC 的内力时,不能以杆BC 为研究对象,因为其上没有已知条件。
本题也可以通过研究杆CDE 和滑轮求解F BC 。
【解答】 以整体为研究对象,受力如图。
)5.1(4)2(,0)(0
,00
,0=-⨯-⨯--⨯=+-==-=∑∑∑r F F r P F M F P F F F F F T Ay B NB Ay Y T Ax x = 其中 F T = P
解得 F A x =1200N ,F A y =150N, F NB =1050N
以杆ADB 为研究对象,受力如图。
0222sin ,0)(=⨯-⨯+⨯=∑Ay NB BC D F F F F M θ
解得 F BC =-1500N
3-27 在图示构架中,各杆单位长度的重量为30N/m ,载荷P =1000N ,A 处为固定端,B 、
C 、
D 处为铰链。
求固定端A 处及B 、C 铰链处的约束反力。
【知识要点】 平面任意力系的平衡方程,构架的平衡问题。
【解题分析】研究整体求得A 处反力。
再研究AC 可列三个独立方程,需补充一个方程。
研究CD ,对点D 取矩可得补充方程。
杆BD 非二力杆。
【解答】 以整体为研究对象,受力如图。
题3-27图
∑∑∑=---==----===0632,0)(0,00
,03
2321P P P M F M P P P P F F F F A A Ay y Ax x
其中 P 1 =P 3 =180N, P 2 =150N
解得 F A x =0 , F A y =1510N, M A =6840N ·m
以杆CD 为研究对象,受力如图。
∑=-+'=024,0)(1P P F F M Cy D
解得 N F Cy
455=' 以杆ABC 为研究对象,受力如图。
∑∑∑=++==++==++=0
36,0)(0,00,0Bx Ax A C Cy By Ay y Cx Bx Ax x F F M F M F F F F F F F F
解得 F B x =-2280N , F B y =-1785N, F C x =2280N 3-29 图示构架,由直杆BC 、CD 及直角弯杆AB 组成,各杆自重不计,载荷分布及尺寸如图。
销钉B 穿透AB 及BC 两构件,在销钉B 上作用一铅垂力F 。
已知q ,a ,M ,且2qa M =。
求固定端A 的约束力及销钉B 对杆BC ,杆AB 的作用力。
【知识要点】 平面任意力系得平衡方程,构架的平衡问题。
【解题分析】 求销钉B 对杆BC 和杆AB 的作用力需把销钉B 与杆AB 、BC 分离。
掌握三角形载荷的处理方法。
【解答】 以杆CD 为研究对象,受力如图。
∑=⨯
-=02,0)(a qa aF F M Cx D 解得 qa F Cx 2
1= 以杆BC 为研究对象(含销钉B ),受力如图。
题3-29图
0,0)(0,0=+-=='-=∑∑Pa a F M F M F F F BAy C Cx BAx x
解得 qa F F BAx BAx 2
1==' qa P F F BAy BAy
+==' 以弯杆AB (不含销钉B )为研究对象,受力如图。
∑∑∑=⨯⨯-⨯'+'-=='-=='-⨯+
=032
130)(0,0032
1,0a a q a F a F M F M F F F F a q F F BAx BAy A A BAy Ay y BAx Ax x , 解得 F A x =-qa ,F A y =P+qa, M A =(P+qa)a
3-35 平面桁架的支座和载荷如图所示。
ABC 为等边三角形,E 、F 为两腰中点,又AD =DB 。
求杆CD 的内力F 。
【知识要点】 平面简单桁架的内力计算。
【解题分析】 本题先以整体为研究对象求得支座B 的反力,然后用截面法截出杆FB ,求
得杆CF 内力,再以点C 为研究对象求得杆CD 内力。
【解答】 以整体为研究对象,受力如图。
题3-35图
∑=⋅⋅
-⋅=060sin 21,0)(0AB F AB F F M NB A 解得 F F FC 2
1= 以节点C 为研究对象,受力如图。
∑∑=---==-=030cos 30cos ,0030sin 30sin ,00000CF CE CD y CE CF x F F F F F F F
解得 F F F CD 866.02
3-=-= 3-38 平面桁架的支座和载荷如图所示,求杆1、2和3的内力。
【知识要点】 平面简单桁架的内力计算。
【解题分析】 截出CDF ,求得杆2,3内力。
再以点C 为研究对象,求得杆1的内力。
【解答】 由截面法截取CDF 部分,受力如图。
题3-38图
32,0)(0
,023=--==-=∑∑aF aF F M F F D x 解得 F F F 3
2,023-== 以节点C 为研究对象,受力如图。
∑=⋅-⋅=032,0)(21a F a F F M F 解得 F F 941-
=。
