第十章电场中导体和电介质课后习题
静电场中的导体与电介质习题课

静电场中的导体和介质习题课
全部分布在外表面。 (2)连接后电荷 +q全部分布在外表面。 )连接后电荷Q+ 全部分布在外表面
Q+q U1 = U 2 = 4πε 0 R3
(3)内球接地,U1=0。内球带电 ´,外球壳内表面- q´, )内球接地, 。内球带电q´ 外球壳内表面- ´ 外表面Q+ ´ 外表面 + q´,
− q′ Q + q′ U1 = + + =0 4πε 0 R1 4πε 0 R2 4πε 0 R3 R1 R2Q q′ = R1 R2 + R3 ( R2 − R1 )
U 2 = −∫
R1 R2
q′
− q′( R2 − R1 ) Edr = ∫ dr = R2 4πε r 2 4πε 0 R1 R2 0
静电场中的导体和介质习题课
例:计算机键盘的键结构如图。按键连有一可移动的金属片。 计算机键盘的键结构如图。按键连有一可移动的金属片。 下面是一固定的金属片,中间是软的绝缘介质( )。两 下面是一固定的金属片,中间是软的绝缘介质(εr=2)。两 )。 块金属片就构成一个平板电容器。当键按下时, 块金属片就构成一个平板电容器。当键按下时,电容器的电容 发生变化,与之相连的电路就能检测出哪一个键被按下, 发生变化,与之相连的电路就能检测出哪一个键被按下,从而 给出相应的信号。设金属片面积为50mm2,两金属片间距 给出相应的信号。设金属片面积为 0.6mm。如果电路能检测出的电容的变化是 。如果电路能检测出的电容的变化是0.25pF,那么需要 , 将键按下多大的距离才能给出必要的信号? 将键按下多大的距离才能给出必要的信号? 解:按键前电容 C = ε r ε 0 S 1 d ε rε 0 S 按键后电容 C2 = d − ∆d
第十章_电荷和静电场课后习题答案

证:由库仑定律得 :
而:
∵ 角很小
∴
故:
即得: 证毕
10-4 在上题中, 如果l = 120 cm,m = 0.010 kg,x = 5.0 cm,问每个小
球所带的电量q为多大?
解:由上题得:
10-5 氢原子由一个质子和一个电子组成。根据经典模型,在正常状态
下,电子绕核作圆周运动,轨道半径是。质子的质量,电子的质量,
∴
10-16 一个半径为R的半球面均匀带电,面电荷密度为s。求球心的电 场强度。
解:由题9-14知:圆环的电场强度为: 10-17 回答下列问题: (1)处于高斯面内的任何位置上的电荷对该高斯面的电通量是否都有贡 献?是否只要电量相同,贡献就相等? (2)处于高斯面外的任何位置上的电荷对该高斯面的电通量是否都无贡 献? (3)假设一个点电荷正好处于高斯面上,那么这个点电荷对该高斯面的 电通量是否有贡献? 答:(1)是的。高斯面内的任何位置上电荷对高斯面的电通量都有贡 献。只要电量相同,电性相同,贡献就相同。
∴ 方向沿轴线方向
故:
∴
(2) ∴
∴
∴ 10-14 一个半径为R的圆环均匀带电,线电荷密度为l。求过环心并垂 直于环面的轴线上与环心相距a的一点的电场强度。 解:如图:圆环上一线元上产生的电场强度为:
与其对称的一线元产生的电场强度为 : ,
两个电场强度的合成为: ∴ 故:
10-15 一个半径为R的圆盘均匀带电,面电荷密度为。求过盘心并垂直 于盘面的轴线上与盘心相距的P点电场强度。 解:由上题知,圆环上电场强度
∴ 10-11 有两个点电荷,电量分别为5.0´10-7C和2.8´10-8C,相距15 cm。求:
(1)一个电荷在另一个电荷处产生的电场强度; (2)作用在每个电荷上的力 已知:点电荷 求: 解: (方向沿两电荷联线向外)
10静电场中的导体和电介质习题解答

第十章 静电场中的导体和电介质一 选择题1. 半径为R 的导体球原不带电,今在距球心为a 处放一点电荷q ( a >R )。
设无限远处的电势为零,则导体球的电势为 ( )20200π4 . D )(π4 . C π4 . B π4 .A R)(a qa R a q a qR a q o --εεεε 解:导体球处于静电平衡,球心处的电势即为导体球电势,感应电荷q '±分布在导体球表面上,且0)(='-+'+q q ,它们在球心处的电势⎰⎰'±'±='='='q q q R R q V 0d π41π4d 00εε 点电荷q 在球心处的电势为 aq V 0π4ε= 据电势叠加原理,球心处的电势aq V V V 00π4ε='+=。
所以选(A )2. 已知厚度为d 的无限大带电导体平板,两表面上电荷均匀分布,电荷面密度均为σ ,如图所示,则板外两侧的电场强度的大小为 ( )00002 . D . C 2 . B 2 .A εd E=εE=E E σσεσεσ== 解:在导体平板两表面外侧取两对称平面,做侧面垂直平板的高斯面,根据高斯定理,考虑到两对称平面电场强度相等,且高斯面内电荷为S 2σ,可得 0εσ=E 。
所以选(C )3. 如图,一个未带电的空腔导体球壳,内半径为R ,在腔内离球心的距离为 d 处(d<R ),固定一电量为+q 的点电荷。
用导线把球壳接地后,再把地线撤去,选无穷远处为电势零点,则球心o 处的电势为( ))Rd (q R d q 11π4 D. 4πq C. π4 B. 0 A.000-εεε 解:球壳内表面上的感应电荷为-q ,球壳外表面上的电荷为零,所以有)π4π4000Rq d q V εε-+=。
所以选( D )4. 半径分别为R 和r 的两个金属球,相距很远,用一根细长导线将两球连接在一起并使它们带电,在忽略导线的影响下,两球表面的电荷面密度之比σR /σr 为 ( )A . R /r B. R 2 / r 2 C. r 2 / R 2 D. r / R解:两球相连,当静电平衡时,两球带电量分别为Q 、q ,因两球相距很远,所以电荷在两球上均匀分布,且两球电势相等,取无穷远为电势零点,则r q R Q 00π4π4εε= 即 rR q Q = Rr r q R Q r R ==22 4/4/ππσσ 所以选(D ) o R d +q . 选择题3图 选择题2图5. 一导体球外充满相对介质电常数为εr 的均匀电介质,若测得导体表面附近场强为E ,则导体球面上的自由电荷面密度σ为 ( )A. ε0 EB. ε0εr EC. εr ED. (ε0εr -ε0) E解:根据有介质情况下的高斯定理⎰⎰∑=⋅q S D d ,取导体球面为高斯面,则有S S D ⋅=⋅σ,即E D r 0εεσ==。
静电场中的导体和介质习题

.该定理表明,静电场是 有势(或保守力) 场.
9.一空气平行板电容器,两极板间距为d,充电后板间电压
为U.然后将电源断开,在两板间平行地插入一厚度为d/3的 金属板,则板间电压变成U' =_2_U__/3__.
10.带有电荷q、半径为rA的金属球A,与一原先
不带电、内外半径分别为rB和rC的金属球壳B同心
静电场中的导体与电介质
一 选择题
1.一带正电荷的物体M,靠近一原不带电的金属导体N,N
的左端感生出负电荷,右端感生出正电荷.若将N的左端
接地,如图所示,则 (A)N上有负电荷入地.
M
N
(B) N上有正电荷入地.
(C) N上的电荷不动.
(D) N上所有电荷都入地. [ B ]
2.如图所示,一带负电荷的金属球,外面同心地罩一
A 点与外筒 : 间的电势差
U 'R 2E dr U R 2d r U lnR 21.5 2 V
R
lnR 2(/R 1)R r lnR 2(/R 1) R
ቤተ መጻሕፍቲ ባይዱ
四 理论推导与证明题 16.一导体A,带电荷Q1,其外包一导体壳B,带电荷Q2,且 不与导体A接触.试证在静电平衡时,B的外表面带电荷为Q1 + Q2.
4Q 1 0R 14 Q 01 R 4Q 0 2R 24 Q 02 R
代入数 : Q 据 1/Q 2得 1/7
两导体表面上的场强最强,其最大场强之比为
E E1 2m ma a x x4Q 01R 12/4Q 02 R22Q Q 1 2R R 2 12 27 4
分别为R1 = 2 cm,R2 = 5 cm,其间充满相对介电常量为εr的各 向同性、均匀电介质.电容器接在电压U = 32 V的电源上,(如
导体电介质习题课

基本概念和规律
1 . 导体静电平衡的条件
(1) 用电场强度描述 0 导体内部任一点的电场强度为零 E 内
导体表面上任一点的电场强度垂直于该点的表面。
E 表面 表
(2) 用电势描述:整个导体是等势体,表面是等势面。 (3) 用电荷分布描述:导体内部没有电荷,电荷只分 布在导体表面。且
( R R R R ) q R R q R R q ' 2 3 1 3 1 2 1 2 q q q 2 3 R R R R R R R R R R R R 1 3 2 3 1 2 1 3 2 3 1 2 R R R R R R 1 2 2 3 1 3
q '1
q '2
q V2 ( R r R ) 4 0 r 1 2
q q 4 0 R 2 4 0 R 3
q 1 1 1 ( ) 4 R R 0 r 2 3
q2
R3
q3
( R r R ) 2 3
q q q r V3 4 0 r 4 0 r 4 0 R 3 q 4 0 R 3
Q2 b W ln 4 L a 0
ab
b a
Q
ab ln 4 a 0L
b ln 4 0 L a Q
2
Q2
Q
L
1 Q2 b 1 ln W 2 4 L a 0 2
3、再把内球接地: 电荷重新分布: ' 由高斯定律: q'2 q 1
q '1
q '2
q '3
R3
R1
由电守恒定律: ' q q '3 q 2 又因内球接地,电势为零
' q q q 3 0 4 0 R 1 4 0 R 2 4 0 R3
第十章 静电场中的导体和电介质习题解答
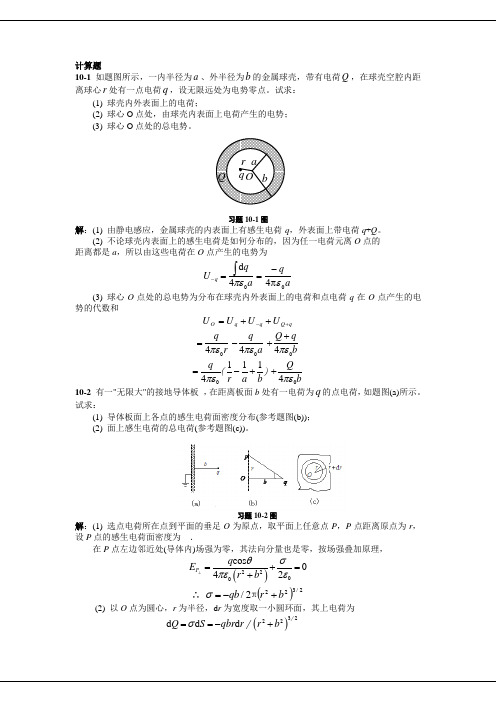
10-1 如题图所示,一内半径为a 、外半径为b 的金属球壳,带有电荷Q ,在球壳空腔内距离球心r 处有一点电荷q ,设无限远处为电势零点。
试求: (1) 球壳内外表面上的电荷;(2) 球心O 点处,由球壳内表面上电荷产生的电势;(3) 球心O 点处的总电势。
习题10-1图解:(1) 由静电感应,金属球壳的内表面上有感生电荷-q ,外表面上带电荷q +Q 。
(2) 不论球壳内表面上的感生电荷是如何分布的,因为任一电荷元离O 点的 距离都是a ,所以由这些电荷在O 点产生的电势为0d 4q qU aπε-=⎰aq04επ-=(3) 球心O 点处的总电势为分布在球壳内外表面上的电荷和点电荷q 在O 点产生的电势的代数和q Q q q O U U U U +-++=04qr πε=04qa πε-04Q qb πε++01114()q r a bπε=-+04Q bπε+ 10-2 有一"无限大"的接地导体板 ,在距离板面b 处有一电荷为q 的点电荷,如题图(a)所示。
试求:(1) 导体板面上各点的感生电荷面密度分布(参考题图(b)); (2) 面上感生电荷的总电荷(参考题图(c))。
习题10-2图解:(1) 选点电荷所在点到平面的垂足O 为原点,取平面上任意点P ,P 点距离原点为r ,设P 点的感生电荷面密度为.在P 点左边邻近处(导体内)场强为零,其法向分量也是零,按场强叠加原理,()220cos 024P q E r b θσεπε⊥=+=+ ∴ ()2/3222/b r qb +-=πσ (2) 以O 点为圆心,r 为半径,d r 为宽度取一小圆环面,其上电荷为 ()3222d d d //Q S qbr r r bσ==-+q Q a bO r()q brrr qb S Q S-=+-==⎰⎰∞2322d d /σ10-3 如题图所示,中性金属球A ,半径为R ,它离地球很远.在与球心O 相距分别为a 与b 的B 、C 两点,分别放上电荷为A q 和B q 的点电荷,达到静电平衡后,问: (1) 金属球A 内及其表面有电荷分布吗?(2) 金属球A 中的P 点处电势为多大?(选无穷远处为电势零点)B C R AP Oq A q Bba习题10-3图解:(1) 静电平衡后,金属球A 内无电荷,其表面有正、负电荷分布,净电荷为零. (2) 金属球为等势体,设金属球表面电荷面密度为. ()()000d 4=4////AP A B S U U S R q a q a σπεπε==⋅+⎰⎰∵d 0AS S σ⋅=⎰⎰∴ ()()04///P A B U q a q a πε=+10-4 三个电容器如题图联接,其中C 1 = 10×10-6 F ,C 2 = 5×10-6 F ,C 3 = 4×10-6 F ,当A 、B 间电压U =100 V 时,试求:(1) A 、B 之间的电容;(2) 当C 3被击穿时,在电容C 1上的电荷和电压各变为多少?ABC 1C 2 C 3U习题10-4图解:(1) =+++=321321)(C C C C C C C 3.16×10-6 F(2) C 1上电压升到U = 100 V ,电荷增加到==U C Q 111×10-3 C10-5 一个可变电容器,由于某种原因所有动片相对定片都产生了一个相对位移,使得两个相邻的极板间隔之比为2:1,问电容器的电容与原来的电容相比改变了多少?(a) (b)习题10-5图解:如图所示,设可变电容器的静片数为n ,定片数为1-n ,标准情况下,极板间的距离为d (图a ),极板相对面积为S 。
川师大学物理第十章 静电场中的导体和电介质习题解
第十章 静电场中的导体和电介质10–1 如图10-1所示,有两块平行无限大导体平板,两板间距远小于平板的线度,设板面积为S ,两板分别带正电Q a 和Q b ,每板表面电荷面密度σ1= ,σ2= ,σ3= ,σ4= 。
解:建立如图10-2所示坐标系,设两导体平板上的面电荷密度分别为σ1,σ2,σ3,σ4。
由电荷守恒定律得12a S S Q σσ+= (1)34b S S Q σσ+= (2)设P ,Q 是分别位于二导体板内的两点,如图10-2所示,由于P ,Q 位于导板内,由静电平衡条件知,其场强为零,即3124000002222P E σσσσεεεε=---= (3)3124000002222Q E σσσσεεεε=++-= (4) 由方程(1)~(4)式得142abQ Q Sσσ+== (5) 232a bQ Q Sσσ-=-= (6) 由此可见,金属平板在相向的两面上(面2,3),带等量异号电荷,背向的两面上(面1,4),带等量同号电荷。
10–2 如图10-3所示,在半径为R 的金属球外距球心为a 的D 处放置点电荷+Q ,球内一点P 到球心的距离为r ,OP 与OD 夹角为θ,感应电荷在P 点产生的场强大小为 ,方向 ;P 点的电势为 。
解:(1)由于点电荷+Q 的存在,在金属球外表面将感应出等量的正负电荷,距+Q 的近端金属球外表面带负电,远端带正电,如图10-4所示。
P 点的场强是点电荷+Q 在P 点产生的场强E 1,与感应电荷在P 点产生的场强E 2的叠加,即E P =E 1+E 2,当静电平衡时,E P =E 1+E 2=0,由此可得21r 2204π(2cos )Qa r ar εθ=-=-+-E E e其中e r 是由D 指向P 点。
因此,感应电荷在P 点产生的场强E 2的大小为图10–4xσ2 4σQQ aQ b 图10-2σ1σ2 σ4σ3 Q a Q b图10-1图10-322204π(2cos )QE a r ar εθ=+-方向是从P 点指向D 点。
第10章 电荷和静电场习题课
(3) 积分值与零势点选取有关 . 选取原则:
电荷有限分布选 U 0 电荷无限分布选 U有限处 0
8
零势点 零势点
Ua E dl Ecosdl
a
a
注意:
• 选取零势点的原则:使场中电势分布有确定值
一般,场源电荷有限分布:选 场源电荷无限分布:不选 许多实际问题中选:
4r2dr
Q2 80r R
18
(1101B)
两个点电荷 q1 40 10-9 C 和 q2 -70 10-9 C ,相距10 cm。
设点A是它们连线的中点,点B 的位置离q1为8.0 cm,离q2为
6.0 cm,求 (1)点A 的电势;(2)点B 的电势。 (设无穷远处电势为0,已知真空中的介电常数)
rr
Ò S
D
dS
r
rS内
q0
D 4πr2 Q
r E
D
D
r0
Q
4π r 0r 2
rˆ
Q
D
r
4πr 2
D 方向:沿径向向外
we
1
2
E2
1 2
r
0
Q
4π r 0r 2
Q2
32π2 r 0r 4
22
如图所示,一半径为R,总电量为q的均匀 带电圆环。
√A. Q
4πε0a
B. Q 2πε0a
C.
Q 4πε0a
2
D. Q 2πε0a2
12
已知厚度为d 的无限大带电导体板,两表面上 σ
大学物理第十章有导体和电介质时的静电场习题解答和分析
第十章习题解答10-1 如题图10-1所示,三块平行的金属板A ,B 和C ,面积均为200cm 2,A 与B 相距4mm ,A 与C 相距2mm ,B 和C 两板均接地,若A 板所带电量Q =3.0×10-7C ,忽略边缘效应,求:(1)B 和C 上的感应电荷?(2)A 板的电势(设地面电势为零)。
分析:当导体处于静电平衡时,根据静电平衡条件和电荷守恒定律,可以求得导体的电荷分布,又因为B 、C 两板都接地,所以有AC AB U U =。
解:(1)设B 、C 板上的电荷分别为Bq 、C q 。
因3块导体板靠的较近,可将6个导体面视为6个无限大带电平面。
导体表面电荷分布均匀,且其间的场强方向垂直于导体表面。
作如图中虚线所示的圆柱形高斯面。
因导体达到静电平衡后,内部场强为零,故由高斯定理得:1A C q q =-2A B q q =-即 ()A B C q q q =-+ ① 又因为: AC AB U U = 而: 2AC AC d U E =⋅AB AB U E d =⋅∴ 2AC AB E E =于是:02C Bσσεε =⋅两边乘以面积S 可得:2C BS S σσεε =⋅即: 2C B q q = ②联立①②求得: 77210,110C B q C q C --=-⨯=-⨯题图10-1题10-1解图d(2) 00222C C A AC C AC AC q d d dU U U U E S σεε =+==⋅=⋅=⋅ 7334122102102.2610()200108.8510V ----⨯=⨯⨯=⨯⨯⨯⨯10-2 如题图10-2所示,平行板电容器充电后,A 和B 极板上的面电荷密度分别为+б和-б,设P 为两极板间任意一点,略去边缘效应,求: (1)A,B 板上的电荷分别在P 点产生的场强E A ,E B ; (2)A,B 板上的电荷在P 点产生的合场强E ; (3)拿走B 板后P 点处的场强E ′。
大学物理下册第10章课后题答案
习题10-3图第10章 静电场中的导体和电介质习 题一 选择题10-1当一个带电导体达到静电平衡时,[ ] (A) 表面上电荷密度较大处电势较高 (B) 表面曲率较大处电势较高(C) 导体内部的电势比导体表面的电势高(D) 导体内任一点与其表面上任一点的电势差等于零 答案:D解析:处于静电平衡的导体是一个等势体,表面是一个等势面,并且导体内部与表面的电势相等。
10-2将一个带正电的带电体A 从远处移到一个不带电的导体B 附近,导体B 的电势将[ ](A) 升高 (B)降低 (C)不会发生变化 (D)无法确定 答案:A解析:不带电的导体B 相对无穷远处为零电势。
由于带正电的带电体A 移到不带电的导体B 附近的近端感应负电荷;在远端感应正电荷,不带电导体的电势将高于无穷远处,因而正确答案为(A )。
10-3将一带负电的物体M 靠近一不带电的导体N ,在N 的左端感应出正电荷,右端感应出负电荷。
若将导体N 的左端接地(如图10-3所示),则[ ](A) N 上的负电荷入地 (B) N 上的正电荷入地 (C) N 上的所有电荷入地 (D) N 上所有的感应电荷入地 答案:A解析:带负电的带电体M移到不带电的导体N附近的近端感应正电荷;在远端感应负电荷,不带电导体的电势将低于无穷远处,因此导体N的电势小于0,即小于大地的电势,因而大地的正电荷将流入导体N,或导体N的负电荷入地。
故正确答案为(A)。
10-4 如图10-4所示,将一个电荷量为q电的导体球附近,点电荷距导体球球心为d。
设无穷远处为零电势,则在导体球球心O点有[ ](A)0E,4πε=qVd(B)24πε=qEd,4πε=qVd(C) 0E,0V(D)24πε=qEd,4πε=qVR答案:A解析:导体球处于静电平衡状态,导体球内部电场强度为零,因此0E。
导体球球心O点的电势为点电荷q及感应电荷所产生的电势叠加。
感应电荷分布于导体球表面,至球心O的距离皆为半径R,并且感应电荷量代数和q∑为0,因此4qVRπε==∑感应电荷。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解 (1) 空气平板电容器的电容
C0
ε0S d
充电后,极板上的电荷和极板间的电场强度为
Q0
CoU
0S
d
U
E0 U / d
(2)插入电介质后,相当于两个电容器串联.由于极 板与电源相接,故电势差不变
Cd
0S d
C
0 r S
U
U1
U2
Q
0S
d
(2) 此过程中外力所作的功,并讨论此过程中的功能 转换关系.
解 (1)极板间的电场为匀强场,且场强不变,因此,
电场的能量密度为
we
1 2
0
E
2
1 2
0
(
0
)2
Q2
20S 2
在外力作用下极板间距从d 被拉开到2d,电场占有空
间的体积,也由V增加到2V,此时电场能量增加
ΔWe
weΔV
Q2
20S 2
S
d
Q2d
20S
(2) 两导体极板带等量异号电荷,外力F 将其缓 缓拉开时,应有F=-Fe ,则外力所作的功为
W
Fe
Δr
QEd
Q2d
2 0 S
外力克服静电引力所作的功等于静电场能量的增加.
10-12 一片二氧化钛晶片,其面积为1.0cm2 ,厚度为0.10mm.把
平行平板电容器的两极板紧贴在晶片两侧.(1) 求电容器的电
容;(2) 当在电容器的两极间加上12 V电压时,极板上的电荷
为多少? 此时自由电荷和极化电荷的面密度各为多少? (3)
求电容器内的电场强度.
解(1) 查表可知二氧化钛的相对电容率ε r=173, 故充满此介质的平板电容器的电容
CCD C3 C4 8 μF
1 1 1 1 CAB CAC CCD C5
求得等效电容CAB =4 μ F.
(2) 由于 QAC QCD QDB QAB,得
U AC
CAB CAC
U AB
4
V
U DB
CAB CDB
U AB
2
V
U CD
CAB CCD
U AB
6
C εrε0S 1.53109 F
(2)
电容器加上U
d
=12
V
的电压时,极板上的电荷
Q CU 1.84 108 C
极板上自由电荷面密度为
σ0
Q S
1.84 108
C
m-2
晶片表面极化电荷密度
σ0
1
1 εr
σ0
1.83104
C
m-2
(3) 晶片内的电场强度为 E U 1.2 105 V m-1
d
10-16 在A点和B点之间有5个电容器,其连接如图所 示.(1) 求A、B 两点之间的等效电容;(2) 若A、
B之间的电势差为12 V,求UAC 、UCD 和UDB .
解(1)由电容器的串、并联
CAC C1 C2 12 μF
V
10-17 有一个空气平板电容器,极板面积为S,间距 为d.现将该电容器接在端电压为U的电源上充电,当
(1) 充足电后;(2) 然后平行插入一块面积相同、
厚度为δ (δ <d)、相对电容率为ε r的电介质板;
(3) 将上述电介质换为同样大小的导体板.分别求
电容器的电容C,极板上的电荷Q 和极板间的电场强
rU
r d
(3) 插入导体达到静电平衡后,导体为等势体,
相当于将极板向上升高 其电容和 Nhomakorabea板上的电荷分别为
C2
ε0S d δ
Q2
ε0S U d δ
导体中电场强度 E2 0
空气中电场强度
E2
U d
δ
10-19 有一电容为0.50 F 的平行平板电容器,两极板
间被厚度为0.01mm的聚四氟乙烯薄膜隔开。(1) 求该 电容器的额定电压(2) 求电容器存储的最大能量。
解 查表知聚四氟乙烯的击穿场强为
Eb 6 10 7V / m
(1) 电容器两极板间电势差为
Umax Ebd 600V
(2)电容器存储的最大能量
We
1 2
CU
2
max
0.09J
10 -23 一平行板空气电容器,极板面积为S,极板间
距为d,充电至带电Q后与电源断开,然后用外力缓缓地 把两极板间距拉开到2d.求:(1) 电容器能量的改变;
Q
0r S
插入电介质后,电容器的电容
C1
Q U
0 r S
r d
极板上的电荷
Q1
C1U
0 r SU
r d
介质内电场强度 E1
1
Q1
0 r S
U
r d
空气中电场强度 E1
0
Q1
0S
