第五节 磁场的能量和能量密度
磁场的能量 磁场能量密度

磁场的能量
L R
K
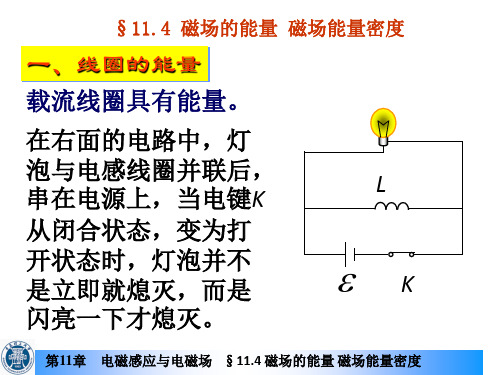
当电键打开后,电源已不再向灯泡供应能量了。 它突然闪亮一下,所消耗的能量从哪里来的?
考察在开关合上后的一段时间内,电路中的电 流滋长过程:
由欧姆定律
dI L dt +
ε
L =I R
R
这一方程的解为:
ε
)
I I )
BATTERY
电池
I = R (1 e
= I (1 e
I1
dI dt
M12
1 B2 dV 2
12
I2
1 2 Wm LI 2
, ,
M k L1L 2
磁场能量: Wm v
总磁 能
1 Wm BH d V 2 1 2 1 L 2 m 2 磁场能量密度: 单位体积中储存的磁场能量 wm 磁能密度:
B wm 2
2
总磁能
Wm
V
B dV 2
2
例1 求同轴传输线之磁能 o I 解: B dV = 2 π rl 2r
t
时间内电源提供的部分能量转化为消耗 0 在电阻 R 上的焦耳-楞次热;
1 2
t
RI 2 d t 是
LI 02 是回路中建立电流的暂态过程中电源电动势克
服自感电动势所作的功,这部分功转化为载流回路的 能量; 当回路中的电流达到稳定值后,断开 K1 ,并同时 接通K 2 ,这时回路中的电流按指数规律衰减,此电 流通过电阻时,放出的焦耳-楞次热为
电磁感应 定律
电动势
d m i dt 动 L( v B ) d l
L
大小与方向 非静电力 f 洛 感生电场
第8章_静磁能1__磁场的能量和能量密度__20101227

0
0 dt
0
0
0
2
0
其中
T
∫ εidt
0
表示 0 → T中,电源所作的功;
1 Li2表示电源在0 → T中提供的转变为磁场的能量。 2
T
∫ i2Rdt
0
表示0 → T中,电流在电阻上作的功;
由此可见,电源所供给的能量,一部分转化为焦耳--楞茨热,另一部分用于反抗自感电动势所作的功,这将 是另一种形式的能量改变的量度。
0
0
注意积分上下限的变换以及M12 = M 21
和自感一样,两个线圈中电源抵抗互感电动势所作 的这部分额外功,也以磁能的形式储存起来,一旦电流中 止,这部分磁能便通过互感电动势作功全部释放出来。
定义:互感磁能
W12 = M12I1I2 = Φ12I2
其中Φ12是载流线圈1产生的磁场通过线圈2的磁通量。
=
1 2
r B1
⋅
r H1
=
1 2
B1H1
=
μ0I 2r2 8π 2a 4
∫ ∫ ∫ ∫ ∫ ∫ Wm1
=
a 0
2π l
ω m1rdϕdrdz
00
=
l 0
μ0I 2 8π 2a4
a
dz
0
2π
r 3dr dϕ
0
=
μ0I 2l 16π
注意
a. 在上面的积分中,根据对称性选取了柱坐标系。
b. 如果电流只分布在导线表面上,则此时 ∑ I = 0,
(rr2
)
⋅
r dS
其可以看成载流线圈2在外磁场 BrS12(由线圈1提供的)中
所具有的静磁能。其实这也就是线圈1和线圈2的互感磁能
《电磁学》第6章 第6.5 磁场的能量和能量密度(1学时)

《电磁学》第六章 §6.5 磁场的能量和能量密度
公式说明: 上面的磁场能量密度公式,虽然由从螺线管中均匀磁场 的特例导出的,但它是适用于各种类型磁场的普遍公式;
第 4页
在任何磁场中,某一点的磁场能量密度,只与该点的磁感 应强度以及磁介质的性质有关, 这也说明了磁能定域于磁场。
wm 各向异性介质中,
B1
I1 B1 , H1; I 2 B2 , H 2
总磁场:
I1
I2
H H1 H 2 , B B1 B2
1 1 B HdV ( B1 B2 ) ( H1 H 2 )dV V V 2 2 1 1 B1 H1 B2 H 2 )dV ( B1 H 2 B2 H1 )dV 2 V 2
第11页
本节作业: pp.436
6.5-3、6.5-6
《电磁学》第六章 §6.5 磁场的能量和能量密度
比较
计算有横截面积的导体回路的自感系数之方法:
第10页
磁能法:
1 1 Wm LI 2 B Hdv 2 2 V
1 L 2 B Hdv I V
平均磁链法(复杂,适合于没有截面积的线电流和面电流情况):
(1)
,式中 1 id ,对磁通积分。 L
公式应用【2】计算自感、互感系数(磁能法)
(1)求自感 L 若空间磁场仅由单一载流回路激发,仅存自感磁能
第 7页
1 2 1 Wm LI B HdV 2 2 V
(2)求互感 M
L
1 I2
V
B HdV
若空间磁场由多个载流回路激发,存在互感磁能
W互 MI1 I 2 0 H1 H 2dV
磁场的能量磁能和磁能密度

磁场的能量磁能和磁能密度在我们生活的这个世界里,磁场是一种看不见、摸不着,但却无处不在的神秘力量。
从地球的磁场保护着我们免受宇宙射线的伤害,到电子设备中的磁性元件发挥着关键作用,磁场的影响无处不在。
而在深入探究磁场的性质时,磁能和磁能密度是两个至关重要的概念。
首先,让我们来理解一下什么是磁能。
简单地说,磁能就是磁场所具有的能量。
想象一下,当我们把一块磁铁靠近一堆铁钉时,铁钉会被磁铁吸引而产生运动。
在这个过程中,磁铁所产生的磁场就是让铁钉运动的“动力源”,而这个“动力源”所蕴含的能量就是磁能。
那磁能是怎么产生的呢?这就要从电流说起。
当电流在导体中流动时,会产生磁场。
而建立这个磁场的过程中,就需要外界输入能量。
就好像我们要把一个重物搬到高处,需要付出力气一样,建立磁场也需要付出能量,而这些被付出的能量就转化为了磁场的能量,也就是磁能。
磁能密度则是描述磁场中单位体积内所蕴含磁能的物理量。
它就像是在说,在磁场的每一小块空间里,到底蕴含了多少磁能。
为了更深入地理解磁能密度,我们可以先来看一个简单的例子——一个长直螺线管。
假设这个螺线管的长度为 L,横截面积为 S,单位长度上的匝数为 n,通有电流 I。
那么,这个螺线管内部的磁场强度 B 可以通过安培环路定理计算得出。
在算出磁场强度 B 之后,我们就可以计算磁能密度 w 了。
磁能密度 w 等于 B 的平方除以2μ,其中μ是磁导率。
通过这样的计算,我们就能知道在这个长直螺线管的每一点上,单位体积内的磁能有多少。
磁能和磁能密度的概念在实际生活中有很多重要的应用。
比如在变压器中,通过改变磁场的强度和分布,实现电能的传输和转换。
变压器中的铁芯就是为了增强磁场,从而提高磁能的传递效率。
在电动机中,磁场与电流相互作用,产生电磁力,使电动机转动。
而设计电动机时,对磁能和磁能密度的合理考虑,可以提高电动机的功率和效率。
在无线充电技术中,也是利用磁场来传递能量。
通过合理设计磁场的分布和强度,实现对电子设备的无线充电。
§11-4 磁场的能量 磁场能量密度
第11章 电磁感应与电磁场 §11.4 磁场的能量 磁场能量密度 章 电磁感应与电磁场
2
例: 计算半径为 R、 、 长为 l、通有电流 I 、 、 磁导率为 µ 的均匀载 流圆柱导体内磁场能 量。 解:由介质中安培环 路定理确定导体内的 磁感应强度 B , 导体内沿磁力线作半 径为 r 的环路, 的环路,
第11章 电磁感应与电磁场 §11.4 磁场的能量 磁场能量密度 章 电磁感应与电磁场
时间内, 在 dt 时间内,电流 i 克服线圈中自感 电动势作的元功为: 电动势作的元功为:
dA = − iε i dt
某一时刻自感Biblioteka 动势为: 某一时刻自感电动势为: di ε i = −L dt 则
0→I
线圈中电流从 0 变化到 I 过程中电流 作的总功为: 作的总功为:
第11章 电磁感应与电磁场 §11.4 磁场的能量 磁场能量密度 章 电磁感应与电磁场
di = Lidi dA = iL dt dt
dA = Lidi
A= ∫
I 0
1 2 dA = ∫ Lidi = LI 2
1 2 A = LI 2
电流作功使线圈能量改变,作功等于末态 电流作功使线圈能量改变, 线圈能量减去初态线圈的能量。 线圈能量减去初态线圈的能量。
ε
K
第11章 电磁感应与电磁场 §11.4 磁场的能量 磁场能量密度 章 电磁感应与电磁场
这是由于线圈中的磁场能量释放给 灯泡。当电键 K 打开时,电路中电流迅 灯泡。 打开时, 速减小,在线圈中产生自感电动势, 速减小,在线圈中产生自感电动势,这 个自感电动势比电源电动势要大, 个自感电动势比电源电动势要大,所以 灯泡比原来还亮一些,最后灯泡熄灭。 灯泡比原来还亮一些,最后灯泡熄灭。 线圈中的能量, 线圈中的能量, 是由于线圈在通电过 L 程中, 程中,电流克服自感 电动势作功, 电动势作功,使线圈 ε K 具有能量。 具有能量。 稳恒电流的功为: 稳恒电流的功为: A = IUt
第五节 磁场的能量和能量密度

第六章磁介质§5 磁场的能量和能量密度(P631)1.目前在实验室里产生E=105伏/米的电场和B=104高斯的磁场是不难做到的。
今在边长为 10厘米的立方体空间里产生上述两种均匀场,问所需的能量各为多少?解:2.利用高磁导率的铁磁体,在实验室产生B=5000高斯的磁场并不困难(1)求这磁场的能量密度ωm;(2)要想产生能量密度等于这个值的电场,问电场强度E的值应为多少?这在实验上容易作到吗?解:3.一导线弯成半径为R= 5.0厘米的圆形,当其中载有I=100安的电流时,求圆心的磁场能量密度ωm。
解:4. 一螺线管长 300毫米,横截面积的直径为 15毫米,有2500匝表面绝缘的导线均匀密绕而成,其中铁芯的磁导率μ=1000。
当它的导线中通有电流2安时,求管中心的磁能密度ωm。
解:5.一同轴线由很长的两个同轴的圆筒构成,内筒半径为 1.0毫米,外筒半径为 7.0毫米,有100安的电流从外筒流去,内筒流回,两筒的厚度可忽略。
两筒之间的介质无磁性(μ=1),求:(1)介质中的磁能密度ωm分布;(2)单位长度( 1米)同轴线所储磁能Wm。
解:6.一根长直导线载有电流I,I均匀分布在它的横截面上。
证明:这导线内部单位长度的磁场能量为:μ0I2/16π。
解:7. 一同轴线由很长的直导线和套在它外面的同轴圆筒构成,导线的半径为a,圆筒的内半径为b,外半径为c。
电流I由圆筒流去,由导线流回;在它们的横截面上,电流都是均匀分布的。
(1)求下列四处每米长度内所储磁能Wm的表达式:导线内,导线和圆筒之间,圆筒内,圆筒外;(2)当a= 1.0毫米,b= 4.0毫米,c= 5.0毫米,I=10安时,每米长度的同轴线中储存磁能多少?解:8. 试验算一下,用上述两种平均磁链法计算例题2的结果,都与磁能法一致。
解:。
第8章_静磁能1__磁场的能量和能量密度__20101227

在物理上有时这样来看,将线圈1看成是外磁场,则
∫∫ 上式可进一步写成: W12 = I 2
r B1
(rr2
)
⋅
r dS
S2
其中 rr2是线圈2的面元 dSr对线圈1的位置矢量,S2 是线
圈流线2所圈张2在的外曲磁面场。这Br1中样所,具我有们的可磁将能该。系统的互能看成是载
后面还会将这一结果进一步推广。
§1. 磁场的能量和能量密度
在第三章中,我们介绍了电容器充电后能储存一定的
电能,即当电容器两极板之间的电压为u时,电容器所储
存的静电能为
We
=
1 2
Cu 2
现在我们已经讨论了自感和互感,自然会提出一个 问题:在电感元件中是否也有能量储存?如果有的话,以 什么形式储存?
下面就来讨论这个问题。
一.一个线圈的静磁能 (也称作自感磁能)
系满足右手定则。
讨论
r
在电介质中,我们得到电偶极子P
量表达式为
rr We = −P ⋅ E
=
1 2
r B1
⋅
r H1
=
1 2
B1H1
=
μ0I 2r2 8π 2a 4
∫ ∫ ∫ ∫ ∫ ∫ Wm1
=
a 0
2π l
ω m1rdϕdrdz
00
=
l 0
μ0I 2 8π 2a4
a
dz
0
2π
r 3dr dϕ
0
=
μ0I 2l 16π
注意
a. 在上面的积分中,根据对称性选取了柱坐标系。
b. 如果电流只分布在导线表面上,则此时 ∑ I = 0,
(( )) ( ) ∑I
磁场能量密度

磁场能量密度磁场能量密度是磁场编码的能量的表达方式,它在电磁学、电力系统设计、无线技术等领域具有广泛的应用。
试想,如果我们能准确掌握磁场的能量密度,那么我们就能设计出更高效、更小型化的电子设备或通讯工具。
首先,我们先来解释一下什么是磁场。
简单来说,磁场是电场的姐妹场,由于电荷的运动(电流)产生的场。
它的存在使得物质之间可以交换能量、动量和角动量,从而发生各种有趣的现象,比如电磁感应、电磁振荡和光的传播等。
然后让我们来探索一下磁场的能量密度。
磁场能量密度定义为单位体积内的磁场能量。
因此,一旦我们知道了磁场的强度和方向,我们就可以通过公式u = B^2 / (2μ) 来计算得出磁场的能量密度。
其中,u 是磁场能量密度赞,B是磁场的磁感应强度,μ是磁导率。
这个公式告诉我们磁场每一处的能量密度都是一样的。
接下来,让我们把焦点转到磁场能量密度的应用。
在电磁学领域,磁场能量密度常常用于设计和优化电力系统。
例如,通过准确测量磁场能量密度,可以有效设计电动机和变压器,提升其效率和性能。
此外,磁场能量密度也被广泛应用于无线通讯技术,例如在设计天线和无线电波传播系统时,就需要考虑磁场能量密度。
最后,我们来讨论一下磁场能量密度的研究潜力。
随着科技的发展和进步,磁场能量密度的研究正在向更小的尺度、更高的精度推进,甚至可以达到纳米或者量子尺度。
例如,一些研究团队正在探索如何利用磁场能量密度来实现更高效的能量转换和存储,以期在未来开展无线充电和高能量无线传输的技术。
总的来说,磁场能量密度是一个极具潜力和价值的研究领域。
通过深入研究和了解,我们能够更好地设计和优化电力系统,开发出更高效、更小型化的电子设备,并推动无线技术的研发和进步。
当然,这个研究领域也对人们的技能和智慧提出了严格的要求,希望每一个研究者都能在这个领域中取得重要的突破,不断推动科技的研发和进步。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五节磁场的能量和能量密度
磁场的能量和能量密度(P631)1、目前在实验室里产生
E=105伏/米的电场和B=104高斯的磁场是不难做到的。
今在边长为10厘米的立方体空间里产生上述两种均匀场,问所需的能量各为多少?解:2、利用高磁导率的铁磁体,在实验室产生
B=5000高斯的磁场并不困难(1)求这磁场的能量密度ωm;(2)要想产生能量密度等于这个值的电场,问电场强度E的值应为多少?这在实验上容易作到吗?解:3、一导线弯成半径为
R=5、0厘米的圆形,当其中载有I=100安的电流时,求圆心的磁场能量密度ωm。
解:4、一螺线管长300毫米,横截面积的直径为15毫米,有2500匝表面绝缘的导线均匀密绕而成,其中铁芯的磁导率μ=1000。
当它的导线中通有电流2安时,求管中心的磁能密度ωm。
解:5、一同轴线由很长的两个同轴的圆筒构成,内筒半径为1、0毫米,外筒半径为7、0毫米,有100安的电流从外筒流去,内筒流回,两筒的厚度可忽略。
两筒之间的介质无磁性(μ=1),求:(1)介质中的磁能密度ωm分布;(2)单位长度(1米)同轴线所储磁能Wm。
解:6、一根长直导线载有电流I,I均匀分布在它的横截面上。
证明:这导线内部单位长度的磁场能量为:μ0I2/16π。
解:7、一同轴线由很长的直导线和套在它外面的同轴圆筒构成,导线的半径为a,圆筒的内半径为b,外半径为c。
电流I由圆筒流去,由导线流回;在它们的横
截面上,电流都是均匀分布的。
(1)求下列四处每米长度内所储磁能Wm的表达式:导线内,导线和圆筒之间,圆筒内,圆筒外;(2)当a=1、0毫米,b=4、0毫米,c=5、0毫米,I=10安时,每米长度的同轴线中储存磁能多少?解:8、试验算一下,用上述两种平均磁链法计算例题2的结果,都与磁能法一致。
解:。
