孔隙压力有效应力和排水
土的应力计算有效应力原理常用资料

1925年,《土力学》
5 有效应力原理
H (1) 侧限应力状态及一维渗流固结
sat
u
uw(Hh) satH w (H h)
H wh
渗透压力: wh
有效应力原理 二. 饱和土中孔隙水压力和有效应力的计算
1.自重应力情况
取土骨架为隔离体
向上渗流: Δh
向下渗流:
H
粘土层 γsat
A
有效应力σ’
Aw 1 A
'u
A
a
PS
PSV
PS
有效应力原理
一. 有效应力原理的基本概念
2. 饱和土的有效应力原理 (1)饱和土体内任一平面上受到的总应力可分为两部分σ’ 和u,并且
'u
超静孔压: u <p
u 是土体发生变形的原因:颗粒间克服摩擦相对滑移、滚动以及在接触点处由于应力过大而破碎均与 有关
一般地, 水不能承受剪应力,对土颗粒间摩擦、土粒的破碎没有贡献
(2)土的变形与强度都只取决于有效应力
σz=u=100MPa
5 有效应力原理
太沙基 – 土力学的奠x基人 xy
(1) 单向压缩应力状态
=γH1+(γsat-γw)Hy2x
y
有效应力原理的基本概念
土19的25应年力,计《算土有力效学z应x》力原理 zy
有效应力原理的讨论
§3.5 有效应力原理
² 孔隙水压 力的作用
² 有效应力 的作用
² 讨论
讨论:
海底与土粒间的接触压力 哪一种情况下大?
1m σz=u=0.01MPa
104m
σz=u=100MPa
有效应力原理的讨论
有效应力原理
第6章 土的孔隙水压力

*
A=
(6.7)
土体的孔隙水压力虽然可以通过上述理论途径确定 但是考虑到各种复杂的因素 从工 程实用角度看 系数 A 和 B 仍需通过试验来确定 黄文熙 1989 年) 对式(6.1)可作如下变换
∆u = B ∆σ 1
(6.8)
其中
B = B[ K 0 + A(1 − K 0 )]
(6.9)
K0 为静止侧压力系数
第6章
土的孔隙水压力
153
∂ ∂h ∂ ∂h 1 ∂e )+ (K y )=− (K x ∂x ∂x ∂y ∂y 1+ e ∂ t
(6.11)
式中 h 为水头 u 为孔隙水压力 t 为时间 e 为孔隙比 式(6.11)中左边为单位时间流进土体的水量 右边为单位时间该土体的体积变形
h= u +y γw
∂ ∂h ∂ ∂h (K x )+ (K y )=0 ∂x ∂x ∂y ∂y
(6.13)
式(6.13)为稳定渗流或骨架不可压缩土体非稳定渗流的拉普位斯方程 结合相应边界条 件 可用有限元法确定坝体各点的孔隙水压力 这方面 有许多成熟的方法和程序 对于粘 性土 则应考虑式(6.11)的右项 这就是以下第 6.3.2 和 6.3.3 节要讨论的内容 6. 3. 2 太沙基固结理论 1. 基本原理 由于
K 0 = ∆σ 3 / ∆σ 1
(6.10)
在土石坝中 可以近似地看作∆σ1 和∆σ3 同步增加或减少 ∆σ3/∆σ1 基本保持不变 这样
B 可视为常数
其值可通过类似应力途径的室内试验测定
6. 3 确定孔隙水压力的理论和方法
6. 3. 1 基本方程 土石坝各运用期的孔隙水压力的确定 属于渗流和固结分析的专门问题 这里仅回顾一 些基本的概念 在二维问题中 反映流量平衡的微分方程式为
有效自重应力计算公式

有效自重应力计算公式
1.排水条件下的有效自重应力计算公式:
排水条件下土体中的孔隙水可以自由排出,因此只有颗粒重力起作用,有效自重应力可用以下公式计算:
σ'=γ*H
其中,σ'表示有效自重应力,γ表示土体的单位重量,H表示土体
的有效高度。
单位重量γ可以通过实测实验获得,有效高度H是指土体
堆积的高度减去排水带(即浸水线以下的部分)的高度。
2.非排水条件下的有效自重应力计算公式:
非排水条件下,土体中的孔隙水不能自由排出,有效自重应力计算需
要考虑孔隙水压力。
σ'=(γ-u)*H
其中,σ'表示有效自重应力,γ表示土体的单位重量,H表示土体
的有效高度,u表示孔隙水压力。
孔隙水压力的计算可以采用以下公式:
u=u0+Δu
其中,u0表示孔隙水静压力,可以通过水压力计等仪器测量得到;
Δu表示孔隙水动压力,可以根据土体的应力路径和试验结果进行估算。
需要注意的是,在进行有效自重应力计算时,需要使用土体的干重而
不是含水量较高的湿重或全重。
此外,有效自重应力的计算公式还要考虑
土体颗粒大小和形状等因素的影响,因此不同的土体类型可能有不同的计算方法。
总之,有效自重应力的计算公式可根据排水条件和非排水条件进行选择,通过合理的应力路径和试验数据的获取,可以得到更准确的有效自重应力值,为工程设计和安全评估提供重要依据。
孔隙水压力与围压的关系

孔隙水压力与围压的关系
孔隙水压力与围压之间存在着密切的关系,这涉及到地下水文
地质学和岩石力学等领域的知识。
首先,孔隙水压力是指岩石或土壤中孔隙中水的压力。
当地下
水位上升时,孔隙水压力会增加;而当地下水位下降时,孔隙水压
力会减小。
孔隙水压力的变化会受到多种因素的影响,包括降雨、
融雪、地下水开采等。
围压则是指地下岩层受到的周围地层和岩石的压力。
围压是由
地层的重力和上覆岩层的压力所造成的,随着深度的增加,围压也
会增加。
孔隙水压力与围压之间的关系可以通过有效应力和孔隙水压力
的关系来描述。
在地下岩层中,有效应力等于围压减去孔隙水压力。
当孔隙水压力增加时,有效应力减小,岩石的强度会减小,从而容
易发生压实、变形或者破裂。
相反,当孔隙水压力减小时,有效应
力增加,岩石的强度会增加。
此外,孔隙水压力与围压还会影响地下水的流动。
当孔隙水压
力高于地表时,地下水会向地表流动,形成泉水或渗泉;而当孔隙水压力低于地表时,地下水则会受到地表水的压力,流向地下。
总的来说,孔隙水压力与围压之间的关系是一个复杂而又密切相关的问题,需要综合考虑地下水文地质学和岩石力学等多方面的知识来进行研究和分析。
第五节有效应力原理
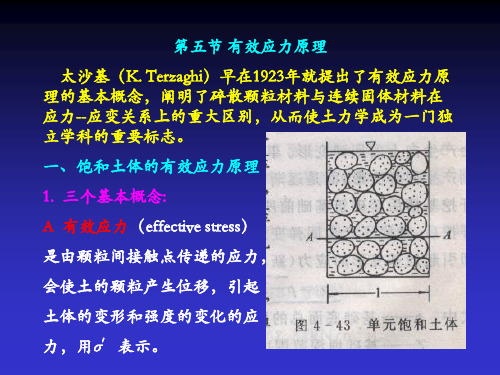
Z 为了模拟饱和土体受到连续均布荷载作用后,在土中 所产生的孔隙水压力以及u与σ′随时间t的变化规律, 1925年太沙基最早提出了一个渗压模型,如图3-24所示。
通过模拟侧限状态下饱和土体的渗流固结过程,可以 得到如下的两点认识:
(1)整个渗流固结过程中u和σ′都是随时间t而不断变 化着的,即u=f(t),σ′=f(t)。渗流固结过程实质上就是 土中两种不同应力形态的转化过程。
推导:
若单位断面积A—A上颗粒接触点面积为a,则孔隙水 压力作用面积为1-a。则有:
u1 a
又a很小,可忽略不计,故: u 上式即为太沙基提出的饱和土体有效应力原理。它是 研究土体固结和强度的重要理论基础。 饱和土体有效应力原理的要点:
1.饱和土体内任一平面上受到的总应力等于有效应力加孔 隙水压力之和;
2.土的变形(压缩)与强度的变化都仅取决于有效应力的 变化。
二、饱和土中孔隙水压力和有效应力的计算 (一)自重应力作用下的两种应力
h2
图3-22a为处于水下的饱和土层,在地面下h2深处的A点, 由于水体和土体自重对地面以下A点处作用的垂向总应 力σ为:
式中:γw--水的重度,kN/m3;γsat--土的饱和重度,kN/m3。 A点处由孔隙水传递的静水压力,即孔隙水压力为:
在渗流产生的渗透力的作用下,其有效应力与渗流作用 的方向有关。当自上而下渗流时,将使有效应力增加,因
而对土体的稳定性有利。反之,若向上渗流则有效应力减 小,对土体的稳定性不利,若使得有效应力减少至0,即 可能发生所谓的流砂和管涌现象,造成地基或边坡的失稳。
三、附加应力作用下孔隙水压力和有效应力的计算
解:1)地下水位以上无 毛细饱和区时的σ、u、σ′ 分布值见下表。σ、u、σ′ 沿深度的分布如下图中实线 所示。
简答题

土力学简答题1. 其它条件相同情况下,超固结粘土的沉降一定小于正常固结粘土的沉降吗?为什么?(10分)答:是的。
(2分)因为和正常固结粘土相比,超固结粘土孔隙比比正常固结土小,如果现有有效应力相同,则在某荷载增量作用下,超固结土是沿再压缩曲线压缩,而正常固结土沿压缩曲线压缩。
由于同一土质,再压缩曲线肯定比压缩曲线缓,即再压缩指数比压缩指数小,因此,超固结粘土沉降比正常固结土小。
(8分)2. 什么是有效应力原理?图中,地基土湿重度、饱和重度和浮重度分别为γ、sat γ和γ',水重度w γ,M 点的测压管水柱高如图所示。
写出M点总应力、孔隙水应力、有效应力、自重应力的计算式。
(8分)答:由外荷在研究平面上引起的法向总应力为б,那么它必由该面上的孔隙力u 和颗粒间的接触面共同分担,即该面上的总法向力等于孔隙力和颗粒间所承担的力之和,即б=б'+u 。
(2分)M 点总应力:12z sat H H σγγ=+ (1分)M 点孔隙水应力:2()w u h H γ=+ (1分)M 点有效应力: 122()zz sat w u H H h H σσγγγ''=-=+-+ (2分) M 点自重应力:12zM H H σγγ'=+ (2分)3. 土坡发生滑动的滑动面有哪几种形式?分别发生在何种情况?没有渗流的情况下的粘性土坡的稳定安全系数可以有哪几种方法计算?(10分)答:土坡发生滑动的滑动面有:圆弧、平面、复合滑动面。
(3分)圆弧滑动通常发生在较均质的粘性土坡中;平面滑动通常发生在无粘性土坡中;复合滑动面发生在土坡土质很不均匀的土坡中。
(4分)没有渗流的情况下,粘性土坡的稳定安全系数计算方法有:φ=0分析法、瑞典条分法、简化毕肖普法。
(3分)4. 地基破坏的型式有哪几种?未修正的太沙基极限承载力公式适用于哪种破坏型式的地基?利用太沙基极限承载力公式具体说明地下水位的位置对承载力是如何的影响?(8分)答:有整体剪切破坏,局部剪切破坏和冲剪破坏。
孔隙压力、有效应力和排水
第六章 孔隙压力、有效应力和排水 引言通常所说的土是由固体颗粒和水两部分组成的,基础或挡墙上的荷载包含土颗粒和孔隙水上面的应力两部分。
在没有土颗粒的船体外表面,法向应力就等于水压力;而在没有水的装有糖的盆底,应力就等于所装的糖的重量。
问题就是土颗粒应力和孔隙水压力的哪种组合决定着土的性质。
要研究这个问题,我们首先研究地基中的应力和水压力。
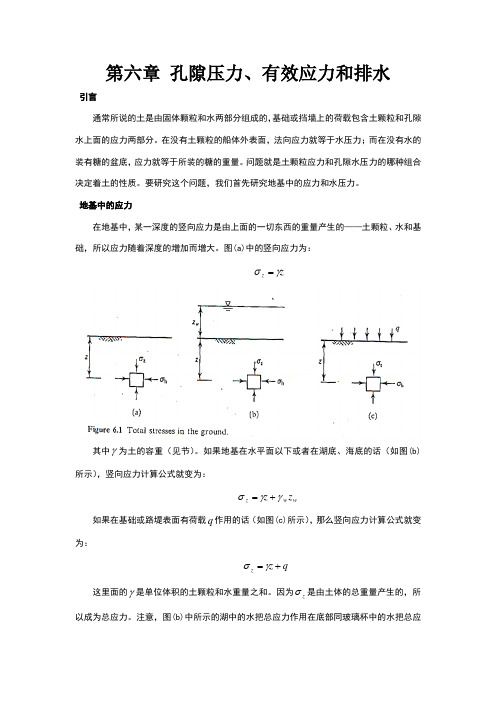
地基中的应力在地基中,某一深度的竖向应力是由上面的一切东西的重量产生的——土颗粒、水和基础,所以应力随着深度的增加而增大。
图(a)中的竖向应力为:z z γσ=其中γ为土的容重(见节)。
如果地基在水平面以下或者在湖底、海底的话(如图(b)所示),竖向应力计算公式就变为:w w z z z γγσ+=如果在基础或路堤表面有荷载q 作用的话(如图(c)所示),那么竖向应力计算公式就变为:q z z +=γσ这里面的γ是单位体积的土颗粒和水重量之和。
因为z σ是由土体的总重量产生的,所以成为总应力。
注意,图(b)中所示的湖中的水把总应力作用在底部同玻璃杯中的水把总应力作用在杯底的方式相同。
土颗粒的重度变化不大,一般来讲,饱和土的3/20m kN ≈γ,干土的3/16m kN ≈γ,水的3/10m kN ≈γ。
同时也有水平向的总应力h σ,但是在z σ和h σ之间没有简单的关系。
在以后的章节我们会对水平向的应力进行研究。
地下水和孔隙水压力饱和土的孔隙水中存在的压力叫做孔隙水压力u 。
在竖管中经常用w h 来简单地代替,如图所示。
当系统处于平衡状态时,竖管内部和外部的水压力相等,因此得到: w w h u γ=当竖管中的水位低于地表面时(如图(a)所示),就称为地下水位。
如果土中水是静止的,那么地下水位面就像湖面一样是水平的。
然而,就像我们后面将要见到的那样,如果地下水位面不是水平的,那么土孔隙中就存在水的渗流。
图(a)中地下水位面处孔隙水压力为零(这就是叫做地下水位),水位以下为正值,问题就出来了:地下水位面以上孔隙水压力是什么样的呢图说明了地表面和地下水位面之间的土中孔隙水压力的变化情况。
有效应力原理

L
p max
min
N M yx A Iy
当e y e, e x 0 p max
min
N A
6e 1 L
N N e B ( ) A LB B 2 2 ( ) 3 2 N 6e 1 A B
矩形面积单向偏心荷载
L
p max
影响因素 计算方法 分布规律
基底压力的影响因素
•大小、方向、分布
荷载条件
基底压力
地基条件
基础条件
•刚度 •形状 •大小 •埋深
•土类、密度、土层结构等
基底压力分布特征
条形基础,竖直均布荷载
基础抗弯刚度EI=0 → M=0; 基础变形能完全适应地基表面的 变形; 基础上下压力分布必须完全相同, 若不同将会产生弯矩。
基底压力分布特征
条形基础,竖直均布荷载
弹性地基,绝对刚性基础 抗弯刚度EI=∞ → M≠0;
反证法: 假设基底压力与荷载 分布相同,则地基变形与柔性 基础情况必然一致;
分布: 中间小, 两端无穷大。
基底压力分布特征
弹塑性地基,有限刚度基础
— 荷载较小 — 荷载较大
砂性土地基
— — — —
粘性土地基
有效应力原理
有效应力’:
土体是由固体颗粒和孔隙水及空气组成的三相 集合体。外荷在土体中产生的应力是通过颗粒 间的接触来传递的。由颗粒间的点接触传递的 应力会使土的颗粒 产生变形,引起土 体的变形和强度的 变化,这种对土体 变形和强度有效的 粒间应力就称为有 效应力’。
A
孔隙水压力U
• 如果土体中的孔隙是互相连通而又充满水,则 孔隙中的水服从静水压力分布规律,这种由孔 隙水传递的应力就称为孔隙水压力U。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章 孔隙压力、有效应力和排水引言通常所说的土是由固体颗粒和水两部分组成的,基础或挡墙上的荷载包含土颗粒和孔隙水上面的应力两部分。
在没有土颗粒的船体外表面,法向应力就等于水压力;而在没有水的装有糖的盆底,应力就等于所装的糖的重量。
问题就是土颗粒应力和孔隙水压力的哪种组合决定着土的性质。
要研究这个问题,我们首先研究地基中的应力和水压力。
地基中的应力在地基中,某一深度的竖向应力是由上面的一切东西的重量产生的——土颗粒、水和基础,所以应力随着深度的增加而增大。
图(a)中的竖向应力为:z z γσ=其中γ为土的容重(见节)。
如果地基在水平面以下或者在湖底、海底的话(如图(b)所示),竖向应力计算公式就变为:w w z z z γγσ+=如果在基础或路堤表面有荷载q 作用的话(如图(c)所示),那么竖向应力计算公式就变为:q z z +=γσ这里面的γ是单位体积的土颗粒和水重量之和。
因为z σ是由土体的总重量产生的,所以成为总应力。
注意,图(b)中所示的湖中的水把总应力作用在底部同玻璃杯中的水把总应力作用在杯底的方式相同。
土颗粒的重度变化不大,一般来讲,饱和土的3/20m kN ≈γ,干土的3/16m kN ≈γ,水的3/10m kN ≈γ。
同时也有水平向的总应力h σ,但是在z σ和h σ之间没有简单的关系。
在以后的章节我们会对水平向的应力进行研究。
地下水和孔隙水压力饱和土的孔隙水中存在的压力叫做孔隙水压力u 。
在竖管中经常用w h 来简单地代替,如图所示。
当系统处于平衡状态时,竖管内部和外部的水压力相等,因此得到:w w h u γ=当竖管中的水位低于地表面时(如图(a)所示),就称为地下水位。
如果土中水是静止的,那么地下水位面就像湖面一样是水平的。
然而,就像我们后面将要见到的那样,如果地下水位面不是水平的,那么土孔隙中就存在水的渗流。
图(a)中地下水位面处孔隙水压力为零(这就是叫做地下水位),水位以下为正值,问题就出来了:地下水位面以上孔隙水压力是什么样的呢?图说明了地表面和地下水位面之间的土中孔隙水压力的变化情况。
在地表面处有一层孔压为零的干土,这种情况很少见到,但是在高潮水面以上的海滩可以发现这种现象。
在地下水面以上的一小部分,由于土中孔隙的毛细作用,土体是饱和的。
在这一区域,孔隙水压力是负值,计算公式如下:w w h u γ-=最应该注意的一点就是饱和土中也可能产生负的孔隙水压力。
这就暗示了水承受了张力,地下水位面以上的土体中的水像毛细试管中的水那样上升。
地下水位面上面饱和区域的高度主要取决于土颗粒的尺寸,更多的取决于孔隙的尺寸:土颗粒和孔隙越小,有负孔隙水压力的饱和土区域的高度就越大,饱和区域顶部和负孔隙水压力就越大。
在干土和饱和土之间存在着非饱和土,包括土颗粒、水和气,一般是空气或者水蒸气。
在这部分,孔隙中的水压和气压是不同的,孔隙水的引力如图所示那样增加或减小。
目前针对非饱和土还没有简单并且令人满意的理论,所以这本书中只研究干土和饱和土。
因为实际的边坡、基础、挡土墙和其它重要的土木工程建筑中,土通常是饱和的,至少在温和的或潮湿的气候条件下是饱和的。
而只有在非常接近地表的土、密室土和干燥炎热的气候条件下的土中才可能存在非饱和土。
有效应力由基础荷载或边坡开挖所产生的总应力可能会导致地面出现移动和失稳现象,这是显而易见的。
但是由于孔隙水压力的变化而导致地面出现移动和失稳现象,这可能是不明显的。
例如,稳定的边坡可能在暴风雨后发生破坏,因为水的抽出导致地面出现沉降,从而地下水位降低,下雨天雨水入渗,孔隙水压力升高(如果有人告诉你雨后发生滑坡是因为雨水对土的润滑作用的话,你就问问他,沙丘里的潮湿砂子的强度为什么比干燥砂土的要大)。
如果土的压缩和强度是随总应力或孔隙水压力的变化而变化的话,就说明土的性质很可能和σ和u 的组合有关。
这种组合应该称为有效应力,因为它对于决定土的性质是有效的。
太沙基(1936)首先揭示了总应力、有效应力和孔隙水压力之间的关系。
他是这样定义有效应力的:所有能够测量到的由应力变化产生的效果,如压缩、扭曲变形、剪切阻力,主要是因为有效应力的变化而导致的。
有效应力'σ和总应力以及孔隙水压力之间的关系为:u -=σσ'。
图是在同一个坐标系下绘制的有效应力和总应力的摩尔应力圆。
因为u -=1'1σσ、u -=3'3σσ,所以两个圆的直径是相等。
点T 和E 代表同一平面上的总应力和有效应力,显然,总剪应力和有效剪应力是相等的。
因此,有效应力为:u -=σσ'ττ='结合第二章所给出的剪应力参数q 和主应力参数p 的定义和公式u -=1'1σσ,可以得到:='p-puq='q从式和式可以看出,总剪切应力和有效剪切应力是相等的,很多学者一直使用剪切应力。
在我的工作和教书生涯中,以及这本书中,我使用'τ和'q表示有效应力,用τ和q表示总应力。
我知道这并不是必要的,但是我发现把总剪切应力和有效剪切应力区别开来是很有用的,尤其是教书时。
有效应力的重要性土力学中有效应力原则是最基础的,它的重要性并不是被夸大的。
这是把由荷载产生的土体性质和由水压力产生的土体性质联系起来的一种方法。
尽管大多数土力学试验在考虑粒间作用力和粒间接触的基础上探讨了有效应力的原则和意义,但是实际上这样做是没有必要的,必要的假设并不一定都能够得到试验验证。
然而,至今仍没有找到证明太沙基最初的假定是错误的依据,至少对于正常应力水平下的饱和土来讲,有效应力原理被认为是最基本的土力学公理。
因为总应力和有效应力是不相等的(除非孔隙水压力为零),把两者区分开来是非常重σ和'τ常用主应力表示,而总应力不用主应力表示。
任何公式都应该含有要的。
有效应力'所有的总应力或所有的有效应力,或者通过孔隙水压力把总应力和有效应力结合起来。
工程师进行设计计算(或学生做考试题目)的时候应该能够弄清楚他们用到的是总应力还是有效应力。
利用图和,并结合公式到这六个公式,可以计算地基中任何地下水位条件下任何深度σ。
如果你做过一些例子,你就会发现如果地下水位低于地表的话,有效的竖向有效应力'z应力主要取决于地下水位。
另一方面,如果地表被水淹没的话,如河流、湖泊或海洋的底部,有效应力大小和水的深度没有关系,这就意味着一个小池塘底部的有效应力和一个水深可能超过5km的海洋底部的有效应力是一样的。
在进行相关计算时要注意自由流动的水(如河水、湖水或海水)对土产生的是总应力(对大坝以及海底),而土孔隙中的水产生孔隙水压力,这些水压力并不一定是相等的。
有效应力的验证考虑到变化量,有效应力公式可以改为:u ∆-∆=∆σσ'上式表明,在保持孔隙水压力不变的条件下改变总应力或者在保持总应力不变的条件下改变孔隙水压力,都会造成有效应力的变化,从而产生可以量测到的影响。
同样要注意到,如果总应力和孔隙水压力的变化量相等的话,有效应力就保持不变,土的状态就不会发生任何变化。
图(a)中,在基础上施加σ∆的荷载,由于地基中的孔隙水压力保持不变,从而产生ρ∆的沉降,因此σσ∆=∆'。
图(b)中,沉降ρ∆是由于抽取地下水产生的,通过抽水使地下水位降低w h ∆,这样孔隙水压力减小了w w h u ∆=∆γ。
从式可以看出,因为0=∆σ,所以孔隙水压力的减小会导致有效应力的增加。
通过有效应力原理可以证明,基础荷载增加σ∆和孔隙水压力减小u ∆所引起的沉降量是相等的。
换句话说,有效应力的改变可以影响土的性质。
图是一个验证有效应力的简单实验。
实验说明了孔隙水压力对深的条形基础的影响能力。
所用的土为粉到中砂,因为如果土很粗的话,当地下水位降低时可能变成非饱和;如果土粒很细的话,在一定时间内,孔隙水压力可能不是相等的。
把砂砾和砂放到水里面,饱和以后打开阀门使水位降低到砂砾。
放置一个重的基础(最好是一个直径40mm ,长80mm 的钢柱)和一个如图所示偏离中心的桩。
关闭阀门,向竖管里面注水,使水位提高。
如果砂和砂砾是饱和的,竖管就会被注满。
随着水位和孔隙水压力的升高,有效应力会降低,两个基础都会破坏。
另一个简单的验证有效应力的简单实验是咖啡豆真空包装袋的刚度和强度实验。
如果是理想的真空的话,袋子相对是很硬而且很结实的,因为负的孔隙压力产生了正的有效应力。
然而,如果你用一个大头针戳一个小洞的话,袋子就变软,这是由于袋子中孔隙压力增大,有效应力减小的缘故。
你也可以用一个自己密封的袋子装上粗糙的砂和砾石作一个同样简单的实验。
体积改变和排水在土由于有效应力的改变而加载和卸载的过程中,体积会发生变化。
然而,因为土颗粒本身的刚度很大,所以土颗粒本身的体积变化是可以忽略的,所以土体积的变化是由颗粒的重新排列和空隙的改变造成的。
在较小的有效应力水平下,土颗粒可能比较松散,而在较高的有效应力水平下就会变得紧密起来,如图所示。
如果孔隙水压力0u 保持不变,那么总应力和有效应力的改变量就相等(σσ∆=∆',见公式)。
如果土颗粒的体积保持不变的话,见图,那么土体积改变量V ∆就等于排出的水的体积w V ∆。
饱和土的体积变化是因为土中水的渗流造成的,所以土体的压缩就像从海绵往外挤水一样。
在实验室里面,水会向土样的边界流动,而在地基中,水会向地表或者土中的自然排水体流动。
例如图8是一个在粘土上修建的路堤,粘土的顶部和底部各有一层作为排水体的砂。
在路堤的修筑过程中,水从粘土向砂土层流动,如图中箭头所示。
当然,必须有足够的时间使水从土中流出,这样才能产生体积变化;同时孔隙水压力也发生了变化。
所以,在路堤的填筑速率、排水速率和土及孔隙压力的变化速率之间必然存在一个关系。
排水荷载、不排水荷载和固结总应力的施加速率和排水速率使决定土的性质的重要因素。
图和是限制条件。
图(a)中总应力增量σ∆施加的非常缓慢,经历了相当长的时间。
这可以代表实验室或现场的加载情况。
如果荷载缓慢施加的话,水就有足够的时间从土中排水。
孔隙水压力就不会发生变化,如图 (c)所示,体积会随着荷载的改变和改变,如图(b)所示。
因为孔隙水压力保持为0u 不变,有效应力随着总应力的变化而变化,如图(d)所示。
当应力保持''0σσ∆+不变时,体积保持为V V ∆-0。
这种相对较慢的荷载叫做排水荷载,因为在荷载施加的过程中,所有的排水都已经完成了。
排水荷载最重要的特征是孔隙水压力保持为0u 不变,这就是所说的稳态孔隙水压力。
图(a)中施加和图相同的总应力增量σ∆,但是施加的速度非常快,没有足够的时间来排水,所以体积保持不变,如图(b)所示。
如果荷载是各向相同的,没有剪切扭曲的话,由于不排水体积不发生变化。
