第八章方差分析
医学统计学 -第08章 方差分析

第一节 方差分析的基本思想
看一个例子
例8-1 为研究钙离子对体重的影响作用,某研究者将36 只肥胖模型大白鼠随机分为三组,每组12只,分别给 予高脂正常剂量钙(0.5%)、高脂高剂量钙(1.0%)和高 脂高剂量钙(1.5%)三种不同的饲料,喂养9周,测其 喂养前后体重的差值。问三组不同喂养方式下大白鼠 体重改变是否不同?
• 三种喂养方式体重改变的平均值各不相同,这种变异 称为组间变异
•
是组内均值
X
与总均值
i
X
之差的平方和
360
340
组间变异反映了:
320
三种喂养方式的差异(影响), 300
同时也包含了随机误差。
280
260
240
k ni
220
SS组间
(Xi X )2
200
i1 j
180
X甲
X
X乙
X丙
甲
乙
丙
3、组内变异(SS组内,variation within groups)
0.05
2、根据公式计算SS、MS及F值,列于方差分析表内(计 算过程省略)
变异来源 总变异 组间 组内(误差)
完全随机设计的方差分析表
平方和 SS 自由度
均方MS
47758.32
35
31291.67
2
15645.83
16466.65
33
498.99
F值
31.36
3、确定P值,作出判断
分子自由度=k-1=2,分母自由度=n-k=33,查F 界值表(方差分析用)
表 8-1 三种不同喂养方式下大白鼠体重喂养前后差值(g)
正常钙(0.5%) 高剂量钙(1.0%) 高剂量钙(1.5%)
第八章:方差分析

SSE xij xi
k ni i 1 j 1
2
计算结果为: SSE = 2708
三个离差平方和的关系
总离差平方和(SST)、组内离差平方和(SSE) 、组间离差平方和 (SSA) 之间的关系:
x
k i 1 j 1
ni
ij
x ni xi x xij x
外包装底色对产品销量是否有显著影响?
市场 北京 上海 深圳 西安 成都 红色 36 35 27 29 38 橙色 28 26 31 30 24 紫色 30 32 28 26 35 蓝色 22 27 20 21 29
什么是方差分析?
【 例 】为了对几个行业的服务质量进行评价,消费者协会 在4个行业分别抽取了不同的企业作为样本。最近一年中消 费者对总共23家企业投诉的次数如下表:
2.
方差分析的基本假定
1. 每个总体都服从正态分布 (每个行业被投诉的次数必须服从正态分布) 2. 各个总体的方差相同 ( 4个行业被投诉次数的方差都相等) 3. 观测值是独立的 (每个行业被投诉的次数与其他行业被投诉的次数独立)
方差分析的基本假设
H 0 : m1 m2 mk H1 : m1 , m2 , , mk 不全相等
2.计算误差
计算全部观测值的均值以及各水平下的组均值 计算总误差 计算组内误差 计算组间误差
计算总误差( SST)
1. 全部观察值 xij 与总平均值 x 的离差平方和 2. 反映全部观察值的离散状况 3. 其计算公式为
SST xij x
k ni i 1 j 1 2
方差分析
差异源
组间 组内
SS
1456.609 2708
第八章 方差分析与相关分析
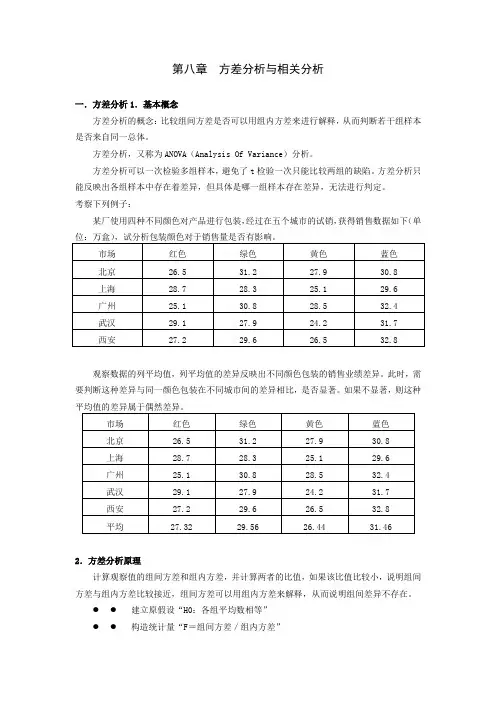
第八章方差分析与相关分析一.方差分析1.基本概念方差分析的概念:比较组间方差是否可以用组内方差来进行解释,从而判断若干组样本是否来自同一总体。
方差分析,又称为ANOVA(Analysis Of Variance)分析。
方差分析可以一次检验多组样本,避免了t检验一次只能比较两组的缺陷。
方差分析只能反映出各组样本中存在着差异,但具体是哪一组样本存在差异,无法进行判定。
考察下列例子:某厂使用四种不同颜色对产品进行包装,经过在五个城市的试销,获得销售数据如下(单观察数据的列平均值,列平均值的差异反映出不同颜色包装的销售业绩差异。
此时,需要判断这种差异与同一颜色包装在不同城市间的差异相比,是否显著。
如果不显著,则这种2.方差分析原理计算观察值的组间方差和组内方差,并计算两者的比值,如果该比值比较小,说明组间方差与组内方差比较接近,组间方差可以用组内方差来解释,从而说明组间差异不存在。
●●建立原假设“H0:各组平均数相等”●●构造统计量“F=组间方差/组内方差”●●在计算组间方差时,使用自由度为(r-1),计算组内方差时,使用自由度为(n-r)。
●●F满足第一自由度为(r-1),第二自由度为(n-r)的F分布。
●●查表,若F值大于0.05临界值,则拒绝原假设,认为各组平均数存在差异。
根据方差计算的原理,生成方差分析表如下:其中:组间离差平方和 SSA (Sum of Squares for factor A) =39.084误差项离差平方和 SSE (Sum of Squares for Error) =76.8455总离差平方和 SST (Sum of Squares for Total)=115.9295P-value值为0.000466,小于0.05,所以拒绝原假设。
3.双因素方差分析观察下列销售数据,欲了解包装方式和销售地区是否对于销售业绩有影响,涉及到双因素的方差分析。
此时需分别计算SSA、SSB与SSE之间的比值是否超过临界值。
生物统计-8第八章单因素方差分析

01
确定因子和水平
确定要分析的因子(独立变量) 和因子水平(因子的不同类别或 条件)。
建立模型
02
03
模型假设
根据因子和水平,建立方差分析 模型。模型通常包括组间差异和 组内误差两部分。
确保满足方差分析的假设条件, 包括独立性、正态性和同方差性。
方差分析的统计检验
01
F检验
进行F检验,以评估组间差异是否 显著。F检验的结果将决定是否拒
生物统计-8第八章单因素方差分析
目录
• 引言 • 方差分析的原理 • 单因素方差分析的步骤 • 单因素方差分析的应用 • 单因素方差分析的局限性 • 单因素方差分析的软件实现
01
引言
目的和背景
目的
单因素方差分析是用来比较一个分类变量与一个连续变量的关系的统计分析方法。通过此分析,我们可以确定分 类变量对连续变量的影响是否显著。
VS
多元性
单因素方差分析适用于单一因素引起的变 异,如果存在多个因素引起的变异,单因 素方差分析可能无法准确反映实际情况。 此时需要考虑使用其他统计方法,如多元 方差分析或协方差分析等。
06
单因素方差分析的软件 实现
使用Excel进行单因素方差分析
打开Excel,输入数据。
点击“确定”,即可得到单因素方差分析 的结果。
输出结果,并进行解释和 解读。
谢谢观看
背景
在生物学、医学、农业等领域,经常需要研究一个分类变量对一个或多个连续变量的影响。例如,研究不同品种 的玉米对产量的影响,或者不同治疗方式对疾病治愈率的影响。
方差分析的定义
定义
方差分析(ANOVA)是一种统计技术,用于比较两个或更多组数据的平均值 是否存在显著差异。在单因素方差分析中,我们只有一个分类变量。
第8章 均值-方差分析

第8章 均值-方差分析
本章制作:陈召洪
本章大纲
偏好与分布 证券组合前沿 证券组合前沿的一些数学性质
8.1 偏好与分布
一般来说,仅仅用证券组合的预期回报率和预期回报率的 方差并不能包含经济行为主体投资行为所需的全部信息。
但是马可维茨通过效用函数和投资收益的分布作了相应假 设之后证明,经济行为主体的预期效用能够仅仅表示为证 券组合的预期回报率和预期回报率的方差的函数。
全刻画,我们必须假定经济行为主体的效用函数是一
个二次型效用函数,即经济行为主体的效用函数或以
表达为 u(z)z(b2)z2
。
此时 E[R3]0
于是经济行为主体的预期效用可以由时期1的财富变 量的两个中心矩来定义
E [ u ( w ~ ) ] E [ w ~ ] b (E [ ( w ~ ]2 )2 ( w ~ )) ( 8 .2 ) 2
h p g w [ ~ r p ] E ( 8 .8 )
其中 g 1D [B (V 1 1 )A (V 1 e)]
w 1D [C (V 1 e)A (V 1 1 )]
从以上(8.8)式人们可以看出, g 是预期收益率为0
的前沿证券组合的权重向量; gw是预期收益率为1
率严格大于最小方差证券组合收益率 A C 的证券组合称之为有
效证券组合;
无效证券组合:那些既不是有效证券组合,又不是最小方差组合 的证券组合称之为无效证券组合。
前沿证券的线性组合也落在证券前沿上。
任意一支有效证券组合的凸组合仍然是一支有效证券组合。因此 有效证券组合的集合是一个凸组合。
8.3 证券组合前沿的一些数学性质
关系式(8.20)、(8.21)、(8.23)是等价的关系式。
第八章_方差分析_8.3
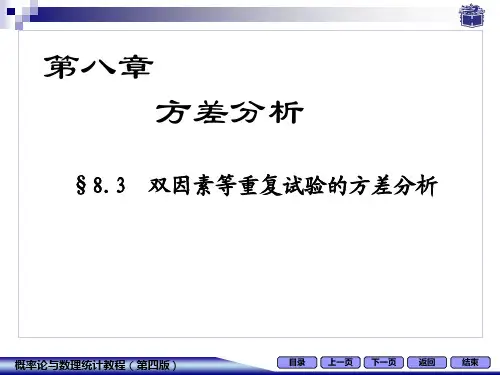
F
值
分 位点
a
显著性
SA SB SI Se ST
l- 1
FA = FB =
S A / (l - 1) S e / lm (r - 1) S B / (m - 1) S e / lm (r - 1) S e / lm (r - 1)
FA 0.05 FA 0.01 FB 0.05 FB 0.01 FI 0.05 FI 0.01
2 s A 是 l 个数据 x 1鬃 x 2鬃L , x l鬃的样本方差; , , 其中
m 2 S B = lr å (x 鬃 - x )2 = lr (m - 1)s B , j j= 1
2 其中 s B 是 m 个数据 x 鬃, x 鬃, L , x 鬃 的样本方差; 1 2 m
概率论与数理统计教程(第四版)
r
i= 1 j = 1
邋
l
m
i= 1 j= 1 k= 1
= S A + S B + S I + Se .
概率论与数理统计教程(第四版)
目录
上一页
下一页
返回
结束
§8.3 双因素等重复试验的方差分析
在上式中
l
S A = mr å (x i 鬃- x )2
称为因素 A 的偏差平方和,它反映了因素 A 的不同水平 所引起的系统误差;
M
xl 21 xl 2 r
M
xlm 1 xlmr
M
M
目录
L
上一页 下一页
M
结束
概率论与数理统计教程(第四版)
返回
§8.3 双因素等重复试验的方差分析
第八章 单因素方差分析
V 4.2 3.2 4.8
4
5
1.0
0.8 1.5
-1.3
-1.1 -0.3
1.8
3.5 11.5
4.1
6.0 29.0
3.3
2.5 18.0 总和 57.0
xi
n
xi2
j 1 2 ij
2.25
1.93
9.00
3.4
132.25
29.43
841.00 324.00
174.46 68.06
1308.50
sx MS e n
品系号
Ⅳ
Ⅴ
Ⅲ
Ⅱ
Ⅰ
平均数
70.8
68.6
67.3
65.3
64.4
顺序号
1
2
3
4
5
df
k
R0.05
Rk
R0.01
Rk
2
2.95
1.165
4.02
1.588
3 20 4
3.10
1.225
4.22
1.667
3.18
1.256
4.33
1.710
5
3.25
1.284
4.40
1.738
5
单因素固定效应模型方差分析表
变异来源
处理间
平方和
自由度
均方
F
F MS A MS e
SSA
a-1
MSA
误差或处理内
总和
SSe
SST
na-a
na-1
MSe
4、平方和的简易计算方法
株号 1 2 3 I -0.4 0.3 -0.2
品 II
第八章 方差分析 SPSS基础教程
Data09-04 p171 本例主要说明均值对比的选择项与结果 可转化成单因素方差分析
协方差分析实例
H 0 :1 2K
FF 0.05(dfb05接受原假设
方差分析中的术语
1、因素 2、水平 3、单元 4、因素的主效应和因素间的交互效应 5、均值比较 6、单元均值、边际均值 7、协方差分析 8、重复测量
方差分析过程
概念: 利用线形回归方法消除混杂因素的影
响后进行的方差分析,这是实际工作中经 常要考虑的问题。 数据背景: p176 数据文件:Data09-06
多维交互效应方差分析实例
数据背景: p179 数据文件:Data09-07
1、One-way过程 2、GLM过程
(1)Univariate过程 (2)Multivariate过程 (3)Repeated Measue (4)Variance Component
第二节 单因素方差分析
单因素方差分析的思想 单因素方差分析的操作 应用举例
1、data09-01 p151 2、data09-02 p159
第三节 简单方差分析
1、基本思想 2、操作步骤 3、应用举例
系统默认方差分析实例
数据背景: 四个种系未成年雌性大白鼠个三只,
每只按一种剂量注射雌激素,一段时间后, 解剖称子宫重量。 Data09-03 p168
2*2析因试验方差分析实例
数据背景: 使用两种药物A和B治疗缺铁性贫血病人的数
第八章 方差分析
第一节 方差分析的基本原理 第二节 单因素方差分析 第三节 简单方差分析
第八章 方差分析
X ij = m j eij
2
SS t 总变异 df t = N 1
SS b 组间(处理)变异 df b = k 1
SS w 组内(误差)变异 df w = N k
均方
平方和 均方 = 自由度 SS e 组内(误差)均方 MS w = MS e = df e SS b 组间(处理)均方 MSb = MStr = df b
2 e 2 e
m =
j m
2
k 1
=
2 j
k 1
2
当H 0为真时,E MS error = E MStreatm ent 当H 0为假时,E MS error E MStreatm ent
平方和的分解 sum of squares
• 平方和的优越性在于其可加性
– 过程:包含27个词的表过3遍后要求被试写下 记住的词
因素“加工方式”有 5 个水平 j= 1 ,2 ,… ,k (k = 5 )
co unting i= 1 ,2 ,… ,n n= 1 0 9 8 6 8 10 4 6 5 7 7 To ta l(Tj) M e an SD V a ria nce 70 7 .0 0 1 .8 3 3 .3 3 rhy ming 7 9 6 6 6 11 6 3 8 7 69 6 .9 0 2 .1 3 4 .5 4 a dje ctiv e 11 13 8 6 14 11 13 13 10 11 110 1 1 .0 0 2 .4 9 6 .2 2 ima g e ry 12 11 16 11 9 23 12 10 19 11 134 1 3 .4 0 4 .5 0 2 0 .2 7 inte ntio na l 10 19 14 5 10 11 14 15 11 11 120 1 2 .0 0 3 .7 4 1 4 .0 0 503 =∑ X 1 0 .0 6 4 .0 1 1 6 .0 6 to ta l
第八章 方差分析与回归分析
第八章 方差分析与回归分析§8.1 方差分析8.1.1 问题的提出举例说明概念因子和水平。
因子:对研究对象产生影响的因素。
水平:因子所处的状态。
8.1.2 单因子方差分析的统计模型在研究中只考察一个因子则称为单因子试验,其中,记因子为A ,设其有r 个水平,记为r A A ,,1 ,在每一水平下考察的指标可以看成一个总体,现有r 个水平,故有r 个总体,假定:(1)每一总体均为正态总体,记为r i N i i ,,2,1),,(2;(2)各总体的方差相同,记222221 r ;(3)从每一总体中抽取的样本是相互独立的,即所有的试验结果ij y 都相互独立。
这些假定都可以用统计方法进行验证。
首先比较各水平下的均值是否相同,即要对如下的一个假设进行检验,不全相等r rH H ,,,::211210在不会引起误解的前提下,1H 通常可以省略不写。
若0H 成立,则称因子A 不显著,否则,称因子A 显著。
对如上的假设进行检验,需要从每一水平下的总体抽取样本,设从第i 个水平下的总体获得m 个试验结果(各个水平下相同),记ij y 表示第i 个总体的第j 次重复试验结果。
共得如下m r 个试验结果:m j r i y ij ,,1,,,1,其中r 为水平数,m 为重复数,i 为水平编号,j 为重复编号。
在水平i A 下的试验结果ij y 与该水平下的指标均值i 一般总是有差距的,记i ij ij y ,ij 称为随机误差,于是有ij i ij y上式称为试验结果ij y 的数据结构式。
把三个假定用于数据结构式就可以写出单因子方差分析的统计模型:),0(,,1,,,1,2 N m j r i y ij ij i ij 相互独立,且都服从诸为了能更好地描述数据,常引入总均值和效应的概念:总均值:诸i 的平均 ri i r r 11 ;称第i 水平下的均值i 与总均值 的差i i a ,r i ,,1为因子A 的第i 水平的主效应,简称为i A 的效应。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
372.59 6
62.1
229.17 7
32.74
18720.97 23758.12 8088.59
48.23 191
7 27.29
6355.43
1122.68 26
43.18
56923.11
k ni
xij
i1 j 1
k
ni
i 1
x
k ni
xi2j
i1 j1 6
(一)变异的分解
2020/8/14
14
理论上,如果F =1或在1附近波动,没 有理由拒绝H0 , 处理因素(无作用);
如果F >>1,或F >F,则P <。
2020/8/14
15
(三)方差分析的基本思想
根据研究目的和设计类型,将全部观察值总的离均 差平方和(总变异)及其自由度分解为多个部分, 除随机误差外,每部分变异可由某因素的作用(或 几个因素的交互作用)加以解释。通过比较不同变 异来源的均方,借助F分布做出统计推断,从而推 断各因素对观察指标有无影响。
61.24 82.35 26.23 25.46
58.65 56.47 46.87 38.79
46.79 61.57 24.36 13.55
37.43 48.79 38.54 19.45
66.54 62.54 42.16 34.56
59.27 60.87 30.33 10.96
20.68
329.92 6
2020/8/14
18
一、完全随机设计
采用完全随机化的分组方法,将全部实验对象分
配到g个处理组(水平组),各组分别接受不同
的处理,实验结束后比较各组均数之间的差别有 无统计学意义,推断处理因素的效应。
2020/8/14
19
完全随机分组的实验设计 (单因素)
(completely random design)
2
表8-1 对照组和各实验组家兔血清ACE浓度比较(U/ml)
对照组 实验组A 实验组B 实验组C
61.24 82.35 26.23 25.46
58.65 56.47 46.87 38.79
46.79 61.57 24.36 13.55
37.43 48.79 38.54 19.45
66.54 62.54 42.16 34.56
i1 j1
设:g 3
n1
n2
n3
ss组内 ( x1 j x1)2 ( x2 j x2 )2 ( x3 j x3 )2
j 1
j 1
j 1
反映随机误差
2020/8/14
10
满足如下关系:
SS总 SS组间 SS组内
总 组间 组内
2020/8/14
11
(二)变异的比较
变异估计量—均方(Mean square ,MS)
组间变异 组内变异
总变异
2020/8/14
7
1.总变异: 反映所有测量值之间总的变异程度。 大 小 用 总 离 均 差 平 方 和 (sum of squares of
deviations from mean,SS)表示
g ni
SS总
X ij X
2
g ni
X ij 2
C
i1 j1
i1 j1
59.27 60.87 30.33 10.96
ni
xij j 1
3229.17
ni
6
x ni i
54.99
xi2j
j1 2020/8/114 8720.97
6 62.1
23758.12
7 32.74
8088.59
48.23 191 7 27.29
6355.43
1122.68 26
N(试验对象)随机化分组
甲处理(n1) 乙处理(n2) 丙处理(n3)
2020/8/14
20
随机化分组的方法
例:将120名试验对象分为4组,采用完全随机分组方法。
k ni
xij
i1 j 1
k
ni
i 1
43.18
x
k ni
56923.11
xi2j
i1 3j1
多样本均数重复进行t检验?
当有g个均数比较时,若进行t 检验, 将会使用m=g(g-1)/2次t检验,若 确定其检验水准为α,则其实际上所 执行的检验水准为1-(1-α)m,犯I
类错误的机率增大
MS组 间 SS组 间 / 组 间
组 间 = 组数-1=G-1
2020/8/14
12
MS组内 SS组内 / 组内
组内 =总例数-组数=N-G
2020/8/14
13
统计量F 值
F
组间变异 组内变异
MS组间 MS组内
, 1
=
组间,
2
=
组内
F 统计量服从F 分布,一般组间变异大 于或等于组内变异,即F≥1。
2020/8/14
4
方差分析的目的
在 H 0 : 1 2 ...g 成立的条件下,通过
分析各处理组之间 X i 的差别大小,推断g个
总体均数有无差别。
2020/8/14
5
一、 方差分析的基本思想
ni
xij j 1
ni
x ni i
xi2j
2020/8j/114
对照组 实验组A 实验组B 实验组C
C
g
(
ni
X ij
)2
/
N
i1 j1
2020/8/14
8
2.组间变异:各处理组由于接受处理的水平不同,
各组的样本均数也大小不等,称为组间变异。其大
小用组间离均差平方和表示
ni
g
g (
X )2 ij
SS组间 ni ( X i X )2
i 1
i 1
j 1
ni
C
设:g 3, (i 1,2,...g)
ss组间 n1(x1 x)2 n2 (x2 x)2 n3 (x3 x)2
产生原因:处理因素效应(可能存在)、随机误差
2020/8/14
9
3.组内变异:在同一处理组中,测量值仍各不相 同,这种变异称为组内变异(误差)。组内变异 用组内离均差平方和表示
SS组内
g ni
( X ij
Xi )2
第八章 方差分析 董英
2020/8/14
1
教学要求
1.掌握方差分析的基本思想。 2.掌握随机化分组方法。 3.掌握完全随机设计、区组设计、析因设计的特点和资料
分析。 4.掌握多重比较方法的选择。 5.掌握各种设计方差分析的SPSS实现及结果解读。 6. 理解析因设计中的主效应、单独效应和交互效应
2020/8/14
2020/8/14
16
二、方差分析应用条件
1.独立性:各样本为相互独立的随机样本; 2.正态性:各样本均来自正态分布总体; 3.方差齐性:相互比较的各样本的总体方差
相等,即具有方差齐性(homogeneity of variance) 。
2020/8/14
17
第二节 完全随机设计资料的方差分析
(completely random design)
