层次分析模型简介及例题
层次分析法例题

某物流企业需要采购一台设备,在采购设备时需要从功能、价格与可维护性三个角度进行评价,考虑应用层次分析法对3个不同品牌的设备进行综合分析评价和排序,从中选出能实现物流规划总目标的最优设备,其层次结构如下图所示。
以A 表示系统的总目标,判断层中1B 表示功能,2B 表示价格,3B 表示可维护性。
1C ,2C ,3C 表示备选的3种品牌的设备。
、9分ij a ij =1/a ji ;a ii =1;i ,j=1,2,…,n显然,比值越大,则要素i 的重要度就越高。
2、构建判断矩阵A判断矩阵是层次分析法的基本信息,也是进行权重计算的重要依据。
根据结构模型,将图中各因素两两进行判断与比较,构造判断矩阵:●判断矩阵B A -(即相对于物流系统总目标,判断层各因素相对重要性比较)如表1所示;●判断矩阵C B -1(相对功能,各方案的相对重要性比较)如表2所示; ●判断矩阵C B -2(相对价格,各方案的相对重要性比较)如表3所示; ●判断矩阵C B -3(相对可维护性,各方案的相对重要性比较)如表4所 示。
表1判断矩阵B A -3●求和法1)将判断矩阵A 按列归一化(即列元素之和为1):b ij =a ij /Σa ij ; 2)将归一化的矩阵按行求和:c i =Σb ij (i=1,2,3….n ); 3)将c i 归一化:得到特征向量W =(w 1,w 2,…w n )T ,w i =c i /Σc i , W 即为A 的特征向量的近似值;4)求特征向量W 对应的最大特征值: ●求根法1)计算判断矩阵A 每行元素乘积的n 次方根;n nj iji aw ∏==1(i=1,2,…,n)2)将i w 归一化,得到∑==ni iii ww w 1;W =(w 1,w 2,…w n )T 即为A 的特征向量的近似值;3)求特征向量W 对应的最大特征值:(1)判断矩阵B A -的特征根、特征向量与一致性检验 ①计算矩阵B A -的特征向量。
层次分析法例题
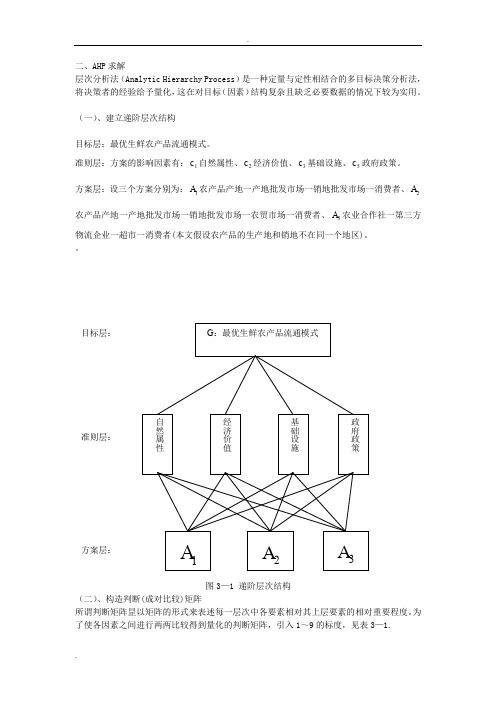
二、AHP 求解 层次分析法(Analytic Hierarchy Process )是一种定量与定性相结合的多目标决策分析法,将决策者的经验给予量化,这在对目标(因素)结构复杂且缺乏必要数据的情况下较为实用。
(一)、建立递阶层次结构目标层:最优生鲜农产品流通模式。
准则层:方案的影响因素有:1c 自然属性、2c 经济价值、3c 基础设施、5c 政府政策。
方案层:设三个方案分别为:1A 农产品产地一产地批发市场一销地批发市场一消费者、2A 农产品产地一产地批发市场一销地批发市场一农贸市场一消费者、3A 农业合作社一第三方物流企业一超市一消费者(本文假设农产品的生产地和销地不在同一个地区)。
。
图3—1 递阶层次结构(二)、构造判断(成对比较)矩阵所谓判断矩阵昰以矩阵的形式来表述每一层次中各要素相对其上层要素的相对重要程度。
为了使各因素之间进行两两比较得到量化的判断矩阵,引入1~9的标度,见表3—1.目标层:准则层:方案层:表3—1 标度值为了构造判断矩阵,作者对6个专家进行了咨询,根据专家和作者的经验,四个准则下的两两比较矩阵分别为:(三)、层次单排序及其一致性检验层次单排序就是把本层所有要素针对上一层某一要素,排出评比的次序,这种次序以相对的数值大小来表示。
对应于判断矩阵最大特征根λmax的特征向量,经归一化(使向量中各元素之和等于1)后记为W。
W的元素为同一层次因素对于上一层次因素某因素相对重要性的排序权值,这一过程称为层次单排序。
能否确认层次单排序,需要进行一致性检验,所谓一致性检验是指对A确定不一致的允许范围。
a,则λ比n 大的越多,A 的不一致性越严重。
用最大特征值对由于λ连续的依赖于ij应的特征向量作为被比较因素对上层某因素影响程度的权向量,其不一致程度越大,引起的判断误差越大。
因而可以用λ―n数值的大小来衡量 A 的不一致程度。
用一致性指标进行检验:max 1nCI n λ-=-。
层次分析法

bn1
bn2 ……
bnn
bij是对于Ak而言,Bi对Bj的相对重要性的数值表示。
Bij通常取1、3、5、7、9及其他们的倒数,其含义为:
尺度
1 3 5 7 9
含义
第i个因素与第j个因素的影响相同 第i个因素比第j个因素的影响稍强 第i个因素比第j个因素的影响强 第i个因素比第j个因素的影响明强 第i个因素比第j个因素的影响绝对地强
层次分析法
一 问题的提出
例1 购物 买钢笔,一般要依据质量、颜色、实用性、价格、
外形等方面的因素选择某一支钢笔。 下馆子,则要依据馆子的饭菜质量、区位条件、档
次、饭菜价格、服务质量等方面因素来选择。
例2 旅游 假期旅游,是去风光秀丽的苏州,还是去迷人的
北戴河,或者是去山水甲天下的桂林,一般会依据景 色、费用、食宿条件、旅途等因素选择去哪个地方。
课题D2
课题可行性B3
难
研财
易
究政
程
周支
度
期持
c3
c4
c5
课题D3
层次分解时注意事项:
如果所选的要素不合理,其含义混淆不清,或 要素间的关系不正确,都会降低AHP法的结果质量, 甚至导致AHP法决策失败。 为保证递阶层次结构的合理性,需注意以下问题: 1、要对问题的影响因素有充分的理解,必要的时 候可以咨询相关的专家; 2、分解简化问题时把握主要因素,不漏不多 3、注意相比较元素之间的强度关系,相差太悬殊 的要素不能在同一层次比较。 4、以上均为完全层次
层次总排序的一致性检验
(1)
(2)
(3)
在(1)式中,CI为层次总排序的一致性指标,CIj为与aj对应 的B层次中判断矩阵的一致性指标;在(2)式中,RI为层次总排 序的随机一致性指标,RIj为与aj对应的B层次中判断矩阵的随 机一致性指标;在(3)式中,CR为层次总排序的随机一致性比例。
经典层次分析法分析及实例教程

当CR 0.1 时,认为层次总排序通过一致性检验。到
此,根据最下层(决策层)的层次总排序做出最后决策。
层次分析法的基本步骤归纳如下
1.建立层次结构模型 该结构图包括目标层,准则层,方案层。
2.构造成对比较矩阵 从第二层开始用成对比较矩阵和1~9尺度。
3.计算单排序权向量并做一致性检验 对每个成对比较矩阵计算最大特征值及其对应的特征向量, 利用一致性指标、随机一致性指标和一致性比率做一致性 检验。若检验通过,特征向量(归一化后)即为权向量; 若不通过,需要重新构造成对比较矩阵。
一般分为三层,最上面为目标层,最下面为方案层,中 间是准则层或指标层。 例1 的层次结构模型
买钢笔
目标层
质颜价外实 量色格形用
准则层
可供选择的笔
方案层
例2 层次结构模型
选择 旅游地
景
费
居
饮
旅
色
用
住
食
途
苏州、杭州、 桂林
目标层Z 准则层A 方案层B
若上层的每个因素都支配着下一层的所有因素,或被下一层所 有因素影响,称为完全层次结构,否则称为不完全层次结构。
A 4 7
2 3
1 3
1 5
2
1
1
1
1
3
1
1
3 5
1 2 5
B1
1 2
1
2
1 5
1 2
1
1
B2
3
1 3 1
1 18 3
8 3 1
1 1 3
B3
1 1
1 1
3
3 3 1
1 3 4
B4
1 3
1
1
层次分析法及其案例分析

2 层次分析法应用实例
5、计算各项指标结构的权值(归一化特征向量) 按照上述第四小点中说明,可将特征值的归一化特征向量作为权重。 计算最大特征向量除高数中讲到的数学方法外,有一个较为简便的方法,即 “求和法" (1)按照纵列求和
A
B1 B2 B3 B4 B5 求和
B1
1 5 0.33333 0.33333 0.142857 6.809524
2、建立层次结构图
为了简化计算步骤,本文在供应商决策分析时,只做关键指标的分析,具体的层 次结构如下图:
目标层(A) 指标层(B) 方案层(C)
合格的供应商
价格指标 质量指标 交货指标 服务指标 硬件资质
供应商1
供应商2
2 层次分析法应用实例
3、建立判断矩阵
(1)建立B层次与A层次的矩阵关系 A、首先对各项指标进行打分( B1: B2,即价格指标、质量指标、交货指标、服 务指标、硬件资质)
B、进行一致性检测,以确保打分时不出现前后的逻辑错误
(1)计算上述矩阵的最大特征值= 5.08
(2)计算一致性指标: CI= - n =0.08/4=0.02( n=5,矩阵的阶 n -1
数),原则上比n越大,说明不一致性越严重
(3)查询随机性一致性指标: RI
n 1 2 3 4 5 6 7 8 9 10
RI 0 0 0.58 0.9 1.12 1.24 1.32 1.41 1.45 1.49
11
1.51
当n=5时,RI=1.12 (4)计算一致性比率:CR=CI/RI=0.02/1.12=0.01785<0.1,一致性成立。 一般认为当CR< 0.1时,认为矩阵的不一致程度在容许范围之内,可用其归一化特 征向量作为权向量,否则要重新构造成对比较矩阵。
层次分析法详解以及例题

构建风险层次结构通过选取的指标可以看出这是一个多目标的且问题涉及到许多因素,各种因素的作用相互,情况复杂。
依据层次分析法处理这类复杂的问题就需要对所涉及的因素指标进行分析:哪些是需相互比较的;哪些是需相互影响的。
把那些需相互比较的因素归成同一类,构造出一个各因素类之间相互联结的层次结构模型。
各因素类的层次级别由其与目标的关系而定:第一层是目标层,也就是国家风险的评价排序第二层是准则层,这一层中是国家风险排序所涉及的国家风险类型,即政治风险、经济风险、社会风险。
第三层是子准则层,这一层是评价衡量准则层中各要素的影响因素及评价指标,即政权凝聚力、腐败状况、相关法律政策、国际关系、官僚主义、经济政策、汇率稳定性、金融环境、内部冲突、外部冲突、民族差异等。
第四层也就是我们要选择的方案即所要选择的并购方案国家。
图5.1风险层次结构模型Fig.5.1 The hierarchical structure model of country risk为了方便计算以及模型的理解,层次结构中各层次均用字母代替,目标层为iA ,准则层为B i ,子准则层为C i ,方案层为D i 。
5.2.2 重要性程度描述为了将上述复杂的多因素综合比较问题转化为简单的两因素相对比较问题。
首先找出所有两两比较的结果,并且把它们定量化;然后再运用适当的数学方法从所有两两相对比较的结果之中求出多因素综合比较的结果。
进行定性的成对比较时,我们将比较结果分为5种等级:相同、稍强、强、明显强、绝对强并将我们所做出的比较结果应用1~9个数字尺度来进行定量化,比较具体含义及相应数字对应如下表:表5.2 AHP重要程度描述表Table 5.2 Described table of AHP important degree 定性比较结果数字定量因素1相较于因素2具有相同的重要性 1因素1与因素2相比,前者重要性稍强 3因素1与因素2相比,前者重要性强 5因素1与因素2相比,前者重要性明显强7因素1与因素2相比,前者重要性绝对强9因素1与因素2相比,相对重要性处于上述等级之间2、4、6、8(续表5.2)定性比较结果数字定量因素1与因素2相比,后者的重要性要稍强、强、明显强、绝对强于前者1/3、1/5、1/7、1/9例如:在准则层中有三个因素政治风险B1、经济风险B2以及社会风险B3,假设如果政治风险B1相较于经济风险B2在风险中的重要性稍强那么就是B1:B2=3:1也就是3。
层次分析法及真题讲解
层次分析法的重要性
解决复杂问题
层次分析法能够有效地处理多目 标、多准则、多约束等复杂决策 问题,尤其在资源分配、政策评 价等领域具有广泛应用。
决策科学化
通过定性与定量相结合的方法, 层次分析法能够使决策过程更加 科学、客观,减少主观因素的影 响。
促进共识
层次分析法有助于决策者与利益 相关者之间达成共识,促进合作 与协调。
实例一:企业并购决策
总结词
层次分析法在企业并购决策中,能够将复杂的决策问题分解为多个层次,通过比 较和判断,确定各因素的权重,从而为决策提供依据。
详细描述
企业并购决策需要考虑多个因素,如目标公司的价值、并购后的协同效应、并购 风险等。层次分析法可以将这些因素分为目标层、准则层和方案层,通过两两比 较和判断,确定各因素的相对重要性,从而得出最优的并购方案。
标准化与规范化
制定层次分析法的标准操作流程和规范,提高其在不同领域的可重 复性和可比性。
应用前景展望
1 2 3
决策支持
层次分析法将继续作为重要的决策支持工具,帮 助决策者进行多目标、多准则的决策分析。
复杂问题解决
面对日益复杂的决策问题,层次分析法将发挥更 大的作用,为解决复杂问题提供有效的方法论支 持。
实例二:投资项目选择
总结词
层次分析法在投资项目选择中,能够综合考虑项目的多个方面,如市场需求、技术可行性、财务指标等,为投资 者提供全面的项目评估。
详细描述
投资者在选择投资项目时,需要考虑多个因素,如市场需求、技术可行性、财务指标等。层次分析法可以将这些 因素分为目标层、准则层和方案层,通过两两比较和判断,确定各因素的相对重要性,从而得出最优的投资项目。
层次分析法的历史与发展
层次分析法模型1
k 层
上 nk 个元素对第 k 1层上第 j 个元素为准则 的排序权重向量, 其中不受 j 元素支配的元 素权重取为零。
3.层次分析法 层次分析法
P
(k ) (k ) (k ) (k ) = ( P , P2 ,, Pn ) 是 nk 1 k 1
× nk 1 阶矩
阵,它表示第 k 层上元素对 k 1层上各元素 的排序。 那末第 k 层上元素对目标的总排序
3.层次分析法 层次分析法
表10.2 平均随机一致性指标R.I.
矩阵阶数
1 2 3 4 5 6 7 8
R.I.
矩阵阶数
0
0
0.52
0.89
1.12
1.26
1.36
1.41
9
10
11
12
13
14
15
R.I.
1.46
1.49
1.52
1.54
1.56
1.58
1.59
3.层次分析法 层次分析法
③计算一致性比例C.R.(consistency ratio)
3.层次分析法 层次分析法
四个步骤的实现方法 : 1.递阶层次结构的建立: 层次可分为三类: (1)最高层:这一层次中只有一个元素,它是问题的预定 最高层: 最高层 目标或理想结果,因此也叫目标层; (2)中间层:这一层次包括了为实现目标所涉及的中间环 中间层: 中间层 节,所需要考虑的准则。该层可由若干层次组成,因而有 准则和子准则之分。这一层也称为准则层; (3)最底层:这一层次包括为实现目标可供选择的各种措 最底层: 最底层 施、决策方案等,因此也称为措施层或方案层。
3.层次分析法 层次分析法
根据以上分析,可把科研课题的选择分为3个层次。
层次分析法例题
二、AHP 求解层次分析法(Analytic Hierarchy Process )是一种定量与定性相结合的多目标决策分析法,将决策者的经验给予量化,这在对目标(因素)结构复杂且缺乏必要数据的情况下较为实用。
(一)、建立递阶层次结构目标层:最优生鲜农产品流通模式。
准则层:方案的影响因素有:1c 自然属性、2c 经济价值、3c 基础设施、5c 政府政策。
方案层:设三个方案分别为:1A 农产品产地一产地批发市场一销地批发市场一消费者、2A 农产品产地一产地批发市场一销地批发市场一农贸市场一消费者、3A 农业合作社一第三方物流企业一超市一消费者(本文假设农产品的生产地和销地不在同一个地区)。
。
图3—1 递阶层次结构(二)、构造判断(成对比较)矩阵所谓判断矩阵昰以矩阵的形式来表述每一层次中各要素相对其上层要素的相对重要程度。
为了使各因素之间进行两两比较得到量化的判断矩阵,引入1~9的标度,见表3—1.目标层:准则层:方案层:表3—1 标度值为了构造判断矩阵,作者对6个专家进行了咨询,根据专家和作者的经验,四个准则下的两两比较矩阵分别为:(三)、层次单排序及其一致性检验层次单排序就是把本层所有要素针对上一层某一要素,排出评比的次序,这种次序以相对的数值大小来表示。
对应于判断矩阵最大特征根λmax的特征向量,经归一化(使向量中各元素之和等于1)后记为W。
W的元素为同一层次因素对于上一层次因素某因素相对重要性的排序权值,这一过程称为层次单排序。
能否确认层次单排序,需要进行一致性检验,所谓一致性检验是指对A确定不一致的允许范围。
a,则λ比n 大的越多,A 的不一致性越严重。
用最大特征值对由于λ连续的依赖于ij应的特征向量作为被比较因素对上层某因素影响程度的权向量,其不一致程度越大,引起的判断误差越大。
因而可以用λ―n数值的大小来衡量 A 的不一致程度。
用一致性指标进行检验:max 1nCI n λ-=-。
其中max λ是比较矩阵的最大特征值,n 是比较矩阵的阶数。
(完整版)层次分析法模板例题
CR=CI/RI
3.0536 0.026810788 0.052068882
一致性检验 Awi/Wi 3.1356 CI=(λ-n)/(n-1) 3.1356 3.1356 3.1356 0.067805422
CR=CI/RI 0.131684027
总排序
Σaibin
0.069712 0.096671 0.016757
0.274628908 0.253415711 0.471955382
CR=CI/RI 0.118696 0.118696
总权重
=A14 按行相乘 开n次方 权重Wi
Awi
6
3.0000 1.4422 0.3806
1.1936
4
8.0000 2.0000 0.5279
1.6551
1
0.0417 0.3467 0.0915
0.2869
3.7889
层次总排序计算
四准则ai
经济效益 社会效益 生态效益 技术要求
三方案bin
0.4821 0.1170 0.2178 0.1831
Awi
1/7 0.2857 0.6586 0.1570
0.4988
1/4 0.1250 0.5000 0.1192
0.3786
1
28.0000 3.0366 0.7238
2.2995
4.1952
=A12 1 2 5
=A13 1/2 1 3
准则层对于目标层的判断矩阵及单排序和一致性检验
=A14 按行相乘 开n次方 权重Wi
CIi Rii(与n有关的常
数) CRi
层次总排序一致性检验
0.0884641 0.001847 0.026811 0.067805
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对权重系数的量化过程
(1)成对比较 从 x1,x2,…xn中任取xi与xj比较它们对于y贡献 (重要程度)的大小,按照以下标度给xi/xj赋值: xi/xj=1,认为“xi与xj重要程度相同” xi/xj=3,认为“xi比xj重要程度略大” xi/xj=5,认为“xi比xj重要程度大” xi/xj=7,认为“xi比xj重要程度大很多” xi/xj=9,认为“xi比xj重要程度绝对大” 当比值为2,4,6,8 时认为介于前后中间状态。
层次分析法简介
• 层次分析法是萨蒂(saaty) 等人20世纪 70年代提出的一种决策方法。它是将半 定性、半定量问题转化为定量问题的有 效途径,它将各种因素层次化,并逐层 比较多种关联因素,为分析和预测事物 的发展提供可的定量依据。 • 层次分析法在决策工作中有广泛的应用。 主要用于确定综合评价的权重系数。层 次分析法所用数学工具主要是矩阵运算。
成对比较阵和权向量 成对比较完全一致的情况
满足 aij a jk aik , i, j, k 1,2,, n 的正互反阵A称一致阵,如 一致阵 性质
(2)建立逆对称矩阵 由xi/xj建立n阶方阵A (3) 迭代 按下列方法求向量迭代序列: e0=( 1/n 1/n … 1/n)T e’k=Aek-1 || e’k||为Aek-1 的n个分量之和 ek= e’k / || e’k|| , k=1,2, … 数列{ ek}是收敛的,记其极限为e.且 记e=(a1 a2 … an) 于是取权重系数wi=ai
例1:评价影视作品
• 在电视节上评价影视作品,用以下三个 评价指标: • x1表示教育性 • x2表示艺术性 • x3表示娱乐性 • 有一名专家经成对,赋值: • x1/x2=1 x1/x3=1 /5 x2/x3=1/3
• 于是得到逆对称矩阵
1 A 1 5
1 3 1 e0 3 1 3
0.467 0.155 0.565 , e2 3.014, e2 0.184 e2 1.991 0.661 0.471 0.156 0.559 , e3 3.018, e3 0.185 e3 1.998 0.659 0.473 0.156 0.561 , e4 3.028, e4 0.185 e4 1.994 0.659
1 1 3
1 5 1 3 1
0.733 Ae0 0.788 e1 3
4.511 e1
0.733 0.162 1 e1 0.788 0.172 4.511 0.665 3
4 3ห้องสมุดไป่ตู้7 1 2 3
1/ 7 1/ 5 1/ 5
3 5 5 A~成对比较阵 1 / 2 1 / 3 A是正互反阵 1 1 1 1
要由A确定C1,… , Cn对O的权向量
成对比较阵和权向量 成对比较的不一致情况
1 A 2
1/ 2 1
4 7
• 由于e4=e3 ,迭代经过4次中止,权系数是 w1=0.156, w2=0.185, w3=0.659 • 相应的综合评价公式是 • Y=0.156x1+0.185x2+0.659x3
• 如果用同样的分制来给作品的三个指 标评分,由以上公式算出的便是作品综 合评分y。
例2. 选择旅游地
如何在3个目的地中按照景色、费用、居 住条件等因素选择.
层次分析法简介
一、层次分析法基本原理
分解
建立 多个因素 层次结构
实际问题
确定
诸因素的相 对重要性
计算 权向量
判断 综合决策
二、层次分析法基本步骤
一、确定权系数 设x1,x2,…xn为对应各因素的决策变量。 其线性组合: y=w1x2+w2x2+ …+wnx 是综合评判函数。 w1,w2, … wn是权重系数,其满足: n wi0 , wi 1
a12 1/ 2 (C1 : C2 )
a13 4 (C1 : C3 )
一致比较
不一致
a23 8 (C2 : C3 )
w1 w2 w2 w2 wn w2 w1 wn w2 wn wn wn
允许不一致,但要确定不一致的允许范围
w1 考察完全一致的情况 w 1 W ( 1) w1 , w2 ,wn w2 A w1 令aij wi / w j T w (w1 , w2 ,wn ) ~ 权向量 wn w1
层次分析法的基本步骤 成对比较阵 和权向量
元素之间两两对比,对比采用相对尺度
设要比较各准则C1,C2,… , Cn对目标O的重要性
Ci : C j aij
选 择 旅 游 地
1 2 A 1/ 4 1/ 3 1/ 3
1/ 2 1
1 A (aij ) nn , aij 0, a ji aij
目标层 O(选择旅游地)
准则层
C1 景色
C2 费用
C3 居住
C4 饮食
C5 旅途
方案层
P1 桂林
P2 黄山
P3 北戴河
“选择旅游地”思维过程的归 纳 • 将决策问题分为3个层次:目标层O,准则层C, 方案层P;每层有若干元素, 各层元素间的关系 用相连的直线表示。
• 通过相互比较确定各准则对目标的权重,及各方 案对每一准则的权重。 • 将上述两组权重进行综合,确定各方案对目标的 权重。 层次分析法将定性分析与定量分析结合起来 完成以上步骤,给出决策问题的定量结果。
