第5章 边界层流动
合集下载
流体力学张兆顺课后答案
流体力学张兆顺课后答案【篇一：流体力学知识点大全】书籍：《全美经典-流体动力学》《流体力学》张兆顺、崔桂香《流体力学》吴望一《一维不定常流》《流体力学》课件清华大学王亮主讲目录：第一章绪论第二章流体静力学第三章流体运动的数学模型第四章量纲分析和相似性第五章粘性流体和边界层流动第六章不可压缩势流第七章一维可压缩流动第八章二维可压缩流动气体动力学第九章不可压缩湍流流动第十章高超声速边界层流动第十一章磁流体动力学第十二章非牛顿流体第十三章波动和稳定性第一章绪论1、牛顿流体：剪应力和速度梯度之间的关系式称为牛顿关系式，遵守牛顿关系式的流体是牛顿流体。
2没有内摩擦，也就没有内耗散和损失。
层流：纯粘性流体，流体分层，流速比较小；湍流：随着流速增加，流线摆动，称过渡流，流速再增加，出现漩涡，混合。
因为流速增加导致层流出现不稳定性。
定常流：在空间的任何点，流动中的速度分量和热力学参量都不随时间改变，3、欧拉描述：空间点的坐标；拉格朗日：质点的坐标；4、流体的粘性引起剪切力，进而导致耗散。
5、无黏流体—无摩擦—流动不分离—无尾迹。
6、流体的特性：连续性、易流动性、压缩性不可压缩流体：d??0dtconst是针对流体中的同一质点在不同时刻保持不变，即不可压缩流体的密度在任何时刻都保持不变。
是一个过程方程。
7、流体的几种线流线：是速度场的向量线，是指在欧拉速度场的描述；同一时刻、不同质点连接起来的速度场向量线；dr?u?x,tdr?u?0迹线：流体质点的运动轨迹，是流体质点运动的几何描述；同一质点在不同时刻的位移曲线；涡线：涡量场的向量线，u,dr???x,t??dr???0涡线的切线和当地的涡量或准刚体角速度重合，所以，涡线是流体微团准刚体转动方向的连线，形象的说：涡线像一根柔性轴把微团穿在一起。
第二章流体静力学1、压强：p?lim?fdf??a?0?ada静止流场中一点的应力状态只有压力。
2、流体的平衡状态：1）、流体的每个质点都处于静止状态，==整个系统无加速度；2）、质点相互之间都没有相对运动，==整个系统都可以有加速度；由于流体质点之间都没有相对运动，导致剪应力处处为零，故只有：体积力(重力、磁场力)和表面力(压强和剪切力)存在。
湍流和层流
ρ v (δ − δ ) − ∫ ρv dy =
2 ∞ ∞ * 0 2 x
δ
∫
δ
0
2 ρ v dy − ∫ (ρ∞v∞ −ρvx )v∞dy − ∫ ρvx dy 2 ∞ ∞ 0 0
δ
δ
= ∫ ρvx (v∞ − vx )dy = ∫ ρvx (v∞ − vx )dy
0Байду номын сангаас
δ
∞
0
二维层流边界层的相似解
• 边界层位移厚度δ*：使粘流所占的通道比无粘（理想流 体）流动应占通道加宽的部分
∞
ρ ∞ v∞δ = ∫ ( ρ ∞ v∞ −ρvx )dy
* 0
* ∗ ∞
δ = ∫ (1 −
* 0
∞
ρv x )dy ρ ∞ v∞
• 物面为曲面物体： δ = δ ( x ) = (1 − ρvx )dy ∫0 ρδ vδ
第五章 层流与湍流边界层
主要内容
• 层流与湍流的基本概念 • 二维层流边界层的相似解 • 二维湍流边界层的主要物理特征及壁面律 • 边界层的动量积分方程 • 边界层的分离
层流与湍流的基本概念
粘性流体与理想流体
平板表面速度型
（a）粘性流体 （b）理想流体
∂v x • 牛顿粘性定律 ∂y • 粘性流体与理想流体的差异：在固体边界上的无滑移条件和流 体内部及流体与固体边界之间的摩擦阻力的存在
• 常微分方程数值解：两点边值问题
δ **
x
vδ x
ν
= ∫ f ′(1 − f ′)dη
0
∞
二维湍流边界层的主要物 理特征及壁面律
湍流边界层的复合层性质
• 湍流边界层：内层和外层（复合层） • 湍流边界层：速度剖面中主要与粘性有关的部分和主要与
传热学-第五章3-4-PPT
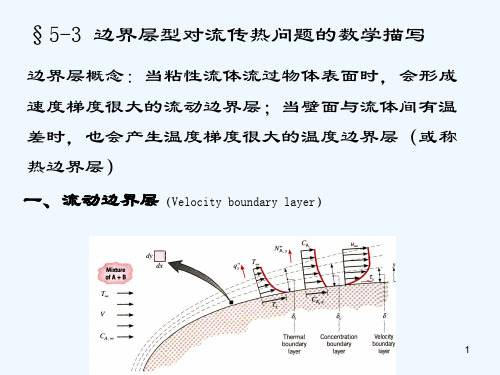
温度：
t 数量级为 1
边界层厚度：δ数量级Δ
18
X方向壁面特征长度：l 数量级为1
二维对流换热，其微 分方程组已导出：
u v 0 x y
（u
u x
v
u y
)
Fx
p x
( 2u
x 2
2u y 2
)
（u
v x
v
v ) y
Fy
p y
(
2v x 2
2v y 2
)
c p u
t x
v
t y
2t x 2
u
t x
v
t y
a
2t y 2
应的定解条件，则 可以求解
dp dx
u
du dx
若 du 0，则 dp 0
dx
dx
23
例如：对于主流场均速 u 、均温 t ，并给定恒定
壁温的情况下的流体纵掠平板换热，即边界条件为
y 0 u 0, v 0, t tw
y u u, t t
求解上述方程组(层流边界层对流换热微分方程组) 可得局部表面传热系数 hx 的表达式
t与 相似，随着 x 增加而增厚,它反映了流
体热量传递的渗透深度。
流动边界层与热边界层的状况决定了热量传 递过程和边界层内的温度分布
10
层流：温度呈抛物线分布
湍流：温度呈幂函数分布 湍流边界层贴壁处的温度梯度明显大于层流
T y
w,t
T y
w, L
故：湍流换热比层流换热强！
11
与 t 的关系：分别反映流体分子和流体微
a
Pr
——普朗特数，反映流体物性对换热 的影响
式中ν 、a 的单位都是 m2 / s，故Pr数是无因次数。
流体力学第五章
5.2 边界层流动
5.2 边界层流动
*
0
u 1 u e e
dy
5.2 边界层流动
**
0
u eue
u 1 u dy e
5.2 边界层流动
平面边界层流动方程
边界层近似假定 1. 纵向偏导数远小于横向偏导数
5.2 边界层流动
边界层分离
理想流体能量转换过程 边界层内粘性对机械能的耗散使得流体微团在逆 压区 MF 段间的某个点处 V 降为零，后来的质点 将改道进入主流区，使来流边界层与物面分离； 在分离点下游区域，受逆压作用而发生倒流。
5.2 边界层流动
边界层分离
分离点：紧邻壁面顺流区与倒流区分界点。 边界层分离的必要条件：粘性、逆压梯度。
湍流边界层摩阻系数大
0.664 C fL Re x
C fT
0.0576 /5 Re 1 x
5.2 边界层流动
边界层分离
边界层流动：流体质点受惯性力、粘性力和压力 作用；粘性力阻滞流体质点运动，使流体质点减 速和失去动能；压力的作用取决于绕流物体形状； 顺压梯度有助于流体加速前进，而逆压梯度阻碍 流体运动。
研究方法：实验、数值(RANS、LES、DNS)
5.1 粘流的基本特性
层流、紊流速度型 紊流粘性应力比层流大
5.2 边界层流动
边界层概念的提出
高 Re流动，惯性力远大于粘性力，研究忽略粘 性的流动有实际意义。 阻力、分离、涡扩散等问题，无粘解与实际相 差甚远。 研究表明：虽然 Re很大，但在靠近物面的薄层 流体内，沿物面法向存在很大的速度梯度，粘 性力与惯性力相当而不可忽略。 Prandtl把物面附近粘性力起重要作用的薄层称 为边界层。
空气动力学基础第五章边界层理论及其近似解读
u v 0 x y
ue u u u ue 2u u v ue 2 t x y t x y
在定常流动情况下，有
u v 0 x y
ue u u 2u u v ue 2 x y x y
5.2、平面不可压缩流体层流边界层方程
0 1 p y
这说明，在高Re数情况下，在边界层内压力沿法向是不变的。
5.2、平面不可压缩流体层流边界层方程
边界层内的压力分布与边界层外边界线上的压力分布相等。也就是， p与y无关，仅是x和t的函数。即
p pe ( x, t )
忽略质量力，Prandtl边界层方程变为
u v 0 x y
0
1 1
0
u dy e ue
这部分主流区增加的流体厚度是由边界层流体排挤入主流区造成的。因 此，称其为排移厚度。 （b）边界层动量损失厚度 在边界层内，在质量流量不变的条件下，理想流体通过的动量为
K i u e udy
0
由于粘性的存在，实际流体通过的动量为
v v v 1 p 2v 2v u v fy 2 2 t x y y x y
选取长度特征L，速度尺度ue，时间尺度t=L/ue，边界层近似假定：
5.2、平面不可压缩流体层流边界层方程
（1）根据边界层定义，纵向偏导数远远小于横向偏导数。
5.1、边界层近似及其特征
Prandtl的边界层概念，为人们如何计入粘性的作用开辟了划时代的途 径，因此称其为粘性流体力学之父。对整个流场提出的基本分区是： （1）整个流动区域可分成理想流体的流动区域（势流区）和粘性流体的 流动区域（粘流区）。 （2）在远离物体的理想流体流动区域，可忽略粘性的影响，按势流理论 处理。 （3）粘性流动区域仅限于物面近区的薄层内，称为边界层。既然是粘流 区，粘性力的作用不能忽略，与惯性力同量级，流体质点作有旋运 动。 2、边界层的特征 （1）边界层定义 严格而言，边界层区与主流区之间无明显界线，通常以速度达到主 流区速度的0.99U作为边界层的外缘。由边界层外缘到物面的垂直距离称 为边界层名义厚度。
传热学第5章
•T
w
•t — 热边界层厚度 •与t 不一定相等
•边界层的传热特性： •在层流边界层内垂直于壁面方向上的热量传递主要依 靠导热。湍流边界层的主要热阻为层流底层的导热热阻 。
1对流换热
•层流：温度呈抛物线分 布•湍流：温度呈幂函数分 布
•湍流边界层贴壁处的温度 梯度明显大于层流
•故：湍流换热比层流换热强！
•边界层内：平均速度梯度很大；
•
y=0处的速度梯度最大
6对流换热
•由牛顿粘性定律：
•速度梯度大，粘滞应力大
•边界层外： u 在 y 方向不变化， u/y=0
•粘滞应力为零 — 主流区
•流场可以划分为两个区： •边界层区：N-S方程
•主流区： u/y=0，=0；无粘性理想流体；
•
欧拉方程
•——边界层概念的基本思想
•强迫对流换热 •自然对流换热
7对流换热
•
(2) 流动的状态 •层流 •：主要靠分子扩散（即导热）。
•湍流 •：湍流比层流对流换热强烈
•
(3) 流体有无相变
•沸腾换热 •凝结换热
8对流换热
• (4) 流体的物理性质
• 1）热导率，W/(mK)， 愈大，对流换热愈强烈；
• 2）密度，kg/m3 • 3）比热容c，J/(kgK)。c反映单位体积流体热容
• 与 t 的关系：分别反映流体分子和流体微团的动量
•
和热量扩散的深度
•普朗特数
2对流换热
•综上所述，边界层具有以下特征：
•( • a) (b) 流场划分为边界层区和主流区。
•流动边界层：速度梯度较大，动量扩散主要区域。
•热边界层：温度梯度较大，热量扩散的主要区域
• (c) 流态：边界层分为层流边界层和湍流边界层 。湍流边界层分为层流底层、缓冲层与湍流核心。
w
•t — 热边界层厚度 •与t 不一定相等
•边界层的传热特性： •在层流边界层内垂直于壁面方向上的热量传递主要依 靠导热。湍流边界层的主要热阻为层流底层的导热热阻 。
1对流换热
•层流：温度呈抛物线分 布•湍流：温度呈幂函数分 布
•湍流边界层贴壁处的温度 梯度明显大于层流
•故：湍流换热比层流换热强！
•边界层内：平均速度梯度很大；
•
y=0处的速度梯度最大
6对流换热
•由牛顿粘性定律：
•速度梯度大，粘滞应力大
•边界层外： u 在 y 方向不变化， u/y=0
•粘滞应力为零 — 主流区
•流场可以划分为两个区： •边界层区：N-S方程
•主流区： u/y=0，=0；无粘性理想流体；
•
欧拉方程
•——边界层概念的基本思想
•强迫对流换热 •自然对流换热
7对流换热
•
(2) 流动的状态 •层流 •：主要靠分子扩散（即导热）。
•湍流 •：湍流比层流对流换热强烈
•
(3) 流体有无相变
•沸腾换热 •凝结换热
8对流换热
• (4) 流体的物理性质
• 1）热导率，W/(mK)， 愈大，对流换热愈强烈；
• 2）密度，kg/m3 • 3）比热容c，J/(kgK)。c反映单位体积流体热容
• 与 t 的关系：分别反映流体分子和流体微团的动量
•
和热量扩散的深度
•普朗特数
2对流换热
•综上所述，边界层具有以下特征：
•( • a) (b) 流场划分为边界层区和主流区。
•流动边界层：速度梯度较大，动量扩散主要区域。
•热边界层：温度梯度较大，热量扩散的主要区域
• (c) 流态：边界层分为层流边界层和湍流边界层 。湍流边界层分为层流底层、缓冲层与湍流核心。
农业物料学-第五章-2010
Re
dv
fl v
2
St
l vt
v
Fr
自由表面流动
gl
Eu
p
v
空化流
2
Ca
v
E
2
体积弹性模量
We
v l
2
自由表面流动 表面张力系数
三、边界层
边界层：又称附面层，是指贴近固体壁面附近的一部分流动区域，在 这部分区域中，速度由固体壁面处的0发展到接近来流的速 度，一般定义为在边界处的流速达到来流流速的99%。在 这部分区域中，由于厚度很小，故速度急剧变化，速度梯 度很大，流体的粘性效应也主要体现在这一区域中。 边界层分类：边界层内的流动也分为层流和紊流，相应的也分为层流 边界层和紊流边界层。对于又有层流又有紊流的边界层又 称为混合边界层。
一、阻力及阻力系数
流体阻力： 升力： 阻力：
F 1 2 cA f v
2
FL
1 2 1 2
cL A f v cr A f v
2
Fr
2
F— 阻力 A— 物体在垂直于相对速度方向上的投影面积 v — 流体与物体的相对速度 c — 阻力系数，与物料形状、表面状态、流体流动状态 等有关 ρf—液体密度
2
Velocity
time
u∞
o o′ u o′′
OL
u b′
b
Zx
c
Boundary-layer thickness Turbulent flow in boundary layer Laminor flow in boundary layer Onset of turbulence
Z′x
Re Re≤1
c
dv
fl v
2
St
l vt
v
Fr
自由表面流动
gl
Eu
p
v
空化流
2
Ca
v
E
2
体积弹性模量
We
v l
2
自由表面流动 表面张力系数
三、边界层
边界层：又称附面层，是指贴近固体壁面附近的一部分流动区域，在 这部分区域中，速度由固体壁面处的0发展到接近来流的速 度，一般定义为在边界处的流速达到来流流速的99%。在 这部分区域中，由于厚度很小，故速度急剧变化，速度梯 度很大，流体的粘性效应也主要体现在这一区域中。 边界层分类：边界层内的流动也分为层流和紊流，相应的也分为层流 边界层和紊流边界层。对于又有层流又有紊流的边界层又 称为混合边界层。
一、阻力及阻力系数
流体阻力： 升力： 阻力：
F 1 2 cA f v
2
FL
1 2 1 2
cL A f v cr A f v
2
Fr
2
F— 阻力 A— 物体在垂直于相对速度方向上的投影面积 v — 流体与物体的相对速度 c — 阻力系数，与物料形状、表面状态、流体流动状态 等有关 ρf—液体密度
2
Velocity
time
u∞
o o′ u o′′
OL
u b′
b
Zx
c
Boundary-layer thickness Turbulent flow in boundary layer Laminor flow in boundary layer Onset of turbulence
Z′x
Re Re≤1
c
第五章 边界层
对于实际流体的流动，无论流动形态是层流还是紊流，真正能求解的问题很少。
这主要是由于流体流动的控制方程本身是非线性的偏微分方程，处理非线性偏微分方程的问题是当今科学界的一大难题，至今还没有找到一套完整的求解方案。
但在实际工程中的大多数问题，是流体在固体容器或管道限定的区域内的流动，这种流动除靠近固体表面的一薄层流体速度变化较大之外，其余的大部分区域内速度的梯度很小。
对于具有这样特点的流动，控制方程可以简化。
首先，由于远离固体壁面的大部分流动区域流体的速度梯度很小，可略去速度的变化，这部分流体之间将不考虑粘性力的存在，视为理想流体，用欧拉方程或伯努利方程就可求解。
而靠近固体壁面的一个薄层——称为流动边界层，在它内部由于速度梯度较大，不能略去粘性力的作用，但可以利用边界层很薄的特点，在边界层内把控制方程简化后再去求解。
这样对整个区域求解的问题就转化为求解主流区内理想流体的流动问题和靠近壁面的边界层内的流动问题。
第一节边界层理论的基本概念一、边界层的定义流体流经固体表面时，靠近表面总会形成一个薄层，在此薄层中紧贴表面的流体流速为零，但在垂直固体表面的方程（法向）上速度增加得很快，即具有很大的速度梯度，甚至对粘度很小的流体，也不能忽略它表现出来的粘性力。
（因此，流体在绕流过固体壁面流动时，紧靠固体壁面形成速度梯度较大的流体薄层称为边界层。
）而在此边界层外，流体的速度梯度很小，甚至对粘度很大的流体，其粘性力的影响也可忽略，流体的流速与绕流固体表面前的流速v0一样。
可以把这部分在边界层外流动的流体运动视为理想流体运动，不考虑粘性力的影响。
边界层内、外区域间没有明显的分界面，而把边界层边缘上的流体流速v x视为v x=0.99v0，因此从固体表面至v x=0.99v0处的垂直距离视为边界层的厚度δ。
二、边界层的形成与特点边界层内的流动可以是层流，也可以是带有层流底层的紊流，还可以是层流、紊流混合的过渡流。
评判边界层层流或紊流的参数为雷诺数Re=vxρ/η，式中v为边界层外边界上流体流速，x为距边界层起点的距离（即流体进入平板的长度）。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
uz uz ( r , z )
②边界层沿层增厚
(z)
③ 流体在管中心加速
第五章 边界层流动 ghp
III．在交汇点之后的边界层流动， 称为充分发展的边界层。 其特征： ① 一维运动：
uz uz ( r )
ur 0
d ② 边界层层厚不再沿程变化为： 2
③ 速度分布不再变化
可能是 抛物线分布 （层流），可能是指数分布（湍流）
第五章 边界层流动
郎格哈尔针对圆管导出进口段长度 Le 的表达式 ：
Le 0.0575 Re d d
层流：
湍流：
式中：
Le 25 40 d
Red dub
第五章 边界层流动 ghp
3．边界层的分离
1）分离现象 2）分离条件 3）分离后果
正是基于上述理由，人们可以在流动分离之前， 对流动加以某种干扰，使这种转化提前发生。 例如在圆球前嵌以金属丝以干扰边界层的流动， 使得边界层从层流转变为湍流，致使阻力系数 显著降低。 因此就有了粗糙圆球的阻力反而小于光滑球的 结果。
4．边界层概念的适用范围
（1）当局部雷诺数Re较小，如≤100时，
由图可见: 在Re较小情况下，边界层呈层流状态，分离点发生在 物体的最大截面处前，在物体后面形成较宽的分离区， 因此相应的压差阻力系数较大。 当Re增加到一定数值后，在流动分离之前的边界层就 可能由层流转变为湍流。 而湍流的强烈混合效应使得分离点后移。此时，虽然 在未分离的区域中摩擦阻力有所增加，但物体后面的 脱体区变窄，从而压差阻力大为下降。 这就是圆柱在Re≈5×105处和圆球在Re≈3×105处阻力 系数突然下降的原因。
现以流体绕长圆柱流动为例，考察边界层分离 的大致过程，见图4-7。
A
E
先考察边界层外压力的变化。由于层薄，层外压力可不 经过改变（损失）的直接传至边界层内，所以层内压力 将随层外压力改变而改变。
在 M 点之前，如 A 点，由于流道截面减小流速加大， 压力变小，即： 如上图所示：
（减压区），流体质点受力情况 p 0 x
粗糙平板
在实际情况下通过做实验加以确定，但其趋势是可以 预测 ，如入口端越钝（就比锐角，圆角临界值大）、 壁面越粗糙、来流速度越大 ，临界距离越大。
在计算上有时为简便起见，当长度方向远大于xc，近 似认为流动直接进入湍流边界层，不考虑层流和过渡 区的影响。
第五章 边界层流动 ghp
2）沿圆管流动的边界层发展
边界层理论不再适用。 （2）一般说来边界层理论只适用分离点 以前。在分离点的下游，由于边界层厚 度大幅度增加，边界层理论因而失效。
第五章 边界层流动
二、沿平板边界层动量微分方程
---- Prandtl 边界层方程
1.
问题的提出 2. 边界层方程的建立 3. 方程的求解 4. 求解结果分析
边界层层外的整个流动区域称为外部流动区域 在该区域内速度梯度（或认为粘度）极小 故认为流动趋于无粘性的理想流体运动。
u x 0 y
0
第五章 边界层流动 ghp
2．速度边界层的发展
1) 沿平板流动
以平板为例讨论边界层的发展情况，见 4-1 图
图4－1 速度边界层的发展过程
第五章 边界层流动 ghp
C .E .
N . S .( x )
ux u y uz + + 0 x y z
uz 0
ux ux ux ux + [ux + uy + uz ] t x y uz uz 0 稳定
2 ux 2 ux 2 ux p g x + ( 2 + + ) 2 2 x x y z 忽略重力 沿平板 量级分析 与 z 无关
如流体以均匀一致的流速流过封闭管道 时，将在管壁形成边界层，并逐渐加厚 直至管中心交汇。
现以圆管内的管流为例，对进口段边界 层的形成与发展过程做一讨论。 沿圆管流动的边界层发展
第五章 边界层流动 ghp
交汇点
进口段长度
图4－5 管进口段的边界层形成与发展
第五章 边界层流动 ghp
18
当流体流经圆管时：
粗糙球的所受阻力与 光滑球所受的阻力哪个更大？
第五章 边界层流动
高尔夫球
从前，有个高尔夫球运动爱好者（同时也是高尔夫球 制造商）为赢得对手，他经常想怎样才能使高尔夫球 打得又快又远又省力。 在一次偶尔的练习机会中，他发现在同样的一击中， 一个已经变得粗糙的高尔夫球比一个新的光滑球飞得 更远，反复的试验证实这并不是偶然现象。 在这一现象的启发下，他制造出一种带有窝纹的高尔 夫球(人造粗糙球)。这种窝纹球一经推出好评如潮， 得到大批定单。 当时人们没能解释这一奇怪现象——粗糙圆球的阻力 反而小于光滑球的阻力。
第五章 边界层流动 ghp
42
简化后的动量传递方程组
通过对方程的简化和量级分析，得到了 适用于边界层内的动量传递方程组
C .E .
N . S .( x )
u x u y + 0 x y
ux ux ux ux + uy v 偏微分方程 2 x y y
图4-1 平板壁面上边界层的形成
第五章 边界层流动 ghp
6
无限大平板上的速度分布
机翼上的速度分布
第五章 边界层流动
分析实验测得的速度分布发现，整个流 场可以明显地分成性质很不相同的两个 流动区域： 1）边界层层内流动 2）边界层层外流动
第五章 边界层流动 ghp
1）边界层流动
边界层内流动特征为：
: L 1 : 100
边界层厚度定义：
边界层厚度有各种不同的定义，根据需要选取。
本课程采用边界层约定厚度定义
其概念是当层内的速度达到来流速度的99%时，即认为
达到了边界层外沿，其距壁面的位置即为边界层厚度
表达式为：
yu
x
u0
0.99
第五章 边界层流动 ghp
2）边界层层外流动
第五章
边界层流动
边界层理论是普朗特 (Prandtl) 于1904年创 立的，由于它的应用性极为广泛，发展极为 迅速，现已成为粘性流体力学的主要发展方 向之一。 边界层理论的主要任务是研究物体在流体 中运动时所受到的摩擦阻力，物体与流体间 的热质交换。 最早提出的边界层概念是速度边界层。此 后的温度边界层和浓度边界层都是在速度边 界层基础上建立的。
第五章 边界层流动
沿物体表面切向速度和沿法线速度梯度变化，见图4-6所示。
在A点处，壁面切向速度为零，法线上的速度梯度大于零；
在E点处壁面速度为零，法线上的速度梯度小于零； 在S点处壁面速度为零，位于曲面法线上的速度梯度也为零； 在SD线上，质点的速度变为零； 在DSE区域内，速度改变方向，在边界层内产生倒流。
12
由图可见，在沿平板流动时，边界层的发展经历了三个阶段。
层流边界层： 0 x x c
在此区域内流体呈有规则的层状流动。 xc 为临界距离，对应的边界层厚度称为临界厚度 c
过渡区：
在该区域内出现不规则涡团运动，流线不再完全是层流状。
湍流边界层：
涡团运动加剧，流线受到剧烈扰动，流动由层流转变为湍流。
2 因为， D + u p S 2 所以此时所有的流体质点沿着流动方向，贴壁面 向前运动。
第五章 边界层流动 ghp
边界层分离示意图
M 点之后，此时由于流道截面变大流速变小，压力沿程
增加进入增压区，即：
p / x 0
流体质点的受力情况，如上图所示。 随着流道截面的增加，反向压差不断增大，最终使得质点 的动能消耗殆尽 ，转而向后运动。而后退的质点又被向前 运动的流体顶住，最终被挤出边界层进入流体内部，形成 一脱体运动现象 ，见图，这一过程称为边界层分离。
I．从入口处建立起边界层，并由四壁同时向管中心发展， 直至交汇于管中心，此时管内流体都处于边界层中。 交汇点离管口距离Le，称为进口段长度。 管内边界层沿程发展情况与沿平板发展不同。
下面根据交汇点前后的特点加以叙述
II. 在交汇点之前的边界层流动称为
正在发展的边界层
其特征：
① 二维运动
ur ur (r , z )
在湍流边界层内，流型并不完全一样：
在紧贴壁面的流层内，剪切应力足以克服涡团的影响， 该层内仍保持层流流动称为层流内层或层流底层。 在层流内层与湍流边界层之间，流体的流动既非层流， 又非完全的湍流，该层称为缓冲层 。 在缓冲层之外的湍流边界层可称为湍流核心层 。
第五章 边界层流动 ghp
① 紧贴物面非常薄的一层区域称为边界层。
P107
在该区域内速度分量
ux 变化非常迅速
因此尽管粘度很小，但因速度梯度极大，导致粘性 应力大，尤其在壁面处。 所以在边界层内粘性力的作用与惯性力同等重要。 由于速度 ux 变化迅速，随着离壁面距离的增加，速
② 层厚非常薄
度迅速恢复到来流速度u0 ，所以边界层的厚度很薄。 通常层厚与前端的距离之比约为：
随着边界层理论的出现，人们揭开了这
个迷底。 现借助于绕长圆柱绕流的实验结果说明 这一现象。
图5-7给出的是由实验得到的圆球和圆柱
阻力系数对雷诺数变化的关系曲线。
阻 力 系 数 突 然 缩 小 柱 ：Re≈5×105 球：Re≈3×105
阻力系数对雷诺数变化的曲线
第五章 边界层流动 ghp
2) 分离条件
①定性分析 所谓边界层分离，顾名思义就是指原来紧贴
壁面运动的边界层流动在某些条件下，脱离壁 面而进入外部流场。 分离出来的流体在物体后面形成尾涡区，从而 产生很大的尾部阻力。 因此有必要研究边界层为什么会从物面分离， 又应该如何防止或推迟分离。 边界层分离