公约数与公倍数的比较
第1讲 公倍数 公约数

第1讲最大公约数、最小公倍数分解质因数一个自然数的因数中,为质数的因数叫做这个数的质因数。
把一个合数,用质因数相乘的形式表示出来,叫做分解质因数。
例如:24=2×2×2×3,75=3×5×5。
例题1:把18个苹果平均分成若干份,每份大于1个,小于18个。
一共有多少种不同的分法?分析:先把18分解质因数:18=2×3×3,可以看出:18的约数是1、2、3、6、9、18,除去1和18,还有4个约数,所以,一共有4种不同的分法。
练习:1,有60个同学分成人数相等的小组去慰问解放军叔叔,每组不少于6人,不多于15人。
有哪几种分法?60=2×2×3×5;6,10,12,152,195个同学排成长方形队伍做早操,行数和列数都大于1,共有几种排法?195=5×39=3×5×133,甲数比乙数大9,两个数的积是792,求甲、乙两数分别是多少。
792=2×396=2×2×2×3×3×11,33,24例题2:一个长方体木块,长2.7米,宽1.8分米,高1.5分米。
要把它切成大小相等的正方体木块,不许有剩余,正方体的棱长最大是多少分米?分析 2.7米=270厘米,1.8分米=18厘米,1.5分米=15厘米。
要把长方体切成大小相等的正方体,不许有剩余,正方体的棱长应该是长、宽、高的公约数。
现要求正方体的棱长最大,所以棱长就是长、宽、高的最大公约数。
(270,18,15)=3,3厘米=0.3分米练习:1,一个长方体木块的长是4分米5厘米、宽3分米6厘米、高2分米4厘米。
要把它切成大小相等的正方体木块,不许有剩余,求所切正方体木块的棱长最长是多少厘米?45cm,36cm,24cm,45=3×3×5,36=2×2×3×3,24=2×2×2×33厘米2,有50个梨,75个橘子和100个苹果,要把这些水果平均分给几个小组,并且每个小组分得的三种水果的个数也相同,最多可以分给几个小组?50=2×5×5,75=3×5×5,100=2×2×5×5,25个小组3,五年级三个班分别有24人、36人、42人参加体育活动,要把他们分成人数相等的小组,但各班同学不能打乱,最多每组多少人?每班各可以分几组?6人例题3:有三根钢管,它们的长度分别是240厘米、200厘米和480厘米,如果把它们截成同样长的小段,每小段最长可以是多少厘米?分析要把三根钢管截成同样长的小段,每小段的长度数应该是240、200和480的公约数,而每小段要取最长,也就是求240、200和480的最大公约数。
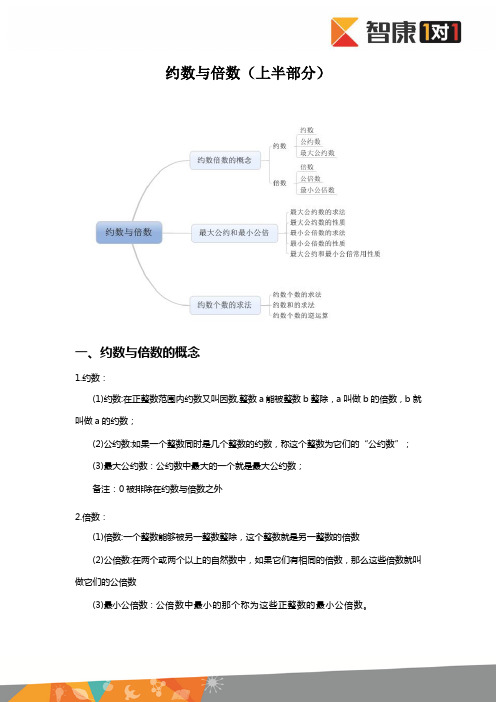
约数与倍 约数与倍 数
0 ;所以 1515 和 600 的最大公约数是
15. (适用于数比较大,不容易直接找到约数的时候) 分数求公约: 先把带分数化成假分数,其他分数不变;求出各个分数的分母的最小公倍数 a;求出各 个分数的分子的最大公约数 b; 2.最大公约数的性质: ①几个数都除以它们的最大公约数,所得的几个商是互质数; ②几个数的公约数,都是这几个数的最大公约数的约数;
例题 2:一个自然数,它的最大的约数和次大的约数的和是 111,这个自然数是________. 【考点】约数 【难度】3 星 【题型】填空
【关键词】2007 年,第十二届,华杯赛,六年级,决赛,第 7 题 【答案】因为 111 是奇数,而奇数=奇数+偶数,所以所求数的最大约数与次大约数必为 一奇一偶。而一个数的最大约数是其自身,而一个数如有偶约数此数必为偶数,而一个偶数 1 的次大约数应为这个偶数的 ,设这个次大约数为 a,则最大约数为 2a,a+2a=111,求 2 得 a=37,2a=74,即所求数为 74。
b 即为所求. a
③几个数都乘以一个自然数 n , 所得的积的最大公约数等于这几个数的最大公约数乘以
n.
例题 1:2004 的约数中,比 100 大且比 200 小的约数是 【考点】约数 【难度】1 星 【题型】填空
。
【关键词】2004 年,希望杯,第二届,五年级,初赛,第 4 题,5 分 【答案】2004=3×4×167,所以结果为 167
例题 5: N 为自然数,且 N 1 , N 2 、……、 N 9 与 690 都有大于 Biblioteka 的公约数. N 的最 小值为多少?
第五讲--最大公约数与最小公倍数

第五讲 最大公约数与最小公倍数【知识导引】一、约数的概念与最大公约数约数又叫因数(在正整数范围内)整数a 能被整数b 整除,a 叫做b 的倍数,b 就叫做a 的约数。
最大公约数:如果一个数既是数a 的约数,又是数b 的约数,称为[a,b]的约数。
几个数公有的因数,叫做这几个数的公因数,其中最大的一个叫做这几个数的最大公因数。
1. 求最大公约数的方法①分解质因数法:先分解质因数,然后把相同的因数连乘起来。
例如:2313711=⨯⨯,22252237=⨯⨯,所以(231,252)3721=⨯=;②短除法:先找出所有共有的约数,然后相乘。
例如:2181239632,所以(12,18)236=⨯=;③辗转相除法:每一次都用除数和余数相除,能够整除的那个余数,就是所求的最大公约数。
用辗转相除法求两个数的最大公约数的步骤如下:先用小的一个数除大的一个数,得第一个余数;再用第一个余数除小的一个数,得第二个余数;又用第二个余数除第一个余数,得第三个余数;这样逐次用后一个余数去除前一个余数,直到余数是0为止。
那么,最后一个除数就是所求的最大公约数(如果最后的除数是1,那么原来的两个数是互质的)。
例如,求600和1515的最大公约数:151********÷=L ;6003151285÷=L ;315285130÷=L ;28530915÷=L ;301520÷=L ;所以1515和600的最大公约数是15。
2. 最大公约数的性质①几个数都除以它们的最大公约数,所得的几个商是互质数;②几个数的公约数,都是这几个数的最大公约数的约数;③几个数都乘以一个自然数n ,所得的积的最大公约数等于这几个数的最大公约数乘以n 。
3. 求一组分数的最大公约数先把带分数化成假分数,其他分数不变;求出各个分数的分母的最小公倍数a ;求出各个分数的分子的最大公约数b ;b a即为所求。
二、倍数的概念与最小公倍数对于整数m ,能被n 整除(n/m ),那么m 就是n 的倍数。
思维数学-公约数与公倍数初步

公约数与公倍数初步知识精讲公约数就是几个数公共的约数,其中最大的一个称为最大公约数;公倍数就是几个数公共的倍数,其中最小的一个称为最小公倍数特别地,1为所有数的公约数。
1、2、3和6都是24和30的公约数,6是最大公约数。
可以发现1、2、3和6都是6的约数。
12和18的公倍数有36,72,108,。
其中36是最小公倍数。
可以发现36、72、108及其他公倍数都是36的倍数。
通常,我们把两个数a、b的最大公约数记为(a,b);a、b的最小公倍数记为[a,b]。
三个数a、b、c的最大公约数记为(a,b,c);a、b、c的最小公倍数记为[a,b,c]如:14和21的最大公约数是7,记作:(14,21)-7;14和21的最小公倍数是42,记作:[14,21]=42。
15、10、21的最大公约数是1,记作:(15,10,21)=1;15、10、21的最小公倍数是210,记作:[15,10,21]=210。
在现实生活中我们常常关心几个数的最大公约数和最小公倍数,那么我们怎样来求几个数的最大公约数和最小公倍数呢?除了直接枚举之外,还有以下几种:短除法、分解质因数法、辗转相除法。
计算两个数的最大公约数及最小公倍数,最常用的方法是短除法。
例题1用短除法计算:(1)(54,90),[54,90];(2)(45,75,90)。
「分析」熟练掌握短除法即可。
练习1用短除法计算:(1)(36,48),[36,48];(2)(28,42,70)。
分解质因数法比较实用,也利于我们分析数的构成。
例题2利用分解质因数法找出下列各组数的最大公约数和最小公倍数。
(1)144和250(2)240、80和96「分析」熟练掌握分解质因数法即可。
练习2利用分解贡因数法找出下列各组数的最大公约数和最小公倍数。
(1)1024和72(2)60、84、90和700如果两个数都比较大,不容易看出来它们的质因数那我们还有第三种方法:辗转相除法。
例题3利用辗转相除法求下列各组数的最大公约数。
最大公约数与最小公倍数的应用

最大公约数与最小公倍数的应用最大公约数(Greatest Common Divisor,简称GCD)和最小公倍数(Least Common Multiple,简称LCM)是数学中常见的概念,在数论和代数学中具有广泛的应用。
它们能够帮助我们解决很多实际问题,从分数化简到找出最优解,都离不开最大公约数和最小公倍数的运用。
本文将详细介绍最大公约数和最小公倍数的定义、计算方法以及一些实际应用案例。
一、最大公约数的定义和计算最大公约数指的是两个或多个整数能够整除的最大的正整数。
如果两个数a和b的最大公约数为d,则表示为GCD(a,b)= d。
最大公约数的计算可以使用欧几里得算法(Euclidean Algorithm)来进行。
欧几里得算法的原理是:假设有两个正整数a和b,其中a > b。
首先,用a除以b得到余数r1,即r1 = a % b。
然后,再用b除以r1得到余数r2,即r2 = b % r1。
接着,再用r1除以r2得到余数r3,以此类推,直到余数为0。
此时,上一步得到的余数r2就是a和b的最大公约数。
例如,求解最大公约数GCD(24,36):24 ÷ 36 = 0 余数2436 ÷ 24 = 1 余数1224 ÷ 12 = 2 余数0因此,GCD(24,36)= 12。
二、最小公倍数的定义和计算最小公倍数是指两个或多个整数的公共倍数中最小的正整数。
如果两个数a和b的最小公倍数为l,则表示为LCM(a,b)= l。
最小公倍数的计算可以通过最大公约数来进行。
最小公倍数与最大公约数的关系是:两个数的乘积等于它们的最大公约数与最小公倍数的积。
即 a × b = GCD(a,b)× LCM(a,b)。
利用这个关系可以得到计算最小公倍数的公式:LCM(a,b)= (a × b)/ GCD(a,b)。
例如,求解最小公倍数LCM(24,36):24 × 36 = 864GCD(24,36)= 12因此,LCM(24,36)= 864 / 12 = 72。
五年级最大公约数和最小公倍数

一、基本概念和知识1.公约数和最大公约数几个数公有的约数,叫做这几个数的公约数;其中最大的一个,叫做这几个数的最大公约数。
例如:12的约数有:1,2,3,4,6,12;18的约数有:1,2,3,6,9,18。
12和18的公约数有:1,2,3,6.其中6是12和18的最大公约数,记作(12,18)=6。
2.公倍数和最小公倍数几个数公有的倍数,叫做这几个数的公倍数;其中最小的一个,叫做这几个数的最小公倍数。
例如:12的倍数有:12,24,36,48,60,72,84,…18的倍数有:18,36,54,72,90,…12和18的公倍数有:36,72,….其中36是12和18的最小公倍数,记作[12,18]=36。
3.互质数如果两个数的最大公约数是1,那么这两个数叫做互质数。
二、例题例1 用一个数去除30、60、75,都能整除,这个数最大是多少?分析∵要求的数去除30、60、75都能整除,∴要求的数是30、60、75的公约数。
又∵要求符合条件的最大的数,∴就是求30、60、75的最大公约数。
解:∵(30,60,75)=5×3=15这个数最大是15。
例2 一个数用3、4、5除都能整除,这个数最小是多少?分析由题意可知,要求的数是3、4、5的公倍数,且是最小的公倍数。
解:∵[3,4,5]=3×4×5=60,∴用3、4、5除都能整除的最小的数是60。
例3 有三根铁丝,长度分别是120厘米、180厘米和300厘米.现在要把它们截成相等的小段,每根都不能有剩余,每小段最长多少厘米?一共可以截成多少段?分析∵要截成相等的小段,且无剩余,∴每段长度必是120、180和300的公约数。
又∵每段要尽可能长,∴要求的每段长度就是120、180和300的最大公约数.(120,180,300)=30×2=60∴每小段最长60厘米。
120÷60+180÷60+300÷60=2+3+5=10(段)答:每段最长60厘米,一共可以截成10段。
最大公约数和最小公倍数的比较
不同点
把所有的除数乘起 来.
把所有的除数和商乘起来.
求两个数的最大公约数和最小公倍数的区别
两个数的最大公约数是它们的公约数中最大 的,它必须包含两个数全部公有的质因数. 所有除数正好是两个数全部公有的质因数, 所以,求最大公约数就要把所有除数乘起 来.
求两个数的最大公约数和最小公倍数的区别
最小公倍数既要包含两个数全部公有的质因数, 又要包含各自独有的质因数.两个数的商分别 是它们独有的质因数.所以求两个数的最小公 倍数要把所有的除数和商乘起来.
最大公约数和最小公倍数的
比
李有琼
较
小学数学第十册
复习 1、下面的数,哪些能被2整除?哪些能被3整除?哪些能被5整除?
5 28
能被2整除的数: 28 能被3整除的数: 42 能被5整除的数: 5 25 42
25
42
2、从上面数中选出分别符合下列条件的几组数,求出各组 数的最大公约数和最小公倍数,并说明是怎么求出的? A、较大数是较小数倍数的: 5 和 25 B、两个数是互质数的: 5和28 和 5 和 42 C、两个数既不互质,较大数又不是较小数倍数的: 28 和 42 28和25 和 25和42 和
练习 很快说出下面每组数的最大公约数和最小公倍 数. 9和15 9和27 7和21 7和12 最大公约数是3,最小公倍数45 最大公约数是9,最小公倍数27 最大公约数是7,最小公倍数21 最大公约数是1,最小公倍数84
修改 因为 7和12是互质数
所以 7和12的最大公约数是1 7和12的最小公倍数是7×12=84
练习 很快说出下面每组数的最大公约数和最小公倍 数. 3和5 最大公约数是1,最小公倍数15 4和6 最大公约数是2,最小公倍数12
最大公约数与最小公倍数比较1
求出下面每组数的最大公约数。 9和30 8和26 17和51 提出: ①什么是最大公约数? ②你是怎样求出每组数的最 大公约数的?
求出下面每组数的最小公倍数。
11和7 10和25 91和13 36和60 ①什么是最小公倍数?
②你是怎样求出每组数的最小公 倍数ห้องสมุดไป่ตู้?
求 28 和 42 的 最 大 公 约 数 和 最 小 公 倍 数 。
1、既能被6整除,又能被9整除的数, 最小是多少?
2、既能整除30,又能整除45的数, 最大是多少?
3、一个数用3、8、10去除,都能整 除,这个数最小是多少?
有两根木棒,分别长12厘米、20厘 米,要把它们截成同样长的小段, 不能有剩余,每根最长多少厘米?
因为求两个数的最小公倍数时,不仅 要包含两个数公有的质因数,还要包 含各自独有的质因数。因此,求两个 数的最小公倍数要把除数和商连乘起 来。
1. 完成例5下面的“做一做”。 2. 完成练习十六的第2题。
分别求出下面每组数的最 大公约数 最小公倍数。
9和12 10和18 13和52 72和26 15和80 8和11
求最大公约数和最小公倍数的 相同点与不同点:
求两个数的最大 求两个数的最小
公约数
公倍数
相同 点
用短除的形式分 解质因数,直到 两个商是互质数
用短除的形式分 解质因数,直到 两个商是互质数
为止。
为止。
不 同 把 所 有 的 除 数 乘 所有的除数和商
点
起来
乘起来。
为什么求最小公倍数要把除数和商连 乘起来?
总结归纳:
(1) 求两个数的最大公约数:一般 先用这两个数公有的质因数连续去 除,一直除到所得的商是互质数为 止,然后把所有的除数连乘起来.
公约数与公倍数的比较课件
计算公约数的方法
辗转相除法
通过不断用大数除以小数,再用 小数去除下一个小数,直到小数 变为1,此时的除数就是最大公
约数。
质因数分解法
将每个数分解为质因数的乘积, 然后找出公共的质因数,将它们
相乘即可得到最大公约数。
特殊值法
对于某些特殊情况,如求两个数 的最大公约数,可以选取一个特 殊值,如两数的差或两数的乘积 ,再通过这些特殊值找到最大公
公约数与公倍数 的比较课件
目录
• 公约数与公倍数的定义 • 公约数的性质与计算 • 公倍数的性质与计算 • 公约数与公倍数的比较 • 实例分析 • 总结与思考
01
公约数与公倍数的定义
公约数的定义
公约数是两个或多个 整数共有的约数。
一个数如果是另一个 数的约数,则称该数 为另一个数的因数。
公约数只考虑正整数 ,不考虑负数和零。
最大公倍数
总结词
最大公倍数是两个或多个整 数的最大的公共倍数。
详细描述
最大公倍数是两个或多个数 的公共倍数中最大的那个, 它可以表示为两个数的乘积 除以它们的最大公约数。
举例
对于数字8和12,它们的最 大公倍数是24。
应用
最大公倍数在解决实际问题 中有着广泛的应用,如周期 性事件的时间计算、分数化 简等。
02
公约数的性质与计算
最大公约数
最大公约数定义
两个或多个整数共有的最大的正整数约数。
最大公约数的性质
它是所有公约数中最大的一个,且所有公约数都是它的约数。
最大公约数的计算方法
辗转相除法、质因数分解法等。
最小公约数
最小公约数定义
两个或多个整数共有的最小的正 整数约数。
最小公约数的性质
公约数与公倍数
奥数公约数和公倍数知识要点:1、几个数公有的约数,叫做这几个数的公约数。
其中最大的一个叫做这几个数的最大公约数。
2、几个数公有的倍数,叫做这几个数的公倍数。
其中最小的一个叫做这几个数的最小公倍数。
3、求最大公约数和最小公倍数的方法:(1)枚举法;(2)分解质因数法(3)短除法。
4、最大公约数和最小公倍数的关系:两个数的最大公约数和最小公倍数的乘积等于这两个数的乘积。
典例巧解例1、有三根木棒,长度分别是1.5米、2.4米、1.8米,王师傅想把它们截成长度相等的小段。
为了最大限度地利用材料,每小段最长是多少分米?一共可以截成多少段?例2、把一块长357厘米、宽105厘米、高84厘米的长方体木料,锯成同样大小的正方体木料,锯后不许有剩余。
正方体的棱长是多少时,用料最省且小木块的体积总和最大?例3、有一批作业本,无论是平均分给10人、12人还是15人,都剩余4本,这批作业本至少有多少本?例4、甲、乙、丙三人环绕操场步行一周,甲要3分钟,乙要4分钟,丙要6分钟。
三人同时同地同向出发环绕操场走,当他们三人第一次相遇时,他们三人分别走了多少圈?例5、狐狸和兔子进行跳跃比赛,狐狸每次跳412米,兔子每次跳234米,它们每秒钟都跳一次,从起点开始,每隔1238米设有一个陷阱。
当它们其中一个掉进陷阱时,另一个跳了多少米?例6、小胡和小涂计算甲、乙两个两位数的乘积,小胡看错了甲数的个位数字,计算结果为1274;小涂看错了甲数的十位数字,计算结果为819.甲数是多少?例7、A、B两个数都含有质因数3和5,它们的最大公约数是75。
已知A有12个约数,B有10个约数,那么A、B两数的和是多少?例8、两个数的最大公约数是6,最小公倍数是144。
有几组这样的数?这两个数各是多少?例9、有一个三位数,如果这个数加上4,就能被4整除;如果这个数减去5,就能被5整除;如果这个数乘以6,就能被6整除;如果这个数除以7,就能被7整除。
这个数最小是多少?例10、两个不同自然数的和是60,它们的最大公约数与最小公倍数的和也是60,这样的自然数共有多少组?竞赛能级训练A级1、若a=b-1(a, b都是自然数,且a≠0),则a和b的最大公约数是(),最小公倍数是()。
