电路分析第三章答案
数字集成电路分析与设计 第三章答案

CHAPTER 3P3.1. The general approach for the first two parameters is to figure out which variables shouldremain constant, so that when you have two currents, you can divide them, and every variable but the ones you want to calculate remain. In this case, since the long-channel transistor is in saturation for all values of V GS and V DS , only one equation needs to be considered:()()2112DS N OX GS T DS W I C V V V Lμλ=-+ For the last two parameters, now that you have enough values, you can just choose oneset of numbers to compute their final values.a. The threshold voltage, V T0, can be found by choosing two sets of numbers with the same V DS ’s but with different V GS ’s. In this case, the first two values in the table can be used.()()()()()()211122222201022001121121.2 1.210000.82800.8DS N OX GS T DS DS N OX GS T DS T DS T DS T T W I C V V V L W I C V V V LV I V I V V μλμλ=-+=-+-⎛⎫-===⎪--⎝⎭ 00.35V T V ∴=b. The channel modulation parameter, λ, can be found by choosing two sets of numberswith the same V GS ’s but with different V DS ’s. In this case, the second and third values in the table can be used.()()221 1.225010.8247DS DS I I λλ+==+ -10.04V λ∴=c. The electron mobility, µn , can now be calculated by looking at any of the first three sets of numbers, but first, let’s calculate C OX .631062-31m 10μm22?.210μm1m 10 0.0351 1.610/2.210OX OX t C F cm--=⨯⨯===⨯Now calculate the mobility by using the first set of numbers.()()()()()()()()()()()()22111021262101111 1.21 1.222210002cm 348V-s 1.610(4.75)1.20.3510.04 1.21DS N OX GS T DS N OX T DS N OX GS T DS W W I C V V V C V L LA I W C V V V L μλμλμμλ-=-+=-+===⨯-+-+d. The body effect coefficient gamma, γ, can be calculated by using the last set of numbers since it is the only one that has a V SB greater than 0V.()()()()244124414411221 1.20.468VDS N OX GS T DS DS GS T N OX DS GS T T GS W I C V V V LI V V W C V LV V V V μλμλ=-+-=+-==-==12000.6VT T T T V V V V γγγ=+-====P3.2. The key to this question is to identify the transistor’s region of operation so that gatecapacitance may be assigned appropriately, and the primary capacitor that will dischargedat a rate of V It C ∂∂= by the current source may be identified. Then, because the nodes arechanging, the next region of operation must be identified. This process continues until the transistor reaches steady state behavior. Region 1:Since 0V GS V = the transistor is in the cutoff region. The gate capacitance is allocated to GB C . Since no current will flow through the transistor, all current will come from the source capacitor and the drain node remains unchanged.68-151010V V 6.67100.6671510s nsSB V I I t C C -∆⨯====⨯=∆⨯ The source capacitor will discharge until 1.1V GS T V V == when the transistor enters thesaturation region. This would require that the source node would be at 3.3 1.1 2.2V S G GS V V V =-=-=.()15961510 3.3 2.2 1.6510s 1.65ns 1010C t V I ---⨯∆=∆=-=⨯=⨯ Region 2:The transistor turns on and is in saturation. The current is provided from the capacitor atthe drain node, while the source node remains fairly constant. The capacitance at the drain node is the same as the source node so the rate of change is given by:68-151010V V 6.67100.6671510s nsSB V I I t C C -∆⨯====⨯=∆⨯ Since the transistor is now in the saturation region, GS V can be computed based on thecurrent flowing through the device.()22 1.1 1.37V 3.3 1.37 1.93VGS T GST S G GS kW I V V LV V V V V =-==+==-=-=This is where the source node settles. This means that most of the current is discharged through the transistor until the drain voltage reaches a value that puts the transistor at the edge of saturation.3.3 1.1 2.2VDS GS TD G T V V V V V V =-=-=-=If we assume that all the current comes from the transistor, and the source node remains fixed, the drain node will then discharge at a rate equal to that of the source node in the first region. Region 3:The transistor is now in the linear region the gate capacitance is distributed equally to both GS C and GD C . and both capacitors will discharge at approximately the same rate.-151510V0.28621510510nsV I A t C μ-∆===∆⨯⨯+⨯The graph is shown below.00.511.522.533.5024681012Time (ns)V o l t a g e (V )P3.3. The gate and drain are connected together so that DS GS V V = which will cause thetransistor to remain in saturation. This is a dc measurement so capacitances are not required. Connect the bulk to ground and run SPICE. P3.4. Run SPICE. P3.5. Run SPICE. P3.6. Run SPICE. P3.7. Run SPICE.P3.8. First, let’s look at the various parameters and identify how they affect V T .∙ L – Shorter lengths result in a lower threshold voltage due to DIBL. ∙ W – Narrow width can increase the threshold voltage.∙ V SB – Larger source-bulk voltages (in magnitude) result in a higher threshold voltage. ∙ V DS –Larger drain-source voltages (in magnitude) result in a lower threshold voltage due to DIBL. The transistor with the lowest threshold voltage has the shortest channel, larger width, smallest source-bulk voltage and largest drain-source voltage. This would be the first transistor listed.The transistor with the highest threshold voltage has the longest channel, smallest width,largest source-bulk voltage and smallest drain-source voltage. This would be the last transistor listed. P3.9. Run SPICE.P3.10. Run SPICE. The mobility degradation at high temperatures reduces I on and the increasemobile carriers at high temperatures increase I off . P3.11. The issues that prompted the switch from Al to Cu are resistance and electromigration.Copper wires have lower resistances and are less susceptible to electromigration problems. Copper on the other hand, reacts with the oxygen in SiO 2 and requires cladding around the wires to prevent this reaction.For low-k dielectrics, the target value future technologies is 2.High-k dielectrics are being developed as the gate-insulator material of MOSFET’s. This is because the current insulator material, SiO 2, can not be scaled any longer due to tunneling effects.P3.12. Self-aligned poly gates are fabricated by depositing oxide and poly before the source anddrain regions are implanted. Self-aligned silicides (salicides) are deposited on top of the source and drain regions using the spacers on the sides of the poly gate. P3.13. To compute the length, simply use the wire resistance equation and solve for L .LR TWRTWL ρρ==First convert the units of ρ to terms of μm. Aluminum:2.7μΩρ=cm 6Ω10μΩ⨯610μm100cm ⨯()()()0.027Ωμm1000.812963μm 2.96mm0.027RTWL ρ=====Copper:1.7μΩρ=cm 6Ω10μΩ⨯610μm100cm ⨯()()()0.017Ωμm1000.814706μm 4.71mm0.017RTWL ρ=====P3.14. Generally, the capacitance equation in terms of permittivity constants and spacing is:k C WL tε=a. 4k = ()()()()230048.8510 3.541100SiO k k C WL TL t S S Sεε-====b. 2k = ()()()()30028.8510 1.771100k k C WL TL t S SSεε-====The plots are shown below.Capacitance vs. Spacing01234567800.511.522.533.544.555.5Spacing (um)C a p a c i t a n c e (f F)。
电路分析基础第四版课后习题答案
i
i1
+ 1V −
2Ω
i3
i2
1Ω
2i
+ 2V −
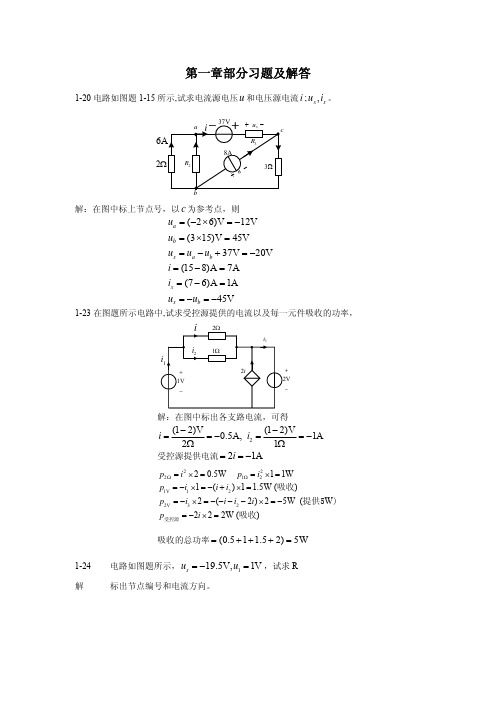
解:在图中标出各支路电流,可得
(1 − 2)V (1 − 2)V = −0.5A, i2 = = −1A 2Ω 1Ω 受控源提供电流 = 2i = −1A i=
p2 Ω = i 2 × 2 = 0.5W
为确定 R,需计算 i4 ,
uce = ucd + ude = 0 ⇒ ude = −ucd = −10u1 = −10V
故
i3 =
udc = −2.5A, i4 = is − i3 = (−3.5 + 2.5)A = −1A 4 R = 0Ω 由此判定
1-33
试用支路电流法求解图题所示电路中的支路电流 i1 , i2 , i3 。
又受控源控制量 i 与网孔电流的关系为 i = i1 − i2
⎧25i1 − 20i2 − 5i3 = 50 ⎪ 代入并整理得: ⎨−5i1 + 9i2 − 4i3 = 0 解得 ⎪−5i − 4i + 10i = 0 2 3 ⎩ 1
受控源电压 受控源功率
⎧i1 = 29.6A ⎨ ⎩i2 = 28A
i2
3Ω
i3
gu
2−5
解
设网孔电流为 i1 , i2 , i3 ,则 i3 = − gu A = −0.1u A ,所以只要列出两个网孔方程
27i1 − 18i2 = 42 −18i1 + 21i2 − 3(−0.1u A ) = 20
因 u A = 9i1 ,代入上式整理得
−15.3i1 + 21i2 = 20
电路分析基础(英文版)课后答案第三章

0 = ¡26i1 ¡ 90i2 + 124i3
[a] Solving, i1 = 5 A; therefore the 80 V source is delivering 400 W to the circuit.
[b] Solving, i3 = 2:5 A; therefore p8− = (6:25)(8) = 50 W
v1 + v1 ¡ v2 = 4:5
1
8
53
54 CHAPTER 3. Techniques of Circuit Analysis
v2 + v2 ¡ v1 + v2 ¡ 30 = 0
12 8
4
Solving, v1 = 6 V v2 = 18 V Thus, i = (v1 ¡ v2)=8 = ¡1:5 A v = v2 + 2i = 15 V
DE 3.8 Use the lower node as the reference node. Let v1 = node voltage across the 7.5 − resistor and v2 = node voltage across the 2.5 − resistor. Place the dependent voltage source inside a supernode between the node voltages v and v2. The node voltage equations are
3
Techniques of Circuit Analysis
Drill Exercises
DE 3.1 [a] 11,8 resistors, 2 independent sources, 1 dependent source
电路分析第三章习题解答
+
10Ω
u1
30Ω
+ uo
78Ω
50V
39Ω
4
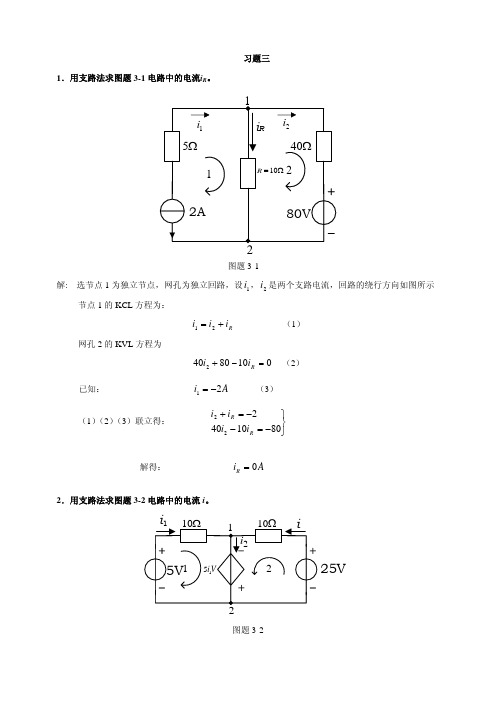
图题 3-11 解:选节点 4 为参考节点,列出节点方程为
u n1 = 50V − 1 1⎞ ⎛ 1 ' u n1 + ⎜ + ⎟u n 2 = −i x 10 ⎝ 30 10 ⎠
(1)
(2)
1 ⎞ ⎛ 1 ' ⎜ + ⎟u n3 = i x 39 78 ⎝ ⎠
50Ω
30Ω
i1 5A
15Ω
30Ω
10Ω
5i 1
图题 3-12 解: (1)原电路等效为下面电路
1
50Ω
2
30Ω
i1 5A
15Ω
30Ω
10Ω
5i1 30
3
选节点 3 作为参考节点,列出节点方程
1 ⎞ 1 ⎛1 u n1 ⎜ + ⎟ − u n 2 = 5 A ⎝ 15 50 ⎠ 50 −
(1)
1 1 1 1 ⎞ 1 ⎛ 1 u n1 + ⎜ + + + ⎟u n 2 = − i1 (2) 50 6 ⎝ 50 30 10 30 ⎠
u n1 = 5i
(1)
1 1 ⎛1 1 1⎞ − u n1 + ⎜ + + ⎟u n 2 − u n3 = 0 (2) 3 6 ⎝3 4 6⎠ 1 30 ⎛1 1⎞ − u n 2 + ⎜ + ⎟u n3 = − ix 6 8 ⎝6 8⎠ u n3 − u n1 = 24
辅助方程: i = (1) (2) (3) (4) (5)联立得: (3)
电路分析试题及答案(第三章)

相量图形:1、下图中,R 1=6Ω,L=0.3H ,R 2=6.25Ω,C=0.012F,u (t)=)10cos(210t ,求稳态电流i 1、i 2和i 3,并画出电路的相量图。
解:V U0010∠= R 2和C 的并联阻抗Z 1= R 2//(1/j ωC )=(4-j3)Ω, 输入阻抗 Z = R 1+j ωL +Z 1 =10Ω,则:A Z U I 0010110010∠=∠== A R Z I I 0211287.368.0-∠== A U C j I 02313.536.0∠== ω 所以:A t i )10cos(21=A t i )87.3610cos(28.02ο-= A t i )13.5310cos(26.02ο+=相量图见上右图2、下图所示电路,A 、B 间的阻抗模值Z 为5k Ω,电源角频率ω=1000rad/s ,为使1U 超前2U 300,求R 和C 的值。
解:从AB 端看进去的阻抗为Cj R Z ω1+=, I213其模值为:Ω=+=k CR Z 5)1(22ω (1) 而2U /1U =)arctan()(112CR CR ωω-∠+由于1U 超前2U 300,所以ωCR =tan300=31 (2)联列(1)、(2)两式得R =2.5k Ω,C =0.231μF3、测量阻抗Z 的电路如下图所示。
已知R=20Ω,R 2=6.5Ω,在工频(f =50Hz)下,当调节触点c 使R ac =5Ω时,电压表的读数最小,其值为30V ,此时电源电压为100V 。
试求Z 及其组成的元件的参数值。
(注意:调节触点c ,只能改变cd U 的实部,电压表读数最小,也就是使实部为零,cd U 为纯虚数,即cdU =±j30V)解:UZR R U R R U ac cd++-=22调节触点c ,只能改变cd U 的实部,其值最小,也就是使实部为零,cd U 为纯虚数,即cdU =±j30V , 因此上式可表示为:±j 30=-25+(100⨯6.5)/(6.5+Z ) 解得:Z=(4.15±j 12.79)Ω 故:R Z =4.15ΩL =40.7mHC =249μF4、电路如下图所示,已知f =1kHz ,U =10V ,U 1=4V ,U 2=8V 。
第3章 电阻电路的一般分析答案
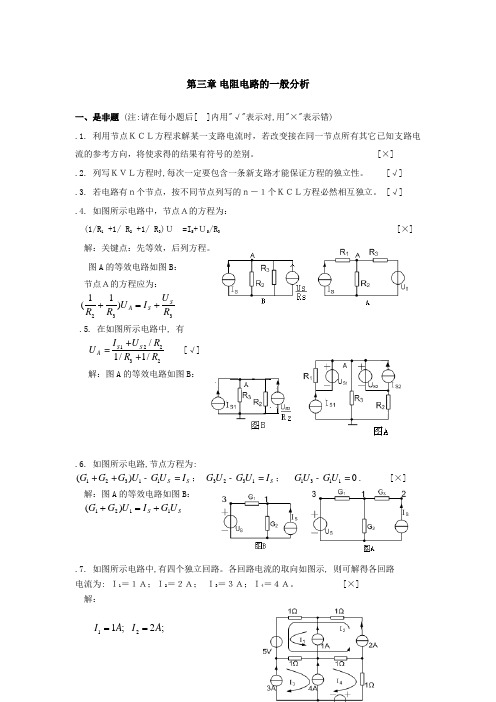
第三章 电阻电路的一般分析一、是非题 (注:请在每小题后[ ]内用"√"表示对,用"×"表示错).1. 利用节点KCL方程求解某一支路电流时,若改变接在同一节点所有其它已知支路电流的参考方向,将使求得的结果有符号的差别。
[×] .2. 列写KVL方程时,每次一定要包含一条新支路才能保证方程的独立性。
[√] .3. 若电路有n个节点,按不同节点列写的n-1个KCL方程必然相互独立。
[√] .4. 如图所示电路中,节点A的方程为: (1/R 1 +1/ R 2 +1/ R 3)U =I S +US /R 3 [×]解:关键点:先等效,后列方程。
图A 的等效电路如图B :节点A的方程应为: 332)11(R U I U R R S S A +=+ .5. 在如图所示电路中, 有 12232/1/1/S S A I U R U R R +=+ [√]解:图A 的等效电路如图B :.6. 如图所示电路,节点方程为:12311()S S G G G U GU I ++-=; 3231S G U G U I -=; 13110GU GU -=. [×]解:图A 的等效电路如图B :S S U G I U G G 1121)(+=+.7. 如图所示电路中,有四个独立回路。
各回路电流的取向如图示, 则可解得各回路 电流为: I1=1A;I2=2A; I3=3A;I4=4A。
[×] 解:;11A I = ;22A I =;33A I = ;7344A I =+=二、选择题(注:在每小题的备选答案中选择适合的答案编号填入该题空白处,多选或不选按选错论).1.对如图所示电路,下列各式求支路电流正确的是 C_。
(A) 12112E E I R R -=+; (B) 222E I R =(C) AB L LUI R =.2. 若网络有b 条支路、n 个节点,其独立KCL方程有_C_个,独立KVL方程有_D__个,共计为_A_个方程。
电路基础第三章
第三章 电路分析的一般方法习题解答3-1 题3-1图所示电路中,已知R 1=R 2=10Ω,R 3=4Ω,R 4=R 5=8Ω,R 6=2Ω,i S1=1Α,u S3=20V ,u S6=40V 。
求各支路电流。
解 以O 点为参考点,选3个网孔作为独立回路,并以顺时针方向作为循行方向,支路电流方程为i 1+i 2+i 6=0- i 2+i 3+i 4=0- i 4+i 5- i 6=0- R 1(i 1+i S1)+R 2i 2+R 3i 3=- u S3- R 3i 3+R 4i 4+R 5i 5=u S3- R 2i 2- R 4i 4+R 6i 6=- u S6代入已知条件得i 1+i 2+i 6=0- i 2+i 3+i 4=0- i 4+i 5- i 6=0- 10i 1+10i 2+4i 3=- 20+10- 4i 3+8i 4+8i 5=20- 10i 2- 8i 4+2i 6=- 40解方程得i 1=1.85A , i 2=1.332A , i 3=- 1.207Ai 4=2.539A ,i 5=- 0.643A ,i 6=- 3.182A3-2 题3-2图所示电路,各元件参数同题3-1。
求各支路电流。
解 以O 点为参考点,选独立回路时,回避无伴电流源所在的网孔,选另外两个网孔为独立回路,以顺时针方向作为回路绕行方向,可得下列支路电流方程R 5 R 4 i 1 i 2 i 6 + U R 6 u S6 i 3 i 4 i 5 R 1 R 2 R 3 i S1 + - u S3 0题3-1图 - U R 6 R 5R 4i 2 i 6 + u S6 i 3i 4 i 5 R 2 R 3i S1 + u S3 -- i S1+i 2+i 6=0- i 2+i 3+i 4=0- i 4+i 5- i 6=0- R 3i 3+R 4i 4+R 5i 5=u S3- R 2i 2- R 4i 4+R 6i 6=- u S6 代入已知条件得- 1+i 2+i 6=0- i 2+i 3+i 4=0- i 4+i 5- i 6=0- 4i 3+8i 4+8i 5=20- 10i 2- 8i 4+2i 6=- 40解方程得i 2=2.2143A , i 3=0.2857A , i 4=1.9286Ai 5=0.7143A , i 6=- 1.2143A3-3 题3-3图所示电路,已知R 1=10Ω,R 2=15Ω,R 3=20Ω,R 4=4Ω,R 5=6Ω,R 6=8Ω,u S2=10V ,u S3=20V ,求各支路电流。
电路分析答案第三章
第三章习题3。
1 如题3.1图所示梯形电路。
⑴ 已知24u V =,求1u 、i 和S u 。
⑵ 已知27S u V =,求1u 、2u 和i 。
⑶ 已知 1.5i A =,求1u 和2u . 解:根据线性电路的性质,设:211u k u = 22u k i = 23s u k u =令: 2V u 2= 可推出 6V u 2= 1A i = 27V u s = 因而可得: 3k 1= 0.5k 2= 27/2k 3= ⑴ 当24u V =时,有: 12V 43u 1=⨯= 2A 40.5i =⨯= 56V 4227u s =⨯=⑵ 当27S u V =时,有: 2V 27272u k 1u s 32=⨯==1A 20.5u k i 22=⨯== 6V 23u k u 211=⨯== ⑶ 当 1.5i A =时,有: 3V 1.50.51i k 1u 22=⨯==9V 33u k u 211=⨯==3。
2 如题3。
2图所示电路,已知9S u V =,3S i A =,用叠加定理求电路i 。
解:S u 单独作用时,有: 1163Su i A ==+ S i 单独作用时,有: 23163S i i A =-=-+ 根据叠加定理可得: 12110i i i =+=-=3.3 如题3.3图所示电路,求电压u .如独立电压源的值均增至原值的两倍,独立电流源的值下降为原值的一半,电压u 变为多少?解:根据KVL 列一个回路113132(32)4u i V A A i =Ω⨯++⨯Ω+-⨯Ω 两个电压源支路可列方程:1131(3)610i i +=-+ 由此可得: 13i A =代入上式得: 33132(323)44u V =⨯++⨯+-⨯⨯=若独立电压源的值均增至原值的两倍,独立电流源的值下降为原值的一半,由上式可知:1132(1.5)620i i +=-+ 解得 13i A = 有: 332 1.52(1.523)44u V =⨯++⨯+-⨯⨯=-3.4 如题3.4图所示电路,N 为不含独立源的线性电路。
电路分析基础习题第三章答案(史健芳)教程文件
电路分析基础习题第三章答案(史健芳)第3章3.1 选择题1.必须设立电路参考点后才能求解电路的方法是( C )。
A.支路电流法B.回路电流法C.节点电压法D.2b法2.对于一个具有n个结点、b条支路的电路,他的KVL独立方程数为( B )个。
A.n-1 B.b-n+1 C.b-nD.b-n-13.对于一个具有n个结点、b条支路的电路列写结点电压方程,需要列写( C )。
A.(n-1)个KVL方程B.(b-n+1)个KCL方程C.(n-1)个KCL方程D.(b-n-1)个KCL方程4.对于结点电压法中的无伴电压源,下列叙述中,( A )是错误的。
A.可利用电源等效变换转化为电流源后,再列写结点电压方程B.可选择该无伴电压源的负极性端为参考结点,则该无伴电压源正极性端对应的结点电压为已知,可少列一个方程C.可添加流过该无伴电压源电流这一新的未知量,只需多列一个该无伴电压源电压与结点电压之间关系的辅助方程即可D.无伴受控电压源可先当作独立电压源处理,列写结点电压方程,再添加用结点电压表示控制量的补充方程5.对于回路电流法中的电流源,下列叙述中,( D )是错误的。
A.对于有伴电流源,可利用电源等效变换转化为电压源后,再列写回路电流方程B.对于无伴电流源,可选择合适的回路,使只有一个回路电流流过该无伴电流源,则该回路电流为已知,可少列一个方程C.对于无伴电流源,可添加该无伴电流源两端电压这一新的未知量,只需多列一个无伴电流源电流与回路电流之间关系的辅助方程即可D.电流源两端的电压通常为零6.对于含有受控源的电路,下列叙述中,( D )是错误的。
A.受控源可先当作独立电源处理,列写电路方程B.在结点电压法中,当受控源的控制量不是结点电压时,需要添加用结点电压表示控制量的补充方程C.在回路电流法中,当受控源的控制量不是回路电流时,需要添加用回路电流表示控制量的补充方程D.若采用回路电流法,对列写的方程进行化简,在最终的表达式中互阻始终是相等的,即:R ij=R ji3.2 填空题1.对于具有n个结点b条支路的电路,可列出 n-1 个独立的KCL方程,可列出 b-n+1 个独立的KVL方程。
电路分析知到章节答案智慧树2023年上海电力大学
电路分析知到章节测试答案智慧树2023年最新上海电力大学第一章测试1.图示电路中,节点A和B之间的电压UAB为()V。
参考答案:-162.图示电路中I= 0 时,电位UA=()V。
参考答案:603.通常所说负载增加,是指负载()增加。
参考答案:功率4.图示电路中S断开时I1= 0A,I=2A。
S闭合时I1=( )A,I=( )A。
()参考答案:0;65.图示电路中,当IS=10A 时,电压U为()V,当IS=8A时电压U为()V。
()参考答案:12;166.电路理论分析的对象是电路模型而不是实际电路。
()参考答案:对7.欧姆定律可表示成U=RI,也可表示成U=-RI,这与采用的参考方向有关。
()参考答案:对8.在节点处各支路电流的方向不能均设为流向节点,否则将只有流入节点的电流而无流出节点的电流。
()参考答案:错9.在电压近似不变的供电系统中,负载增加相当于负载电阻减少。
()参考答案:对10.理想电压源的端电压是由它本身确定的,与外电路无关,因此流过它的电流则是一定的,也与外电路无关。
()参考答案:错第二章测试1.图示电路AB间的等效电阻为()。
参考答案:14Ω2.电路如图所示,A、B端的等效电阻R=()。
参考答案:4Ω3.电路如图所示,可化简为()参考答案:3Ω电阻4.如图所示电路中,当电阻R2增加时电流I将()。
参考答案:增加5.图示电路中,就其外特性而言,()。
参考答案:b、c等效6.两只额定电压为110V的电灯泡串联起来总可以接到220V的电压源上使用。
()参考答案:错7.电流相等的两个元件必属串联,电压相等的两个元件必属并联。
()参考答案:错8.一个不含独立源的电阻性线性二端网络(可以含受控源)总可以等效为一个线性电阻。
()参考答案:对9.一个含独立源的电阻性线性二端网络(可以含受控源)总可以等效为一个电压源与一个电阻串联或一个电流源与一个电阻并联。
()参考答案:对10.已知图示电路中A、B两点电位相等,则AB支路中必然电流为零。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章习题3.1 如题3.1图所示梯形电路。
⑴ 已知24u V =,求1u 、i 和S u 。
⑵ 已知27S u V =,求1u 、2u 和i 。
⑶ 已知 1.5i A =,求1u 和2u 。
解:根据线性电路的性质,设:211u k u = 22u k i = 23s u k u =令:2V u 2= 可推出 6V u 2= 1A i = 27V u s = 因而可得: 3k 1= 0.5k 2= 27/2k 3= ⑴ 当24u V =时,有: 12V 43u 1=⨯= 2A 40.5i =⨯= 56V 4227u s =⨯=⑵ 当27S u V =时,有: 2V 27272u k 1u s 32=⨯==1A 20.5u k i 22=⨯== 6V 23u k u 211=⨯== ⑶ 当 1.5i A =时,有: 3V 1.50.51i k 1u 22=⨯==9V 33u k u 211=⨯==3.2 如题3.2图所示电路,已知9S u V =,3S i A =,用叠加定理求电路i 。
解:S u 单独作用时,有: 1163Su i A ==+ S i 单独作用时,有: 23163S i i A =-=-+ 根据叠加定理可得: 12110i i i =+=-=3.3 如题3.3图所示电路,求电压u 。
如独立电压源的值均增至原值的两倍,独立电流源的值下降为原值的一半,电压u 变为多少?解:根据KVL 列一个回路113132(32)4u i V A A i =Ω⨯++⨯Ω+-⨯Ω 两个电压源支路可列方程:1131(3)610i i +=-+ 由此可得: 13i A =代入上式得: 33132(323)4u V =⨯++⨯+-⨯⨯= 若独立电压源的值均增至原值的两倍,独立电流源的值下降为原值的一半,由上式可知:1132(1.5)620i i +=-+ 解得 13i A = 有: 332 1.52(1.523)4u V =⨯++⨯+-⨯⨯=-3.4 如题3.4图所示电路,N 为不含独立源的线性电路。
已知:当12S u V =、4S i A =时,0u V =;当12S u V =-、2S i A =-时,1u V =-;求当9S u V =、1S i A =-时的电压u 。
解:根据线性电路的叠加定理,有:12S S u k u k i =+将已知数据代入,有:120124k k =+ 121122k k -=-- 联立解得: 116k =212k =- 因而有: 1162S S u u i =- 将9S u V =、1S i A =-代入可得: 119(1)262u V =--=3.5 如题3.5图所示电路,已知当开关S 在位置1时,I=40mA ;当S 在位置2时,I=-60mA ;求当S 在位置3时的I 解:设电源S U 和S I 对电流I 的贡献为I 根据线性电路的叠加定理,有:/I I kU =+其中U 为开关外接电源的作用。
开关S 在位置1时,有 /400I k =+⨯ 此时可将U 视为0开关S 在位置2时,有/604I k -=- 由上可解得: 25k = /40I = 当S 在位置3时,6U V =,则有:/40256190I I k U m A=+=+⨯=3.6 如题3.6图所示电路,若/8x i i =,求电阻x R解:运用置换定理将电路变为如下图所示。
根据叠加定理电压x u 可看成电流源8x i 和x i 共同 作用,即 ///x x xu u u =+ /xu 由电流源8x i 单独作用,//x u 电流源x i 单独作用。
根据分流关系,有:/158108552416815101510x xxx x x i i u i i i ⨯⨯=⨯-⨯=-=++//1510[(105)//(55)]61510xx x x u i i i ⨯=-++⨯=-⨯=-+因而有:///862x x x x x x u u ui i i =+=-=故得: 2xx xu R i ==Ω3.7 如题3.7图所示电路,当L R 分别为1Ω、2Ω和5Ω时,求其上电流L I 分别为多少?解:将电流源变换为电压源形式,再根据 叠加原理,有:22//R 2//R 222//R 2//R 10U U U L L L L L2L1L +++=+= 整理可得: LLL R 16R U +=当Ω=1R 时,有: 3A R 16R U I LL L L =+== 当Ω=2R 时,有: 2A R 16R U I LL L L =+== 当Ω=1R 时,有: 1A R 16R U I LL L L =+==3.8 如题 3.8图所示电路,N 为不含独立源的线性电路,已知输出电压/2S u u =;若在输出端接上5Ω电阻,则/3S u u =。
问在输出端接3Ω电阻时,输出电压u 与输入电压S u 的关系如何?解:从输出端进行戴文宁等效,有/sLs L u R R R u += 当∞→L R 时,/2S u u =,可得 /2u u s /s =当Ω=5R L 时,/3S u u =,代入上式可求得:Ω=52.R s 因此,当Ω=3R L 时,有s s /s L s L u 1132u 2.533u R R R u =⨯+=+=3.9 如题3.9图所示电路,当R=12Ω时其上电流为I 。
若要求I 增至原来值的3倍,而电路中除R 外的其他部分均不变,则此时的电阻R 为多少?解:从R 两端进行戴文宁等效,可得等效电源 s /su 61u -=,等效电阻Ω=3R 0 根据等效电路,当Ω=12R 有 s 0/su 901-R R u I =+=而 0/sR Iu R -=,若3I I →,则有: Ω=-⨯=23u 9013-u 61-R ss3.10 求如题3.10图所示各电路ab 端的戴维宁等效电路和诺顿等效电路。
解:对图(a)电路进行诺顿等效,求ab 两端的短路电流,如图可知: 21OC I I I += 而 6A 424I 1==A 16333//6624I 2=+⨯+=可得: 7A I I I 21O C =+=求电压源短路时,ab 两端的等效电阻: Ω=+=28//)63//6//(4R 0 对图(b)电路进行戴文宁等效,3.11 如题3.11(a)图所示线性有源二端电路N ,其伏安关系如题3.11(b)图所示。
试求它的戴维宁等效电路。
解:根据戴文宁等效电路,端口 电压、电流的约束关系为:O C 0u u +R i = 当i 0=时,有 OC u -15V = 当u 0=时,有 OC0u R =0.5i=Ω3.12 如题3.12图所示线性时不变电阻电路,已知当2cos(10)S i t A =、2L R =Ω时,电流[4(10)2]L i cod t A =+;当4S i A =、4L R =Ω时,电流8L i A =;问当5S i A =、10L R =Ω时,电流L i 为多少?解:从负载两端进行诺顿等效,根据线性 电路的齐次性,等效电流源为:S SC ki i =则有: S L 00SC L 00L ki R R R i R R R i +=+=t=0时,2A i S =,6A i L =,2L R =Ω代入上式 有 k 2R R 2600+= ① 再将4S i A =、4L R =Ω时,8L i A =代入上式 有 k 4R R 4800+= ② 联解①式和②式,可得: 6k = Ω=2R 0因而有: S LL i R 226i += 当5S i A =,10L R =Ω时,可得5A 510226i L =+=3.13 如题3.13图所示电路,已知8u V =,求电阻R 。
解:从电阻R 两端进行戴文宁等效,其 开路电压为:OC 3(24)//62u =18183+2+43(24)//62412V+⨯+⨯⨯+++ =()//6等效电阻为:0R =4//(26//3)2+=Ω 则可得:RR ROC u u =+ 解得: R 4=Ω33.14 如题 3.14图所示电路,N 为含有独立源的线性电阻电路。
已知当9L R =Ω时其上获得最大功率为1W ,求N 的戴维宁等效电路。
解:将电路等效为如图所示,根据功率 最大传输定理,有:L 0010R R R //1010R ==+可解得: 0R 90=Ω又有: 2L m a xLu P 4R = u 为L R 两端的开路电压,可解得:L u =6V =± 根据等效电路可知: OC 010u u -10+10R +10=()解得: OC u -30V = 或 OC u -150V =3.15 如题3.15图所示电路,L R 可任意改变,问L R 等于多大时其上获得最大功率,并求出该最大功率。
解:对L R 两端进行戴文宁等效,首先 求开路电压OC U ,有:OC R U =25U +20⨯+而 R R U =2-0.1U 10⨯()解得 R U =10V 可得:OC U =40V 再求等效电阻0R ,如右图所示,有:RU =5IU⨯+ 而此时 R R U =I-0.1U 10⨯() 解得 R U =5I 故得 0UR ==10IΩ 根据最大功率传输定理,当L 0R =R =10Ω时, 可获得最大功率,为:22O m a xL U 40P ===40W 4R 410C⨯3.16 如题3.16图所示电路,S U 、S I 均未知,已知当4L R =Ω时电流2L I A =。
若L R 可任意改变,问L R 等于多大时其上获得最大功率,并求出该最大功率。
解:从L R 两端进行戴文宁等效 可知 0R 2//2+1=2=Ω 又有 OCL 0Lu I R +R = 代入已知数据可得: OC u 12V = 根据最大功率传输定理,有当 L 0R R =2=Ω 时可获得最大功率 为 2OC LmaxL u 12P ==18W 4R 42=⨯3.17 如题3.17图所示电路,N 为含独立源的线性电阻电路。
已知当受控电流源系数1β=时,电压20u V =;当1β=-时,电压12.5u V =。
求β为何值时外部电路从N 获得最大功率,并求出该功率。
解:将电路N 进行戴文宁等效,并将受控源 转换为电压源形式,有OC110u -10I I 20+10+R β= 得: OC10u I 30+10+R β= 又有: 11u 10I +(20+10)I β= 得: 1uI 10+30β=可得: OC 0u u30+10+R 10+30ββ=将1β=,20u V =;1β=-,12.5u V =代入,有OC 0u 2040+R 40= 和 OC 0u 12.520+R 20=联立求解可得: OC u 50V = 0R 60=Ω再求电路N 的等效电阻L R11u-10I I 20+10β=可求得: L 1uR =30+10I β= 当L 0R R =60=Ω 时可获得最大功率,则有: L R =30+10=60β 解得:=3β 最大功率为: 2OC LmaxL u 50P ==10.42W 4R 460=⨯ 3.18如题3.18图所示电路,R N 仅由线性电阻组成。
