材料力学作业
材料力学书面作业
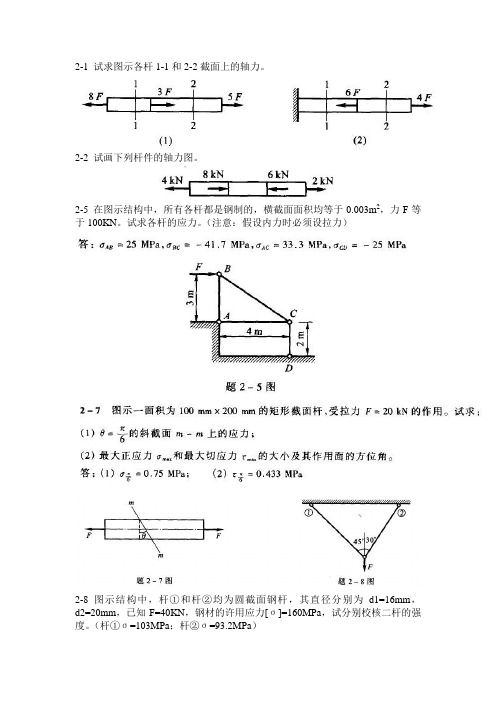
2-1 试求图示各杆1-1和2-2截面上的轴力。
2-2 试画下列杆件的轴力图。
2-5 在图示结构中,所有各杆都是钢制的,横截面面积均等于0.003m2,力F等于100KN。
试求各杆的应力。
(注意:假设内力时必须设拉力)2-8 图示结构中,杆①和杆②均为圆截面钢杆,其直径分别为d1=16mm,d2=20mm,已知F=40KN,钢材的许用应力[σ]=160MPa,试分别校核二杆的强度。
(杆①σ=103MPa;杆②σ=93.2MPa)2-9 图示为钢杆组成的桁架,已知F=20KN,钢材的许用应力[σ]=160MPa。
试求CD所需的横截面面积。
(A=125mm2)2-10 图示结构中,AB和BC均为直径d=20mm的钢杆,钢材许用应力[σ]=160MPa。
试求该结构的许用荷载[F]。
([F]=35.5KN)2-13 图示钢杆的横截面面积为200mm2,钢的弹性模量E=200GPa。
试求各段杆的应变、伸长及全杆的总伸长。
3-3 图示铆接接头中,已知F=60KN,t=12mm,b=80mm,铆钉直径d=16mm,铆钉材料的许用切应力[τ]=140MPa,许用挤压应力[σ]=300MPa,板的许用拉应力bs[σ]=160MPa。
试分别校核铆钉和板的强度。
3-5 图示一正方形截面的混凝土柱,浇注在混凝土基础上。
基础分两层,每层厚为t。
已知F=200KN,假定地基对混凝土板的反力均匀分布,混凝土的许用切应力[τ]=1.5MPa。
试计算为使基础不被破坏,所需的厚度t值。
(t=95.5mm)3-8 试画下列各杆的扭矩图。
3-13 图示受扭圆杆中,d=100mm,材料的许用切应力[τ]=40MPa。
试校核该杆的强度。
(τmax=35.7MPa)3-15 圆杆受力如图所示,已知材料的许用切应力[τ]=40MPa,切变模量G=8×104MPa,单位长度杆的许用扭转角[θ]=1.2°/m。
试求杆所需的直径。
材料力学(1)(专升本)阶段性作业1

材料力学(1)(专升本)阶段性作业1总分:100分得分:11分一、单选题1. 下列结论中正确的是()。
(6分)(A) 内力是应力的代数和;(B) 内力是矢量,而应力是标量;(C) 内力必大于应力;(D) 应力是内力的集度,是精确的描述内力分布情况的物理量;内力和应力的量纲不同。
参考答案:D2. 关于变形和位移的关系,下面不正确的结论是()。
(6分)(A) 若物体产生位移,则必定同时产生变形;(B) 若物体各点均无位移,则该物体必无变形;(C) 若物体产生变形,则物体内必有一些点有位移。
(D) 通常要了解物体的变形,必须分析物体的变形位移。
参考答案:A3. 小变形的确切含义是()。
(6分)(A) 小变形是指:构件材料在弹性变形范围内的变形量;(B) 小变形是指:结构上点的位置与其原始位置相比为微小的变化量;(C) 小变形是指:一维构件内各点在垂直于其轴线方向的变形量;(D) 小变形是指:构件的变形量与构件自身的主要尺寸相比较要小得多的变形量。
参考答案:D4. 一悬臂梁B端在横向载荷作用下弯曲变形,如题一、4图(a)所示。
若根据力线平移定理,将力平移到C截面处,同时附加一个力偶,附加力偶的力偶矩为,如题一、4图_____所示。
这样做对研究原梁的变形(图(a)所示)有影响或无影响的区段是_______。
(6分)(A) AC段有影响,CB段无影响;(B) AC段有影响,CB段也有影响;(C) AC段无影响,CB段无影响;(D) AC段无影响,但CB段有影响;参考答案:D您的回答:D 正确5. 图示结构A、B、C三处铰支,在载荷作用下产生变形,而在和两杆横截面m-m和n-n上必然产生内力。
和两杆的变形属于何类基本变形,下列说法正确的是()。
(6分)(A) AB杆扭转,BC杆轴向拉伸;(B) AB杆弯曲,BC杆轴向压缩;(C) AB杆弯曲,BC杆轴向拉伸;(D) AB杆弯曲,BC杆扭转;参考答案:C6. 在图示简易吊车的横梁上作用载荷F,载荷可以左右移动。
材料力学课后作业

和弯矩方程绘制剪力图和弯矩图。
32、如图示,设q、a均为己知。求:梁的剪力方程和弯矩方程并根据剪力方程
和弯矩方程绘制剪力图和弯矩图。
33、如图示,设q、a均为己知。求:梁的剪力方程和弯矩方程并根据剪力方程
和弯矩方程绘制剪力图和弯矩图。
《材料力学》课后作业
1、试作图示各杆的轴力图。
2、求图示各杆 和 横截面上的轴力,并作轴力图。
答案:
3、 求图示阶梯状直杆横截面 、 和 上的轴力,并作轴力图。如横截面面积 , , ,求各横截面上的应力。
答案:
4、 图示一混合屋架结构的计算简图。屋架的上弦用钢筋混凝土制成。下面的拉杆和中间竖向撑杆用角钢构成,其截面均为两个 的等边角钢。已知屋面承受集度为 的竖直均布荷载。求拉杆 和 横截面上的应力。
40、割刀在切割工件时,受到F=1KN的切削力作用,割刀尺寸如图所示,若割刀的许用弯曲正应力〔σ〕=200MPa。试校核割刀的弯曲正应力强度。
答案:σmax=200MPa
41、图示为一承受纯弯曲的铸铁梁,其截面为⊥形,材料的拉伸和压缩许用应力之比
〔σ+〕/〔σ-〕=1/4。求水平翼板的合理宽度b。
答案:b=510mm
答案:σA=σD=-163.5MPaσB=38.8 MPaσC=58.8 MPa
38、矩形截面的悬臂梁受集中力和集中力偶作用,如图所示。试求Ⅰ-Ⅰ截面和固定端Ⅱ-Ⅱ截面上A、B、C、D四点处的正应力。
答案:I-I截面:σA=-7.41MPaσB=4.94MPaσC=0σD=7.41MPa
I-I截面:σA=9.26MPaσB=-6.18MPaσC=0σD=-9.26MPa
《材料力学 》在线作业参考资料

一、单选题(共 10 道试题,共 20 分。
)V1. 如图:A. AB. BC. CD. D正确答案:C 满分:2 分2.材料的持久极限与试件的()无关A.材料B.变形形式C.循环特征D.最大应力正确答案:D 满分:2 分在相同的交变载荷作用下,构件的横向尺寸增大,其()。
A.工作应力减小,持久极限提高;B.工作应力增大,持久极限降低;C.工作应力增大,持久极限提高;D.工作应力减小,持久极限降低。
正确答案:D 满分:2 分4.圆截面杆受扭转作用,横截面任意一点(除圆心)的切应力方向()A.平行于该点与圆心连线B.垂直于该点与圆心连线C.不平行于该点与圆心连线D.不垂直于该点与圆心连线正确答案:B 满分:2 分在以下措施中()将会降低构件的持久极限A.增加构件表面光洁度;B.增加构件表面硬度;C.加大构件的几何尺寸;D.减缓构件的应力集中正确答案:C 满分:2 分6. 如图2:A. AB. BC. CD. D正确答案:A 满分:2 分7.截面上的切应力的方向()A.平行于截面B.垂直于截面C.可以与截面任意夹角D.与截面无关正确答案:A 满分:2 分8. 如图3:A. AB. BC. CD. D正确答案:A 满分:2 分9. 如图1:A. AB. BC. CD. D正确答案:C 满分:2 分10.脆性材料的破坏应力是()A.比例极限B.弹性极限C.屈服极限D.强度极限正确答案:D 满分:2 分二、判断题(共 40 道试题,共 80 分。
)V1.拉伸(压缩)和弯曲组合变形时中性轴一定不过截面的形心。
A.错误B.正确正确答案:B 满分:2 分2.. 用力法解超静定问题时,由于有标准形式的正则方程,故不需要考虑静力平衡、变形几何和物理关系三个方面。
A.错误B.正确正确答案:A 满分:2 分3.当受力构件内最大工作应力低于构件的持久极限时,通常构件就不会发生疲劳破坏的现象。
A.错误B.正确正确答案:B 满分:2 分4.力法的正则方程是解超静定问题的变形协调方程。
材料力学作业(1-4章)

第一章 绪 论一、选择题1 构件的强度是指( ),刚度是指( ),稳定性是指( )。
A. 在外力作用下构件抵抗变形的能力B. 在外力作用下构件保持其原有的平衡状态的能力C. 在外力作用下构件抵抗破坏的能力2 根据均匀性假设,可认为构件的( )在各点处相同。
A. 应力B. 应变C. 材料的弹性常数D. 位移 3 下列结论中正确的是( )A. 内力是应力的代数和B. 应力是内力的平均值C. 应力是内力的集度D. 内力必大于应力 4 下列说法中,正确的是( )A. 内力随外力的改变而改变。
B. 内力与外力无关。
C. 内力在任意截面上都均匀分布。
D. 内力在各截面上是不变的。
5 图示两单元体虚线表示其A. α,α 受力后的变形情况,两单元体切应变γ ( )、计算题1、如图所示,在杆件的斜截面m-m 上,任一点A 处的应力p =120 MPa ,其方位角θ=20°,试求B. 0,α C. 0,-2αD. α,2α二该点处的正应力σ与切应力τ。
2、已知杆内截面上的内力主矢为F R 与主矩M 如图所示,且均位于x-y 平面内。
试问杆件截面上 、板件ABCD 的变形如图中虚线A’B’C’D’所示。
试求棱边AB 与AD 的平均正应变以及A 点处直存在哪种内力分量,并确定其大小。
图中之C 点为截面形心。
3角BAD 的切应变。
第二章 拉伸与压缩一、选择题和填空题1、轴向拉伸杆件如图所示,关于应力分布正确答案是_________。
A 1-1、2-2面上应力皆均匀分布;B 1-1面上应力非均匀分布,2-2面上应力均匀分布;C 1-1面上应力均匀分布,2-2面上应力非均匀分布;D 1-1、2-2面上应力皆非均匀分布。
2、图示阶梯杆AD 受三个集中力作用,设AB 、BC 、CD 段的横截面积分别为3A 、2A 、A ,则三段的横截面上。
A 轴力和应力都相等B 轴力不等,应力相等C 轴力相等,应力不等D 轴力和应力都不等3、在低碳钢拉伸曲线中,其变形破坏全过程可分为4个变形阶段,它们依次是 、 、 、 。
华南理工 网络 材料力学作业1

参考答案:×问题解析:3图示桁架中3杆的内力为0。
()参考答案:√1.图示扭转杆固定端截面的扭矩为15kN-M。
()参考答案:√问题解析:2.等截面圆轴作匀速转动,转速n=200r/min,传递的功率为60kw,作用在轴上的外力偶矩为2864.7N.m。
()参考答案:√1.梁AB受力如图所示,截面1-1剪力和弯矩分别为FS1=-qa, M1=-qa2/2 。
()答题:对. 错. (已提交)参考答案:√问题解析:2.图示简支梁,其正确的弯矩图如图所示。
()参考答案:×问题解析:3.图示受力梁的支座约束力、剪力图、弯矩图均正确。
()参考答案:√1.图示杆件的内力有轴力和扭矩。
()答题:对. 错. (已提交)参考答案:×问题解析:2.图示杆件的内力有轴力和弯矩。
()答题:对. 错. (已提交)参考答案:×问题解析:1.静定轴向拉(压)杆横截面上的应力与杆件材料的力学性能有关。
()参考答案:×问题解析:2.已知变截面圆杆受力如图所示,d=38mm,D=65mm,AB段和BC段横截面的应力是相同的。
()参考答案:×问题解析:3.边长为200mm的正方形杆件受力如图示,杆件横截面上最大压应力为 7.5MPa。
()参考答案:√1.拉压杆的最大切应力发生在与轴线成450的斜截面上,且。
()参考答案:√1.边长为200mm的正方形杆件受力如图示(同题2图),材料可认为符合胡克定律,其弹性模量E=10GPa,杆件总变形为1.05mm。
()参考答案:√问题解析:2.轴向拉(压)杆,受力和变形关系满足胡克定律,即。
()参考答案:×问题解析:3.变截面直杆受力如图所示,可用公式求杆的总伸长量。
参考答案:×1.图示的杆系结构中,按强度条件计算,最危险的杆件是4杆。
()参考答案:×1.图示两端固定的等截面直杆,其横截面面积为A,该杆受轴力FP作用。
材料力学试卷部分作业答案1
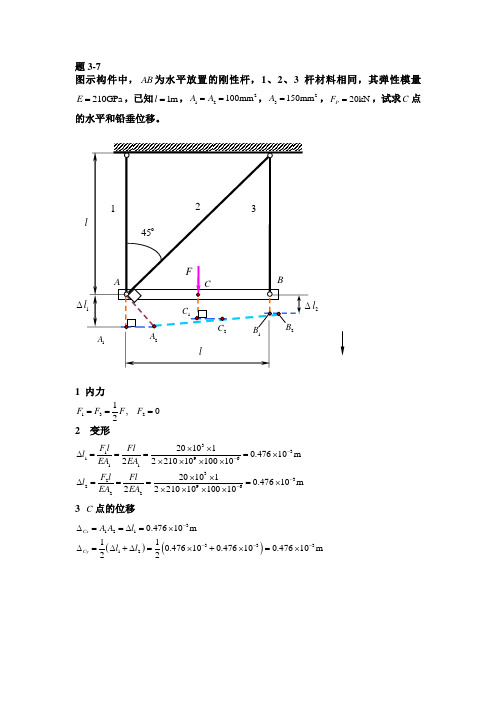
题3-7图示构件中,AB 为水平放置的刚性杆,1、2、3杆材料相同,其弹性模量210GPa E =,已知1m l =,212100mm A A ==,23150mm A =,20kN P F =,试求C 点的水平和铅垂位移。
1 内力1321,02F F F F ===2 变形3311961133229622201010.47610m 222101010010201010.47610m 222101010010F l Fl l EA EA F l Fl l EA EA ----⨯⨯∆====⨯⨯⨯⨯⨯⨯⨯∆====⨯⨯⨯⨯⨯3 C 点的位移()()3121333120.47610m 110.476100.476100.47610m 22Cx CyA A l l l ----∆==∆=⨯∆=∆+∆=⨯+⨯=⨯∆2l题11-2题11-3yz题12-16 如图12-44,两根材料相同、截面面积相等的简支梁,一根是整体矩形梁,另一根是矩形截面叠合梁。
热布吉叠合梁间的摩擦,试问:(1)这两种梁截面上的弯曲正应力是怎样分布的? (2)这两种梁能承受的荷载相差多少?解 1. 画弯矩图,最大弯矩在中间截面1max 12max 211,44M F l M F l ==2. 整梁的强度条件 应力分布如图a[][]21max 11max121/42/63z bhM F l F W bh lσσσ==≤∴≤3.叠合梁的最大应力和强度: 危险面也在中面,由于上下梁截面相同,弯曲相同()a b ρρ=,所以上下截面受到的弯矩max a M 、max b M 相同,于是可画出应力分布如图b 。
由于截面总弯矩为2max M ,所以max max 2max 2/2/8a b M M M F l ===叠合梁的强度条件为()[][]2max 22max22/813/2/6a az bhM F l F W lb h σσσ==≤∴≤14241maxσ1maxσ2max σ2max2max可见 [][]122F F =12-6 铸铁梁的荷载及截面尺寸如图所示。
材料力学课程作业及答案4

材料力学作业4 单项选择题第1题下列哪项措施不能提高压杆稳定性:___。
A、减小压杆支撑间的长度B、减弱压杆的约束条件C、选择合理的截面形状D、合理选用压杆的材料答案:B第2题下列哪项措施可以提高构件的疲劳强度:___。
A、减缓应力集中B、增加构件尺寸C、降低表面质量答案:A第3题下列哪项措施不能提高构件的抗冲击能力:___。
A、减小构件的刚度B、增加构件的弹性模量C、增加构件的体积答案:B第4题下图所示的连续梁的静不定次数为___。
A、1B、2C、3D、4答案:B判断题第5题构件在发生疲劳破坏前,会出现明显的塑性变形。
答案:错误第6题构件外形的变化不会改变构件的持久极限。
答案:错误第7题虚位移表示这种位移是由其他原因引起,且和梁上的原有载荷相关。
答案:错误第8题在虚功原理中,与材料性质也是相关的。
答案:错误第9题对于既是外力静不定又是内力静不定的情况,应当同时接触外多余约束和内多余约束,才能形成静定基。
答案:正确第10题轴向受压的细长直杆当压力过大时,可能突然变弯,失去原直线形式的平衡状态,此状态称为失稳。
答案:正确第11题杆愈细长,其临界力越小,愈容易失稳。
答案:正确第12题杆端的约束愈强,压杆的临界压力就愈低。
答案:错误第13题压杆的柔度愈大,其愈容易失稳。
答案:正确第14题机器设备中零件的工作应力随时间作随机性变化,,这种应力称为交变应力。
答案:错误第15题交变应力作用下材料抵抗疲劳破坏的能力,称为疲劳强度。
答案:正确填空题第16题两根尺寸和材料均相同的细长压杆,弹性模量=200Gpa,直径d=80mm。
下端固定,上端与刚性很大的横梁固连,压杆长度L=1.2m,则细长压杆的临界力为___。
答案:689kN第17题变形固体的功能原理为:外力功=___。
答案:变形能第18题对于任何弹性体,其外力功 = ___广义力 X 广义位移。
答案:0.5第19题列出两个常用的结构位移变形能法:___和___。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
材料力学作业Company Document number:WUUT-WUUY-WBBGB-BWYTT-1982GT2-4 木架受力如图所示,已知两立柱横截面均为100m m ×100mm 的正方形。
试求:(1)绘左、右立柱的轴力图;(2)求左、右立柱上、中、下三段内横截面上的正应力。
解:(1)求立柱各节点的受力为了求出ACEG 立柱(左立柱)和BDFH 立柱(右立柱)中的内力和应力,首先对各杆受力进行分析如下图2-4a 所示,并求出数值。
取AB 为研究对象,由平衡方程∑=0)(F m A,0211=⨯'-⨯BF F ①∑=0Y ,01=-'+'F F F B A②联合①和②解得,KN F F B A5='='。
又由牛顿第三定律得,KN F F AA 5='=,KN F FB B 5='=。
同理可得,KN F F CC 9='=,KN F FD D 3='=;KN F FE E 4='=,KNF F F F 12='=。
(2)绘左、右立柱的轴力图取左立柱(ACEG 立柱)为研究对象。
采用截面法,画受力图如图2-4b 所示,求得 )(5KN F N A AC -=-=;)(1495KN F F N C A CE -=--=--=;)(10495KN F F F N E C A EG -=+--=+--=。
同理又取右立柱(BDFH 立柱)为研究对象。
采用截面法求得)(5KN F N B BD -=-=;)(235KN F F N D B BD -=+-=+-=;)(141235KN F F F N F D B FH -=-+-=-+-=。
画轴力图如图左立柱所示和如图右立柱所示。
(3)求左、右立柱上、中、下三段内横截面上的正应力由轴向拉压正计算公式AN=σ应力得,左立柱上、中、下正应力:MPa mm N A N AC 5.010********3-=⨯⨯-==左上σ; MPa mm N A N CE 4.1100100101423-=⨯⨯-==左中σ; MPa mmN A N EG 1100100101023-=⨯⨯-==左下σ。
右立柱上、中、下正应力:MPa mm N A N 5.010*********BD -=⨯⨯-==右上σ;MPa mm N A N F 2.010********3D -=⨯⨯-==右中σ; MPa mm N A N FH 4.1100100101423-=⨯⨯-==右下σ。
2-9 图示的构架中,AB 为刚性杆,CD 杆的刚度为EA ,试求:(1)CD 杆的伸长;(2)C 、B 两点的位移。
解:(1)CD杆的伸长取ACB 刚性杆为研究对象,画受力图如图2-9a 所示。
由平衡条件∑=0)(F m A,230sin =⨯-⨯︒⋅a F a N CD 得,F N CD 4=⋅。
CD 杆的伸长⋅∆CD l 为:EAFaEA a F EA l N l CD CD CD ⋅=︒⨯==⋅∆33830cos /4。
(2)C 、B 两点的位移ACB 杆位移关系如图2-9b 所示。
CDCD C l l ∆=︒∆=230sin /δ;CD B C l ∆==42δδ。
杆,结构承受载荷为F=50KN 。
设计要求强度安全系数n ≥2,并要求刚性杆只能向下平移而不能转动,竖向位移又不允许超过1mm 。
试计算AC 杆和BD 杆所需的横截面面阿积。
材料的路力学性能如下:AC 杆:E=200MPa σs =200MPa σb =400MPa BD 杆:E=200MPa σs =400MPa σb =600MPa 解:(1)求AC 杆和BD 杆的轴力取AB 杆为研究对象,AC 杆和BD 杆皆为拉杆,由平衡条件∑=0)(F m A,051=⨯-⨯BD F F ①∑=0Y ,0=-+F F FBD AC②联合①和②解得,KN F F AC 4054==;KN F F BD 1051==。
(2)由刚度条件设计AC 杆和BD 杆的横截面面积 刚度条件:][l A E l N l i i i i i ∆≤=∆→iii i E l l N A ][∆≥,则 253310420*********][mm E l l N A AC AC AC AC⨯=⨯⨯⨯⨯=∆≥;24331042001108.01010][mm E l l N A BD BD BD BD⨯=⨯⨯⨯⨯=∆≥。
所以 AC BD A A 10=。
(3)由强度条件设计AC 杆和BD 杆的横截面面积 强度条件:n A N si i i i σσσ=≤=][→siii nN A σ≥,则 2340020010402mm nN A sACACAC =⨯⨯=≥σ;235040010102mm nN A sBD BD BD =⨯⨯=≥σ。
综上刚度与强度要求考虑,250mm A BD =,2500mm A AC =。
2-19 图示结构中各杆的刚度EA 相同,试求各杆的轴力。
解:取节点C 为研究对象,画受力图如图2-19(b )a 所示,列平衡方程为∑=0X ,045sin 45sin =︒⋅+︒⋅-CB CAN N, ①∑=0Y ,045cos 45cos =-︒⋅+︒⋅CECB CA N N N , ②变形协调条件为 CA CD l l ∆=︒⋅∆45cos ③︒⋅=⋅=∆45cos EA lN EA l N l CA CA CA CA ,EAlN F EA l N l l l CE CE ED CE CD ⋅-+⋅-=∆+∆=∆)( ④ 图2-19C联立①、②、③和④得F N N CB CA 207.0==(+),F N CE 293.0=(﹣),F N CD 707.0=(+)。
2-21 图示结构中钢杆1、2、3的横截面面积均为A=200mm 2,长度l=1m ,E=200GPa 。
杆3因制造不准而比其余两根短了δ=0.8mm 。
试求将杆3安装在刚性梁上后三杆的轴力。
解:取刚性梁为研究对象,画受力图如图2-21a 所示,列平衡方程:∑=0)(1F m,0232=⨯-⨯a F a F ①∑=0Y ,②2-21b 所122)(ll l l ∆+∆+∆+∆=δ ③物理方程为EA l F l 11=∆,EA lF l 22=∆,EAl F l 33=∆ ④ 联立①、②、③和④得)(33.531KN F F ==(﹢);)(66.102KN F =(﹣)。
3-4 两块钢板搭接如图所示。
已知两板的宽度均为b=180mm ,厚度分别为t 1=16mm ,t 2=18mm ,铆钉直径d=25mm ,所有构件的材料的许用应力均为:[τ]=100MPa,[σc ]=280MPa ,[σ]=140MPa 。
试求:(1)接头的许用载荷;(2)若铆钉的排列次序相反(即自左向右,第一列是两只,第二列是三只铆钉),则接头的许用载荷为多大解:假设每颗铆钉受力一样。
(1) 求接头的许用载荷由剪切强度条件][4/5/2τπτ≤==d F A Q Q 得N d F 3221024542510054][5⨯=⨯⨯=≤ππτ。
由挤压强度条件 ][5/1C C C C dt F A P σσ≤==得 N dt F C 311056016252805][5⨯=⨯⨯⨯=≤σ。
考虑拉压强度。
板1和板2的轴力图如图3-4a 所示。
由板1求允许载荷:][)3(1σσ≤-==t d b FA N → N t d b F 311023516)253180(140)3]([⨯=⨯⨯-⨯=-≤σ;又由板2求允许载荷:][)3(5/32σσ≤-==t d b F A N →N t d b F 321044118)253180(14035)3]([35⨯=⨯⨯-⨯⋅=-≤σ][)2(2σσ≤-==t d b F A N → 所以 许用载荷[F]=235KN 。
(2)若铆钉的排列次序相反(即自左向右,第一列是两只,第二列是三只铆钉),则接头的许用载荷剪切强度和挤压强度计算同前。
考虑拉压强度。
板1和板2的轴力图如图3-4a 所示。
由板1求允许载荷:][)2(1σσ≤-==t d b F A N → N t d b F 311029116)252180(140)2]([⨯=⨯⨯-⨯=-≤σ;][)3(5/31σσ≤-==t d b F A N →N t d b F 311039216)253180(14035)3]([35⨯=⨯⨯-⨯⋅=-≤σ又由板2求允许载荷:][)3(2σσ≤-==t d b FA N → 所以 许用载荷[F]=245KN 。
3-8 矩形截面(30m m ×5mm )的低碳钢拉伸试件如图所示。
试件两端开有圆孔,孔内插有销钉,载荷通过销钉传递至试件。
试件和销钉材料相同,其强度极限σb =400MPa ,许用应力[σ]=160MPa ,[τ]=100MPa ,[σC ]=320MPa 。
在试验中为了确保试件在端部不被破坏,试设计试件端部的尺寸a 、b 和销钉的直径d 。
解:(1)求所需拉力F由N A F b 31060)503(040⨯=⨯⨯=≥中σ。
(2)求销钉直径d 由剪切强度条件][42τπτ≤==d F A Q Q 得,)(6.2710010604][43mm Fd =⨯⨯⨯=≥πτπ;由挤压强度条件][C C C C dt F A P σσ≤==得,)(5.3732051060][3mm t F d C =⨯⨯=≥σ 所以销钉直径取[d]=40mm 。
(3)求边尺寸a 和b 由由剪切强度条件][2ττ≤==ta F A Q Q 得,)(60100521060][23mm t F a =⨯⨯⨯=≥τ。
由由拉压强度条件][)(σσ≤-==d b t FA N 得,)(1154016051060][3mm d t F b =+⨯⨯=+≥σ。
4-1圆轴受力如图所示m KN M ⋅=11,m KN M ⋅=6.02,m KN M ⋅=2.03,m KN M ⋅=2.04。
(1)作轴的扭矩图。
(2)若外力偶矩1M 、2M 的位置互换,扭矩图有何变化 解:(1)作轴的扭矩图 如图4-1a 所示。
图4-1图(2扭矩为max 1000T N m =⋅。
4-10 两段直径均为d=100mm 的圆轴用法兰和螺栓连接成传动轴,如图所示。
已知轴受扭时最大切应力τMax =70MPa ,螺栓的直径d 1=20mm ,并布置在D =200mm 的圆周上,设螺栓的许用切应力为[τ]=60MPa ,试求所需螺栓的个数。
解:(1)求圆轴上的扭矩16/3d MMaxπτ= → mm N d M Max .10374.1167010016733⨯=⨯⨯==πτπ。
