系统辨识试验
哈工大系统辨识实验三

zl=[z(3:16)]'
hl1=-z(2:15)'
hl2=-z(1:14)'
hl3=u(2:15)'
hl4=u(1:14)'
Hl=[hl1,hl2,hl3,hl4];
theta=((Hl'*Hl)^-1)*Hl'*zl;
disp('辨识后得到的参数:')
disp(theta)
end
function m=m_xulie(n,k)%n为M序列的阶数k为序列的长度
………………………………………………………………………………………….....(2)
设
,
则式(2)可写为
…………………………………………………………………………….(3)
式中:y为N维输出向量; 为N维噪声向量; 为 维参数向量; 为 测量矩阵。为了尽量减小噪声 对 估值的影响,应取 ,即方程数目大于未知数数目。
通过本次上机实验课程,我体会到了最小二乘法辨识是一种近代的系统辨识方法,其优点是只需要考虑系统的输入输出特性,而不强调系统的内部机理。适用于单输入单输出系统的差分方程模型中的参数估计。
最后感谢老师在指导我们上机实验当中所付出的努力。
当系统中没有白噪声时,理论上应该得到准确的参数,我们把模型中的v(k)项剔除,得到以下的辨识结果:
这说明当不存在白噪声时,可以精确获得精确的估计值 ,估计值 的均方差随着噪声的均方差的增大而增大。
8
在这次上机实验当中,我们跟着老师学会了运用最小二乘法实现对系统的参数的估计,估计结果与系统的实际参数存在一定的偏差,原因是白噪声对系统的干扰造成的。
x(j)=X(n);
end
x=-2*x+ones(1,k);
系统辨识实验报告
i=1:800; figure(1) plot(i,Theta(1,:),i,Theta(2,:),i,Theta(3,:),i,Theta(4,:),i,Theta(5,:),i,T title('待估参数过渡过程') figure(2) plot(i,Pstore(1,:),i,Pstore(2,:),i,Pstore(3,:),i,Pstore(4,:),i,Pstore(5,: title('估计方差变化过程')
最小二乘法建模:
二、三次实验 本次实验要完成的内容: 1.参照index2,设计对象,从workspace空间获取数据,取二阶,三阶 对象实现最小二乘法的一次完成算法和最小二乘法的递推算法(LS and RLS); 2.对设计好的对象,在时间为200-300之间,设计一个阶跃扰动,用最 小二乘法和带遗忘因子的最小二乘法实现,对这两种算法的特点进行说 明; 实验内容结果与程序代码: 利用LS和RLS得到的二阶,三阶参数 算法 阶次 A1 A2 A3 B0 B1 B2 B3 LS 二阶 -0.78420.1373 -0.00360.5668 0.3157 RLS 二阶 -0.78240.1373 -0.00360.5668 0.3157 LS 三阶 -0.4381-0.12280.0407 -0.00780.5652 0.5106 0.1160
测试对象流程图 实验结果为:
2、加入噪声干扰 搭建对象
实验结果:
加入噪声干扰之后水箱输出不平稳,有波动。
实验二:相关分析法 搭建对象:
处理程序: for i=1:15 m(i,:)=UY(32-i:46-i,1);
end y=UY(31:45,2); gg=ones(15)+eye(15); g=1/(25*16*2)*gg*m*y; plot(g); hold on; stem(g); 实验结果: 相关分析法
系统辨识基础实验指导书

实验一 离散模型的参数辨识一、实验目的1. 掌握随机序列的产生方法。
2. 掌握最小二乘估计算法的基本原理。
3. 掌握最小二乘递推算法。
二、实验内容1. 基于Box--Jinkins 模型模拟一个动态过程,动态过程取为各种不同的情况,输入信号采用M 序列,实验者可尝试不同周期的M 序列。
信噪比、观测数据长度也由实验者取为各种不同情况。
2. 模拟生成输入输出数据。
3. 根据仿真过程的噪声特性,选择一种模型参数估计算法,如RLS 、RIV 、RELS 、RGLS 、COR-LS 、STAA 、RML 或MLS 等,估计出模型的参数。
三、实验器材计算机 1台四、实验原理最小二乘法是一种经典的有效的数据处理方法。
它是1795年高斯(K.F.Guass )在预测行星和彗星运动的轨道时提出并实际使用的。
最小二乘法也是一种根据实验数据进行参数估计的主要方法。
这种方法容易被理解,而且由于存在唯一解,所以也比较容易实现。
它在统计学文献中还被称为线性回归法,在某些辨识文献中还被称为方程误差法。
正如各个学科都用到系统辨识技术建立模型一样,最小二乘法也用于很多场合进行参数估计,虽然不一定是直接运用,但很多算法是以最小二乘为基础的。
在系统辨识和参数估计领域中,最小二乘法是一种最基本的估计方法。
它可用于动态系统,也可用于静态系统;可用于线性系统,也可用于非线性系统;可用于离线估计,也可用于在线估计。
在随机的环境下利用最小二乘法时,并不要求知道观测数据的概率统计信息,而用这种方法所获得的估计结果,却有相当好的统计性质。
在系统辨识和参数估计领域中,应用最广泛的估计方法是最小二乘法和极大似然法,而其他的大多数算法都与最小二乘法有关。
最小二乘法采用的模型为11()()()()()A z y k B z u k e k --=+最小二乘估计是在残差二乘方准则函数极小意义下的最优估计,即按照准则函数ˆˆˆˆ()()min T T J ee Y Y ΦθΦθ==--= 来确定估计值ˆθ。
系统辨识实验三

《系统辨识》课程报告题目:最小二乘参数估计法班级:工控08.1姓名:学号:日期:2011.6.1成都信息工程学院控制工程学院最小二乘参数估计摘要:最小二乘法提供了一个估算方法,使之能得到一个在最小方差意义上与实验数据最好拟合的数学模型。
最小二乘的一次性完成辨识算法,他的特点是直接利用已经获得的观测数据进行运算处理。
求出一个使各次实际观测和计算值之间的差值的平方乘以度量其精度的数值以后的和为最小的数值,求出带辨识参数。
最小二乘辩识方法在系统辩识领域中先应用上已相当普及,方法上相当完善,可以有效的用于系统的状态估计,参数估计以及自适应控制及其他方面。
关键词:最小二乘法,AIC 准则,M 序列1 引言:最小二乘法是 1795 年高斯在预测星体运行轨道最先提出的 , 它奠定了最小二乘估计理论的基础 . 到 20 世纪 60 年代瑞典学者 Austron 把这个方法用于动态系统的辨识中 , 在这种辨识方法中 , 首先给出模类型 , 在该类型下确定系统模型的最优参数 .这种具有格式规范的辨识方法可以演绎成递推形式 .递推最小二乘算法计算量小 , 可以用于在线辨识 , 即使辨识对象随时间发生化 , 模型也可以对其进行跟踪断地进行更新和修正辨识参数 , 从而成为一种被广泛采用的辨识方法,最小二乘法有一次完成算法和递推算法,其中 一次完成算法存在一定的局限性,工业系统辨识常采用递推算法进行系统辨识。
2 实验原理:由于运用最小二乘一次完成算法进行系统参数辨识的时候,存在一定的限定条件,并且需要用到全部的观测数据,每采样一次就需要增添一组新的观察数据,所以引入递推最小二乘法来辨识系统参数,递推最小二乘法是用旧的估计值加上修正值得到的新的估计值,用新的测量数据对上一次的估计结果进行修正,直到估计值达到需要的精度为止。
2.1根据汉格尔矩阵估计模型的阶次设一个可观可控的SISO 过程的脉冲响应序列为{个g(1),g(2),……g(L)},可以通过汉格尔(Hankel )矩阵的秩来确定系统的阶次。
系统辨识实验二

《系统辨识》实验二要点实验二 递推最小二乘估计(RLS)及模型阶次辨识(F-Test )一、实验目的① 通过实验,掌握递推最小二乘参数辨识方法 ② 通过实验,掌握F-Test 模型阶次辨识方法二、实验内容1、仿真模型实验所用的仿真模型如下: 框图表示模型表示)()2(5.0)1()2(7.0)1(5.1)(k v k u k u k z k z k z λ+-+-=-+-- 其中u (k )和z (k )分别为模型的输入和输出变量;v (k )为零均值、方差为1、服从正态分布的白噪声;λ为噪声的标准差(实验时,可取0.0、0.1、0.5、1.0);输入变量u (k )采用M 序列,其特征多项式取1)(4⊕⊕=s s s F ,幅度取1.0。
2、辨识模型辨识模型的形式取)()()()()(11k e k u z B k z z A +=--为方便起见,取n n n b a ==,即nn nn zb z b z b z B z a z a z a z A ------+++=++++= 22112211)(1)(根据仿真模型生成的数据{}L k k u ,,1),( =和{}L k k z ,,1),( =,辨识模型的参数n n b b b a a a ,,,,,,2121 和;并确定模型阶次n ,同时估计出模型误差)(k e 的方差(应近似等于模型噪声)(k v 的方差,即为2λ)和模型的静态增益K 。
3、辨识算法① 采用递推遗忘因子法:[][][]⎪⎪⎩⎪⎪⎨⎧--=+--=--+-=-)1()()(1)()()1()()()1()()1()()()()1()(1k k k μk μk k k k k k k k k z k k k P h K I P h P h h P K h K τττθθθ 其中,遗忘因子10≤<μ(具体值根据情况自已确定);数据长度L 可取100、300、500;初始值⎩⎨⎧==IP 2)0()0(a εθ。
系统辨识实验报告30288
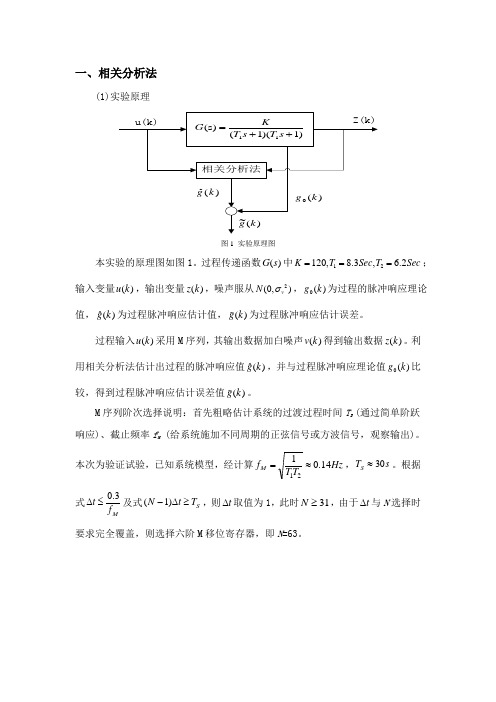
一、相关分析法(1)实验原理图1 实验原理图本实验的原理图如图1。
过程传递函数()G s 中12120,8.3, 6.2K T Sec T Sec ===;输入变量()u k ,输出变量()z k ,噪声服从2(0,)v N σ,0()g k 为过程的脉冲响应理论值,ˆ()gk 为过程脉冲响应估计值,()g k 为过程脉冲响应估计误差。
过程输入()u k 采用M 序列,其输出数据加白噪声()v k 得到输出数据()z k 。
利用相关分析法估计出过程的脉冲响应值ˆ()gk ,并与过程脉冲响应理论值0()g k 比较,得到过程脉冲响应估计误差值()g k 。
M 序列阶次选择说明:首先粗略估计系统的过渡过程时间T S (通过简单阶跃响应)、截止频率f M (给系统施加不同周期的正弦信号或方波信号,观察输出)。
本次为验证试验,已知系统模型,经计算Hz T T f M 14.0121≈=,s T S 30≈。
根据式Mf t 3.0≤∆及式S T t N ≥∆-)1(,则t ∆取值为1,此时31≥N ,由于t ∆与N 选择时要求完全覆盖,则选择六阶M 移位寄存器,即N =63。
(2)编程说明图2 程序流程图(3)分步说明 ① 生成M 序列:M 序列的循环周期63126=-=N ,时钟节拍1t Sec ∆=,幅度1a =,移位寄存器中第5、6位的内容按“模二相加”,反馈到第一位作为输入。
其中初始数据设为{1,0,1,0,0,0}。
程序如下:② 生成白噪声序列: 程序如下:③ 过程仿真得到输出数据:如图2所示的过程传递函数串联,可以写成形如121211()1/1/K Gs TT s T s T =++,其中112KK TT =。
图2 过程仿真方框图程序如下:④ 计算脉冲响应估计值:互相关函数采用公式)()(1)(10k i y i x Nr k R N r i xy +⋅⋅=∑-⋅=,互相关函数所用的数据是从第二个周期开始的,其中r 为周期数,取1-3之间。
系统辨识试验

2.用普通最小二乘法(OLS )法辨识对象数学模型 选择的仿真对象的数学模型如下)()2(5.0)1()2(7.0)1(5.1)(k v k u k u k z k z k z +-+-=-+--其中,)(k v 是服从正态分布的白噪声N )1,0(。
输入信号采用4阶M 序列,幅度为1。
选择如下形式的辨识模型)()2()1()2()1()(2121k v k u b k u b k z a k z a k z +-+-=-+-+设输入信号的取值是从k =1到k =16的M 序列,则待辨识参数LSθˆ为LS θˆ=L τL 1L τL z H )H H -(。
其中,被辨识参数LSθˆ、观测矩阵z L 、H L 的表达式为 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=2121ˆb b a a LSθ , ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=)16()4()3(z z z L z , ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------=)14()2()1()15()3()2()14()2()1()15()3()2(u u u u u u z z z z z z LH 程序框图如下所示:参考程序:%olsu=[-1,1,-1,1,1,1,1,-1,-1,-1,1,-1,-1,1,1]; %系统辨识的输入信号为一个周期的M 序列z=zeros(1,16); %定义输出观测值的长度for k=3:16z(k)=1.5*z(k-1)-0.7*z(k-2)+u(k-1)+0.5*u(k-2); %用理想输出值作为观测值endsubplot(3,1,1) %画三行一列图形窗口中的第一个图形stem(u) %画出输入信号u的经线图形subplot(3,1,2) %画三行一列图形窗口中的第二个图形i=1:1:16; %横坐标范围是1到16,步长为1plot(i,z) %图形的横坐标是采样时刻i, 纵坐标是输出观测值z, 图形格式为连续曲线subplot(3,1,3) %画三行一列图形窗口中的第三个图形stem(z),grid on%画出输出观测值z的经线图形,并显示坐标网格u,z%显示输入信号和输出观测信号%L=14%数据长度HL=[-z(2) -z(1) u(2) u(1);-z(3) -z(2) u(3) u(2);-z(4) -z(3) u(4) u(3);-z(5) -z(4) u(5) u(4);-z(6) -z(5) u(6) u(5);-z(7) -z(6) u(7) u(6);-z(8) -z(7) u(8) u(7);-z(9) -z(8) u(9) u(8);-z(10) -z(9) u(10) u(9);-z(11) -z(10) u(11) u(10);-z(12) -z(11) u(12) u(11);-z(13) -z(12) u(13) u(12);-z(14) -z(13) u(14) u(13);-z(15) -z(14) u(15) u(14)] %给样本矩阵HL赋值ZL=[z(3);z(4);z(5);z(6);z(7);z(8);z(9);z(10);z(11);z(12);z(13);z(14);z(15);z(16)]% 给样本矩阵zL赋值%calculating parameters%计算参数c1=HL'*HL; c2=inv(c1); c3=HL'*ZL; c=c2*c3 %计算并显示%DISPLAY PARAMETERSa1=c(1), a2=c(2), b1=c(3), b2=c(4) %从中分离出并显示a1 、a2、 b1、 b2%End注:由于输出观测值没有任何噪音成分,所以辨识结果也无任何误差,同学们可以在输出观测值中添加噪音,观察ols的辨识效果。
系统辨识实验报告

系统辨识实验报告自动化0903班09051302 李姣实验一、系统辨识的经典方法系统的模块如图:(1)、对系统的传递函数进行辨识。
对于一阶系统而言,未加入干扰信号时,其稳定值 t0=20.0,h0=42.2040, 加入干扰信号后其稳定值为 t=40,h1=60.4937。
现在分别取两个点为y1=30%对应的实际点为 h1’=42.2040+(60.4937-42.2040)*30%=47.6909; 根据实际测试值,选取h1’=47.8909,t1’=20.6,对应的 y1’=(47.89*09-42.2040)/(60.4939-42.2040)=0.3109 所以第一个点的取值为 y1’=0.3109;t1’=0.6; 同理可得第二个点的数值为 y2’=0.8033;t2’=2.7; 由公式 :可得 T=1.6750;=0; 由公式可得 k=1.82899(2)、对传递函数进行检验下面对系统的辨识结果进行验证,用一个幅值为10的阶跃信号进行验证,程序如下: num=[1.82899]; den=[1.675,1];()()()()()()2112211212t t T ln 1Y ln 1Y t ln 1Y t ln 1Y ln 1Y ln 1Y -⎧=⎪---⎪⎨---⎪τ=⎪---⎩()y y K u u∞∆==∆∆t=[0:0.1:10];[y,x,t]=step(num,den,t);plot(t,10*y)grid on;title('一阶系统模型的验证');xlabel('仿真时间');ylabel('系统的响应值');set(gca,'xtick',[0:0.5:10]);set(gca,'ytick',[0:1:20]);所得的仿真图形如下,实际系统加入测试信号后0.5s,从workspace中可发现系统的响应值为h=47.0929-42.2040=4.8889;验证是的对应仿真值为h’=4.4720;其误差大小为:(4.8889-4.4720)/4.8889*100%=8.536%;同理,当仿真时间为3.8s时,h=16.3993;h’=16.398;误差大小为:(16.3993-16.398)/16.3993*100%=0.08%;所以经过验证个,可以确定该辨识结果可以反应该系统的传递函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、用普通最小二乘法(OLS)法辨识对象数学模型选择得仿真对象得数学模型如下)()2(5.0)1()2(7.0)1(5.1)(k v k u k u k z k z k z +-+-=-+--其中,)(k v 就是服从正态分布得白噪声N )1,0(。
输入信号采用4阶M 序列,幅度为1。
选择如下形式得辨识模型)()2()1()2()1()(2121k v k u b k u b k z a k z a k z +-+-=-+-+设输入信号得取值就是从k =1到k =16得M 序列,则待辨识参数LSθˆ为LS θˆ=L τL 1L τL z H )H H -(。
其中,被辨识参数LSθˆ、观测矩阵z L 、H L 得表达式为 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=2121ˆb b a a LS θ , ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=)16()4()3(z z z L z , ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------=)14()2()1()15()3()2()14()2()1()15()3()2(u u u u u u z z z z z z L H 程序框图如下所示:参考程序:%olsM 序列z=zeros(1,16); %for k=3:16 z(k)=1、endsubplot(3,1,1) %stem(u) %subplot(3,1,2) %画三行一列图形窗口中得第二个图形i=1:1:16; %横坐标范围就是1到16,步长为1plot(i,z) %图形得横坐标就是采样时刻i, 纵坐标就是输出观测值z, 图形格式为连续曲线subplot(3,1,3) %画三行一列图形窗口中得第三个图形stem(z),grid on%画出输出观测值z得经线图形,并显示坐标网格u,z%显示输入信号与输出观测信号%L=14%数据长度HL=[-z(2) -z(1) u(2) u(1);-z(3) -z(2) u(3) u(2);-z(4) -z(3) u(4) u(3);-z(5) -z(4) u(5) u(4);-z(6) -z(5) u(6) u(5);-z(7) -z(6) u(7) u(6);-z(8) -z(7) u(8) u(7);-z(9) -z(8) u(9) u(8);-z(10) -z(9) u(10) u(9);-z(11) -z(10) u(11) u(10);-z(12) -z(11) u(12) u(11);-z(13) -z(12) u(13) u(12);-z(14) -z(13) u(14) u(13);-z(15) -z(14) u(15) u(14)] %给样本矩阵HL赋值ZL=[z(3);z(4);z(5);z(6);z(7);z(8);z(9);z(10);z(11);z(12);z(13);z(14);z(15);z(16)]% 给样本矩阵zL赋值%calculating parameters%计算参数c1=HL'*HL; c2=inv(c1); c3=HL'*ZL; c=c2*c3 %计算并显示%DISPLAY PARAMETERSa1=c(1), a2=c(2), b1=c(3), b2=c(4) %从中分离出并显示a1 、a2、 b1、 b2%End注:由于输出观测值没有任何噪音成分,所以辨识结果也无任何误差,同学们可以在输出观测值中添加噪音,观察ols得辨识效果。
同时,可以尝试增加输入信号得数量,瞧辨识结果有何变化。
实验二 基于RLS 法得系统辨识数字仿真实验一、实验目得1、深入理解系统辨识中相关分析法及最小二乘法得相关内容。
2、学会用Matlab 或C 语言等进行系统辨识得仿真研究二、实验设备装有相应软件得计算机。
三、实验原理1、 考虑如下图所示得仿真对象:图中,(v )(1-z G = ⎪⎪⎩⎪⎪⎨⎧=+==---1)(5.00.1)()(111z D z z z B z A 选择上图所示得辨识模型。
仿真对象选择如下得模型结构:)()2()1()2()1()(2121k v k u b k u b k z a k z a k z +-+-=-+-+ (2) 其中,)(k v 就是服从正态分布得白噪声N )1,0(。
输入信号采用4位移位寄存器产生得M 序列,幅度为0、03。
按式(3))()2(5.0)1()2(7.0)1(5.1)(k v k u k u k z k z k z +-+-=-+-- (3)构造h (k );加权阵取单位阵I Λ=L ;利用如下公式计算K (k )、)(ˆk θ与P (k ),计算各次参数辨识得相对误差,精度满足要求后停机。
递推最小二乘法得推导公式如下:(1)()()(1)(1)1(1)()(1)(1)()(1)(1)()(1)()(1)[][1](1)T k k k k k T k k k k k k Tk k k k k k y xK P x x P x P P k k x P θθθ∧∧∧+++-++++++=++-=+=-+ (4) 2、阶得辨识 前面所讨论得系统辨识方法,都就是假定模型得阶次就是已知得,因此仅仅要求估计差分方程得系数。
但实际上,系统得阶次就是很难被准确知道得。
因为对阶次得理解程度就是直接与一个线性差分方程得准确结构有关得,所以有关阶次得确定也可以称为系统结构得确定。
经验指出,一个模型得阶次不准,就可能在控制系统设计时发生严重问题。
故在辨识过程中,模型得阶次就是否合适就是必须加以检验得。
一般阶得方法中,常用得有这么几种:零极点相消法、目标函数法与F 检验法。
下面只介绍其中得目标函数法。
当我们用不同阶得模型给系统得输入——输出观测数据进行最小二乘拟合时,会得到不同得估计误差:因此利用J 极小化确定阶就是很自然得。
实验表明,假设模型具有大于1而小于max N 得阶n,当n 取1,2,…时, 若随着n 得增加, 在ˆn(阶得估计量)-1时,J 最后一次出现陡峭得下降,往后J 就近似地保持不变或者只有微小得下降(见下图),则取ˆn n=。
也就就是说,模型阶次得确定可以直接依次计算阶次n =1,2,…时得最小二乘估计ˆn以及相应得损失函数J ,然后选择当J 下降不明显时得阶次作为合适得模型阶次n,这种方法也叫确定阶得估计准则方法,有很广得应用。
Jn 四、实验内容1、 用递推最小二乘法2、 对象阶得辨识。
五、实验要求∑===Nk T EE k e J 12)(1、熟悉系统辨识中得相关内容。
2、掌握Matlab或C语言等进行系统辨识仿真研究得一般步骤。
3、实验前基本应完成相关得编程任务,实验时调试相应程序。
4、修改相应参数与随机噪声幅度,观察并分析结果。
5、软件包人机界面得开发与设计。
(选做)六、实验步骤1、首先要熟悉一下MATLAB得运行环境:1)File->New->M-File打开M文件编辑窗口2)输入自己编写得程序3)点击run按钮,如果程序出错则调试程序,如果运行正常得话则观察程序得运行结果2、用递推最小二乘法(RLS)法辨识对象数学模型在这个实验中,我们采用以下模型进行仿真:y=1.5*y[k-1]-0.7*y[k-2]+0*u[k]+1.0*u[k-1]+0.5*u[k-2]+e[k] (5),它x3=y2;%第三个移位积存器得输入就是第2个移位积存器得输出x4=y3;%第四个移位积存器得输入就是第3个移位积存器得输出y(i)=y4;%取出第四个移位积存器幅值为"0"与"1"得输出信号,if y(i)>0、5,u(i)=-0、03;%如果M序列得值为"1"时,辨识得输入信号取“-0.03”else u(i)=0、03;%当M序列得值为"0"时,辨识得输入信号取“0.03”end%小循环结束y1=x1;y2=x2;y3=x3;y4=x4;%为下一次得输入信号做准备end%大循环结束,产生输入信号ufigure(1);%第1个图形stem(u),grid on%以径得形式显示出输入信号并给图形加上网格z(2)=0;z(1)=0;%取z得前两个初始值为零for k=3:15;%循环变量从3到15z(k)=1、5*z(k-1)-0、7*z(k-2)+u(k-1)+0、5*u(k-2);%给出理想得辨识输出采样信号end%RLS递推最小二乘辨识c0=[0、001 0、001 0、001 0、001]';%直接给出被辨识参数得初始值,即一个充分小得实向量p0=10^6*eye(4,4);%直接给出初始状态P0,即一个充分大得实数单位矩阵E=0、000000005;%相对误差E=0、000000005c=[c0,zeros(4,14)];%被辨识参数矩阵得初始值及大小e=zeros(4,15);%相对误差得初始值及大小for k=3:15; %开始求Kh1=[-z(k-1),-z(k-2),u(k-1),u(k-2)]'; x=h1'*p0*h1+1; x1=inv(x); %开始求K(k)k1=p0*h1*x1;%求出K得值d1=z(k)-h1'*c0; c1=c0+k1*d1;%求被辨识参数ce1=c1-c0;%求参数当前值与上一次得值得差值e2=e1、/c0;%求参数得相对变化e(:,k)=e2; %把当前相对变化得列向量加入误差矩阵得最后一列c0=c1;%新获得得参数作为下一次递推得旧参数c(:,k)=c1;%把辨识参数c 列向量加入辨识参数矩阵得最后一列p1=p0-k1*k1'*[h1'*p0*h1+1];%求出 p(k)得值p0=p1;%给下次用if e2<=E break;%若参数收敛满足要求,终止计算end%小循环结束end%大循环结束c%显示被辨识参数e%显示辨识结果得收敛情况%分离参数a1=c(1,:); a2=c(2,:); b1=c(3,:); b2=c(4,:); ea1=e(1,:); ea2=e(2,:); eb1=e(3,:); eb2=e(4,:);figure(2);%第2个图形i=1:15;%横坐标从1到15plot(i,a1,'r',i,a2,':',i,b1,'g',i,b2,':') %画出a1,a2,b1,b2得各次辨识结果title('Parameter Identification with Recursive Least Squares Method')%图形标题figure(3); %第3个图形i=1:15; %横坐标从1到15plot(i,ea1,'r',i,ea2,'g',i,eb1,'b',i,eb2,'r:') %画出a1,a2,b1,b2得各次辨识结果得收敛情况title('Identification Precision') %图形标题注:同样这个程序使用得输出信号也没有噪音,所以辨识得结果没有误差,请同学们在输出信号中加入噪音,再使用RLS对其辨识,观察辨识结果,进行分析。
