机械振动大作业.
机械振动作业
实际背景：汽车拖车在凹凸不平的道路上行驶，车身颠簸得厉害，容易损坏机件，甚至驾驶员失去对方向的控制而发生危险。
汽车可能有的振源 ：第一，发动机非均匀运动，或发动机与车体的共振；第二，路面不平，地面对车轮的作用。
由于振动，使得汽车的车体发生共振，所以，汽车的共振频率检测是振动工程中一项重要的技术。
除了了解车体的振动情况外，主要要掌握各种不同路面的路况谱，这可通过实地检测而获得。
根据路况谱可计算出车在行驶过程中所受到的作用力F ，并根据车体模型通过计算选出阻尼c 与弹性k 。
由于F 很复杂，可能有多种频率或方向的成分，因此，可能要用多个c 与k 。
现将实际问题转化为数学模型，求振幅比。
汽车的拖车在波形道路上行驶，已知拖车的质量满载时为 1000kg =m 1，空载时为 kg 250m 2=，悬挂弹簧的刚度为kN/m 350=k ，阻尼比在满载时为5.01=ζ，车速为 km/h 100= v ，5m =l ，路面呈正弦波形，可表示为l z a x f π2sin =。
求： 拖车在满载和空载时的振幅比？f z解： 由公式：lz a x f π2sin=得 汽车行驶的路程可表示为：vt z =t lv a x f π2sin = 路面的激励频率：s rad l v /9.342==πω 得：km c c cr ξξ2== c 、k 为常数，因此 ξ 与m 成反比， 因此得到空载时的阻尼比为： 0.12112==m m ξξ 满载和空载时的频率比： 87.11011===km s ωωω 93.02022===k m s ωωω 因为有：km c cr 2= 02ξω=mc 所以当：满载时阻尼比5.01=ξ空载时阻尼比0.12=ξ 满载时频率比87.11=s 空载时频率比93.02=s 记：满载时振幅 1B ，空载时振幅2B 有：68.0)2()1()2(12112212111=+-+=s s s a B ζζ13.1)2()1()2(12222222222=+-+=s s s a B ζζ 因此满载和空载时的振幅比： 60.021=B B。
哈工大机械振动基础大作业
《机械振动基础》大作业（2015年春季学期）题目基于MATLAB求系统特性姓名学号班级专业机械设计制造及其自动化报告提交日期哈尔滨工业大学报告要求1.请根据课堂布置的2道大作业题，任选其一，拒绝雷同和抄袭；2.报告最好包含自己的心得、体会或意见、建议等；3.报告统一用该模板撰写，字数不少于3000字，上限不限；4.正文格式：小四号字体，行距为倍行距；5.用A4纸单面打印；左侧装订，1枚钉；6.课程报告需同时提交打印稿和电子文档予以存档，电子文档由班长收齐，统一发送至：。
7.此页不得删除。
评语：成绩（15分）：教师签名：年月日解多自由度矩阵的认识体会。
二、MATLAB程序图：>> m=[];k1=[];k=[];c=[];c1=[];for i=1:9a=input('输入质量矩阵m：');m(i,i)=a;end ;for j=1:9b=input('输入刚度系数k：');k1(1,j)=b;endfor l=1:8k(l,l)=k1(l)+k1(l+1);k(9,9)=k1(9);k(l+1,l)=-k1(l+1);k(l,l+1)=-k1(l+1);k(9,8)=-k1(9);k(8,9)=-k1(9);end ;syms w;B=k-w^2*m %系统的特征矩阵BY=det(B); %展开行列式W=solve(Y); %求解whlW=length(W);[V,D]=eig(k,m);for I=1:9for J=1:9V(J,I)=V(J,I)/V(5,I);endendVW三 MATLAB结果输入输出：程序输入内容：输入质量矩阵m：1输入质量矩阵m：2输入质量矩阵m：3输入质量矩阵m：4输入质量矩阵m：5输入质量矩阵m：6输入质量矩阵m：7输入质量矩阵m：8输入质量矩阵m：9输入刚度系数k：10输入刚度系数k：11输入刚度系数k：12输入刚度系数k：13输入刚度系数k：14输入刚度系数k：15输入刚度系数k：16输入刚度系数k：17输入刚度系数k：18Matlab 输出界面截图：输出结果：B =[ 21-w^2, -11, 0, 0, 0, 0, 0, 0, 0][ -11, 23-2*w^2, -12, 0, 0, 0, 0, 0, 0][ 0, -12, 25-3*w^2, -13, 0, 0,0, 0, 0][ 0, 0, -13, 27-4*w^2, -14, 0, 0, 0, 0][ 0, 0, 0, -14, 29-5*w^2, -15, 0, 0, 0][ 0, 0, 0, 0, -15, 31-6*w^2, -16, 0, 0][ 0, 0, 0, 0, 0, -16,33-7*w^2, -17, 0][ 0, 0, 0, 0, 0, 0, -17, 35-8*w^2, -18][ 0, 0, 0, 0, 0, 0, 0, -18, 18-9*w^2]V =W =.224079.403四. 心得体会：（一）利用Matlab 进行多自由度振动分析的体会：MATLAB是一种高性能软件平台,是一种面向科学与工程的高级语言,它集数值分析、矩阵运算、信号处理和图形显示于一体,构成了一个功能强大、方便、界面友好的用户环境。
机械振动大作业——简支梁的各情况分析
机械振动大作业姓名：徐强学号：SX1302106专业：航空宇航推进理论与工程能源与动力学院2013年12月简支梁的振动特性分析题目:针对简支梁、分别用单、双、三、十个自由度以及连续体模型，计算其固有频率、固有振型。
单、双、三自由度模型要求理论解；十自由度模型要求使用李兹法、霍尔茨法、矩阵迭代法、雅可比法、子空间迭代法求解基频；连续体要求推导理论解，并通过有限元软件进行数值计算。
解答：一、 单自由度简支梁的振动特性如图1，正方形截面（取5mm ×5mm ）的简支梁，跨长为l =1m ，质量m 沿杆长均匀分布，将其简化为单自由度模型，忽略阻尼，则运动微分方程为0=+••kx x m ,固有频率ωn =eqeq m k ，其中k 为等效刚度，eq m 为等效质量。
因此，求出上述两项即可知单自由度简支梁的固有频率。
根据材料力学的结果，由于横向载荷F 作用在简支梁中间位置而引起的变形为）（224348EI F -)(x l x x y -=（20l x ≤≤）, 48EI F -3max l y =为最大挠度，则： eq k =δF=348EIl梁本身的最大动能为：）（224348EI F -)(x l xx y -==）（223max43x l l x y -T max =2×dx x y l m l 220)(21⎭⎬⎫⎩⎨⎧•⎰=2max 351721•y m ）（如果用eq m 表示简支梁的质量等效到中间位置时的大小，它的最大动能可表示为：T max =2max21•y m eq所以质量为m 的简支梁，等效到中间位置的全部质量为： m m eq 3517=故单自由度简支梁横向振动的固有频率为：ωn =eqeq m k =3171680mlEImk图1 简支梁的单自由度模型二、 双自由度简支梁的振动特性如图2，将简支梁简化为双自由度模型，仍假设在简支梁中间位置作用载荷，根据对称性，等效质量相等,因此只要求出在3/l 处的等效质量即可。
机械振动基础作业(有答案-全版)
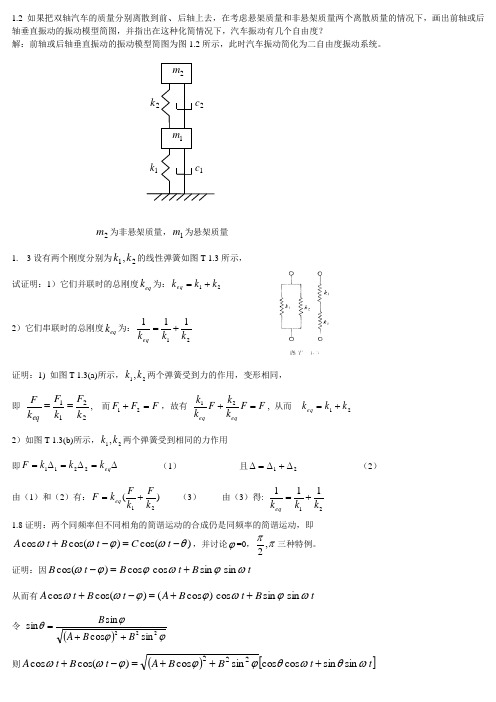
1.2 如果把双轴汽车的质量分别离散到前、后轴上去，在考虑悬架质量和非悬架质量两个离散质量的情况下，画出前轴或后轴垂直振动的振动模型简图，并指出在这种化简情况下，汽车振动有几个自由度？解：前轴或后轴垂直振动的振动模型简图为图1.2所示，此时汽车振动简化为二自由度振动系统。
2m 为非悬架质量，1m 为悬架质量1. 3设有两个刚度分别为21,k k 的线性弹簧如图T-1.3所示， 试证明：1）它们并联时的总刚度eq k 为：21k k k eq +=2）它们串联时的总刚度eq k 为：21111k k k eq +=证明：1) 如图T-1.3(a)所示，21,k k 两个弹簧受到力的作用，变形相同， 即2211k F k F k F eq ==, 而F F F =+21，故有 F F k kF k k eq eq =+21, 从而 21k k k eq +=2）如图T-1.3(b)所示，21,k k 两个弹簧受到相同的力作用 即∆=∆=∆=eq k k k F 2211 （1）且21∆+∆=∆ （2）由（1）和（2）有：)(21k Fk F k F eq += （3） 由（3）得:21111k k k eq += 1.8证明：两个同频率但不同相角的简谐运动的合成仍是同频率的简谐运动，即)cos()cos(cos θωϕωω-=-+t C t B t A ，并讨论ϕ=0，ππ,2三种特例。
证明：因t B t B t B ωϕωϕϕωsin sin cos cos )cos(+=-从而有t B t B A t B t A ωϕωϕϕωωsin sin cos )cos ()cos(cos ++=-+令 ()ϕϕϕθ222sin cos sin sin B B A B ++=则()[]t t B B A t B t A ωθωθϕϕϕωωsin sin cos cos sin cos )cos(cos 222+++=-+=())cos(sin cos 222θωϕϕ-++t B B A令C=()ϕϕ222sin cos B B A ++，则有 )cos()cos(cos θωϕωω-=-+t C t B t A当ϕ=0时，C=A+B ；当ϕ=2π时，22B A C +=，22BA arcsin +=B θ ；当ϕ=π时，B A -=C ，0=θ1.13汽车悬架减振器机械式常规性能试验台，其结构形式之一如图T-1.13所示。
机械振动分析与应用作业二
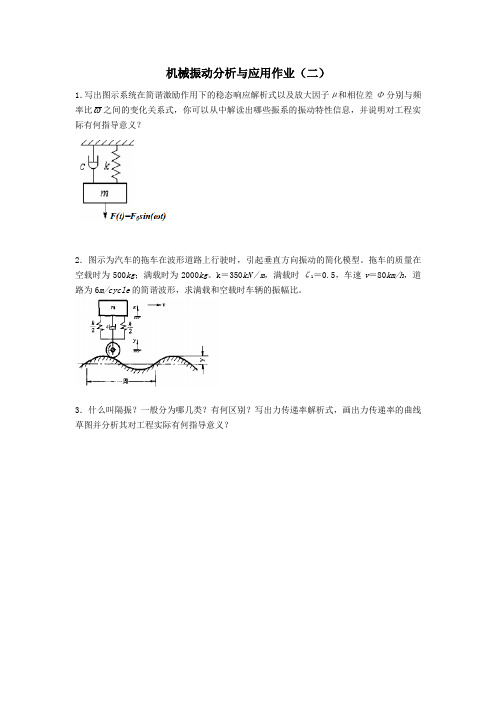
机械振动分析与应用作业（二）1．写出图示系统在简谐激励作用下的稳态响应解析式以及放大因子µ和相位差Φ分别与频率比 之间的变化关系式，你可以从中解读出哪些振系的振动特性信息，并说明对工程实际有何指导意义？2．图示为汽车的拖车在波形道路上行驶时，引起垂直方向振动的简化模型。
拖车的质量在空载时为500kg；满载时为2000kg。
k＝350kN／m，满载时ζ1＝0.5，车速v＝80km/h，道路为6m/cycle的简谐波形，求满载和空载时车辆的振幅比。
3．什么叫隔振？一般分为哪几类？有何区别？写出力传递率解析式，画出力传递率的曲线草图并分析其对工程实际有何指导意义？“柴油机推进轴系自由扭振计算”大作业1．已知条件1）主机型号：上海船厂Sulzer 6RTA58缸径/冲程：580mm/1700mm连杆长宽比：λ=0.327发火顺序：1-6-2-4-3-5单缸往复运动重量G：44100N标定功率/标定转速：7293kw/105r/min前飞轮+轴段转动惯量：J1=2597kg.m2单位气缸转动惯量：J2=J3=J4=J5=J6=J7=4741.1 kg.m2飞轮+1/2中间轴转动惯量：J8=6585 kg.m2曲轴、主轴颈、曲柄销直径：600mm单位曲柄柔度：e23=e34=e45=e56=e67=0.1485×10-8Rad/N.m自由端轴段柔度：e12=0.10503×10-8Rad/N.m第六缸与飞轮间的轴段柔度：e78=0.168×10-8Rad/N.m2）轴段中间轴基本直径/长度：430mm/5700mm柔度：e89=1.6814×10-8Rad/N.m轴段集中转动惯量（法兰+1/2中间轴+1/2桨轴）：J9=378.505 kg.m2螺旋桨轴基本直径/长度：520mm /612.5mm=1.02357×10-8Rad/N.m柔度：e9，10加入螺旋桨中的1/2桨轴转动惯量：J10=413.83 kg.m2 3）螺旋桨直径/桨叶（D P/Z P）：6m/4螺距比（H P/ D P）：0.778盘面比（A S/A）：0.511重量：143619N螺旋桨转动惯量（干）：21136.85 kg.m2附连水系数：1.232．计算1）自由振动单节点、双节点固有频率、振型图、应力尺标。
机械振动现象练习题(含答案)
机械振动现象练习题(含答案)1. 一个弹簧常数为3000 N/m, 质量为0.2 kg的物体，在弹簧下端受到一个向下的力2 sin(10t) N，其中t为时间（秒）。
求物体的振动方程。
根据牛顿第二定律，可以得到物体的振动方程为：m * x'' + k * x = F(t)其中，m是物体的质量，x是物体的位移，x''是位移对时间的二阶导数，k是弹簧的常数，F(t)是作用在物体上的外力。
根据题目中给出的数据，代入上述公式，我们可以得到：0.2 * x'' + 3000 * x = 2 sin(10t)这就是物体的振动方程。
2. 一个质点在受到一个力F(t) = 0.1 cos(3t) N的作用下进行振动，已知质点的质量为0.5 kg。
求质点的角频率和振动周期。
根据振动方程的形式，我们可以知道物体的振动频率和周期与力的形式有关。
在这个题目中，我们可以看出力的形式为cos(3t)，它是一个正弦函数。
如果将cos(3t)函数展开，我们可以得到下面的表达式：F(t) = a cos(wt)其中，a是振幅，w是角频率。
根据题目中给出的数据，我们可以得到：a = 0.1 N，w = 3 rad/s由于振动的频率与角频率之间是有关联的，振动的周期T可以表示为：T = 2π/w代入上述数据，我们可以得到：T = 2π/3 s这就是质点的振动周期。
3. 一个质点质量为0.3 kg，在一竖直方向上的弹簧中振动，弹簧的劲度系数为2000 N/m。
当质点受到一个外力F(t) = 0.5 cos(5t) N时，求质点的振动方程。
根据题目中给出的数据，我们可以得到：m = 0.3 kg，k = 2000 N/m，F(t) = 0.5 cos(5t)代入振动方程的一般形式，我们可以得到：0.3 * x'' + 2000 * x = 0.5 cos(5t)这就是质点的振动方程。
机械振动作业(教师用)
第1讲机械振动时间：60分钟1．弹簧振子在光滑水平面上做简谐运动，在振子向平衡位置运动的过程中()．A．振子所受的回复力逐渐增大B．振子的位移逐渐增大C．振子的速度逐渐减小D．振子的加速度逐渐减小解析分析这类问题，关键是首先抓住回复力与位移的关系，然后运用牛顿运动定律逐步分析．在振子向平衡位置运动的过程中，振子的位移逐渐减小，因此，振子所受回复力逐渐减小，加速度逐渐减小，但加速度方向与速度方向相同，故速度逐渐增大．答案 D2．一质点做简谐运动时，其振动图象如图1-1-17所示．由图可知，在t1和t2时刻，质点运动的()．图1-1-17A．位移相同B．回复力相同C．速度相同D．加速度相同解析从题图中可以看出在t1和t2时刻，质点的位移大小相等、方向相反．则有，在t1和t2时刻质点所受的回复力大小相等、方向相反，加速度大小相等、方向相反，A、B、D错误；在t1和t2时刻，质点都是从负最大位移向正最大位移运动，速度方向相同，由于位移大小相等，所以速度大小相等，C正确，本题答案为C.答案 C3．如图1-1-18是一做简谐运动的物体的振动图象，下列说法正确的是()．1-1-18A．振动周期是2×10－2 sB．前2×10－2 s内物体的位移是－10 cmC．物体的振动频率为25 HzD．物体的振幅是10 cm解析物体做简谐运动的周期、振幅是振动图象上明显标识的两个物理量，由题图知，周期为4×10－2s，振幅为10 cm，频率f＝1T＝25 Hz，选项A错误，C、D正确；前2×10－2 s内物体从平衡位置又运动到平衡位置，物体位移为0，选项B错误．答案CD4．(2011·上海卷，5)两个相同的单摆静止于平衡位置，使摆球分别以水平初速v1、v2(v1＞v2)在竖直平面内做小角度摆动，它们的频率与振幅分别为f1、f2和A1、A2，则()．A．f1＞f2，A1＝A2B．f1＜f2，A1＝A2C．f1＝f2，A1＞A2D．f1＝f2，A1＜A2解析单摆的频率由摆长决定，摆长相等，频率相等，所以A、B错误；由机械能守恒，小球在平衡位置的速度越大，其振幅越大，所以C正确、D错误．答案 C5．如图1-1-19所示为某弹簧振子在0～5 s内的振动图象，由图可知，下列说法中正确的是()．图1-1-19A．振动周期为5 s，振幅为8 cmB．第2 s末振子的速度为零，加速度为负向的最大值C．第3 s末振子的速度为正向的最大值D．从第1 s末到第2 s末振子在做加速运动解析根据题图象可知，弹簧振子的周期T＝4 s，振幅A＝8 cm，选项A错误；第2 s末振子到达负的最大位移处，速度为零，加速度最大，且沿x轴正方向，选项B错误；第3 s末振子经过平衡位置，速度达到最大，且向x轴正方向运动，选项C正确；从第1 s末到第2 s末振子经过平衡位置向下运动到达负的最大位移处，速度逐渐减小，选项D错误．答案 C6．图1-1-20为一弹簧振子的振动图象，由此可知()．图1-1-20A．在t1时刻，振子的动能最大，所受的弹性力最大B．在t2时刻，振子的动能最大，所受的弹性力最小C．在t3时刻，振子的动能最大，所受的弹性力最小D．在t4时刻，振子的动能最大，所受的弹性力最大解析从题图象的横坐标和纵坐标可知此图是振动图象，它所描述的是一个质点在不同时刻的位置，t2和t4是在平衡位置处，t1和t3是在最大位移处，根据弹簧振子振动的特征，弹簧振子在平衡位置时的速度最大，加速度为零，即弹性力为零；在最大位移处，速度为零，加速度最大，即弹性力为最大，所以B正确．答案 B7．下表记录了某受迫振动的振幅随驱动力频率变化的关系，若该振动系统的固有频率为f固，则().A．f固＝60 Hz B．60 Hz<f固<70 HzC．50 Hz<f固<60 Hz D．以上三项都不对解析从图所示的共振曲线，可判断出f驱与f固相差越大，受迫振动的振幅越小；f驱与f固越接近，受迫振动的振幅越大．并从中看出f驱越接近f固，振幅的变化越慢．比较各组数据知f驱在50 Hz～60 Hz范围内时，振幅变化最小，因此，50 Hz<f固<60 Hz，即C选项正确．答案 C8. (1)将一个电动传感器接到计算机上，就可以测量快速变化的力，用这种方法测得的某单摆摆动时悬线上拉力的大小随时间变化的曲线如图1-2-21所示．某同学由此图象提供的信息作出的下列判断中，正确的是________．图1-2-21A．t＝0.2 s时摆球正经过最低点B．t＝1.1 s时摆球正经过最低点C．摆球摆动过程中机械能减小D．摆球摆动的周期是T＝1.4 s(2)如图1-2-22所示为同一地点的两单摆甲、乙的振动图象，下列说法中正确的是________．图1-2-22A．甲、乙两单摆的摆长相等B．甲摆的振幅比乙摆大C．甲摆的机械能比乙摆大D．在t＝0.5 s时有正向最大加速度的是乙摆解析(1)悬线拉力在经过最低点时最大，t＝0.2 s时，F有正向最大值，故A 选项正确，t＝1.1 s时，F有最小值，不在最低点，周期应为T＝1.0 s，因振幅减小，故机械能减小，C选项正确．(2)振幅可从题图上看出甲摆振幅大，故B对．且两摆周期相等，则摆长相等，因质量关系不明确，无法比较机械能．t＝0.5 s时乙摆球在负的最大位移处，故有正向最大加速度，所以正确答案为A、B、D.答案(1)AC(2)ABD9．(2012·浙江温州二模，19)图1-1-23在光滑水平面上有两个完全相同的弹簧振子a和b，O1、O2为其平衡位置，如图1-1-23所示．今将a向右拉伸4 cm，将b向右压缩2 cm，同时由静止释放，不计空气阻力．下列说法正确的是()．A．两弹簧振子的小球经过平衡位置时的速度相同B．两弹簧振子的小球每次都在平衡位置处相遇C．两弹簧振子的小球不一定在平衡位置处相遇D．在振动过程中的任一时刻，a的机械能与b的机械能不会相等解析初始时刻势能不同，根据机械能守恒，平衡位置动能也不同，任意时刻机械能不同，A错，D对；周期与振幅无关，所以周期相同，每次都同时刻到达平衡位置，B对，C错．答案BD10．有一弹簧振子在水平方向上的BC之间做简谐运动，已知BC间的距离为20 cm，振子在2 s内完成了10次全振动．若从某时刻振子经过平衡位置时开始计时(t＝0)，经过14周期振子有正向最大加速度．图1-1-25(1)求振子的振幅和周期；(2)在图1125中作出该振子的位移—时间图象；(3)写出振子的振动方程．解析(1)振幅A＝10 cm，T＝210s ＝0.2 s.(2)四分之一周期时具有正的最大加速度，故有负向最大位移．如图所示．(3)设振动方程为y＝A sin(ωt＋φ)当t＝0时，y＝0，则sin φ＝0得φ＝0，或φ＝π，当再过较短时间，y为负值，所以φ＝π所以振动方程为y＝10sin(10πt＋π) cm.答案(1)10 cm0.2 s(2)如解析图(3)y＝10sin(10πt＋π) cm11．简谐运动的振动图线可用下述方法画出：如图1-1-26(1)所示，在弹簧振子的小球上安装一枝绘图笔P，让一条纸带在与小球振动垂直的方向上匀速运动，笔P在纸带上画出的就是小球的振动图象．取振子水平向右的方向为振子离开平衡位置的位移正方向，纸带运动的距离代表时间，得到的振动图线如图1126(2)所示．图1-1-26(1)为什么必须匀速拖动纸带？(2)刚开始计时时，振子处在什么位置？t＝17 s时振子相对平衡位置的位移是多少？(3)若纸带运动的速度为2 cm/s，振动图线上1、3两点间的距离是多少？(4)振子在______ s末负方向速度最大；在______ s末正方向加速度最大；2.5s时振子正在向______方向运动．(5)写出振子的振动方程．解析(1)纸带匀速运动时，由x＝v t知，位移与时间成正比，因此在匀速条件下，可以用纸带通过的位移表示时间．(2)由图(2)可知t＝0时，振子在平衡位置左侧最大位移处；周期T＝4 s，t＝17 s时位移为零．(3)由x＝v t，所以1、3两点间距x＝4 cm.(4)3 s末负方向速度最大；加速度方向总是指向平衡位置，所以t＝0或t＝4 s时正方向加速度最大；t＝2.5 s时，振子向－x方向运动．(5)x ＝10sin ⎝ ⎛⎭⎪⎫π2t －π2 cm.答案 (1)在匀速条件下，可以用纸带通过的位移表示时间 (2)左侧最大位移 零 (3)4 cm (4)3 0或4 －x (5)x ＝10sin ⎝ ⎛⎭⎪⎫π2t －π2 cm1．在做“用单摆测定重力加速度”的实验中，有人提出以下几点建议： A ．适当加长摆线B ．质量相同、体积不同的摆球，应选用体积较大的C ．单摆偏离平衡位置的角度不能太大D ．当单摆经过平衡位置时开始计时，经过一次全振动后停止计时，用此时间间隔作为单摆振动的周期其中对提高测量结果精确度有利的是________．解析 适当加大摆线长度，有利于把摆球看成质点，在摆角小于10°的条件下，摆球的空间位置变化较大，便于观察，A 正确；摆球体积越大，所受空气阻力越大，对质量相同的摆球其影响越大，B 错误；摆角应小于10°，C 正确；本实验采用累积法测量周期，若仅测量一次全振动，由于球过平衡位置时速度较大，难以准确记录，且一次全振动的时间太短，偶然误差较大，D 错误． 答案 AC5.某同学在做“探究单摆周期与摆长的关系”的实验中，先测得摆线长78.50 cm ，摆球直径2.0 cm.然后将一个力电传感器接到计算机上，实验中测量快速变化的力，悬线上拉力F 的大小随时间t 的变化曲线如图1-5-9所示．图1-5-9(1)该摆摆长为________ cm. (2)该摆摆动周期为________ s.(3)测得当地重力加速度g 的值为________ m/s 2.(4)如果测得g值偏小，可能原因是()．A．测摆线长时摆线拉得过紧B．摆线上端悬点未固定好，摆动中出现松动C．计算摆长时，忘记了加小球半径D．读单摆周期时，读数偏大解析(1)摆长＝摆线长＋小球半径＝78.50 cm＋1.0 cm＝79.50 cm.(2)由Ft变化图线可知，T＝1.8 s.(3)g＝4π2lT2＝4×3.142×79.501.82cm/s2≈9.68 m/s2.(4)由g＝4π2lT2可知g值偏小的可能原因是：l的测量值偏小，B、C正确，A错误，也可能是T值偏大，D对．答案(1)79.50(2)1.8(3)9.68(4)BCD。
机械振动试题(含答案)(1)
机械振动试题(含答案)(1)一、机械振动 选择题1．如图所示，在一根张紧的水平绳上，悬挂有 a 、b 、c 、d 、e 五个单摆，让a 摆略偏离平衡位置后无初速释放，在垂直纸面的平面内振动；接着其余各摆也开始振动，当振动稳定后，下列说法中正确的有（ ）A ．各摆的振动周期与a 摆相同B ．各摆的振动周期不同，c 摆的周期最长C ．各摆均做自由振动D ．各摆的振幅大小不同，c 摆的振幅最大2．如图所示，质量为m 的物块放置在质量为M 的木板上，木板与弹簧相连，它们一起在光滑水平面上做简谐振动，周期为T ，振动过程中m 、M 之间无相对运动，设弹簧的劲度系数为k 、物块和木板之间滑动摩擦因数为μ，A ．若t 时刻和()t t +∆时刻物块受到的摩擦力大小相等，方向相反，则t ∆一定等于2T 的整数倍 B ．若2T t ∆=，则在t 时刻和()t t +∆时刻弹簧的长度一定相同 C ．研究木板的运动，弹簧弹力充当了木板做简谐运动的回复力 D ．当整体离开平衡位置的位移为x 时，物块与木板间的摩擦力大小等于m kx m M+ 3．用图甲所示的装置可以测量物体做匀加速直线运动的加速度，用装有墨水的小漏斗和细线做成单摆，水平纸带中央的虚线在单摆平衡位置的正下方。
物体带动纸带一起向左运动时，让单摆小幅度前后摆动，于是在纸带上留下如图所示的径迹。
图乙为某次实验中获得的纸带的俯视图，径迹与中央虚线的交点分别为A 、B 、C 、D ，用刻度尺测出A 、B 间的距离为x 1；C 、D 间的距离为x 2。
已知单摆的摆长为L ，重力加速度为g ，则此次实验中测得的物体的加速度为（ ）A ．212()x x g L π-B ．212()2x x g L π-C ．212()4x x g L π-D ．212()8x x g Lπ- 4．如图所示，弹簧下面挂一质量为m 的物体，物体在竖直方向上做振幅为A 的简谐运动，当物体振动到最高点时，弹簧正好处于原长，弹簧在弹性限度内，则物体在振动过程中A ．弹簧的弹性势能和物体动能总和不变B ．物体在最低点时的加速度大小应为2gC ．物体在最低点时所受弹簧的弹力大小应为mgD ．弹簧的最大弹性势能等于2mgA5．如图所示是扬声器纸盆中心做简谐运动的振动图象，下列判断正确的是A ．t =2×10-3s 时刻纸盆中心的速度最大B ．t =3×10-3s 时刻纸盆中心的加速度最大C ．在0〜l×10-3s 之间纸盆中心的速度方向与加速度方向相同D ．纸盆中心做简谐运动的方程为x =1.5×10-4cos50πt （m ）6．在做“用单摆测定重力加速度”的实验中，有人提出以下几点建议，可行的是（ ） A ．适当加长摆线B ．质量相同，体积不同的摆球，应选用体积较大的C ．单摆偏离平衡位置的角度要适当大一些D ．当单摆经过平衡位置时开始计时，经过一次全振动后停止计时，用此时间间隔作为单摆振动的周期7．图(甲)所示为以O 点为平衡位置、在A 、B 两点间做简谐运动的弹簧振子，图(乙)为这个弹簧振子的振动图象，由图可知下列说法中正确的是( )A．在t=0.2s时，弹簧振子可能运动到B位置B．在t=0.1s与t=0.3s两个时刻，弹簧振子的速度相同C．从t=0到t=0.2s的时间内，弹簧振子的动能持续地增加D．在t=0.2s与t=0.6s两个时刻，弹簧振子的加速度相同8．悬挂在竖直方向上的弹簧振子，周期T=2s，从最低点位置向上运动时刻开始计时，在一个周期内的振动图象如图所示，关于这个图象，下列哪些说法是正确的是（）A．t=1.25s时，振子的加速度为正，速度也为正B．t=1.7s时，振子的加速度为负，速度也为负C．t=1.0s时，振子的速度为零，加速度为负的最大值D．t=1.5s时，振子的速度为零，加速度为负的最大值9．如图所示，一端固定于天花板上的一轻弹簧，下端悬挂了质量均为m的A、B两物体，平衡后剪断A、B间细线，此后A将做简谐运动。
机械振动练习题
1机械振动练习题(一)1、在水平方向上振动的弹簧振子如图1所示，受力情况是()图1 图2 图3A.重力、支持力和弹簧的弹力B.重力、支持力、弹簧弹力和回复力C.重力、支持力和回复力D.重力、支持力、摩擦力和回复力2、做简谐运动的质点在通过平衡位置时，下列物理量中具有最大值的物理量是（ ）A.动能B.加速度C.速度D.位移3、一简谐运动的图象如图2所示，在0.1—0.15 s 这段时间内( )A.加速度增大，速度变小，加速度和速度的方向相同B.加速度增大，速度变小，加速度和速度方向相反C.加速度减小，速度变大，加速度和速度方向相同D.加速度减小，速度变大，加速度和速度方向相反4、一个质点在平衡位置O 点附近做简谐运动，如图3所示，若从O 点开始计时，经过3 s 质点第一次经过M 点；再继续运动，又经过2 s 它第二次经过M 点.则该质点第三次经过M 点所需要的时间是（ )A.8 sB.4 sC.14 sD.310s5、甲、乙两弹簧振子质量相等，其振动图象如图4所示，则它们振动的机械能大小关系是E 甲_________E 乙（填“＞”“＝”或“＜”）；振动频率的大小关系是f 甲_________f 乙；在0—4 s 内，甲的加速度为正向最大的时刻是____________，乙的速度为正向最大的时刻是____________.2图4 图5 图66、.如图5所示为一弹簧振子的振动图象，规定向右的方向为正方向，试根据图象分析以下问题：（1）如图6所示的振子振动的起始位置是________，从初始位置开始，振子向________（填“右”或“左”）运动.（2）在图6中，找出图象中的O 、A 、B 、C 、D 各对应振动过程中的哪个位置？即O 对应_________，A 对应_________，B 对应_________，C 对应________，D 对应________.（3）在t=2 s 时，振子的速度的方向与t=0时速度的方向_________.（4）质点在前4 s 内的位移等于_________.7、一弹簧振子沿x 轴振动，振幅为4 cm 。
机械振动大作业
F为Coriolis力与离心力等项目之和，τ
为广义主动力向量，
p为广义坐标向量
抑制原理
定义Pa、Pp分别为刚性和柔性广义坐标
向量,M、K、F、S按同样维数分块为刚性、
柔性及耦合部分;
得：
M aa a M ap p Fa a p p
M pp p K p Pp P M pa a Fp p p
振动理论与应用
S313070039
王鹏
什么是机械振动
机械振动：是指物体（或物体
系）在平衡位置（或平均位置） 附近来回往复的运动。
什么是机械振动理论
机械振动理论：是研究机械振
动的理论、技术及设备的一门的 学科。它是机械振动学、振动利 用工程等的理论基础。
机械振动研究的内容
如何提高机械系统的抗振能力; 如何防止系统产生共振; 如何避免系统自振; 减振与隔振; 冲击与冲击隔离; 噪声控制与振动利用;
仿真
机器人的尺寸为: l1=l2=l4=2m l3=l5=10m,A=P4 各杆质量为: m1=40kg,m2=m4=2kg,m3=m5=10kg 柔性杆参数为: EI=10000
仿真
仿真中设定起始位姿为: pa0=(0,0,0,0,0,0,0)T, 目标位姿为: paf= 12,6,P6,P3,P6,P3,P6T。 轨迹优化算法的各项参数为: n0=8, pop_size=30, epoch=1000, nmax=80, N=100。
i 0
n
轨迹描述
设定最前和最后3个控制点为： Pa0=Pa1=Pa2=Pa0； Pa(n-2)=Pa(n-1)=Pan=Paf；
p aj ,0 j i 3 p aj (1 ) p aj ( j 1) j p aj , i 2 j i, s s j p ( j 1), i 1 j n 1 j sj 3 sj a
高中物理选修3-4机械振动练习题典型题带答案
高中物理机械振动练习题一．选择题（共25小题）1．如图所示，PQ为一竖直弹簧振子振动路径上的两点，振子经过P点时的加速度大小为6m/s2，方向指向Q点；当振子经过Q点时，加速度的大小为8m/s2，方向指向P点。
若PQ之间的距离为14cm，已知振子的质量为1kg，则以下说法正确的是（）A．振子经过P点时所受的合力比经过Q点时所受的合力大B．该弹簧振子的平衡位置在P点正下方7cm处C．振子经过P点时的速度比经过Q点时的速度大D．该弹簧振子的振幅一定为8cm2．如图甲所示，在升降机的顶部安装了一个能够显示拉力大小的传感器，传感器下方挂上一轻质弹簧，弹簧下端挂一质量为m的小球，若升降机在匀速运行过程中突然停止，并以此时为零时刻，在后面一段时间内传感器显示弹簧弹力F随时间t变化的图象如图乙所示，g为重力加速度，忽略一切阻力，则（）A．升降机停止前在向上运动B．0～t1和时间内小球处于失重状态，t1～t2时间内小球处于超重状态C．t2～t3的时间内弹簧弹性势能变化量等于重力势能变化量D．t3～t4时间内小球向下运动，加速度减小3．如图所示图线Ⅰ、图线Ⅱ为两单摆分别做受迫振动的共振曲线，下列判断正确的是（）A．若摆长为1m的单摆在地球上做受迫振动，则其共振曲线为图线ⅠB．若图线Ⅱ是单摆在地球上做受迫振动的共振曲线，则该单摆摆长约为0.5mC．若两单摆分别在月球上和地球上做受迫振动，则图线Ⅰ一定是在月球上的单摆的共振曲线D．若两单摆是在地球上同一地点做受迫振动，则两单摆摆长之比h1：h2＝25：44．如图所示，水平弹簧振子以坐标原点O为水平位置，沿x轴在M、N之间做简谐运动，其运动方程为x＝5sin（2πt+）cm，则（）A．t＝0.5s时，振子的位移最小B．t＝1.5s时，振子的加速度最小C．t＝2.25s时，振子的速度沿x轴负方向D．t＝0到t＝1.5s的时间内，振子通过的路程为15cm5．甲、乙两位同学分别使用图中左图所示的同一套装置，观察单摆做简谐运动时的振动图象，已知两人实验时所用的摆长相同，落在同一木板上的细砂分别形成的曲线如图N1、N2所示。
哈工大机械振动大作业详解
H a r b i n I n s t i t u t e o f T e c h n o l o g y机械振动大作业课程名称：机械振动班级：1208105 班作者：付帅磊学号：1120810523 指导教师：陈照波于东设计时间：2015.11.12哈尔滨工业大学第一次大作业1.The amplitude of vibration of an undamped system is measured to be 1 mm. the phase shift is measured to be 2 rad and the frequency 5 rad/sec. Calculate the initial conditions.解：由题意知，无阻尼振动位移方程为：)sin(ϕω+=t A x n对无阻尼单自由度振动，2020⎪⎪⎭⎫ ⎝⎛+=n v x A ω，⎪⎪⎭⎫ ⎝⎛=-001tan v x n ωϕ。
其中m A 001.0=，rad 2=ϕ。
解得m x 3010909.0-⨯=，s m v /10081.230-⨯-=。
所以)25sin(001.0)(+=t t x图1.ing the equation: “t A t A t x ωωsin cos )(21+=”to evaluate the constant 1A and2A in terms of the initial conditions.解：2sin 5cos 001.02cos 5sin 001.0)25sin(001.0)(t t t t x +=+=所以mm A 909.02sin 1==，mm A 416.02cos 2-==。
3.An automobile is modeled as 1000 kg mass supported by a stiffness k=400000N/m. When it oscillates, the maximum deflection is 10 cm. when loaded with the passengers, the mass becomes 1300 kg. Calculate the change in the frequency, velocity, amplitude, and acceleration if the maximum deflection remain 10 cm.解：设0=t 时，汽车处于平衡位置且有向上运动趋势，即0)0(=x ，0)0(>x。
机械振动大作业
《机械振动基础》大作业（2015年春季学期）题目基于MATLAB求系统特性姓名学号班级专业机械设计制造及其自动化报告提交日期2015年5月7哈尔滨工业大学报告要求1.请根据课堂布置的2道大作业题，任选其一，拒绝雷同和抄袭；2.报告最好包含自己的心得、体会或意见、建议等；3.报告统一用该模板撰写，字数不少于3000字，上限不限；4.正文格式：小四号字体，行距为1.25倍行距；5.用A4纸单面打印；左侧装订，1枚钉；6.课程报告需同时提交打印稿和电子文档予以存档，电子文档由班长收齐，统一发送至：liuyingxiang868@。
7.此页不得删除。
评语：成绩（15分）：教师签名：年月日求解多自由度矩阵的认识体会。
二、MATLAB程序图clearclose%--定义质量阵和刚度阵m1 = 2;m2 = 3;m3 = 5;m4 = 8;m5 = 4;m6 = 7;m7 = 7;m8 = 11;k1 = 25;k2 = 30;k3 = 45;k4 = 60;k5 = 70;k6 = 90;k7 = 100;k8 = 110; {}{u+u Km = [m1 0 0 0 0 0 0 0;0 m2 0 0 0 0 0 0;0 0 m30 0 0 0 0;...0 0 0 m4 0 0 0 0;0 0 0 0 m5 0 0 0;0 0 00 0 m6 0 0;...0 0 0 0 0 0 m7 0;0 0 0 0 0 0 0 m8];k = [k1+k2,-k2,0,0,0,0,0,0;-k2,k2+k3,-k3,0,0,0,0,0;...0,-k3,k3+k4,-k4,0,0,0,0;0,0,-k4,k4+k5,-k5,0,0,0;...0,0,0,-k5,k5+k6,-k6,0,0;0,0,0,0,-k6,k6+k7,-k7,0;...0,0,0,0,0,-k7,k7+k8,-k8;0,0,0,0,0,0,-k8,k8];[V,D]=eig(k,m); %%--特征频率DD和振型VVfor j=1:1:8w(j)=sqrt(D(j,j)); %---特征频率fprintf('wn%d = %6.4f\n',j,w(j)); %--从小到大依次输出8个固有频率值for i=1:1:8absV(i,j)=abs(V(i,j));endendmax=max(absV); %--为了归一化取振幅最大值for j=1:1:8for i=1:1:8V(i,j)= V(i,j)/max(j); %--振幅归一化endendfigurex=1:8;for a=1:8subplot(2,4,a),plot(x,V(x,a)); %分为2*4的子图;并画出图形hold on;grid on;title('振型图');end三、MATLAB结果输入输出wn1 = 0.4332wn2 = 1.7823wn3 = 3.2255wn4 = 4.1038wn5 = 5.2021wn6 = 6.2638wn7 = 6.5306wn8 = 7.5722四、心得体会1)学习机械振动课程的体会振动的强弱用振动量来衡量，振动量可以是振动体的位移、速度或加速度。
振动作业安全操作规程
振动作业安全操作规程振动作业是一种常见的工业作业，它利用振动设备产生机械振动，用于料筒、料斗、输送装置等工业设备中。
在振动作业中，工人需要通过设备的振动来达到一定的目的，但同时也必须严格遵守相关的安全操作规程，以确保工作人员的安全和设备的正常运行。
1. 穿戴防护装备在进行振动作业之前，工人必须穿戴符合标准的个人防护装备。
这包括安全鞋、安全帽、护目镜、耳塞等。
这些防护装备能够有效保护工人免受振动设备产生的噪音、飞溅物和其他危害物的伤害。
2. 进行设备检查在开启振动设备之前，必须进行设备的全面检查，确保设备处于良好的工作状态。
工人应该检查设备的电源、控制装置、机械部件等，确保它们没有损坏或存在潜在的问题。
如果发现问题，应及时进行维修或更换。
3. 正确操作设备在进行振动作业时，工人必须遵循设备的操作指南和安全规程。
工人应该了解设备的工作原理和操作方法，熟悉各个控制装置的功能，确保能够正确、安全地操作设备。
同时，工人还应该注意设备的工作状态，及时进行调整和处理异常情况。
4. 定期维护设备设备的定期维护是保证振动作业安全的重要措施。
在振动作业过程中，设备往往会受到较大的振动和冲击，容易出现磨损、松动等问题。
因此，工人需要定期对设备进行检修、紧固和润滑，确保设备的正常运行和安全性能。
5. 做好应急准备尽管工人在振动作业时采取了一系列的安全措施，但事故仍然有可能发生。
因此，工人需要做好应急准备，知道应对突发情况的方法和步骤。
工人应该熟悉设备的停机、断电等紧急操作，掌握急救知识和技能，确保在事故发生时能够及时采取正确的措施，保护自己和他人的安全。
振动作业安全操作规程是保证工人安全和设备正常使用的重要指导。
在振动作业中，工人必须遵守相关安全规定，着装合适的防护装备，进行设备检查，正确操作设备，定期维护设备，做好应急准备。
只有这样，才能保证振动作业的安全和高效进行。
总之，振动作业是一项具有一定危险性的工作，但只要遵守安全规程，采取相应的安全措施，就能保证工作人员的安全。
机械振动作业
1.如图所示,竖立在水平地面上的轻弹簧,下端与地面固定,将一个金属球放置在弹簧顶端(球与弹簧不粘连),并用力向下压球,使弹簧作弹性压缩,稳定后用细线把弹簧拴牢.烧断细线,球将被弹起,脱离弹簧后能继续向上运动.那么该球从细线被烧断到刚脱离弹簧的这一运动过程中( ).(A)球所受合力的最大值不一定大于球的重力值(B)在某一阶段内球的动能减小而它的机械能增加(C)球刚脱离弹簧时的动能最大(D)球刚脱离弹簧时弹簧的弹性势能最小2.如图所示,物体放在轻弹簧上,沿竖直方向在A、B之间作简谐运动,今物体在A、B之间的D点和c点沿DC方向运动(D、C图上未画出)的过程中,弹簧的弹性势能减少了3.0J,物体的重力势能增加了1.0J,则在这段运动过程中( ).(A)物体经过D点时的运动方向是指向平衡位置的(B)物体的动能增加了4.0J(C)D点的位置一定在衡位置以上(D)物体的运动方向可能是向下的3.单摆振动的回复力是( ).(A)摆球所受的重力(B)摆球重力在垂直悬线方向上的分力(C)悬线对摆球的拉力(D)摆球所受重力和悬线对摆球拉力的合力4．如图所示在竖直平面内，有一段光滑圆弧轨道MN，它所对应的圆心角小于5o，P是MN的中点，也是圆弧的最低点，在N、P之间一点Q和P之间搭一光滑斜面，将两个小球（可视为质点）分别同时由Q点和M点静止释放，则两个小球相遇点一定在（）A．斜面PQ上一点B．PM弧上的一点C．P点D．条件不足，无法判定5．一弹簧振子做简谐运动，周期为T，下列叙述中正确的是（）A、若t时刻和(t+△t)时刻振子运动位移的大小相等，方向相同，则△t一定等于T的整数倍B、若t时刻和(t+△t)时刻振子运动速度的大小相等，方向相反，则△t一定等于T/2的整数倍C、若△t=T，则t时刻和(t+△t)时刻振子运动的加速度一定相等D、若△t=T/2，则t时刻和(t+△t)时刻弹簧的长度一定相等6.如图所示,质量分别为m、M的两物块用轻弹簧相连,其中M放在水平地面上,m处于竖直光滑的导轨内.今将m向下压一段距离后放手,它就在导轨内上下作简谐运动,且m到达最高点时,M对地面的压力刚好为零,试问:(1)m的最大加速度多大?(2)M对地面的最大压力多大?答案:(1)()mgMm+(2)2(m+M)g。
10机械振动作业 吉林大学大物答案
。则第二个简谐振动的振 10 ；第一、第二两个简谐振动的位 幅为____cm 。 相差为____ 2
9. 一简谐振动的旋转矢量图如图所示，振幅矢 量长2cm，则该简谐振动的初位相为 。 4 2 振动方程为 x 2 * 10 cos( t ) 。
4
10. 物体的共振角频率与系统自身性质以及 阻尼大小 有关。系统的 阻尼 越大，共振时
2
4 4 T t t 3 32
1
5. 一质点同时参与两个在同一直线上的 谐振动，其振动方程分别为 7 x 4 cos( 2 t ), x 3 cos( 2 t ) 1 2 6 6 则关于合振动有结论：［］
A.振幅等于1cm, 初相等于
A1
A A2
B.振幅等于7cm,
2 2 2 2 2 2
A cos( 3 t )， 2. 一简谐振动的表达式为 x 已知 t 0 时的初位移为 0.04 m，初速度为 0.09m/s，则振幅A＝ ，初相 __ _。 v 3 2 2 0 2 A x v 0 . 05 m tan 0 0 / x 4 0
4.两个相同的弹簧以相同的振幅作谐振 动，当挂着两个质量相同的物体时其能 相同 ，当挂着两个质量不同的物体仍 量____ 相同 ，振动 以相同的振幅振动，其能量____ 不同 。 频率____
5. 一弹簧振子作简谐振动，振幅为A，周期为T， 运动方程用余弦函数表示，若t=0时， (1)振子在负的最大位移处，则初位相为____。 (2)振子在平衡位置向正方向运动，则初位相为 2。 _____ (3)振子在位移A/2处，向负方向运动，则初位 3。 相为_____ 6.（不要求）将复杂的周期性振动分解为一系列 的 简谐振动之和 ；从而确定出该振动包含的 频率成分以及各频率对应的振幅的方法，称为 频谱分析 。
机械振动大作业
《机械振动基础》大作业（2015年春季学期）题目多自由度系统的固有频率与固有振型姓名学号班级专业报告提交日期哈尔滨工业大学报告要求1.请根据课堂布置的2道大作业题，任选其一，拒绝雷同和抄袭；2.报告最好包含自己的心得、体会或意见、建议等；3.报告统一用该模板撰写，字数不少于3000字，上限不限；4.正文格式：小四号字体，行距为1.25倍行距；5.用A4纸单面打印；左侧装订，1枚钉；6.课程报告需同时提交打印稿和电子文档予以存档，电子文档由班长收齐，统一发送至：liuyingxiang868@。
7.此页不得删除。
评语：成绩（15分）：教师签名：年月日一、 参数选择在该作业中，我选取了7个自由度系统，其他参数如下：取N=7，M1=2Kg ，M2=3Kg ，M3，M5=6Kg ，M6=7Kg ，M7=8Kg K1=20N/m ，K2=30N/m ，K3=40N/m ，K4=5m K7=20N/m 。
并且令初始相位角全部为0。
方程。
如上图所示系统，其刚度矩阵为代入所给定的数据，为用刚度系数法来求刚度矩阵中的元素Kij 时，Kij 表示在第j 点处发生单位位移时，需在i1222233334100000000000000N NN NN k k k k k k k k k k k k k k k -+-⎡⎤⎢⎥-+-⎢⎥⎢⎥-+=⎢⎥⎢⎥⎢⎥+-⎢⎥-⎢⎥⎣⎦K点处施加力的大小。
这对于质量-弹簧系统的多自由度系统建立振动微分方程是非常简便的，不必进行隔离体分析列方程，就可建立起运动方程。
若系统存在阻尼，则与弹簧并行的还应画出阻尼器。
对于黏性阻尼，阻尼矩阵的每一个元素cij 可以如下求得:当第j 个质量具有单位速度而其他质量的速度均为零时，要克服第j 个质量的阻尼器阻力而需在第i 个质量上施加的力的大小。
然后把阻尼力这一项加到运动方程中去，即可得到有阻尼的多自由度系统运动微分方程用刚度系数法同样也可以建立扭转振动系统微分方程，只需将作用力F 变成作用力矩M ，单位位移变成单位角位移，按上述方法分析即可质量矩阵可用类似的过程得到代入数据得质量矩阵为：1234()5678i i N m Diag ≤≤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦M所以可列出该系统的矩阵方程为：{}{}{}+=0M x K x （1）3、求解固有频率与固有振型1、固有频率设系统各质量块按照同频率和同相位作简谐振动，即：sin()i i x A t ωϕ=+代入式（1）得，1234()5678i i N m Diag ≤≤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦M222111111212211222212112222222222111222()()()0()()()0()()()0n n n n n n n n n n nn nn n K m A K m A K m A K m A K m A K m A K m A K m A K m A ωωωωωωωωω⎧-+-++-=⎪-+-++-=⎪⎨⎪⎪-+-++-=⎩这是一个关于Ai 的n 元线性齐次方程组。
机械振动作业的职业危害防控指南
机械振动作业的职业危害防控指南随着工业的快速发展与机械设备的广泛应用，许多从事机械振动作业的工作者面临着职业危害的风险。
机械振动可以对工作者的健康产生负面影响，包括损害听力、引起神经病变以及影响心血管系统等。
因此，为了保护从事机械振动作业的工作者的健康，本文将提供一份职业危害防控指南。
一、机械振动危害的认识机械振动是指机械设备工作时产生的振动，其主要来源于旋转和往复运动的机械件。
机械振动可以被分为手臂振动和全身振动两种类型。
手臂振动主要来自于使用电动工具等设备，而全身振动则主要来自于驾驶特种设备或长期暴露在振动环境中。
二、机械振动职业危害机械振动作业对工作者的健康会产生不可忽视的危害。
长期暴露在机械振动环境中可能会导致工人患上手臂振动综合征和全身振动症。
手臂振动综合征会导致手臂麻木、手指发麻、肩膀酸痛等，在严重的情况下还可能引发手部肌肉功能受限。
而全身振动症的症状包括腰背酸痛、疲劳、运动困难以及消化系统问题等。
此外，机械振动还会对听力产生损害，并有可能对神经系统和心血管系统造成不可逆转的伤害。
三、机械振动作业的危害防控措施为了有效防控机械振动作业带来的职业危害，以下措施应该被采取：1. 设计阶段控制在机械设备的设计阶段，应该考虑采用抗振措施来减少机械振动对工作者的影响，例如通过优化设计来降低振动频率和幅度、采用减振器等。
2. 工作时间控制对于从事机械振动作业的工作者，应该限制他们的振动暴露时间。
长时间的暴露于机械振动环境中会增加职业危害的风险。
因此，应该通过轮班制度、工作时间安排等方式来减少对工作者的长期振动暴露。
3. 工作设备控制应该选用能够降低振动的工作设备，例如带有振动减少装置的工具。
此外，还应该定期检查和维护工作设备，确保其振动水平符合相关的标准和要求。
4. 工作环境控制工作场所的环境对于机械振动的防控非常重要。
应该采取隔离工作场所和振动源的措施，例如通过添加隔离墙来减少机械振动的传递。
机械振动大作业——简支梁的各情况分析2
机械振动大作业姓名：徐强学号：SX1302106专业：航空宇航推进理论与工程能源与动力学院2013年12月简支梁的振动特性分析题目:针对简支梁、分别用单、双、三、十个自由度以及连续体模型，计算其固有频率、固有振型。
单、双、三自由度模型要求理论解；十自由度模型要求使用李兹法、霍尔茨法、矩阵迭代法、雅可比法、子空间迭代法求解基频；连续体要求推导理论解，并通过有限元软件进行数值计算。
解答：一、 单自由度简支梁的振动特性如图1，正方形截面（取5mm ×5mm ）的简支梁，跨长为l =1m ，质量m 沿杆长均匀分布，将其简化为单自由度模型，忽略阻尼，则运动微分方程为0=+••kx x m ,固有频率ωn =eqeq m k ，其中k 为等效刚度，eq m 为等效质量。
因此，求出上述两项即可知单自由度简支梁的固有频率。
根据材料力学的结果，由于横向载荷F 作用在简支梁中间位置而引起的变形为）（224348EI F -)(x l x x y -=（20l x ≤≤）, 48EI F -3max l y =为最大挠度，则： eq k =δF=348EIl 梁本身的最大动能为：）（224348EI F -)(x l x x y -==）（223max43x l lx y -T max =2×dx x y l m l 220)(21⎭⎬⎫⎩⎨⎧•⎰=2max 351721•y m ）（ 如果用eq m 表示简支梁的质量等效到中间位置时的大小，它的最大动能可表示为：T max =2max21•y m eq所以质量为m 的简支梁，等效到中间位置的全部质量为： m m eq 3517=故单自由度简支梁横向振动的固有频率为：ωn =eqeq m k =3171680ml EImk图1 简支梁的单自由度模型二、 双自由度简支梁的振动特性如图2，将简支梁简化为双自由度模型，仍假设在简支梁中间位置作用载荷，根据对称性，等效质量相等,因此只要求出在3/l 处的等效质量即可。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
《机械振动基础》大作业（2014年春季学期）题目基于MATLAB求系统特性姓名李超学号1110910706班级1108107专业机械设计制造及其自动化报告提交日期2014年4月23哈尔滨工业大学报告要求1.请根据课堂布置的2道大作业题，任选其一，拒绝雷同和抄袭；2.报告最好包含自己的心得、体会或意见、建议等；3.报告统一用该模板撰写，字数不少于3000字，上限不限；4.正文格式：小四号字体，行距为1.25倍行距；5.用A4纸单面打印；左侧装订，1枚钉；6.课程报告需同时提交打印稿和电子文档予以存档，电子文档由班长收齐，统一发送至：shanxiaobiao@。
7.此页不得删除。
评语：成绩（15分）：教师签名：年月日求解多自由度矩阵的认识体会。
二、MATLAB程序图m=[];k1=[];k=[];c=[];c1=[];% 质量矩阵的输入for i=1:10a=input('输入质量矩阵m：');m(i,i)=a;end%刚度矩阵的输入for j=1:10b=input('输入刚度系数k：');k1(1,j)=b;endfor l=1:9k(l,l)=k1(l)+k1(l+1);k(10,10)=k1(10);k(l+1,l)=-k1(l+1);k(l,l+1)=-k1(l+1);k(10,9)=-k1(10);k(9,10)=-k1(10);end%阻尼矩阵的输入syms w;B=k-w^2*m %系统的特征矩阵BY=det(B); %展开行列式W=solve(Y); %求解whlW=length(W);[V,D]=eig(k,m);for I=1:10for J=1:10V(J,I)=V(J,I)/V(5,I);endendVW三、MATLAB结果输入输出1.输入质量矩阵m：12.输入质量矩阵m：13.输入质量矩阵m：14.输入质量矩阵m：15.输入质量矩阵m：16.输入质量矩阵m：17.输入质量矩阵m：18.输入质量矩阵m：19.输入质量矩阵m：110.输入质量矩阵m：111.输入刚度系数k：112.输入刚度系数k：113.输入刚度系数k：114.输入刚度系数k：115.输入刚度系数k：116.输入刚度系数k：117.输入刚度系数k：118.输入刚度系数k：119.输入刚度系数k：120.输入刚度系数k：121. B =22.[ 2 - w^2, -1, 0, 0, 0, 0, 0, 0, 0,0]23.[ -1, 2 - w^2, -1, 0, 0, 0, 0, 0, 0,0]24.[ 0, -1, 2 - w^2, -1, 0, 0, 0, 0, 0,0]25.[ 0, 0, -1, 2 - w^2, -1, 0, 0, 0, 0,0]26.[ 0, 0, 0, -1, 2 - w^2, -1, 0, 0, 0,0]27.[ 0, 0, 0, 0, -1, 2 - w^2, -1, 0, 0,0]28.[ 0, 0, 0, 0, 0, -1, 2 - w^2, -1, 0,0]29.[ 0, 0, 0, 0, 0, 0, -1, 2 - w^2, -1,0]30.[ 0, 0, 0, 0, 0, 0, 0, -1, 2 - w^2,-1]31.[ 0, 0, 0, 0, 0, 0, 0, 0, -1, 1 -w^2]32. 133.V =a)0.2191 0.5550 -1.2074 -1.0000 2.2470 1.0713 -3.1581 -0.8019 3.77960.2956b)0.4334 1.0000 -1.7702 -1.0000 1.0000 -0.1601 2.3076 1.0000 -6.2457-0.5649c)0.6379 1.2470 -1.3879 0.0000 -1.8019 -1.0473 1.4720 -0.4450 6.54130.7840d)0.8282 1.2470 -0.2646 1.0000 -1.8019 0.3166 -3.3832 -0.4450 -4.5636-0.9335e)1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.00001.0000f)0.3412 -0.1894 0.4255 0.0000 -0.4255 -0.1894 0.3412 0.3412 0.18940.4255g)0.3780 0.0000 0.3780 0.3780 0.0000 -0.3780 -0.3780 0.0000 -0.3780-0.3780h)0.4063 0.1894 0.1286 0.3780 0.4255 0.2459 -0.0650 -0.3412 0.43520.2969i)0.4255 0.3412 -0.1894 0.0000 0.1894 0.3412 0.4255 0.4255 -0.3412-0.1894j)0.4352 0.4255 -0.4063 -0.3780 -0.3412 -0.2969 -0.2459 -0.1894 0.12860.065034.W =35. 1.97766165245025709013948576586836.-0.7306820487327900290894759978595437.-1.652477548631989743890325147545438.-0.1494601871728485085818794914695339. 1.466103743659652657044862978541340.-1.911145611572281465622668107534941. 1.911145611572281465622668107534942.0.1494601871728485085818794914695343.-1.466103743659652657044862978541344.0.7306820487327900290894759978595445. 1.652477548631989743890325147545446.-1.97766165245025709013948576586847. 148.-149.7/(9*(108^(1/2)*((7*i)/108) + 7/54)^(1/3)) + ((108^(1/2)*7*i)/108 + 7/54)^(1/3) -1/350.7/(9*(108^(1/2)*((7*i)/108) - 7/54)^(1/3)) + ((108^(1/2)*7*i)/108 - 7/54)^(1/3) + 1/3-7/(18*(108^(1/2)*((7*i)/108) + 7/54)^(1/3)) - ((108^(1/2)*7*i)/108 + 7/54)^(1/3)/2 + (3^(1/2)*(7/(9*(108^(1/2)*((7*i)/108) + 7/54)^(1/3)) -((108^(1/2)*7*i)/108 + 7/54)^(1/3))*i)/2 - 1/3-7/(18*(108^(1/2)*((7*i)/108) + 7/54)^(1/3)) - ((108^(1/2)*7*i)/108 + 7/54)^(1/3)/2 - (3^(1/2)*(7/(9*(108^(1/2)*((7*i)/108) + 7/54)^(1/3)) -((108^(1/2)*7*i)/108 + 7/54)^(1/3))*i)/2 - 1/3b)1/3 - ((108^(1/2)*7*i)/108 - 7/54)^(1/3)/2 +(3^(1/2)*(7/(9*(108^(1/2)*((7*i)/108) - 7/54)^(1/3)) - ((108^(1/2)*7*i)/108 -7/54)^(1/3))*i)/2 - 7/(18*(108^(1/2)*((7*i)/108) - 7/54)^(1/3))c)1/3 - ((108^(1/2)*7*i)/108 - 7/54)^(1/3)/2 -(3^(1/2)*(7/(9*(108^(1/2)*((7*i)/108) - 7/54)^(1/3)) - ((108^(1/2)*7*i)/108 -7/54)^(1/3))*i)/2 - 7/(18*(108^(1/2)*((7*i)/108) - 7/54)^(1/3))四、心得体会1)学习机械振动课程的体会机械振动是设计和研制飞机、直升机、和导弹等飞行器的必须妥善解决的重要工程问题，本课程作为一门专业基础课程，其教学目的与任务是要求学生学习和掌握机械振动的基本理论，初步具有把机械系统振动、噪声等实际问题抽象为理论模型，并利用所学到的理论知识和方法来分析和解决实际机械系统振动噪声问题的能力，学会机械振动噪声的测试分析及实验方法和技能。
培养学生对机械系统动态问题的认识和分析能力，并且提高学生在学校和将来解决实际问题的能力。
本学期上课，我们主要学习了以下课程第一章绪论第二章基础理论第三章单自由度系统的振动第四章二自由度系统的振动第五章多自由度系统的振动第六章连续弹性体振动及有限元法第七章工程振动测试和实验机械振动是指机械系统(即力学系统)中的振动，任何力学系统，只要它具有弹性和惯性，都可能发生振动，这种力学系统称为振动系统。
振动应用举例★心脏的搏动、耳膜和声带的振动★声音的产生、传播和接收★桥梁和建筑物在阵风或地震激励下的振动★飞机和船舶在航行中的振动★机床和刀具在加工时的振动★各种动力机械的振动★控制系统中的自激振动振动危害☆振动会影响精密仪器设备的功能，降低加工精度，加剧构件的疲劳和磨损，缩短机器和结构物的使用寿命☆振动可能引起结构的大变形破坏，有的桥梁曾因振动而坍毁☆飞机机翼的颤振、机轮的抖振往往造成事故☆车、船和机舱的振动会劣化乘载条件☆强烈的振动噪声会形成严重的公害。
以下是我对机械振动这门课程的概念总结：离散系统：具有集中参数元件所组成的系统。
连续系统：由分布参数元件组成的系统非线性振动系统:指该系统的振动只能用非线性微分方程描述按激励类型：自由、受迫、自激、参数按响应类型：固有、简谐、周期、混沌、随机按系统系统：线性、非线性、确定性、随机第一类：已知系统模型和外载荷求系统响应，称为响应计算（分析）或正问题。
第二类：已知输入和输出求系统特性，称为系统识别或参数识别，又称为第一类逆问题。
第三类：已知系统特性和响应求载荷，称为载荷识别（振动环境预测），又称为第二类逆问题惯性元件：集中质量和转动惯量都属于惯性元件特点是完全刚性且无阻尼，在振动过程中储存或释放动能。