(完成)二阶电路响应的三种(欠阻尼、过阻尼及临界阻尼)状态轨迹及其特点
二阶电路响应的三种状态轨迹和特点

二阶电路响应的三种状态轨迹和特点二阶电路是指由两个电感和两个电容元件构成的电路,它是电路中的一种常见类型。
在二阶电路中,电感和电容的存在导致电路的自然频率,从而影响电路的响应特性。
在电流或电压变化的情况下,二阶电路的响应可以分为三种状态:欠阻尼、过阻尼和临界阻尼。
下面将详细介绍这三种状态的轨迹和特点。
1.欠阻尼状态:
欠阻尼状态的特点包括:
-振荡幅度逐渐减小,最终稳定在一些特定值。
-振荡周期较长。
-被激励信号的频率在自然频率的附近。
2.过阻尼状态:
过阻尼状态的特点包括:
-响应快速收敛到稳定状态,没有振荡。
-没有振荡的存在使得响应更加平滑。
-被激励信号的频率通常远离自然频率。
3.临界阻尼状态:
临界阻尼状态的特点包括:
-响应最快地收敛到稳态,没有振荡。
-没有过冲和回弹的存在。
-被激励信号的频率通常接近自然频率。
综上所述,二阶电路的响应可以分为欠阻尼、过阻尼和临界阻尼三种状态。
每种状态具有不同的响应轨迹和特点,这取决于电路的自然频率和被激励信号的频率。
深入了解这些状态对于分析和设计电路至关重要。
仿真实验二二阶电路响应
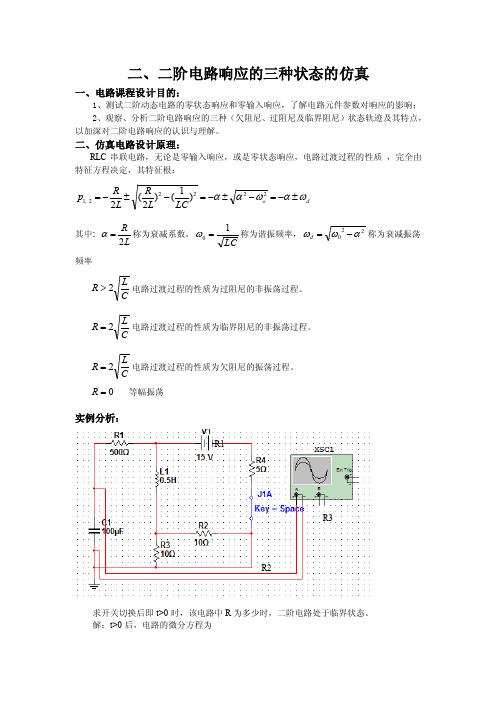
二、二阶电路响应的三种状态的仿真一、电路课程设计目的:1、测试二阶动态电路的零状态响应和零输入响应,了解电路元件参数对响应的影响;2、观察、分析二阶电路响应的三种(欠阻尼、过阻尼及临界阻尼)状态轨迹及其特点,以加深对二阶电路响应的认识与理解。
二、仿真电路设计原理:RLC 串联电路,无论是零输入响应,或是零状态响应,电路过渡过程的性质 ,完全由特征方程决定,其特征根:d o LCL R L R p ωαωαα±-=-±-=-±-=22222,1)1()2(2 其中: L R 2=α称为衰减系数,LC10=ω称为谐振频率,220αωω-=d 称为衰减振荡频率 CL R 2>电路过渡过程的性质为过阻尼的非振荡过程。
CL R 2=电路过渡过程的性质为临界阻尼的非振荡过程。
C L R 2=电路过渡过程的性质为欠阻尼的振荡过程。
0=R 等幅振荡实例分析:求开关切换后即t>0时,该电路中R 为多少时,二阶电路处于临界状态。
解:t>0后,电路的微分方程为R1R2R3Ai i V u u u dtdu C R dt u d LC c c c c c 5)0()0(25)0()0(0'22=-=+=-=+=++ Ate e e te A e A e A C t i Ve t e t A A u A A p p p C L R LC L R L R Cp R LCp t t t t t t t t c )5.5006975.35405.3535(10)()()5.354020()(5.35402542.141,42.14121)(2p 0142.14142.14142.141422142.14142.141212121'2''2,1'2-----------=-+--=+=+=∴==-===Ω==∴-±-==++δδδδδ,为两个相等的实根。
完成二阶电路响应的三种欠阻尼过阻尼及临界阻尼状态轨迹及其特点

完成二阶电路响应的三种欠阻尼过阻尼及临界阻尼状态轨迹及其特点二阶电路是由两个电感、两个电容和一个电阻组成的电路。
其响应可以分为欠阻尼、过阻尼和临界阻尼三种状态。
下面将分别介绍这三种状态的轨迹及其特点。
1.欠阻尼状态:欠阻尼状态下,电路的阻尼系数小于临界阻尼,电路呈现振荡状态。
其响应的轨迹是在零点附近进行周期性的振荡,并且振荡幅值逐渐减小,最终趋于稳定。
欠阻尼状态下的二阶电路具有以下特点:(1)有振荡的频率:欠阻尼状态下的二阶电路会以一定的频率进行振荡,频率与电路元件的参数相关。
(2)振荡幅值逐渐衰减:由于缺乏能量的输入,振荡幅值会逐渐减小,最终趋于稳定。
(3)频率响应中心频率:欠阻尼状态下的二阶电路的响应会在一些特定的频率上具有最大振幅,称为中心频率。
(4)稳定时间较长:由于振荡幅值的衰减过程较长,欠阻尼状态下的二阶电路需要一段时间才能趋于稳定。
2.过阻尼状态:过阻尼状态下,电路的阻尼系数大于临界阻尼,电路呈现过度阻尼的响应。
其响应的轨迹是在零点周围进行减振并趋于稳定,没有振荡现象。
过阻尼状态下的二阶电路具有以下特点:(1)没有振荡现象:过阻尼状态下的二阶电路不会出现振荡,响应会直接趋于稳定。
(2)稳定时间较短:由于振荡现象的缺失,过阻尼状态下的二阶电路不需要过多的时间来达到稳定状态。
(3)没有中心频率:过阻尼状态下的二阶电路没有特定的中心频率,响应在整个频率范围内逐渐趋于零。
3.临界阻尼状态:临界阻尼状态下,电路的阻尼系数等于临界阻尼,电路响应既不振荡也不过度阻尼,而是以最快的速度达到稳定。
其响应的轨迹是在零点的附近进行振荡,振荡幅值逐渐减小,最终趋于稳定。
临界阻尼状态下的二阶电路具有以下特点:(1)最快的稳定时间:临界阻尼状态下的二阶电路响应以最快的速度达到稳定,不会出现过渡过程。
(2)无振荡现象:临界阻尼状态下的二阶电路虽然在响应过程中会振荡,但振幅逐渐减小,不会形成持续的振荡。
(3)没有中心频率:临界阻尼状态下的二阶电路没有特定的中心频率,响应在整个频率范围内逐渐趋于零。
(完成)二阶电路响应的三种(欠阻尼、过阻尼及临界阻尼)状态轨迹及其特点

真验二之阳早格格创做二阶电路赞同的三种(短阻僧、过阻僧及临界阻僧)状态轨迹及其特性一、真验手段1、流利掌握二阶电路微分圆程的列写及供解历程;2、掌握RLC二阶电路整输进赞同及电路的过阻僧、临界阻僧战短阻僧状态;3、教会利用MULTISIM仿真硬件流利分解电路,更加是电路中各电压电流的变更波形.二、真验本理用二阶线性常微分圆程形貌的电路称为二阶电路,二阶电路中起码含有二个储能元件.二阶电路微分圆程式一个含有二次微分的圆程,由二阶微分圆程形貌的电路称为二阶电路.分解二阶电路的要领仍旧是修坐二阶微分圆程,并利用初初条件供解得到电路的赞同.二阶圆程普遍皆为齐次圆程.齐次圆程的通解普遍分为三种情况:(RLC串联时)1、为二个没有等的真根(称过阻僧状态)此时,,二阶电路为过阻僧状态.2、为相等真根(称临界状态)此时,,二阶电路为临界状态.3、为同轭复根(称短阻僧状态)此时,二阶电路为短阻僧状态.那三个状态正在二阶电路中式一个要害的数据,它决断了电路中电流电压关系以及电流电压波形.三、真验真质电路中启关S关合已暂.t=0时将S挨启,并丈量.1、短阻僧状态(R=10Ω,C=10mF,L=50mH)如图所示,为短阻僧状态时的二阶电路图.波形图展示了短阻僧状态下的战波形(橙色线条为电容电压衰减波形,白色线条为电感电压衰减波形).2、临界阻僧(R=10Ω,C=10mF,L=0.25mH)如图所示,为临界状态的二阶电路图.图展示了临界状态下的的波形.波形图展示了临界状态下的战波形.3、过阻僧状态(R=10Ω,C=1mF,L=1mH)如图所示,为过阻僧状态下的二阶电路图.波形图展示了临界状态下的战波形图.四、真验分解由本理公式以及仿真截止,咱们不妨考证得出1)当二阶电路为短阻僧状态时,其特性圆程特性根为一对于复根,且为同轭复根.2)当二阶电路为过阻僧状态时,其特性圆程特性根为二个没有等的真根.3)当二阶电路为临界阻僧状态时,其特性圆程特性根为相等真根五、真验报告1、归纳、分解真验要领取截止正在真验历程中,真验需要举止多次电路的变换.真验时需要留神审慎,以预防堕落.正在真验截止中,大部分取表面相切合,但是仍存留些微缺面(简略定量分解).2、心得体验及其余通过本次真验的教习,尔认识了二阶电路微分圆程的列写及供解历程,认识了RLC二阶电路整输进赞同及电路的过阻僧、临界阻僧战短阻僧状态,更流利天力用仿真仪器分解电路,那将对于以来的仿真正在验有要害的前提效率.。
邓 仿真实验2二阶电路响应的三种

四、对比分析与结论
1、分析实验: 本实验这要是观察三种阻态下的波形, 由于引入了可变电阻使电路的转换非常方便。 在 进行波形分析时,由于测的是电感的电压和电流,所以主要从电路的电流变化来看,我们很 容易就能理解电感的充放电过程。 2、实验总结: 通过本次实验的学习, 我熟悉了二阶电路微分方程的列写及求解过程, 了解了 RLC 二阶 电路的响应及电路的过阻尼、 临界阻尼和欠阻尼状态, 更熟练地利用仿真软件分析电路的动 态变化。 在实验中我先是用的并联电路但由于公示用错改用了串联电路, 终于得到正确的波 形,在这个实验上也花费了很多的时间。由此也学会,具体题目具体分析,不要一味的套用 公式。
用二阶线性常微分方程描述的电路称为二阶电路, 二阶电路中至少含有两个不同类型的 储能元件。 二阶电路微分方程式一共含有两个二次微分的方程。 分析二阶电路的方法是建立 二阶微分方程,并利用初始条件求解得到电路的响应。在解二阶方程式时,我们通常是先解 齐次方程。 齐次方程的通解一般分为三种情况: (RLC 串联时) 1、S1 ≠ S2 为两个不等的实根: f = A 1 eS 1 t + A 2 eS 2 t 此时,R > 2
L C
=2
10 −3 1000×10 −12
= 2kΩ
1)欠阻尼状态(R=400Ω ,C=1000pF,L=1mH) 如图所示,为欠阻尼状态时的二阶电路图,以及其在方波激励下的波形。 本次实验的测量值为:电感点电流(蓝色)以及电感电压(红色) 。
单个波形放大为:
由波形图可知在欠阻尼的情况下 (方波激励) , 电感两端电压和电流都是振荡的减小的。
二、二阶电路响应的三种(欠阻尼、过阻尼及临界阻尼)状
态轨迹及其特点
一、仿真实验目的
完成二阶电路响应的三种欠阻尼、过阻尼及临界阻尼状态轨迹及其特点.docx

实验二二阶电路响应的三种(欠阻尼、过阻尼及临界阻尼)状态轨迹及其特点一、实验目的1、熟练掌握二阶电路微分方程的列写及求解过程;2、掌握 RLC 二阶电路零输入响应及电路的过阻尼、临界阻尼和欠阻尼状态;3、学会利用 MULTISIM 仿真软件熟练分析电路, 尤其是电路中各电压电流的变化波形。
二、实验原理用二阶线性常微分方程描述的电路称为二阶电路, 二阶电路中至少含有两个储能元件。
二阶电路微分方程式一个含有二次微分的方程, 由二阶微分方程描述的电路称为二阶电路。
分析二阶电路的方法仍然是建立二阶微分方程, 并利用初始条件求解得到电路的响应。
二阶方程一般都为齐次方程。
齐次方程的通解一般分为三种情况: ( RLC 串联时)1、S 1 S 2 为两个不等的实根(称过阻尼状态)f hS t S tA 1e 11 A 2 e 12 此时, R 2 L,二阶电路为过阻尼状态。
C2、 S 1 S 2为相等实根(称临界状态) f h ( A 1 A 2 )e t此时, R 2L ,二阶电路为临界状态。
C 3、 S 1、2j 为共轭复根(称欠阻尼状态) f h sin( t)e t此时 R2 L ,二阶电路为欠阻尼状态。
C 这三个状态在二阶电路中式一个重要的数据, 它决定了电路中电流电压关系以及电流电压波形。
三、实验内容电路中开关 S 闭合已久。
t=0 时将 S 打开,并测量。
1、欠阻尼状态( R=10Ω,C=10mF,L=50mH)如图所示,为欠阻尼状态时的二阶电路图。
波形图展示了欠阻尼状态下的U C和 U L波形(橙色线条为电容电压衰减波形,红色线条为电感电压衰减波形) 。
2、临界阻尼( R=10Ω ,C=10mF,L=0.25mH)如图所示,为临界状态的二阶电路图。
图展示了临界状态下的U C的波形。
波形图展示了临界状态下的U C和 U L波形。
3、过阻尼状态( R=10Ω,C=1mF,L=1mH)如图所示,为过阻尼状态下的二阶电路图。
实验二 二阶电路响应的三种状态轨迹及其特点

实验报告二 二阶电路响应的三种状态轨迹及其特点
1、电路课程设计目的
观察二阶电路响应的三中状态电压电流波形。
2、设计电路原理与说明
二阶电路是含有两个独立储能元件的电路,描述电路行为的方程是二阶线性常微分方程。
设计电路图如下: U 0
L
图一 C
L R 2>时,过阻尼非振荡放电 C
L R 2<时,欠阻尼非振荡放电 C L R 2
=时,临界阻尼放电 若取200L mH =、5C F μ=,则当400R =Ω时为临界阻尼状态。
故此次仿真分别选用100Ω 400Ω 700Ω的电阻进行测试。
3、电路课程设计仿真内容与步骤及结果
(1)接好电路,设置电感、电容值;
图二
(2)选择700Ω电阻,观察电感的电压及电流波形;
图三
(3)选择100Ω电阻,观察电感的电压及电流波形;
图四
(4)选择400 电阻,观察电感的电压及电流波形;
图五
综上,波形符合理论结果。
4、仿真结果与理论分析对比及仿真中的注意事项
仿真结果与理论计算相一致。
仿真中用到了单刀双掷开关,在实际测试时要留意开关的切换,同时由于此次仿真中利用到了示波器,而且所测波形在很小的一段范围内,所以在操作是要注意开关和示波器的相互配合,这样才容易得到理想波形图。
5、电路课程设计总结
通过这次仿真,我们深一层次的认识了二阶电路的三种状态特性,并观察了各个状态的电路波形图。
二阶电路由于设计到二阶常微分方程,计算方面相当麻烦,我们在研究时可以借助示波器等器材做辅助,帮助我们理解掌握新知识。
完成二阶电路响应的三种欠阻尼过阻尼与临界阻尼状态轨迹和特点

完成二阶电路响应的三种欠阻尼过阻尼与临界阻尼状态轨迹和特点二阶电路是指由两个电感和两个电容构成的电路,常见的二阶电路包括二阶低通滤波器、二阶高通滤波器、振荡器等。
二阶电路的响应包括三种状态:欠阻尼、临界阻尼和过阻尼。
1.欠阻尼状态欠阻尼状态是指二阶电路的阻尼比小于临界阻尼时的状态。
在欠阻尼状态下,电路的阻尼比大于1,电路会发生振荡。
欠阻尼状态下的二阶电路的特点是:振荡频率为固定值,振荡衰减的幅度随时间增大而减小。
2.临界阻尼状态临界阻尼状态是指二阶电路的阻尼比等于1时的状态。
在临界阻尼状态下,电路不会发生振荡,且电路的响应最快。
临界阻尼状态下的二阶电路的特点是:响应时间最短,过渡过程最平稳。
3.过阻尼状态过阻尼状态是指二阶电路的阻尼比大于1时的状态。
在过阻尼状态下,电路不会发生振荡,且电路的响应速度较慢。
过阻尼状态下的二阶电路的特点是:响应时间较长,过渡过程较缓慢。
在二阶电路中,三种状态的轨迹可以通过绘制相应的阻尼比图来表示。
对于欠阻尼状态,阻尼比小于1,而相位角是一个正弦曲线。
对于临界阻尼状态,阻尼比等于1,相位角是一个直线。
对于过阻尼状态,阻尼比大于1,而相位角是两个阶梯曲线。
从特性角度来看,欠阻尼状态下的二阶电路是有振荡的,可以用于振荡器的设计;临界阻尼状态下的二阶电路响应最快,过渡过程最平稳,适用于需要快速响应的系统;过阻尼状态下的二阶电路响应时间较长,过渡过程较缓慢,适用于需要较长时间稳定的系统。
总结起来,二阶电路的响应包括欠阻尼、临界阻尼和过阻尼三种状态。
不同状态下的响应轨迹和特点有所不同,分别适用于不同的应用场景。
在实际设计中,需要根据系统需求选择合适的阻尼比来获得所需的响应特性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二
二阶电路响应的三种(欠阻尼、过阻尼及临界阻尼)状态轨迹及其特点
一、实验目的
1、熟练掌握二阶电路微分方程的列写及求解过程;
2、掌握RLC 二阶电路零输入响应及电路的过阻尼、临界阻尼和欠阻尼状态;
3、学会利用MULTISIM 仿真软件熟练分析电路,尤其是电路中各电压电流的变化波形。
二、实验原理
用二阶线性常微分方程描述的电路称为二阶电路,二阶电路中至少含有两个储能元件。
二阶电路微分方程式一个含有二次微分的方程,由二阶微分方程描述的电路称为二阶电路。
分析二阶电路的方法仍然是建立二阶微分方程,并利用初始条件求解得到电路的响应。
二阶方程一般都为齐次方程。
齐次方程的通解一般分为三种情况:(RLC 串联时)
1、 21S S ≠ 为两个不等的实根(称过阻尼状态)
t S t S h e A e A f 211121+= 此时,C
L R 2>,二阶电路为过阻尼状态。
2、 σ==21S S 为相等实根(称临界状态)
t h e A A f σ)21+=
( 此时,C
L R 2=,二阶电路为临界状态。
3、 ωσj S ±-=21、为共轭复根(称欠阻尼状态)
t h e t f σβω-+=)sin( 此时C
L R 2<,二阶电路为欠阻尼状态。
这三个状态在二阶电路中式一个重要的数据,它决定了电路中电流电压关系
以及电流电压波形。
三、实验内容
电路中开关S 闭合已久。
t=0时将S 打开,并测量。
1、欠阻尼状态(R=10Ω,C=10mF,L=50mH )
如图所示,为欠阻尼状态时的二阶电路图。
波形图展示了欠阻尼状态下的C U 和L U 波形(橙色线条为电容电压衰减波形,红色线条为电感电压衰减波形)。
2、临界阻尼(R=10Ω,C=10mF,L=0.25mH )
如图所示,为临界状态的二阶电路图。
图展示了临界状态下的C U 的波形。
波形图展示了临界状态下的C U 和L U 波形。
3、过阻尼状态(R=10Ω,C=1mF,L=1mH )
如图所示,为过阻尼状态下的二阶电路图。
波形图展示了临界状态下的C U 和L U 波形图。
四、实验分析
由原理公式以及仿真结果,我们可以验证得出
1)当二阶电路为欠阻尼状态时,其特征方程特征根为一对复根,且为共轭
复根。
2)当二阶电路为过阻尼状态时,其特征方程特征根为两个不等的实根。
3)当二阶电路为临界阻尼状态时,其特征方程特征根为相等实根
五、实验报告
1、总结、分析实验方法与结果
在实验过程中,实验需要进行多次电路的转换。
实验时需要小心谨慎,以防止出错。
在实验结果中,大部分与理论相符合,但仍存在些微误差(省略定量分
析)。
2、心得体会及其他
通过本次实验的学习,我熟悉了二阶电路微分方程的列写及求解过程,熟悉了RLC二阶电路零输入响应及电路的过阻尼、临界阻尼和欠阻尼状态,更熟练地利用仿真仪器分析电路,这将对以后的仿真实验有重要的基础作用。
如有侵权请联系告知删除,感谢你们的配合!。
