最佳旅游线路数学建模
数学建模层次分析法旅游景点选址举例
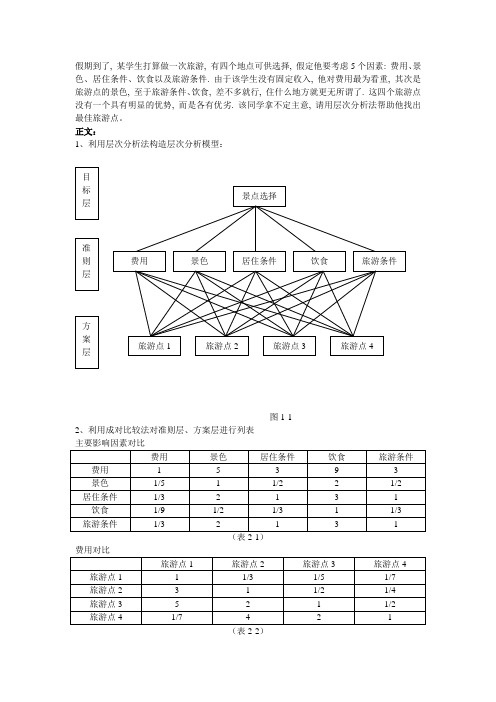
假期到了, 某学生打算做一次旅游, 有四个地点可供选择, 假定他要考虑5个因素: 费用、景色、居住条件、饮食以及旅游条件. 由于该学生没有固定收入, 他对费用最为看重, 其次是旅游点的景色, 至于旅游条件、饮食, 差不多就行, 住什么地方就更无所谓了. 这四个旅游点没有一个具有明显的优势, 而是各有优劣. 该同学拿不定主意, 请用层次分析法帮助他找出最佳旅游点。
正文:1、利用层次分析法构造层次分析模型:图1-12、利用成对比较法对准则层、方案层进行列表费用对比(表2-3)(表2-4)(表2-5)旅游条件对比2.构造成对比较判断矩阵(1) 建立准则层对目标层的成对比较判断矩阵153931/511/221/21/321311/91/21/311/31/32131A ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦(2) 建立方案层对准则层的成对比较判断矩阵111/31/51/7311/21/45211/21/7421B ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭211/24321551/41/5111/31/511B ⎛⎫⎪ ⎪= ⎪ ⎪⎝⎭316581/61121/51171/81/21/71B ⎛⎫⎪⎪= ⎪⎪⎝⎭ 4111/31/3111/21/532113511B ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭ 512121/211/2112121/211/21B ⎛⎫⎪⎪= ⎪ ⎪⎝⎭3.计算层次单排序权重向量并做一致性检验先利用Mathematica 计算矩阵A 的最大特征值及特征值所对应的特征向量. 输入A={{1.0,5,3,9,3},{1/5,1,1/2,2,1/2},{1/3,2,1,3,1},{1/9,1/2,1/3,1,1/3},{1/3,2,1,3,1}} T=Eigensystem[j]//Chop 输出{{5.00974,-0.0048699+0.22084™,-0.0048699-0.22084™,0,0}, {{0.88126,0.167913,0.304926,0.0960557,0.304926},{0.742882,-0.223286-0.278709™,-0.165421+0.346134™,0.151384-0.057689™,-0.165421+0.346134™},{0.742882,-0.223286+0.278709™,-0.165421-0.346134™,0.151384+0.057689™,-0.165421-0.346134™},{-0.993367,0,0.0719207,0.0662245,0.0605282}, {0.884443,0,-0.380934,-0.0589629,0.263009}}}得出A 的最大特征值为max λ=5.00974,及其对应的特征向量x={0.88126,0.167913,0.304926,0.0960557,0.304926}T输入Clear[x]; x=T[[2,1]];W1=x/Apply[Plus,x]得到归一化之后的的特征向量()1w ={0.502119,0.0956728,0.173739,0.0547301,0.173739}T计算一致性指标max 1nCI n λ-=-, ,00974.5,5max ==λn 故.002435.0=C I查表(见表3-1)得到相应的随机一致性指标 1.12RI =所以 002174.0)2(==RICICR ()20.1CR <通过了一致性检验,即认为A 的一致性程度在容许的范围之内, 可以用归一化后的特征向量()1w 作为排序权重向量.下面再求矩阵)5,,2,1( =j B j 的最大特征值及特征值所对应的特征向量 输入B1={{1.0,1/3,1/5,1/7},{3,1,1/2,1/4},{5,2,1,1/2},{1/7,4,2,1}} B2={{1,1/2,4,3},{2,1,5,5},{1/4,1/5,1,1},{1/3,1/5,1,1}} B3={{1,6,5,8},{1/6,1,1,2},{1/5,1,1,7},{1/8,1/2,1/7,1}} B4={{1,1,1/3,1/3},{1,1,1/2,1/5},{3,2,1,1},{3,5,1,1}} B5={{1,2,1,2},{1/2,1,1/2,1},{1,2,1,2},{1/2,1,1/2,1}} T1=Eigensystem[B1]//Chop T2=Eigensystem[B2]//Chop T3=Eigensystem[B3]//Chop T4=Eigensystem[B4]//Chop T5=Eigensystem[B5]//Chop 输出{{3.82325,0.0883772+0.544064™,0.0883772-0.544064™,0}, {{0.111267,0.283002,0.536902,0.786934},{-0.0248134-0.0681165™,-0.141793+0.0729826™,-0.154388+0.121345™,0.964755}, {-0.0248134+0.0681165™,-0.141793-0.0729826™,-0.154388-0.121345 ™,0.964755}, {0,0.299667,-0.832409,0.466149}}}{{4.02113,-0.0105652+0.291301™,-0.0105652-0.291301™,0}, {{0.495852,0.84036,0.149575,0.159851},{-0.234515+0.517899™,0.805208,-0.109665-0.110941™,0.0407277 -0.0493071 ™}, {-0.234515-0.517899 ™,0.805208,-0.109665+0.110941 ™,0.0407277 +0.0493071 ™}, {0,-0.953463,-0.0953463,0.286039}}}{{4.25551,-0.110262+1.03317™,-0.110262-1.03317™,-0.0349818}, {{0.941183,0.179553,0.276018,0.0758271},{0.898054,0.136097 +0.0728034 ™,-0.309669+0.2519 ™,-0.0331642-0.0960598™}, {0.898054,0.136097-0.0728034™,-0.309669-0.2519™,-0.0331642+0.0960598™}, {0.958653,-0.256222,0.123505,-0.00904772}}}{{4.08009,-0.0400469+0.570251™,-0.0400469-0.570251™,0}, {{0.214349,0.214031,0.59059,0.747963},{0.00228339-0.0861419™,-0.0895045+0.220107™,-0.388206-0.387638™,0.796962}, {0.00228339+0.0861419™,-0.0895045-0.220107™,-0.388206+0.387638 ™,0.796962}, {-0.424264,0,0.565685,0.707107}}}{{4.,0,0,0},{{0.632456,0.316228,0.632456,0.316228}, {0.116296,0.629208,-0.687356,-0.343678}, {-0.92582,0.154303,0.308607,0.154303}, {-0.92582,0.154303,0.308607,0.154303}}}分别得出其最大特征值1B λ=3.82325,2B λ= 4.02113,3B λ= 4.25551,4B λ= 4.08009,5λ= 4, 以及其特征向量如下:B1=({0.111267,0.283002,0.536902,0.786934})TB2=({0.495852,0.84036,0.149575,0.159851})T B3=({0.941183,0.179553,0.276018,0.0758271})T B4=({0.214349,0.214031,0.59059,0.747963})T B5=({0.632456,0.316228,0.632456,0.316228})T其中.5,,2,1),,,(321 ==i x x x x i i i i 为求出归一化后的特征向量, 输入Clear[B1,B2,B3,B4,B5]; B1=T1[[2,1]];w1=B1/Apply[Plus,B1] B2=T2[[2,1]];w2=B2/Apply[Plus,B2] B3=T3[[2,1]];w3=B3/Apply[Plus,B3] B4=T4[[2,1]];w4=B4/Apply[Plus,B4] B5=T5[[2,1]];w5=B5/Apply[Plus,B5] 输出{{4.,0,0,0},{{0.632456,0.316228,0.632456,0.316228}, {0.116296,0.629208,-0.687356,-0.343678}, {-0.92582,0.154303,0.308607,0.154303}, {-0.92582,0.154303,0.308607,0.154303}}}w1= {0.0647614,0.164718,0.312497,0.458024}Tw2={0.301313,0.510659,0.0908919,0.0971363}Tw3= {0.639138,0.121931,0.187438,0.0514926}Tw4= {0.121311,0.121132,0.334246,0.423311}Tw5= {0.333333,0.166667,0.333333,0.166667}T计算一致性指标(1,2,3,4,5)1i i nCI i n λ-==-,其中4n =,输入 lamda={T1[[1,1]],T2[[1,1]],T3[[1,1]],T4[[1,1]],T5[[1,1]]}CI=(lamda-4)/(4-1)//Chop 则可以得到1CI =-0.0589181,2CI = 0.00704344,3CI =0.0851688,4CI =0.0266979,5CI =0查表(见表3-1)得到相应的随机一致性指标0.90(1,25)i RI i ==计算一致性比率(),1,2,,5ii iCI CR i RI ==,输入CR=CI/0.90 相应可得到12345-0.0654646,0.00782605,0.094632,0.0296643,0CR CR CR CR CR =====因0.1,(1,2,,5)i CR i <=通过了一致性检验. 即认为)5,,2,1( =j B j 的一致性程度在容许的范围之内, 可以用归一化后的特征向量作为其排序权重向量.4、计算层次总排序权重向量并做一致性检验购买个人电脑问题的第三层对第二层的排序权重计算结果列于表4-1(表4-1)以矩阵表示第三层对第二层的排序权重计算结果为()30.06476140.3013130.6391380.1213110.3333330.1647180.5106590.1219310.1211320.1666670.3124970.09089190.1874380.3342460.3333330.4580240.09713630.05149260.4233110.166667w ⎛⎫⎪⎪= ⎪⎪⎝⎭)3(W 即是第三层对第二层的权重向量为列向量组成的矩阵. 最下层(第三层)对最上层(第一层)的总排序权向量为()()231w w W =为了计算上式, 输入W2=Transpose[{w1,w2,w3,w4,w5}]; W3=W2.W1则从输出结果得到W3={0.236941,0.188335,0.274378,0.300347}为了对总排序权向量进行一致性检验, 计算(3)(1)125(.,.,,.)CI C I C I C I w =输入 CI.W1 输出(3)CI = -0.0126517再计算(3)15[,,]1RI RI RI W =输入RI=Table[0.90,{j,5}]; RI.W1则从输出结果得到(3)0.90RI =最后计算(3)(2)(3)(3)/CR CR CI RI =+可得(3)CR = -0.0118834因为,1.0.)3(<RC 所以总排序权重向量符合一致性要求的范围.根据总排序权重向量的分量取值,旅游点4的电脑是建模者对这三种品牌机的首选。
数学建模景区路线规划论文

景区路线规划摘要本文主要研究最短旅游路线的设计问题。
在满足题目中的条件下,找到最佳的路径且用最短的距离是我们追求的目标。
毕竟,能否设计出合理且令人满意的旅游路径,对景区的经济效益和长远发展有着密切的关系。
对此本文用数学联系实际,建立数学模型,设计出相对科学的景区旅游景点路线,来解决此类问题。
对于问题一,从题目中我们了解到我们要设计出6种只含4个景点的最短路径,且至少包括两个特色景点,而旅游内容相近的同类景点如1,6和9,10又不能同时出现。
根据这些条件,我们运用floyd算法的原理,通过matlab编程,建立带权邻接矩阵,再用插入顶点的方法构造出距离矩阵,同时也能求出插入点矩阵,最终得到初步符合条件的旅游套餐。
再经过用Excel软件对得出的数据进行分类,整理,排序,最终得出符合题意的6种旅游套餐。
同时,在我们对景点的组合中可以发现,有多种景点组合都存在游览顺序不同而导致的行程不同的现象。
对这种游览顺序不同,但游览的景点是相同的情况,我们视其为同一种旅游套餐。
对于问题二,题目要求我们设计出6种不同旅游套餐,并在在景区特色景点的客流容纳人数是其他景点的两倍的情况下计算出各种套餐的人数比例,使得景点的客流量基本均衡,且总行程尽可能短。
对此我们0-1变量的思想表示是否游览某个景点,从而推出总行程尽可能短的约束条件,再用Lingo编程对模型进行求解,得出初步可能的旅游套餐。
然后再引入方差的思想,方差是描述数据离散程度的量,方差越小各景点的客流量越均衡。
所以,我们接下来可以利用 6 个旅游套餐中所有景点的客流量的方差来刻画景点客流量的均衡程度,要使方差尽量小,首先6个套餐应覆盖尽量多的景点,再由每种套餐的比例来约束方差,使得方差尽量小。
由此,我们可以建立关于游客量的方程和关于方差的函数。
然后再对之前得出的旅游套餐使用综合评判的方法,并经过灵敏度的分析,得出符合要求的6种旅游套餐。
关键词 floyd算法 Exce软件 matlab软件 0-1变量 Lingo软件一、问题重述图1某景区有10个景点,各景点的交通示意图如图1。
旅游线路规划建模题

第二次模拟竞赛注意事项:
8月30日早晨前提交论文至causxjm@
按照2015年全国数学建模竞赛格式要求写作
尽量用word文档或PDF文件,处理过程一般结果放在附件中,文件夹名:赵一钱二李四A,
30日上午答辩8点半,要求每组都讲一下,每组5分钟,控制好时间,把自己组的创新点、主要结果讲清楚就可以。
A 山东旅游问题
山东是东夷文化的主要发源地,更是齐鲁文化的诞生地,其悠久的历史文化和富饶壮美的山泉水海湖泊,孕育了一代代圣哲贤达。
王先生夫妇打算暑假到山东旅游。
1、请为他们设计合适的旅游路线,使他们在暑假一个月的时间里花最少的钱游览尽可能多的地方,并估算除吃饭之外的费用。
2、如果他们打算今、明两年暑假完成对山东的旅游,请你为他们设计合适的旅游线路,使在山东境内的交通费用尽量的节省。
3、如果某机构组织人员对山东考察,用于交通的时间和前两种情况相同,单考察时间是旅游观光时间的四倍,请您们为他们设计合适的考察路线,为便于尽早完成考察任务,最少需要分几组考察。
4、旅游部门为迎接“十一黄金周”(游程为5-10天),准备为山东省外的游客组织多条旅游路线以分散游客,提高接待的质量。
在假设参加你们设计的各条路线的游客人数与整条路线的接待能力成比例的条件小,请你们为旅游部门设计合适的、准备向游客推介的全部旅游路线(可以考虑游玩线路、交通、价格、游玩时间、推荐点位等)。
山东主要景点分布图,各旅游点之间的路程、每个景点的最佳逗留时间等信息可以上网自己收集。
你也可以自己对题目作进一步的完善。
运用数学模型优化旅游线路设计

运用数学模型优化旅游线路设计
一、最短路径算法
在旅游线路设计中,最短路径算法可以用于寻找旅游路线中的最短路径。
以图的方式
表示旅游路线,通过算法得到旅游者能够最短时间到达各个景点的路径,从而为旅游者提
供更高效的旅游体验。
该算法主要用于处理两点之间的最短路径问题。
二、线性规划算法
三、遗传算法
四、模拟退火算法
在进行旅游线路设计时,我们也需要注意以下几点:
1. 考虑旅游者的喜好和需求,量身定制旅游线路;
2. 合理安排旅游的时间和成本,避免浪费时间和金钱;
3. 考虑景点间的距离和交通情况,合理安排旅游路线;
4. 考虑景点的开放时间和规定,避免因为时间问题错过美景;
5. 考虑旅游的季节和天气情况,避免因为天气问题影响旅游效果。
总之,通过运用数学模型优化旅游线路设计,可以为旅游者提供更加优质的旅游体验。
同时,在进行旅游线路设计时,我们也需要充分考虑旅游者的需求和情况,以确保为旅游
者提供有效的服务和建议。
运用数学模型优化旅游线路设计

运用数学模型优化旅游线路设计旅游线路设计是一项复杂的任务,需要考虑众多因素,如旅游景点的位置、时间、距离等。
而数学模型可以帮助我们优化旅游线路的设计,使得旅游线路更加合理、高效。
我们可以运用图论模型来解决旅游线路中的路径选择问题。
图论是研究顶点和边之间关系的数学分支,可以通过建立图模型来描述旅游景点之间的距离、连通关系等。
在图模型中,每个旅游景点可以表示为一个顶点,而两个旅游景点之间的距离则可以表示为边的权重。
通过使用最短路径算法,比如Dijkstra算法或Floyd-Warshall算法,我们可以找到从一个旅游景点到另一个旅游景点的最短路径,从而确定游览的顺序和路径。
我们可以运用约束优化模型来考虑旅游线路中的时间限制和资源分配问题。
约束优化模型可以将旅游线路设计问题转化为一个数学优化问题,通过设定目标函数和约束条件来找到最优解。
我们可以将每个旅游景点的吸引力、游览时间和交通成本等视为目标函数的参数,然后通过设置约束条件来限制旅游线路的总时间、总费用等。
通过求解这个优化问题,我们可以得到一个最优的旅游线路设计方案。
我们还可以运用网络流模型来解决旅游线路中的资源分配问题。
网络流模型是一种用于描述资源流动和分配的数学模型,可以帮助我们合理分配旅游资源,如交通工具、食宿设施等。
通过建立一个网络图模型,将旅游景点和资源之间的关系转化为节点和边,我们可以使用最大流算法来确定每个旅游景点所需的资源量,从而实现资源的均衡和合理分配。
运用数学模型可以帮助我们优化旅游线路的设计。
通过运用图论模型解决路径选择问题、约束优化模型解决时间限制和资源分配问题,以及网络流模型解决资源分配问题,我们可以得到一个更加合理、高效的旅游线路设计方案。
这些数学模型的运用,不仅可以提高旅游线路的满意度和效益,还可以为旅游行业的发展提供科学依据。
数学建模旅游问题C2

数学建模旅游问题C2【摘要】旅游的最佳线路的选择会直接决定旅行者的旅行时间和金钱的花费,设计合理可行的旅游线路则使这一费用的唯一标准,由于实际纷繁复杂的景点,交通,时间等对方面因素的综合影响和相互作用下,通过“点线图”将复杂的现实景点和路线表示在便于处理的简单的只有点和线组成的图中,便于我们运用一定的数学工具进行最优化处理。
通过综合各方面的信息、资源,并对其进行相应的处理整合如“点线图”,在保证合理,准确,有效,详实的同时,将抽象的,复杂的实际概念和数据量,转化为有价值的,精确的时间和费用值。
这样“点线图”中每一个点就对应地包含其最佳停留时间和花费情况,其中为了合理的表示花费,构造“城市分”的概念来表示。
而每一条线也都对应地包含所花费的时间和费用,这些数量通过表格给出,在求取最优解时视为相应点或线的特性。
为了难保证这种转化的实际意义和有效性,准确性,通过多方数据的综合分析、平均,共同得到的综合得到。
在“点线图”的基础上,做出必要假设和的基础上,将图形做进一步的简化分区,将一个图形分成若干个子图,对图进行处理,把问题拆减。
利用已经比较成熟的Dijstra算法,找到其它城市距离中心城市(这里使乌鲁木齐)的最小距离,然后利用避图法找到最小树,这样在路线周围,结合图形特点,围绕近似路线周围作局部搜索,在大大减少数据运算的情况下,得到相对最优解。
对得到的最优解进行检验,验证其确实是比较优的线路。
即基本处理过程为:抽象图形分解图找到近似算法子图中在近似算法得到路径周围搜索调整边界检验路线分析建模、解模的整个过程,合理地分析可以得到,方法可以被推广到其它更加复杂的环境。
【关键词】:点线图城市分旅行推销员问题哈密顿 Dijkstra算法,避图法3010151.问题随着我国经济的不断增长,节假日外出旅游已经成为当今时代的热点和亮点,而伴随者出游人数的不断增多,产生了一系列的与旅游线路安排,设计,选择的有关的问题,旅游地旅游部门,旅行社,随团游客,自助游者都希望可以构建一个和谐的旅游线路和行程,使所有的人达到最大的满足。
运用数学模型优化旅游线路设计

运用数学模型优化旅游线路设计随着人们生活质量的提高和旅游意识的增强,旅游业已经成为一个快速发展的行业。
为了满足人们对旅游的不断需求,旅游线路设计成为了一个重要的环节。
如何设计出更具吸引力和经济效益的旅游线路成为了旅游从业者们关注的问题。
在优化旅游线路设计中,数学模型被广泛应用。
数学模型是将现实问题转化为数学形式,然后进行数学计算和分析的工具。
通过构建合适的数学模型,可以更加全面、客观地考虑各种相关因素,从而优化旅游线路设计。
数学模型可以帮助选择最佳出行路线。
对于一条旅游线路来说,其涉及的景点众多,选择不同的出发点和游览顺序可能会导致全程距离和时间的差异。
通过数学模型,可以计算出每种出发点和游览顺序对应的旅行时间和距离,并基于这些数据进行比较,从而选择出最佳的出行路线。
数学模型可以帮助确定最佳游览时间。
不同的景点在不同的时间段内可能会存在拥堵或人流量过少的情况。
为了避免这些问题,我们可以构建一个数学模型,根据历史数据和游览线路的特点,预测每个景点的游览人数,并根据人数变化和游览时间的关系,确定最佳游览时间。
数学模型还可以与经济模型相结合,帮助确定最佳价格策略。
在旅游线路设计中,不同的价格可能会影响游客对线路的选择和参与度。
通过数学模型和经济模型的分析,可以计算出不同价格对应的游客数量和收益,并找出最佳价格策略,从而最大化利润。
数学模型还可以帮助优化旅游线路的时间安排。
在一天的旅游时间中,不同景点的游览时间可能是不同的,而且还需要考虑各种交通和休息等因素。
通过构建数学模型,我们可以分析不同景点的游览时间和各种因素之间的关系,并优化安排旅游线路的时间,以便游客能够更好地享受旅游过程。
B题-最佳旅游路线设计

2011年第八届苏北数学建模联赛承诺书我们仔细阅读了第八届苏北数学建模联赛的竞赛规则。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与本队以外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们愿意承担由此引起的一切后果。
我们的参赛报名号为:2795参赛组别:本科参赛队员(签名) :队员1:队员2:队员3:2011年第八届苏北数学建模联赛编号专用页参赛队伍的参赛号码:竞赛统一编号(由竞赛组委会送至评委团前编号):竞赛评阅编号(由竞赛评委团评阅前进行编号):2011年第八届苏北数学建模联赛题目旅游线路的优化设计摘要随着我国全面建设小康社会的推进,人民的生活质量不断提高,旅行游览活动作为一种新型的高级社会消费形式逐步受到人们的亲睐。
旅游作为一种经济活动,游客如何在时间和费用有限的情况下最大程度的享受旅游的乐趣显得尤其重要。
本文从实际情况出发,建立了离散型目标优化模型和动态规划模型,对模型进行了全方面的论述,并针对本题不同的要求设计出相应的旅游行程表。
建模过程中,首先用科学分析的方法,确定主要因素并对其作数学抽象,再针对各因素综合运用多种数学方法进行分析求解。
第一,我们用主要目标法建立了“离散型单目标优化模型”,并分别确定了五个问题的目标函数以及约束条件;第二,我们将旅游景点看作地图中的点,利用图论中著名的哈密顿回路问题和顺序递推的方法建立了“动态优化模型”;第三,通过查询数据,并利用数理统计的方法求解模型中的参数,从而得出一个与实际接近的完整数学模型。
求解问题过程中,首先把路途时间(路费)、景点停留时间(门票)、住宿时间(住宿费用)和其它时间(其它费用)综合考虑,借鉴历史上著名的货郎担问题的解法巧妙的将路程优化问题转化旅游时间和旅游费用的优化问题,在利用“Floyd算法”时分别将旅游时间和旅游费用作为权成功解决问题一与问题二。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最佳旅游路线设计摘要本文主要研究最佳旅游路线的设计问题。
在满足相关约束条件的情况下,花最少的钱游览尽可能多的景点就是我们追求的目标。
基于对此的研究,建立数学模型,设计出最佳的旅游路线。
第一问给定时间约束,要求为主办方设计合适的旅游路线。
我们建立了一个最优规划模型,在给定游览景点个数的情况下以人均总费用最小为目标。
再引入0—1变量表示就是否游览某个景点,从而推出交通费用与景点花费的函数表达式,给出相应的约束条件,使用lingo编程对模型求解。
推荐方案:成都→都江堰→青城山→丹巴→乐山→成都,人均费用为949元(此处不考虑旅游人数对游览费用的影响)。
第二问放松时间约束,要求代表们游遍所有的景点,该问题也就成了典型的货郎担(TSP)问题。
同样使用第一问的模型,改变时间约束,使用lingo编程得到最佳旅游路线为:成都→乐山→峨眉→海螺沟→康定→丹巴→四姑娘山→青城山→都江堰→九寨沟→黄龙→成都,人均费用为3243元。
第三问要求在第一问的基础上充分考虑代表们的旅游意向,建立模型求解。
通过对附件一数据的观察,我们使用综合评判的方法,巧妙地将代表们的意愿转化为对相应旅游景点的权重,再对第一问的模型稍加修改,编程求出对应不同景点数的最佳路线。
推荐路线:成都→乐山→都江堰→青城山→丹巴→成都,人均费用为927元。
对于第四问,由于参观景点的人数越多每人承担的费用越少,因此我们要考虑的就是尽量使得两组代表在共同旅游的时间内在相同的景点游览。
正就是基于此,我们建立模型求解。
推荐路线:第一组:成都→乐山→丹巴→都江堰→青城山→成都第二组:成都→都江堰→青城山→峨眉→乐山→成都,两组在都江堰会合并且共同游览了都江堰与青城山,人均费用为971元。
第五问中,首先我们修改了不合理数据,并用SPSS软件对缺省数据进行了时间序列预测。
其次我们合理定义了阴雨天气带来的损失,以人均总花费最小与阴雨天气带来的损失最小为目标,建立加权双目标规划模型。
推荐路线:成都→康定→青城山→都江堰→乐山→成都,相应人均消费987元,阴雨天气带来的损失为1、6。
本文思路清晰,模型恰当,结果合理、由于附件所给数据的繁杂,给数据的整理带来了很多麻烦,故我们利用Excel排序,SPSS预测,这样给处理数据带来了不少的方便。
本文成功地对0—1变量进行了使用与约束,简化了模型建立难度,并且可方便地利用数学软件进行求解。
此外,本文建立的模型具有很强普适性,便于推广。
关键词:最佳路线TCP问题综合评判景点个数最小费用1 问题重述今年暑假,西南交通大学数学系要召开“××学术会议”,届时来自国内外的许多著名学者都会相聚成都。
在会议结束后,主办方希望能安排这些远道而来的贵宾参观四川省境内的著名自然与人文景观,初步设想有如下线路可供选择: 一号线:成都→九寨沟、黄龙;二号线:成都→乐山、峨嵋;三号线:成都→四姑娘山、丹巴;四号线:成都→都江堰、青城山;五号线:成都→海螺沟、康定;每条线路中的景点可以全部参观,也可以参观其中之一。
不仅如此,一起参观景点的人数越多,每人承担的费用也会越小。
结合上述要求,请您回答下列问题:一、请您们为主办方设计合适的旅游路线,使会议代表在会议结束后的10天时间内花最少的钱游尽可能多的地方。
二、如果有一些会议代表的时间非常充裕(比如一个月),她们打算将上述旅游景点全部参观完毕后才离开四川,请您们为她们设计合适的旅游路线,使在四川境内的交通费用尽量地节省。
三、主办方在会议开始前对所有参会的100位代表旅游意向进行了调查,调查数据见附件1所示。
充分考虑这些代表的意愿,请您们为主办方设计代表们合适的旅游路线,使她们在会议结束后的10天时间内花最少的钱游尽可能多的地方。
四、由于会议安排原因,附件1中的后50位代表要拖后四天时间才能去旅游观光(每人旅游总时间保持不变)。
请在问题三基础上考虑时间滞后因素,为主办方设计合适的旅游路线,使代表们在10天的时间里花最少的钱游尽可能多的地方。
五、在旅游过程中最担心出现阴雨天气,这种气候环境就是最不适合旅游的。
因此,在出发前,主办方询问了四川省气象局这五条旅游线路降雨的概率,具体数据见附件2。
请在问题三的基础上增加气候因素,为主办方设计合适的旅游路线,使代表们在10天的时间里花最少的钱游尽可能多的地方,同时因阴雨天气而带来的旅游不便损失降为最低。
2 问题分析2、1问题背景的理解:根据对题目的理解我们可以知道,旅游的总费用包括交通费用与在景点游览时的费用,而在确定了要游览的景点的个数后,所以我们的目标就就是在满足所有约束条件的情况下,求出成本的最小值。
2、2问题一与问题二的分析:问题一要求我们为主办方设计合适的旅游路线,使会议代表在会议结束后的10天时间内花最少的钱游尽可能多的地方。
在这里我们的做法就是在满足相应的约束条件下,先确定游览的景点数,然后计算出在这种情况下的最小花费。
这样最终会得出几种最佳方案,而组织方可以根据自己的实际情况进行选择。
问题二实质上就是在问题一的基础上改变了时间约束,即代表们要游览所有的景点,我们完全可以使用与问题一同样的方法进行求解。
2、3问题三的分析:问题三要求我们在问题一的基础上充分考虑代表们对各个景点的意愿来设计最佳旅游路线,而代表们的意愿由附件1给出。
对于意愿,我们的做法就是将其转化为相应的权重,然后乘以相应的旅游景点的花费,再利用问题一的模型得出几种最佳方案供主办方选择。
2、4问题四与问题五的分析:问题四将100名代表平均分成了两组,而第二组则晚了四天出发。
由于题目中告诉我们参观景点的人数越多,每人承担的费用越少,因此我们应该考虑使两组同时在外旅游就是尽量在同一景点游览,来减少旅游总费用。
基于此思想建立模型求解即可。
问题五在问题三的基础上考虑了天气的因素,因为阴雨会给代表们带来一定的损失,因此该问又增加了一个使损失最小的目标。
我们在定义这个损失后,对总费用与损失两个目标分别加权,以最小为目标求出相应的方案即可。
3 模型假设1、所给的5条路线每条路线中的景点可以全部参观,也可以参观其一;2、参观景点的人数越多,每人承担的费用越少;3、数学系使用旅游大巴安排代表们往返于各个旅游景点,其交通费用、在景点的花费、在景点的逗留时间参照当地客运公司及旅行社的数据;4、代表们所乘坐的旅游大巴平均时速为50km/h,平均费用为0、3元/km;5、一个景点直接到达另外一个景点就是指,途中经过的其她景点只就是一个转站地,而并不进行游览;6、在限定的时间内,代表们最终要返回成都,并且假设成都就是代表们肯定要去的一个旅游景点;7、假设参观景点的人数每增加一人,每个代表在景点的费用就减少原价的1‰; 8、代表们在途中与游览景点的时间为12小时,而另外12小时为休息、用餐及其她琐事时间。
4 符号说明i ,j ——第i 个或者第j 个景点, i ,j =1,2, (11)分别表示成都、九寨沟、黄龙、乐山、峨嵋、四姑娘山、丹巴、都江堰、青城山、海螺沟、康定;c ——每个会议代表的旅游总花费;i t ——每个会议代表在第i 个景点的逗留时间; i c ——每个会议代表在i 个景点的总消费;ij t ——从第i 个景点到第j 个景点路途中所需时间;ij c ——从第i 个景点到第j 个景点所需的交通费用;⎩⎨⎧=01ij r其他个景点个景点到达第代表们直接从第j i 5 模型建立及求解5、1 问题一:5、1、1 目标函数的确立:经过对题目分析,我们可以知道本题所要实现的目标就是,使会议代表在10天时间内花最少的钱游览尽可能多的地方。
显然,花费最少与游览的景点尽量多就是该问题的两个目标。
因此,我们的做法就是在满足相应的约束条件下,先确定游览的景点数,然后计算出在这种情况下的最小花费。
这样最终会得出几种旅游路线,而组织方可以根据自己的实际情况进行选择。
游览的总费用由2部分组成,分别为交通总费用与在旅游景点的花费。
我们定义:m ——每个代表的旅游总花费;1m ——每个代表的交通总费用;2m ——每个代表的旅游景点的花费; 从而得到目标函数: Min m =1m +2m (1)交通总花费因为ij c 表示从第i 个景点到第j 个景点所需的交通费用,而ij r 就是判断代表们就是否从第i 个景点直接到第j 个景点的0—1变量,因此我们可以很容易的得到交通总费用为:∑∑==⨯=1111111i j ij ij c r m(2)旅游景点的花费因为i c 表示会议代表们在i 个景点的总消费,ij r 也可以表示出代表们就是否到达过第i 个与第j 个景点,而整个旅游路线又就是一个环形,因此()∑∑==+⨯111111i j jiijc c r 实际上将代表们在所到景点的花费计算了两遍,从而我们可得旅游景点的花费为:()∑∑==+⨯⨯=111111221i j j i ij c c r m从而我们可以得到目标函数为:Min m =1m +2m=∑∑==⨯111111i j ij ij c r +()∑∑==+⨯⨯11111121i j j i ij c c r5、1、2 约束条件:①时间约束由题目可知,代表们在川的旅游时间应该不多于10天(120小时),而这些时间包括在路途中的时间与在旅游景点逗留的时间。
因为ij t 表示从第i 个景点到第j 个景点路途中所需时间,所以路途中所需总时间为∑∑==⨯111111i j ij ij t r ;i t 表示会议代表们在第i 个景点的逗留时间,故代表们在旅游景点的总逗留时间为()∑∑==+⨯⨯11111121i j j i ij t t r 。
因此,总的时间约束为: ∑∑==⨯111111i j ij ij t r +()∑∑==+⨯⨯11111121i j j i ij t t r ≤120 ②旅游景点数约束根据假设,整个旅游路线就是环形,即最终代表们要回到成都,因此∑∑==111111i j ijr即表示代表们旅游的景点数,这里我们假定要旅游的景点数为n (n =2,3,……,11)。
因此旅游景点数约束为:∑∑===111111i j ijn r(n =2,3, (11)③0——1变量约束我们可以把所有的景点连成一个圈,而把每一个景点瞧做圈上一个点。
对于每个点来说,只允许最多一条边进入,同样只允许最多一条边出来,并且只要有一条边进入就要有一条边出去。
因此可得约束:=∑iij r 1≤∑jij r (i ,j =1,2, (11)当1=i 时,因为成都就是出发点,所以11=∑=i ij r ;1=j 时,因为代表们最终要回到成都,所以11=∑=j ij r 。
综合以上可知,=∑i ijr1≤∑jijr(i ,j =1,2, (11)11=∑=i ijr11=∑=j ij r同样,当i ,2≥j 时,根据题意不可能出现1==ji ij r r ,即不可能出现游客在两地间往返旅游,因为这样显然不满足游览景点尽量多的原则。
